数字电路与系统设计(张顺兴)第六章习题答案
数字电路答案第六章

第六章可编程逻辑器件PLD可编程逻辑器件PLD是由用户借助计算机和编程设备对集成电路进行编程,使之具有预定的逻辑功能,成为用户设计的ASIC芯片。
近年来,可编程逻辑器件从芯片密度上、速度上发展相当迅速,已成为集成电路的一个重要分支。
本章要求读者了解PLD器件的工作原理,掌握用可编程逻辑器件设计数字电路的方法。
为掌握使用电子设计自动化和可编程逻辑器件设计电路系统的后续课程打下良好的基础。
第一节基本知识、重点与难点一、基本知识(一)可编程逻辑器件PLD基本结构可编程逻辑器件PLD包括只读存储器ROM、可编程只读存储器PROM、可编程逻辑阵列PLA、可编程阵列逻辑PAL、通用阵列逻辑GAL和可擦写编程逻辑器件EPLD等。
它们的组成和工作原理基本相似,其基本结构由与阵列和或阵列构成。
与阵列用来产生有关与项,或阵列把所有与项构成“与或”形式的逻辑函数。
在数字电路中,任何组合逻辑函数均可表示为与或表达式,因而用“与门-或门”两级电路可实现任何组合电路,又因为任何时序电路是由组合电路加上存储元件(触发器)构成的,因而PLD的“与或”结构对实现数字电路具有普遍意义。
(二)可编程逻辑器件分类1.按编程部位分类PLD有着大致相同的基本结构,根据与阵列和或阵列是否可编程,分为三种基本类型:(1)与阵列固定,或阵列可编程;(2)与或阵列均可编程;(3)与阵列可编程,或阵列固定。
2.按编程方式分类(1)掩膜编程;(2)熔丝与反熔丝编程;(3)紫外线擦除、电可编程;(4)电擦除、电可编程;(5)在系统编程(Isp)。
(三)高密度可编程逻辑器件HDPLD单片高密度可编程逻辑器件HDPLD(High Density Programmable Logic Device)芯片内,可以集成成千上万个等效逻辑门,因此在单片高密度可编程逻辑器件内集成数字电路系统成为可能。
HDPLD器件在结构上仍延续GAL的结构原理,因而还是电擦写、电编程的EPLD 器件。
《数字电路-分析与设计》1--10章习题及解答(部分)_北京理工大学出版社
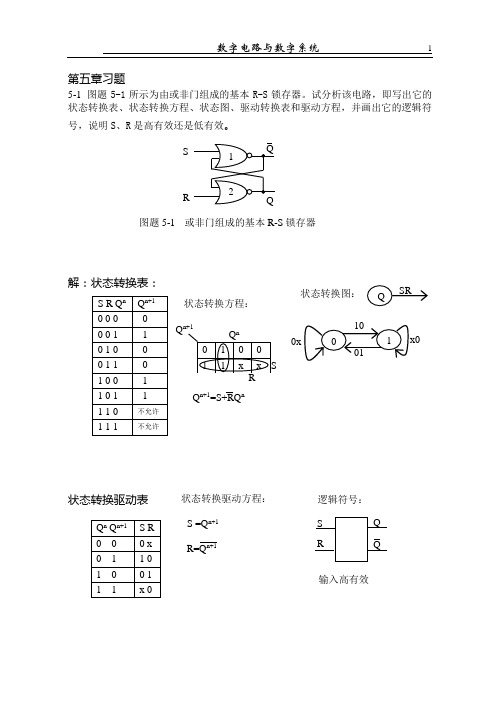
第五章习题5-1 图题5-1所示为由或非门组成的基本R-S 锁存器。
试分析该电路,即写出它的状态转换表、状态转换方程、状态图、驱动转换表和驱动方程,并画出它的逻辑符号,说明S 、R 是高有效还是低有效。
解:状态转换表:状态转换驱动表5-2 试写出主从式R-S 触发器的状态转换表、状态转换方程、状态图、驱动转换表和驱动方程,注意约束条件。
解:与R-S 锁存器类似,但翻转时刻不同。
5-3 试画出图5.3.1所示D 型锁存器的时序图。
解:G=0时保持,G=1时Q=D 。
图题5-1 或非门组成的基本R-S 锁存器S R状态转换方程:Q n+1Q n+1=S+RQ n状态转换图: S =Q n+1R=Q n+1 状态转换驱动方程: 逻辑符号: 输入高有效 G D Q图题5-3 D 型锁存器的时序图5-4试用各种描述方法描述D锁存器:状态转换表、状态转换方程、时序图、状态转换驱动表、驱动方程和状态转换图。
5-5锁存器与触发器有何异同?5-6试描述主从式RS触发器,即画出其功能转换表,写出状态方程,画出状态表,画出逻辑符号。
5-7试描述JK、D、T和T'触发器的功能,即画出它们的逻辑符号、状态转换表、状态转换图,时序图,状态转换驱动表,写出它们的状态方程。
5-8试分析图5.7.1(a) 所示电路中虚线内电路Q’与输入之间的关系。
5-9试分析图5.7.1(b)所示电路的功能,并画出其功能表。
5-10试用状态方程法完成下列触发器功能转换:JK→D, D→T, T→D, JK→T, JK→T’, D→T’。
解:JK→D:Q n+1=JQ+KQ,D:Q n+1=D=DQ+DQ。
令两个状态方程相等:D=DQ+DQ =JQ+KQ。
对比Q、Q的系数有:J=D,K=D逻辑图略。
5-11试用驱动表法完成下列触发器功能转换:JK→D, D→T, T→D, JK→T, JK→T’, D→T’。
解:略。
5-12用一个T触发器和一个2-1多路选择器构成一个JK触发器。
数字电路与系统设计课后习题答案

1、7将下列个数分别转换成十六进制数:(11111111)2,(377)8,(255)10
解:结果都为(FF)16
1、8转换下列各数,要求转换后保持原精度:
解:(1、125)10=(1、0010000000)10——小数点后至少取10位
(0010 1011 0010)2421BCD=(11111100)2
A-B=(90)10-(47)10=(43)10
C×D=(84)10×(6)10=(504)10
C÷D=(84)10÷(6)10=(14)10
两种算法结果相同。
1、11试用8421BCD码完成下列十进制数的运算。
解:(1)5+8=(0101)8421BCD+(1000)8421BCD=1101 +0110=(1 0110)8421BCD=13
(2)9+8=(1001)8421BCD+(1000)8421BCD=1 0001+0110=(1 0111)8421BCD=17
(3)58+27=(0101 1000)8421BCD+(0010 0111)8421BCD=0111 1111+0110=(1000 0101)8421BCD=85
(4)9-3=(1001)8421BCD-(0011)8421BCD=(0110)8421BCD=6
1、1将下列各式写成按权展开式:
(352、6)10=3×102+5×101+2×100+6×10-1
(101、101)2=1×22+1×20+1×2-1+1×2-3
(54、6)8=5×81+54×80+6×8-1
《数字电路与系统设计》第6章习题答案
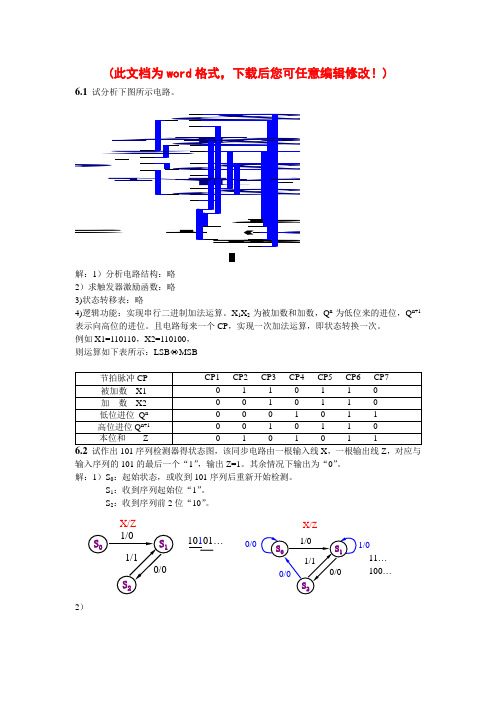
l ee t h e \1210101…X/Z0/01/0X/Z11…100…6.3对下列原始状态表进行化简: (a)解:1)列隐含表: 2)进行关联比较3)列最小化状态表为:a/1b/0b b/0a/0aX=1X=0N(t)/Z(t)S(t)解:1)画隐含表: 2)进行关联比较: 6.4 试画出用MSI 移存器74194构成8位串行 并行码的转换电路(用3片74194或2片74194和一个D 触发器)。
l ee t-h e \r 91行''' 试分析题图6.6电路,画出状态转移图并说明有无自启动性。
解:激励方程:略 状态方程:略状态转移图 该电路具有自启动性。
6.7 图P6.7为同步加/减可逆二进制计数器,试分析该电路,作出X=0和X=1时的状态转移表。
解:题6.7的状态转移表X Q 4nQ 3nQ 2nQ 1nQ 4n +1Q 3n +1Q 2n +1Q 1n +1Z 0 0 0 0 0 1 1 1 1 1 0 1 1 1 1 1 1 1 0 0 0 1 1 1 0 1 1 0 1 0 0 1 1 0 1 1 1 0 0 0 0 1 1 0 0 1 0 1 1 0 0 1 0 1 1 1 0 1 0 0 0 1 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 0 0 0 0 1 0 0 0 0 1 1 1 0 0 0 1 1 1 0 1 1 0 0 0 0 1 1 0 0 1 0 1 0 0 0 1 0 1 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 1 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 0 0 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 0 0 1 1 1 0 1 0 1 1 1 1 0 0 0 0 1 1 0 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 1 0 1 0 1 1 0 1 1 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 1 1 1 0 1 1 1 1 0 0 1 1 1 1 0 1 1 1 1 1 11 1116.8分析图6.8电路,画出其全状态转移图并说明能否自启动。
《数字电子技术基础》2版习题答案 6章习题解答
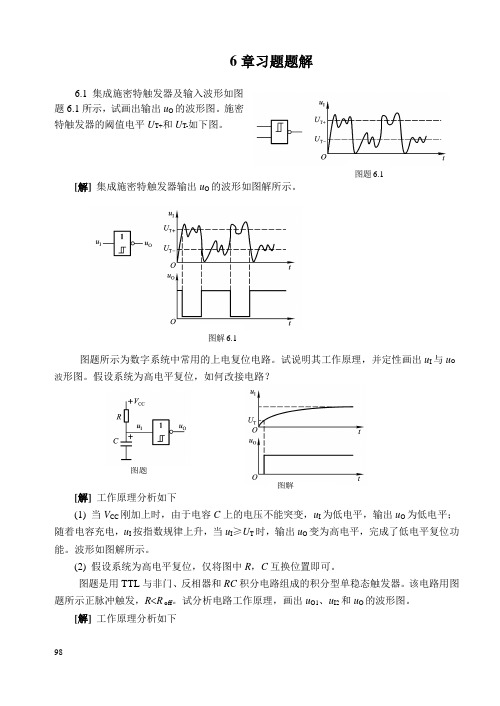
6章习题题解6.1 集成施密特触发器及输入波形如图题6.1所示,试画出输出u O的波形图。
施密特触发器的阈值电平U T+和U T-如下图。
图题6.1 [解]集成施密特触发器输出u O的波形如图解所示。
图解6.1图题所示为数字系统中常用的上电复位电路。
试说明其工作原理,并定性画出u I与u O 波形图。
假设系统为高电平复位,如何改接电路?图题图解[解] 工作原理分析如下(1) 当V CC刚加上时,由于电容C上的电压不能突变,u I为低电平,输出u O为低电平;随着电容充电,u I按指数规律上升,当u I≥U T时,输出u O变为高电平,完成了低电平复位功能。
波形如图解所示。
(2) 假设系统为高电平复位,仅将图中R,C互换位置即可。
图题是用TTL与非门、反相器和RC积分电路组成的积分型单稳态触发器。
该电路用图题所示正脉冲触发,R R off。
试分析电路工作原理,画出u O1、u I2和u O的波形图。
[解]工作原理分析如下9899触发信号未到来时,u I 为低电平,输出u O 为高电平;正触发脉冲到来时,u O1翻为低电平,此时由于u I2仍为高电平,输出u O 为高电平不变,电容通过R 放电,当u I2下降到U T 时〔u I 仍为高电平〕,输出u O 翻为高电平,暂稳态过程结束。
u O1、u I2和u O 的波形见图解。
6.4 集成单稳态触发器74121组成的延时电路如图题6.4所示,要求 (1)计算输出脉宽的调节范围; (2)电位器旁所串电阻有何作用?[解] (1) 输出脉宽:W ext ext W 0.70.7()t R C R R ==+,分别代入R W =0和22k Ω计算,可得t W的调节范围为:W 3.6mS 19mS t ≤≤。
(2) 电阻R 起保护作用。
假设无R ,当电位器调到零时,假设输出由低变高,那么电容C 瞬间相当于短路,V CC 将直接加于内部门电路输出而导致电路损坏。
6.5 集成单稳态触发器74121组成电路如图题6.5所示,要求(1)计算u O1、u O2的输出脉冲宽度;(2)假设u I 如图中所示,试画出输出u O1、u O2的波形图。
3-数字电路与系统设计 课后答案(张顺兴) 东南大学出版

第 2 章习题答案.doc
2.1 有A、B、C三个输入信号,试列出下列问题的真值表,并写出最小项表达式∑m( )。
(1)如果 A、B、C 均为 0 或其中一个信号为 1 时。输出 F=1,其余情况下 F=0。 (2)若 A、B、C 出现奇数个 0 时输出为 1,其余情况输出为 0。 (3)若 A、B、C 有两个或两个以上为 1 时,输出为 1,其余情况下,输出为 0。 解:F1(A,B,C)=∑m(0,1,2,4)
(1)F(ABC)=A+BC (2)F(ABCD)=(B+⎯C)D+(⎯A+B) C (3)F(ABC)=A+B+C+⎯A+B+C 解:(1)F(ABC)=∑m(3,4,5,6)
(2) F(ABCD)=∑m(1,3,5,6,7,9,13,14,15) (3) F(ABC)=∑m(0,2,6)
2.9 将题 2.8 中各题写成最大项表达式,并将结果与 2.8 题结果进行比较。
2.6 已知⎯ab+a⎯b=a⊕b,⎯a⎯b+ab=a~b,证明:
(1)a⊕b⊕c=a~b~c (2)a⊕b⊕c=⎯a~⎯b~⎯c
证明:略
2.7试证明:
(1)若⎯a⎯b+ a b=0 则 a x+b y=a⎯x + b⎯y (2)若⎯a b+a⎯b=c,则⎯a c + a⎯c=b 证明:略
2.8 将下列函数展开成最小项之和:
1.9 用下列代码表示(123)10,(1011.01)2:
解:(1)8421BCD 码: (123)10=(0001 0010 0011)8421BCD (1011.01)2=(11.25)10=(0001 0001.0010 0101)8421BCD
数字电路及系统设计课后习题答案

1.1 将下列各式写成按权展开式:2 1 0 -1(352.6 ) io=3X 102+5X 101+2X 10°+6X 10(101.101 ) 2=1 X 22+1x 2O+1X 2-1+1x 2-3( 54.6 )8=5X 81+54X 80+6X 8-12 1 0 -1 -2(13A.4F)16=1X162+3X161+10X 160+4X16-1+15X16-21.2 按十进制0~17 的次序,列表填写出相应的二进制、八进制、十六进制数。
解:略1.3 二进制数00000000~11111111 和0000000000~1111111111 分别可以代表多少个数?解:分别代表28=256和210=1024个数。
1.4 将下列个数分别转换成十进制数:1111101000)2,(1750) 8,( 3E8)16解:( 1111101000)2=( 1000)10( 1750)8= ( 1000)10(3E8)16=(1000)101.5 将下列各数分别转换为二进制数: ( 210)8,( 136)10,( 88)16解:结果都为:(10001000)21.6 将下列个数分别转换成八进制数:(111111)2,(63)10,(3F)16解:结果都为(77)81.7 将下列个数分别转换成十六进制数:(11111111)2,(377)8 ,(255)10 解:结果都为(FF)161.8 转换下列各数,要求转换后保持原精度:解:(1.125 )10=(1.0010000000 )10 ——小数点后至少取10 位(0010 1011 0010 )2421BCD= (11111100)2(0110.1010 )余 3 循环BC[M= ( 1.1110 ) 21.9 用下列代码表示(1 23)10,(1011.01 )2:解:(1) 8421BCD码:(123 )10= (0001 0010 0011 )8421BCD(1011.01 )2=(11.25)10=(0001 0001.0010 0101 )8421BCD(2) 余3 BCD码(123) io= (0100 0101 0110 )余3BCD(1011.01 ) 2=( 11.25 ) 10=(0100 0100.0101 1000 )余3BcD1.10 已知A=(1011010) 2,B=( 101111) 2,c=(1010100) 2,D=( 110) 2(1)按二进制运算规律求A+B, A-B, C X D, C一D,(2)将A B、C D转换成十进制数后,求A+B, A-B, C X D,C- D,并将结果与(1)进行比较。
数字逻辑电路与系统设计第6章习题及解答.docx

第6章题解:6.1试用4个带异步清零和置数输入端的负边沿触发型JK 触发器和门电路设计一个异步余 3BCD 码计数器。
题6・1解:余3BCD 码计数器计数规则为:0011->0100->—1100-0011-*-,由于釆用 异步清零和置数,故计数器应在1101时产生清零和置数信号,所设计的电路如图题解6.1 所示。
题6.2试用中规模集成异步十进制计数器74290实现模48计数器。
题6.2解:图题解6. 16.3试用D触发器和门电路设计一个同步4位格雷码计数器。
题6.3解:根据格雷码计数规则,\Q1Q OQsQ>\00011110000000011000111111100111\QlQoQ.3Q>\00011110000001011111111110100000X^iQoQ3Q>\00011110000111010001110111100001\QlQoQ.3Q>\00011110001100010011111100100011 Qi Qo计数器的状态方程和驱动方程为:er1=D.=+型Q”+Q;莎er1=D2=+Q©+N Q;N QT = D L+ Q;Q;Q;; +Qj = D o = Q^Q;1+按方程画出电路图即可,图略。
6.5试用4位同步二进制计数器74163实现十二进制计数器。
74163功能表如表6.4所示。
题6・5解:可采取同步清零法实现。
电路如图题解6.5所示。
题6.6解:题6.4解:反馈值为1010c卜一进制计数器CLKCLR LD ENT ENP>c a[―<>40) a D DTC=\5图题解6. 5RCO74163当M=1时:六进制计数器八进制计数器6.7试用4位同步二进制计数器74163和门电路设计一个编码可控计数器,当输入控制变 量M=0时,电路为8421 BCD 码十进制计数器,M=1时电路为5421 BCD 码十进制计数器, 5421BCD 码计数器状态图如下图P6.7所示。
