一元一次方程初中数学竞赛专题讲座(26份初中数学竞赛教程)

合集下载

一元一次方程[初中数学竞赛专题讲座

学科：奥数教学内容：一元一次方程【内容综述】一元一次方程是最简单的方程，它是进一步学习方程、不等式和函数的基础，许多方程都是通过变形后转化为一元一次方程来解的。

本期主要介绍一些解一元一次方程的基本方法和技巧。

只含有一个未知数（又称为一元），且其次数是1的方程叫做一元一次方程，任何一个一元一次方程总可以化为的形式，这是一元一次方程的标准形式（最简形式）。

解一元一次方程的一般步骤：（1）去分母；（2）去括号；（3）移项；（4）合并同类项，化为最简形式；（5）方程两边同除以未知数的系数，得出方程的解。

【要点讲解】§1 含参量的一元一次方程含有参变量的方程在求解时往往需分类讨论，关于的方程。

因为未注明，所以它的解有下面三种情况：（1）当时，方程有唯一解；（2）当时，方程的解为任意数；（3）当，时，方程无解。

★例1解关于χ的方程。

思路这是含参量的一元一次方程，需分类讨论。

解：把原方程变形为即当，即且时，方程有唯一解；当且，即且时，方程无解；当且，即时，方程的解为任意数。

★★例2若a，b，c是正数，解方程。

解法一：原方程两边乘以abc，得到方程,移项合并同类项得即由，，知,即。

解法2：对原方程左端的每一项减去1，得即∵由，，知∴∴说明通过细心观察方程的自身特点，巧妙地分析为3个，为3个，使原方程易于求解。

★★例3k为何正数时，方程的解是正数？思路当方程有唯一解时，此解的正负可由a，b的取值确定：（1）若b=0时，方程的解是零；反之，若方程的解是零，b=0成立。

（2）若时，则方程的解是正数；反之，若方程的解是正数，则成立。

（3）若时，则方程的解是负数；反之，若方程的解是负数，则成立。

解：按未知数χ整理方程得要使方程的解为正数，需要不等式的左端因为，所以只要或时上式大于零，所以当或时，原方程的解是正数，因此或，即为所求。

§2 含有绝对值符号的一次方程解含有绝对值符号的一次方程时，可利用绝对值的定义脱去绝对值符号，转化为普通的一元一次方程。

七年级数学竞赛讲座：第四讲一元一次方程

第四讲一元一次方程方程是中学数学中最重要的内容．最简单的方程是一元一次方程，它是进一步学习代数方程的基础，很多方程都可以通过变形化为一元一次方程来解决．本讲主要介绍一些解一元一次方程的基本方法和技巧．用等号连结两个代数式的式子叫等式．如果给等式中的文字代以任何数值，等式都成立，这种等式叫恒等式．一个等式是否是恒等式是要通过证明来确定的．如果给等式中的文字(未知数)代以某些值，等式成立，而代以其他的值，则等式不成立，这种等式叫作条件等式．条件等式也称为方程．使方程成立的未知数的值叫作方程的解．方程的解的集合，叫作方程的解集．解方程就是求出方程的解集．只含有一个未知数(又称为一元)，且其次数是1的方程叫作一元一次方程．任何一个一元一次方程总可以化为ax=b(a≠0)的形式，这是一元一次方程的标准形式(最简形式)．解一元一次方程的一般步骤：(1)去分母；(2)去括号；(3)移项；(4)合并同类项，化为最简形式ax=b；(5)方程两边同除以未知数的系数，得出方程的解．一元一次方程ax=b的解由a，b的取值来确定：(2)若a=0，且b=0，方程变为0·x=0，则方程有无数多个解；(3)若a=0，且b≠0，方程变为0·x=b，则方程无解．例1解方程解法1从里到外逐级去括号．去小括号得去中括号得去大括号得解法2按照分配律由外及里去括号．去大括号得化简为去中括号得去小括号得例2已知下面两个方程3(x+2)=5x，①4x－3(a－x)=6x－7(a－x) ②有相同的解，试求a的值．分析本题解题思路是从方程①中求出x的值，代入方程②，求出a的值．解由方程①可求得3x－5x=－6，所以x=3．由已知，x=3也是方程②的解，根据方程解的定义，把x=3代入方程②时，应有4×3－3(a－3)=6×3－7(a－3)，7(a－3)－3(a－3)=18－12，例3已知方程2(x+1)=3(x－1)的解为a+2，求方程2[2(x+3)－3(x－a)]=3a的解．解由方程2(x+1)=3(x－1)解得x=5．由题设知a+2=5，所以a=3．于是有2[2(x+3)－3(x－3)]=3×3，－2x=－21，例4解关于x的方程(mx－n)(m+n)=0．分析这个方程中未知数是x，m，n是可以取不同实数值的常数，因此需要讨论m，n 取不同值时，方程解的情况．解把原方程化为m2x+mnx－mn－n2=0，整理得m(m+n)x=n(m+n)．当m+n≠0，且m=0时，方程无解；当m+n=0时，方程的解为一切实数．说明含有字母系数的方程，一定要注意字母的取值范围．解这类方程时，需要从方程有唯一解、无解、无数多个解三种情况进行讨论．例5解方程(a+x－b)(a－b－x)=(a2－x)(b2+x)－a2b2．分析本题将方程中的括号去掉后产生x2项，但整理化简后，可以消去x2，也就是说，原方程实际上仍是一个一元一次方程．解将原方程整理化简得(a－b)2－x2=a2b2+a2x－b2x－x2－a2b2，即 (a2－b2)x=(a－b)2．(1)当a2－b2≠0时，即a≠±b时，方程有唯一解(2)当a2－b2=0时，即a=b或a=－b时，若a－b≠0，即a≠b，即a=－b时，方程无解；若a－b=0，即a=b，方程有无数多个解．例6已知(m2－1)x2－(m+1)x+8=0是关于x的一元一次方程，求代数式199(m+x)(x－2m)+m的值．解因为(m2－1)x2－(m+1)x+8=0是关于x的一元一次方程，所以m2－1=0，即m=±1．(1)当m=1时，方程变为－2x+8=0，因此x=4，代数式的值为199(1+4)(4－2×1)+1=1991；(2)当m=－1时，原方程无解．所以所求代数式的值为1991．例7 已知关于x的方程a(2x－1)=3x－2无解，试求a的值．解将原方程变形为2ax－a=3x－2，即 (2a－3)x=a－2．由已知该方程无解，所以例8k为何正数时，方程k2x－k2=2kx－5k的解是正数？来确定：(1)若b=0时，方程的解是零；反之，若方程ax=b的解是零，则b=0成立．(2)若ab＞0时，则方程的解是正数；反之，若方程ax=b的解是正数，则ab＞0成立．(3)若ab＜0时，则方程的解是负数；反之，若方程ax=b的解是负数，则ab＜0成立．解按未知数x整理方程得(k2－2k)x=k2－5k．要使方程的解为正数，需要(k2－2k)(k2－5k)＞0．看不等式的左端(k2－2k)(k2－5k)=k2(k－2)(k－5)．因为k2≥0，所以只要k＞5或k＜2时上式大于零，所以当k＜2或k＞5时，原方程的解是正数，所以k＞5或0＜k＜2即为所求．例9若abc=1，解方程解因为abc=1，所以原方程可变形为化简整理为化简整理为说明像这种带有附加条件的方程，求解时恰当地利用附加条件可使方程的求解过程大大简化．例10若a，b，c是正数，解方程解法1原方程两边乘以abc，得到方程ab(x－a－b)+bc(x－b－c)+ac(x－c－a)=3abc．移项、合并同类项得ab[x－(a+b+c)]+bc[x－(a+b+c)]+ac[x－(a+b+c)]=0，因此有[x－(a+b+c)](ab+bc+ac)=0．因为a＞0，b＞0，c＞0，所以ab+bc+ac≠0，所以x－(a+b+c)=0，即x=a+b+c为原方程的解．解法2将原方程右边的3移到左边变为－3，再拆为三个“－1”，并注意到其余两项做类似处理．设m=a+b+c，则原方程变形为所以即x－(a+b+c)=0．所以x=a+b+c为原方程的解．说明注意观察，巧妙变形，是产生简单优美解法所不可缺少的基本功之一．例11设n为自然数，[x]表示不超过x的最大整数，解方程：分析要解此方程，必须先去掉[ ]，由于n是自然数，所以n与(n+1)…，n[x]都是整数，所以x必是整数．解根据分析，x必为整数，即x=[x]，所以原方程化为合并同类项得故有所以x=n(n+1)为原方程的解．例12已知关于x的方程且a为某些自然数时，方程的解为自然数，试求自然数a的最小值．解由原方程可解得a最小，所以x应取x=160．所以所以满足题设的自然数a的最小值为2．练习四1．解下列方程：*2．解下列关于x的方程：(1)a2(x－2)－3a=x+1；4．当k取何值时，关于x的方程3(x+1)=5－kx，分别有：(1)正数解；(2)负数解；(3)不大于1的解．。

初一数学竞赛系列讲座8

初一数学竞赛系列讲座8初一数学竞赛系列讲座(8)解一次方程（组）与一次不等式（组）一、知识要点1、一元一次方程方程中或者不含分母，或者分母中不含未知数，将它们经过去分母、去括号、移项、合并同类项等变形后，能化为最简形式ax=b(a ≠0)，它只含有一个未知数，并且未知数的次数是1，系数不等于0，我们把这一类方程叫做一元一次方程。

解一元一次方程的一般步骤是：分母、去括号、移项、合并同类项、系数化成1。

2、方程ax=b(a 、b 为常数)的解的情形当a ≠0时，方程ax=b 有唯一解a bx当a=0，b=0时，方程ax=b 有无数多个解，即方程的解为任何有理数。

当a=0，b ≠0时，方程ax=b 无解。

3、一次方程组解一次方程组的基本思想是“消元”，常用方法有“代入消元法”和“加减消元法”4、不定方程不定方程(组)是指未知数的个数多于方程个数的方程(组)。

它的解往往有无穷多个，不能唯一确定，对于不定方程(组)，我们常常限定当时，方程无解。

43,43≠=n m评注：含参方程必须对参数进行讨论。

例3 解方程组 (1) ⎪⎩⎪⎨⎧=-+==(2) 5434(1) 432z y x z y x (2) ⎪⎩⎪⎨⎧=++=++=++(3) 201633(2)143163(1) 103316z y x z y x z y x分析：第一个方程组的(1)式是一个连比式，对于连比式常用连比设k 法来解决。

第二个方程组的各式系数较大，直接用代入消元或加减消元比较繁，观察这个方程组的特点，将三式相加可得x+y+z ，然后再用三式去分别减可得x 、y 、z 的值。

解：(1)设k z k y k x k z y x 4,3,2432======，则，代入(2)得k=5∴x=10，y=15，z=20∴原方程组的解为⎪⎩⎪⎨⎧===201510z y x(2) (1)+(2)+(3)得22 (x+y+z)=44，所以x+y+z=2 所以3 (x+y+z)=6 (4)(1)-(4)得13x=4，则x=134(2)-(4)得13y=8，则y=138(3)-(4)得13z=14，则z=1314所以原方程组的解为⎪⎪⎪⎩⎪⎪⎪⎨⎧===1314138134z y x 评注：解方程组时，应对方程组的整体结构进行分析，从整体上把握解题方向。

七年级数学上册竞赛系列讲座第六讲一元一次方程

第6讲一元一次方程笔记：一元一次方程是代数方程中最基础的部分，是后继学习的基础，其基本内容包括：解方程、方程的解及其讨论。

解一元一次方程有一般程序化的步骤，我们在解一元一次方程时，既要学会按部就班（严格按步骤）地解方程，又要能随机应变（灵活打乱步骤）解方程。

当方程中的系数是用字母表示时，这样的方程叫含字母系数的方程。

含字母系数的一元一次方程总可化为ax=b 的形式，继续求解时，一般要对字母系数a,b 进行讨论：1、当0≠a 时，方程有唯一解：ab x =； 2、当00≠=b a 且时，方程无解；3、当00==b a 且时，方程有无数个解。

习题：1、当1=b 时，关于x 的方程78)32()23(-=-+-x x b x a 有无数多个解，则a 等于（）A 、2B 、2-C 、32- D 、不存在 2、已知关于x 的方程b x a x a 3)5()1(2+-=-有无数多个解，那么=a ；=b 。

3、如果方程x a a x 3200442003-=+的根（解）是1=x ，则=a 。

4、关于x 的方程09=-p x 的根（解）是p -9，则p = 。

5、已知a 是任意有理数，在下面各题中：①方程0=ax 的解是1=x ；②方程a ax =的解是1=x ；③ ax ax 11==的解是方程；④a x a =方程的解是1±=x 。

结论正确的个数是（）A 、0B 、1C 、2D 、36、已知关于x 的一次方程07)83=++b a （无解，则ab 是（）A 、正数B 、非正数C 、负数D 、非负数7、（华杯赛试题）若01)204)=--=++x m k x m k 和（（是关于x 的同解方程，则2-mk 的值是。

8、（希望杯试题）当1-=x 时，代数式8323+-bx ax 的值为18，这时，代数式269+-a b 等于（）A 、28B 、28-C 、32D 、32-9、若a 3的倒数与392-a 互为相反数，则a 等于（） A 、23 B 、23- C 、3 D 、9 10、（14届希望杯）方程231)153(123661-=⎥⎦⎤⎢⎣⎡+--x x x 的解是（） A 、1415 B 、1415- C 、1445 D 、1445- 总结：灵活地解一元一次方程时常用到以下方法和技巧：（1）若括号内含有分数，则由外向内先去括号，再去分母；（2）若有多重括号，则去括号与合并同类项可交替进行；（3）恰当用整体思想，即把含有未知数的代数式看做一个整体进行变形；（4）当分母中含有小数，可用分数的基本性质化成整数。

初一数学竞赛讲义(一元一次方程)

第1讲一元一次方程一、一元一次方程的解法一元一次方程的解法一般有去分母，去括号，移项，合并同类项等步骤，但在解题过程中不要生搬硬套，往往需要我们活用所学方法，灵活解决问题。

例1、解方程200620072005275253212=⨯++⨯+⨯+⨯xxxx x二、一元一次方程根的存在性一元一次方程最终都可化成ax=b 的形式，显然当a ≠0时，方程有唯一的根a b；当a=0且b=0时，方程有无数根；当a=0且b ≠0时，方程无根；例2、当b=1时，关于x 的方程a （3x-2）+b （2x-3）=8x-7有无数多个解，求a 的值。

例3、如果a 、b 为定值，关于x 的方程6232bk x a kx -+=+，无论k 为何值，它的根总是1，求a 、b 的值。

例4、解关于x 的方程a b a b x b a x =---，其中a ≠0，b ≠0。

例5、已知3=--+--+--b ac x a cb xc ba x ，且0111≠++c b a ，求x-a-b-c 的值。

三、一元一次方程的整数解例6、若k 为整数，则使得方程（k-1999）x=2001-2000x 的解也是整数的k 值有几个？例7、已知p 、q 都是质数，则以x 为未知数的一元一次方程px+5q=97的解是1，求代数式p 2-q 的值。

四、含绝对值的一元一次方程例8、解方程312=+-x x例9、解方程532=+++x x练习1、已知ax 2+5x+14=2x 2-2x+3a 是关于x 的一元一次方程，则其解是多少？2、已知方程5x-2m=mx-4-x 的解在2与10之间（不包括2和10），求m 。

3、一个六位数左端的数字是1，如果把左端的数字移到右端，那么所得的六位数等于原数的3倍，则原数是什么？4、求自然数n a a a 21，使得122121122121n n a a a a a a ⨯=⨯。

5、关于x 的方程mx+4=3x-n ，分别求m 、n 为何值时，原方程（1）有惟一解（2）有无数解（3）无解6、方程1-x+x的解有哪些？2=-37、已知关于x的方程2a（x-1）=（5-a）x+3b有无数多解，试求a、b的值。

数学竞赛专题讲座七年级第7讲一元一次方程(含答案)

第5讲一元一次方程当方程中的系数是用字母表示时，这样的方程叫含字母系数的方程，含字母系数的一元一次方程总可以化为b ax =的形式，继续求解时，一般要对字母系数a 、b 进行讨论：1．当0≠a 时，方程有惟一解ab x =；2．当0,0≠=b a 时，方程无解； 3．当0,0==b a 时，方程有无数个解．例题讲解【例1】(1)已知关于x 的方程x a x x 4)3(23=⎥⎦⎤⎢⎣⎡--和1851123=--+x a x 有相同的解，那么这个解是． (北京市“迎春杯”竞赛题)（2）如果20042003)1(11216121=+++++n n ，那么n ＝． (江苏省竞赛题)【例2】当1=b 时，关于x 的方程78)32()23(-=-+-x x b x a 有无数多个解，则a 等于( )． A ．2 B ．2- C ．32- D ．不存在 (“希望杯”邀请赛试题)【例3】是否存在整数k ，使关于x 的方程x x k 516)5(-=+-；在整数范围内有解?并求出各个解．【例4】解下列关于x 的方程． (1)84-=+ax b x ； (4≠a ) (2)nx mx =-1； (3))2(41)(31m x n x m +=-．【例5】已知q p 、都是质数，并且以x 为未知数的一元一次方程975=+q px 的解是1，求代数式410140++q p的值． (“希望杯”邀请赛试题) 【例6】如图，8块相同的长方形地砖拼成一个长方形，每块长方形地砖的长和宽分别是多少？基础训练一、基础夯实1.已知x=-1是关于x的方程7x3-3x2+kx+5=0的解,则k3+2k2-11k-85=______.2.计算器上有一个倒数键1/x,能求出输入的不为零的数的倒数(注:有时需先按shift或2nd键,再按1/x键,才能实现此功能,下面不再说明).例如,输入2,按下键1/x,则得0.5,现在计算器上输入某数,再依下列顺序按键: 1/x-1=1/x-1= ,在显示屏上的结果为-0.75,则原来输入的某数是____ ___. (第17届江苏省竞赛题)3.方程16(20x+50)+23(5+2x)-12(4x+10)=0的解为______;解方程12｛12[12(12x-3)-3]-3｝-3=0,得x=_______.4.已知关于x的方程2a(x-1)=(5-a)x+3b有无数多个解,那么a=_____,b=_ ____. (“希望杯”邀请赛试题)5.和方程x-3=3x+4不同解的方程是( ).A.7x-4=5x-11B.13x++2=0 C.(a2+1)(x-3)=(3x+4)(a2+1) D.(7x-4)(x-1)=(5x-11)(x-1)6.已知a是任意有理数,在下面各题中，结论正确的个数是( ).(1)方程ax=0的解是x=1 (2)方程ax=a的解是x=1(3)方程ax=1的解是x=1a(4)方程│a│x=a的解是x=±1A.0B.1C.2D.3 (江苏省竞赛题)7.方程x-16[36-12(35x+1)]=13x-2的解是( ).A.1514 B.-1514 C. 4514 D.- 45148.已知关于x 的一次方程(3a+8b)x+7=0无解,则ab 是( ).A.正数B.非正数C.负数D.非负数 9.解下列关于x 的方程:(1)ax-1=bx ; (2)4x+b=ax-8; (3)k(kx-1)=3(kx-1).10.a 为何值时,方程3x +a=2x -16(x-12)有无数多个解?无解?二、能力拓展11.已知方程2(x+1)=3(x-1)的解为a+2,那么方程2[2(x+3)-3(x-a)]=3a•的解为_______.12.•已知关于x•的方程9x-•3=•kx+•14•有整数解,•那么满足条件的所有整数k=_______. (“五羊杯”竞赛题) 13.已知14+4(11999+1x )=134,那么代数式1872+48·(19991999xx +)的值为_________. 14.若(3a+2b)x 2+ax+b=0是关于x 的一元一次方程,且有惟一解,则x=_____. 15.有4个关于x 的方程,其中同解的两个方程是( ).(1)x-2=-1 (2)(x-2)+(x-1)=-1+(x-1) (3)x=0 (4)x-2+11x -=-1+11x - A.(1)与(2) B.(1)与(3) C.(1)与(4) D.(2)与(4) 16.方程12x ⨯+23x ⨯+…+19951996x⨯=1995的解是( ). A.1995 B.1996 C.1997 D.1998 17.已知a+2=b-2=2c=2001,且a+b+c=2001k ,那么k 的值为( ). A.14 B.4 C.-14D.-4 (第15届江苏省竞赛题)18.若k 为整数,则使得方程(k-1999)x=2001-2000x 的解也是整数的k 值有( ).A.4个B.8个C.12个D.16个 (第12•届“希望杯”邀请赛试题)19.若干本书分给小朋友,每人m 本,则余14本;每人9本,则最后一人只得6本,•问小朋友共几个?有多少本书?20.下边横排有12个方格,每个方格都有一个数字,•已知任何相邻三个数字的和都是20,求x 的值. (上海市竞赛题)X 10E HG F E D C B A5三、综合创新21.如果a 、b 为定值,关于x 的方程23kx a +=2+6x bk-,无论k 为何值,它的解总是1, 求a 、b 的值. (山东省竞赛题)22.将连续的自然数1～1001按如图的方式排列成一个长方形阵列,•用一个正方形框出16个数,要使这个正方形框出的16个数之和分别等于:(1)1988;(2)1991;(•3)2000;(4)2080.这是否可能?若不可能,试说明理由;若可能,请写出该方框16个数中的最小数与最大数. (2002年河北省竞赛题)1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28…… ……995 996 997 998 999 1000 1001提高训练1．已知a x x x ax 32213522+-=++是关于x 的一元一次方程，那么关于y 的一元一次方程931054-=--ay y ay 的解是________．2．如图是一个数表，现用一个长方形在数表中任意框出4个数，则：（1）a 、c 的关系是：__________；（2）当32=+++d c b a 时，=a ______．3．（1）方程023424231=-----xx x 的解是____ __．（2）在有理数范围内定义一个运算“※”其规则为a ※b =2b a +，则方程4※（x ※2）=21的解__ _.4．若方程x mx x m =+--8)1(22是关于x 的一元一次方程，则代数式12008--m m 的值为（）． A ．1或1- B ．1 C ．1- D ．2 （广西竞赛题） 5．已知关于x 的方程)(23a x ax -=+的解满足032=--x ，则a 的值为（）．A ． 5-B ．1C ．5-或1-D ．5-或1 6．对任意四个有理数a 、b 、c 、d ，定义新运算：bc ad d c b a -=，已知18142=-x x ，则=x （）． A ．1- B ．2 C ．3 D ．4 （希望杯竞赛题）7．若2=x 是方程110742316191=⎭⎬⎫⎩⎨⎧+⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛++a x 的解，则a =______．8．已知06)3()9(22=+---x m x m 是以x 为未知数的一元一次方程，如果m a ≤，那么m a m a -++的值为______．（华罗庚杯竞赛题）9．以x 为未知数的方程0200820072007=++b a x （a 、b 为有理数，且0>b ）有正整数解，则ab 是（）． A ．负数 B ．非负数 C ．正数 D ．零（希望杯竞赛题） 10．关于x 的一元一次方程20112012200920102007200820052006xx x x -+-=-+-的解（）． A ．是一个大于1000的数 B ．是一个两位的自然数C ．是一个大于0且小于2的数D ．不存在（五羊杯竞赛题） 11．解关于x 的方程3-=++++++++bac x a c b x c b a x ．（广西竞赛题）12．当a 取符合03≠+na 的任意数时，式子32+-na ma 的值都是一个定值，其中6=-n m ，求m 、n 的值．dc b a 24252627281920212223141516171810111213876594。

数学竞赛专题讲座七年级第7讲一元一次方程（含答案）

数学竞赛专题讲座七年级第7讲⼀元⼀次⽅程（含答案）第七讲⼀元⼀次⽅程早在300多年前法国数学家笛卡尔有⼀个伟⼤的设想：⾸先把宇宙万物的所有问题都转化为数学问题；其次，把所有的数学问题转化为代数问题；最后，把所有的代数问题转化为解⽅程．虽然笛卡尔“伟⼤设想”没有实现，但是充分说明了⽅程的重要性．⼀元⼀次⽅程（linear equation with one unknown ）是代数⽅程中最基础的部分，是后续学习的基础，其基本内容包括：解⽅程、⽅程的解及其讨论．解⼀元⼀次⽅程有⼀般程序化的步骤，我们在解⼀元⼀次⽅程时，既要学会按部就班(严格按步骤)地解⽅程，⼜要能随机应变(灵活打乱步骤)解⽅程．当⽅程中的系数是⽤字母表⽰时，这样的⽅程叫含字母系数的⽅程，含字母系数的⼀元⼀次⽅程总可以化为b ax =的形式，继续求解时，⼀般要对字母系数a 、b 进⾏讨论：1．当0≠a 时，⽅程有惟⼀解ab x =；2．当0,0≠=b a 时，⽅程⽆解； 3．当0,0==b a 时，⽅程有⽆数个解．如果其他⼈也像我⼀样不迷信权威，持久⽽深⼊地探索数学真理，那么他们也将做出我所做的发现．——C ．F ．⾼斯C ．F ．⾼斯（1777-1855），著名的德国数学家，在代数、⼏何和近代数论等数学领域中做过许多开创性的⼯作．例题讲解【例1】(1)已知关于x 的⽅程x a x x 4)3(23=--和1851123=--+x a x 有相同的解，那么这个解是． (北京市“迎春杯”竞赛题)（2）如果20042003)1(11216121=+++++n n ，那么n ＝． (江苏省竞赛题) 思路点拨 (1)设法建⽴关于a 等式，再解关于a 的⽅程求出a 的值；(2)恰当地解关于n 的⼀元⼀次⽅程．链接：对于⼀般解题步骤与解题技巧来说，前者是通法，后者是技巧；前者是基础，后者是机智．只有真正掌握⼀般步骤，才能“熟能⽣巧”．⽅程的解是⽅程理论中的⼀个重要概念，解题中要学会从两个⽅⾯去应⽤：(1)求解：通过解⽅程，求出⽅程的解进⽽解决问题； (2)代解：将⽅程的解代⼊原⽅程进⾏解题．【例2】当1=b 时，关于x 的⽅程78)32()23(-=-+-x x b x a 有⽆数多个解，则a 等于( )．A ．2B ．2-C ．32- D ．不存在 (“希望杯”邀请赛试题)思路点拨将1=b 代⼈原⽅程，整理所得⽅程，就⽅程解的个数情况建⽴a 的等式．【例3】是否存在整数k ，使关于x 的⽅程x x k 516)5(-=+-；在整数范围内有解?并求出各个解．思路点拨把⽅程的解x ⽤k 的代数式表⽰，利⽤整除的知识求出k ．【例4】解下列关于x 的⽅程． (1)84-=+ax b x ； (4≠a ) (2)nx mx =-1； (3))2(41)(31m x n x m +=-．思路点拨⾸先将⽅程化为b ax +的形式，然后注意每个⽅程中字母系数可能取值的情况进⾏讨论．【例5】已知q p 、都是质数，并且以x 为未知数的⼀元⼀次⽅程975=+q px 的解是1，求代数式410140++q p 的值． (“希望杯”邀请赛试题)思路点拨⽤代解法可得到q p 、的关系式，进⽽综合运⽤整数相关知识分析．链接：同⼀个⽅程在不同的数集范围内求解，其解集往往是不同的．对于含字母系数的⽅程，我们不但可讨论⽅程根的个数，⽽且还可以探求解的性态，如整数解、正数解，负数解，解这类问题，常常要⽤到整数知识、枚举、分类讨论等⽅法。

七年级一元一次方程竞赛讲座2

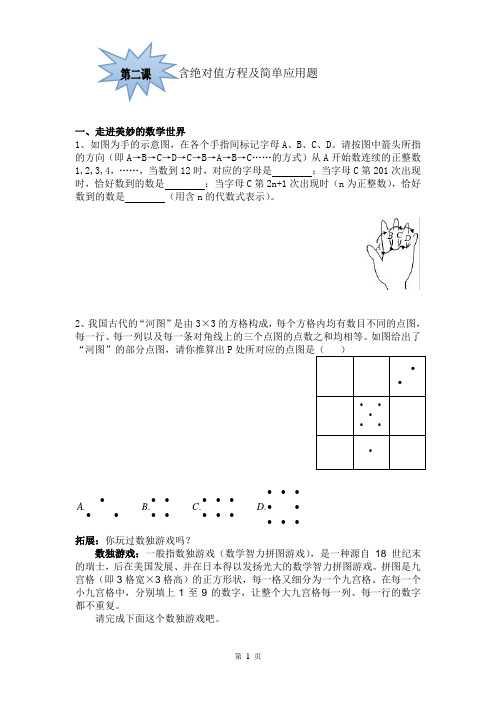
含绝对值方程及简单应用题一、走进美妙的数学世界1、如图为手的示意图，在各个手指间标记字母A 、B 、C 、D 。

请按图中箭头所指的方向（即A →B →C →D →C →B →A →B →C ……的方式）从A 开始数连续的正整数1,2,3,4，……，当数到12时，对应的字母是；当字母C 第201次出现时，恰好数到的数是；当字母C 第2n+1次出现时（n 为正整数），恰好数到的数是（用含n 的代数式表示）。

2、我国古代的“河图”是由3×3的方格构成，每个方格内均有数目不同的点图，每一行、每一列以及每一条对角线上的三个点图的点数之和均相等。

如图给出了“河图”的部分点图，请你推算出P 处所对应的点图是（）∙∙∙∙∙∙∙∙∙∙∙.A ∙∙∙∙.B ∙∙∙∙∙∙.C ∙∙∙∙∙∙∙∙.D拓展：你玩过数独游戏吗？数独游戏：一般指数独游戏（数学智力拼图游戏），是一种源自18世纪末的瑞士，后在美国发展、并在日本得以发扬光大的数学智力拼图游戏。

拼图是九宫格（即3格宽×3格高）的正方形状，每一格又细分为一个九宫格。

在每一个小九宫格中，分别填上1至9的数字，让整个大九宫格每一列、每一行的数字都不重复。

请完成下面这个数独游戏吧。

1 32 9 5 6 1 8 4 2 8 2 4 7 1 4 6 2 53 5 7 2 1 6 1 645 8 7 9 2 3 4 3 8 9 5 1 25379二、含绝对值的一元一次方程绝对值是初中数学最活跃的概念之一，能与数学中许多知识关联而产生新的问题，我们把绝对值符号中含有未知数的方程叫做含绝对值符号的方程，简称绝对值方程。

解绝对值方程的基本方法：一是设法去掉绝对值符号，将绝对值方程转化为常见的方程求解；一是数形结合，借助于图形的直观性求解。

前者是通法，后者是技巧。

解绝对值方程时，常常要用到绝对值的几何意义、去绝对值的符号法则、非负数的性质、绝对值常用的基本性质等与绝对值相关的知识、技能和方法。

初三数学竞赛：一元一次方程进阶

第 10 讲一元一次方程进阶知识总结归纳一 . 含字母系数的一次方程的解法关于 x 的方程ax b（1）当 a 0 时，方程有唯一解x b ；a（2）当 a b 0时，方程的解为任意实数；（3）当 a 0且 b0 时，方程无解．二. 对于特殊的一元一次方程，可以用验根法解方程，即代入某数验证它就是方程的根，然后说明此方程有唯一解（一次项系数不为 0）.三. 当一个一元一次方程有两个或者两个以上的解时，它必有无穷多个解，即它的一次项系数和常数都为 0.四 . 整数根的两种解法：方法 1：先解方程，然后把解的代数式适当变形，根据整数的整除性求解；方法 2：直接把方程化成一个整式，利用因式分解的方法求解 .典型例题一.解方程例题 1解方程：xx 3 2 3x . 246例题 2解方程：3[ 2( x 2 )4] 1. 233x x 31 6 xx例题 3解方程： x 2423 232例题 4解方程：1x1x1x x52 2356例题 5解方程：x x x x223342009200912010例题 611112013 ；解方程：（ y 1)（ y 2)（ y 3)（ y 2013)2342014二.含参数的方程例题 7解下列关于x的方程．（1）mx 1 nx；（2）4x b ax 8；（ 3）1m( x n)1(x 2m)；34例题 8解关于 x 的方程x ax bb，其中 a0 ， b 0 .b a a例题 9解关于x的方程:(mx n)(m n)0 .例题 10 解关于x的方程 : (a x b)( a b x) ( a2x)(b2x)a2 b2三.解的情况的讨论例题 11 关于x的方程 mx4 3x n ，分别求m、n为何值时，原方程：（1）有惟一解；（2）有无数解；（ 3）无解 .例题 12 已知关于x的方程2a x1 5 a x 3b 无穷多解，求 a 、b .例题 13 已知关于x的方程2m 3x 2 1 2n 1 x 无穷多解，求 m 、 n .例题 14 已知关于x的方程a(2x1) 3x 2无解，试求 a 的值．例题 15 证明：若一元一次方程ax b 有两个不同的解x1和 x2，求证：这个方程必有有无数多个解。

初中数学竞赛辅导第四讲一元一次方程含答案.doc.docx

初中数学竞赛辅导第四讲一元一次方程1、解方程：1x1x1x23x3.2343242、已知方程 3 x 2 5x 和 4x 3 a x 6x 7 a x 有相同的解，求 a 的值。

3、已知方程 2 x 1 3 x 1 的解为a+2，求方程 2 2 x 3 2 x a3a 的解。

4、解关于x 的方程mx n m n0 。

5、解方程： a x b a b x a 2x b2x a 2b 2。

6 、已知m2 1 x 2m 1 x 8 0 是关于x的一元一次方程，求代数式199 m x x 2m m 的值。

7、关于 x 的方程a 2x 1 3x 2 无解，试求 a 的值。

8、 k 为何正数时，方程k 2 x k 22kx5k 的解是正数？9、若abc2ax2bx2cx。

1 ，解方程bc b 11ab a 1ca a 1x a b x b c x c a3。

10、若 a、b、c 是正数，解方程a bc11、设 n 为自然数， [x] 表示不超过x 的最大整数，解方程x 2 x 3 x 4 xn x n2n 1 2。

212、已知关于x 的方程，且 a 为某些自然数时，方程5 xa8 x142 的解为自然数，试25求自然数 a 的最小值。

答案：1、 x22。

92、 a4 1。

2 3、 x110 。

24、（ 1）当 m n0 ，且 m 0 时，方程有唯一解 xn 0 时，且 m 0 时，；（ 2）当 m n m方程无解；（ 3）当 m n 0 时，方程的解为一切实数。

5、（）当 a2b20 时，方程有唯一解ab；（）当 a 2 b 20 时，则方程无解或有1x2a b无数多个解。

6、 1991。

3 7、 a 。

28、 k 5 或 0 k 2 。

9、 x1。

210、 x a b c 。

11、 x n n 1 。

12、 2。

训练题：1、解下列方程：1 1 1 x0.4x0.9x 5 0.02 x 0.0312 （ 1）31（ 2）0.520.034（ 3）1 1 1 1x 1 6 4 12 3 4 52、解下列关于 x 的方程：（ 1） a 2 x23 a x 1 （） axb3x 2ab1 （） x bx a2323a2b3、 a 为何值时，方程 xax1 x 12 有无数多个解？无解？32 64、当 k 取何值时，关于x 的方程3 x 1 5kx ，分别有（1）正数解；（2）负数解；（3）不大于 1 的解。

初一数学竞赛培训第7讲-一元一次方程

数学兴趣小组教案第三讲一元一次方程初一数学兴趣小组(2课时)一、教学目标1 学会根据方程的结构特点，灵活的选择解法和求解顺序；2 通过方程的认识和训练，了解“未知”可以转化为“已知”的思想方法；3 提高应用数学知识解决实际问题的能力。

二、教学重点根据方程的结构特点选择合适的求解方法和技巧三、教学难点能恰当的选取合适的解方程的方法并理解方程中的转化的思想四、教学方法启发教授五、教学手段六、教学过程（一）复习引入1回忆方程的有关概念（方程的解和解方程）；2总结一元一次方程的一般求解方法；（1）最简方程的求解---系数化1；（2）等号两边是多项式方程---移项，合并同类项；（3）含有括号的方程---去括号；（4）含有分式的方程----去分母；（5）系数是小数---系数化整；（6）含有绝对值---去绝对值号；（7）含有字母系数方程—分类讨论。

３几个有关于上一讲有理数的几个练习：（１）１＋３＋５＋．．．＋ｎ（２）２＋22＋32＋．．．＋n2 （３）200820071...431321211⨯++⨯+⨯+⨯ （４）10210...164834221+++++ （二）教授新知识1基础知识（1）换元法求解一元一次方程例题1先求解如下方程：043531221=----+x x x 解：去分母，得：6(x+1)-4(3x-1)-3(5-3x)=0;去括号，得：6x+6-12x+4-15+9x=0;移项，合并同类项，得：７ｘ＝５；系数化１，得：ｘ＝５／７．下面，我们看另一个一元一次方程：0465314212=----+y y y 这个方程和我们刚才求解的方程在结构上非常相似，只需将２ｙ换成ｘ就是上面的方程。

练习１，利用换元方法求解下面的方程：（１）042531342132=+----+-y y y （２）0403.053102.02101.0=----+y y y （３）)3(413)1(21)2(31+-=+-+x x x 小结：解答某个数学问题，需要用到换元方法时，应当认真，细致的观察题目的结构特征，选取合适的辅助元。

七年级数学竞赛专家讲座第3讲与一元一次方程有关的问题 (1)

第三讲：与一元一次方程有关的问题一、知识回顾一元一次方程是我们认识的第一种方程，使我们学会用代数解法解决一些用算术解法不容易解决的问题。

一元一次方程是初中代数的重要内容，它既是对前面所学知识——有理数部分的巩固和深化，又为以后的一元二次方程、不等式、函数等内容打下坚实的基础。

典型例题：二、典型例题例1．若关于x 的一元一次方程2332x k x k --+=1的解是x=-1，则k 的值是（） A ．27 B ．1 C ．-1311D ．0 分析：本题考查基本概念“方程的解” 因为x=-1是关于x 的一元一次方程2332x k x k --+=1的解，所以12313)1(2=--+--⨯k k ，解得k=-1311例2．若方程3x-5=4和方程0331=--x a 的解相同，则a 的值为多少？分析：题中出现了两个方程，第一个方程中只有一个未知数x ，所以可以解这个方程求得x 的值；第二个方程中有a 与x 两个未知数，所以在没有其他条件的情况下，根本没有办法求得a 与x 的值，因此必须分析清楚题中的条件。

因为两个方程的解相同，所以可以把第一个方程中解得x 代入第二个方程，第二个方程也就转化为一元一次方程了。

解：3x-5=4， 3x=9， x=3因为3x-5=4与方程 0331=--x a 的解相同所以把x=3代人0331=--x a 中即03331=--a 得3-3a+3=0，-3a=-6，a=2例3.（方程与代数式联系）a 、b 、c 、d 为实数，现规定一种新的运算 bc ad dc b a -=. （1）则2121-的值为；（2）当185)1(42=-x 时，x = .分析：（1）即a=1，b=2，c=-1，d=2，因为bc ad d c b a -=，所以2121-=2-（-2）=4（2）由185)1(42=-x 得：10-4（1-x ）=18所以10-4+4x=18，解得x=3例4．（方程的思想）如图，一个瓶身为圆柱体的玻璃瓶内装有高a 厘米的墨水，将瓶盖盖好后倒置，墨水水面高为h 厘米，则瓶内的墨水的体积约占玻璃瓶容积的（）A ．b a a +B ．b a b +C ．h a b+ D ．h a h + 分析：左右两个图中墨水的体积应该相等，所以这是个等积变换问题，我们可以用方程的思想解决问题解：设墨水瓶的底面积为S ，则左图中墨水的体积可以表示为Sa设墨水瓶的容积为V ，则右图中墨水的体积可以表示为V-Sb于是，Sa= V-Sb ，V= S(a+b)由题意，瓶内的墨水的体积约占玻璃瓶容积的比为ba ab a S Sa V Sa +=+=)(例5．小杰到食堂买饭，看到A 、B 两窗口前面排队的人一样多，就站在A 窗口队伍的里面，过了2分钟，他发现A 窗口每分钟有4人买了饭离开队伍，B 窗口每分钟有6人买了饭离开队伍，且B 窗口队伍后面每分钟增加5人。

一元一次方程初中数学竞赛专题讲座(26份初中数学竞赛教程)