2011年暑假生活初高中衔接内容考试数学试题
初升高数学暑假衔接(人教版)综合测试第1章:集合与常用逻辑用语(学生版)

第1章:集合与常用逻辑用语基础检测卷(试卷满分150分,考试用时120分钟)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求.1.下列说法正确的有()①1∈N *N ;③32∈Q ;④2+∉R ;⑤π∈Q A .1个B .2个C .3个D .4个2.下面有四个结论:①集合N 中最小数为1;②若N a -∉,则N a ∈;③若N a ∈,N b ∈,则a b +的最小值为2;④所有的正数组成一个集合.其中正确结论的个数为()A .0B .1C .2D .33.命题“2,10x x ∃∈+<R ”的否定是()A .2,10x x ∀∈+<R B .2,10x x ∀∈+≥R C .2,10x x ∃∈+>R D .2,10x x ∃∈+≥R 4.已知集合{}(,)|0,0M x y x y xy =+<>和{}(,)|0,0P x y x y =<<,那么()A .P M ⊆B .M P ⊆C .M P =D .M P≠5.已知{}2{1,2},0A B x x ax b ==++=∣,若A B ⊆,则()A .1,2a b ==-B .2,2a b ==-C .3,2a b =-=D .1,2a b =-=6.已知集合{}1,2,3,4,5,6A =,{}2,3B =,{}2,4,6C =,则()A B C = ð()A .{}2,4,6B .{}1,3,4,5,6C .{}4,6D .{}27.设全集U 及集合M 与N ,则如图阴影部分所表示的集合为()A .M N⋂B .M N ⋃C .U M N ðD .()U M N ð8.设p :2x >或23x <;q :2x >或1x <-,则p ⌝是q ⌝的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知,x y 都是非零实数,x y xy z x y xy =++可能的取值组成的集合为A ,则下列判断错误的是()A .3,1A A ∈-∉B .3,1A A ∈-∈C .3,1A A∉-∈D .3,1A A∉-∉10.已知全集U =R ,集合A 、B 满足A ⫋B ,则下列选项正确的有()A .A B B = B .A B B⋃=C .()U A B Ç=ÆðD .()R A B ⋂=∅ð11.下列命题正确的是()A .“1a >”是“11a<”的充分不必要条件B .命题“21,1x x ∀<<”的否定是“21,1x x ∃<≥”C .设,x y ∈R ,则“2x ≥且2y ≥”是“224x y +≥”的必要而不充分条件D .设,a b ∈R ,则“0a ≠”是“0ab ≠”的必要而不充分条件12.下列命题的否定为假命题的是()A .对任意的x ∈R ,2104x x -+≥B .所有的正方形都是矩形C .存在2R,220x x x ∈++≤D .至少有一个实数x ,使310x +=三、填空题:本题共4小题,每小题5分,共20分13.设,R a b ∈,{}{}1,,1,P a Q b ==--,若P Q =,则a b -=_________.14.集合{|(2)0}A x x x =-=,则集合A 的子集的个数为________.15.数集{}21,,a a a -中的元素a 不能取的值是__________.16.已知集合{}2220 A x mx x =++=中有两个元素,则实数m 满足的条件为_____.四.解答题:本小题共6小题,共70分。
2011年全国各地中考数学试卷分类汇编第42章学科结合与高中衔接问题

2011年全国各地中考数学试卷分类汇编第42章学科结合与高中衔接问题一、选择题1. (2011台湾全区,30)如图(十三),ΔABC中,以B为圆心,BC长为半径画弧,分别交AC、AB 于D、E两点,并连接BD、DE.若∠A=30∘,AB=AC,则∠BDE的度数为何?A.45 B.52.5 C.67.5 D.75【答案】C2. (2011贵州安顺,9,3分)正方形ABCD边长为1,E、F、G、H分别为边AB、BC、CD、DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x. 则y关于x的函数图象大致是()A.B.C.D.【答案】C3. (2011河北,11,3分)如图4,在矩形中截取两个相同的圆作为圆柱的上、下底面,剩余的矩形作为圆柱的侧面,刚好能组合成圆柱.设矩形的长和宽分别为y和x,则y与x的函数图象大致是()图4xxxxA.B.C.D.【答案】A3. (2011重庆市潼南,10,4分) 如图,在平面直角坐标系中,四边形OABC 是菱形, 点C 的坐标为(4,0),∠AOC = 60°,垂直于x 轴的 直线l 从y 轴出发,沿x 轴正方向以每秒1个单位长 度的速度向右平移,设直线l 与菱形OABC 的两边分 别交于点M,N (点M 在点N 的上方),若△OMN 的面积为S ,直线l 的运动时间为t 秒(0≤t ≤4),则 能大致反映S 与t 的函数关系的图象是【答案】C4. (2011台湾台北,23)如图(八),三边均不等长的ABC ∆,若在此三角形内找一点O ,使得OAB ∆、OBC ∆、OCA ∆的面积均相等。
判断下列作法何者正确?A . 作中线AD ,再取AD 的中点OB . 分别作中线AD 、BE ,再取此两中线的交点OC .分别作AB 、BC 的中垂线,再取此两中垂线的交点O D . 分别作A ∠、B ∠的角平分线,再取此两角平分线的交点O 【答案】B 二、填空题 1. 2. 3. 4. 5.三、解答题1. (2011重庆綦江,26,12分)在如图的直角坐标系中,已知点A (1,0);B (0,-2),将线段AB 绕点A按逆时针方向旋转90°至AC .⑴ 求点C 的坐标; ⑵ 若抛物线2212++-=ax x y 经过点C . ①求抛物线的解析式;②在抛物线上是否存在点P (点C 除外)使△ABP 是以AB 为直角边的等腰直角三角形?若存在,求出所有点P 的坐标;若不存在,请说明理由.【答案】:解:(1)过点C 作CD ⊥x 轴,垂足为D ,在△ACD 和△BAO 中,由已知有∠CAD +∠BAO =90°,而∠ABO +∠BAO =90°∴∠CAD =∠ABO ,又∵∠CAD =∠AOB =90°,且由已知有CA =AB ,∴△ACD ≌△BAO ,∴CD =OA =1,AD =BO =2,∴点C 的坐标为(3,-1)(2)①∵抛物线2212++-=ax x y 经过点C (3,-1),∴2332112++⨯-=-a ,解得21=a ∴抛物线的解析式为221212++-=x x y解法一:② i) 当A 为直角顶点时 ,延长CA 至点1P ,使AB AC AP ==1,则△1ABP 是以AB 为直角边的等腰直角三角形,如果点1P 在抛物线上,则1P 满足条件,过点1P 作1P E ⊥x 轴, ∵1AP =AC ,∠1EAP =∠DAC ,∠EA P 1=∠CDA =90°, ∴△A EP 1≌△DCA ,∴AE =AD =2, 1EP =CD =1,∴可求得1P 的坐标为(-1,1),经检验1P 点在抛物线上,因此存在点1P 满足条件; ii ) 当B 点为直角顶点时,过点B 作直线L ⊥BA ,在直线L 上分别取AB BP BP ==32,得到以AB 为直角边的等腰直角△2ABP 和等腰直角△3ABP ,作F P 2⊥y 轴,同理可证△F BP 2≌△ABO∴,22==BO F P BF =OA =1,可得点2P 的坐标为(-2,-1),经检验2P 点在抛物线上,因此存在点2P 满足条件.同理可得点3P 的坐标为(2,-3),经检验3P 点不在抛物线上. 综上:抛物线上存在点1P (-1,1),2P (-2,-1)两点,使得△1ABP 和△2ABP是以AB 为直角边的等腰直角三角形.解法二:(2)②(如果有用下面解法的考生可以给满分) i) 当点A 为直角顶点时,易求出直线AC 的解析式为2121+-=x y 由⎪⎪⎩⎪⎪⎨⎧++-=+-=2212121212x x y x y 解之可得1P (-1,1) (已知点C 除外)作E P 1⊥x 轴于E ,则AE =2, E P 1=1, 由勾股定理有又∵AB =5,∴AB AP =1,∴△AB P 1是以AB 为直角边的等腰三角形;ii )当B 点为直角顶点时,过B 作直线L ∥AC 交抛物线于点2P 和点3P ,易求出直线L 的解析式为221--=x y ,由⎪⎪⎩⎪⎪⎨⎧++-=--=221212212x x y x y 解得21-=x 或42=x∴2P (-2,-1),3P (4,-4)作F P 2⊥y 轴于F ,同理可求得AB BP ==52∴△AB P 2是以AB 为直角边的等腰三角形作H P 3⊥y 轴于H ,可求得AB BP ≠=+=5242223,∴Rt △3ABP 不是等腰直角三角形,∴点3P 不满足条件.综上:抛物线上存在点1P (-1,1),2P (-2,-1)两点,使得△1ABP 和△2ABP 是以角AB 为直边的等腰直角三角形.2. (2011广东省,22,9分)如图,抛物线2517144y x x =-++与y 轴交于点A ,过点A 的直线与抛物线交于另一点B ,过点B 作BC ⊥x 轴,垂足为点C (3,0). (1)求直线AB 的函数关系式;(2)动点P 在线段OC 上,从原点O 出发以每钞一个单位的速度向C 移动,过点P 作⊥x 轴,交直线AB 于点M ,抛物线于点N ,设点P 移动的时间为t 秒,MN 的长为s 个单位,求s 与t 的函数关系式,并写出t 的取值范围;(3)设(2)的条件下(不考虑点P 与点O ,点G 重合的情况),连接CM ,BN ,当t 为何值时,四边形BCMN 为平等四边形?问对于所求的t 的值,平行四边形BCMN 是否为菱形?说明理由.【解】(1)把x=0代入2517144y x x =-++,得1y = 把x=3代入2517144y x x =-++,得52y =,∴A 、B 两点的坐标分别(0,1)、(3,52)设直线AB 的解析式为y kx b =+,代入A 、B 的坐标,得1532b k b =⎧⎪⎨+=⎪⎩,解得112b k =⎧⎪⎨=⎪⎩所以,112y x =+(2)把x=t 分别代入到112y x =+和2517144y x x =-++ 分别得到点M 、N 的纵坐标为112t +和2517144t t -++∴MN=2517144t t -++-(112t +)=251544t t -+即251544s t t =-+∵点P 在线段OC 上移动,∴0≤t ≤3.(3)在四边形BCMN 中,∵BC ∥MN∴当BC=MN 时,四边形BCMN 即为平行四边形由25155442t t -+=,得121,2t t ==即当12t =或时,四边形BCMN 为平行四边形当1t =时,PC=2,PM=32,PN=4,由勾股定理求得CM=BN=52,此时BC=CM=MN=BN ,平行四边形BCMN 为菱形;当2t =时,PC=1,PM=2,由勾股定理求得此时BC ≠CM ,平行四边形BCMN 不是菱形;所以,当1t =时,平行四边形BCMN 为菱形.3. (2011湖南怀化,24,10分)在矩形AOBC 中,OB=6,OA=4,分别以OB ,OA 所在直线为x 轴和y 轴建立如图所示的平面直角坐标系,F 是边BC 上的一个动点(不与B ,C 重合),过F 点的反比例函数)0(>=k xky 的图像与AC 边交于点E. (1) 求证:AE×AO=BF×BO ; (2) 若点E 的坐标为(2,4),求经过O 、E 、F 三点的抛物线的解析式;(3) 是否存在这样的点F ,使得将△CEF 沿EF 对折后,C 点恰好落在OB 上?若存在,求出此时的OF长;若不存在,请说明理由.【答案】(1)证明:由题意知,点E 、F 均在反比例函数)0(>=k xky 图像上,且在第一象限,所以AE×AO=k ,BF×BO=k ,从而AE×AO=BF×BO.(2)将点E 的坐标为(2,4)代入反比例函数)0(>=k xky 得k=8, 所以反比例函数的解析式为xy 8=. ∵OB=6,∴当x=6时,y=34,点F 的坐标为(6,34). 设过点O 、E 、F 三点的二次函数表达式为)0(2≠++=a c bx ax y ,将点O (0,0),E (2、4),F (6,34)三点的坐标代入表达式得:⎪⎪⎩⎪⎪⎨⎧=++=++=346364240c b a c b a c 解得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=092694c b a ∴经过O 、E 、F 三点的抛物线的解析式为:x x y 926942+-=. (1) 如图11,将△CEF 沿EF 对折后,C 点恰好落在OB 边于点C′.过点E 作EH ⊥OB 于点H.设CE=n ,CF=m ,则AE=6-n ,BF=4-m由(1)得AE×AO=BF×BO ∴(6-n)×4=(4-m)×6 ,解得n=1.5m. 由折叠可知,CF=C′F=m ,CE=C′E=1.5m ,∠EC′F=∠C=90° 在Rt △EHC′中,∠EC′H+∠C′EH=90°,又∵∠EC′H+∠EC′F+FC′B=180°,∠EC′F=90° ∴∠C′EH=FC′B ∵∠EHC′=C′BF=90° ∴△EC′H ∽△C′FB ,∴FC C E B C EH ''=' ∴5.15.1==''='mmF C C E B C EH , ∵由四边形AEHO 为矩形可得EH=AO=4 ∴C ′B=38. 在Rt △BC′F 中,由勾股定理得,C′F 2=BF 2+C′B 2,即m 2=(4-m)2+238⎪⎭⎫⎝⎛解得:m=926BF=4-926=910, 在Rt △BOF 中,由勾股定理得,OF 2=BF 2+OB 2,即OF 2=62+2910⎪⎭⎫ ⎝⎛=813016.∴OF=97542∴存在这样的点F ,OF=97542,使得将△CEF 沿EF 对折后,C 点恰好落在OB 上. 4. (2011江苏淮安,28,12分)如图,在Rt △ABC 中,∠C=90°,AC=8,BC=6,点P 在AB 上,AP=2.点E 、F 同时从点P 出发,分别沿P A 、PB 以每秒1个单位长度的速度向点A 、B 匀速运动,点E 到达点A 后立即以原速度沿AB 向点B 运动,点F 运动到点B 时停止,点E 也随之停止.在点E 、F 运动过程中,以EF 为边作正方形EFGH ,使它与△ABC 在线段AB 的同侧,设E 、F 运动的时间为t 秒(t >0),正方形EFGH 与△ABC 重叠部分面积为S .(1)当t=1时,正方形EFGH 的边长是 ;当t=3时,正方形EFGH 的边长是 ; (2)当0<t ≤2时,求S 与t 的函数关系式; (3)直接答出:在整个运动过程中.......,当t 为何值时,S 最大?最大面积是多少? A【答案】(1)2;6; (2) 当0<t ≤611时(如图),求S 与t 的函数关系式是:S=EFGH S 矩形=(2t )2=4t 2;当611<t≤65时(如图),求S与t的函数关系式是:S=EFGHS矩形-S△HMN=4t2-12×43×[2t-34(2-t)]2=2524t2+112t-32;当65<t≤2时(如图),求S与t的函数关系式是:S= S△ARF -S△AQE =12×34(2+t) 2-12×34(2-t) 2=3t.(3)由(2)知:若0<t≤611,则当t=611时S最大,其最大值S=144121;若611<t≤65,则当t=65时S最大,其最大值S=185;若65<t≤2,则当t=2时S最大,其最大值S=6.综上所述,当t=2时S最大,最大面积是6.5. (2011山东临沂,26,13分)如图,已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C.(1)求抛物线的解析式;(2)若点D在抛物线上,点E在抛物线的对称轴上,且以A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;(3)P是抛物线上第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P使得以点P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.解:(1)∵抛物线过原点O ,∴可设抛物线的解析式为y =ax 2+bx ,将A (-2,0),B (-3,3)代入,得⎩⎨⎧.3b 3a 90b 2a 4=-,=-解得⎩⎨⎧.2b 1a =,=∴此抛物线的解析式为y =x 2+2x .……………………(3分)(2)如图,①当AO 为边时,∵以A 、O 、D 、E 为顶点的四边形是平行四边形,∴DE ∥AO ,且DE =AO =2,…………………………………………( 4分) 点E 在对称轴x =-1上,∴点D 的横坐标为1或-3,…………………………………………( 5分) 即符合条件的点D 有两个,分别记为:D 1,D 2, 而当x =1时,y =3;当x =-3时,y =3, ∴D 1(1,3),D 2(-3,3).…………………………………………(7分) ②当AO 为对角线时,则DE 与AO 互相平分, 又点E 在对称轴上,且线段AO 的中点横坐标为-1,由对称性知,符合条件的点D 只有一个,即顶点C (-1,,1), 综上所述,符合条件的点D 共有三个,分别为D 1(1,3),D 2(-3,3),C (-1,,1).………………………………………………………(8分)③存在.…………………………………………………………………(9分)6. (2011上海,24,12分)已知平面直角坐标系xOy(如图),一次函数334y x=+的图像与y轴交于点A,点M在正比例函数32y x=的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.(1)求线段AM的长;(2)求这个二次函数的解析式;(3)如果点B在y轴上,且位于点A下方,点C在上述二次函数的图像上,点D在一次函数334y x=+的图像上,且四边形ABCD是菱形,求点C的坐标.【答案】(1)一次函数334y x=+,当x=0时,y=3.所以点A的坐标为(0,3).正比例函数32y x=,当y =32时,x=1.所以点M的坐标为(1,32).如下图,AM=.(2)将点A (0,3)、M (1,32)代入y =x 2+bx +c 中,得 3312c b c =⎧⎪⎨++=⎪⎩,. 解得523b c ⎧=-⎪⎨⎪=⎩,.即这个二次函数的解析式为2532y x x =-+. (3)设B(0,m )(m <3),C(n ,2532n n -+),D(n ,334n +).则AB =3m -,DC =D C y y -=2134n n -,AD =54n .因为四边形ABCD 是菱形,所以AB =DC =AD .所以21334534m n n m n ⎧-=-⎪⎪⎨⎪-=⎪⎩,. 解得1130m n =⎧⎨=⎩,;(舍去)12122m n ⎧=⎪⎨⎪=⎩,.将n =2代入2532y x x =-+,得C y =2.所以点C 的坐标为(2,2). 7. (2011四川乐山26,13分)已知顶点为A(1,5)的抛物线2y ax bx c =++经过点B(5,1).(1)求抛物线的解析式;(2)如图(15.1),设C,D 分别是x 轴、y 轴上的两个动点,求四边形ABCD 周长的最小值(3)在(2)中,当四边形ABCD 的周长最小时,作直线CD.设点P(x,y)(x>0)是直线y=x 上的一个动点,Q 是OP 的中点,以PQ 为斜边按图(15.2)所示构造等腰直角三角形PRQ. ①当△PBR 与直线CD 有公共点时,求x 的取值范围;②在①的条件下,记△PBR 与△COD 的公共部分的面积为S.求S 关于x 的函数关系式,并求S 的最大值。
初高中数学衔接测试题

高一《初高中数学衔接读本》测试卷一.选择题1. 下列各式正确的是 ( ) A 、a a =2 B 、a a ±=2 C 、a a =2 D 、22a a =2. 已知754z y x ==,则=-+++zy x z y x ( )A 、9B 、716 C 、38D 、8 3. 二次函数y =ax 2+bx+c (a ≠0)的图象如图所示,则下列结论:①a>0;②c>0;•③b 2-4ac>0,其中正确的个数是( )A 、0个B 、1个C 、 2个D 、3个4. 如图,△ABC 中,∠BAC=90°,AD ⊥BC 于D , 若AB=2,BC=3,则CD 的长是( )A .83B .23C .43D .535. 已知321+=a ,则a a a a a a a a 112121222--+---+-化简求值的结果是 ( ) A 、 0 B 、 31- C 、 3 D 、 13-- 6. 若多项式b x x -+1732分解因式的结果中有一个因式为4+x ,则b 的值为( )A 、20B 、-20C 、13D 、-137.当34x =时,代数式223111(2)(42)x x x x x-+++的值为( )A 、16B 、384C 、32D 、40 8. 把多项式1222+--b a a 分解因式,结果是( ) A 、)1)(1(++-+b a b a B 、)1)(1(-+--b a b a C 、)1)(1(++--b a b a D 、)1)(1(+---b a b a9. 已知二次函数的图象开口向下,且过点A (1,1),B (3,1),C ),4(1y -,D ),2(2y -,E ),5(3y ,则1y ,2y ,3y 的大小关系是( )A 、1y < 2y <3y B 、2y < 1y < 3yC 、3y <1y <2y D 、3y < 2y <1y10. 将函数图象上的所有点向左移动一个单位,再向下移动两个单位得到的函数解析式为4722++=x x y ,则原函数的解析式为( ) A 、111122++=x x y B 、7322++=x x y C 、1322++=x x y D 、51122++=x x y11.已知:如图,△ABC 中,D 在AC 上,且AD :DC =1:2, E 为BD 的中点,AE 的延长线交BC 于F ,则BF :FC =( )A 、2:1B 、3:1C 、4:1D 、5:1 12.给出下列命题,其中正确的有( )①重心到顶点与对边中点的距离之比为2:1;②等边三角形的外接圆的半径和内切圆半径之比为1:2; ③等腰三角形的内心、重心和外心同在底边的高线上; ④直角三角形的外心是斜边的中点,垂心是直角的顶点; A 、0个 B 、1个 C 、 2个 D 、3个二.填空题 13. 化简381--=____________ ,324- =___________; 14. 如果2a b c x y z ===,则456456a b cx y z+++-= ; 15. 如图,梯形ABCD 中,DC ∥AB ,DC =3cm ,AB =6cm ,且MN ∥PQ ∥AB ,DM =MP =PA , 则MN = ,PQ = 。
2011年暑假八年级升九年级数学测试题(最新)

12011暑假八年级升九年级辅导班数学综合检测题 姓名__________ 得分____________一、选择题(本题共10小题,每小题4分,共40分)1.若分式112--x x 的值为0,则x 的值为( )A . 1B . -1C . ±1D .22.下列运算正确的是A .a 3•a 2=a 6B .(x 3)3=x 6C .x 5+x 5=x 10D .(-ab )5÷(-ab )2 =-a 3b 33. 计算1÷()2111mm m+∙--的结果果 A .-m 2-2m -1B .-m 2+2m -1C .m 2-2m -1D .m 2-14.任意给定一个非零实数,按下列程序计算,最后输出的结果是( )A.mB.1m +C.1m -D. 2m5.不等式组⎩⎨⎧≥+<-0302x x 的解集在数轴上正确..表示的是 6. 直角三角形两直角边边长分别为6cm 和8cm ,则连接这两条直角边中点的线段长为( ) A .10cm B .3cmC .4cmD .5cm2125a7.反比例函数y=xk(k>0)在第一象限内的图象如图,点M 是图象上一点,MP 垂直x 轴于点P ,如果△MOP 的面积为1,那么k 的值是( ) A .1 B . 2 C .4 D8.如图:已知,平行四边形ABCD 中,CE ⊥AB ,E 为垂足,如果∠A=125°,则∠BCE 的度数是( )A .25°B .55°C .35°D .30°9.汶川地震后,吉林电视台法制频道在端午节组织发起“绿丝带行动”,号召市民为四川受灾的人们祈福.人们将绿丝带剪成小段,并用别针将折叠好的绿丝带别在胸前,如图所示,绿丝带重叠部分形成的图形是( ) A 、正方形 B 、等腰梯形 C 、菱形 D 、矩形10.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分....a 的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )A 、1213a ≤≤B 、1215a ≤≤C 、512a ≤≤D 、513a ≤≤ 二、填空题(本题共4小题,每小题5分,共20分)11.2005年新版人民币中一角硬币的直径约为0.022m ,用科学记数法表示为 ____ m . 12..因式分解:22a b ab b ++=_____________________.13.某校规定学生期末数学总评成绩由三部分构成:卷面成绩、课外论文成绩、平日表现成绩(三部分所占比例如图),若方方的三部分得分依次是92、80、•84,则她这学期期末数学总评成绩是 _________ . 14.如图,直线L 1、L 2、L 3分别过正方形ABCD 的三个顶点A 、D 、C ,且相互平行,若L 1、L 2的距离为1,L 2、L 3的距离为2,则正方形的边长为 .AEBCD第8题图第7题图3三、解答题(第15、16、17、18小题每题10分;第19、20小题每题15分;第21小题20分,满分90分) 15.先化简,再求值:21211x x ---,其中x=-2 【解】16.如图,已知平行四边形ABCD 中,点E 为BC 边的中点, 连结DE 并延长DE 交AB 延长线于F . 求证:CD BF =.证明:17.如图,已知∠AOB,OA =OB ,点E 在OB 边上, 四边形AEBF 是矩形.请你只用无刻度...的直尺在图 中画出∠AOB 的平分线(请保留画图痕迹).18.如图,在平面直角坐标系中,网格中每一个 小正方形的边长为1个单位长度,(1) 请在所给的网格内画出以线段AB 、BC 为 边的菱形并写出点D 的坐标 ; (2)线段BC 的长为 ; (3)菱形ABCD 的面积为 .F19.一次学科测验,学生得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格.成绩达到9分为优秀.这次测验中甲乙两组学生成绩分布的条形统计图如下(1)请补充完成下面的成绩统计分析表:(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要高于甲组.请你给出三条支持乙组学生观点的理由.【解】20.江南生态食品加工厂收购了一批质量为10000千克的某种山货,根据市场需求对其进行粗加工和精加工处理,已知精加工的该种山货质量比粗加工的质量3倍还多2000千克.求粗加工的该种山货质量.【解】421.如图所示,在直角梯形ABCD中,AD//BC,∠A=90°,AB=12,BC=21,AD=16。
初中高中衔接数学试卷

一、选择题(每题5分,共50分)1. 下列函数中,是奇函数的是()A. y = x^2B. y = |x|C. y = x^3D. y = 2x2. 已知等差数列的前三项分别为2,5,8,则该数列的公差是()A. 1B. 2C. 3D. 43. 若直角三角形的两条直角边长分别为3和4,则斜边长为()A. 5B. 6C. 7D. 84. 已知一个圆的半径为r,则该圆的面积S与半径r的关系为()A. S = πr^2B. S = 2πrC. S = πrD. S = 4πr5. 若等比数列的前三项分别为2,6,18,则该数列的公比是()A. 2B. 3C. 4D. 66. 已知函数y = ax^2 + bx + c的图象开口向上,且顶点坐标为(-1, 4),则a的取值范围是()A. a > 0B. a < 0C. a = 0D. a ≥ 07. 已知等差数列的前n项和为S_n,若S_5 = 15,S_10 = 50,则该数列的首项a_1为()A. 1B. 2C. 3D. 48. 若函数y = kx + b的图象经过点A(1, 2),B(3, 4),则该函数的斜率k为()A. 1B. 2C. 3D. 49. 已知直角三角形的两条直角边长分别为3和4,斜边上的高为h,则h的取值范围是()A. 0 < h < 3B. 0 < h < 4C. 0 < h < 5D. 0 < h < 610. 若等比数列的前三项分别为2,6,18,则该数列的通项公式为()A. a_n = 2 3^(n-1)B. a_n = 2 2^(n-1)C. a_n = 6 3^(n-1)D. a_n = 6 2^(n-1)二、填空题(每题5分,共50分)1. 若函数y = ax^2 + bx + c的图象开口向上,且顶点坐标为(-1, 4),则a = _______,b = _______,c = _______。
2011年8-9月高一暑假数学作业答案(仅供参考)

仅供参考,有些题目没有练习一1. S←A+B+C S←S/32. 将设计好的算法清晰直观地描述出来3. 24. 15. 66. 3 88. 8π9. 75 21 3210. 当i×(i+2)=624时i和i+2的值24 2611. 412. 2013. 6314. 1 1.5 1.5 2练习二1. m=02. 1+1/2+1/1×2×3+…1/1×2×3×…×n3. 214. 9 115. 12 36. 47. 0.38. 6.429. 2550 250010. 12711. 略12. y=「100(1+1.2%)」n次方Read n=10y←「100(1+1.2%)」n次方Print y练习三1. 简单随机抽样2. 系统抽样3. 0.9 0.74.9.5~13.55. 0.36. 10%7. 95008. 169. 28 2810. 1011. 9012. 570013. 3014. 1)将总体中的个体从001至400编号2)在随机数表中任选一个数作为开始3)从选定的数开始按一定方向读下去,若得到的号码在编号中,则取出;若得到的号码不在编号中或前面已取出,则跳过,如此进行下去,直到取满为止4)根据选定的号码抽取样本15. 中200青120老8014. 略练习四1. 2平均数X-3平均数Y+12. (1)3. 2√34. (1)5. 99966. (2)7. 3+平均数X+1 9s28. 9.5 5.39. S2<S1<S310. 10,1111 2/512. 37,2013. 6014.(1)甲99.3 乙99.6(2)甲95%乙90%(3)s甲2=5.31 s乙2=8.64 甲稳定15.(1)甲86 乙(2)方差:甲43 乙86标准差:甲7 乙9(3)甲成绩均衡16.略练习五2. 2/33. 1/24. n/N5. 4/96. 11/217. 1/128. 16/45 28/45 17/45 44/459. 7 1/610. 14/1511. 1/27312. 1/213. 3/414. 1/36015. 3/10 3/5 7/1016. 3/5 12/2517. 7/45 7/15 8/1518. 1/2 9/1019. 400辆 7/10 3/4练习六1. 0.52. 1减√3/33. π/84. (2)5. 5/426. π/167. 0.6 0.88. 55/569. (AB AC BD BC) BD10. 1/25011. (3√3)/4π12. 1-π/1613. 2/314. π/415. 1/5 3/5 4/516. 6/7 1 1/217. 1/3 5/618. √3/3 5/819. 12/49练习七1. 105或15°2. 494. 等边三角形5. 30°6. 2√37. 2√37 或 2√138. 19. (2,2√3)10. 4√3/711. 212. 60°13. 30°14. 2 (根号下2 /2,根号下3 /2)15. 假设角C等于60°则ab=40由余弦定理得a+b=13所以三边分别为5 7 816. 1)cosC=cos2A=1/8 sinC=√63/8 sinA=√7/4 所以c/a=3/22)a=4 c=6由余弦定理得b=4或b=617. 见最后18. 1)sinB=12/13sinC=3/5sinA=sin(B+C)=sinBcosC+coSBsinC =33/652)b=20/11a S=1/2absinC=33/2所以BC=11/219.略练习八1. 60°2. √373. 1+√34. 2个5. 2个6. (10,20)7. 垂直于河岸8. 400/3米9. 7√2 /210. 100√311. 1012 2/3小时13. 6014. 2-√315——18 略练习九2. 153. -2/34. 55.55. 456. 60007. -28. 1-4n9. an=4n-210. -111. 1212. 7213. 1214. 415. 当n≥2时Sn-1=(n-1) 2+(n-1)-2=n2+2n+1+n-1-2=n2-n-2S n -S(n-1)=n2+n-2-n2+n+2=2nan=2n当n=1时Sn=0an=0,n=1an=2n,n≥216. d=116-112=4an≥450112+(n-1)4≥450(n-1)4≥338n-1≥84.5n≥85.5n属于正整数n=86an≤600112-(n-1)4≤600(n-1)4≤488n-1≤122n=123123-86+1=3817.S10=140 S奇=125 S偶=15S偶-S奇=n/2×d-110=5d d=-22S 10=5(a5+a6)140=5(a5+a5+d)28=2a5-2250=2a5a5=25所以a6=318. 1) S12=12(a1+a12)/2>06(a1+a12)>0a 3+a10>0a10>-12a3+7d>-12 7d>-24 d>-24/7S 13=13(a1+a13)/2<013/2(a1+a13)<0a 3+a11<0a 11<-12a3+8d<-12 8d<-24d<-3-24/7<d<-3 2)S1 最大因为d<0所以S1>S2>S3>…>S1219. 1)2bn =bnSn-Sn2S n 2-bnSn+2bn=0S n (Sn-bn)+2bn=0S n ×S(n-1)=2bnS n ×S(n-1)+(Sn-S(n-1))=01+2(1/S(n-1)-1/Sn)=01/Sn -1/S(n-1)=1/2Sn=2/n+1bn=-2/n(n+1)2) n(n+1)/2≤81n(n+1)≤162所以a81为第13行第3列a 79=a81/q方a 79=b13=-1/91q=2第13行为a79到a91所以S91-S79=-45练习十1. 202. 21/163. 1354. 105. 126. 27. 138. a(1+r)(2+r)…(7+r)9. 45/410. 13/1611. (2n-1)/(3n-1)13. 114. 7练习十一1. (-2,3)2. R3. m≤14. {x|X〈-2或x≥1}5. (0,1)6. 97. [0,1]8. X〉1或0<X<19. -7<a<2410.{x|x≤-6或x>2}11.(-1,2)12. x>1/a或x<1/b13. (-2,-1)∪(1,3)14. {x|x<b或x>-a}15. 略练习十二1. A≤G2. 1/43. 44. a≤-4或a≥45. 1/66. M≥N7. 38. 109. 110. (3,5)11. -212. 18√313. 1/214. 4 12 1615. 最大4+2b+c16. (ab+cd)(ac+bd)=a方bc+b方ad+c方ad+d方bc=bc(a方+d方)+ad(b方+c 方)≥2bc根号(a方×d方)+2ad根号(b方×c方)=4abcd当且仅当a=d,b=c时等号成立练习十三1. 62. -2<a<13. -2<a<14. 25. 16. 47. a≥98. k<-5/2 huo k>19. (-2,-1/3)10. 311. 412. ab≥913. 0<x<1/ai14. 9练习十四1. 242. √2/23. n的n次方4. 605. 496. -1/27. 2√28. 49. 410. 1511. -912. 2n13. x<b或x>-a14. 19下面是部分大题目答案,对照已写出的的题目内容在练习册上找到对应题目,是按顺序来的,从22页起/这是一个搜题网站,不会的题目可将第一句话输入找,找不到再用百度、google、搜搜、搜狗、搜狐等搜索引擎找请对应要找的科目设△ABC的内角A、B C所对的边分别为a、b、c,且acosB-bcosA=3/5/testdetail/156585/已知数列{a n}中,S n+1=4a n+2(n=1,2,3,…),a1=1/view/d16226e2524de518964b7dbd.html23题设a1、d为实数,首相为a1,公差为d的等差数列{a n}的前n项和为S n,满足S5S6+15=0 /z/q210022430.htm已知数列{a n}中,a1=1,a2=2,且a n+1=(1+q)a n-qa n-1(n≥2,q≠0)(1)设b n=a n+1-a n(n∈N*),证明{b n}是等比数列/testdetail/239824/关于x的不等式(x-2a)(x-a2-1)≤0与x2-3(a+1)x+2(3a+1)≤0(a∈r)/question/174469084.html已知函数f(x)=lg【(m2-1)x2+(m+1)x+1】,若f(x)的定义域为R,求实数m的取值范围/question/178738348.html不等式|x+3|- |x-1|≤a2-3a对任意实数x恒成立,求实数a的取值范围/z/q222372632.htm已知在区间【1/2,2】上,函数f(x)= x2+bx+c(b,c∈R)与g(x)= x2+x+1/x在同一点取得相同的最小值/testdetail/241883/某种汽车购车时的费用为10万元,每年的保险、养路、汽油费用共9千元/testdetail/217210/某海滨城市附近海面有一台风,据监测,当前台风中心位于城市的东南偏/testdetail/142849/某单位决定投资3200元建一仓库(长方形形状),高度恒定,它的后墙利用旧墙不花钱/testdetail/224295/某单位用2160万元购得一块空地,计划在该块地上建造一栋至少10层、每层2000平方米的楼房/testdetail/137608/已知函数f(x)=log a x(a>0,且a≠1)x∈(0,+∝)/z/q216627139.htm某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用12万元/testdetail/134979/如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分)/testdetail/239628/数列{a n}为等差数列,a n为正整数,其前n项和为S n,数列{b n}为等比数列/testdetail/137694/已知数列{a n}满足a1=0,a2=2,且对任意m、n∈N+都有a2m-1+a2n-1=2a m+n-1+2(m-n)2/view/f08c38f80242a8956bece4a7.html21题等比数列{a n}的前n项和为S n,已知对任意的n∈N+,点(n,S n),均在函数y=bx+r(b>0且b≠1,b,r均为常数)的图像上第一小题/view/e6d7381ca76e58fafab00334.html20题围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修)/testdetail/247510/。
初高中衔接型数学试题(8)及参考答案
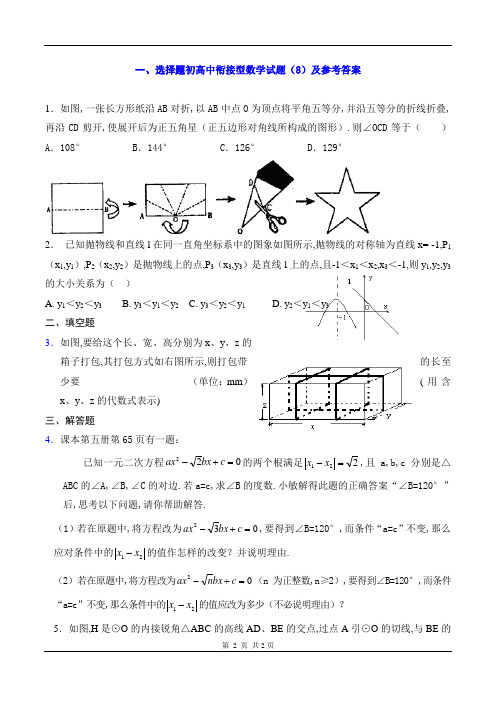
一、选择题初高中衔接型数学试题(8)及参考答案1.如图,一张长方形纸沿AB 对折,以AB 中点O 为顶点将平角五等分,并沿五等分的折线折叠,再沿CD 剪开,使展开后为正五角星(正五边形对角线所构成的图形).则∠OCD 等于( )A .108°B .144°C .126°D .129°2. 已知抛物线和直线l 在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x= -1,P 1(x 1,y 1),P 2(x 2,y 2)是抛物线上的点,P 3(x 3,y 3)是直线l 上的点,且-1<x 1<x 2,x 3<-1,则y 1,y 2,y 3的大小关系为( )A. y 1<y 2<y 3B. y 3<y 1<y 2C. y 3<y 2<y 1D. y 2<y 1<y 3二、填空题3.如图,要给这个长、宽、高分别为x 、y 、z 的箱子打包,其打包方式如右图所示,则打包带的长至少要____________________ (单位:mm )(用含x 、y 、z 的代数式表示)三、解答题4.课本第五册第65页有一题:已知一元二次方程022=+-c bx ax 的两个根满足221=-x x ,且a,b,c 分别是△ABC 的∠A,∠B,∠C 的对边.若a=c,求∠B 的度数.小敏解得此题的正确答案“∠B=120°”后,思考以下问题,请你帮助解答.(1)若在原题中,将方程改为032=+-c bx ax ,要得到∠B=120°,而条件“a=c ”不变,那么应对条件中的21x x -的值作怎样的改变?并说明理由.(2)若在原题中,将方程改为02=+-c bx n ax (n 为正整数,n ≥2),要得到∠B=120°,而条件“a=c ”不变,那么条件中的21x x -的值应改为多少(不必说明理由)?5.如图,H 是⊙O 的内接锐角△ABC 的高线AD 、BE 的交点,过点A 引⊙O 的切线,与BE 的延长线相交于点P,若AB 的长是关于x 的方程0)1cos (cos 363622=+-+-C C x x 的实数根。
2011年暑期初升高衔接结业考试

2010年暑期初升高衔接结业考试一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分)。
1. 已知全集U ={0,2,4,6,8,10},集合A ={2,4,6},B ={1},则(U A )∪B 等于 (A ){0,1,8,10} (B ){1,2,4,6} (C ){0,8,10} (D )Φ2. 下列关系中正确的个数为①0∈{0},②Φ{0},③{0,1}⊆{(0,1)},④{(a ,b )}={(b ,a )}(A )1 (B )2 (C )3 (D )4 3. 不等式(x +1)(2-x )>0的解集为(A ){|12}x x x <->或 (B ){|21}x x x <->或 (C ){|21}x x -<< (D ){|12}x x -<<4. 方程组⎩⎨⎧=-=+3242y x y x 的解集为(A ) {2,1} (B ) {1,2} (C ){(2,1)} (D )(2,1)5. 下列四个函数中,与y =x 表示同一函数的是A.y =(x )2B.y =33xC.y =2xD.y =xx 26. 函数f (x )=x 2+2(a -1)x +2在区间(-∞,4]上递减,则a 的取值范围是A.[-3,+∞]B.(-∞,-3)C.(-∞,5]D.[3,+∞)7. 下列对应中是集合A 到集合B 的映射的个数为①A ={1,3,5,7,9},B ={2,4,6,8,10},对应法则f :x →y = x +1,x ∈A ,y ∈B ; ②A ={x |00<x <900},B ={y |0<y <1},对应法则f :x →y = sinx ,x ∈A ,y ∈B ; ③A ={x |x ∈R },B ={y |y ≥0},对应法则f :x →y = x 2,x ∈A ,y ∈B .(A )0 (B )1 (C )2 (D )38.已知g (x )=1-2x, f [g (x )]=)0(122≠-x xx ,则f (21)等于 ( )A .1B .3C .15D .30 9.设函数f (x )是(-∞,+∞)上的减函数,又若a ∈R ,则( )A .f (a )>f (2a )B .f (a 2)<f (a)C .f (a 2+a )<f (a )D .f (a 2+1)<f (a )10、定义域为R 的函数f(x)是偶函数,且在[0,5]上是增函数,在[5,+∞]上是减函数,又f(5)=2,则函数f(x) ( )A .在[-5,0]上是增函数且有最大值2B .在[-5,0]上是减函数且有最大值2C .在[-5,0]上是增函数且有最小值2D .在[-5,0]上是减函数且有最小值2 二、填空题(本大题共5小题,每小题5分,共25分)11..若1)(2++=x x x f ,则)2(f = _________;=)1(af _________;=-)(b a f _________;=))2((f f _________.12.函数2y x =13. 已知函数f (n )=⎩⎨⎧<+≥-),10)](5([),10(3n n f f n n 其中n ∈N ,则f (8) =14. 在物理实验课上,小明用弹簧称将铁块A 悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧称的读数y (单位N )与铁块被提起的高度x (单位cm )之间的函数关系的大致图象是_________________15、下列几个命题:①函数x x f 1)(=在定义域内为单调减函数;②函数y =是偶函数,但不是奇函数;③函数()f x 的值域是[2,2]-,则函数(1)f x +的值域为[3,1]-;④函数()f x 的定义域为]4,2[-,则函数)43(-x f 的定义域是]8,10[-. 其中不正确的命题的序号为__________三、解答题:(解答应写出文字说明、证明过程或演算步骤)16. (本题满分13分) 设全集U =R ,集合{}{}{}13,04,A x x B x x C x x a =-≤≤=<<=<。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年暑假生活初高中衔接内容考试数 学 试 题命题人:南安一中 黄荣祥 2011-7-31本试卷第I 卷(选择题)和第II 卷(非选择题)两部分,满分150分;答卷时间120分钟。
注意事项:1.答题前,考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名。
考生要认真 核对答题卡上粘贴的条形码的“准考证号,姓名”与考生本人准考证号,姓名是否一致。
2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动, 用橡皮擦干净后,再选涂其他答案标号,第Ⅱ卷用0.5毫米黑色签字笔在答题卡上书写作答, 在试题卷上作答,答案无效。
3.考试结束,考生必须将试题卷和答题卡一并交回。
第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中, 只有一个项是符合题目要求的。
1.已知反比例函数y =xa(a ≠0)的图象,在每一象限内,y 的值随x 值的增大而减少,则一次函数y =-a x +a 的图象不经过( ) A .第一象限 B .第二象限 C. 第三象限 D . 第四象限2. 已知二次函数y =ax 2+bx +c (a ≠0)的图象如图,则下列结论中正确的是()A .a >0B .当x >1时,y 随x 的增大而增大C .c <0D .3是方程ax 2+bx +c =0的一个根 3. 不等式112x <的解集是( ) A .(,2)-∞ B .(,2)-∞⋃(2,)+∞ C.(0,2) D .(2,)+∞4. 已知一元二次方程20(0)ax bx c a ++= >的两个实数根1x 、2x 满足124x x +=和321=⋅x x ,那么二次函数2(0)y ax bx c a =++ >的图象有可能是( )A .B .C .D .5.(2011福建高考题)若关于x 的方程x 2+mx+1 =0有两个不相等的实数根,则实数m 的 取值范围是( )A .(-1,1)B .(-2,2)C .(-∞,-2)∪(2,+∞)D .(-∞,-1)∪(1,+∞) 6. 已知关于x 的方程x 2+bx +a =0有一个根是-a (a≠0),则a -b 的值为( ) A .-1 B .0 C .1 D .27. 在R 上定义运算⊙:a ⊙b =ab +2a +b ,则满足x ⊙(x -2)<0的实数x 的取值范围为( ) A .(0,2) B .(-∞,-2)∪(1,+∞) C .(-2,1) D .(-1,2) 8. 若a <b <0,则下列不等式成立的是( ) A .b a 11< B .1>b a C .1<baD .ab <1 9. 关于x 的不等式02<++b ax x 的解集为}21|{<<x x ,则不等式012>++bx ax 的解为( )A .)31,1(- B .)1,31(- C .),1()31,(+∞⋃--∞ D .),31()1,(+∞⋃--∞ 10.方程xx 212=+解的情况是( ) A .仅有一正根 B .有两正根 C .有一正根和一负根 D .无解 11. 已知函数y=ax 2+bx +c (a ≠0)的图象经过点(-1,3)和(1,1)两点,若0<c <1,则a 的取值范围是( )A .(1,3)B .(1,2)C .[2,3)D .[1,3]12. 已知函数()()()()22113513x x y x x ⎧--⎪=⎨--⎪⎩≤>,则使y=k 成立的x 值恰好有三个,则k 的值为( )A .0B .1C .2D .3第II 卷(非选择题 共90分)注意事项:用0.5毫米黑色墨水签字笔在答题卡上书写作答,在试题卷上作答,答案无效。
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上。
13.分解因式:6x ²-x -1= .14.若210ax bx +-<的解集为{12}x x -<<,则a = ,b = .15. 一个函数的图象如图所示,给出以下结论: ①当0x =时,函数值最大;②当02x <<时,函数y 随x 的增大而减小; ③存在001x <<,当0x x =时,函数值为0. 其中正确的结论是 (填写序号).16. 已知关于x 的方程2(3)0x ax a -++=有两个根,且一个根比3-小,另一个根比3-大,则实数a 的取值范围是_______ _____.三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或验算步骤.17.(本题满分12分)记函数f (x )=132++-x x 的定义域为A ,求A .18.(本题满分12分)已知2243,30()33,0165,16x x x f x x x x x x ⎧++-≤<⎪=-+≤<⎨⎪-+-≤≤⎩.(I)画出函数的草图;(II)根据函数图像,求函数的单调区间和最值.19.(本题满分12分)已知关于x 的方程x 2-2(k -1)x+k 2=0有两个实数根x 1,x 2. (I)求k 的取值范围;(II)若12121x x x x +=-,求k 的值.20.(本题满分12分)解关于x 的不等式(2)(2)0x ax -->.21.(本题满分12分)如果函数f x x ()()=-+112定义在区间[]t t ,+1上,求f x ()的最小值.22.(本题满分14分)已知函数f (x )=ax 2+x -a ,a ∈R . (I)若函数f (x )有最大值178,求实数a 的值; (II)解不等式f (x )>1(a ∈R ).2011年暑假生活初高中衔接内容考试数学试题参考答案审核人:肖泽中 2011-7-31 一、选择题 1-6 C D B C C A 7-12 C B B A B D 二、填空题13. (2x -1)(3x +1) 14. 11,22a b ==-.15. ②③ 16. (3,2][6,)--⋃∞.[解析] 解:令2()(3)f x x ax a =-++,则由题知2()4(3)032(3)4120a a a f a ⎧∆=--+≥⎪-⎪->-⎨⎪-=+>⎪⎩ ∴实数a 的取值范围是(3,2][6,)--⋃∞. 三、解答题 17.解:由2-13++x x ≥0, 得11+-x x ≥0, 它等价于(1)(1)0,10.x x x -+≥⎧⎨+≠⎩即x <-1或x ≥1∴A=(-∞,-1)∪[1,+ ∞] 18.略19.解:(1)依题意,得0≥即22[2(1)]40k k ---≥,解得12k ≤.(2)解法一:依题意,得212122(1),x x k x x k +=-=.以下分两种情况讨论:①当120x x +≥时,则有12121x x x x +=-,即22(1)1k k -=-解得121k k == ∵12k ≤∴121k k ==不合题意,舍去②120x x +<时,则有()12121x x x x +=--,即()22(1)1k k -=-- 解得121,3k k ==- ∵12k ≤,∴ 3.k =- 综合①、②可知k=﹣3.解法二:依题意可知122(1)x x k +=-.由(1)可知12k ≤∴2(1)0k -<,即120x x +< ∴22(1)1k k --=-解得121,3k k ==- ∵12k ≤,∴ 3.k =- 20. 【点拨】 不等式的解及其结构与a 相关,所以必须分类讨论. 【解析】 1° 当0a =时,原不等式化为20x -<,其解集为{2}x x <; 2°当0a <时,由于22a >,原不等式化为2(2)()0x x a --<,解集为2{|2}x x a << 3°当01a <<时,由于22a <,原不等式化为2(2)()0x x a -->,解集为{2x x <或2}x a> 4°当1a =时,原不等式化为2(2)0x ->,解集为{2}x x ≠; 5°当1a >时,由于22a >,原不等式化为2(2)()0x x a-->, 其解集为2{|x x a<或2}x >. 综上所述,原不等式的解集为:1° 当0a =时,其解集为{2}x x <; 2°当0a <时,解集为2{|2}x x a<< 3°当01a <<时,解集为{2x x <或2}x a>; 4°当1a =时,解集为{2}x x ≠;5°当1a >时,其解集为2{|2}x x x a<>或.21. 解:函数f x x ()()=-+112,其对称轴方程为x =1,顶点坐标为(1,1),图象开口向上。
如图6所示,若顶点横坐标在区间[]t t ,+1左侧时,有1<t 。
当x t =时,函数取得最小值f x f t t ()()()min ==-+112。
如图7所示,若顶点横坐标在区间[]t t ,+1上时,有t t ≤≤+11, 即01≤≤t 。
当x =1时,函数取得最小值f x f ()()min ==11。
如图8所示,若顶点横坐标在区间[]t t ,+1右侧时,有t +<11,即t <0。
当x t =+1时,函数取得最小值f x f t t ()()min =+=+112综上讨论,f x t t t t t ()(),,min=-+>≤≤+<⎧⎨⎪⎩⎪1111011022 22.【点评】讨论时分类要合理,要注意不重不漏.解:(1)a ≥0时不合题意,f (x )=a ⎝⎛⎭⎫x +12a 2-1+4a24a , 当a <0时,f (x )有最大值,且-1+4a 24a =178,解得a =-2或a =-18.(2)f (x )>1,即ax 2+x -a >1, (x -1)(ax +a +1)>0,①当a =0时,解集为{x |x >1}; ②当a >0时,(x -1)⎝⎛⎭⎫x +1+1a >0, 解集为{x |x >1或x <-1-1a};③当a =-12时,(x -1)2<0,解集为∅;④当-12<a <0时,(x -1)⎝⎛⎭⎫x +1+1a <0, 解集为{x |1<x <-1-1a};⑤当a <-12时,(x -1)⎝⎛⎭⎫x +1+1a <0, 解集为{x |-1-1a <x <1}.。
