理论力学碰撞习题及答案
高中生碰撞测试题及答案

高中生碰撞测试题及答案一、选择题(每题2分,共20分)1. 根据牛顿第一定律,物体在不受外力作用时将保持()状态。
A. 静止B. 匀速直线运动C. 静止或匀速直线运动D. 变速运动答案:C2. 一个物体的动量是()。
A. 物体的质量与速度的乘积B. 物体的质量与加速度的乘积C. 物体的质量与位移的乘积D. 物体的质量与力的乘积答案:A3. 以下哪项是描述物体运动状态的物理量?()A. 质量B. 速度C. 密度D. 温度答案:B4. 一个物体从静止开始做匀加速直线运动,若初速度为零,加速度为a,则在时间t内,物体的位移s与时间t的关系是()。
A. s = 0.5at^2B. s = at^2C. s = atD. s = 2at答案:A5. 根据牛顿第二定律,物体的加速度与作用力成正比,与物体的质量成反比。
若作用力增大到原来的两倍,物体的质量不变,则物体的加速度将()。
A. 增大到原来的两倍B. 减小到原来的一半C. 保持不变D. 无法确定答案:A6. 一个物体在水平面上做匀速直线运动,若摩擦力增大,则物体的运动状态将()。
A. 保持不变B. 速度增大C. 速度减小D. 停止运动答案:C7. 根据能量守恒定律,一个物体在没有外力作用的情况下,其机械能()。
A. 会增加B. 会减少C. 保持不变D. 无法确定答案:C8. 一个物体在竖直方向上做自由落体运动,其加速度是()。
A. 向上的B. 向下的C. 为零D. 无法确定答案:B9. 一个物体在水平面上做匀速圆周运动,其向心力的方向是()。
A. 指向圆心B. 指向圆外C. 与速度方向相同D. 与速度方向相反答案:A10. 根据牛顿第三定律,作用力和反作用力的大小()。
A. 相等B. 不相等C. 相等但方向相反D. 无法确定答案:C二、填空题(每题2分,共20分)1. 牛顿第一定律也被称为______定律。
答案:惯性2. 物体的动量等于其质量与______的乘积。
力学试题动量守恒和碰撞

力学试题动量守恒和碰撞力学试题:动量守恒和碰撞一、引言力学是物理学的一个重要分支,主要研究物体的运动规律和相互作用。
其中,动量守恒和碰撞是力学中的基础概念,对于解决与物体运动和相互作用相关的问题具有重要作用。
本文将通过几个力学试题,探讨动量守恒和碰撞的相关原理和应用。
二、题目一:弹性碰撞问题题目描述:一个质量为m1的小球以速度v1与一个质量为m2的小球以速度v2在平直的光滑水平面上发生完全弹性碰撞,求发生碰撞后两个小球的速度。
解析:根据动量守恒定律,碰撞前后的动量总和保持不变。
设碰撞前两个小球的动量分别为p1和p2,碰撞后为p1'和p2',则有:m1v1 + m2v2 = m1p1' + m2p2' (1)根据弹性碰撞的特性,碰撞后小球的动量满足以下条件:m1v1 + m2v2 = m1v1' + m2v2' (2)结合方程(1)和方程(2),可以解得碰撞后两个小球的速度v1'和v2'。
三、题目二:完全非弹性碰撞问题题目描述:一个质量为m1的小球以速度v1与一个质量为m2的小球以速度v2在光滑平面上发生完全非弹性碰撞,两小球粘连在一起运动,求粘连后的速度。
解析:完全非弹性碰撞意味着碰撞后两个小球将粘连在一起,视为一个整体运动。
根据动量守恒定律:m1v1 + m2v2 = (m1 + m2)V其中,V表示粘连后小球组成整体的速度。
根据上述等式解得粘连后的速度V。
四、题目三:动量守恒与角动量守恒的关系题目描述:在一个封闭系统中,一个物体撞击另一个物体,碰撞时既有动量守恒又有角动量守恒,请阐述两者之间的关系。
解析:动量守恒和角动量守恒是力学中两个重要的守恒定律。
在封闭系统中,如果一个物体对另一个物体施加一个作用力,这个作用力同时改变了两个物体的动量和角动量,但总的动量和总的角动量保持不变。
这是因为力矩的产生会导致角动量的变化。
五、总结通过以上力学试题的分析,我们深入理解了动量守恒和碰撞的原理。
动量守恒定律和碰撞问题(解析版)

动量守恒定律和碰撞问题特训目标特训内容目标1 动量守恒的条件(1T—4T)目标2 弹性碰撞动碰静模型(5T—8T)目标3 弹性碰撞动碰动模型(9T—12T)目标4 完全非弹性碰撞模型(13T—16T)目标5 类碰撞问题(17T—20T)【特训典例】一、动量守恒的条件1.在光滑水平面上,A、B两小车中间有一轻弹簧(弹簧不与小车相连),如图所示,用手抓住小车并将弹簧压缩后使小车处于静止状态,将小车及弹簧看成一个系统,下列说法中不正确的是()A.两手同时放开后,系统总动量始终为零B.先放开左手,再放开右手后,动量不守恒C.先放开左手,后放开右手,总动量向左D.无论何时放手,两手放开后,系统总动量都保持不变【答案】B【详解】A.若两手同时放开A、B两小车,系统所受合外力为零,系统动量守恒,由于系统初动量为零,则系统总动量为零,A正确,不符合题意;BC.先放开左手,系统所受合外力向左,系统所受合外力的冲量向左,再放开右手,系统总动量向左,因为两手放开后,系统所受合外力为零,系统动量守恒,B错误,符合题意,C正确,不符合题意;D.无论何时放手,两手放开后,系统所受合外力为零,系统动量守恒,系统总动量保持不变,D正确,不符合题意。
故选B。
2.如图所示,A、B两物体的质量之比A BM M=,原来静止在平板小车C上,A、B间有一根被压缩的:1:2弹簧,地面光滑。
当弹簧突然释放后,A、B两物体被反向弹开,则A、B两物体滑行过程中()A .若A 、B 与平板车上表面间的动摩擦因数相同,A 、B 组成的系统动量守恒B .若A 、B 与平板车上表面间的动摩擦因数之比为2:1,A 、B 组成的系统动量守恒,机械能守恒C .若A 、B 所受的动摩擦力大小相等,A 、B 组成的系统动量守恒D .若A 、B 所受的动摩擦力大小不相等,则A 、B 、C 组成的系统动量不守恒 【答案】C【详解】A .若A 、B 与平板车上表面间的动摩擦因数相同,则有A B 12M g M g µµ=由于A 、B 受到的滑动摩擦力大小不相等,可知A 、B 组成的系统受到的合外力不为零,A 、B 组成的系统动量不守恒,故A 错误; B .若A 、B 与平板车上表面间的动摩擦因数之比为2:1,则有A A B B M g M g µµ=由于A 、B 受到的滑动摩擦力大小相等,可知A 、B 组成的系统受到的合外力为零,A 、B 组成的系统动量守恒,但A 、B 的动能都在增加,A 、B 组成的系统机械能增加,故B 错误;C .若A 、B 所受的动摩擦力大小相等,可知A 、B 组成的系统受到的合外力为零,A 、B 组成的系统动量守恒,故C 正确;D .若A 、B 所受的动摩擦力大小不相等,但摩擦力是A 、B 、C 组成的系统的内力,A 、B 、C 组成的系统受到的合外力一定为零,A 、B 、C 组成的系统动量一定守恒,故D 错误。
碰撞与动量守恒经典例题解析

动量知识点应用一、应用动量解释判断现象的例题解析【例1】 如图6-4所示,两小球质量均为m ,A 和B 是完全相同两根绳.若缓慢地竖直拉②球,则绳____先断;若突然快速竖直下拉②球,则绳____先断.解:第一空应填:A ;第二空应填:B .说明 第一空较容易填写,第二空要应用动量定理解释的物理现象.由其表达式F·Δt=Δp 可知.当=∆p 恒定时,tF ∆∝1,即作用时间越短,其相互作用力就越大。
这便是第二种情况,B 绳先断的原因.而此种情况为什么A 绳没先断呢,原因是①球尽管受到B 球较大力的作用,但是作用时间极短(Δt→0),故①球仍保持静止(Δp=0),因此A 绳的形变与原来状态相同,自然不会断.【例2】 质量为1kg 的物体原来静止,受到质量为2kg 的、速度是1m /s 的运动物体碰撞,碰后两物体的总动能不可能是 [ ]A .1JB .43JC .32JD .31J 答案:D .说明 两物体碰撞过程中动量一定守恒,而碰撞后总机械能最大值应与碰撞前相同(发生弹性碰撞,应为1J );最小值应是完全非弹性碰撞时碰撞后系统总的机械能,其值应为:①m 1v 1+m 2v 2=(m 1+m 2)v ②可见,两物体碰撞后总能量为所以,选D项.【例3】如图6-5所示,光滑平板小车质量为M,以速度v匀速运动,质量为m的物块相对静止地放在小车前端后,小车最终速度为[]答案:B.说明当系统所受合外力为零时,系统动量守恒.系统中各物体间的作用力的冲量将使各个物体的动量发生变化,而不能影响系统总的动量.从题中可知小车和物块间水平方向上无力作用,故小车动量不变,保持原来的速度.如认为物块在小车上,小车和物块的动量就要改变,速度就要改变,这是很危险的错误.一定要深刻理解动量定理以及与动量守恒定律关系.二、动量定理应用问题的例题解析【例4】小球质量为m=0.5kg,以v=20m/s的速度垂直打在水平地面上,经Δt=0.2s又竖直弹起,离地速度为v′=10m/s.小球对地面的平均打击力多大?解以小球为研究对象,动量变化时,受力情况如图6-6所示.选取竖直向上为正方向,根据动量定理:F′击Δt-mgΔt=mv′-(-mv)【例5】如图6-7所示,重物质量为m,滑块质量为M,与桌面间动摩擦因数为μ,m由静止释放经t秒落地.绳子的拉力多大?解不论M或m都满足动量定理.以m为研究对象,受力情况如图6-7中所示,以运动方向为正方向,则mg·t-T·t=mv①以M为研究对象,受力情况如图6-7所示,则T·t-μMg·t=Mv②①+②式得mg·t-μMg·t=(M+m)v③由③式得将v值代入①式得说明上面两例意在说明动量定理的解题步骤的可行性:不论单一体或是“连接体”,只要满足动量定理就按动量定理解题步骤处理.从例5中③式可见,“整体法”的应用:将两个物体视为一整体,其方程的建立同样按动量定理解题步骤.注意其内力不做分析.【例6】质量为m A=1kg的木块A和质量为m B=2kg的木块B靠在一起放在光滑水平面上,如图6-8所示.今有一子弹以某一速度射入木块,子弹穿过A木块需时间t A=0.1s,穿过B木块需时间t B=0.2s.若子弹在木块中所受阻力恒为f=3000N,问(1)在0.1s内,木块A对木块B的推力多大?(2)木块B最终速度多大?解(1)子弹刚打入木块A时,木块B只受A对其的推力FAB,根据动量定理,有F AB·t A=m B v A①以A和B两木块为一整体研究,只受子弹作用力f′,则同样根据动量定理,有f′·t A=(m A+m B)v A②由①、②两式解得F AB=2000(N)v A=100(m/s)(2)当子弹由A木块穿出进入B木块时,B木块只受子弹作用力f′作用.则根据动量定理,有:f′·t B= m B v B - m B v A三、动量守恒定律应用问题的例题解析【例7】如图6-9所示,在光滑水平面上停着A、B两小车,质量分别为3kg与2kg,在B车右端有一质量为1kg的物体C,C与B之间的动摩擦因数为0.3,A、B之间用质量不计的细线连接,当使A向右以2m/s速度运动时线突然被拉紧(时间极短),问(1)线拉紧瞬时,B物体的速度多大?(2)C物体速度多大?解(1)以A、B为系统研究,系统动量守恒:m A v A=(m A+m B)v B(2)以A、B、C为系统研究,动量守恒,有m A v A=(m A+m B+m C)v C【例8】质量为M的气球上有一质量为m的人,气球与人共同静止在离地面高H的空气中.如果从气球上放下一条不计质量的细绳,以使人能沿绳安全地滑到地面.绳子至少需要多长?解设需绳长为L,人下滑过程,以气球与人为系统,在竖直方向上动量守恒,人与气球初、末态位置如图6-10所示.可建立方程:说明(1)例7中,A和B相互作用时,尽管B物体受到C物体的摩擦力作用,但作用时间极短,对B物体动量变化无影响.因此,A和B总动量不变.(2)例7在求C物体速度时,A、B、C三物体为系统,摩擦力是内力,不影响系统动量守恒.(3)例8主要强调,如果系统动量守恒,其各个物体的速度可用平均速度代替.计算时必须以地面为参照物.四、动量、机械能、碰撞问题的例题解析【例9】质量为m1的小球以速度v1在光滑平面上向静止在该平面上的、质量为m2的小球碰去(如图6-11所示),求m1和m2发生正碰过程中最大弹性势能.解两球相碰过程中,弹性势能最大时两球间距离最小,速度相同.以m1和m2为系统,水平方向动量守恒,选v1方向为正方向,则根据动量守恒定律,有m1v1=(m1+m2)v①系统机械能守恒:②由①、②式得:解得:【例10】质量为M=16kg的平板车B原来静止在光滑水平面上.另一个质量为m=4kg的物体A以v0=5.0m/s的水平初速度滑上平板车的一端,如图6-12所示.若物体A与平板车间动摩擦因数为μ=0.5,g=10m/s2.要使A不能从B 的另一端落下,B车至少应多长?解当物体A与小车速度相同时,A物体刚好运动至小车最右端,此种情况小车长L为最短长度,则mv0=(M+m)v①由于物体A与小车间有摩擦,因此系统机械能不守恒,发生能量转化,故②由①、②式解得(过程略)L=2(m)【例11】质量为m的滑块与质量为M(M>m)的长木板间的动摩擦因数为μ,滑块与木板一起以v0的速度在光滑的水平面上向右滑行,如图6-13所示.木板到达墙角与墙发生碰撞,碰撞后长木板以原速率弹回,设木板足够长.长木板碰墙后到滑块相对木板静止的整个过程中,滑块(相对地)通过的路程多长?解由题意可知,滑块运动过程是:M与墙相碰后以v0返回向左滑行,而滑块仍以v0向右滑行(因为碰撞时间很短,不能改变m的运动状态).由于摩擦力冲量作用使m速度变为零,然后m随M向左运动,最后相对M静止.因此滑块经过的路程是两个过程滑块经过位移的和(设s1为第一过程位移;s2为第二过程位移).由以上四个式解得【例12】 质量为M ,长为L 的木板上放一滑块m ,今将木板放在光滑的水平面上,用恒力F 推木板(如图6-14所示),滑块m 与木板间动摩擦因数为μ,m 离开木板时速度多大?解 以滑块为研究对象,根据动能定理,有221)(m M mv L s mg =-μ ① 以木板为研究对象,根据动能定理,有221M M M Mv mgs Fs =-μ ② 分别以m 和M 为研究对象,应用动量定理,有μmgt =mv m ③F·t - μmgt =Mv M ④由①、②、③、④联立解得说明 在研究系统动量守恒的同时,要兼顾系统机械能是否守恒.如果两个守恒同时成立,则列方程组:如果动量守恒,机械能不守恒,则列方程组:方程Wf=ΔE中Wf为系统克服内摩擦力所做功.计算时要注意:此功等于摩擦力乘以两物体间相对位移.如果两个守恒定律均不成立,则列方程组:【例13】如图6-15所示,子弹质量为m,以速度v m射向静止在光滑水平面上的质量为M的木块,子弹在木块中运动所受阻力恒为f.欲使子弹穿不出木块,木块的厚度至少多大?解法一设子弹刚好穿不出时木块厚为L,子弹刚好穿不出末速度应与木块相同,则mv m=(M+m)v①②解法二子弹穿不出木块,子弹与木块有共同速度,如图6-15所示,则L=s m - s M①以木块为研究对象,根据动能定理,有②以子弹为研究对象,根据动能定理,有③以子弹和木块为系统研究,动量守恒:mv m=(M+m)v④由①、②、③、④式解得(过程略)说明此题为成题,这里只说明子弹与木块相互作用过程中能量间转化情况.解法二中,③式表示子弹克服阻力做功而动能减少——动能定理.由解法一中②式得即可见,子弹机械能(动能)减少,一部分增加了木块的动能,另一部分转化为系统内能(ΔE内=fL).系统克服阻力做功完成了系统机械能向系统内能的转化.系统克服阻力做功的大小等于系统内能的增加(功能原理).另外,从解法二中可以看到:摩擦力(或介质阻力)可以做正功,也可以做负功.但是摩擦力(或介质阻力)对系统所做功必然是负功.。
碰撞练习题

一、选择题1. 两个物体发生碰撞,下列哪种情况下,碰撞是弹性碰撞?A. 两个物体的速度都变为零B. 两个物体的动能守恒C. 两个物体碰撞后仍保持相对静止D. 两个物体的速度方向发生改变但大小不变2. 下列哪个公式描述了动量守恒定律?A. F = maB. p = mvC. E = mc²D. Δp = FΔt3. 两个质量分别为m1和m2的物体发生完全非弹性碰撞,碰撞后它们的共同速度为v,则碰撞前两物体的速度分别为:A. v1 = m1v, v2 = m2vB. v1 = m2v, v2 = m1vC. v1 = (m1 + m2)v / m1, v2 = (m1 + m2)v / m2D. v1 = (m1 + m2)v / m2, v2 = (m1 + m2)v / m14. 下列哪种情况下,碰撞过程中动能不守恒?A. 弹性碰撞B. 完全非弹性碰撞C. 弹性碰撞和非弹性碰撞D. 碰撞过程中没有外力作用5. 两个质量分别为m1和m2的物体发生碰撞,碰撞前速度分别为v1和v2,碰撞后速度分别为v1'和v2',则动量守恒定律可以表示为:A. m1v1 + m2v2 = m1v1' + m2v2'B. m1v1 m2v2 = m1v1' m2v2'C. m1v1 + m2v2 = m1v1' m2v2'D. m1v1 m2v2 = m1v1' + m2v2'二、填空题1. 碰撞过程中,动量守恒定律的数学表达式为:______。
2. 弹性碰撞中,动能守恒定律的数学表达式为:______。
3. 完全非弹性碰撞中,两个物体的共同速度为______。
4. 碰撞过程中,如果两个物体的质量相等,则它们的速度变化量______。
5. 碰撞过程中,如果两个物体的速度方向相反,则它们的动量大小______。
三、计算题1. 两个质量分别为2kg和3kg的物体发生弹性碰撞,碰撞前速度分别为5m/s和3m/s,求碰撞后两个物体的速度。
碰撞问题练习题

碰撞问题练习题碰撞问题一直是力学中的重要内容,本文将提供一些碰撞问题的练习题,帮助读者巩固力学知识并提升解题能力。
1. 弹性碰撞问题:有两个质量相同的小球,质量分别为m,初始速度分别为v1和v2。
它们进行完全弹性碰撞后,两球的最终速度是多少?解析:在完全弹性碰撞中,动量和动能守恒。
设最终速度分别为v1'和v2',则根据动量守恒定律有m*v1 + m*v2 = m*v1' + m*v2';根据动能守恒定律有1/2*m*v1^2 + 1/2*m*v2^2 = 1/2*m*v1'^2 +1/2*m*v2'^2。
通过解这两个方程组,可以得到v1'和v2'的值。
2. 完全非弹性碰撞问题:有两个质量分别为m1和m2的小球,初始速度分别为v1和v2。
它们进行完全非弹性碰撞后,两球的最终速度是多少?解析:在完全非弹性碰撞中,动量守恒,但动能不守恒。
设最终速度为v,则根据动量守恒定律有m1*v1 + m2*v2 = (m1 + m2)*v。
通过解这个方程可以得到v的值。
3. 壁面弹性碰撞问题:有一个质量为m的小球以速度v与垂直于地面的墙壁碰撞,碰撞后小球以速度v'反弹。
如果碰撞时间为Δt,求墙壁对小球的平均冲量。
解析:平均冲量可以通过动量变化量来计算。
设小球碰撞前后的动量分别为p和p',则平均冲量为Δp/Δt = (p' - p)/Δt = (mv' - mv)/Δt。
4. 碰撞系数问题:弹性碰撞中,定义碰撞系数e为速度反向后的物体速度与碰撞前速度的比值。
设两个小球质量分别为m1和m2,初始速度分别为v1和v2,在碰撞过程中,小球1的速度反向后变为v1',小球2的速度反向后变为v2'。
求碰撞系数e。
解析:碰撞系数e可以通过速度变化量来计算。
根据动量守恒定律和定义可以得到mv1 - mv1' = -m1v1' - m2v2',mv2 - mv2' = -m1v1' -m2v2'。
弹性碰撞和非弹性碰撞(同步练习)(含答案解析) (4)
1.5课 弹性碰撞和非弹性碰撞解题要点梳理:碰撞三原则1.系统动量守恒原则:碰撞前后系统的总动量守恒:22112211v m v m v m v m '+'=+; 2.动能不增加原则:碰撞后系统的总动能小于或等于碰撞前系统的总动能,即系统的总动能不增加:22221122221121212121v m v m v m v m '+'≥+; 3.速度要合理原则:(1)若碰后两物体同向运动,则碰撞后后面物体的速度一定小于或等于前面物体的速度(否则碰撞没有结束,还要发生碰撞):2121v v v v '≤'> (2)碰前两物体相向运动,碰后两物体的运动方向不可能都不改变。
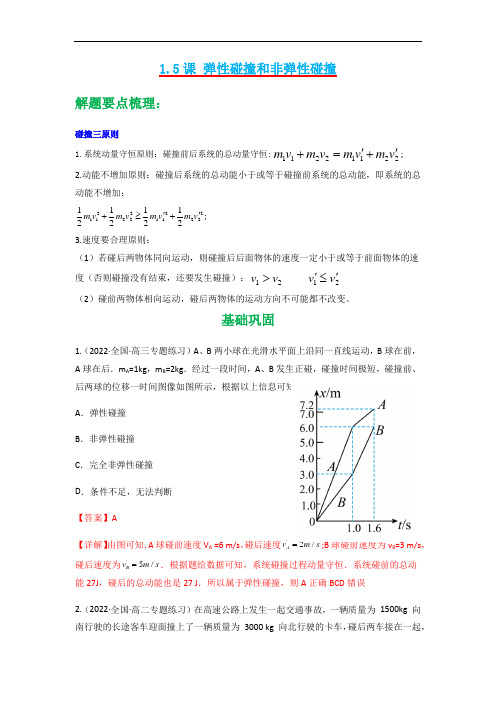
基础巩固1.(2022·全国·高三专题练习)A 、B 两小球在光滑水平面上沿同一直线运动,B 球在前,A 球在后.m A =1kg ,m B =2kg .经过一段时间,A 、B 发生正碰,碰撞时间极短,碰撞前、后两球的位移一时间图像如图所示,根据以上信息可知碰撞类型属于( ) A .弹性碰撞 B .非弹性碰撞 C .完全非弹性碰撞 D .条件不足,无法判断 【答案】A【详解】由图可知.A 球碰前速度V A =6 m/s ,碰后速度'2/Av m s =;B 球碰前速度为v B =3 m/s ,碰后速度为'5/B v m s =.根据题给数据可知,系统碰撞过程动量守恒.系统碰前的总动能27J ,碰后的总动能也是27 J .所以属于弹性碰撞,则A 正确BCD 错误2.(2022·全国·高二专题练习)在高速公路上发生一起交通事故,一辆质量为 1500kg 向南行驶的长途客车迎面撞上了一辆质量为 3000 kg 向北行驶的卡车,碰后两车接在一起,并向南滑行了一段距离后停止。
根据测速仪的测定,长途客车碰前以 20 m/s 的速度行驶,由此可判断卡车碰前的行驶速率为( ) A .小于 10 m/sB .大于 10 m/s 小于 20m/sC .大于 20 m/s 小于30m/sD .大于 30 m/s 小于 40 m/s【答案】A【详解】长途客车与卡车发生碰撞,系统内力远大于外力,碰撞过程系统动量守恒,选择向南为正方向,根据动量守恒定律,有12)mv Mv m M v -=+(,因而120mv Mv -> 代入数据,可得12150020m/s=10m/s 3000mv v M ⨯=<,故选A 。
物理碰撞试题及答案

物理碰撞试题及答案1. 两个质量分别为 \( m_1 \) 和 \( m_2 \) 的小球在光滑水平面上发生完全弹性碰撞,碰撞前 \( m_1 \) 的速度为 \( v_1 \),\( m_2 \) 的速度为 \( v_2 \)。
碰撞后 \( m_1 \) 和 \( m_2 \) 的速度分别是多少?答案:根据动量守恒和能量守恒,碰撞后的速度 \( v_1' \) 和\( v_2' \) 可以通过以下公式计算:\[ v_1' = \frac{(m_1 - m_2)v_1 + 2m_2v_2}{m_1 + m_2} \]\[ v_2' = \frac{(m_2 - m_1)v_2 + 2m_1v_1}{m_1 + m_2} \]2. 一个质量为 \( m \) 的小球从高度 \( h \) 处自由下落,与地面碰撞后反弹,反弹高度为 \( h' \)。
若碰撞是完全非弹性的,求反弹后小球的速度。
答案:完全非弹性碰撞意味着小球与地面碰撞后粘在一起,因此反弹后的速度为零。
3. 一辆质量为 \( M \) 的汽车以速度 \( V \) 与一辆静止的质量为\( m \) 的汽车发生碰撞,两车碰撞后速度相同。
求碰撞后两车的速度。
答案:根据动量守恒定律,碰撞后两车的速度 \( v \) 可以通过以下公式计算:\[ v = \frac{MV}{M + m} \]4. 一颗质量为 \( m \) 的子弹以速度 \( v \) 射入一块静止的木块中,木块的质量为 \( M \)。
如果子弹和木块在碰撞后一起移动,求碰撞后它们的共同速度。
答案:根据动量守恒定律,碰撞后子弹和木块的共同速度 \( v' \)可以通过以下公式计算:\[ v' = \frac{mv}{m + M} \]5. 一颗质量为 \( m \) 的小球以速度 \( v \) 沿着光滑水平面运动,与一个质量为 \( M \) 的静止小球发生碰撞。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
碰撞习题参考答案及解答
1.质量为50g 的弹丸,以400m/s 的速度射入球内,速度的方向如图示。
球的质量为4kg ,经历时间t =0.05s 后撞击终止。
求(a )绳子拉力的平均增量;(b )碰撞后球的速度;(c )碰撞后球所升起的高度。
提示:用碰撞时的动量定理可计算绳子拉力的平均增量和碰撞后球的速度。
碰撞后求球所升起的高度是非碰撞的问题,可用机械能守恒或动能定理求得。
答案:(a )283N , (b )3 .49m/s , (c) 0.621m
2.图示两球,分别由两不等长绳索悬挂,球A 的质量m A =4.5kg ,球B 的质量m B =1.5kg 。
现将球A 拉起至θA =60°,并将它无初速释放,与仍在铅垂位置的球B 相撞。
已知k =0.90。
求(a )球B 升起的最大偏角θB ;(b )悬挂球B 的绳内的最大拉力。
提示:本题分为三个阶段来分析求解:(1)用动能定理先求出碰撞前瞬时小球A 的速度;(2)碰撞结束瞬时球B 的速度,据此求得悬挂球B 的绳内的最大拉力;(3)用动能定理求碰撞结束后球B 升起的最大偏角θB 。
答案:(a) θB =76.2o , (b)1.37max =F N
3.撞击机的摆,由钢铸圆盘A 和圆杆B 组成。
钢铸圆盘的半径为10cm ,厚为5cm 。
圆杆B 的半径为2cm ,长为90cm 。
问用该机器击打碎石,其所在水平面与转轴O 的距离l 应多大方能使轴不受碰撞?碰撞的方向可视为水平。
答案:cm 90.6 , 18842250 , 207995 , cm 77==
===ma
J l J ma a O
O ρρ a 为质心距转轴O 的距离,J O 为摆对转轴O 的转动惯量,ρ为材料密度。
4.质量为m 1的滑块A 置于光滑的水平面上,它与质量为m 2长为l 的均质杆AB 铰接,如图所示,系统初始静止,杆AB 铅垂,m 1=2m 2。
今有一冲量为I 的水平碰撞力作用于杆的B 端。
试求碰撞结束时,滑块A 的速度。
解:取整体为研究对象如图(b ),由水平方向的碰撞时的动量定理
I v m v m C A =+21 (1)
取杆AB 为研究对象如图(c ),由碰撞时对轴A 的动量矩定理
I l lv m l m C ⋅=+2222
1
121ω (2) 又由运动学关系 ωl v v A C 2
1
+= (3)
联立式(1)、(2)和(3)解得
2
2
2
930,913,
92lm I
m I v m I
v C A =
→=
←−
=ω 负号表示方向与图示方向相反。
