正弦电流电路激励
电路在正弦激励下非正弦稳态响应

电路在正弦激励下非正弦稳态的响应田社平1,孙盾2,张峰1(1上海交通大学电子信息与电气工程学院 上海 200240;2浙江大学电气工程学院 杭州 310027)摘要:基于作者的教学实践,讨论了电路在正弦激励下产生非正弦稳态的响应的各种情况。
零状态动态电路存在正弦稳态响应的充要条件为,响应的象函数Y (s )存在且仅存在一对共轭虚极点,而Y (s )的其它极点均位于复平面的开左半平面上。
通过实例说明了在正弦激励下产生非正弦稳态的响应的情形。
电路本文的讨论对丰富正弦稳态电路分析的教学内容,加深学生对相关知识的理解,具有良好的助益。
关键词:正弦激励;非正弦稳态响应;电路 中图分类号: TM13 文献标识码 ANon-sinusoidal Steady-state Response of Circuit with Sinusoidal ExcitationTIAN She-ping 1, SUN Dun 2, ZHANG Feng 1(1School of Electronic, Information and Electrical Engineering, Shanghai Jiao Tong Univ., Shanghai 200240, China; 2College ofElectrical and Electronic Eng ,Zhejiang Univ.,Hangzhou 310027,China )Abstract: Based on the teaching practice, various situations of non-sinusoidal steady-state response of circuit with sinusoidal excitation are discussed. The necessary and sufficient condition for the existence of sinusoidal steady-state response in a zero-state dynamic circuit is that the Laplace transform of the response which is Y (s ) exists and has only one pair of conjugate virtual poles, while the other poles of Y (s ) lie on the left open plane of the complex plane. Several examples are given to illustrate the non-sinusoidal steady-state response with sinusoidal excitation. The discussion is helpful to enrich the teaching content of sinusoidal steady-state circuit analysis and deepen students' understanding of relevant knowledge.Key words: sinusoidal excitation; non-sinusoidal steady-state response; circuit 处于正弦稳态的电路称为正弦稳态电路。
电路分析23

d e j t ) Re[ d ( A e j t )] Re(j A e j t ) Re( A dt dt
引理包含两个内容:取实部运算和求导可交 A e j t 对t的导数等于该函数与jω的 换;复数函数 乘积。
电 路 分 析 课 件
d e j t ) Re[ d ( A e j t )] Re(j A e j t ) Re( A dt dt d e j t ) d Re[ A e j( t ) ] Re( A m dt dt d [ Am cos( t )] dt Am sin( t )
t RC
UCm cos( t u )
(t 0)
K由初始条件确定
K uC (0) U Cm cos u
代入得到电容电压uC(t)的全响应为
uC (t ) [uC (0) UCm cos u ] e
t RC
UCm cos( t u )
t 0
相量法求微分方程特解的方法与步骤如下: 1. 用KCL,KVL和VCR写出电路方程(例如2b 方程,网孔方程,结点方程等),以感兴趣的电压电 流为变量,写出n阶微分方程。
2. 用相量表示同一频率的各正弦电压电流,将 n阶微分方程转换为复系数代数方程。 3. 求解复系数代数方程得到所感兴趣电压或电 流的相量表达式。 4. 根据所得到的相量,写出正弦电压或电流的 瞬时值表达式。
电 路 分 析 课 件
§10-2
正弦稳态响应
一、正弦电流激励的RC电路分析
如图所示RC电路,电路达到稳定状态,在t=0 时刻断开开关,正弦电流iS(t)=ISmcos( t+ψi)作用 于RC电路,求电容电压uC(t)的响应。
第三章 正弦交流电路-1

一.电阻元件
i
根据欧姆定律,线性电阻上的电压与电流
成正比关系,即 i u R
图3-10
当电压和电流均用相量表示时,欧姆定律
的相量表示式为 第(23)页
•
•
I
U
R
u
R
电阻元件
上式表明,电阻元件上电压和电流的相位相同,
如图3-11所示。
设 i 2ISint
u 2USint 图3-11
电阻元件吸收的瞬时功率为
方法二: 运用矢量运算
Y I2m B
C I3m
10 50
I1m
A
5
0 60 30
X
i1 I1m OA矢量 i2 I2m OB矢量 i3 I3m OC矢量
根据矢量图
I3m 14.6
3 50 于是i3 14.6CoS(t 50)
+j
I3m
方法三.运用复数运算:
11.16
I1m 5e j30
只要有幅值与初相位两个要素就足以表示各电压 与电流之
间的关系,因此我们约定:用式(3-1)中的复常数 Ie ji 表
示正弦电流 i 2ISint i ,并用下列记法
•
I Ie ji I i
(3-2)
上式中I• m不仅是一个复数,而且表示了一个正弦量,所以给它
一个专有名称——相量。代表正弦电流的相量称之为电流相量,
U
的正方向如图3-13(a)所示。
u,i
(b) 0
u
i
t
i ii
i
+ -- +
p- + + 储能 放能 储能 放能
根据楞次定律得出
u
eL
电路 正弦激励下一阶电路的响应

f 2 (t ) y f 2 (t )
时不变电路的延时不变性
f (t t 0 ) y f (t t 0 )
杜阿密尔积分(叠加积分): 适用于f(t)为解析表示式时计算电路的零 t 状态响应。
y f (t ) f (0) g (t ) f ( )g (t )d
arctan RC
Um US 1 (RC )
2
4
uC (t ) Ke st Um sin( t )
s 1 1 RC
uS
K U0 U m sin
arctan RC
Um US 1 (RC )
2
求得全响应
uC (t ) (U 0 U m sin )e
duc 1 1 uc U s sin t dt RC RC
uS
则
齐次解: 特解: 完全解:
uCh (t ) Ke uCp (t ) Um sin( t )
st
uC (t ) uCh (t ) uCp (t )
Ke st Um sin( t )
s 1 1 RC
(t )
C
uC
–
uC (0-)=0
线性电路的线性性质
1 RC i(t ) e (t ) R
t
如果
则 如果
a1 f1 (t ) a2 f 2 (t ) a1 y f 1 (t ) a2 y f 2 (t )
f (t ) y f (t )
则
f1 (t ) y f 1 (t )
iL
U (1 e R
S
Rt L
)
(t0)
16
正弦交流电知识点整理
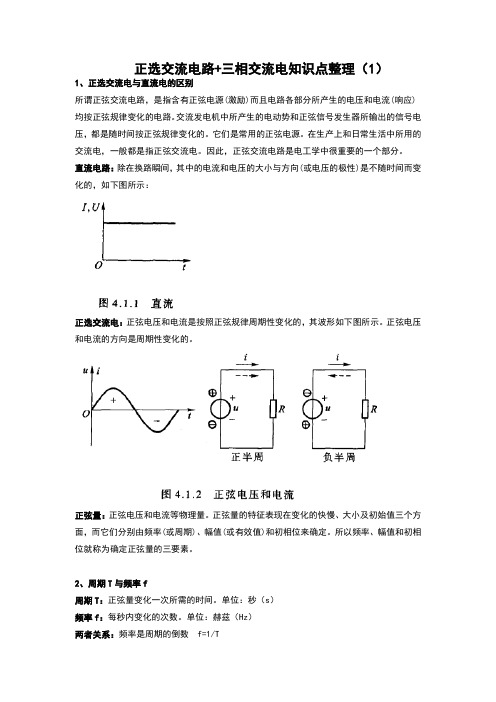
正选交流电路+三相交流电知识点整理(1)1、正选交流电与直流电的区别所谓正弦交流电路,是指含有正弦电源(激励)而且电路各部分所产生的电压和电流(响应)均按正弦规律变化的电路。
交流发电机中所产生的电动势和正弦信号发生器所输出的信号电压,都是随时间按正弦规律变化的。
它们是常用的正弦电源。
在生产上和日常生活中所用的交流电,一般都是指正弦交流电。
因此,正弦交流电路是电工学中很重要的一个部分。
直流电路:除在换路瞬间,其中的电流和电压的大小与方向(或电压的极性)是不随时间而变化的,如下图所示:正选交流电:正弦电压和电流是按照正弦规律周期性变化的,其波形如下图所示。
正弦电压和电流的方向是周期性变化的。
正弦量:正弦电压和电流等物理量。
正弦量的特征表现在变化的快慢、大小及初始值三个方面,而它们分别由频率(或周期)、幅值(或有效值)和初相位来确定。
所以频率、幅值和初相位就称为确定正弦量的三要素。
2、周期T与频率f周期T:正弦量变化一次所需的时间。
单位:秒(s)频率f:每秒内变化的次数。
单位:赫兹(Hz)两者关系:频率是周期的倒数 f=1/T高频炉的频率是200- 300kHz;中频炉的频率是500-8000Hz;高速电动机的频率是150-2000Hz; 通常收音机中波段的频率是530-1600kHz ,短波段是2.3-23MHz;移动通信的频率是900MHz和1800MHz; 在元线通信中使用的频率可高 300 GHz。
正弦量变化的其他表达方式:角频率正弦量变化的快慢除用周期和频率表示外,还可用角频率ω来表示。
因为一周期内经历了 2π弧度(图 4.1.3) ,所以角频率为:上式表示 T,f,ω三者之间的关系,只要知道其中之一,则其余均可求出。
3、幅值与有效值正弦量在任一瞬间的值称为瞬时值,用小写字母来表示,如 i , U 及 e 分别表示电流、电压及电动势的瞬时值。
瞬时值中最大的值称为幅值或最大值,用带下标 m 的大写字母来表示,如Im, Um 及 Em 分别表示电流、电压及电动势的幅值。
什么是正弦稳态电路(精)

二、研究正弦稳态电路的意义
正弦电压和电流产生容易,与非电量转换方便,在实用 电路中使用广泛。 复杂信号皆可分解为若干不同频率正弦信号之和,因此可 利用叠加定理将正弦稳态分析推广到非正弦信号激励下的电 路响应。
三、正弦稳态电路的分析方法
采用相量分析法,引入相量的概念以后,在电阻电路 中应用的公式、定理均可以运用于正弦稳态电路。
试求 i3 (t ),并作出各电流相量的相量图。
解:由 i1 (t ) 、 i2 (t ) 的时域形式,得:
I1 20 I 2 2120
i1 (t )
i2 (t )
i3 (t )
由KCL的相量形式,得:
I3 I1 I 2 20 2120 2 1 j 3 2 120 A
u2 (t ) 2U 2 cos(t 2 )
相位差定义为:
12 (t 1 ) (t 2 ) 1 2
同频正弦量的相位差等于它们的初相之差,是一个与 时间无关的常数
比较两正弦量的相位差时应注意: (1)两正弦量必须是同类型的函数
(2)两正弦量必须具有相同的频率
i iR u(t) iC C iL L
R=15Ω,C=83.3μF,L=30mH,求电流I. 解:利用KCL相量关系,有:
I I R IC I L
U 120 j120 V 2
U j120 IR j8 A R 15 I C j CU j 1000 (83.3 106 ) ( j120) 10 A U j120 IL 4A 3 j L j1000 (30 10 )
定理4
若A、B为复常数,若在所有的时刻都满足
Re[ Ae jt ] Re[ Be jt ]
任务一 认识正弦交流电【 正弦交流电路的基本概念和基本定律】
复数的引入
i 1
x21;
x 无解
我们引入这样一个数 i ,把 i 叫做虚数单位,并且规定:
复数:A=a+bi
i21;
i表示电流
A=a+jb
18
复数的表示形式
代数表示:4种
几何表示
(1)直角坐标形式表示: Im
A=a+jb
b
实部 虚部
(2)极坐标形式表示:
0
A 复平面
a Re
A ry
模
幅角
(3)指数形式表示:
)A
6
π
)V
3
u2 =100
解:
2sin(100t 2π )V 3
I&1 =50
π 6
A
U&1 =100
π 3
V
U&2
=100-
2π 3
V
U 2
相量图
U 1
I 1
3
6
2 3
32
已知相量,求瞬时值。
例3:已知两个频率都为1000 Hz的正弦电流其相量形式为:
i 、i I1 = 100 -60°A I2 = 10 30° A 求: 1 2
A B (a1 jb1) (a2 jb2 ) 实部与实部相减
例
(a1 a2 ) j(b1 b2 ) 虚部与虚部相减
(1) (4+j5)-(2+j3)
Im
几何表示 A
=(4-2)+j(5-3) =2+j2
A-B
(2) (m+jn )-(6 + j7) =(m-6)+j(n-7)
B
0
Re
电路 第二章 正弦交流电路(1)
所以交流电的有效值就是与它热效应相等的直流电的数值, 它们之间的关系由焦耳-楞次定律确定。为了区别,交流电 流、电压和电动势的有效值分别用大写字母I、U、E表示。 设正弦电流i=Imsin(ωt+ψ),通过计算可知,正弦电流的有 效值是其最大值的1/√2倍,如图2—9(c)所示,即 I=Im/√2 =0.707Im (2—9) 同理,正弦电压和电动势的有效值分别为 U=Um/√2 ; E=Um/√2 在工程上,主要使用有效值,今后不加特别声明,交流电 的大小均指有效值。从交流电流表和电压表上读取的数值也 是有效值。电气设备所标明的交流电压、电流数值也都是有 效值。可以证明有效值为正弦量在一个周期内的方均根值, 即它不随时间变化,因此,和最大值比较,有效值更为实用。
15
相量也可以用复平面上的有向线段来表示。如图所示。这种 用来表示相量的图形,叫相量图,相量图与力学和物理学中 的向量图相似。但是,相量表示的是随时间作正弦变动的函 数,而向量指的是力、电 场强度等空间向量。 2 因为实际工程中,常采用正弦量的有效值,而且最大值与 有效值之间有着固定的 2关系,所以有效值相量应用较多。 它等于最大值相量除以 2 ,即 U=Um/ 2 同理 I=Im/ 2
上式表明,为了保证电动势的频率稳定,必须保 持发电机转速稳定。 周期T、频率f及角频率ω反映了正弦量随时间作 ω 周期性交变的快慢。各国在电力工业上所用交流 电的频率都规定了各自的标准。我国和有些国家 电力工业的标准频率为50Hz,称为工频。一般我 们讲交流电时,如果不加说明,指的就是50Hz的 工频。还有一些国家工频采用60Hz。
采用适当的磁极形状,使电枢表面的磁感应强度B 沿圆周按正弦规律分布,如图 (a)所示。由于铁芯 的磁导率远大于空气的磁导率,故磁力线的方向 与铁芯表面垂直。在磁极之间的分界面O~O',B= 0,称为磁中性面。在磁极的轴线上,磁感应强度 具有最大值Bm 。设线圈的一条有效边AA'(切割磁 力线的部分)和转轴所组成的平面,与磁中性面的 夹角为α,则AA'边所处位置的磁感应强度为(见图 2—2) B=Bmsinα 当电枢被原动机拖动,在磁场中以逆时 针方向作 等速旋转时,电枢线圈有效 边因切 割磁力线而产生感 应电动势。其表达式为 e=Emsinωt (2—1)
电工学第4章
i1与i2 同相 i1与i2 反相
i1 ωt o ψ1 ψ2 ϕ i i2 ωt
ψ2 o ψ1
注意:不同频率的正弦量比较无意义。 注意:不同频率的正弦量比较无意义。
[例题] 正弦电流 =100sin(6280t − π)mA,指出它的周期 例题] i , 4 频率,角频率幅值 有效值初相位画出波形图 , , , , . 解:Im =100mA i 100(mA) Im = 100=70.7mA I= 2 2 ω=6280rad/s oπ f = ω = 6280=1000Hz =1kHz 4 2π 2π T= 1 = 1 =0.001s=1ms f 1000 ψ=− π 4
4.1.2 幅值与有效值
幅值: 幅值:Im、Um、Em 有效值: 有效值:与交流热效应相等的直流定义为交流电的 有效值。 有效值。
幅值必须大写, 幅值必须大写, 下标加 m。
= I 2 RT ∫0 i R dt
T 2
交流
直流
则有
I =
Im 1 T 2 2 有效值必 = Imsin ωt dt = 2 须大写 T ∫0 Um Em 同理: 同理: U = E= 2 2 注意:交流电压、电流表的刻度、 注意:交流电压、电流表的刻度、数据为有效值
r ψ
a
A = r cos ψ + j r sin ψ = r (cos ψ + jsin ψ)
jψ
由欧拉公式: 由欧拉公式 cos ψ = e 可得: 可得 (3)
= cos ψ + jsin ψ 指数式 A = r ej ψ e
jψ
+e 2
−j ψ
ej ψ − e− j ψ , sin ψ = 2j
正弦交流电路公式总结
正弦交流电路公式总结
正弦交流电路中的主要公式和概念包括:
1. 周期和频率:
周期(T):交变电流完成一次周期性变化(线圈转一周)所需的时间,
单位是秒(s),公式为T=2π/ω。
频率(f):交变电流在1s内完成周期性变化的次数,单位是赫兹(Hz)。
周期和频率的关系:T=1/f。
2. 正弦式交变电流的函数表达式(线圈在中性面位置开始计时):
电动势e随时间变化的规律:e=Emsinωt。
负载两端的电压u随时间变化的规律:u=Umsinωt。
电流i随时间变化的规律:i=Imsinωt。
其中ω等于线圈转动的角速度,Em=nBSω。
3. 在纯电阻性电路中,当电路与电源之间不再有能量的交换时,电路呈电阻性。
以上内容仅供参考,如需更具体全面的信息,建议查阅电路学相关书籍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Um i R (t ) cos( t Ψ u ) R
i( t ) U m (1 R ) 2 (C) 2 cos( t Ψ u arctg(RC))
The branch voltage and current change at the same angular frequency!!!
Feel Safe?
π Um CU m cos( t Ψ u ) R cos( t Ψ u ) 2 U m (1 R)2 (C )2 cos( t Ψ uarctg(RC ))
SCADA/EMS DTS
1. “+”、“-” of sinusoids
i (t ) i1 (t ) i2 (t )+...+in (t )
Two pains!
I m1 cos(t i1 ) I m 2 cos(t i 2 ) ...+I mn cos(t in ) ?
2. Differentiation and integration of sinusoids
duC (t ) iC ( t ) C ? dt
直流I
R
交流i
R
W RI T
2
W Ri ( t )dt
2 0
T
电流有效 值定义为
1 T 2 I i (t )dt T 0
def
有效值也称均方根值 (root-meen-square)
同样,可定义电压有效值:
正弦电流、电压的有效值 设 i(t)=Imcos( t+ )
1 U T
1 t i L (t) uL ( t )d ? L
iC(t) + _ i(t) iR(t) R C
u(t)
u R (t ) uC (t ) u(t ) U m cos(t Ψ u )
π iC (t ) CU m cos( t Ψ u ) 2
Charles Steinmetz (1865 ~1923)
乘法:模相乘,角相加。
A1 | A1 | θ 1 | A1 | e | A1 | j( θ 1θ 2 ) e jθ 2 A2 | A2 | θ 2 | A2 | e | A2 | | A1 | θ 1 θ 2 | A2 |
除法:模相除,角相减。
(3) 旋转因子:
复数 ej =cos +jsin =1∠ Im
(2)正弦信号是一种基本信号,任何变化规律复杂的信号 可以分解为按正弦规律变化的分量。
f ( t ) Ak cos(kt k )
k 1
n
对正弦电路的分析研究具有重要的理 论价值和实际意义。
2. 正弦量的三要素
i(t)=Imcos( t+)
(1) 幅值 (amplitude) (振幅、 最大值)Im 反映正弦量变化幅度的大小。 (2) 角频率(angular frequency)ω
u, i u i
0
0 j= /2:
t
u, i u
i 0
u 领先 i /2, 不说 u 落后 i 3/2; i 落后 u /2, 不说 i 领先 u 3/2。
t
同样可比较两个电压或两个电流的相位差。
例
计算下列两正弦量的相位差。 解
(1) i1 ( t ) 10 cos(100 t 3 4) i2 ( t ) 10 cos(100 t 2)
相位变化的速度, 反映正弦量变化快慢。
2 f 2 T
单位: rad/s ,弧度 / 秒 i Im O T 2
(3) 初相位(initial phase angle) 反映正弦量的计时起点, 常用角度表示。
/
tt
同一个正弦量,计时起点不同,初相位不同。
i(t)=Imcos( t+)
复数运算 (1)加减运算——采用代数形式 Im A2
图解法
若
则
A1=a1+jb1, A2=a2+jb2
A1±A2=(a1±a2)+j(b1±b2)
若 0
A1 Re
(2) 乘除运算——采用极坐标形式
A1=|A1| 1 ,A2=|A2| 2
A1 A2 1 2
jθ 1
则:
A1 A2 A1 e j1 A2 e j 2 A1 A2 e j (1 2 )
Use complex number to represent sinusoids!!!
2.Review the complex number
Im b Im
A
b
A
|A|
0 a Re
0 a Re
A a jb
A | A | e
j
| A |
3.用复数表示正弦量
A( t ) I m e j( t )
1 f T
周期T :重复变化一次所需的时间。 单位:s,秒 频率f :每秒重复变化的次数。 单位:Hz,赫(兹)
正弦电流电路
激励和响应均为正弦量的电路(正弦 稳态电路)称为正弦电路或交流电路。 (Sinusoidal Steady-State)
研究正弦电路的意义: (1)正弦稳态电路在电力系统和电子技术领域占有十分重 要的地位。 优点: 1)正弦函数是周期函数,其加、减、求导、积分 运算后仍是同频率的正弦函数 2)正弦信号容易产生、传送和使用。
( 2) i1 ( t ) 10 cos(100 t 300 ) i2 ( t ) 10 sin(100 t 150 ) ( 3) u1 ( t ) 10 cos(100 t 300 ) u2 ( t ) 10 cos(200 t 450 ) (4) i1 ( t ) 5 cos(100 t 30 )
j 300 (1500 ) 1200
i2 ( t ) 3 cos(100 t 30 )
0
两个正弦量进行相位比较时应满足同频率、同函数、同符 号,且在主值范围比较。
4. 周期性电流、电压的有效值
周期性电流、电压的瞬时值随时间而变,为了衡量其 平均效果工程上采用有效值来表示。 物 理 意 义 周期电流、电压有效值(effective value)定义
交流电
1. What is AC?
/
i
T
O
t
2. What is first, AC or DC? 3. Why is AC?
a) Gegerator b) Voltage Transformer
第8章
重点:
相量法
1. 正弦量的表示、相位差; 2. 正弦量的相量表示 3. 电路定理的相量形式;
u( t ) 2U cos( t θ ) U Uθ
4. 问题的解决
(1)正弦量的加减 j t R e ( I e ) 1 i1 (t ) I1m cos( t Ψ1 ) i2 (t ) I 2m cos( t Ψ 2 ) Re( I 2 e j t ) i(t ) i1 (t ) i2 (t ) R ?e( I 1 e jt ) Re( I 2 e jt )
(2)测量中,交流测量仪表指示的电压、电流读数一 般为有效值。 (3)区分电压、电流的瞬时值、最大值、有效值的符号。
i , Im , I
U=380V,
Um537V。
8.3 向量法的基础
1. 问题的提出:
已知: u( t ) U m cos(t Ψ u ) 求解各支路电压、电流
+ _ i(t)
u(t)
R
C
du( t ) π 则 iC ( t ) C CU m sin( t Ψ u ) CU m cos( t Ψ u ) dt 2
u (t ) U m 则 iR (t ) cos( t Ψ u ) R R 则 i ( t ) iC ( t ) i R ( t )
故 +j, –j, -1 都可以看成旋转因子。
, e
j
2
cos
j sin
I
j
8.2
1. 正弦量
瞬时值表达式:
正弦量
i
波形: T O
i(t)=Imcos( t+)
正弦量为周期函数
/
t
f(t)=f ( t+kT)
周期T (period)和频率f (frequency) :
8.1 复数
1. 复数及运算
复数A的表示形式 Im b 0 a A
A=a+jb
(j 1 为虚数单位)
Im b A |A|
Re
0
a
Re
A a jb
j
A | A | e j
A | A | e | A | (cos j sin ) a jb
A | A | e j | A |
def
T
0
u ( t )dt
2
1 I T
T
0
I cos ( t Ψ ) dt
2 m 2
T 0
T
0
cos ( t Ψ ) dt
2
1 cos 2( t Ψ ) 1 dt t 2 2
T 0
1 T 2
1 2 T Im I Im 0.707 I m T 2 2
欧拉公式: I m cos(t ) jI m sin( t Ψ ) ej =cos +jsin
j( t Ψ )
Re[ A( t )] I m cos( t Ψ ) i(t)
