第11章Logistic回归分析教学案例
《SPSS统计分析》第11章 回归分析

返回目录
多元逻辑斯谛回归
返回目录
多元逻辑斯谛回归的概念
回归模型
log( P(event) ) 1 P(event)
b0
b1 x1
b2 x2
bp xp
返回目录
多元逻辑斯谛回归过程
主对话框
返回目录
多元逻辑斯谛回归过程
参考类别对话框
保存对话框
返回目录
多元逻辑斯谛回归过程
收敛条件选择对话框
创建和选择模型对话框
返回目录
曲线估计
返回目录
曲线回归概述
1. 一般概念 线性回归不能解决所有的问题。尽管有可能通过一些函数
的转换,在一定范围内将因、自变量之间的关系转换为线性关 系,但这种转换有可能导致更为复杂的计算或失真。 SPSS提供了11种不同的曲线回归模型中。如果线性模型不能确 定哪一种为最佳模型,可以试试选择曲线拟合的方法建立一个 简单而又比较合适的模型。 2. 数据要求
线性回归分析实例1输出结果2
方差分析
返回目录
线性回归分析实例1输出结果3
逐步回归过程中不在方程中的变量
返回目录
线性回归分析实例1输出结果4
各步回归过程中的统计量
返回目录
线性回归分析实例1输出结果5
当前工资变量的异常值表
返回目录
线性回归分析实例1输出结果6
残差统计量
返回目录
线性回归分析实例1输出结果7
返回目录
习题2答案
使用线性回归中的逐步法,可得下面的预测商品流通费用率的回归系数表:
将1999年该商场商品零售额为36.33亿元代入回归方程可得1999年该商场 商品流通费用为:1574.117-7.89*1999+0.2*36.33=4.17亿元。
logistic回归分析实例操作

Logistic回归分析二分类(因变量Y有(如发病1与未发病0)两种可能出现的结果)资料的Logistic回归分析,至于多分类Logistic回归分析,与二分类操作过程类似,只是在数据编制及分析方法选择处不同。
分析的一般步骤:变量的编码哑变量的设置和引入各个自变量的单因素分析变量的筛选交互作用的引入建立多个模型选择较优的模型模型应用条件的评价输出结果的解释实例操作11.1 某研究人员在探讨肾细胞癌转移的有关临床病理因素研究中,收集了一批行根治性肾切除术患者的肾癌标本资料,现从中抽取26例资料作为示例进行logistic回归分析。
1.各变量及其赋值说明x1:确诊时患者的年龄(岁)x2:肾细胞癌血管内皮生长因子(VEGF),其阳性表述由低到高共3个等级(1-3)x3:肾细胞癌组织内微血管数(MVC)x4:肾癌细胞核组织学分级,由低到高共4级(1-4)x5:肾细胞癌分期,由低到高共4期(1-4)y:肾细胞癌转移情况(有转移y=1; 无转移y=0)。
为二分类变量。
若作单因素的Logistic回归分析,也就是分别作Y与各自变量间的回归分析,如Y与X1、Y与X2等的单因素Logistic回归分析。
2.建立数据库3.分析步骤(1)(2)上图中若为单因素回归分析,只需在Covariates协变量框内导入单一自变量如X1即可。
(3)4.分析结果(1)数据描述Case Processing SummaryUnweighted Cases a N PercentSelected Cases Included in Analysis 26 100.0Missing Cases 0 .0Total 26 100.0Unselected Cases 0 .0Total 26 100.0a. If weight is in effect, see classification table for the total number of cases.Dependent Variable EncodingOriginal Value Internal Value无转移0转移 1(2)Block 1: Method = Forward Stepwise (Likelihood Ratio)Omnibus Tests of Model CoefficientsChi-square df Sig.Step 1 Step 15.538 1 .000Block 15.538 1 .000Model 15.538 1 .000Step 2 Step 6.178 1 .013Block 21.716 2 .000Model 21.716 2 .000表示两步变量的引入均有统计学意义,方法合理。
论文经典方法:Logistic回归分析及其应用PPT课件

04.02.2021
.
5
简单的解决方法
固定其他因素,研究有影响的一两个因 素; 分层分析:按1~2个因素组成的层进行 层内分析和综合。 统计模型
04.02.2021
.
6
寻找合适的模型
进行logit变换
p
logit(p) = ln( 1—-—p ), p为y=1所对应的概率 0.1
logit(0.1) = ln( ——— ) = ln(0.1/0.9) 1 - 0.1
称此为logistic回归模型
04.02.2021
.
8
P = ez / (1 + ez ) ea+b1x1+b2x2+… +bkxk
P = 1 + ea+b1x1+b2x2+… +bkxk
此为非条件logistic回归模型 应用于成组数据的分析
04.02.2021
.
9
自变量取定一些值时,因变量取0、1的概率就是 条件概率,对条件概率进行logistic回归,称为
04.02.2021
.
11
分析的一般步骤
变量的编码 哑变量的设置和引入 各个自变量的单因素分析 变量的筛选 交互作用的引入 建立多个模型 选择较优的模型 模型应用条件的评价 输出结果的解释
04.02.2021
.
12
1.变量的编码
变量的编码要易于识别 注意编码的等级关系 改变分类变量的编码,其分析的意 义并不改变。 牢记编码
04.02.2021
.
31
条件logistic回归
研究中有N个配比组,每组中n个病 例配m个对照者。这时,各个研究 对象发生某事件的概率即为条件概 率。 适用于 配比设计的病例-对照研究 精细分层设计的队列研究
图文举例详细讲解Logistic曲线的回归分析
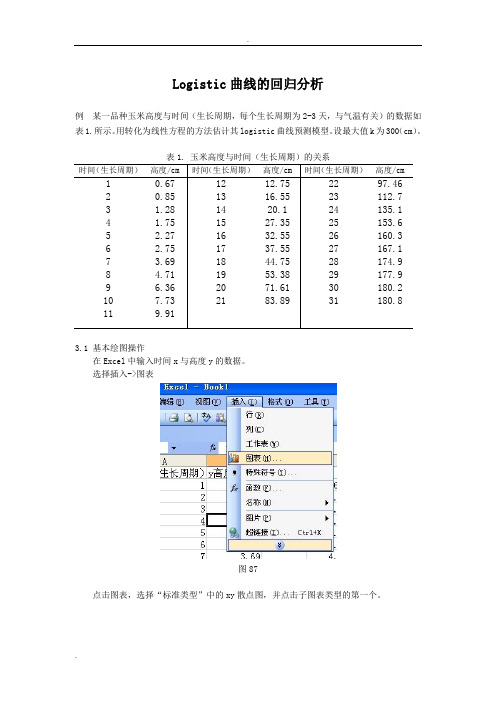
Logistic 曲线的回归分析例 某一品种玉米高度与时间(生长周期,每个生长周期为2-3天,与气温有关)的数据如表1.所示。
用转化为线性方程的方法估计其logistic 曲线预测模型。
设最大值k 为300(cm )。
表1. 玉米高度与时间(生长周期)的关系时间(生长周期) 高度/cm 时间(生长周期) 高度/cm 时间(生长周期) 高度/cm12 3 4 5 6 7 8 9 10 11 0.67 0.85 1.28 1.75 2.27 2.75 3.69 4.71 6.36 7.73 9.9112 13 14 15 16 17 18 19 20 21 12.75 16.55 20.1 27.35 32.55 37.55 44.75 53.38 71.61 83.89 22 23 24 25 26 27 28 29 30 31 97.46 112.7 135.1 153.6 160.3 167.1 174.9 177.9 180.2 180.83.1 基本绘图操作在Excel 中输入时间x 与高度y 的数据。
选择插入->图表图87点击图表,选择“标准类型”中的xy 散点图,并点击子图表类型的第一个。
图88 点击下一步,得到如图89。
图 89点击下一步。
图90分别点击标题、网格线、图例进行修改,然后点击下一步。
图91点击完成。
图92右击绘图区,修改绘图区格式,双击做表格,修改坐标轴刻度,最后的散点图。
图93观察散点图,其呈S 型曲线,符合logistic 曲线。
采用转化为线性方程的方法求解模型。
3.2 Logistic 曲线方程及线性化Logistic 曲线方程为:1atk y me-=+ (12)(1) 将数据线性化及成图转化为线性方程为:01'y a a t =+ (13)其中,'ln(/1)y k y =-,0ln a m =,1a a =-具体操作为:向excel 表格中输入y ’数据。
Logistic回归分析及应用讲课文档

第三十页,共76页。
第三十一页,共76页。
第三十二页,共76页。
第三十三页,共76页。
第三十四页,共76页。
第三十五页,共76页。
第三十六页,共76页。
3、逐步Logistic回归分析
(1)向前法(forward selection)
开始方程中没有变量,自变量由 少到多一个一个引入回归方程。按自 变量对因变量的贡献(P值的大小)由 小到大依次挑选,变量入选的条件是 其P值小于规定进入方程的P界值Enter, 缺省值 P(0.05)。
除变量量纲的影响,为此计算标准化回归系数
bi' bi *Si / Sy,其中 Si为Xi的标准差 Sy为y的标准差。
第十五页,共76页。
5.假设检验
• (1)回归方程的假设检验
• H0:所有 i0,i0,1,2,,p H1:某个 i 0
• 计算统计量为:G=-2lnL,服从自由度等于n-p
• 的 2 分布
• 对子号
病例
对照
•
x1 x2 x3 x1 x2 x3
•1
13 0
101
•2
03 1
130
•3
01 2
020
•…
… … … ………
• 10
22 2
000
• 注:X1蛋白质摄入量,取值:0,1,2,3
•
X2不良饮食习惯,取值:0,1,2,3
•
X3精神状况 ,取值:0,1,2
•
第十页,共76页。
Logistic回归
Logit(P)=-9.7544+2.5152X1+3.9849X2+0.1884X31.3037X4.
logistic回归分析及其应用-41页文档资料

21.03.2020
2
F(y) :因变量的logit值
1.00
0.75
0.50
0.25
0.00 -4.00 -2.00 0.00 2.00 4.00
X:自变量
21.03.2020
如果一定要进 行直线回归也 可以做出结果, 但此时效果不 佳。当自变量 取一定值时, 因变量的预测 值可能为负数。
21.03.2020
14
2.哑变量的设置和引入
哑变量,又称指示变量或设计矩阵。 有利于检验等级变量各个等级间的变 化是否相同,但主要适合于无序分类变 量。 一个k分类的分类变量,可以用k-1个 哑变量来表示。
21.03.2020
15
哑变量的设置
教育程度:文盲,小学,初中,高中以上
教育程度 X1
X2
X3
文盲:0 0
0
0
小学:1 1
0
0
初中:2 0
1
0
高中:3 0
0
1
以文盲作为参考组
21.03.2020
16
以高中作为参照
教育程度
X1
X2
X3
文盲:010 Nhomakorabea0
小学:1
0
1
0
初中:2
0
0
1
高中:3
0
0
0
21.03.2020
17
SPSS提供的方法
Indicator: 默认。以第1 或最后1类作对照,其他每类 与对照比较; Sample: 以第1 或最后1类作对照,其他每类与对照比 较,但反映平均效应。 Difference: 除第1类外各分类与其前各类平均效应比较; Helmert: 除最后1类外各分类与其前各类平均效应比较; Repeated: 除第1类外各分类与其前一类比较; Polynomial: 假设类间距相等,用于数值型变量。 Deviation: 以第1 或最后1类作对照,其余每类与总效 应比较。
logistic回归分析PPT精品课程课件讲义

问题的提出(续)
• 但在医学研究中常碰到因变量的取值仅有两个, 如是否发病、死亡或痊愈等;
• 分析“母亲怀孕期间体重增加”对“新生儿出 生低体重”的影响
二、概念的引入
• 如按线性回归思想建立模型: P=α +βX • P的意义是发生出生低体重的概率
• 在线性回归模型中,X的取值是任意的,P值可能大 于1或小于0,无法从医学意义进行解释, 显然不适 宜用线性回归建立预测模型。
表明ECG异常者CHD发病是正常者的2.056倍。 (3) 比较各变量对方程贡献的大小: 根据标化的值大小,确定各因素对CHD发病影响的 大小。在此项研究中,危险因素中吸烟对方程贡献最大 ,其他依次为相对体重、年龄、 胆固醇、ECG和BP。
4) 用于预测发病率: 可根据该公式预测某人在不同因素暴露条件下 CHD的发病率。如某受试者A暴露于因素xi的情况 为: X=(45, 210, 130, 100, 120, 0, 0) 利用该模型计算该受试者A在暴露上述各种研究因 素的条件下,12年间CHD的发病率为: PA1 = 1/{1+exp[-(-13.2573 + 0.1216 x 45 + 0.0070 x 210 + +0.7206 x 0)]} = 1/[1+exp(-2.9813)] = 0.048
小 结
• (1)logistic回归分析要求因变量是二分变量,或任何取值
为0或1的属性数据。
• (2)logistic回归分析中对自变量的正态性、方差齐性不作
要求,对自变量类型也不作要求;
• (3)自变量与因变量(y)之间是非线性关系,但是与logit y之
间应符合线性关系。
1. 定群研究资料分析…弗明汉心脏研究 742 名居住在弗明汉年龄为 40-49 岁的男性,在各自暴露不 同水平的影响因素(详见下表中的7种因素),经 12年追踪观察 CHD发病情况。根据此742名受试者每人暴露各项因素的水平 和 CHD 发病与否的资料,采用多因素 LOGISTIC 回归模型进
《logistic回归》课件

易于理解和实现: 由于基于逻辑函数,模型输出结 果易于解释,且实现简单。
Logistic回归的优势与不足
• 稳定性好: 在数据量较小或特征维度较高 时,Logistic回归的预测结果相对稳定。
Logistic回归的优势与不足
01
不足:
02
对数据预处理要求高: 需要对输入数据进行标准化或归一化处理,以 避免特征间的尺度差异对模型的影响。
模型假设
01
线性关系
因变量与自变量之间存在线性关系 。
无自相关
因变量与自变量之间不存在自相关 。
03
02
无多重共线性
自变量之间不存在多重共线性,即 自变量之间相互独立。
随机误差项
误差项是独立的,且服从二项分布 。
04
模型参数求解
最大似然估计法
通过最大化似然函数来求解模型参数。
梯度下降法
通过最小化损失函数来求解模型参数。
特征选择与降维
在处理大数据集时,特征选择和降维是提高模 型性能和可解释性的重要手段。
通过使用诸如逐步回归、LASSO回归等方法, 可以自动选择对模型贡献最大的特征,从而减 少特征数量并提高模型的泛化能力。
降维技术如主成分分析(PCA)可以将高维特 征转换为低维特征,简化数据结构并揭示数据 中的潜在模式。
迭代法
通过迭代的方式逐步逼近最优解。
牛顿法
利用牛顿迭代公式求解模型参数。
模型评估指标
准确率
正确预测的样本数占总样本数的比例 。
精度
预测为正例的样本中实际为正例的比 例。
召回率
实际为正例的样本中被预测为正例的 比例。
F1分数
精度和召回率的调和平均数,用于综 合评估模型性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 了解条件Logistic回归的应用; • 掌握条件Logistic回归的SAS程序;
概述
• 线性回归模型和广义线性回归模型要求因变量是
连续的正态分布变量,且自变量和因变量呈线性 关系。当因变量是分类型变量时,且自变量与因 变量没有线性关系时,线性回归模型的假设条件 遭到破坏。这时,最好的回归模型是Logistic回归 模型,它对因变量的分布没有要求,从数学角度 看,Logistic回归模型非常巧妙地避开了分类型变 量的分布问题,补充完善了线性回归模型和广义 线性回归模型的缺陷。从医学研究角度看, Logistic回归模型解决了一大批实际应用问题,对 医学的发展起着举足轻重的作用。
• 多元线性回归的局限性 • 经典流行病学统计分析方法—分层分析的局限性
1.两种主要的流行病学设计 1)病历对照研究 2)队列研究
2.判断结局(疾病)和暴露(因素)联系强弱的指标 1) 相对危险度:RR = p1 / p0 p1: 暴露于某个危险因素下发病的概率 p0: 不暴露于某个危险因素下发病的概率(对照) 2)比值比:
五、Logistic 回归模型的统计学检 验
{e α/[1+ e α] }c {1/ [1+ e α] }d
取对数,有 Ln (L) = a (α + β) – a ln[1+e(α + β) ]– b ln[1+e (α + β)]
+ c α – c ln [1+e α ] – d ln[1+e α ]
对以上似然函数分别求对α 和 β的一阶偏导数,再令两个偏导数为零, 就可以解得α 和 β的估计值。
331
———————————————————————————————————
2 = 17. 88 P〈0. 01
40岁以上服用OC的比例远小于40岁以下组。
Mantel-Haenszel分层分析法
按年龄分层,可以得到下表:
—————————————————————————————————
〈40岁
≥40岁
用发病概率来表示四格表,可以得到四格表的另外一种表示形式:
四格表的另外一种表达形式(1)
————————————————————————————
发病(y=1)
不发病(y=0)
————————————————————————————
暴露(x=1)
p1
1- p1
不暴露(x=0)
p0
1- p0
—————————————————————————————
暴露者发病概率: p1 = exp(α + βx)/[1+ exp(α + βx)]
暴露者不发病概率: q0= 1- p1 = 1/ [1+ exp(α + βx)];
不暴露者发病概率: p0 = exp(α)/[1+ exp(α)]
不暴露者不发病概率: q0= 1- p0 = 1/[1+ exp(α)] ;
OR = {P(D=1|E=1)/P(D=0|E=1)} / {P(D=1|E=0)/P(D=0|E=0)}
D=1: 患某种疾病, D=0:不患某种疾病 E=1: 暴露于某个危险因素, E=0: 不暴露于某个危险因素 可以简单地表述成:OR = (p1 / q1) / (p0 / q0)
p1 : 暴露于某个危险因素下发病的概率 q1 : 暴露于某个危险因素下不发病的概率 p0 : 不暴露于某个危险因素下发病的概率 q0 : 不暴露于某个危险因素下不发病的概率
回归系数的流行病学意义是:在其它自变量都 不变的条件下,当因素X变化一个测量单位时所引起的 OR值自然对数的改变量。
三、Logistic 回归和OR值间的关系
ln1pp = 1x1
p e1x1 1 p
ORX1 =
p q X11 X11
...... px11 ...... 1 px11
e 1x1
如果当分层后各层的OR值经过一致性检验发现: 各层间的OR值有统计学差异,这时说明分析因素在 分层因素的不同水平上与结局变量的联系强度是不同 的,这时分层因素和研究因素存在这交互作用(效应 修饰作用)。这时应该分层报告OR值,而不能计算 调整OR值。
分层分析的局限性
❖只能控制少数因素(分层因素过多,
建立的logistic 回归方程形式为:
Logit P = -0.2478 + 1.3107 x X取值:1 使用过雌激素
0 未使用过雌激素
使用过雌激素的Logit 为: Logit P(x=1) = -0.2478 + 1.3107 = 1.063 即:Ln (p1/q1) = 1.063 所以,使用过雌激素的比值(odds) 为:
1/ [1+ e (α + β)]
不暴露(x=0) e α/[1+ e α]
1/ [1+ e α]
——————————————————————————————
因为四格表的四个实际数为a,b,c及d, 故可构造似然函数为:
L = {e(α + β)/[1+ e (α + β)] }a {1/ [1+ e (α + β)] }b
用发病概率来表示四格表,可以得到四格表的另外一种表示形式:
四格表的另外一种表达形式(2)
——————————————————————————————
发病(y=1)
不发病(y=0)
——————————————————————————————
暴露(x=1) e(α + β)/[1+ e (α + β)]
————————————————————————————
暴露(x=1)
a
b
不暴露(x=0)
c
d
合计
—————————————————
a+c
b+d
—————————————————————————————
暴露者发病概率 p1 = a /(a+b); 不暴露者发病概率 p0= c/(c+d)
OR= ad/(bc)
非条件Logistic回归
• 医学研究中经常需要分析分类型变量的问题。比如,生存
与死亡、有病与无病、有效与无效、感染与未感染等二分 类变量。研究者关心的问题是,哪些因素导致了人群中有 些人患某种病而有些人不患某种病,哪些因素导致了某种 治疗方法出现治愈、显效、好转和无效等不同的效果等。 这类问题,实质上是一个回归问题,因变量就是上述提到 的这些分类型变量,自变量x是与之有关的一些因素。但 是,这样的问题却不能直接用线性回归分析方法解决,其 根本原因在于因变量是分类型变量,严重违背了线性回归 分析对数据的假设条件。那么应该怎样解决这个问题呢?
第11章 Logistic回归分析
学习目标
• 了解Logistic回归模型的建立和假设检验; • 了解Logistic回归模型的应用领域; • 掌握Logistic回归模型系数的解释,及回归系数与
OR值之间的关系;
• 掌握Logistic回归过程步; • 掌握哑变量的设置和结果的解释; • 掌握多元Logistic回归模型的逐步过程法和系数的
非条件Logistic回归
• 研究者将所研究的问题转换一个角度,不
是直接分析y与x的关系,而是分析y取某个
值的概率P与x的关系。例如,令y为1,0变
量,y=1表示有病,y=0表示未患病;x是
与患病有关的危险因素。如果P表示患病的 概率,即P=prob(y=1),那么研究患病 的概率P与危险因素x的关系就不是很困难
所以不暴露时, Logit(P0) = α , 比值(odds) = exp(α)
则,暴露对于不暴露的比值比(odds ratio)为: OR = exp(α + β ) / exp(α) = exp(β)
举例2 使用雌激素与子宫内膜癌病例对照研究
(病例对照,曾光《现代流行病学方法与应用》,P76)
————————————
————————————
MI 非MI 合计
MI 非MI 合计
—————————————————————————————————
服OC 21 17 38
18 7 25
未—服—O—C——2—6———59———8—5——8—8———9—5———1—8—3
——
合计 47 76 123 106 102 208
不同年龄组内服用避孕药的比例
——————————————————————————
年龄
服OC
不服OC
合计
——————————————————————————
〈40
38(0.31) 85
123
≥40
25(0.12) 183
208
——————————————————————————
合计
63
268
= p q X10 X10
px10
= e 1x1
1 px10
e 1 1
= e 10
=e1
假设建立了如下的logistic回归方程:
Logit P = α + βx
x 为二分变量,当暴露时,取值为1;
不暴露时,取值为0。
所以暴露时,
Logit(P1) = α + β, 比值(odds) = exp(α + β )
—————————————————————————
OR(1) = 2.803 2 (1)= 6.77 OR(2) = 2.776 2 (2)= 5.03
ORMH = (ai*di/ni) / (bi *ci/ni) ORMH =2.79
