高考真题立体几何文科
高考文科数学专题5 立体几何 高考文科数学 (含答案)
专题五 立体几何第一讲 空间几何体1．棱柱、棱锥 (1)棱柱的性质侧棱都相等，侧面是平行四边形；两个底面与平行于底面的截面是全等的多边形；过不相邻的两条侧棱的截面是平行四边形；直棱柱的侧棱长与高相等且侧面与对角面是矩形． (2)正棱锥的性质侧棱相等，侧面是全等的等腰三角形，斜高相等；棱锥的高、斜高和斜高在底面内的射影构成一个直角三角形；棱锥的高、侧棱和侧棱在底面内的射影也构成一个直角三角形；某侧面的斜高、侧棱及底面边长的一半也构成一个直角三角形；侧棱在底面内的射影、斜高在底面内的射影及底面边长的一半也构成一个直角三角形． 2．三视图(1)三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线．画三视图的基本要求：正俯一样长，俯侧一样宽，正侧一样高； (2)三视图排列规则：俯视图放在正视图的下面，长度与正视图一样；侧视图放在正视图的右面，高度和正视图一样，宽度与俯视图一样． 3．几何体的切接问题(1)解决球的内接长方体、正方体、正四棱柱等问题的关键是把握球的直径即棱柱的体对角线长．(2)柱、锥的内切球找准切点位置，化归为平面几何 问题．4．柱体、锥体、台体和球的表面积与体积(不要求记忆) (1)表面积公式①圆柱的表面积 S ＝2πr (r ＋l )； ②圆锥的表面积S ＝πr (r ＋l )；③圆台的表面积S ＝π(r ′2＋r 2＋r ′l ＋rl )； ④球的表面积S ＝4πR 2. (2)体积公式①柱体的体积V ＝Sh ；②锥体的体积V ＝13Sh ；③台体的体积V ＝13(S ′＋SS ′＋S )h ；④球的体积V ＝43πR 3.1． (2013·广东)某四棱台的三视图如图所示，则该四棱台的体积是( )A ．4 B.143C.163D ．6答案 B解析 由三视图知四棱台的直观图为由棱台的体积公式得：V ＝13(2×2＋1×1＋2×2×1×1)×2＝143.2． (2013·四川)一个几何体的三视图如图所示，则该几何体的直观图可以是( )答案 D解析由三视图可知上部是一个圆台，下部是一个圆柱，选D.3． (2013·江西)如图，正方体的底面与正四面体的底面在同一平面α上，且AB∥CD，正方体的六个面所在的平面与直线CE，EF相交的平面个数分别记为m，n，那么m＋n＝( )A．8 B．9 C．10 D．11答案 A解析取CD的中点H，连接EH，HF.在四面体CDEF中，CD⊥EH，CD⊥FH，所以CD⊥平面EFH，所以AB⊥平面EFH，所以正方体的左、右两个侧面与EF平行，其余4个平面与EF相交，即n＝4.又因为CE与AB在同一平面内，所以CE与正方体下底面共面，与上底面平行，与其余四个面相交，即m＝4，所以m＋n＝4＋4＝8.4． (2013·新课全国Ⅱ)一个四面体的顶点在空间直角坐标系O－xyz中的坐标分别是(1,0,1)，(1,1,0)，(0,1,1)，(0,0,0)，画该四面体三视图中的正视图时，以zOx平面为投影面，则得到正视图可以为( )答案 A解析根据已知条件作出图形：四面体C1－A1DB，标出各个点的坐标如图(1)所示，可以看出正视图为正方形，如图(2)所示．故选A.5． (2013·福建)已知某一多面体内接于球构成一个简单组合体，如果该组合体的正视图、侧视图、俯视图均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是________．答案12π解析由三视图知，该几何体为正方体和球组成的组合体，正方体的对角线为球的直径．所以2R＝23，即R＝3，球的表面积为S＝4πR2＝12π.题型一空间几何体的三视图例1(1)(2012·广东)某几何体的三视图如图所示，它的体积为( )A．12πB．45πC．57πD．81π(2)(2012·陕西)将正方体(如图(1)所示)截去两个三棱锥，得到如图(2)所示的几何体，则该几何体的左(侧)视图为( )审题破题根据三视图先确定原几何体的直观图和形状，然后再解题．答案(1)C (2)B解析 (1)由三视图知该几何体是由圆柱、圆锥两几何体组合而成，直观图如图所示． 圆锥的底面半径为3，高为4，圆柱的底面半径为3，高为5，∴V ＝V 圆锥＋V 圆柱＝13Sh 1＋Sh 2＝13×π×32×4＋π×32×5＝57π.(2)还原正方体后，将D 1，D ，A 三点分别向正方体右侧面作垂线．D 1A 的射影为C 1B ，且为实线，B 1C 被遮挡应为虚线．反思归纳 将三视图还原成直观图是解答该类问题的关键，其解题技巧是对常见简单几何体及其组合体的三视图，特别是正方体、长方体、圆柱、圆锥、棱柱、棱锥、球等几何体的三视图分别是什么图形，数量关系有什么特点等都应该熟练掌握，会画出其直观图，然后由三视图验证．变式训练1 若某几何体的三视图(单位：cm)如图所示，则此几何体的体积是________ cm 3.答案 18解析 由几何体的三视图可知，该几何体由两个直四棱柱构成，其直观图如图所示．上底面直四棱柱的长是3 cm ，宽是3 cm ，高是1 cm ，故其体积为9 cm 3，下底面直四棱柱的高是3 cm ，长是1 cm ，宽是3 cm ，其体积为9 cm 3.故该几何体的体积为V ＝18 cm 3. 题型二 空间几何体的表面积和体积例2 如图所示，已知E 、F 分别是棱长为a 的正方体ABCD —A 1B 1C 1D 1的棱A 1A 、CC 1的中点，求四棱锥C 1—B 1EDF 的体积．审题破题 本题可从两个思路解题：思路一：先求出四棱锥C 1—B 1EDF 的高及其底面积，再利用棱锥的体积公式求出其体积； 思路二：先将四棱锥C 1—B 1EDF 化为两个三棱锥B 1—C 1EF 与D —C 1EF ，再求四棱锥C 1—B 1EDF 的体积．解 方法一 连接A 1C 1，B 1D 1交于点O 1，连接B 1D ，过O 1作。
高考真题立体几何文科
文科立体几何4、如图,矩形ABCD中,ABE AD 平面⊥,2===BC EB AE ,F 为CE 上的点,且ACE BF 平面⊥、C1 (Ⅰ)求证:BCEAE平面⊥;(Ⅱ)求证;BFDAE平面//;(Ⅲ)求三棱锥BGFC-的体积、5、如图所示,在棱长为2的正方体1111ABCD A B C D-中,E、F分别为1DD、DB的中点.(Ⅰ)求证://EF平面11ABC D;(Ⅱ)求证:1EF B C⊥;(III)求三棱锥EFCBV-1的体积.6、如图,在四棱锥ABCDP-中,底面ABCD就是正方形,侧棱⊥PD底面ABCD,1==DCPD,E就是PC的中点,作PBEF⊥交PB于点F.(I) 证明: PA∥平面EDB;(II) 证明:PB⊥平面EFD;(III) 求三棱锥DEFP-的体积.7、如图, 在三棱柱111ABC A B C-中,3AC=,1CC⊥平面ABC,4BC=,5AB=,14AA=,点D就是AB的中点,(1)求证:1AC BC⊥;(2)求证:11AC CDBP平面;(3)求三棱锥11C CDB-的体积。
8、如图,四边形ABCD为矩形,AD⊥平面ABE,AE＝EB＝BC＝2,F且BF⊥平面ACE.(1)求证:AE⊥BE;(2)求三棱锥D－AEC的体积;A BDEFA1B1(3)设M 在线段AB 上,且满足AM ＝2MB,试 在线段CE 上确定一点N,使得MN ∥平面DAE 、9、如图,在四棱锥P —ABCD 中,底面ABCD 就是菱形,∠ABC=60°,PA=AC=a,PB=PD=a 2,点E,F分别在PD,BC 上,且PE:ED=BF:FC 。
(1)求证:PA ⊥平面ABCD; (2)求证:EF//平面PAB 。
10、正方形ABCD 所在平面与三角形CDE 所在平面相交于CD ,AE ⊥平面CDE ,且3AE =,6AB =.(1)求证:AB ⊥平面ADE ;(2)求凸多面体ABCDE 的体积.11、如图的几何体中,AB ⊥平面ACD ,DE ⊥平面ACD ,△ACD 为等边三角形,22AD DE AB ===,F 为CD 的中点.(1)求证://AF 平面BCE ; (2)求证:平面BCE ⊥平面CDE ; (3)求这个几何体的体积. 1213、已知直角梯形ABCD 中,AB ∥CD ,AB ⊥BC ,AB ＝1,BC ＝2,CD ＝1＋3,过A 作AE ⊥CD ,垂足为E ,G 、F 分别为AD 、CE 的中点,现将△ADE 沿AE 折叠,使DE ⊥EC 、ABCDE(1)求证:BC ⊥平面CDE ; (2)求证:FG ∥平面BCD ; (3)求四棱锥D －ABCE 的体积、17、如图4,在边长为1的等边三角形ABC 中,,D E 分别就是,AB AC 边上的点,AD AE =,F 就是BC 的中点,AF 与DE 交于点G ,将ABF ∆沿AF 折起,得到图 4GEF ABCD如图5所示的三棱锥A BCF -,其中22BC =、 (1) 证明:DE //平面BCF ; (2) 证明:CF ⊥平面ABF ; (3) 当23AD =时,求三棱锥F DEG -的体积F DEG V -、 18、如图,直三棱柱ABC-A 1B 1C 1中,D,E 分别就是AB,BB 1的中点、(1) 证明: BC 1//平面A 1CD;(2) 设AA 1= AC=CB=2,AB=2,求三棱锥C 一A 1DE 的体积、19、如图,四棱锥P ABCD -的底面ABCD 就是边长为2的菱形,60BAD ∠=o 、已知2,6PB PD PA === 、(Ⅰ)证明:PC BD ⊥(Ⅱ)若E 为PA 的中点,求三菱锥P BCE -的体积、19.G1、G4、G3[2014·安徽卷] 如图1-5所示,四棱锥P - ABCD 的底面就是边长为8的正方形,四条侧棱长均为217、点G ,E ,F ,H 分别就是棱PB ,AB ,CD ,PC 上共面的四点,平面GEFH ⊥平面ABCD ,BC ∥平面GEFH 、图 5DGBFCAE图1-5(1)证明:GH ∥EF ;(2)若EB ＝2,求四边形GEFH 的面积.20.G1、G5[2014·重庆卷] 如图1-4所示四棱锥P ABCD 中,底面就是以O 为中心的菱形,PO ⊥底面ABCD ,AB ＝2,∠BAD ＝π3,M 为BC 上一点,且BM ＝12、(1)证明:BC ⊥平面POM ;(2)若MP ⊥AP ,求四棱锥P -ABMO 的体积.图1-417.G2、G8[2014·陕西卷] 四面体ABCD 及其三视图如图1-4所示,平行于棱AD ,BC 的平面分别交四面体的棱AB ,BD ,DC ,CA 于点E ,F ,G ,H 、图1-4(1)求四面体ABCD 的体积; (2)证明:四边形EFGH 就是矩形.17.G4 、G5[2014·北京卷] 如图1-5,在三棱柱ABCA1B1C1中,侧棱垂直于底面,AB⊥BC,AA1＝AC＝2,BC＝1,E,F分别就是A1C1,BC的中点.图1-5(1)求证:平面ABE⊥平面B1BCC1;(2)求证:C1F∥平面ABE;(3)求三棱锥EABC的体积.16.G4、G5[2014·江苏卷] 如图1-4所示,在三棱锥P -ABC中,D,E,F分别为棱PC,AC,AB 的中点.已知P A⊥AC,P A＝6,BC＝8,DF＝5、求证:(1)直线P A∥平面DEF;(2)平面BDE⊥平面ABC、图1-418.G4、G11[2014·新课标全国卷Ⅱ] 如图1-3,四棱锥P -ABCD中,底面ABCD为矩形,P A ⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设AP＝1,AD＝3,三棱锥P -ABD的体积V＝34,求A到平面PBC的距离.18.G5,G4[2014·山东卷] 如图1-4所示,四棱锥P ABCD 中,AP ⊥平面PCD ,AD ∥BC ,AB ＝BC ＝12AD ,E ,F 分别为线段AD ,PC 的中点.图1-4(1)求证:AP ∥平面BEF ; (2)求证:BE ⊥平面P AC 、18.G4、G5[2014·四川卷] 在如图1-4所示的多面体中,四边形ABB 1A 1与ACC 1A 1都为矩形.(1)若AC ⊥BC ,证明:直线BC ⊥平面ACC 1A 1、(2)设D ,E 分别就是线段BC ,CC 1的中点,在线段AB 上就是否存在一点M ,使直线DE ∥平面A 1MC ？请证明您的结论.图1-419.G5,G7[2014·福建卷] 如图1-6所示,三棱锥A BCD 中,AB ⊥平面BCD ,CD ⊥BD 、 (1)求证:CD ⊥平面ABD ;(2)若AB ＝BD ＝CD ＝1,M 为AD 中点,求三棱锥A - MBC 的体积.19.G5、G7[2014·辽宁卷] 如图1-4所示,△ABC与△BCD所在平面互相垂直,且AB＝BC ＝BD＝2,∠ABC＝∠DBC＝120°,E,F,G分别为AC,DC,AD的中点.图1-4(1)求证:EF⊥平面BCG;(2)求三棱锥D -BCG的体积.19.G5 G11[2014·全国新课标卷Ⅰ] 如图1-4,三棱柱ABCA1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C、图1-4(1)证明:B1C⊥AB;(2)若AC⊥AB1,∠CBB1＝60°,BC＝1,求三棱柱ABC -A1B1C1的高.19.G5 G11[2014·全国新课标卷Ⅰ] 如图1-4,三棱柱ABCA1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C、图1-4(1)证明:B1C⊥AB;(2)若AC⊥AB1,∠CBB1＝60°,BC＝1,求三棱柱ABC -A1B1C1的高.18.G1,G4,G5[2015·北京卷] 如图1-5,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC＝BC＝2,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;(2)求证:平面MOC⊥平面VAB;(3)求三棱锥V-ABC的体积.18.G1,G4,G5[2015·四川卷] 一个正方体的平面展开图及该正方体的直观图的示意图如图1-2所示.(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);(2)判断平面BEG与平面ACH的位置关系,并证明您的结论;(3)证明:直线DF⊥平面BEG、图1-218.G4,G5,G11[2015·广东卷] 如图1-3,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD＝PC＝4,AB＝6,BC＝3、(1)证明:BC∥平面PDA;(2)证明:BC⊥PD;(3)求点C到平面PDA的距离.图1-316.G4、G5[2015·江苏卷] 如图1-2,在直三棱柱ABC - A 1B 1C 1中,已知AC ⊥BC ,BC ＝CC 1,设AB 1的中点为D ,B 1C ∩BC 1＝E 、求证:(1)DE ∥平面AA 1C 1C ;(2)BC 1⊥AB 1、图1-218.G5[2015·全国卷Ⅰ] 如图1-5,四边形ABCD 为菱形,G 为AC 与BD 的交点,BE ⊥平面ABCD 、(1)证明:平面AEC ⊥平面BED ;(2)若∠ABC ＝120°,AE ⊥EC, 三棱锥E - ACD 的体积为63,求该三棱锥的侧面积.18.G5[2015·陕西卷] 如图1-5(1),在直角梯形ABCD 中,AD ∥BC ,∠BAD ＝π2,AB ＝BC ＝12AD ＝a ,E 就是AD 的中点,O 就是AC 与BE 的交点.将△ABE 沿BE 折起到图(2)中△A 1BE 的位置,得到四棱锥A 1 BCDE 、(1)证明:CD ⊥平面A 1OC ;(2)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1 BCDE 的体积为362,求a 的值.图1-5 20.G5、G7[2015·重庆卷] 如图1-4,三棱锥P - ABC 中,平面P AC ⊥平面ABC ,∠ABC ＝π2,点D ,E 在线段AC 上,且AD ＝DE ＝EC ＝2,PD ＝PC ＝4,点F 在线段AB 上,且EF ∥BC 、(1)证明:AB ⊥平面PFE ;(2)若四棱锥P - DFBC 的体积为7,求线段BC 的长.图1-419.G12[2015·安徽卷] 如图1-5,三棱锥P -ABC 中,P A ⊥平面ABC ,P A ＝1,AB ＝1,AC ＝2,∠BAC ＝60°、(1)求三棱锥P -ABC 的体积;(2)证明:在线段PC 上存在点M ,使得AC ⊥BM ,并求PM MC的值.图1-519.G1、G4[2016·全国卷Ⅲ] 如图1-5,四棱锥P - ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB ＝AD ＝AC ＝3,P A ＝BC ＝4,M 为线段AD 上一点,AM ＝2MD ,N 为PC 的中点.(1)证明:MN ∥平面P AB ;(2)求四面体N - BCM 的体积.图1-518.G4,G5[2016·北京卷] 如图1-4,在四棱锥P - ABCD 中,PC ⊥平面ABCD ,AB ∥DC ,DC ⊥AC 、(1)求证:DC ⊥平面P AC 、(2)求证:平面P AB ⊥平面P AC 、(3)设点E 为AB 的中点,在棱PB 上就是否存在点F ,使得P A ∥平面CEF ？说明理由.18.G4,G5[2016·山东卷] 在如图1-5所示的几何体中,D 就是AC 的中点,EF ∥DB 、(1)已知AB ＝BC ,AE ＝EC ,求证:AC ⊥FB ;(2)已知G ,H 分别就是EC 与FB 的中点,求证:GH ∥平面ABC 、图1-517.G7、G4、G5[2016·四川卷] 如图1-4,在四棱锥P - ABCD 中,P A ⊥CD ,AD ∥BC ,∠ADC＝∠P AB ＝90°,BC ＝CD ＝12AD 、 (1)在平面P AD 内找一点M ,使得直线CM ∥平面P AB ,并说明理由;(2)证明:平面P AB ⊥平面PBD 、图1-418.G5[2016·全国卷Ⅰ] 如图1-4,已知正三棱锥P - ABC 的侧面就是直角三角形,P A ＝6,顶点P 在平面ABC 内的正投影为点D ,D 在平面P AB 内的正投影为点E ,连接PE 并延长交AB 于点G 、(1)证明:G 就是AB 的中点;(2)作出点E 在平面P AC 内的正投影F (说明作法及理由),并求四面体PDEF 的体积.图1-419.G5[2016·全国卷Ⅱ] 如图1-4,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE ＝CF ,EF 交BD 于点H 、将△DEF 沿EF 折到△D ′EF 的位置.(1)证明:AC ⊥HD ′;(2)若AB ＝5,AC ＝6,AE ＝54,OD ′＝22,求五棱锥D ′ABCFE 的体积.图1-411、【2017课标1,文18】如图,在四棱锥P-ABCD 中,AB//CD ,且90BAP CDP ∠=∠=o .(1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,90APD ∠=o ,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积. 12、【2017课标II,文18】如图,四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底面ABCD ,01,90.2AB BC AD BAD ABC ==∠=∠= (1)证明:直线//BC 平面PAD ;(2)若△PAD 面积为27,求四棱锥P ABCD -的体积、13、【2017课标3,文19】如图,四面体ABCD 中,△ABC 就是正三角形,AD =CD .(1)证明:AC ⊥BD ;(2)已知△ACD 就是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.14、【2017山东,文18】(本小题满分12分)由四棱柱ABCD -A 1B 1C 1D 1截去三棱锥C 1- B 1CD 1后得到的几何体如图所示,四边形ABCD 为正方形,O 为AC 与BD 的交点,E 为AD 的中点,A 1E ⊥平面ABCD ,(Ⅰ)证明:1A O ∥平面B 1CD 1;(Ⅱ)设M 就是OD 的中点,证明:平面A 1EM ⊥平面B 1CD 1、15、【2017天津,文17】如图,在四棱锥P ABCD -中,AD ⊥平面PDC ,AD BC ∥,PD PB ⊥,1AD =,3BC =,4CD =,2PD =、(I)求异面直线AP 与BC 所成角的余弦值;(II)求证:PD ⊥平面PBC ;(Ⅲ)求直线AB 与平面PBC 所成角的正弦值、16、【2017北京,文18】如图,在三棱锥P –ABC 中,PA ⊥AB ,PA ⊥BC ,AB ⊥BC ,PA =AB =BC =2,D 为线段AC 的中点,E 为线段PC 上一点.(Ⅰ)求证:PA ⊥BD ;(Ⅱ)求证:平面BDE ⊥平面PAC ;(Ⅲ)当PA ∥平面BD E 时,求三棱锥E –BCD 的体积.。
高考文科立体几何题汇总（含答案）
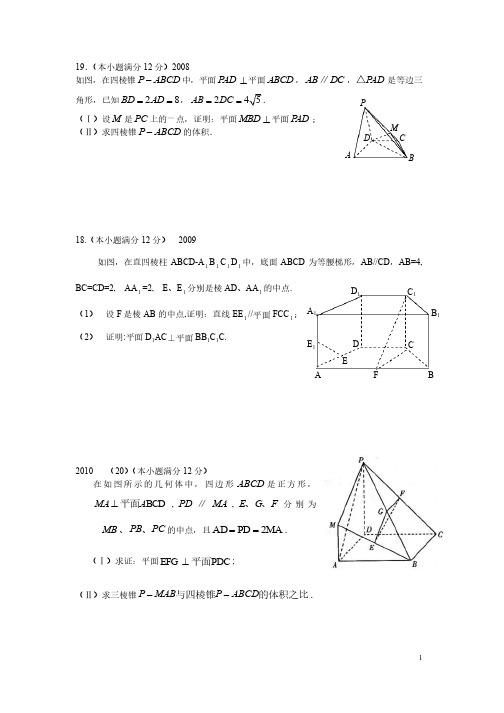
19．（本小题满分12分）2008 如图，在四棱锥P ABCD -中，平面PAD ^平面ABCD ，AB DC ∥，P AD △是等边三角形，已知28BD AD ==，245AB DC ==．（Ⅰ）设M 是PC 上的一点，证明：平面MBD ^平面PAD ； （Ⅱ）求四棱锥P ABCD -的体积．的体积．18.（本小题满分12分）分） 2009 如图，在直四棱柱ABCD-A 1B 1C 1D 1中，底面ABCD 为等腰梯形，AB//CD ，AB=4, BC=CD=2, AA 1=2, E 、E 1分别是棱AD 、AA 1的中点. （1） 设F 是棱AB 的中点,证明：直线EE 1//平面FCC 1； （2） 证明:平面D 1AC ⊥平面BB 1C 1C. 2010 （20）（本小题满分12分）分）在如图所示的几何体中，四边形ABCD 是正方形，BCD A MA 平面^,PD ∥MA ,E G F 、、分别为MB 、PC PB 、的中点，且2MA PD AD ==．（Ⅰ）求证：平面PDC EFG 平面^; （Ⅱ）求三棱锥的体积之比与四棱锥ABCD P MAB P --．A B C M P D EA B C F E 1 A 1 B 1 C 1 D 1 D 2011 19．（本小题满分12分）分）如图，在四棱台1111ABCD A B C D -中，1D D ^平面ABCD ，底面ABCD 是平行四边形，AB=2AD ，11AD=A B ，BAD=Ð60° （Ⅰ）证明：1AA BD ^；（Ⅱ）证明：11CC A BD ∥平面．2012 (19) ( (本小题满分本小题满分12分)如图，几何体E ABCD -是四棱锥，△ABD 为正三角形，,CB CD EC BD =^. (Ⅰ)求证：BE DE =；(Ⅱ)若∠120BCD =°，M 为线段AE 的中点，的中点， 求证：DM ∥平面BEC .53238545545523163 ACM PDOEA B C F 1 1 C 1 D 1 D F 1 EC 1 1 C 1 D 1 D 所以CC 1⊥AC,因为底面ABCD 为等腰梯形，AB=4, BC=2, F 是棱AB 的中点,所以CF=CB=BF ，△BCF 为正三角形，为正三角形， 60BCF Ð=°,△ACF 为等腰三角形，且30ACF Ð=°所以AC ⊥BC, 又因为BC 与CC 1都在平面BB 1C 1C 内且交于点C, 所以AC ⊥平面BB 1C 1C,而AC Ì平面D 1AC, 所以平面D 1AC ⊥平面BB 1C 1C. 2010 （20）本小题主要考查空间中的线面关系，考查线面垂直、）本小题主要考查空间中的线面关系，考查线面垂直、面面垂直的判定及几面面垂直的判定及几何体体积的计算，考查试图能力和逻辑思维能力。
(整理)高考文科数学立体几何_(答案详解).
选择题1.（12年四川卷）如图，半径为R 的半球O 的底面圆O 在平面α内，过点O 作平面α的垂线交半球面于点A ，过圆O 的直径CD 作平面α成45角的平面与半球面相交，所得交线上到平面α的距离最大的点为B ，该交线上的 一点P 满足60BOP ∠=，则A 、P 两点 间的球面距离为 （ ）A. RB. 4R πC. RD. 3R π 2.（12年广东卷）某几何体的三视图如图1所示，它的体积为( )A. 72πB. 48πC. 30πD. 24π3.（12年重庆卷）设四面体的六条棱的长分别为1，1，1，1和a 且长为a的棱与长为的棱异面，则a 的取值范围是（ ）A.B.C.D.4.（12年浙江卷）已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积是（ ） A.1cm 3 B.2cm 3 C.3cm 3 D.6cm3图1C5.（12年浙江卷）设l 是直线，αβ，是两个不同的平面 （ ）A.若l ∥α，l ∥β，则α∥βB. 若l ∥α，l ⊥β，则α⊥βC. 若α⊥β，l ⊥α，则l ⊥βD. 若α⊥β， l ∥α，则l ⊥β6.（12年新课标卷）如图，网格上小正方形的边长为1，粗线画出的是某几何体的三视图，则几何体的体积为（ ）A .6B .9C .12D .187. 某三棱锥的三视图如图所示，该三棱锥的表面积是（ ）A．28+ B．30+ C．56+ D ．60+ 8.（12年福建卷）一个几何体的三视图形状都相同，大小均等，那么这个几何体不可以是（ ）A ．球B ．三棱锥C ．正方体D ．圆柱 9.（12年湖南卷）某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能．．．是（ ）10.（12年江西卷）若一个几何体的三视图如图所示，则此几何体的体积为 ( ) A B C DA ．112 B.5 C.4 D. 9211.（12年大纲卷）已知正四棱柱1111ABCD A B C D -中，2AB =，1CC =E 为1CC 的中点，则直线1AC 与平面BED 的距离为（ ）A ．2 BCD ．1 12.（12年陕西卷）将正方体（如图1所示）截去两个三棱锥，得到图2所示的几何体，则该几何体的左视图为（ ）填空题1．（12年湖北卷）已知某几何体的三视图如图所示，则该几何体的体积为 .左视图主视图俯视图侧视图正视图俯视图2.（12年四川卷）如图，在正方体1111ABCD A B C D -中，M 、N 分别是CD ，1CC 的中点，则异面直线1A M 与DN 所成的角的大小是____________.3.（12年山东卷）如图，正方体1111D C B A ABCD -的棱长为1，E 为线段C B 1上的一点，则三棱锥1DED A -的体积为___________ .4.（12年安徽卷）某几何体的三视图如图所示，该几何体的体积是_____.5.（12年江苏卷）如图，在长方体1111ABCD A B C D -中，3cm AB AD ==，12cm AA =，则四棱锥11A BB D D -的体积为 cm 3．NA 1A B CC 1 A 1 侧（左）视图正（主）视图 4俯视图 5 4 26.（12年辽宁卷）一个几何体的三视图如图所示，则该几何体的体积为_______________.7.（12年辽宁卷）已知点P A B C D ，，，，是球O 表面上的点，PA ABCD ⊥平面，四边形ABCD是边长为.若PA =，则OAB ∆的面积为______________. 8.（12年大纲卷）已知正方形1111ABCD A B C D -中，,E F 分别为1BB ，1CC 的中点，那么异面直线AE 与1D F 所成角的余弦值为 ．9.（12年上海卷）一个高为2的圆柱，底面周长为2π，该圆柱的表面积为 . 10.（12年天津卷）一个几何体的三视图如图所示（单位：m ），则该几何体的体积 3m.2.（12年山东卷）(本小题满分12分)如图，几何体E ABCD -是四棱锥，△ABD 为正三角形，,CB CD EC BD =⊥. (Ⅰ)求证：BE DE =；(Ⅱ)若∠120BCD =︒，M 为线段AE 的中点， 求证：DM ∥平面BEC .3.（12年广东卷）(本小题满分13分)如图所示，在四棱锥P ABCD -中，AB ⊥平面PAD ，//,AB CD PD AD =，E 是PB 中点，F 是DC 上的点，且12DF AB =，PH 为PAD ∆中AD 边上的高. （1）证明：PH ⊥平面ABCD ； （2）若1,1PH AD FC ===，求三棱锥E BCF -的体积； （3）证明：EF ⊥平面PAB ． 6.（12年新课标卷）（本小题满分12分） 如图，三棱柱111ABC A B C -中，侧棱垂直底面，o 90ACB ∠=，112AC BC AA ==，D 是棱1AA 的 中点.(Ｉ) 证明：平面BDC ⊥平面1BDC（Ⅱ）平面1BDC 分此棱柱为两部分，求这两部分体积的比.选择题1.【答案】A【分析】由已知可知，AOP CBD ⊥面面，∴cos cos cos AOP AOB BOP =∠∠∠，带入数据得12cos ==224AOP ∠，arccos 4AP R ∴=. 2. 【答案】C【分析】几何体是半球与圆锥叠加而成它的体积为32141π3π330π233V =⨯⨯+⨯⨯= 3.【答案】：A【分析】：如图所示，取,EF 分别为,PC AB 的中点，依题意可得PB BC ⊥，所以 GEAB FCPD H2BE ==.在BEF ∆中，BF BE <，所以2AB BF =<4. 【答案】C【分析】由题意判断出，底面是一个直角三角形，两个直角边分别为1和2，整个棱锥的高由侧视图可得为3，所以三棱锥的体积为11123132⨯⨯⨯⨯=. 5.【答案】B【分析】利用排除法可得选项B 是正确的，∵l ∥α，l ⊥β，则α⊥β．如选项A ：l ∥α，l ∥β时，α⊥β或α∥β；选项C ：若α⊥β，l ⊥α时，l ∥β或l β⊂；选项D ：若α⊥β，l ∥α时，l ∥β或l ⊥β．6. 【答案】B【分析】由三视图知，其对应几何体为三棱锥，其底面为一边长为6，底边上高为3的等腰三角形，棱锥的高为3，故其体积为1163332⨯⨯⨯⨯=9，故选B. 7. 【答案】B 【分析】从所给的三视图可以得到该几何体为三棱锥，本题所求表面积为三棱锥四个面的面积之和.利用垂直关系和三角形面积公式，可得：=10=10=10S S S S 后右左底，，，因此该几何体表面积30S =+，故选B .8. 【答案】D【分析】圆的正视图（主视图）、侧视图（左视图）和俯视图均为圆；三棱锥的正视图（主视图）、侧视图（左视图）和俯视图可以为全等的三角形； 正方体的正视图（主视图）、侧视图（左视图）和俯视图均为正方形； 圆柱的正视图（主视图）、侧视图（左视图）为矩形，俯视图为圆.9. 【答案】D【分析】本题是组合体的三视图问题，由几何体的正视图和侧视图均相同，原图下面部分应为圆柱或直四棱柱，上面是圆柱或直四棱柱或下底是直角的三棱柱，A ，B ，C 都可能是该几何体的俯视图，D 不可能是该几何体的俯视图，因为它的正视图上面部分应为中间有条虚线的矩形..10. 【答案】C【分析】通过观察几何体的三视图可知，该几何体是一个底面为六边形（2条对边长为1，其余4），高为1的直棱柱.所以该几何体的体积为112122142V sh ⎛⎫==⨯+⨯⨯⨯⨯= ⎪⎝⎭，故选D.11. 【答案】D【分析】因为底面的边长为2，高为,AC BD ，得到交点为O ，连接EO ，1//EO AC ，则点1C 到平面BDE 的距离等于C 到平面BDE 的距离，过点C 作CH OE ⊥，则CH 即为所求，在三角形OCE 中，利用等面积法，可得1CH =，故选答案D. 12.【答案】B【分析】显然从左边看到的是一个正方形，因为割线1AD 可见，所以用实线表示；而割线1B C 不可见，所以用虚线表示．故选B ．填空题1. 【答案】12π【分析】该几何体的左中右均为圆柱体，其中左右圆柱体全等，是底面半径为2，高为1的 圆柱体；中间部分是底面半径为1，高为4的圆柱体，所以所求的体积为：22π212π14=12πV =⨯⨯⨯+⨯⨯.2. 【答案】o 90【分析】方法一：连接D 1M ，易得DN ⊥A 1D 1 ，DN ⊥D 1M ，所以，DN ⊥平面A 1MD 1，又A 1M ⊂平面A 1MD 1，所以，DN ⊥A 1M ，故夹角为o 90 方法二：以D 为原点，分别以DA ， DC ， DD 1为x ， y ， z 轴，建立空间直角坐标系D —xyz .设正方体边长为2，则D （0，0，0），N （0，2，1），M （0，1，0），A 1（2，0，2）故1(0,2,1)(2,1,2)DN MA ==-， 所以， 111cos ,0DN MA DN MA DN MA <>==，故DN ⊥A 1M ，所以夹角为o 90.3. 【答案】61【分析】求1DED A -的体积，显然为定值，也就是说三棱锥的底面面积与三棱锥的高都为定值，因此，我们需要找一个底面为定值的三角形，三角形1ADD 的面积为21（为定值），而E 点到底面1ADD 的高恰为正方体的高为1（为定值），因此体积为61. 4. 【答案】56 【分析】该几何体是底面是直角梯形，高为4的直四棱柱，几何体的的体积是：()12544562V =⨯+⨯⨯=5. 【答案】6【分析】∵长方体底面ABCD 是正方形 ，∴△ABD 中BD cm ，BD 边上的高（它也是四棱锥11A BB D D -的高）∴四棱锥11A BB D D -的体积为123⨯6. 【答案】12π+【分析】由三视图可知该几何体为一个长方体和一个等高的圆柱的组合体，其中长方体的长、宽、高分别为4、3、1，圆柱的底面直径为2，高位1，所以该几何体的体积为3411112ππ⨯⨯+⨯⨯=+7.【答案】【分析】点P A B C D O 、、、、为球内接长方体的顶点，14O OAB ∴∆球心为该长方体对角线的中点，的面积是该长方体对角面面积的，164OAB AB PA S ∆===⨯=8. 【答案】35【分析】首先根据已知条件，连接DF ，则由//DF AE 可知1DFD ∠或其补角为异面直线AE 与1D F 所成的角，设正方体的棱长为2，则可以求解得到112DF D F DD ===，再由余弦定理可得22211115543cos 2255D F DF D D DFD D F DF +-+-∠===⋅⨯.9. 【答案】π6【分析】根据该圆柱的底面周长得底面圆的半径为1=r ，所以该圆柱的表面积为：22π2π4π2π6πS rh r =+=+=.10. 【答案】30【分析】由三视图可知这是一个下面是个长方体，上面是个平躺着的底面为直角梯形的直四棱柱构成的组合体.长方体的体积为24243=⨯⨯，直四棱柱的体积是6412)21(=⨯⨯+，所以几何体的总体积为30.2. 【证明】(Ⅰ)设BD 的中点为O ，连接,OC OE , 则由BC CD CO BD =知垂直 又CE BD ⊥，所以BD OCE ⊥平面 所以BD OE ⊥，即OD 是BE 的垂直平分线BE DE =所以(Ⅱ)取AB 的中点为N ，连接MN ,DN ONM因为M 是AE 的中点，，所以//MN BE 因为ABD ∆是等边三角形，所以DN ⊥AB由o o 12030BCD CBD ∠=∠=知，所以o 90ABC ∠=，即BC ⊥AB所以ND //BC所以平面MND //平面BEC ，故DM //平面BEC3. 【解】（1）AB ⊥平面PAD ，PH ⊂面PAD PH AB ⇒⊥ 又,PH AD ADAB A PH ⊥=⇒⊥面ABCD（2）E 是PB 中点⇒点E 到面BCF 的距离1122h PH ==三棱锥E BCF -的体积1111113326212BCF V S h FC AD h ∆=⨯=⨯⨯⨯⨯=⨯= （3）过D 作DG PA G ⊥于，连接EG ，易得EG PAD ⊥面 由AB ⊥平面PAD ⇒面PAD ⊥面PAB DG ⇒⊥面PAB E P B E GP A A B P是的中点，⊥，⊥ 11//,//////22EG AB DF AB EG DF DG EF ⇒⇒⇒ 得：EF ⊥平面PAB6. 【解】（Ⅰ）由题设知1BC CC ⊥，BC AC ⊥，1CC AC C =∩，∴BC ⊥面11ACC A又∵1DC ⊂面11ACC A ，∴1DC BC ⊥，由题设知01145A DC ADC ∠=∠=，∴1CDC ∠=090，即1DC DC ⊥，又∵DC BC C =∩，∴1DC ⊥面BDC ， ∵1DC ⊂面1BDC ，∴面BDC ⊥面1BDC ；（Ⅱ）设棱锥1B DACC -的体积为1V ，AC =1，由题意得，1V =1121132+⨯⨯⨯=12，由三棱柱111ABC A B C -的体积V =1，精品文档精品文档 ∴11():V V V =1:1，∴平面1BDC 分此棱柱为两部分体积之比为1:1.。
(版)高考试题汇编文科数学立体几何
〔2021全国1文〕16. ACB 90，P为平面ABC外一点，PC 2，点P到ACB两边AC,BC的距离均为3，那么P到平面ABC的距离为 .答案：2解答：如图，过P点做平面ABC的垂线段，垂足为O，那么PO的长度即为所求，再做PE CB,PF CA，由线面的垂直判定及性质定理可得出OE CB,OF CA，在RtPCF中，由PC 2,PF 3，可得出CF 1，同理在RtPCE中可得出CE 1，结合 ACB 90，OE CB,OF CA可得出OE OF 1，OC2，PO PC2OC2 2〔2021全国1文〕19.如图直四棱柱ABCD A1B1C1D1的底面是菱形，AA14,AB 2，BAD60o，E,M,N分别是BC,BB1,A1D的中点.1〕证明：MN//平面C1DE2〕求点C到平面C1DE的距离.答案：见解析解答：〔1〕连结AC,BD相交于点，再过点M作MH//CE交BC于点，再连结GH，NG.1111111E,M,N分别是BC,BB1,A1D的中点.于是可得到NG//C1D，GH//DE，于是得到平面NGHM//平面C1DE，由QMN平面NGHM，于是得到MN//平面C1DE1/19〔2〕QE为BC中点，ABCD为菱形且BAD60oDE BC，又QABCD A1B1C1D1为直四棱柱，DECC1DEC1E，又QAB2,AA14，DE3,C1E17，设点C到平面C1DE的距离为h 由V CC1DE V C1DCE得11317113432h1 432解得h1717所以点C 417到平面C1DE的距离为17〔2021全国2文〕7.设,为两个平面，那么//的充要条件是()A.内有无数条直线与平行B.内有两条相交直线与平行C.,平行于同一条直线D.,垂直于同一平面答案：B解析:根据面面平行的判定定理易得答案.〔2021全国2文〕16.中国有悠久的金石文化，印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体〞〔图1〕.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体表达了数学的对称美.图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的外表上，且此正方体的棱长为 1.那么该半正多面体共有个面，其棱长为.(此题第一空2分，第二空3分.)2/19答案： 262 1解析：由图2 结合空间想象即可得到该正多面体有26个面；将该半正多面体补成正方体后，根据对称性列方程求解 .〔2021全国2文〕17.如图，长方体ABCDA 1B 1C 1D 1的底面ABCD是正方形，点E 在棱AA 1上，BE ⊥EC 1.〔1 〕证明：BE 平面EB 1C1〔2 〕假设AEAE 1,AB3,求四棱锥EBB 1C 1C 的体积.答案： 看解析 看解析解答：〔1〕证明：因为B 1C 1C 面A 1B 1BA ，BE面A 1B 1BA∴B 1C 1⊥BE 又C 1EB 1C 1 C 1，∴BE平面EB 1C 1；〔2〕设AA2a 那么BE2922222a ，C 1E18+a ，C 1B94a1222∴a，∴11 因为C 1B=BEC 1E3V EBB 1C 1CS BB 1C 1Ch363=18333/19(版)高考试题汇编文科数学立体几何〔2021全国3文〕8.如图，点N为正方形ABCD的中心，ECD为正三角形，平面ECD平面ABCD,M是线段ED的中点，那么〔〕A.BM EN，且直线B.BM EN，且直线C.BM EN，且直线D.BM EN，且直线【答案】B【解析】分析】BM,ENBM,ENBM,ENBM,EN是相交直线是相交直线是异面直线是异面直线利用垂直关系，再结合勾股定理进而解决问题．【详解】∵BDE ，N为BD中点M为DE中点，BM，EN共面相交，选项C DCD于O，，为错．作EO连接ON，过M作MF OD于F．连BF，Q平面CDE平面ABCD．EO CD,EO平面CDE，EO平面ABCD，MF平面ABCE，【MFB与EON均为直角三角形．设正方形边长为2，易知EO3,0N1EN2，MF3,BF2295BM3247．24244BM EN，应选B．【点睛】此题为立体几何中等问题，考查垂直关系，线面、线线位置关系.4/19〔2021全国3文〕16.学生到工厂劳动实践，利用3D打印技术制作模型.如图，该模型为长方体ABCD A1B1C1D1挖去四棱锥O EFGH后所得的几何体，其中O为长方体的中心，E,F,G,H分别为所在棱的中点，AB=BC=6cm,AA1=4cm，3D打印所用原料密度为/cm3，不考虑打印损耗，制作该模型所需原料的质量为___________g.【答案】118．8【解析】【分析】根据题意可知模型的体积为四棱锥体积与四棱锥体积之差进而求得模型的体积，再求出模型的质量.【详解】由题意得，四棱锥O-EFGH的底面积为46412312cm2，其高为点O到底面BB1C1C的距12离为3cm，那么此四棱锥的体积为V112312cm2．又长方体ABCD A1B1C1D1的体积为3V2466144cm2，所以该模型体积为V V2V114412132cm2，其质量为132．【点睛】此题牵涉到的是3D打印新时代背景下的几何体质量，忽略问题易致误，理解题中信息联系几何体的体积和质量关系，从而利用公式求解．〔2021全国3文〕19.图1是由矩形ADEB,RtABC和菱形BFGC组成的一个平面图形，其中AB 1,BE BF 2，FBC60o，将其沿AB,BC折起使得BE与BF重合，连结DG，如图2.〔1〕证明图2中的A,C,G,D四点共面，且平面ABC平面BCGE；〔2〕求图2中的四边形ACGD的面积.【答案】(1)见详解；(2)4.5/19【解析】【分析】(1)因为折纸和粘合不改变矩形ABED ，RtVABC 和菱形BFGC 内部的夹角，所以 AD//BE ，BF//CG 依然成立，又因E 和F 粘在一起，所以得证.因为AB 是平面BCGE 垂线，所以易证.(2) 欲求四边形ACGD 的面积，需求出CG 所对应的高，然后乘以CG 即可。
立体几何测试题(文科)
立体几何文科试题一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的． 1、设有直线m 、n 和平面α、β.下列四个命题中，正确的是( )A.若m ∥α,n ∥α,则m ∥nB.若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥βC.若α⊥β，m ⊂α,则m ⊥βD.若α⊥β，m ⊥β，m ⊄α,则m ∥α 2、已知直线,l m与平面αβγ，，满足//l l m βγαα=⊂ ，，和mγ⊥，则有A ．αγ⊥且l m⊥ B ．αγ⊥且//m β C ．//m β且lm⊥ D ．//αβ且αγ⊥3.若()0,1,1a =- ，()1,1,0b = ，且()a b a λ+⊥，则实数λ的值是（ ）A .－1 B.0 C.1 D.－24、已知平面α⊥平面β，α∩β= l ，点A ∈α，A ∉l ，直线AB ∥l ，直线AC ⊥l ，直线m ∥α，m ∥β，则下列四种位置关系中，不一定．．．成立的是（ ） A. AB ∥m B. AC ⊥m C. AB ∥β D. AC ⊥β5一个几何体的三视图及长度数据如图，则几何体的表面积与体积分别为()3,27+A ()328，+B()2327，+C ()23,28+D6、已知长方体的表面积是224cm ，过同一顶点的三条棱长之和是6cm ，则它的对角线长是（ ）A. B. 4cm C. D.7、已知圆锥的母线长5l cm =，高4h cm =，则该圆锥的体积是____________3cmA. 12π B 8π C. 13π D. 16π8、某几何体的三视图如图所示，当ba +取最大值时，这个几何体的体积为 （ ）A ．61 B ．31 C ．32 D ．219、已知,,,A B C D 在同一个球面上,,AB BCD ⊥平面,BC CD ⊥若6,AB =AC =8A D =,则,B C 两点间的球面距离是 （ ）A. 3πB. 43π C. 23π D. 53π10、四面体A B C D 的外接球球心在C D 上，且2C D =，3=AB ，在外接球面上A B ，两点间的球面距离是（ ） A ．π6B ．π3C ．2π3D ．5π611、半径为2cm 的半圆纸片做成圆锥放在桌面上，一阵风吹倒它，它的最高处距桌面（ ） A ．4cmB ．2cmC ．cm 32D ．cm 312、 有一正方体，六个面上分别写有数字1、2、3、4、5、6，有三个人从不同的角度观察的结果如图所示.如果记3的对面的数字为m ，4的对面的数字为n ，那么m+n 的值为（ ） A ．3B ．7C ．8D ．11二．填空题：本大题共4个小题。
高考立体几何文科大题及答案
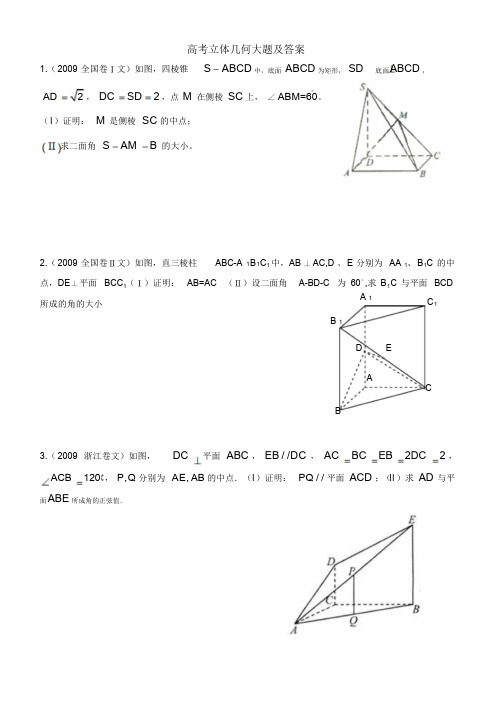
高考立体几何大题及答案1.（2009 全国卷Ⅰ文）如图，四棱锥S ABCD中，底面ABCD 为矩形，SD 底面ABCD ，AD 2 ，DC SD 2，点M 在侧棱SC上，∠ABM=60。
（I）证明：M 是侧棱SC的中点；求二面角S AM B的大小。
2.（2009 全国卷Ⅱ文）如图，直三棱柱ABC-A 1B1C1 中，AB ⊥AC,D 、E 分别为AA 1、B1C 的中点，DE⊥平面BCC1（Ⅰ）证明：AB=AC （Ⅱ）设二面角A-BD-C 为60°,求B1C 与平面BCD所成的角的大小A 1 C1 B 1D EAC B3.（2009 浙江卷文）如图，DC 平面ABC ，EB / /DC ，AC BC EB 2DC 2 ，ACB 120 ，P,Q 分别为AE, AB 的中点．（I）证明：PQ / / 平面ACD ；（II ）求AD 与平面ABE所成角的正弦值．4.（2009 北京卷文）如图，四棱锥P ABCD 的底面是正方形，PD 底面ABCD ，点E 在棱PB 上.（Ⅰ）求证：平面AEC 平面PDB ；（Ⅱ）当PD 2AB 且 E 为PB 的中点时，求AE 与平面PDB 所成的角的大小.5.（2009 江苏卷）如图，在直三棱柱ABC A1B1C1 中，E、F 分别是 A B 、A1C 的中点，点D1在B C 上，A1D B1C1 1 。
求证：（1）EF∥平面ABC ；（2）平面A FD 平面BB1C1C .16.（2009安徽卷文）如图，ABCD的边长为2的正方形，直线l与平面ABCD平行，g和F式l上的两个不同点，且EA=ED，FB=FC，和是平面ABCD内的两点，和都与平面ABCD垂直，（Ⅰ）证明：直线垂直且平分线段AD：（Ⅱ）若∠EAD=∠EAB=60°，EF=2，求多面体ABCDEF的体积。
7.（2009江西卷文）如图，在四棱锥P ABCD中，底面ABCD是矩形，PA平面ABCD，PA AD4，AB2．以BD的中点O为球心、BD为直径的球P面交PD于点M．（1）求证：平面ABM⊥平面PCD；（2）求直线PC与平面ABM所成的角；M（3）求点O到平面ABM的距离．DAOBC8.（2009四川卷文）如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，△ABE是等腰直角三角形，AB AE,FA FE,AEF45（I）求证：EF平面BCE；（II）设线段CD、AE的中点分别为P、M，求证：PM∥平面BCE（III）求二面角F BD A的大小。
(完整版)—高考全国卷Ⅰ文科数学立体几何专题复习(附详细解析)
2012-2018年新课标全国卷Ⅰ文科数学汇编立体几何一、选择题【2017，6】如图，在下列四个正方体中,A ，B 为正方体的两个顶点，M ，N ,Q 为所在棱的中点，则在这四个正方体中,直接AB 与平面MNQ 不平行的是（）【2016，7】如图所示,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径．若该几何体的体积是28π3，则它的表面积是（） A ．17π B ．18π C ．20π D ．28π【2016，11】平面α过正方体1111ABCD A BC D -的顶点A ,α∥平面11CB D ，α平面ABCD m =，α平面11ABB A n =,则,m n 所成角的正弦值为(）A ．3 B ．22C ．3D ．13【2015，6】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委M 依垣内角,下周八尺，高五尺，问”积及为M 几何？”其意思为：“在屋内墙角处堆放M （如图,M 堆为一个圆锥的四分之一)，M 堆底部的弧长为8尺,M 堆的高为5尺，M 堆的体积和堆放的M 各位多少？”已知1斛M 的体积约为1．62立方尺,圆周率约为3，估算出堆放的M 有（ ) A ．14斛 B ．22斛 C ．36斛 D ．66斛【2015，11】圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体的三视图中的正视图和俯视图如图所示，若该几何体的表面积为16+20π，则r =( ) B A ．1 B ．2 C ．4 D ．8【2015，11】【2014，8】【2013,11】【2012，7】【2014，8】如图，网格纸的各小格都是正方形，粗实线画出的一个几何体的三视图，则这个几何体是（ ）A ．三棱锥B ．三棱柱C ．四棱锥D ．四棱柱【2013，11】某几何体的三视图如图所示，则该几何体的体积为（）．A ．16＋8π B．8＋8π C．16＋16π D．8＋16π【2012，7】如图，网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图，则此几何体的体积为A ．6B ．9C ．12D ．15【2012，8】平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2,则此球的体积为（）A ．6πB ．43πC ．46πD ．63π【2018，5】已知圆柱的上、下底面的中心分别为O 1,O 2，过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,该圆柱的表面积为A. 12π B. 12π C. 8π D. 10π【2018，9】某圆柱的高为2，底面周长为16，其三视图如右图,圆柱表面上的点M 在正视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A 。
文科立体几何大题高考真题
文科立体几何大题高考真题1（19年全国1卷）如图直四棱柱1111ABCD A B C D -的底面是菱形，14,2AA AB ==，60BAD ∠=，,,E M N 分别是11,,BC BB A D 的中点.（1）证明：//MN 平面1C DE（2）求点C 到平面1C DE 的距离.&[.2（19年全国2）如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1.（1）证明：BE ⊥平面EB 1C 1；（2）若AE =A 1E ，AB =3，求四棱锥11E BB C C 的体积．` ￥—>3（18年全国1）如图，在平行四边形ABCM中，3AB AC==，90ACM=︒∠，以AC 为折痕将△ACM折起，使点M到达点D的位置，且AB DA⊥．（1）证明：平面ACD⊥平面ABC；（2）Q为线段AD上一点，P为线段BC上一点，且23BP DQ DA==，求三棱锥Q ABP-的体积．；#）4．（18全国卷2）如图，在三棱锥P ABC -中，AB BC ==，4PA PB PC AC ====，O 为AC 的中点．（1）证明：PO ⊥平面ABC ；（2）若点M 在棱BC 上，且MB MC 2=，求点C 到平面POM 的距离．~，'—5（2017•新课标Ⅰ）如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，且四棱锥P﹣ABCD的体积为，求该四棱锥的侧面积．、* >6（2017•新课标2）如图，四棱锥P ABCD -中，侧面PAD 为等边三角形且垂直于底面ABCD ，12AB BC AD ==，90BAD ABC ∠=∠=。
（1） 证明：直线//BC 平面PAD ；（2） 若PCD ∆的面积为27，求四棱锥P ABCD -的体积。
立体几何近12年全国真题(及答案文科)
综上所述，总有 ．
15.【解析】（Ⅰ）如图：
…………… 3分
（Ⅱ）所求多面体体积
．
（Ⅲ）证明：在长方体 中，
连结 ，则 ．
因为 分别为 ， 中点，所以 ，
从而 ．又 平面 ，所以 面 ．
16.【解析】（Ⅰ）因为 是等边三角形， ，
所以 ，
可得 ．
如图，取 中点 ，连结 ， ，
37.（2018年全国Ⅰ卷第18题）如图，在平行四边形 中， ， ，以 为折痕将△ 折起，使点 到达点 的位置，且 ．
（1）证明：平面 平面 ；
（2） 为线段 上一点， 为线段 上一点，且 ，求三棱锥 的体积．
38.（2018年全国Ⅱ卷第19题）如图，在三棱锥 中， ，
， 为 的中点．
（1）证明： 平面 ；
26.（2017年全国Ⅰ卷第16题）已知三棱锥 的所有顶点都在球O的球面上，SC是球O的直径.若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥 的体积为9，则球O的表面积为________.
27.（2015年全国Ⅰ卷第18题）如图四边形ABCD为菱形，G为AC与BD交点， .
（ ）证明：平面 平面 ；
9.（2013年全国Ⅱ卷第16题）已知两个圆锥有公共底面，且两圆锥的顶点和底面的圆周
都在同一个球面上．若圆锥底面面积是这个球面面积的 ，则这两个圆锥中，体积较小者
的高与体积较大者的高的比值为______________．
10.（2017年全国Ⅰ卷第6题）如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直接AB与平面MNQ不平行的是
（ ）若 ，
三棱锥 的体积为 ，
高三立体几何习题(文科含答案)
23正视图 图1侧视图 图22 俯视图 2图3立几习题21假设直线l 不平行于平面a ，且l a ∉，则 A ．a 内的所有直线与异面 B ．a 内不存在与l 平行的直线 C ．a 内存在唯一的直线与l 平行 D ．a 内的直线与l 都相交 2.1l ，2l ，3l 是空间三条不同的直线，则以下命题正确的选项是〔A 〕12l l ⊥，23l l ⊥13//l l ⇒〔B 〕12l l ⊥，23//l l ⇒13l l ⊥〔C 〕233////l l l ⇒1l ，2l ，3l 共面〔D 〕1l ，2l ，3l 共点⇒1l ，2l ，3l 共面3．如图1 ~ 3，某几何体的正视图〔主视图〕，侧视图〔左视图〕和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体的体积为 A ．3 B ．4 C ．3 D ．24.某几何体的三视图如下图，则它的体积是〔 〕 A.283π- B.83π-D.23π5、如图，在四棱锥ABCD P -中，平面PAD ⊥平面ABCD ，AB=AD ，∠BAD=60°，E 、F 分别是AP 、AD的中点 求证：〔1〕直线E F ‖平面PCD ； （2）平面BEF ⊥平面PAD5〔本小题总分值13分〕如图，ABEDFC为多面体，平面ABED与平面ACFD垂直，点O在线段AD上，OD=，△OAB，△OAC，△ODE，△ODF都是正三角形。
OA=，21∥；〔Ⅰ〕证明直线BC EF-的体积.〔Ⅱ〕求棱锥F OBED6.〔本小题共14分〕如图，在四面体PABC中，PC⊥AB，PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.〔Ⅰ〕求证：DE∥平面BCP；〔Ⅱ〕求证：四边形DEFG为矩形；〔Ⅲ〕是否存在点Q，到四面体PABC六条棱的中点的距离相等？说明理由.7．〔本小题总分值12分〕如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB。
立体几何(文科专用)(解析版)
专题09 立体几何1.【2019年高考全国Ⅱ卷文数】设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 B ．α内有两条相交直线与β平行 C ．α，β平行于同一条直线 D ．α，β垂直于同一平面 【答案】B【解析】由面面平行的判定定理知：α内两条相交直线都与β平行是αβ∥的充分条件，由面面平行性质定理知，若αβ∥，则α内任意一条直线都与β平行，所以α内两条相交直线都与β平行是αβ∥的必要条件，故选B ．【名师点睛】本题考查了空间两个平面的判定与性质及充要条件，渗透直观想象、逻辑推理素养，利用面面平行的判定定理与性质定理即可作出判断．面面平行的判定问题要紧扣面面平行判定定理，最容易犯的错误为定理记不住，凭主观臆断，如：“若,,a b a b αβ⊂⊂∥，则αβ∥”此类的错误．2．【2019年高考全国Ⅲ卷文数】如图，点N 为正方形ABCD 的中心，△ECD 为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，则（）A ．BM =EN ，且直线BM ，EN 是相交直线B ．BM ≠EN ，且直线BM ，EN 是相交直线C ．BM =EN ，且直线BM ，EN 是异面直线D ．BM ≠EN ，且直线BM ，EN 是异面直线【答案】B【解析】如图所示，作EO CD ⊥于O ，连接ON ，BD ，易得直线BM ，EN 是三角形EBD 的中线，是相交直线.过M 作MF OD ⊥于F ，连接BF ，平面CDE ⊥平面ABCD ，,EO CD EO ⊥⊂平面CDE ，EO ∴⊥平面ABCD ，MF ⊥平面ABCD ，MFB ∴△与EON △均为直角三角形．设正方形边长为2，易知3,12EO ON EN ===,，35,,722MF BF BM ==∴=，BM EN ∴≠，故选B ．【名师点睛】本题考查空间想象能力和计算能力，解答本题的关键是构造直角三角形.解答本题时，先利用垂直关系，再结合勾股定理进而解决问题．3．【2019年高考江苏卷】如图，长方体1111ABCD A B C D -的体积是120，E 为1CC 的中点，则三棱锥E −BCD的体积是 ▲ .【答案】10【解析】因为长方体1111ABCD A B C D -的体积为120，所以1120AB BC CC ⋅⋅=，因为E 为1CC 的中点，所以112CE CC =，由长方体的性质知1CC ⊥底面ABCD ，所以CE 是三棱锥E BCD -的底面BCD 上的高，所以三棱锥E BCD -的体积1132V AB BC CE =⨯⋅⋅=111111201032212AB BC CC =⨯⋅⋅=⨯=. 【名师点睛】本题蕴含“整体和局部”的对立统一规律.在几何体面积或体积的计算问题中，往往需要注意理清整体和局部的关系，灵活利用“割”与“补”的方法解题.由题意结合几何体的特征和所给几何体的性质可得三棱锥的体积.4．【2019年高考全国Ⅱ卷文数】如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1．（1）证明：BE ⊥平面EB 1C 1；（2）若AE =A 1E ，AB =3，求四棱锥11E BB C C -的体积． 【答案】（1）见详解；（2）18.【解析】（1）由已知得B 1C 1⊥平面ABB 1A 1，BE ⊂平面ABB 1A 1，故11B C BE ⊥．又1BE EC ⊥，所以BE ⊥平面11EB C ． （2）由（1）知∠BEB 1=90°.由题设知Rt △ABE ≌Rt △A 1B 1E ， 所以1145AEB A EB ︒∠=∠=，故AE =AB =3，126AA AE ==.作1EF BB ⊥，垂足为F ，则EF ⊥平面11BB C C ，且3EF AB ==． 所以，四棱锥11E BB C C -的体积1363183V =⨯⨯⨯=． 【名师点睛】本题主要考查线面垂直的判定，以及四棱锥的体积的求解，熟记线面垂直的判定定理，以及四棱锥的体积公式即可，属于基础题型.一、考向分析：二、考向讲解考查内容解 题 技 巧 几何 体表 面积 与体 积1、空间几何体表面积的求法（1）以三视图为载体的几何体的表面积问题，关键是分析三视图确定几何体中各元素之间的位置关系及数量。
高考真题文科数学汇编：立体几何
高考真题文科数学汇编：立体几何 一、选择题 1.【2019高考新课标文7】如图， 网格纸上小正方形的边长为1， 粗线画出的是某几何体的三视图， 则此几何体的体积为（ ）()A 6 ()B 9 ()C 12 ()D 18【答案】B2.【2019高考新课标文8】平面α截球O 的球面所得圆的半径为1， 球心O 到平面α的距离为2， 则此球的体积为（A ）6π （B ）43π （C ）46π （D ）63π【答案】B3.【2019高考全国文8】已知正四棱柱1111ABCD A B C D -中 ， 2AB =， 122CC =， E 为1CC 的中点， 则直线1AC 与平面BED 的距离为（A ）2 （B ）3 （C ）2 （D ）1【答案】D4.【2019高考陕西文8】将正方形（如图1所示）截去两个三棱锥， 得到图2所示的几何体， 则该几何体的左视图为 （ ）8.【答案】B.5.【2019高考江西文7】若一个几何体的三视图如图所示， 则此几何体的体积为A ．112 B.5 C.4 D. 92 【答案】D6.【2019高考湖南文4】某几何体的正视图和侧视图均如图1所示， 则该几何体的俯视图不可能．．．是【答案】D7.【2019高考广东文7】某几何体的三视图如图1所示， 它的体积为A. 72πB. 48πC. 30πD. 24π【答案】C8.【2019高考福建文4】一个几何体的三视图形状都相同， 大小均等， 那么这个几何体不图1 正视图 俯视图侧视图5 5 635 56 3可以是A 球B 三棱锥C 正方体D 圆柱【答案】D.9.【2019高考重庆文9】设四面体的六条棱的长分别为1， 1， 1， 1， 2和a 且长为a 的棱与长为2的棱异面， 则a 的取值范围是（A ）(0,2) （B ）(0,3) （C ）(1,2)（D ）(1,3)【答案】A10.【2019高考浙江文3】已知某三棱锥的三视图（单位：cm ）如图所示， 则该三棱锥的体积是A.1cm 3B.2cm 3C.3cm 3D.6cm 3【答案】C11.【2019高考浙江文5】 设l 是直线， a ， β是两个不同的平面A. 若l ∥a ， l ∥β， 则a ∥βB. 若l ∥a ， l ⊥β， 则a ⊥βC. 若a ⊥β， l ⊥a ， 则l ⊥βD. 若a ⊥β, l ∥a ， 则l ⊥β【答案】B12.【2019高考四川文6】下列命题正确的是（ ）A 、若两条直线和同一个平面所成的角相等， 则这两条直线平行B 、若一个平面内有三个点到另一个平面的距离相等， 则这两个平面平行C 、若一条直线平行于两个相交平面， 则这条直线与这两个平面的交线平行D 、若两个平面都垂直于第三个平面， 则这两个平面平行【答案】C13.【2019高考四川文10】如图， 半径为R 的半球O 的底面圆O 在平面α内， 过点O 作平面α的垂线交半球面于点A ， 过圆O 的直径CD 作平面α成45o角的平面与半球面相交， 所得交线上到平面α的距离最大的点为B ， 该交线上的一点P 满足60BOP ∠=o ， 则A、P两点间的球面距离为（）A、2 arccos4 RB、4RπC、3arccos3R D、3Rπ【答案】A14.【2019高考北京文7】某三棱锥的三视图如图所示，该三棱锥的表面积是（A）28+5B）30+5C）56+5D）60+5【答案】B二、填空题15.【2019高考四川文14】如图，在正方体1111ABCD A B C D-中，M、N分别是CD、1CC的中点，则异面直线1A M与DN所成的角的大小是____________。
立体几何（文科）高考真题
立体几何（文科）高考真题1若直线l 不平行于平面a ，且l a Ë，则，则(A) a 内的所有直线与l 异面异面 (B) (B) a 内不存在与l 平行的直线平行的直线 (C) a 内存在唯一的直线与l 平行平行 (D) (D) a 内的直线与l 都相交相交2.2.已知平面已知平面a 截一球面得圆M ，过圆心M 且与a 成060，二面角的平面b 截该球面得圆N ，若该球的半径为4，圆M 的面积为4p ，则圆N 的面积为的面积为(A)7p (B)9p (c)11p (D)13p3.将长方体截去一个四棱锥，得到的几何体如右图所示，则该几何体的左视图为（将长方体截去一个四棱锥，得到的几何体如右图所示，则该几何体的左视图为（ ）4.如图，正方体ABCD-A 1B 1C 1D 1中，AB =2，点E 为AD 的中点，点F 在CD 上，若EF ∥平面AB 1C ，则线段EF 的长度等于_____________. 5.5.已知正方体已知正方体1111ABCD A B C D -中，中，E E 为11C D 的 中点，则异面直线AE 与BC 所成的角的余弦值为所成的角的余弦值为6. 如图，在四棱台1111ABCD A B C D -中，1D D ^平面ABCD ，底面ABCD 是平行四边形，AB=2AD ，11AD=A B ，BAD=Ð60°.（Ⅰ）证明：1AA BD ^； （Ⅱ）证明：11CC A BD ∥平面.60°BAONM7．如图3，在圆锥PO 中，已知2,PO O = 的直径 2,,AB C AB D AC =Ð 点在上,且CAB=30为的中点．的中点． （I ）证明：;AC POD ^平面（II ）求直线OC 和平面PAC 所成角的正弦值．所成角的正弦值． 8.如图如图,,在四棱锥P-ABCD 中,底面ABCD 为平行四边形为平行四边形,,45ADC Ð=,AD=AC=1,O 为AC 的中点,PO ,PO⊥平面⊥平面ABCD,PO=2,M 为PD 的中点的中点. .(Ⅰ)证明PB PB∥平面∥平面ACM ; (; (ⅡⅡ)证明AD AD⊥平面⊥平面PAC; (Ⅲ)求直线AM 与平面ABCD 所成角的正切值所成角的正切值. .9.如图，四棱锥P-ABCD 中，P A ⊥底面ABCD ，AB ⊥AD ，点E 在线段AD 上，且CE ∥AB 。
(完整版)高考文科立体几何证明专题
立体几何专题1．如图 4，在边长为 1 的等边三角形 ABC 中， D , E 分别是 AB, AC 边上的点， AD AE ，F 是 BC 的中点， AF 与 DE 交于点G ，将 ABF 沿 AF 折起，获取如图5 所示的三棱锥A BCF ，其中 BC2 ．2(1) 证明： DE // 平面 BCF ；(2) 证明： CF 平面 ABF ；(3) 2时，求三棱锥 FDEG 的体积 V F DEG ．当 AD3ADGEBFC图 4【剖析】（ 1）在等边三角形ABC 中， ADAEAD AE ,A BCF 中DB在折叠后的三棱锥EC也成立， DE / / BC ,Q DE平面 BCF ，BC 平面 BCF ，DE / / 平面 BCF ；AGEDFCB图 5（2 ）在等边三角形ABC 中， F 是 BC 的中点，所以 AFBC 1 ①， BF CF.2Q 在三棱锥 ABCF 中， BC2， BC 2 BF 2 CF 2 CF BF ②2Q BF CF F CF 平面 ABF ；（ ）由（ ）可知 GE / /CF ，结合（ 2）可得 GE平面 DFG.3 1VF DEGV E1 11 1 1 1 3 13 DFG3 DG FG GF2 3 3 2332423【剖析】 这个题是入门级的题，除了立体几何的内容， 还观察了平行线分线段成比率这个平面几何的内容 .2．如图 5 所示，在四棱锥P-ABCD 中,AB平面PAD,AB CD,PD=AD,E是PB的中点，F是 DC 上的点且 DF= 1AB,PH 为PAD 中 AD 边上的高．2（1）证明： PH 平面 ABCD ；（2）若PH=1，AD= 2 ,FC=1，求三棱锥E-BCF 的体积；（3）证明：EF平面PAB．解： (1)PH 为PAD中的高PH AD又 AB面PAD，PH平面PADPH ABAB AD A所以PH平面ABCD(2):过 B 点做 BG BG CD ，垂足为 G ；连接 HB, 取 HB 中点 M ，连接 EM ，则 EM 是BPH 的中位线由(1)知： PH平面ABCDEM平面 ABCDＥＭ平面 BCF即 EM 为三棱锥E - BCF底面上的高ＥＭ＝1PH1 22SBCF 1FC ? BG =11 22 222 1V E BCF? S BCF ? EM1 2 13 2 2212.（3）：取 AB 中点 N， PA 中点 Q，连接 EN ， FN ，EQ， DQ AB // CD , CD平面PADAB平面PAD，PA平面PADAB PA又EN 是 PAB 的中位线EN // PAAB EN1又DF AB四边形NADF是距形AB FNEN FN NAB平面NEF又 EF平面NEFEF AB四边形NADF是距形AB NF 3、如图，已知三棱锥 A —BPC 中，AP ⊥ PC ， AC ⊥ BC ，M为 AB 中点， D 为 PB 中点，且△ PMB 为正三角形。
高考数学最新真题专题解析—立体几何(文科)
高考数学最新真题专题解析—立体几何（文科）考向一 线面夹角【母题来源】2022年高考全国甲卷（文科）【母题题文】 在长方体1111ABCD A B C D -中，已知1B D 与平面ABCD 和平面11AA B B 所成的角均为30，则（ ） A. 2AB AD =B. AB 与平面11AB C D 所成的角为30C. 1AC CB =D. 1B D 与平面11BB C C 所成的角为45︒ 【答案】D【试题解析】【详解】如图所示：不妨设1,,AB a AD b AA c ===，依题以及长方体的结构特征可知，1B D 与平面ABCD 所成角为1B DB ∠，1B D 与平面11AA B B 所成角为1DB A ∠，所以11sin 30c b B D B D==，即b c =，22212B D c a b c ==++2a c =． 对于A ，AB a ，AD b ，2AB AD =，A 错误；对于B ，过B 作1BE AB ⊥于E ，易知BE ⊥平面11AB C D ，所以AB 与平面11AB C D 所成角为BAE ∠，因为2tan c BAE a ∠==30BAE ∠≠，B 错误； 对于C ，223AC a b c =+=，2212CB b c c =+=，1AC CB ≠，C 错误； 对于D ，1B D 与平面11BB C C 所成角为1DB C ∠，112sin 22CD a DB C B D c ∠===，而1090DB C <∠<，所以145DB C ∠=．D 正确． 故选：D ．【命题意图】本题主要考查直线与平面夹角，是一道容易题.【命题方向】这类试题在考查题型上选择题、填空题、解答题形式出现，试题难度不大，多为中低档题，重点考查线面夹角的求法问题. 【得分要点】（1）找斜线在平面中的射影； （2）求斜线与其射影的夹角； 考向二 线面平行、垂直的证明【母题来源】2022年高考全国乙卷（文科）【母题题文】 如图，四面体ABCD 中，,,AD CD AD CD ADB BDC ⊥=∠=∠，E 为AC 的中点．（1）证明：平面BED ⊥平面ACD ；（2）设2,60AB BD ACB ==∠=︒，点F 在BD 上，当AFC △的面积最小时，求三棱锥F ABC -的体积． 【试题解析】【小问1详解】由于AD CD =，E 是AC 的中点，所以AC DE ⊥.由于AD CD BD BD ADB CDB =⎧⎪=⎨⎪∠=∠⎩，所以ADB CDB ≅△△，所以AB CB =，故AC BD ⊥，由于DE BD D ⋂=，,DE BD平面BED ，所以AC ⊥平面BED ，由于AC ⊂平面ACD ，所以平面BED ⊥平面ACD . 【小问2详解】依题意2AB BD BC ===，60ACB ∠=︒，三角形ABC 是等边三角形， 所以2,1,3AC AE CE BE ====由于,AD CD AD CD =⊥，所以三角形ACD 是等腰直角三角形，所以1DE =.222DE BE BD +=，所以DE BE ⊥，由于AC BE E ⋂=，,AC BE ⊂平面ABC ，所以DE ⊥平面ABC . 由于ADB CDB ≅△△，所以FBA FBC ∠=∠，由于BF BF FBA FBC AB CB =⎧⎪∠=∠⎨⎪=⎩，所以FBA FBC ≅，所以AF CF =，所以EF AC ⊥，由于12AFCS AC EF =⋅⋅，所以当EF 最短时，三角形AFC 的面积最小值.过E 作EF BD ⊥，垂足为F ，在Rt BED △中，1122BE DE BD EF ⋅⋅=⋅⋅，解得32EF =，所以223131,2222DF BF DF ⎛⎫=-==-= ⎪ ⎪⎝⎭，所以34BF BD =. 过F 作FH BE ⊥，垂足为H ，则//FH DE ，所以FH ⊥平面ABC ，且34FH BF DE BD ==， 所以34FH =,所以11133233324F ABC ABCV SFH -=⋅⋅=⨯⨯=【命题意图】本题考查线面平行、垂直的证明.【命题方向】这类试题在考查题型多以解答题形式出现，多为中档题，是历年高考的必考题型． 常见的命题角度有：（1）线面平行的证明；（2）线面垂直的证明；（3）面面平行的证明；（4）面面垂直的证明. 【得分要点】（1）利用线面、面面平行的判定定理与性质定理； （2）利用线面、面面垂直的判定定理与性质定理. 真题汇总及解析 一、单选题1．（2022·内蒙古·乌兰浩特一中模拟预测（文））已知,αβ为空间的两个平面，直线,l ααβ⊄⊥，那么“l ∥α”是“l β⊥”的（ ）条件 A ．必要不充分 B ．充分不必要C ．充分且必要D ．不充分也不必要【答案】A 【解析】 【分析】根据空间线面位置关系，结合必要不充分条件的概念判断即可. 【详解】当直线,l ααβ⊄⊥，l ∥α，则l β//，l 与β相交，故充分性不成立； 当直线l α⊄，且αβ⊥，l β⊥时，l ∥α，故必要性成立， ⸫“l ∥α”是“l β⊥”的的必要不充分条件. 故选：A.2．（2022·贵州·贵阳一中模拟预测（文））在正方体1111ABCD A B C D -中，M 为1A D 的中点，则直线CM 与11A C 所成的角为（ ） A ．π2B ．π3C ．π4D ．π6【答案】D 【解析】 【分析】11AC AC ∥，所求角为ACM∠，利用几何体性质，解CMA 即可【详解】设正方体棱长为1，连接11,,AC AC AC CM ∴与11A C 所成角即是CM 与AC 所成角，22222221162,,1,2222AC AM CM AM CM AC ⎛⎫⎛⎫===++=∴+= ⎪ ⎪⎝⎭⎝⎭，CMA ∴为Rt △，1πsin ,26AM ACM ACM AC ∠∠==∴= 故选：D3．（2022·青海·模拟预测）已知四面体ABCD 的所有棱长都相等，其外接球的6π，则下列结论错误的是（ ） A ．四面体ABCD 的棱长均为2 B ．异面直线AC 与BD 2 C ．异面直线AC 与BD 所成角为60︒D ．四面体ABCD 的内切球的体积等于6π27【答案】C 【解析】 【分析】对于A, 设该四面体的棱长为a ，表示出高，根据其外接球的体积等于6π，求得外接球半径，即可求得a ,判断A;对于B, 分别取BD,AC 的中点为E,F ,连接EF ,求得EF 的长，即可判断；对于C ，证明线面垂直即可证明异面直线AC 与BD 互相垂直，即可判断;对于D ，利用等体积法求得内切球半径，即可求得内切球体积，即可判断. 【详解】如图示，设该四面体的棱长为a ，底面三角形BCD 的重心为G ,该四面体的外接球球心为O ，半径为R ，连接AG ,GB,OB ,AG 为四面体的高，O 在高AG 上，在Rt AGB △中，2223336,()33BG AG a a ===-, 在Rt OGB △中，22263()()R R =-+，解得6R = ， 6π，即34π6π3R ,故336R =故38,2a a == ，故A 正确； 分别取BD,AC 的中点为E,F ,连接EF ,正四面体ABCD 中，AE=EC ,故EF AC ⊥ ,同理EF BD ⊥, 即EF 为AC,BD 的公垂线，而3232CE =⨯= , 则2222(3)12EF CE CF =-=-= ,故B 正确；由于,AE BD CE BD ⊥⊥ , AE CE ⊂，平面ACE ,故BD ⊥平面ACE , 又AC ⊂平面ACE ,所以BD AC ⊥，即异面直线AC 与BD 所成角为90︒ ，故C 错误； 设四面体内切球的半径为r ,而263AG =,故11433BCDBCDSr SAG ⨯⨯⨯=⨯⨯，故646AG r a ==， 所以四面体ABCD 的内切球的体积等于3344666ππ()π3327r a ==，故D 正确， 故选：C4．（2022·湖北·华中师大一附中模拟预测）如图，正方体1111ABCD A B C D -中，P 是1A D 的中点，则下列说法正确的是（ ）A ．直线PB 与直线1A D 垂直，直线PB ∥平面11B DC B ．直线PB 与直线1D C 平行，直线PB ⊥平面11AC D C ．直线PB 与直线AC 异面，直线PB ⊥平面11ADC B D ．直线PB 与直线11B D 相交，直线PB ⊂平面1ABC【答案】A 【解析】 【分析】根据空间的平行和垂直关系进行判定. 【详解】连接11111,,,,DB A B D B D C B C ；由正方体的性质可知1BA BD =，P 是1A D 的中点，所以直线PB 与直线1A D 垂直；由正方体的性质可知1111//,//DB D B A B D C ，所以平面1//BDA 平面11B D C ， 又PB ⊂平面1BDA ，所以直线PB ∥平面11B D C ，故A 正确；以D 为原点，建立如图坐标系，设正方体棱长为1，()111,1,,0,1,122PB D C ⎛⎫==- ⎪⎝⎭显然直线PB 与直线1D C 不平行，故B 不正确；直线PB 与直线AC 异面正确，()1,0,0DA =，102PB DA ⋅=≠，所以直线PB 与平面11ADC B 不垂直，故C 不正确；直线PB与直线B D异面，不相交，故D不正确；11故选：A.5．（2022·安徽·合肥市第八中学模拟预测）下列四个命题，真命题的个数为（）（1）如果一条直线垂直于一个平面内的无数条直线，则这条直线垂直于该平面；（2）过空间一定点有且只有一条直线和已知平面垂直；（3）平行于同一个平面的两条直线平行；（4）a与b为空间中的两条异面直线，点A不在直线a，b上，则过点A有且仅有一个平面与直线a，b都平行．A．0 B．1 C．2 D．3【答案】B【解析】【分析】根据线面垂直的定义即可判断命题(1)；根据线面垂直的性质定理即可判断命题(2)；根据空间中线面的位置关系即可判断命题(3)；结合图形即可判断命题(4). 【详解】命题(1)：由直线垂直平面的定义可知，若直线垂直于一个平面的任意直线，则该直线垂直于该平面，故命题(1)错误；命题(2)：由直线与平面垂直的性质定理可知，过空间一定点有且只有一条直线与已知平面垂直，故命题(2)正确；命题(3)：平行于同一个平面的两条直线，可能平行，可能相交，也可能异面，故命题(3)错误；命题(4)：如图，当点A在如图上底面时，不存在平面同时平行于直线a、b；点A不在异面直线a、b上，若点A在直线a、b之间，则可以确定一个平面同时平行于直线a、b；若点A在直线a、b的外侧，也可以确定一个平面同时平行于直线a、b，故命题(4)错误.故选：B.6．（2022·河南安阳·模拟预测（文））如图，在四面体ABCD中，90BCD AB∠=︒⊥，平面BCD，AB BC CD==，P为AC的中点，则直线BP与AD所成的角为（）A．π6B．π4C．π3D．π2【答案】D【解析】【分析】根据给定条件，证明BP⊥平面ACD即可推理计算作答.【详解】在四面体ABCD中，AB⊥平面BCD，CD⊂平面BCD，则AB CD⊥，而90BCD∠=︒，即BC CD⊥，又AB BC B⋂=，,AB BC⊂平面ABC，则有CD⊥平面ABC，而BP⊂平面ABC，于是得CD BP ⊥，因P 为AC 的中点，即AC BP ⊥，而AC CD C =，,AC CD ⊂平面ACD ，则BP ⊥平面ACD ，又AD ⊂平面ACD ，从而得BP AD ⊥， 所以直线BP 与AD 所成的角为π2. 故选：D7．（2022·四川成都·模拟预测）如图，网格纸上小正方形的边长为1，粗实线画出的是某三棱锥的三视图，A ，B ，C ，D 是该三棱锥表面上四个点，则直线AC 和直线BD 所成角的余弦为（ ）A ．0B ．13C ．13-D 22【答案】A 【解析】 【分析】由三视图还原几何体，根据线面垂直的判定有BG ⊥面AGD ，线面垂直的性质可得BG AC ⊥，再由线面垂直的判定和性质得AC BD ⊥，即可得结果. 【详解】由三视图可得如下几何体：BG AG ⊥，BG DG ⊥，AG DG G =，则BG ⊥面AGD ，又AC ⊂面AGD ，则BG AC ⊥，而AC GD ⊥， 由BG GD G ⋂=，则AC ⊥面BGD ，又BD ⊂面BGD ， 所以AC BD ⊥，故直线AC 和直线BD 所成角的余弦为0. 故选：A8．（2022·山东潍坊·三模）我国古代数学名著《九章算术》中给出了很多立体几何的结论，其中提到的多面体“鳖臑”是四个面都是直角三角形的三棱锥．若一个“鳖臑”的所有顶点都在球O 的球面上，且该“鳖臑”的高为2，底面是腰长为2的等腰直角三角形．则球O 的表面积为（ ） A ．12π B ．43π C ．6π D ．26π【答案】A 【解析】 【分析】作出图形，设在三棱锥A BCD -中，AB ⊥平面BCD ，BC CD ⊥且2BC CD ==，2AB =，证明出该三棱锥的四个面均为直角三角形，求出该三棱锥的外接球半径，结合球体表面积公式可得结果. 【详解】 如下图所示：在三棱锥A BCD -中，AB ⊥平面BCD ，BC CD ⊥且2BC CD ==，2AB =， 因为AB ⊥平面BCD ，BC 、BD 、CD ⊂平面BCD ，则AB BC ⊥，AB BD ⊥，CD AB ⊥，CD BC ⊥，AB BC B ⋂=，CD平面ABC ，AC ⊂平面ABC ，AC CD ∴⊥，所以，三棱锥A BCD -的四个面都是直角三角形，且2222BD BC CD =+=，2223AD AB BD =+=，设线段AD 的中点为O ，则12OB OC AD OA OD ====， 所以，点O 为三棱锥A BCD -的外接球球心，设球O 的半径为R ，则132R AD ==，因此，球O 的表面积为2412R ππ=. 故选：A. 二、填空题9．（2022·四川成都·模拟预测（理））如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的表面积为________.【答案】816283++ 【解析】 【分析】根据三视图可知这是一个四面体，根据长度即可根据三角形面积公式求每一个面的面积，进而可得表面积. 【详解】该几何体的直观图是正方体中的四面体ABCD ，4,42,43AB AD BD BC CD AC ======，()21113448,44282,44282,42832224ABD ABC ADC DBCS S SS =⨯⨯==⨯⨯==⨯⨯==⨯= 故答案为： 816283++.10．（2022·上海普陀·二模）已知一个圆锥的侧面积为2π，若其左视图为正三角形，则该圆锥的体积为________. 3π3 【解析】 【分析】由圆锥侧面积公式求得底面半径12r =3.【详解】由题设，令圆锥底面半径为r ，则体高为3r ，母线为2r ， 所以12222r r ππ⨯⨯=，则12r =，故圆锥的体积为2133324r r ππ⨯⨯=. 故答案为：324π 11．（2022·黑龙江·佳木斯一中模拟预测（理））如图，在正方体1111ABCD A B C D -中，点F 是棱1AA 上的一个动点，平面1BFD 交棱1CC 于点E ，则下列正确说法的序号是___________.①存在点F 使得11A C ∥平面1BED F ； ②存在点F 使得1B D ∥平面1BED F ； ③对于任意的点F ，都有EF BD ⊥；④对于任意的点F 三棱锥1E FDD -的体积均不变. 【答案】①③④ 【解析】 【分析】①，找到点F 为1AA 的中点时，满足11A C ∥平面1BED F ；②，证明出11,BD B D 相交，得到不存在点F 使得1B D ∥平面1BED F ；③，作出辅助线，证明线面垂直，进而得到线线垂直； ④，得到三棱锥1E FDD -的体积等于正方体体积的16，为定值. 【详解】当点F 为1AA 的中点，此时点E 为1CC 的中点，此时连接EF ，可得：11A C EF ， 因为11A C ⊄平面1BED F ，EF ⊂1BED F ，所以11A C ∥平面1BED F ，①正确；连接11,BD B D ，因为11//BB DD ，且11BB DD =，所以四边形11BB D D 为平行四边形， 所以11,BD B D 相交， 因为1BD ⊂平面1BED F ，所以不存在点F 使得1B D ∥平面1BED F ，②错误连接AC ，BD ，则AC ⊥BD ，又1AA ⊥平面ABCD ，BD ⊂平面ABCD ， 所以1AA ⊥BD ， 因为1AA AC A =， 所以BD ⊥平面11AAC C ，因为EF ⊂平面11AAC C ， 所以BD ⊥EF ，③正确；连接DF ，EF ，ED ，则无论点F 在1A A 的何处，都有1112DFD SDD AD =⋅，是定值，为正方形11ADD A 面积的一半，又高等于CD ，故体积也为定值，为正方体体积的16，④正确.故选：①③④12．（2022·甘肃·武威第六中学模拟预测（文））如图，在长方体1111ABCD A B C D -中，E ，F 是棱CD 上的两个动点，点E 在点F 的左边，且满足122EF DC BC ==，给出下列结论：①11B D ⊥平面1B EF ；②三棱锥11D B EF -的体积为定值； ③1A A //平面1B EF ； ④平面11A ADD ⊥平面1B EF . 其中所有正确结论的序号是______. 【答案】②④ 【解析】 【分析】根据线面位置关系、面面位置关系判断命题①③④，由棱锥体积公式判断②． 【详解】11B D 与11D C 显然不垂直，而11//EF C D ，因此11B D 与EF 显然不垂直，从而11B D ⊥平面1B EF 是错误的，①错；1111D B EF B D EF V V --=，三棱锥11B D EF -中，平面1D EF 即平面11CDD C ，1B 到平面11CDD C 的距离为11B C 是定值，1D EF 中，EF 的长不变，1D 到EF 的距离不变，面积为定值，因此三棱锥体积是定值，②正确；平面1B EF 就是平面11B A DC ，而1AA 与平面11B A DC 相交，③错；长方体中CD ⊥平面11A D DA ，CD ⊂平面11B A DC ，所以平面11A D DA ⊥平面11B A DC ，即平面11A ADD ⊥平面1B EF ，④正确． 故答案为：②④．三、解答题13．（2022·四川成都·模拟预测（文））如图，四棱锥P ABCD -中，四边形ABCD 为直角梯形，,PB PD 在底面ABCD 内的射影分别为,AB AD ，222PA AB AD CD ．(1)求证：PC BC ⊥； (2)求D 到平面PBC 的距离． 【答案】(1)证明见解析 3【解析】 【分析】（1）由题意可证AD PA ⊥、AB PA ⊥，则可得PA ⊥面ABCD ，即可知PA BC ⊥，又AC BC ⊥则可得BC ⊥面PAC ，即可证PC BC ⊥.（2）分别计算出BCD S 与PBC S ，再利用等体积法D PBC P BCD V V --=即可求出答案. (1)因为PB 在底面ABCD 内的射影为AB ，所以面PAB ⊥面ABCD ， 又因为AD AB ⊥，面PAB ⋂面ABCD AB =，AD ⊂面ABCD 所以AD ⊥面PAB ，又因PA ⊂面PAB 因此AD PA ⊥， 同理AB PA ⊥，又AB AD A ⋂=,AD ⊂面ABCD ,AB 面ABCD 所以PA ⊥面ABCD ，又BC ⊂面ABCD ,所以PA BC ⊥，连接AC ，易得2AC =45BAC ∠=，又2AB =， 故AC BC ⊥，又PA AC A =,PA ⊂面PAC ,PA ⊂面PAC 因此BC ⊥面PAC ， 又PC ⊂面PAC 即PC BC ⊥；(2)在RT PAC 中426PC =+=在RT ACB 中422BC =-把D 到平面PBC 的距离看作三棱锥D PBC -的高h ， 由等体积法得，D PBC P BCD V V --=，故1133PBC BCD S h S PA ，即123213622BCD PBCS PA h S ，故D 到平面PBC 的距离为33． 14．（2022·青海·海东市第一中学模拟预测（文））如图，在四棱锥P ABCD -中，平面PCD ⊥平面ABCD ，PCD 为等边三角形，22CD AB ==，2AD =，90BAD ADC ∠=∠=︒，M 是棱PC 上一点．(1)若2MC MP =，求证：//AP 平面MBD ．(2)若MC MP =，求点P 到平面BDM 的距离．【答案】(1)证明见解析22 【解析】【分析】（1）连接AC ，记AC 与BD 的交点为H ，连接MH ，先证明//AP MH ，再由线面平行的判定定理即可证明.（2）由等体积法B DMP P BMD V V --=，即可求出点P 到平面BDM 的距离.(1)连接AC ，记AC 与BD 的交点为H ，连接MH ．由90BAD ADC ∠=∠=︒，得//AB CD ，12AB AH CD HC ==，又12PM MC =，则AH PM HC MC =， ∴//AP MH ，又MH ⊂平面MBD ，PA ⊄平面MBD ，∴//AP 平面MBD ．(2) 由已知易得3BD DM ==，3BM =，所以在等边BMD 中，BM 边上的高为32h =，所以BMD 的面积为13333224BMD S =⨯⨯=△， 易知三棱锥B PDM -的体积为116132326B DMP V -=⨯⨯⨯⨯=， 又因为B DMP P BMD V V --=，所以点P 到平面BDM 的距离为3223P BMD BMD V d S -==△． 15．（2022·贵州·贵阳一中模拟预测（文））如图，四棱锥P ABCD -中，平面,PAB ABCD ⊥平面,AB CD ∥,AB AD ⊥3,3,2,60AB AD AP CD PAB ====∠=︒.M 是CD 中点，N 是PB 上一点.(1)若3,BP BN =求三棱锥P AMN -的体积；(2)是否存在点N ,使得MN 平面PAD ,若存在求PN 的长；若不存在，请说明理由.【答案】(1)1；(2)存在，73=PN . 【解析】 【分析】 （1）证得点M 到平面PAB 的距离是3AD =，进而可求出结果； （2）证得//MN PE ，进而可证出MN //平面PAD ，从而可求出PN 的长.(1)P AMN M PAN V V --=， 由面PAB ⊥面ABCD 且交线是AB ，又DA AB ⊥，DA ⊂面PAB ， 所以DA ⊥平面PAB ，又MD //AB ， ∴点M 到平面PAB 的距离是3AD =， 又3BP BN =，则22123sin603332APN APB S S ==⨯⨯⨯⨯=， ∴三棱锥P AME -的体积13313=⨯⨯=. (2)存在.//,3,2AB DC AB CD==，连接BM并延长至于AD交于点E，//DM AB，∴在EAB中：13 EM DMEB AB==，∴在PBE△中：在PB上取点N，使得23 BN BMBP BE==，而13PN PB=，则//MN PE，又MN⊄平面PAD，PE⊂平面PAD，MN∴//平面PAD，在PAB△中，2212322372PB=+-⨯⨯⨯=7PN∴=。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
文科立体几何4、如图，矩形ABCD 中，ABE AD 平面⊥，2===BC EB AE ，F 为CE 上的点，且ACE BF 平面⊥.（Ⅰ）求证：BCE AE 平面⊥； （Ⅱ）求证；BFD AE 平面//； （Ⅲ）求三棱锥BGF C -的体积.ABCDEFGAB CD PE F5、如图所示，在棱长为2的正方体1111ABCD A B C D -中，E 、F 分 别为1DD 、DB 的中点．(Ⅰ)求证：//EF 平面11ABC D ； (Ⅱ)求证：1EF B C ⊥； （III ）求三棱锥EFC B V -1的体积．6、 如图，在四棱锥ABCD P -中，底面ABCD 是正方形，侧棱⊥PD 底面ABCD ，1==DC PD ，E 是PC 的中点，作PB EF ⊥交PB 于点F ．(I) 证明： PA ∥平面EDB ；(II) 证明：PB ⊥平面EFD ；(III) 求三棱锥DEF P -的体积．ABDEFA 1B 1第7题图7、 如图, 在三棱柱中，，1CC ⊥平面ABC ，，,， 点是的中点，（1）求证：；（2）求证：； （3）求三棱锥的体积。
8. 如图，四边形ABCD 为矩形，AD ⊥平面ABE ，AE ＝EB ＝BC ＝2，F 为CE 上的点， 且BF ⊥平面ACE ． (1)求证：AE ⊥BE ；(2)求三棱锥D －AEC 的体积；(3)设M 在线段AB 上，且满足AM ＝2MB ，试 在线段CE 上确定一点N ，使得MN ∥平面DAE.111ABC A B C -3AC =4BC =5AB =14AA =D AB 1AC BC ⊥11AC CDB 平面11C CDB -BCADEF M9、如图，在四棱锥P —ABCD 中，底面ABCD 是菱形，∠ABC=60°，PA=AC=a ，PB=PD=a 2，点E ，F 分别在PD ，BC 上，且PE ：ED=BF ：FC 。
（1）求证：PA ⊥平面ABCD ； （2）求证：EF//平面PAB 。
10、正方形所在平面与三角形所在平面相交于，平面，且，．（1）求证：平面；（2）求凸多面体的体积．ABCD CDE CD AE ⊥CDE 3AE =6AB =AB ⊥ADE ABCDE A B CD E11、如图的几何体中，平面，平面，△为等边三角形，22AD DE AB ===，为的中点．（1）求证：平面；（2）求证：平面平面； （3）求这个几何体的体积．12AB ⊥ACD DE ⊥ACD ACDF CD //AF BCE BCE ⊥CDE13、已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB＝1，BC＝2，CD＝1＋3，过A作AE⊥CD，垂足为E，G、F分别为AD、CE的中点，现将△ADE沿AE折叠，使DE⊥EC.(1)求证：BC⊥平面CDE；(2)求证：FG∥平面BCD；(3)求四棱锥D－ABCE的体积.17、如图4,在边长为1的等边三角形ABC 中,,D E 分别是,AB AC 边上的点,AD AE =,F 是BC 的中点,AF 与DE 交于点G ,将ABF ∆沿AF 折起,得到如图5所示的三棱锥A BCF -,其中22BC =. (1) 证明:DE //平面BCF ; (2) 证明:CF ⊥平面ABF ; (3) 当23AD =时,求三棱锥F DEG -的体积F DEG V -.18、如图,直三棱柱ABC-A 1B 1C 1中,D,E 分别是AB,BB 1的中点.(1) 证明: BC 1//平面A 1CD;(2) 设AA 1= AC=CB=2,AB=2,求三棱锥C 一A 1DE 的体积.图 4GEF ABCD图 5DGBFCA E19、如图,四棱锥P ABCD -的底面ABCD 是边长为2的菱形,60BAD ∠=.已知2,PB PD PA === .(Ⅰ)证明:PC BD ⊥(Ⅱ)若E 为PA 的中点,求三菱锥P BCE -的体积.19．G1、G4、G3[2014·安徽卷] 如图15所示，四棱锥P ABCD 的底面是边长为8的正方形，四条侧棱长均为217.点G ，E ，F ，H 分别是棱PB ，AB ，CD ，PC 上共面的四点，平面GEFH ⊥平面ABCD ，BC ∥平面GEFH .图15(1)证明：GH ∥EF ；(2)若EB ＝2，求四边形GEFH 的面积．20．G1、G5[2014·重庆卷] 如图14所示四棱锥P ABCD 中，底面是以O 为中心的菱形，PO ⊥底面ABCD ，AB ＝2，∠BAD ＝π3，M 为BC 上一点，且BM ＝12.(1)证明：BC ⊥平面POM ；(2)若MP ⊥AP ，求四棱锥图17．G2、G8[2014·陕西卷] 四面体ABCD 及其三视图如图14所示，平行于棱AD ，BC 的平面分别交四面体的棱AB ，BD ，DC ，CA 于点E ，F ，G ，H .图14(1)求四面体ABCD 的体积；(2)证明：四边形EFGH 是矩形．17．G4 、G5[2014·北京卷] 如图15，在三棱柱ABCA1B1C1中，侧棱垂直于底面，AB⊥BC，AA1＝AC＝2，BC＝1，E，F分别是A1C1，BC的中点．图15(1)求证：平面ABE⊥平面B1BCC1；(2)求证：C1F∥平面ABE；(3)求三棱锥EABC的体积．16．G4、G5[2014·江苏卷] 如图14所示，在三棱锥P ABC中，D，E，F分别为棱PC，AC，AB的中点．已知P A⊥AC，P A＝6，BC＝8，DF＝5.求证：(1)直线P A∥平面DEF；(2)平面BDE⊥平面ABC.图1418．G4、G11[2014·新课标全国卷Ⅱ] 如图13，四棱锥P ABCD 中，底面ABCD 为矩形，P A ⊥平面ABCD ，E 为PD 的中点．(1)证明：PB ∥平面AEC ；(2)设AP ＝1，AD ＝3，三棱锥P ABD 的体积V ＝34，求A 到平面PBC 的距离．18．G5，G4[2014·山东卷] 如图14所示，四棱锥P ABCD 中，AP ⊥平面PCD ，AD ∥BC ，AB ＝BC ＝12AD ，E ，F 分别为线段AD ，PC 的中点．图14(1)求证：AP ∥平面BEF ； (2)求证：BE ⊥平面P AC .18．G4、G5[2014·四川卷] 在如图14所示的多面体中，四边形ABB1A1和ACC1A1都为矩形．(1)若AC⊥BC，证明：直线BC⊥平面ACC1A1.(2)设D，E分别是线段BC，CC1的中点，在线段AB上是否存在一点M，使直线DE∥平面A1MC？请证明你的结论．图1419．G5，G7[2014·福建卷] 如图16所示，三棱锥ABCD中，AB⊥平面BCD，CD ⊥BD.(1)求证：CD⊥平面ABD；(2)若AB＝BD＝CD＝1，M为AD中点，求三棱锥A MBC的体积．19．G5、G7[2014·辽宁卷] 如图14所示，△ABC和△BCD所在平面互相垂直，且AB ＝BC＝BD＝2，∠ABC＝∠DBC＝AC，DC，AD的中点．(1)求证：EF⊥平面BCG；(2)求三棱锥D BCG的体积．19．G5 G11[2014·全国新课标卷Ⅰ] 如图14，三棱柱ABCA1B1C1中，侧面BB1C1C 为菱形，B1C的中点为O，且AO⊥平面BB1C1C.图14(1)证明：B1C⊥AB；(2)若AC⊥AB1，∠CBB1＝60°，BC＝1，求三棱柱ABC A1B1C1的高．19．G5 G11[2014·全国新课标卷Ⅰ] 如图14，三棱柱ABCA1B1C1中，侧面BB1C1C 为菱形，B1C的中点为O，且AO⊥平面BB1C1C.图14(1)证明：B1C⊥AB；(2)若AC⊥AB1，∠CBB1＝60°，BC＝1，求三棱柱ABC A1B1C1的高．18．G1，G4，G5[2015·北京卷] 如图15，在三棱锥VABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC＝BC＝2，O，M分别为AB，VA的中点．(1)求证：VB∥平面MOC；(2)求证：平面MOC⊥平面VAB；(3)求三棱锥VABC的体积．18．G1，G4，G5[2015·四川卷] 一个正方体的平面展开图及该正方体的直观图的示意图如图12所示．(1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；(2)判断平面BEG与平面ACH的位置关系，并证明你的结论；(3)证明：直线DF⊥平面BEG.图1218．G4，G5，G11[2015·广东卷] 如图13，三角形PDC所在的平面与长方形ABCD所在的平面垂直，PD＝PC＝4，AB＝6，BC＝3.(1)证明：BC∥平面PDA；(2)证明：BC⊥PD；(3)求点C到平面PDA的距离．图1316．G4、G5[2015·江苏卷] 如图12，在直三棱柱ABC A1B1C1中，已知AC⊥BC，BC ＝CC1，设AB1的中点为D，B1C∩BC1＝E.求证：(1)DE∥平面AA1C1C；(2)BC1⊥AB1.18．G5[2015·全国卷Ⅰ] 如图15，四边形ABCD为菱形，G为AC与BD的交点，BE⊥平面ABCD.(1)证明：平面AEC⊥平面BED；(2)若∠ABC＝120°，AE⊥EC, 三棱锥E ACD的体积为63，求该三棱锥的侧面积．18．G5[2015·陕西卷] 如图15(1)，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝π2，AB＝BC ＝12AD ＝a ，E 是AD 的中点，O 是AC 与BE 的交点．将△ABE 沿BE 折起到图(2)中△A 1BE的位置，得到四棱锥A 1 BCDE .(1)证明：CD ⊥平面A 1OC ；(2)当平面A 1BE ⊥平面BCDE 时，四棱锥A 1 BCDE 的体积为362，求a 的值．图1520．G5、G7[2015·重庆卷] 如图14，三棱锥P ABC 中，平面P AC ⊥平面ABC ，∠ABC ＝π2，点D ，E 在线段AC 上，且AD ＝DE ＝EC ＝2，PD ＝PC ＝4，点F 在线段AB 上，且EF ∥BC .(1)证明：AB ⊥平面PFE ；(2)若四棱锥P DFBC 的体积为7，求线段BC 的长．图1419．G12[2015·安徽卷] 如图15，三棱锥PABC中，P A⊥平面ABC，P A＝1，AB＝1，AC＝2，∠BAC＝60°.(1)求三棱锥PABC的体积；(2)证明：在线段PC上存在点M，使得AC⊥BM，并求PMMC的值．图1519．G1、G4[2016·全国卷Ⅲ] 如图15，四棱锥P ABCD中，P A⊥底面ABCD，AD∥BC，AB＝AD＝AC＝3，P A＝BC＝4，M为线段AD上一点，AM＝2MD，N为PC的中点．(1)证明：MN∥平面P AB；(2)求四面体N BCM的体积．图15DC⊥AC.(1)求证：DC⊥平面P AC.(2)求证：平面P AB⊥平面P AC.(3)设点E为AB的中点，在棱PB上是否存在点F，使得P A∥平面CEF？说明理由．18．G4，G5[2016·山东卷] 在如图15所示的几何体中，D是AC的中点，EF∥DB.(1)已知AB＝BC，AE＝EC，求证：AC⊥FB；(2)已知G，H分别是EC和FB ABC.∠ADC ＝∠P AB ＝90°，BC ＝CD ＝12AD .(1)在平面P AD 内找一点M ，使得直线CM ∥平面P AB ，并说明理由； (2)证明：平面P AB ⊥平面PBD .图1418．G5[2016·全国卷Ⅰ] 如图14，已知正三棱锥P ABC 的侧面是直角三角形，P A ＝6，顶点P 在平面ABC 内的正投影为点D ，D 在平面P AB 内的正投影为点E ，连接PE 并延长交AB 于点G .(1)证明：G 是AB 的中点；(2)作出点E 在平面P AC 内的正投影F (说明作法及理由)，并求四面体PDEF 的体积．图1419．G5[2016·全国卷Ⅱ] 如图14，菱形ABCD 的对角线AC 与BD 交于点O ，点E ，F 分别在AD ，CD 上，AE ＝CF ，EF 交BD 于点H .将△DEF 沿EF 折到△D ′EF 的位置．(1)证明：AC ⊥HD ′；(2)若AB ＝5，AC ＝6，AE ＝54，OD ′＝22，求五棱锥D ′ABCFE 的体积．图1411.【2017课标1，文18】如图，在四棱锥P-ABCD 中，AB//CD ，且90BAP CDP ∠=∠=．（1）证明：平面PAB ⊥平面PAD ；（2）若PA =PD =AB =DC ，90APD ∠=，且四棱锥P-ABCD 的体积为83，求该四棱锥的侧面积．12.【2017课标II ，文18】如图，四棱锥P ABCD -中，侧面PAD 为等边三角形且垂直于底面ABCD ,01,90.2AB BC AD BAD ABC ==∠=∠= （1）证明：直线//BC 平面PAD ;（2）若△PAD 面积为P ABCD -的体积.13.【2017课标3，文19】如图，四面体ABCD 中，△ABC 是正三角形，AD =CD ．（1）证明：AC ⊥BD ；（2）已知△ACD 是直角三角形，AB =BD ．若E 为棱BD 上与D 不重合的点，且AE ⊥EC ，求四面体ABCE 与四面体ACDE 的体积比．14.【2017山东，文18】（本小题满分12分）由四棱柱ABCD -A 1B 1C 1D 1截去三棱锥C 1- B 1CD 1后得到的几何体如图所示,四边形ABCD 为正方形,O 为AC 与BD 的交点,E 为AD 的中点,A 1E ⊥平面ABCD ,（Ⅰ）证明：1A O ∥平面B 1CD 1;（Ⅱ）设M 是OD 的中点,证明：平面A 1EM ⊥平面B 1CD 1.15.【2017天津，文17】如图，在四棱锥P ABCD -中，AD ⊥平面PDC ，AD BC ∥，PD PB ⊥，1AD =，3BC =，4CD =，2PD =.（I ）求异面直线AP 与BC 所成角的余弦值； （II ）求证：PD ⊥平面PBC ；（Ⅲ）求直线AB 与平面PBC 所成角的正弦值.16.【2017北京，文18】如图，在三棱锥P–ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．（Ⅰ）求证：PA⊥BD；（Ⅱ）求证：平面BDE⊥平面PAC；（Ⅲ）当PA∥平面BD E时，求三棱锥E–BCD的体积．。