可靠性工程之可修复系统的可靠性.ppt
合集下载
第三章可修复系统的可靠性课件
...
Pnn
如果系统的初始状态是ei,经过n次转移后处于ej 的概率是此转移期间所有通道v的概率和,记作:
Pijn Piv Pvjn1
v
设以 Pijn 为元素组成的矩阵为 Pn 以 Pij1 为元素组成的矩阵为 P
则: Pn Pn
可靠性设计
例3-1
1 2
已知e1,e2,e3三个状态,其状态转移图 如图所示。初始状态为E(0)=(1,0,0),求由e1 出发至第二步转移后各状态的概率。
XP X
四、吸收状态的平均转移次数(或平均时间)可 靠 性 设 计
吸收状态:
当转移过程达到某一状态,再也不能向其 他状态转移时,称此状态为吸收状态。
要求在吸收状态时由ei转移到ej所需的平均转移 次数,须先求出M矩阵。
m11 m12 ... m1k
M
I
Q1
m21
m22
...
m2k
ml1
4 8
P132
P11P131
P12 P231
P13 P331
10 2
1 2
1 4
0
1 2
1 8
三、极限概率及各态历经性
E(n) E(0)Pn
可靠性设计
例3-2 某设备状态转移图如图所示,如初始状态向量
E0 1 0 ,求各次转移后设备所处的状态。
解: 其转移矩阵为:
1/2
1 1
P
2
2
2 3
5 5
1
4
3
2 2 2 2 8 8 8
方法二
Pijn Piv Pvjn1
v
可靠性设计
该题目中,v=1,2,3;n=2。
P112
系统工程导论第十章系统可靠性.ppt

❖ 3.故障时间
❖ (1)平均故障前时间(mean time to fault, MTTF)。是不可修复的产品在发生故障前时间的均值。 它是在规定的条件下和规定的时间内,产品的寿命 单位总数与故障产品总数之比。
❖ (2)平均故障间隔时间(mean time between faults,MTBF),是可修复产品在相邻两次故障之间 的平均工作时间。
❖ 对于电子元器件而言,随着环境变化、电源电 压变化等,不仅有漂移性变化,还伴随着储存和使 用时间在进行着不可逆的特性参数值退化的变化。
❖ 4.环境防护设计
❖ 环境条件就是指产品在储存、运输和工作过程 中可能遇到的一切外界影响。环境条件对产品的可 靠性有着重大的影响。如:温度、湿度、霉菌、盐 雾、尘埃、电磁干扰等。所以要进行抗干扰设计、 “三防”设计等。
造、使用和维修的整个过程之中。可靠性技术是一门综合性的工程技术,
是系统工程的一个重要组成部分。
❖ 10.2.2 系统可靠性的含义
❖
系统可靠性指的是系统在规定条件下和规定时间内完成
规定功能的能力。
❖
狭义上讲,可靠的反义就是容易发生故障。尽可能设计
与制造不发生故障的系统,这是可靠性工作的目的,而与此
有关的一切工程方法就是可靠性技术。产品和系统在使用过
❖ 为了提高系统可靠性,从设计角度还可采取以 下措施。
❖ 1.优选元器件
❖ 在系统设计时,根据给定的环境条件和可靠性 要求,尽可能采用已经正式投入生产的、工艺上成 熟的元器件;尽可能采用已经标准化的元器件,并 且尽可能减少元器件串联环节;尽可能采用高可靠 性的新技术成果,如超微型电子管、固体电路等。
❖ 4.冷储备
❖ 如图10-19所示,两个(或更多个)相同元 件A、B并联但不同时工作,当工作元件失效 时,系统立即切换到备份元件上,备份元件 开始工作,这样,系统的功能得以继续维持。 这种储备方式称为冷储备,即非工作储备。 切换动作可以手动或自动,但是都需要有检 测故障的传感器C与切换开关K。
第4章系统可靠性设计PPT课件

则单元分配的可靠度为:
Ri (Rs )1 n (i 1, 2, , n)
(4-68)
第16页/共23页
(2)并联系统
对于并联系统,由式(4-8)可知:
Rs 1 (1 Ri )n
故单元应分配的可靠度
为:
Ri 1 (1 Rs )1 n (i 1, 2, , n)
:
第17页/共23页
2. 按相对失效概率分配可靠度
n
Fs (1 R1 )(1 R2 ) (1 Rn ) (1 Ri ) i 1
所以并联系统的可靠度为
n
Rs 1 Fs 1 (1 Ri ) i 1
(4-7)
当 R 1 R 2 R n R 时,则有
Rs 1 (1 R)n
(4-8)
由此可知,并联系统的可靠度 Rs 随单元数量的增加和单元可靠度 的增加而增加。
设各元件的复杂度为 Ci (i 1, 2, , n) 。 因为各元件的失效概率 正比于其复杂度 则对串联系统有下式成立
,即 Fia kCi ,
n
n
Rsa (1 Fia ) (1 kCi )
i 1
i 1
(a)
第20页/共23页
由于 是已知的,而 可由元件的结构复杂程度以及零部件的 数目大小定出,也是已知的,
第15页/共23页
1. 平均分配法
平均分配法是对系统中的全部单元分配以相等的可靠度。
(1)串联系统 当系统中n 个单元具有近似的复杂程度、重要性以及制造成本时, 则可用平均分配法分配系统各单元的可靠度。 该分配法是按照系统中各单元的可靠度均相等的原则进行分配。 对由n 个单元组成的串联系统,若知系统可靠度为Rs ,由于
可靠性预测是一种预报方法,它是从所得的失效率数据预报一个 元件、部件、子系统或系统实际可能达到的可靠度,即预报这些元件 或系统等在特定的应用中完成规定功能的概率。
可修复系统可靠性概要78页PPT

可修复系统可靠性概要
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ;权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊,可是金 子可以 拉着它 的鼻子 走。— —莎士 比
Hale Waihona Puke 谢谢你的阅读❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ;权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊,可是金 子可以 拉着它 的鼻子 走。— —莎士 比
Hale Waihona Puke 谢谢你的阅读❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
第七章 可修复系统的可靠性

G 1 M
维修率与无维修度函数关系:
维修率与维修度函数关系:
d ln G d
0 M 1 e
d
沈阳理工大学装备工程学院
第7章 可修复系统的可靠性
维修时间的分布函数
维修时间受很多因素的影响,如维修产品、部位、损坏 程度、维修人员的素质、维修工具、设备、工作环境条件及 维修组织管理水平等。因此尽管是同样故障位置上的相同零 件,且由同一个工人进行维修,两次维修所用时间也不一样。 维修时间为随机变量服从一定的分布规律,一般按指数分布 和对数正态分布处理。
沈阳理工大学装备工程学院
第7章 可修复系统的可靠性
• 维修时间T服从指数分布 修复率: 维修度函数: 维修密度函数: 平均修复时间:
M 1 e m e
MTTR
1
沈阳理工大学装备工程学院
第7章 可修复系统的可靠性
• 维修时间T服对数正态分布 ~ N , 2 ln 维修密度函数: m
故障 R 修复 系统的状态转移图
沈阳理工大学装备工程学院
F
第7章 可修复系统的可靠性
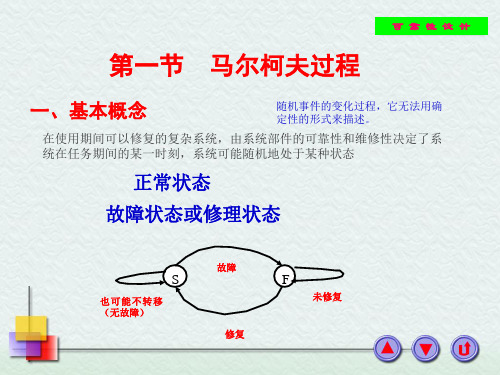
由于系统由一种状态转移到另一种状态的过程是 完全随机的,这种随机转移的过程就称为随机过程, 即随时间t而变化的一组随机变量X(t)。 在研究系统故障-工作两种状态互相转换的过程引 入马尔柯夫过程。
沈阳理工大学装备工程学院
沈阳理工大学装备工程学院
第7章 可修复系统的可靠性
• 维修度
可维修产品在规定的使用条件下,在规定的时间内,按 规定的程序和方法进行维修时,保持或恢复到能完成规定功 能状态的概率。一般将维修度记为M,是维修时间τ的函数, 故称M (τ)为维修度函数。 令维修时间为随机变量T,则产品从发生故障后开始维 修,到某一时刻τ以内能完成修复的概率为
维修及可靠性管理要点ppt课件

制定的的总体方案的计划与实施。
常用的维修策略有基于时间或工作量的维修策略;
基于故障的维修策略;基于状态的维修策略。第一种通
常为预防维修模式,第二种为事后维修模式,第三种则
为状态监测维修模式。在企业中三种策略都不可或缺,
对于一般设备或故障损失较小的设备可采用基于故障的
策略,主要生产设备可采用基于时间、工作量的策略,
维修材料费用比 = 企业年度维修材料费用×100%
企业维修年度总费用
维修工时费用比= 企业年度维修总工时
企业年度维修总费用
×100%
1-84
11
上述两项参数分别反映了单位维修费用中维修材 料及维修工时所占的比例,通过不同企业(部门)之 间的考核可以分析、判断维修材料及维修工时费用的 合理性,据此制订相应的费用控制措施。这两项参数 可由企业财务部门及设备维修管理部门共同进行统计 并考核。
和现代化改装等手段,维修可以使资产的利用更加强
化。
维修还可以为避免产生废物作出贡献。制造产品
1-84
6
而不产生废物,这是生态工业所追求的目标,而没有
维修工程在模拟和消耗过程方面的研究成果是不可能
实现的。这些成就体现在:
1、改进产品的设计:
改型(重新制造)和改进装备(修改设计,现代
化改装);实现产品的多功能化:采用标准化设计;
是:
技术上可行;
经济上合理;
生态上允许:
与各项法规相适应;
符合社会/公众/政治的需要。
二. 设备维修的参数系统 设备维修中的参数系统(或称指标体系)是维修 管理目标的重要组成部分,借助于维修参数及参数系
1-84
8
统可对维修管理中某一环节的计划与实际情况进行评 估和比较,为管理层在维修方面的决策提供依据。我 国企业现有的以设备完好率为中心的参数体系已难以 全面考核和评估新形势下维修管理中如费用控制、计 划程度、劳动组织、物质管理等诸多方面的管理水平 和经济效果,因而有必要对现有的参数系统加以补充 和完善,使之适应新形势下维修管理工作发展的需要。
第七章可修复系统的可靠性(精)
沈阳理工大学装备工程学院
第7章 可修复系统的可靠性
3) 0.95
1 2
1 2
e
ln 2
2 2
平均修复时间: 修复时间标准差: 维修度:
e
2
e
2 2
e
2
1
ln
M m d z
0
z
沈阳理工大学装备工程学院
第7章 可修复系统的可靠性
第7章 可修复系统的可靠性
可修复系统是指系统的组成单元发生故障之后, 经过修理使系统恢复到正常工作状态。
系统的修复时间是一个随机变量。影响因素: 1)故障发生的原因、部位、程度。 2)系统所处的环境。 3)维修设备及修理人员水平。 修复时间的长短和修复质量高低将影响设备的 可靠性水平。
沈阳理工大学装备工程学院
若已知维修密度函数m(τ ),则
M m d
0
o
维修度函数
沈阳理工大学装备工程学院
第7章 可修复系统的可靠性
• 修复率
修复率是指维修时间达到某一时刻τ尚未修复的产品,在 该时刻τ后的单位时间内完成修复的概率。记作μ( τ ),称为 修复率函数,也称维修率。
1 P T 1 lim lim P T T 0 0 PT
PT M
0 M 1
沈阳理工大学装备工程学院
若在同一时刻τ的维修度值越大,说明该产品修好的可能性越大。
第7章 可修复系统的可靠性
• 维修密度函数
如果维修度函数M (τ)连续可导,则M (τ)得导数即 为维修密度函数。
第7章 可修复系统的可靠性
3) 0.95
1 2
1 2
e
ln 2
2 2
平均修复时间: 修复时间标准差: 维修度:
e
2
e
2 2
e
2
1
ln
M m d z
0
z
沈阳理工大学装备工程学院
第7章 可修复系统的可靠性
第7章 可修复系统的可靠性
可修复系统是指系统的组成单元发生故障之后, 经过修理使系统恢复到正常工作状态。
系统的修复时间是一个随机变量。影响因素: 1)故障发生的原因、部位、程度。 2)系统所处的环境。 3)维修设备及修理人员水平。 修复时间的长短和修复质量高低将影响设备的 可靠性水平。
沈阳理工大学装备工程学院
若已知维修密度函数m(τ ),则
M m d
0
o
维修度函数
沈阳理工大学装备工程学院
第7章 可修复系统的可靠性
• 修复率
修复率是指维修时间达到某一时刻τ尚未修复的产品,在 该时刻τ后的单位时间内完成修复的概率。记作μ( τ ),称为 修复率函数,也称维修率。
1 P T 1 lim lim P T T 0 0 PT
PT M
0 M 1
沈阳理工大学装备工程学院
若在同一时刻τ的维修度值越大,说明该产品修好的可能性越大。
第7章 可修复系统的可靠性
• 维修密度函数
如果维修度函数M (τ)连续可导,则M (τ)得导数即 为维修密度函数。
可修复系统可靠性概要PPT文档78页
可修复系统可靠性概要
41、俯仰终宇宙,不乐复何如。 42、夏日长抱饥,寒夜无被眠。 43、不戚戚于贫贱,不汲汲于富贵。 44、欲言无予和,挥杯劝孤影。 45、盛年不重来,一日难再晨。及时 当勉励 ,岁月 不待人 。
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚25、学习源自劳动,是充满思想的劳动。——乌申斯基
谢谢!
41、俯仰终宇宙,不乐复何如。 42、夏日长抱饥,寒夜无被眠。 43、不戚戚于贫贱,不汲汲于富贵。 44、欲言无予和,挥杯劝孤影。 45、盛年不重来,一日难再晨。及时 当勉励 ,岁月 不待人 。
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚25、学习源自劳动,是充满思想的劳动。——乌申斯基
谢谢!
可靠性工程基础(王金武主编)PPT模板
1.6 可靠 性与质量管
理
1.4 可靠 性研究的重
要意义
1.5 可靠 性工程的技
术内涵
1.1 可靠 性的基本概
念
1.2 可靠 性的特点
1.3 可靠 性的发展
第1章 绪论
复习思考题1
06
第2章 可靠性的基本理论
第2章 可靠性的 基本理论
2.1 可靠性特征量 2.2 维修性特征量 2.3 有效性特征量 2.4 可靠性中常见的失效分布 复习思考题2
第10章 软件可 靠性工程
10.7 容错设计 10.8 软件可靠性测试 复习思考题10
15
第11章 可靠性试验
第11章 可靠性试验
A
11.1 概 述
B
11.2 可 靠性寿命
试验
C
11.3 加 速寿命试
验
D
11.4 可 靠性增长
试验
E
11.5 可 靠性筛选
试验
F
11.6 可 靠性抽样
试验
第11章 可靠性 试验
参考文献
18
附录
附录
19
封底
封底
LOGO
感谢聆听
09
第5章 机械结构可靠性设计
可第
靠 性
章
设 计
机 械
结
构
5
01
5.1 概述
04
5.4 静强 度概率可靠
性设计
02
5.2 应力 与强度的分
布
05
5.5 疲劳 强度的概率 可靠性设计
03
5.3 可靠 性系数与可
靠度
06
复习思考题 5
10
第6章 典型机械零件的可靠性设计
可靠性系统工程PPT
设计目标范围 … …… …… …… …… …
……………
项目增长
实施要素
01 横向监控
工作项目之间的内在逻辑关系
02 纵向监控
整个供应链的要求监控
03 监控主体
政府/企业;企业/供应商;用户/产品
04 监控方法
定性检查单/定量跟踪线条
25
规范体系 Standard
特性
安全性 保障性 可靠性 测试性 维修性
550K
寿命周期 500K 费用($)
450K
400K
… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… … …………………………………………………………………………………………………………………………
主任设计师确认 军代表监控
主任师,T1专家 系统确定,4所会签,主
任设计师确认
预计结果满足整机 对系统的要求
否 问题分类
改进建议表
报质量部 是
分析,改进
纳入监控流程
建议改进措施归零表
系统基本可靠性预计报告
实施要素
什么部门、什么人? 什么时候? 做什么工作? 用什么方法/工具? 向谁要什么输入? 得到什么输出? 输出给谁用?
实施要素
可靠性技术(续)
可靠性增长试验 可靠性强化试验 环境应力筛选试验 寿命试验 加速寿命试验 加速退化试验 可靠性鉴定试验 可靠性验收试验 可靠性评估
测试性技术
故障诊断设计 故障预测设计
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1 马尔可夫过程
3.1 马尔可夫过程
3.1 马尔可夫过程
转移矩阵
Pij(t)称为从状态i到状态j的转移函数,由转移函数的 全体组成的矩阵称为转移矩阵。如对n个状态系统的转移
矩阵为n×n阶方阵,可写为:
P11 P12 P1n
P P21
P22
P
2n
马尔可夫链的概念及转移概率
p01:在系统内没有顾客的条件下,经Δt后有一顾客进入系统 的概率, p01=q.
p10:系统内恰有一顾客正在接受服务的条件下,经Δt后系统 内无人进入的概率, 等于在Δt间隔内顾客因服务完毕而离去, 且无人进入系统的概率, p10=p(1-q).
p11:系统内恰有一顾客的条件下,在Δt间隔内, 因服务完毕 而离去,而另一顾客进入系统, 或者正在接受服务的顾客将继 续要求服务,且无人进入系统的概率,p11=pq+(1-p)(1-q).
3.2 状态转移图
由此可写出系统的转移矩阵为:
转移矩阵Pij也表示事件ei 发生的条件下,事件ej发生的条件概率:Pij=P(ej|ei) ; 矩阵 P:行是起始状态,由小到大;列是到达状态,由小到大排列,建立P时应与转移 图联系起来。
3.2 状态转移图
例2
对于一可修系统,失效率和修复率λ、μ为常数, 试画出状态转移图:
与始点u 无关,则称该马尔可夫过程是齐次的。
或者,齐次马尔可夫过程
如果马尔可夫过程的转移概率函数或转移概率密度,只与 转移前后的状态及相应的二个时刻的时间差有关,而与二个 时刻无关,即
F(x2 ; t2 | x1 ; t1)= F(x2 | x1 ; t2 -t1) f(x2 ; t2 | x1 ; t1)= f(x2 | x1 ; t2 -t1)
统实际上是不可能的
马尔可夫链的概念及转移概率
再设有无顾客来到与服务是否完毕是相互独立的. 如何用马氏链描述这一服务系统? 设 Xn≡X(nΔt), 表 示 时 间 nΔt 时 系 统 内 的 顾 客 数 。 则 {Xn,n=0,1,2,…} 是 随 机 过 程 , 状 态 空 间 I={0,1,2,3}. 由 于 当 Xn=i,i∈I已知时,Xn+1所处的状态概率分布只与Xn=i有关,而 与时间nΔt以前所处的状态无关,所以该随机过程是一个齐次 马氏链. 怎样计算此马氏链的一步转移概率? 记p00:在系统内没有 顾客的条件下,经Δt后仍无顾客的概率, p00=1-q.
P n1
Pn2
Pnn
性质(2)说明一步转移概率矩阵中任一行元素之和为1. 通常称满足(1)、(2)性质的矩阵为随机矩阵.
3.1 马尔可夫过程
三条假设
a) ,为常数(即寿命和维修时间服从指数分布) b) 部件和系统取正常和故障两种状态。 c) 在相当小的t内,发生两个或两个以上部件同时进行状态转移的概率是t的高
阶无穷小,此概率可以忽略不计。
3.1 马尔可夫过程
3.2 状态转移图
例1 如一台机器,运行到某一时刻t时,可能的状态为:
e1-正常; e2-故障。如机器处于e1状态的概率P11=4/5, 则e1向e2转移的概率P12=1-P11=1/5;反过程,如机器处 于e2状态,经过一定时间的修复返回e1 状态的概率是3/5, P21=3/5( 维 修 度 M()); 则 修 不 好 仍 处 于 e2 状 态 的 概 率 是 P22=1-P21=2/5.
服务规则: 先到先服务,后来者需在等候室依次排队. 假定需要服务的顾客到达系统, 发现系统内已有3个顾客(1
个在接受服务, 2个在等候室排队),则该顾客即离去. 设时间间隔Δt内有一个顾客进入系统的概率为q,有一原来
被服务的顾客离开系统(即服务完毕)的概率为p. 又设当Δt充分小,在时间间隔内多于一个顾客进入或离开系
可靠性工程之可修复系统的可靠 性
第三章 可修复系统的可靠性
3.1 马尔可夫过程 3.2 状态转移图 3.3 n步转移后系统各状态概率 3.4 单部件可修系统 3.5 串联可修系统 3.6 并发生故障后,经过修理可以使系 统恢复至正常工作状态,如下图所示。如果工作时间和修 复时间都服从指数分布,就可以借助马尔可夫过程来描述。
P{x(tn)=in|x(t1)=i1,x(t2)=i2,…,x(tn-1)=in-1} =P{x(tn)=in|x(tn-1)=in-1} i1,i2,…,in∈E
则称{x(t),t≥0}为离散状态空间E上连续时间马尔可夫过程。
3.1 马尔可夫过程
齐次马尔可夫过程
如果对任意t,u≥0,均有 P{x(t+u)=j|x(u)=i}=Pij(t) i,j∈E
称具有这种特性的马尔可夫过程为齐次马尔可夫过程。
3.1 马尔可夫过程
齐次马氏过程的性质
P ( 1)0 1; ij
n
( 2) Pij 1 j 1
可以证明,对系统寿命以及故障后的修复时间均服 从指数分布时,则系统状态变化的随机过程{x(t),t≥0}是 一个齐次马尔可夫过程。
(2)式中对j求和,是对状态空间I的所有可能状态进行的
3.1 马尔可夫过程
马尔可夫过程定义
马尔可夫过程是一类“后效性”的随机过程。简单 地说,在这种过程中系统将来的状态只与现在的状态 有关,而与过去的状态无关。或者说,若已知系统在t0 时刻所处的状态,那么t> t0时的状态仅与时刻t0的状态 有关。
3.1 马尔可夫过程
马尔可夫过程的数学描述
设{x(t),t≥0}是取值在E={0,1,2,…}或E={0,1,2,…,N}上的 一个随机过程。若对任意n个时刻点0≤t1<t2<…<tn 均有:
e1——正常; e2——故障。
3.2 状态转移图
由此可写出:
此时转移矩阵P也称为微系数矩阵
通常令Δt=1,则有 1
P
1
由此可知,状态转移图是求解(写出)转移矩阵的基础。
随机到达者 等候室 服务台离去者
系统
马尔可夫链的概念及转移概率
例排队模型 设服务系统,由一个服务员和只可能容纳两个人的等候室组成.
