圆曲线放样
圆曲线放样实习报告

圆曲线测设实习报告一、实习内容及目的1.运用全站仪实地将设计的圆曲线通过坐标法放样出五大桩点及线路中线上的部分中桩点坐标。
2.结合课堂知识运用公式计算五大桩点坐标及中桩点坐标。
3.能运用坐标旋转公式将线路独立坐标系下的中桩点坐标转换到相应的线路坐标系坐标下。
4.能了解并运用“公路坐标计算系统V2.3 Build 328”软件进行曲线坐标计算。
5.沿曲线前进方向测设支导线用于曲线中桩点坐标的放样。
6.在曲线交点及支导线上的控制点上分别对曲线进行放样比较两次放样的偏差大小。
二、实习仪器拓普康全站仪*1 配套脚架铝合金脚架*2 对中杆*1 对中基座*1 棱镜*2 皮尺*2 计算器*1三、实习过程1.在直线段部分的两边分别选择两个转点用于交会定出曲线交点。
并在所选择的点上做好标志,将全站仪架设在靠近圆曲线的那个交点上,后视另一个转点定向;然后倒镜用棱镜在曲线交点附近位于视线上的直线上放出两个桩点。
用相同的方式在另一端直线部分架设仪器并在交点放出两个桩点。
然后在放出的四个交点上用皮尺交叉的拉出交点(需要注意交会交点的时候皮尺有一定的宽度,所以对准的时候要用相同边的皮尺交会。
)然后将全站仪架设在交点上分别照准直线上的两个转点,如果三点一线则表示放出的交点精度比较高。
2.将仪器架设在交点上用盘左盘右法测出两条直线的夹角β,用180 -β便可以得到曲线的转向角α。
小组根据自己所在的地段设计合适的曲线半径和缓和曲线长。
然后根据课本P165页相应公式可以算出曲线的综合要素。
3.将仪器架设在交点上根据算出的切线长T定出直缓点(ZH)的位置并做好标志;同样的方式在另一端直线上找出缓直点(HZ)。
4.将仪器架设在ZH点上后视转点(或前视交点)定向,然后从ZH点沿着圆曲线前进方向布设支导线用于圆曲线上中桩点的放样。
定向之后盘左盘右分别测出相应的转折角和距离。
建立以ZH点为坐标原点的独立直角坐标系用于曲线上中桩点坐标的计算,以及支导线上各点的坐标计算。
圆曲线的施工放样

偏角法在圆曲线施工放样中的应用随着人们审美观念的改变,人们建造房屋,不局限于四四方方的建筑,把外观设计成各种曲线、流线形,其中最常见的是圆曲线。
圆曲线的施工放样比较复杂,实地放样前需进行一定的内业计算,根据图纸的尺寸及设计要求,确定圆曲线主点的元素,然后,根据工程的特点,从便于施工放样出发,建立不同的坐标方式和计算公式。
现介绍保定高开区某建筑的圆曲线部分的施工放样。
由设计图纸可知,圆曲线的半径R=560m,圆曲线夹角a=28030’,曲线的主点A、B已经在轴线测量时定出,主要是对曲线上加密点的测设,在这里,我主要是采用偏角法测设加密点位。
1、计算测设数据由已知可计算也圆曲线的切线长T和曲线长L,T=Rtga/2=304.06mL=Raл/180=278.546m△3 c△2△1 cφφφA根据平面几何原理,偏角(弦切角)等于所夹弧的圆心角的一半,则偏角△与弦长C的计算公式分别为:△=φ/2C=2Rsinφ/2每隔一定的弧长l测设一点,即把圆弧分成n等份,则l=L/n,那么曲线上各点的偏角为第一点偏角的整数倍,即△1=a/2n=180*l/2ЛR△2=2△1△3=3△1……△n=n△1=a/2加密时,把圆曲线分成20等份,即把半圆分成10等份,则分偏角依次为:a/4=7007’30”△1=0042’45” △2=1025’30”△3=2008’15” △4=2051’00”△5=3033’45” △6=4016’30”△7=4059’15” △8=5042’00”△9=6024’45” △10=7007’30”C=2Rsin△1=13.927m。
2、实测1)在起点A上安置经纬仪,瞄准转折点定出切线方向,并使水平度盘读数为0000’00”。
2)顺时针方向转动照准部,使度盘的读数为0042’45”,并沿视线方向测设13.927m的水平距离,定出圆曲线上的第一点。
3)继续转动照准部,使水平度盘的读数为1025’30”,从第一点测设13.927m的水平距离与视线方向相交,定出第二点。
解析圆曲线坐标及其放样方法

解析圆曲线坐标及其放样方法圆曲线坐标是一种特殊的几何坐标系,它是由一条曲线经过的坐标点组成的。
圆曲线是几何学中的概念,它是一种更贴近自然环境的曲线形状。
其定义是,某一点到曲线所经过的其它点的距离和曲线上某一点到原点O的距离的乘积,此乘积总是常数。
圆曲线坐标的概念是,只要点所形成的距离可以满足圆曲线坐标的定义,它们就是圆曲线坐标。
因此,可以建立一组具有该坐标定义的点,这些点就构成了一条圆曲线。
二、圆曲线坐标的放样方法圆曲线放样方法是将圆曲线上的点按照一定的规律分布以得到一个平面、立体的效果的技术方法。
通常,圆曲线放样方法分为两种:一种是空间放样法,另一种是平面放样法。
空间放样法是将圆曲线上的点放置在一个三维空间中,通过空间放样可以将一条圆曲线变成贴近自然环境的曲线形状。
这种放样方法可以得到更加真实的效果。
平面放样法是把圆曲线上的点放置在一个二维平面上,从而组成一个半圆形。
此外,还可以利用软件进行放样,把圆曲线以图像的形式在屏幕上重现出来,从而得到一个真实的效果。
三、应用圆曲线坐标及其放样方法在工程设计中有着广泛应用。
比如,由于具有平滑曲线的独特特点,它们常常被用来作为管道设计,机械设计和船舶设计等工程设计中的基础几何形状。
此外,它也被用作绘制几何图形的参数化方案,从而能够方便的计算出几何图形的形状参数,进而更加精确地绘制几何图形。
四、总结圆曲线坐标及其放样方法可以帮助我们设计出更加平滑的几何图形,从而更加真实地绘制几何图形。
此外,它还被广泛应用于工程设计中,用于管道设计、机械设计和船舶设计等工程设计中的基础几何形状。
综上所述,圆曲线坐标及其放样方法可被广泛应用到几何图形的设计和工程设计以及其它领域。
公路圆曲线中、边桩坐标及放样计算 (全新版)
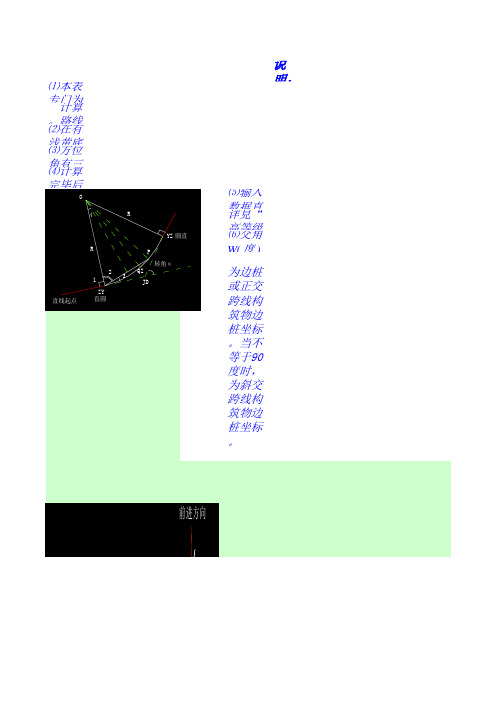
明:
⑴本表专门为圆曲线中、边桩坐标及放样计算而设计,只需输入转点的里程桩号、坐标及 计算。路线右转时R、转角输入正值,当路线左转时,R、转角输入负值。
⑵在有浅黄底色的单元格内输入数据,其它颜色的单元格为计算结果显示区,不能输入数
⑶方位角有三种值均可使用,第一种有正角,第二种为度、分、秒,秒的计算有误差,约
显示区,不能输入数据。
秒的计算有误差,约为0.2秒。
并删除不用数据等才可打印,可缩小比例。
用先删除后输入方法。
用说明”。
断面线与路线的夹角,见下图。当等于 90 度时,
。当不等于90度时,为斜交跨线构筑物边桩坐标。
为07年3月前,就可以不要注册了。
为边桩或正交跨线构筑物边桩坐标。当不等于90度时,
前进方向
P1(XP1,YP1) T W 公路中线 P0(XP0,YP0) T P2(XP2,YP2)Z 桥涵轴线 高速公路跨线建筑物轴线平面图
用时系统时间改为07年3月前,就可
的里程桩号、坐标及转角,圆曲线半径R,直线起点的坐标、桩打印前需进行值与数据格式复制并删除不用数据等才
O 4 R YZ 圆直 R P 转角α 2 1 直线起点 ZY 直圆 3 QZ JD
⑸输入数据直接覆盖原有数据,不用先删除后输入方法 详見“高等级公路测量计算程序使用说明”。
⑹交角 W( 度 ) 系指前进方向左侧横断面线与路线的夹
道路中线圆曲线放样方案
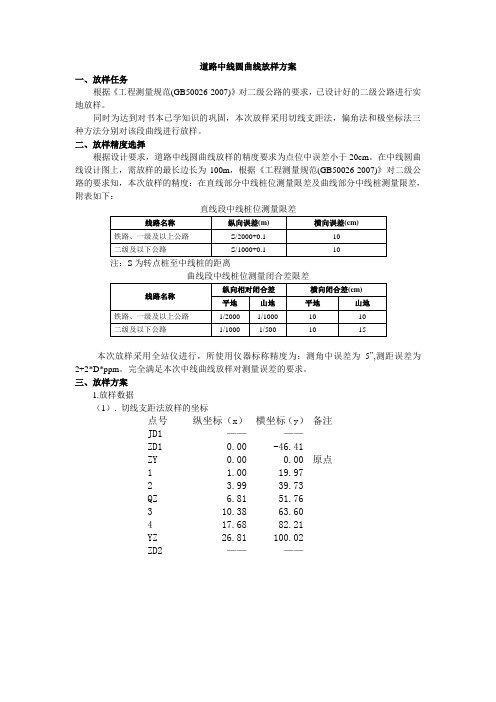
道路中线圆曲线放样方案一、放样任务根据《工程测量规范(GB50026-2007)》对二级公路的要求,已设计好的二级公路进行实地放样。
同时为达到对书本已学知识的巩固,本次放样采用切线支距法,偏角法和极坐标法三种方法分别对该段曲线进行放样。
二、放样精度选择根据设计要求,道路中线圆曲线放样的精度要求为点位中误差小于20cm。
在中线圆曲线设计图上,需放样的最长边长为100m,根据《工程测量规范(GB50026-2007)》对二级公路的要求知,本次放样的精度:在直线部分中线桩位测量限差及曲线部分中线桩测量限差,附表如下:本次放样采用全站仪进行,所使用仪器标称精度为:测角中误差为5”,测距误差为2+2*D*ppm。
完全满足本次中线曲线放样对测量误差的要求。
三、放样方案1.放样数据(1). 切线支距法放样的坐标点号纵坐标(x)横坐标(y)备注JD1 ————ZD1 0.00 -46.41ZY 0.00 0.00 原点1 1.00 19.972 3.99 39.73QZ 6.81 51.763 10.38 63.604 17.68 82.21YZ 26.81 100.02ZD2 ————(2).偏角法放样的角度与距离点号偏角(°′″)距离备注JD1 ————ZD1 ————ZY 00 00 00 0.00 原点1 02 51 52 19.992 05 43 44 39.93QZ 07 29 57 52.213 09 16 14 64.444 12 08 06 84.09YZ 15 00 00 103.55ZD2 ————(3).任意站极坐标法点号角(°′″)距离备注JD1 28 03 45 207.06ZD1 00 00 00 205.31ZY 13 03 51 200.001 18 47 35 200.002 24 31 19 200.00QZ 28 03 45 200.003 31 36 10 200.004 37 19 54 200.00YZ 43 03 58 200.00ZD2 56 07 50 205.312.放样步骤(一)切线支距法放样放样部位:道路中线圆曲线。
圆弧放样

[摘要]在实际的工程应用当中,如果曲线较长,地形变化大,放样曲线的三个主点已不能满足设计和施工的需要,还需要按照一定的桩距,在曲线上测设整桩和加桩。
这个过程称为圆曲线的详细测设。
偏角法是进行圆弧曲线放样的一种最重要的方法。
[关键词]偏角法放样圆弧曲线当路线由一个方向转到另一个方向时,必须用曲线来连接。
曲线的形式较多,其中,圆曲线是最基本的的一种平面曲线。
偏角根据所测右角计算;圆曲线半径R根据地形条件和工程要求选定。
根据偏角和半径,可以计算其他各个元素。
圆曲线的测设分两步进行,先测设曲线上起控制作用的主点;依据主点再测设曲线上每隔一定距离的里程桩,详细地标顶曲线位置。
为了在实地测设圆曲线的主点,需要知道切线长、曲线长及外距,这些元素称为主点测设元素。
一般情况下,当地形变化不大,曲线长度小于40m时,测设曲线的三个主点已经能够满足设计和施工的需要。
如果曲线较长,地形变化大,则除了测定三个主点以外,还需要按照一定的桩距,在曲线上测设整桩和加桩,这个过程称为圆曲线的详细测设。
圆曲线详细测设的方法很多,有极坐标法、直角坐标法、偏角法等。
其中偏角法是最基本、最重要的方法,也是在实际工程中广泛应用的一种方法。
用偏角法测设圆曲线上的细部点是以曲线的起点(或终点)作为测站,计算出测站至曲线上任一细部点的弦线与切线的夹角——弦切角(称为偏角)和弦长或相邻细部点的弦长,据此确定点的位置。
曲线上的细部点即曲线上的里程桩,一般按曲线半径R规定弧长为lo的整桩。
lo一般规定为5m,10m和20m,R越小,lo也越小。
用偏角法测设圆曲线的细部点,因测设距离的方法不同,分为长弦偏角法和短4偏角法两种。
前者测设测站至细部点的距离(长弦),适合于用经纬仪加测距仪(或用全站仪);后者测社设相邻细部点之间的距离(短弦),适合于用经纬仪加钢尺。
在实际的工程实践当中,为了追求美观,为了与当地的环境与自然相协调,为了有一定的美学价值,一些旅游建筑、大型的公共建筑和标志性建筑往往把其外轮廓立面做成圆弧形。
第四节圆曲线放样

60 3000 切线长 T 150 * tan 87 .48 m 2
ZY
JD
α
T
E0
L
QZ
YZ
曲线长 L 150 * 60 3000 *
603000 外矢矩 E 150 * (sec 1) 23.64 m 2
切曲差D 2 * 87.48- 158.39 16.57m
•
检查:
QZ
4
26
• ※ 置镜于YZ 点,(如图11-7),测设另一半曲线,偏
角要反拨:逆时针方向转动照准部,使度盘读
数为360°- δi 。
• 检查:弦长丈量是从点到点如 : YZ-1,1-2,2-3„iQZ
QZ 360
4
•
•
在QZ点的总偏角为:
应检核所测设的 QZ 点点位是否闭合 , 如超 限,须及时检查原因,重新测设。
K 180 1= · 2 2R 2 2 1
(11-2)
3 3 1 n n 1
※整弦:里程为 20m 倍数的两相邻曲线点间的弦长 (曲线点间距20m对应的弦长)。
※分弦:有一端里程不为 20m 倍数的两相邻曲线点 间的弦长。
17
•
•
• • •
通常要求曲线点设置在整数(如20m 的倍数)里程上 ,即里程 尾数为00, 20, 40, 60, 80m等点上。
27
二、切线支距法测设圆曲线(稍后)
• (切线支距法适用于地势较 平坦的地区)
1.测设原理:切线支距法即直 角坐标法。 (1)切线坐标系:见图11-8
坐标原点:曲线起点ZY或曲线 终点YZ;
曲线放样方法

实验:曲线放样实验仪器与工具:全站仪、花杆、测钎、红蓝铅笔、钉子、斧头等实验目的与要求:1、掌握偏角法放样单圆曲线测设过程2、掌握偏角法放样单圆曲线的测设数据的计算方法实验内容与步骤:1、根据给定的曲线半径R=80m和转角α=68°42′,计算其余曲线要素。
2、计算主点里程(其中JD里程为DK3+284.56)直圆(ZY)点里程 = JD里程– T曲中(QZ)点里程 = 直圆(ZY)点里程+ L/2圆直(YZ)点里程 = 曲中(QZ)点里程 + L/23、准备偏角法放样数据里程弧长偏角水平度盘读数备注ZY:QZ:QZ:YZ:4、主点的测设1)将全站仪安置在交点JD对中整平。
2)定ZY点和YZ点。
分别以线路的两个切线方向定向,自交点起分别沿线路的切向方向量取切线长T,定出ZY和YZ点3)定QZ点。
以线路的一个切线方向定向,度盘配置为0º0′0″,顺转望远镜,当水平度盘读数为1(180)2α-时,定出角分线方向,量外矢距E定出曲线中点QZ。
5、偏角法测设曲线细部点2180(sec1)22T R tgRLE Rq T Lααπα=⨯⨯⨯=︒=-=-1)将仪器置于ZY点,盘左位置用望远镜瞄准JD,置水平度盘读数为0º0′0″。
2)检查:瞄准QZ点,其水平度盘读数应为α/4,瞄准YZ点,其水平度盘读数应为α/2,误差应在±1ˊ之内。
若超限,仪器应重新移至JD处,重新测设圆曲线主点。
3)旋转仪器,使度盘读数为第1细部点的偏角,将钢尺零点对准ZY点,将花杆放在钢尺的刻度为弦长C1处,左右移动花杆使其对准望远镜的视线,所得点位即为细部点1。
4)旋转仪器,使度盘读数为第2细部点的偏角,将钢尺零点对准细部点1点,将花杆放在钢尺的刻度为弦长C处,左右移动花杆使其对准望远镜的视线,所得点位即为细部点2。
以后各点,可依此类推。
5)检查:继续进行以后各桩点的测设工作,按上法测至QZ点,检查分弦长度是否与计算值相符,其误差应小于1/1000,即(分弦之差/ 曲线半长)<(1/1000),若误差超限,则应分析原因,重新测设。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆曲线放样
在施工时,还需要放出曲线上除主点之外的若干点,称为轴线的详细放样。
常用的方法有偏角法和直角坐标法等。
⑴偏角法——利用偏角(弦切角)和弦长交会的方式来放样轴线。
(图10-6)
圆曲线起点为B,终点为E,转点为P。
为把曲线上各放样点里程凑成整数,曲线长度分为首尾两段零头弧长S1、S2和n段相等的弧长之和,即:
L=S1+nS+S2
S1、S2所对圆心角为φ1、φ2,S所对圆心角为φ。
放样数据按下式计算:
的弦长计算公式:
圆曲线上各点的偏角(弦切角等于弦长所对圆心角的一半)为:
放样过程:将仪器安置于圆曲线起点ZY(即B点)上,后视JD(P)点,并将水平度盘置于零,拨角∠PB1,在此方向上量取d1,得1点;然后,再拨角∠PB2,钢尺零点对准1点,以d为半径,摆动钢尺到经纬仪方向线上,得2点;再拨角∠PB3,钢尺零点对准2点,以d为半径,摆动钢尺到经纬仪方向线上,得3点;依此类推…
当拨角∠PBE时,视线应当通过圆曲线的终点YZ点。
YZ点至圆曲线上最后一个细部点的距离应为d2。
以此检查放样质量。
⑵直角坐标法——切线支距法,以曲线起点ZY或终点YZ为坐标原点,以切线为x轴,切线的垂线为y轴,如图10-17所示。
根据坐标xi、yi放样曲线上各细部点。
设各细部点之间的弧长为S,所对应的圆心角为φ,则
已知R,又给定S值后,即可求出待放样的细部点坐标。
S值一般为10m、20m、30m等整数值。
放样前可按上述公式计算,将计算得结果列表备用。
放样步骤如下:
①检核先前放样的三个主点ZY、QZ、YZ的点位有无错误。
②用钢尺沿切线ZY-JD方向放样x1、x2、x3等,并在地面上标定出垂足点m、n、p等。
③在垂足m、n、p等处用经纬仪、直角尺法作切线的垂线,分别在各自的垂线上放样y1、y2、y3等,以桩定细部点1、2、3等。
为了避免支线过长,影响放样精度,可用同法,从YZ-JD切线方向上放样曲线的另一半弧上的细部点。
