解析圆曲线坐标及其放样方法
圆曲线细部放样方法的探讨

w r la d me u e n o t n d ic e ig e o o i e e t.S t a e r a l ee e c o et g o tm a u e n ftn e o k o d a a rme tc s ,a n r a n c n l c b n f s o i h s rma k b er fr n ef rs t n — u e s rme to n l n s s n i i u
D s nadR sa hIstt, hny 74 0 ,C ia ei n eer tue Z a ge 3 00 hn ) g c ni
Ab t a t T i p p r p e e t e t o fcr ua u v e t g o t n a u e n ,a d i p l ain s r c : hs a e rs n sa n w me h d o i lrc r es t n - u d me s r me t n sa p i t .C mp rn h a i c i a t c o o ai gt t et d - o r
称之 为坐标 法 。下 面对 坐标 法 、 角 法 和切 线 支距 偏
法各 法 的具 体操作 叙述如 下 。
面 曲线 。平 面曲线 又 分为 圆 曲线 和缓 和 曲线 2种 , 圆 曲线 是具有 一定 曲率 半 径 的 圆弧 ; 和 曲线 一 般 缓 是 用来连 接直线 和 圆弧 的 , 曲率 半 径 由无 穷 大 变 其 化 至 圆曲线半 径 。在实 际 工作 中 , 由于 水利 工 程 自
ZHANG u—pe F ng
( h s B a c f a s rv c l t o sra o n y r o e Ivs gt n T e1 t r ho n uP oi i e C nev t n a dH do w r n et ai , n G n a Wa r i p i o
圆曲线与综合曲线的放样方法

2 1 年 2月 00
测 绘 与 空 间地 理 信 息
G EOMAT C & S IS PAT AL l I NFORM ATI ON TECHNOL ocY
Vo . 3, .1 1 3 No
Fe b.,2 0 01
圆 曲线 与 综 合 曲线 的 放 样 方 法
史 磊
( 哈尔滨 市勘察测绘 研究院 , 黑龙 江 哈尔滨 10 1 ) 5 0 0
摘
要 : 过 对 工 程 测 量 中 曲线 测 设 的 各 种 方 法 总 结 , 述 了 曲线 放 样 的数 学 原 理 及 程 序 编 制 方 法 。 分 别 介 绍 通 论
了 圆 曲线 、 合 曲线 放 样 方 法 的 过 程 。探 讨 了一 种 放 样 缓 和 曲线 及 其 边 线 的 方 法 , 法 在 实 际 工 作 中有 良好 的 综 此
A b tac :Th o g n lzn h rncp e fe i e rng s r e i g a u sr t r u h a ay ig t e p i il so ngn e i u v y n nd s mm aii g v ro sm eh dsfrs ti u h ur e n en rzn a u t o o e t i ng o tt e c v si — g n e ig s r e ig,hs pa rdic s e he i e rn u yn t i pe s u s d t mah m ais rncp e n o r m ev lpi eh ds o e tn utc r e .I nto v te tc p i il a d prg a d e o ng m to fr s ti g o u v s t r ・ i du e h r c d e o etig o tcr ulrc r e a d o c d t e p o e ur fs tn u ic a u v n c mpo ie c r e, s use nd o t o r s tig o tt r nsto u v st u v dic s d a ki fme h d f etn u he ta iin c r e o a d isbo n r i h h sa h e e l efc si a tc lwo k a d m e h c u a y rqur menso h e in o n i e n ur n t u day wh c a c i v d wel fe t n prc ia r n tt e a c r c e ie t n t e d sg fe gne r g s — i
圆曲线与综合曲线的放样方法

[1]吕云林.建筑工程测量[M].武汉:武汉工业大学出版 社,1998.
[2]杨三卫.张宏志,毛启礼.工程测量[M].北京:中国建筑 工业出版社,1985.
[3]邵自修.工程测量[M].北京i冶金工业出版社,1999. [4]陈龙飞,金其坤.工程测量[M].北京:同济大学出版
社,1990. [5]周荣沾主编.城市道路设计[M]பைடு நூலகம்北京:人民交通出版
GEOMATICS&SPATIAL INFORMATION TECHNOLOGY
v。I.33。N。.1 Feb.,2010
圆曲线与综合曲线的放样方法
史磊
(哈尔滨市勘察测绘研究院。黑龙江哈尔滨1卯olo)
摘要:通过对工程测量中曲线测设的各种方法总结,论述了曲线放样的数学原理及程序编制方法。分别介绍
了圆曲线、综合曲线放样方法的过程。探讨了一种放样缓和曲线及其边线的方法,此法在实际工作中有良好的
万方数据
包括曲线起点Zy(也称圆点),曲线中点qz(也称曲中 点),曲线终点蹈(也称圆直点)。
如果这3点的位置确定了,这个曲线的位置也就固定 了,所以称为曲线主点。
圆曲线主点位置的测设:先要根据外业观测的转角a 和设计时选定的曲线半径R,求出以下数据以后才能进行 测设,由几何关系得出:
r=R.tan詈
置=R×sin(/印)
K:R—R cos(妇);月[1-cos(ie)]=2R sin2(等)
妒2了1800×百七
s=2R sin旦2
式中,=1,2,3,…,no
Fig.2
图2直角坐标定位图 The positioning using rectan甜e coordinates
上述数据可用计算机编程序算得,亦可以尺,矗为引 数查“曲线测设用表”获得。
公路圆曲线中、边桩坐标及放样计算 (全新版)
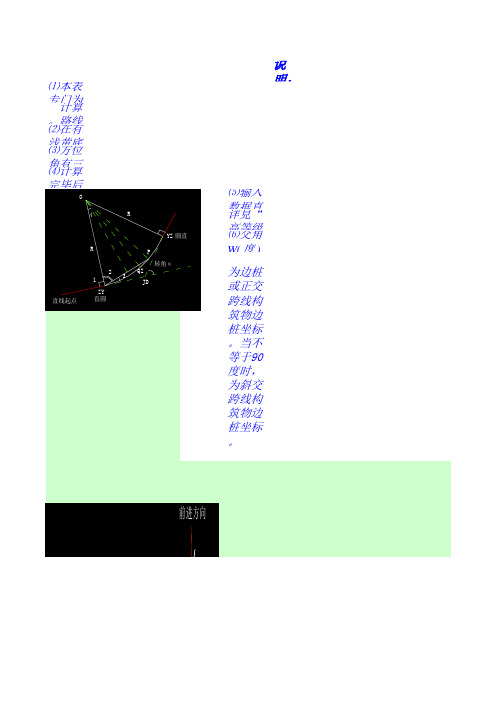
明:
⑴本表专门为圆曲线中、边桩坐标及放样计算而设计,只需输入转点的里程桩号、坐标及 计算。路线右转时R、转角输入正值,当路线左转时,R、转角输入负值。
⑵在有浅黄底色的单元格内输入数据,其它颜色的单元格为计算结果显示区,不能输入数
⑶方位角有三种值均可使用,第一种有正角,第二种为度、分、秒,秒的计算有误差,约
显示区,不能输入数据。
秒的计算有误差,约为0.2秒。
并删除不用数据等才可打印,可缩小比例。
用先删除后输入方法。
用说明”。
断面线与路线的夹角,见下图。当等于 90 度时,
。当不等于90度时,为斜交跨线构筑物边桩坐标。
为07年3月前,就可以不要注册了。
为边桩或正交跨线构筑物边桩坐标。当不等于90度时,
前进方向
P1(XP1,YP1) T W 公路中线 P0(XP0,YP0) T P2(XP2,YP2)Z 桥涵轴线 高速公路跨线建筑物轴线平面图
用时系统时间改为07年3月前,就可
的里程桩号、坐标及转角,圆曲线半径R,直线起点的坐标、桩打印前需进行值与数据格式复制并删除不用数据等才
O 4 R YZ 圆直 R P 转角α 2 1 直线起点 ZY 直圆 3 QZ JD
⑸输入数据直接覆盖原有数据,不用先删除后输入方法 详見“高等级公路测量计算程序使用说明”。
⑹交角 W( 度 ) 系指前进方向左侧横断面线与路线的夹
圆弧放样

[摘要]在实际的工程应用当中,如果曲线较长,地形变化大,放样曲线的三个主点已不能满足设计和施工的需要,还需要按照一定的桩距,在曲线上测设整桩和加桩。
这个过程称为圆曲线的详细测设。
偏角法是进行圆弧曲线放样的一种最重要的方法。
[关键词]偏角法放样圆弧曲线当路线由一个方向转到另一个方向时,必须用曲线来连接。
曲线的形式较多,其中,圆曲线是最基本的的一种平面曲线。
偏角根据所测右角计算;圆曲线半径R根据地形条件和工程要求选定。
根据偏角和半径,可以计算其他各个元素。
圆曲线的测设分两步进行,先测设曲线上起控制作用的主点;依据主点再测设曲线上每隔一定距离的里程桩,详细地标顶曲线位置。
为了在实地测设圆曲线的主点,需要知道切线长、曲线长及外距,这些元素称为主点测设元素。
一般情况下,当地形变化不大,曲线长度小于40m时,测设曲线的三个主点已经能够满足设计和施工的需要。
如果曲线较长,地形变化大,则除了测定三个主点以外,还需要按照一定的桩距,在曲线上测设整桩和加桩,这个过程称为圆曲线的详细测设。
圆曲线详细测设的方法很多,有极坐标法、直角坐标法、偏角法等。
其中偏角法是最基本、最重要的方法,也是在实际工程中广泛应用的一种方法。
用偏角法测设圆曲线上的细部点是以曲线的起点(或终点)作为测站,计算出测站至曲线上任一细部点的弦线与切线的夹角——弦切角(称为偏角)和弦长或相邻细部点的弦长,据此确定点的位置。
曲线上的细部点即曲线上的里程桩,一般按曲线半径R规定弧长为lo的整桩。
lo一般规定为5m,10m和20m,R越小,lo也越小。
用偏角法测设圆曲线的细部点,因测设距离的方法不同,分为长弦偏角法和短4偏角法两种。
前者测设测站至细部点的距离(长弦),适合于用经纬仪加测距仪(或用全站仪);后者测社设相邻细部点之间的距离(短弦),适合于用经纬仪加钢尺。
在实际的工程实践当中,为了追求美观,为了与当地的环境与自然相协调,为了有一定的美学价值,一些旅游建筑、大型的公共建筑和标志性建筑往往把其外轮廓立面做成圆弧形。
第四节圆曲线放样

60 3000 切线长 T 150 * tan 87 .48 m 2
ZY
JD
α
T
E0
L
QZ
YZ
曲线长 L 150 * 60 3000 *
603000 外矢矩 E 150 * (sec 1) 23.64 m 2
切曲差D 2 * 87.48- 158.39 16.57m
•
检查:
QZ
4
26
• ※ 置镜于YZ 点,(如图11-7),测设另一半曲线,偏
角要反拨:逆时针方向转动照准部,使度盘读
数为360°- δi 。
• 检查:弦长丈量是从点到点如 : YZ-1,1-2,2-3„iQZ
QZ 360
4
•
•
在QZ点的总偏角为:
应检核所测设的 QZ 点点位是否闭合 , 如超 限,须及时检查原因,重新测设。
K 180 1= · 2 2R 2 2 1
(11-2)
3 3 1 n n 1
※整弦:里程为 20m 倍数的两相邻曲线点间的弦长 (曲线点间距20m对应的弦长)。
※分弦:有一端里程不为 20m 倍数的两相邻曲线点 间的弦长。
17
•
•
• • •
通常要求曲线点设置在整数(如20m 的倍数)里程上 ,即里程 尾数为00, 20, 40, 60, 80m等点上。
27
二、切线支距法测设圆曲线(稍后)
• (切线支距法适用于地势较 平坦的地区)
1.测设原理:切线支距法即直 角坐标法。 (1)切线坐标系:见图11-8
坐标原点:曲线起点ZY或曲线 终点YZ;
圆曲线坐标计算(坐标正算法)

2、计算方法 根据交点里程和圆曲线要素计算主点里程。
公路习惯推算方法:
曲线测设是指每隔一定距离测设一个曲线点以在地面上标志曲线平面位置。
现阶段曲线测设主要采用全站仪或GPS进行,而这两种方法所需测设资料是曲线点的坐标,故实施测设前必须计算曲线点的坐标。
四、单圆曲线测设资料计算
1、基本要求 中桩间距:即相邻两曲线点间的距离,一般为 20 米,地形复杂时为 10 米。施工时可按规范或标书要求进行。 桩号:即曲线点的里程,必须是中桩间距的整倍数。 例如:ZY点里程为18+197.36,中桩间距为20m,则第一点里程为________________________________。 第二点里程为______________________________。 依此类推。
18+200
18+220
2、曲线点坐标计算
已知条件:起点、终点及各交点的坐标。
JD1
起点
终点
ZY2
YZ2
ZY1
YZ1
QZ2
JD2
S1-2
T1
T2
X
Y
O
QZ2
1)计算ZY、YZ点坐标
JD1
起点
终点
ZY2
YZ2
ZY1
YZ1
QZ2
JD2
S1-2
T1
T2
X
Y
O
QZ2
通用公式:
JD1
起点
终点
ZY2
YZ2
ZY1
YZ1
QZ2
JD2
S1-2
T1
T2
X
Y
O
QZ2
ZY- i
ZY- JD
公路圆曲线简易放样方法
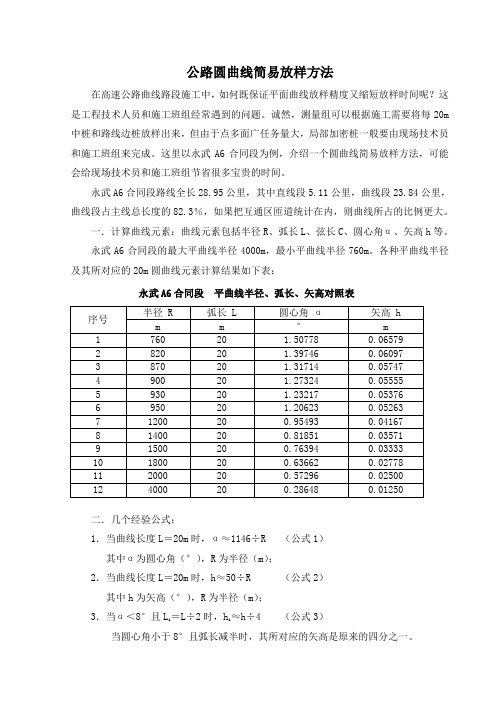
公路圆曲线简易放样方法在高速公路曲线路段施工中,如何既保证平面曲线放样精度又缩短放样时间呢?这是工程技术人员和施工班组经常遇到的问题。
诚然,测量组可以根据施工需要将每20m 中桩和路线边桩放样出来,但由于点多面广任务量大,局部加密桩一般要由现场技术员和施工班组来完成。
这里以永武A6合同段为例,介绍一个圆曲线简易放样方法,可能会给现场技术员和施工班组节省很多宝贵的时间。
永武A6合同段路线全长28.95公里,其中直线段5.11公里,曲线段23.84公里,曲线段占主线总长度的82.3%,如果把互通区匝道统计在内,则曲线所占的比例更大。
一.计算曲线元素:曲线元素包括半径R、弧长L、弦长C、圆心角α、矢高h等。
永武A6合同段的最大平曲线半径4000m,最小平曲线半径760m。
各种平曲线半径及其所对应的20m圆曲线元素计算结果如下表:永武A6合同段平曲线半径、弧长、矢高对照表二.几个经验公式:1.当曲线长度L=20m时,α≈1146÷R (公式1)其中α为圆心角(°),R为半径(m);2.当曲线长度L=20m时,h≈50÷R (公式2)其中h为矢高(°),R为半径(m);3.当α<8°且Li =L÷2时,hi≈h÷4 (公式3)当圆心角小于8°且弧长减半时,其所对应的矢高是原来的四分之一。
三.准备放样工具:钢尺(50m)1把,测量距离用;尼龙线绳50m以上,挂线用;手锤(2~3p)1把,钉子若干,确定点位用。
四.曲线桩加密方法:举一个路基边沟曲线段加密的例子。
为了简便,放样时以设计半径代替边沟曲线半径。
严格来说,由于边沟位于路基的两侧,其曲线半径与路基中线的曲线半径并不相等,但通过计算可知,20m路段两者矢高之差在0~5mm之间,施工中可以忽略不计。
本人多年前在浆砌边沟施工放样时用加密曲线点的方法逐段缩小矢高数值,当加密到曲线的矢高小于10mm时,边沟外观线形圆滑顺畅,令人满意。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解析圆曲线坐标及其放样方法
圆曲线坐标是一种特殊的几何坐标系,它是由一条曲线经过的坐标点组成的。
圆曲线是几何学中的概念,它是一种更贴近自然环境的曲线形状。
其定义是,某一点到曲线所经过的其它点的距离和曲线上某一点到原点O的距离的乘积,此乘积总是常数。
圆曲线坐标的概念是,只要点所形成的距离可以满足圆曲线坐标的定义,它们就是圆曲线坐标。
因此,可以建立一组具有该坐标定义的点,这些点就构成了一条圆曲线。
二、圆曲线坐标的放样方法
圆曲线放样方法是将圆曲线上的点按照一定的规律分布以得到一个平面、立体的效果的技术方法。
通常,圆曲线放样方法分为两种:一种是空间放样法,另一种是平面放样法。
空间放样法是将圆曲线上的点放置在一个三维空间中,通过空间放样可以将一条圆曲线变成贴近自然环境的曲线形状。
这种放样方法可以得到更加真实的效果。
平面放样法是把圆曲线上的点放置在一个二维平面上,从而组成一个半圆形。
此外,还可以利用软件进行放样,把圆曲线以图像的形式在屏幕上重现出来,从而得到一个真实的效果。
三、应用
圆曲线坐标及其放样方法在工程设计中有着广泛应用。
比如,由于具有平滑曲线的独特特点,它们常常被用来作为管道设计,机械设计和船舶设计等工程设计中的基础几何形状。
此外,它也被用
作绘制几何图形的参数化方案,从而能够方便的计算出几何图形的形状参数,进而更加精确地绘制几何图形。
四、总结
圆曲线坐标及其放样方法可以帮助我们设计出更加平滑的几何图形,从而更加真实地绘制几何图形。
此外,它还被广泛应用于工程设计中,用于管道设计、机械设计和船舶设计等工程设计中的基础几何形状。
综上所述,圆曲线坐标及其放样方法可被广泛应用到几何图形的设计和工程设计以及其它领域。
