2019秋小学数学12.1 全等三角形 (4)
12.1三角形全等的条件(四HL)
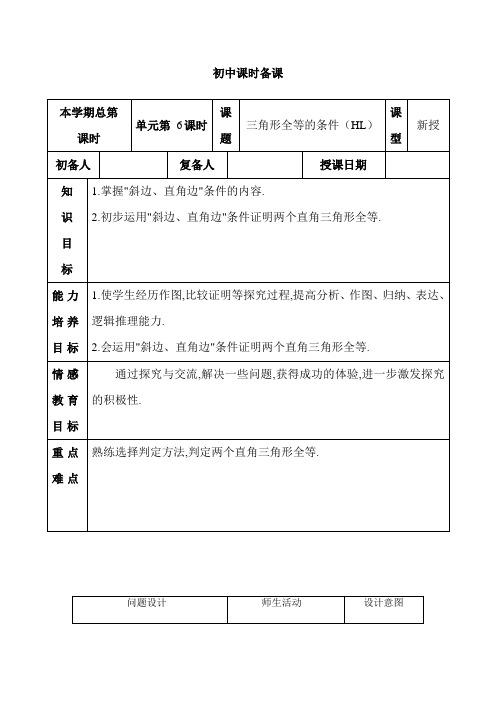
⑴作∠MC´N=90°;
⑵在射线C´M上取B´C´=BC;
⑶以B´为圆心,AB为半径画弧,
交射线C´N于点A´;
⑷连接A´B´.
3.探索发现的规律:
斜边和一条直角边对应相等的两个直角三角形全等。
简写为“斜边、直角边”或“HL”。
三、典例讲析
如图:AC⊥BC,BD⊥AD,AC=BD.求证:BC=AD
初中课时备课
本学期总第课时
单元第6课时
课题
三角形全等的条件(HL)
课型
新授
初备人
复备人
授课日期
知
识
目
标
1.掌握"斜边、直角边"条件的内容.
2.初步运用"斜边、直角边"条件证明两个直角三角形全等.
能力培养目标
1.使学生经历作图,比较证明等探究过程,提高分析、作图、归纳、表达、逻辑推理能力.
2.会运用"斜边、直角边"条件证明两个直角三角形全等.
2.两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?为什么?
3.思考:
如图,△ABC中,∠C =90°,
直角边是_____、_____,斜边是______。
4.问题:
对于直角三角形,是不是有其他证明全等的方法呢?
二、动动手、探新知
1、任意画出一个Rt△ABC,∠C=90°。再画一个Rt△A´B´C´,使得∠C´= 90°,B´C´=BC,A´B´= AB。
教师强调在三角形前面加上Rt。
学生独立分析
找学生说解题思路
教师板演规范步骤学生独立完成一源自学生板演引导学生将知识系统化
练习2先让学生将文字语言转化成几何语言,写成已知和求证的形式。
全等三角形性质教案

证明:∵△ABC≌△EFD
∴AB=EF
(全等三角形的对应边相等。)
∴AB-AE=EF-AE
(等量减等量,差相等。)
即BE=FA
二次备课
小结
本节主要讲了全等形的概念及全等三角形的性质。
全等形:能够完全重合的两个图形叫做全等形.
(形状、大小完全相同的图形叫做全等形)
全等三角形:能够完全重合的两个三角形叫做全等三角形
3、全等三角形的性质:
全等三角形的对应边相等.
全等三角形的对应角相等
4、巩固练习
教学反思(要求:经验总结、问题分析、改进措施)
情感态度与价值观:通过全等形和全等三角形的学习,认识和熟悉生活中的全等图形, 认识生活和数学的关系,激发学生学习数学的兴趣。
重点
认识全等三角形,掌握全等三角形的性质,准确快速找到对应边,对应角
难点
让学生掌握全等三角形的性质,并准确快速的找到对边,对应角
教学
方法
讲授法,合作交流法
教具准备
教案,课件、彩色粉笔
课题
12.1 全等三角形
课时安排
第(1)课时
共(2)课时
教
学
目
标
知识与技能:1、了解全等 形和全等三角形的概念,掌握全等形的性质
2、能正确表示两个全等三角形,能找出全等三角形的对应元素
3、能运用全等性质进行简单的推理和计算,解决一些实际问题。
过程与方法:通过将两个全等的三角形平移,旋转和翻折等位置变换,让学生从中体会图形的变换思想,逐步培养学生动态的研究几何图形的意识。
注意:记两个三角形全等时,通常把对应顶点的字母写在对应的位置上.
【问题】你能找出图⑴中其他的对应顶点、对应边和对应角吗?怎样表示图⑵⑶中的两个全等三角形,并找出对应顶点、对应边和对应角.
12.1全等三角形全等三角形的性质(教案)

本节课旨在让学生在掌握全等三角形知识的基础上,全面提升学科核心素养,为学生的终身发展奠定基础。
三、教学难点与重点
1.教学重点
(1)全等三角形的定义:理解全等三角形的含义,掌握全等三角形的判定条件。
-举例:强调全等三角形是大小和形状完全相同的三角形,要求学生对SSS、SAS、ASA、AAS、HL五种判定方法熟练掌握。
2.教学难点
(1)全等三角形的判定方法的区分与应用:学生容易混淆SSS、SAS、ASA、AAS、HL五种判定方法,不知道在具体情况下如何选择。
-举例:通过典型例题和练习,帮助学生区分各种判定方法,并指导他们在实际问题中灵活运用。
(2)全等三角形性质的应用:学生在解决问题时,往往不知道如何运用全等三角形的性质。
-举例:针对这一问题,设计不同类型的题目,指导学生运用全等三角形的观察和想象全等三角形的过程中,可能存在一定的困难。
-举例:利用几何画板、实物模型等教具,帮助学生培养空间想象能力。
(4)团队合作能力的培养:学生在小组讨论和合作探究过程中,可能存在沟通不畅、分工不明确等问题。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了全等三角形的基本概念、判定方法和在实际中的应用。同时,我们也通过实践活动和小组讨论加深了对全等三角形的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
五、教学反思
在上完这节课后,我进行了深入的思考。首先,我发现学生们对全等三角形的定义和性质的理解程度参差不齐。在讲授过程中,我尽量用简单明了的语言解释全等三角形的判定方法,并通过实例让学生们更好地理解。但我也意识到,对于一些学生来说,这些概念仍然难以消化。在今后的教学中,我需要更加关注这部分学生,采用更为直观和生动的方式,帮助他们真正掌握全等三角形的判定方法和性质。
12-1 全等三角形 课件(共26张PPT)

知识梳理
例题 1:如图所示,△ ≌△ ,指出所有的对应边和对应角.
AB与DC,AC与DB,BC与CB是对应边;
∠ABC与∠DCB,∠A与∠D,∠ACB与∠DBC是对应角。
【解答】(1)已知△ABC≌△DCB,故公共边BC和CB
是对应边,它们所对的∠A和∠D是对应角,最短边
【结论】本题考查了全等三角形的性质及
比较角的大小,解题的关键是找到两全等
三角形的对应角、对应边.
80°
.
知识梳理
例题4:如图,将长方形ABCD沿AE折叠,使D点落在BC边上的F点处,
如果∠BAF = 60°,那么∠DAE= 15°
角
例题5:如图,△ ABC ≌△ ADE,则AB = AD ,∠E =
知识梳理
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合
的边叫做对应边,重合的角叫做对应角。例如,图中的△ 和△
全等,记作△ ≌ ,其中点和点,点和点,点
和点是对应顶点;和,和,和是对应边;∠和
∠,∠和∠,∠和∠是对应角.
∠BAE = 130°,∠BAD = 50°,则∠BAC=
。
80°
∠C
,若
知识梳理
例题6:如图,已知△ ABC ≌△ EBF,AB ⊥ CE,ED ⊥ AC,∠A = 24°,
则:(1)AB =
EB ,BC = BF ,∠C = 66 °,∠EFB = 66 °;
(2)若AB = 5cm,BC = 3cm,则AF = 2cm 。
AB和DC是对应边,它们所对的∠ACB和∠DBC是对应
角,余下的一对边和一对角分别是对应边和对应角.
(2)根据书写规范可知点A和点D,点B和点C,点C
12.1全等三角形
第十二章全等三角形12.1全等三角形要点感知1能够 _____________________ 叫做全等形•两个图形是否全等只与这两个图形的形状和大小有关,与图形所在位置无关•预习练习1-1下列各图形中,不是全等图形的是()飪3必倉令令翩影A H C D要点感知2能够 ____________ 的两个三角形叫做全等三角形•平移、翻折、旋转前后的图形_______ •把两个全等的三角形重合在一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.预习练习2-1如图所示,△ ABC与厶DEF全等,可记作厶ABC _ △DEF其中点A与点—是对应顶点,/ B与____ 是对应角,AC与__ 对应边.要点感知3全等三角形的 ______ 相等;全等三角形的______ 相等•预习练习3-1如图,已知△ ABD BA ECF则相等的边有__________________ ;相等的角有________________________知识点1认识全等形及全等三角形2•如图所示,将△ ABC沿AC对折,点B与点E重合,则全等的三角形有()A.1对B.2对C.3对D.4对3•如图所示,△ AOC^^ BOD, C, D是对应点,下列结论错误的是()A.Z A与/ B是对应角B.Z AOC与/ BOD是对应角C.OC与OB是对应边D.OC与OD是对应边知识点2全等三角形的性质4.如图,△ ABC^^ DEF,BE=4,AE=10 DE的长是()A.5B.4C.3D.2夺童milsi•下列图形中与已知图形全等的是()5.已知图中的两个三角形全等,则/ a度数是()D.50 °A.72°B.60°AC.58°/代广衣 /6.如图,b△ ACB^ A'cCB',/ BCB' = 30°,则/ ACA'的度数是8•若△ ABC与厶DEF全等,A和E, B和D分别是对应点,则下列结论错误的是()A.BC=EFB./ B=/ DC./ C=/ FD.AC=EF9•若△ ABG^A DEF且△ ABC的周长为20,AB= 5,BC= 8,则DF长为()A.5B.8C.7D.5 或810. 如图,已知△ ABD^A CDB,且AB、CD是对应边,下面四个结论中不正确的是()A A ABD和厶CDB的面积相等B A ABD和厶CDB的周长相等C./ A+/ ABD=/ C+/ CBDD.AD// BC且AD= BC11. _____________________________________________________ 如图,已知△ ABC^^ BAD,BC=AD写出其他的对应边 ___________________________________________________ 和对应角______________________12. _______________________________________________________ 如图是用七巧板拼成的一艘帆船,其中全等的三角形共有 _________________________________________________ 对.7•如图所示,△ ABg A DEF若AB= DE,/ B= 50°,/ 8 70°,/ E= 50 ° ,AC= 2 cm,求/ D 的度数及DF 的长•13. ________________________________________________________________________ 如图,已知△ AEB^^ DFC, AE丄BC, DF丄CB,/ C= 28°,则/ A 的度数是 __________________________14. _______________________________________________________________________________________ 如图所示,若△ ABD^A ACE/ B与/ C是对应角,若AE= 5 cm,BE= 7 cm, / ADB= 100 °,则/ AEC=________________________________________________________________________________________ , AC= _____________________________________________________________________________________15. 如图所示,已知△ ABD^A ACD,且B, D, C在同一条直线上,那么AD与BC是怎样的位置关系?为什么?B D C16. 如图,△ ABC^A ADE, / DAC=60°,Z BAE=100°, BC、DE相交于点F,求/ DFB的度数.挑战自我17. 如图所示,A, D, E三点在同一直线上,且△ BAD^A ACE,试说明:(1)BD= DE+ CE;(2)△ ABD满足什么条件时,BD// CE?参考答案课前预习要点感知1完全重合的两个图形预习练习1-1 A要点感知2完全重合全等预习练习2-1也 D / E DF要点感知3 对应边对应角预习练习3-1 A B=EC,AD=EF,BD=C/A=/ E,/ B=/ ECF/ ADB=/ F当堂训练1 .B2 .C 3.C 4.A 5 .D 6.30 °7. •/△ABC^A DEF/. / B=/ E,/ C=/ F,/ A=/ D,DF= AC= 2 cm.•••/ B= 50°,/ C= 70°, •••/ A= 180°-50°-70°= 60°,.•./ D=/ A= 60°.课后作业8.A 9 .C 10.C11 .AC=BD,AB=B& C=Z D,Z CAB=Z DBA,/ABC=Z BAD12. 2 13.62°14.100° 12 cm15 .AD丄BC理由如下:•••/ ADB与/ ADC是对应角,且/ ADB+/ ADC=180°, •••/ ADB=/ ADC=90° .••• AD丄BC.16 .•••△ ABC^^ ADE,:/ B=/ D,/ BAC=Z DAE. 又/ BAD=/ BAC/ CAD, / CAE=/ DAE-/ CAD,•/ BAD=/ CAE.•••/ DAC=60°,/ BAE=100°,1•/ BAD=—(/ BAE-/ DAC) =20° .2•••在△ ABG和厶FDG中,/ B=/ D,/ AGB=/ FGD,•/ DFB=/ BAD=20° .17. (1)v^ BAD^A ACE, • BD=AE, AD=CE.又••• AE=AD+DE •- BD=CE+DE.(2)A ABD满足/ ADB=90° 时,BD// CE理由:•••/ ADB=90°, •/ BDE=180° -90° =90° . 又•••△BAD^AACE, •/ CEA=Z ADB=90°.•/ CEA=/ BDE,「. BD// CE.。
第04讲 全等三角形的判定(原卷版)

第04讲全等三角形的判定一、全等三角形判定1——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).要点:如图,如果''A B =AB,''A C =AC,''B C =BC,则△ABC≌△'''A B C .二、全等三角形判定2——“边角边”1.全等三角形判定2——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).要点:如图,如果AB =''A B ,∠A=∠'A ,AC =''A C ,则△ABC≌△'''A B C .注意:这里的角,指的是两组对应边的夹角.2.有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB=AB,AC=AD,∠B=∠B,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.三、全等三角形判定3——“角边角”全等三角形判定3——“角边角”两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).要点:如图,如果∠A=∠'A ,AB=''A B ,∠B=∠'B ,则△ABC≌△'''A B C .四、全等三角形判定4——“角角边”1.全等三角形判定4——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)要点:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果DE∥BC,那么∠ADE=∠B,∠AED=∠C,又∠A=∠A,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.五、判定方法的选择1.选择哪种判定方法,要根据具体的已知条件而定,见下表:已知条件可选择的判定方法一边一角对应相等SAS AAS ASA 两角对应相等ASA AAS两边对应相等SAS SSS2.如何选择三角形证全等(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;(2)可以从已知出发,看已知条件确定证哪两个三角形全等;(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.一、“SSS ”证明三角全等例1.如图,ABC 中,AB AC =,BE EC =,直接使用“SSS ”可判定()A .ABD ACD △≌△B .ABE ACE △≌△C .BED CED △≌△D .ABE EDC≌例2.如图,在ACE △和BDF V 中,AE BF =,CE DF =,要利用“SSS ”证明ACE BDF V V ≌,需增加的一个条件可以是()A .AB BD =B .DC AC =C .AB CD =D .AC BC=例3.如图,木工师傅常用角尺平分任意一个角,做法如下:如图,在AOB ∠的边OA OB 、上分别取OM ON =,移动角尺,使角尺的两边相同的刻度分别与M 、N 重合,得到AOB ∠的平分线OP .做法中用到的三角形全等的判定方法是()A .SSSB .SASC .ASAD .HL例4.已知AOB ∠.下面是“作一个角等于已知角,即作A O B AOB '''=∠∠”的尺规作图痕迹.该尺规作图的依据是()A .SASB .SSSC .AASD .ASA例5.一个三角形的三边长为5,x ,14,另一个三角形的三边长为5,10,y ,如果由“SSS ”可以判定两个三角形全等,则x y +的值为()A .15B .19C .24D .25例6.如图,AD BC 、交于点O ,AC BD BC AD ==,.求证:C D ∠=∠.例7.如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,AB AE =,AC AD =,BC DE =,48C ∠=︒,求D ∠.二、“SAS ”证明三角全等例8.如图,已知12∠=∠,AC AB =,则ABD ACD △≌△的依据是()A .ASAB .AASC .SSSD .SAS例9.如图,AB 与CD 相交于点O ,且O 是AB CD ,的中点,则AOC 与BOD 全等的理由是()A .SASB .ASAC .SSSD .HL例10.如图,若AB DE =,BC EF =,B E ∠=∠,则判定ABC DEF ≌△△的方法是()A .AASB .ASAC .SASD .SSS例11.如图,若已知AE AC =,用“SAS ”说明ABC ADE △≌△,还需要的一个条件是()A .BC DE =B .AB AD =C .BO DO =D .EO CO=例12.如图,点A 、B 、C 、D 在同一直线上,AF DE =,A D ∠=∠,AC DB =.求证:ABF DCE △△≌.例13.如图,已知点B ,E ,C ,F 在同一直线上,BE CF =,ABC DFE ∠=∠,AB DF =.求证:ABC DFE △≌△.例14.如图,在ABC 中,AB AC =,点D 、E 都在边BC 上,且BE CD =,求证:AD AE =.例15.如图,AD BC ,相交于点O ,OB OC OA OD ==,,延长AD 到F ,延长DA 到E ,AE DF =,连接CF BE ,.求证BE CF ∥.三、“AAS 、ASA ”证明三角全等例16.如图,已知12∠=∠,B C ∠=∠,不正确的等式是()A .AB AC =B .BAE CAD ∠=∠C .BE DC =D .BD DE=例17.小刚把一块三角形玻璃打碎成了如图所示的三块,现要到玻璃店取配一块完全一样的玻璃,那么最省事的办法是()A .带①去B .带②去C .带③去D .带①和②去例18.已知D 是ABC 的边AB 上一点,DF 交AC 于点E ,DE EF =,FC AB ∥,若2BD =,5CF =,则AB 的长为()A .1B .3C .5D .7例19.已知,如图,AB AE =,AB DE ∥,ACB D ∠=∠,求证:ABC EAD △△≌.例20.如图,12∠=∠,34∠∠=,求证AC AD =.∵34∠∠=,∴180︒-______180=︒-______,∴ABD ABC ∠=∠.在ABD △和ABC 中,____________________________________∠=∠⎧⎪=⎨⎪∠=∠⎩,∴ABD ABC ≅△△().∴______=______.例21.已知:如图,A ,E ,F ,B 在同一条直线上,CE AB DF AB AE BF A B ⊥⊥=∠=∠,,,.求证:CE DF =.例22.如图,在四边形ABCD 中,AD BC ∥,点E 为对角线BD 上一点,A BEC ∠=∠,且AD BE =.求证:ABD ECB ≌.一、单选题1.如下,给定三角形的六个元素中的三个元素,画出的三角形的形状和大小完全确定的是()①三边;②两角及其中一角的对边;③两边及其夹角;④两边及其中一边的对角.A .①②③B .①②④C .①③④D .②③④2.如图,在△ABC 与△ADC 中,若BAC DAC ∠=∠,则下列条件不能判定△ABC 与△ADC 全等的是()A .B D ∠=∠B .BCA DCA ∠=∠C .BC DC =D .AB AD =3.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是().A .带①去B .带②去C .带③去D .①②③都带4.如图,E 、B 、F 、C 四点在一条直线上,EB =FC ,AC DF ∥,再添一个条件仍不能证明△ABC ≌△DEF 的是()A .AB ED ∥B .DF =AC C .ED =AB D .∠A =∠D 5.如图,在ABC 和DEC 中,已知AB DE =,添加两个条件仍不能使ABC DEC ≌△△的是()A .BC EC =,B E ∠=∠B .BC EC =,AC DC =C .BC DC =,AD ∠=∠D .BE ∠=∠,A D ∠=∠6.如图,AB AC =,点D 、E 分别在AB 、AC 上,补充一个条件后,仍不能判定△ABE 与△ACD 全等的是()A .BC ∠=∠B .AD AE =C .BE CD =D .AEB ADC∠=∠7.如图,已知方格纸中是4个相同的正方形,则1∠与2∠的和为()A .45︒B .60︒C .90︒D .100︒8.在下列各组的三个条件中,能判定△ABC 和△DEF 全等的是()A .AC=DF ,BC=DE ,∠B =∠D B .∠A =∠F ,∠B =∠E ,∠C =∠D C .AB=DF ,∠B =∠E ,∠C =∠F D .AB=EF ,∠A =∠E ,∠B =∠F9.根据下列已知条件,能画出唯一的△ABC 的是()A .3cm AB =,7cm BC =,4cm AC =B .3cm AB =,7cm BC =,8cm AC =C .30A ∠=︒,3cm AB =D .30A ∠=︒,100B ∠=︒,50C ∠=︒10.如图,在方格纸中,以AB 为一边作△ABP ,使之与△ABC 全等,从P 1,P 2,P 3,P 4四个点中找出符合条件的点P ,则点P 有()A .1个B .2个C .3个D .4个11.如图,在△ABC 与△AEF 中,AB =AE ,BC =EF ,∠ABC =∠AEF ,∠EAB =40°,AB 交EF 于点D ,连接EB .下列结论:①∠FAC =40°;②AF =AC ;③∠EBC =110°;④AD =AC ;⑤∠EFB =40°,正确的个数为()个.A .1B .2C .3D .412.如图1,已知AB=AC ,D 为∠BAC 的平分线上一点,连接BD 、CD ;如图2,已知AB=AC ,D 、E 为∠BAC 的平分线上两点,连接BD 、CD 、BE 、CE ;如图3,已知AB=AC ,D 、E 、F 为∠BAC 的平分线上三点,连接BD 、CD 、BE 、CE 、BF 、CF ;…,依次规律,第n 个图形中全等三角形的对数是()A .nB .2n-1C .()12n n +D .3(n+1)二、填空题13.如图,已知AC DB =.要使ABC DCB ≅ .只需添加的一个条件是______.14.三角形全等的判定方法——“角边角”(即ASA )指的是_______________________________15.如图,要测量水池宽AB ,可从点A 出发在地面上画一条线段AC ,使AC AB ⊥,再从点C 观测,在BA 的延长线上测得一点D ,使ACD ACB ∠=∠,这时量得120m AD =,则水池宽AB 的长度是__m .16.如图,点D 是△ABC 的边AB 上一点,FC ∥AB ,连接DF 交AC 于点E ,若CE =AE ,AB =7,CF =4,则BD 的长为________.17.填表.已知两个对应相等的边或角应寻找的条件证明三角形全等的依据两边SAS SSS一角及其对边AAS一角及其邻边SASAAS 或ASA两角ASA 或AAS 18.在ABC 与DEF 中,,,,3cm,5cm A D B E BC EF AB AC ∠=∠∠=∠===,那么DE =______cm .19.如图,在ABC 中,CE 平分ACB ∠,CE AD ⊥于点E ,若ABC 的面积为212cm ,则阴影部分的面积为________2cm .20.如图,Rt △ABC 中,∠BAC=90°,AB=AC ,点D 为BC 的中点,点E 、F 分别在边AB 和边AC 上,且∠EDF=90°,则下列结论一定成立的是_______①△ADF ≌△BDE②S 四边形AEDF =12S △ABC ③BE+CF=AD④EF=AD三、解答题21.已知:如图,A 、B 、C 、D 四点在一条直线上,且AB =CD ,∠A =∠D ,∠ECA =∠FBD .求证:AE =DF .22.如图,在△ABC 中,已知∠ABC =∠ACB ,BD 、CE 分别平分∠ABC 、∠ACB ,那么△BDC 与△CEB 全等吗?为什么?解:因为BD 、CE 分别平分∠ABC 、∠ACB (已知),所以∠DBC=12(),∠ECB=12().由∠ABC=∠ACB(已知),所以∠DBC=∠ECB().在△BDC与△CEB中,,(),().所以△BDC≌△CEB(ASA).23.如图,两车从路段A,B的两端同时出发,以相同的速度行驶,相同时间后分别到达C,D两地,两车行进的路线平行.那么C,D两地到路段AB的距离相等吗?为什么?24.已知:如图,A、F、C、D在同一直线上,AB∥DE,AB=DE,AF=CD,求证:(1)BC=EF;(2)BC∥EF.25.如图,在△ABC和△DEF中,边AC,DE交于点H,AB∥DE,AB=DE,BE=CF.(1)若∠B =55°,∠ACB =100°,求∠CHE 的度数.(2)求证:△ABC ≌△DEF .26.已知:如图,在△AOB 和△COD 中,OA =OB ,OC =OD ,∠AOB =∠COD =50°.(1)求证:AC =BD ;(2)求∠APB 的度数.27.如图,AD 为△ABC 的中线,DE 平分∠ADB ,DF 平分∠ADC ,BE ⊥DE ,CF ⊥DF .(1)求证;DE ⊥DF ;(2)求证:△BDE ≌△DCF ;(3)求证:EF ∥BC .28.已知:等边△ABC 边长为3,点D 、点E 分别在射线AB 、射线BC 上,且BD =CE =a (0<a <3),将直线DE 绕点E 顺时针旋转60°,得到直线EF 交直线AC 于点F .(1)如图1,当点D 在线段AB 上,点E 在线段BC 上时,说明BD +CF =3的理由.(2)如图2,当点D 在线段AB 上,点E 在线段BC 的延长线上时,请判断线段BD ,CF 之间的数量关系并说明理由.(3)当点D 在线段AB 延长线上时,线段BD ,CF 之间的数量关系又如何?请在备用图中画图探究,并直接写出线段BD ,CF 之间的数量关系.29.如图,已知ABC 中,20cm AB AC ==,16cm BC =,点D 为AB 的中点.(1)如果点P 在线段BC 上以6cm /s 的速度由B 点向C 点运动,同时点Q 在线段CA 上由C 向A 点运动.①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP V 是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP V 全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC 三边运动,求经过多长时间点P 与点Q 第一次在ABC 的哪条边上相遇?30.(1)如图1,∠MAN =90°,射线AE 在这个角的内部,点B 、C 在∠MAN 的边AM ,AN 上,且AB =AC ,CF ⊥AE 于点F ,BD ⊥AE 于点D .求证:ABD CAF ≅ .(2)如图2,点B 、C 在∠MAN 的边AM 、AN 上,点E 、F 在∠MAN 内部射线AD 上,∠1,∠2分别是ABE △,CAF V 的外角,已知AB =AC ,∠1=∠2=∠BAC ,求证:ABE CAF ≅ ;(3)如图3,在ABC 中,AB =AC ,AB >BC ,点D 在边BC 上,CD =2BD ,点E 、F 在线段AD 上,12BAC ∠=∠=∠,若ABC 的面积是15,则ACF 与BDE 的面积之和是_________.一、单选题1.(2022·浙江金华·统考中考真题)如图,AC 与BD 相交于点O ,,OA OD OB OC ==,不添加辅助线,判定ABO DCO △≌△的依据是()A .SSSB .SASC .AASD .HL2.(2022·四川成都·统考中考真题)如图,在ABC 和DEF 中,点A ,E ,B ,D 在同一直线上,AC DF ∥,AC DF =,只添加一个条件,能判定ABC DEF ≌△△的是()A .BC DE =B .AE DB =C .A DEF ∠=∠D .ABC D∠=∠二、填空题3.(2022·黑龙江·统考中考真题)如图,在四边形ABCD 中,对角线AC ,BD 相交于点O ,OA OC =,请你添加一个条件________,使△≌△AOB COD .4.(2021·黑龙江齐齐哈尔·统考中考真题)如图,AC AD =,12∠=∠,要使ABC AED ≌△△,应添加的条件是_________.(只需写出一个条件即可)三、解答题5.(2022·福建·统考中考真题)如图,点C ,F 在BE 上,BF EC =,=AB DE ,B E ∠=∠.求证:A D ∠=∠.6.(2021·四川宜宾·统考中考真题)如图,已知OA =OC ,OB =OD ,∠AOC =∠BOD .求证:△AOB ≌△COD .7.(2019·江苏南通·统考中考真题)如图,有一池塘,要测池塘两端A ,B 的距离,可先在平地上取一个点C ,从点C 不经过池塘可以直接到达点A 和B .连接AC 并延长到点D ,使CD CA =.连接BC 并延长到点E ,使CE CB =.连接DE ,那么量出DE 的长就是A ,B 的距离.为什么?8.(2011·辽宁丹东·中考真题)如图,在△ABC 中,D 为BC 的中点,过D 点的直线GF 交AC 于点F ,交AC 的平行线BG 于点G ,DE ⊥GF ,并交AB 于点E ,连接EG ,EF .(1)求证:BG =CF .(2)请你猜想BE +CF 与EF 的大小关系,并说明理由.。
12.1 全等三角形
41.一直割舍不下一件事,永远成不了! 42.扫地,要连心地一起扫! 43.不为模糊不清的未来担忧,只为清清楚楚的现在努力. 44.当你停止尝试时,就是失败的时候. 45.心灵激情不在,就可能被打败. 46.凡事不要说"我不会"或"不可能",因为你根本还没有去做! 47.成功不是靠梦想和希望,而是靠努力和实践. 48.只有在天空最暗的时候,才可以看到天上的星星. 49.上帝说:你要什么便取什么,但是要付出相当的代价. 50.现在站在什么地方不重要,重要的是你往什么方向移动。 51.宁可辛苦一阵子,不要苦一辈子. 52.为成功找方法,不为失败找借口. 53.不断反思自己的弱点,是让自己获得更好成功的优良习惯。 54.垃圾桶哲学:别人不要做的事,我拣来做! 55.不一定要做最大的,但要做最好的. 56.死的方式由上帝决定,活的方式由自己决定! 57.成功是动词,不是名词! 28、年轻是我们拼搏的筹码,不是供我们挥霍的资本。 59、世界上最不能等待的事情就是孝敬父母。 60、身体发肤,受之父母,不敢毁伤,孝之始也; 立身行道,扬名於后世,以显父母,孝之终也。——《孝经》 61、不积跬步,无以致千里;不积小流,无以成江海。—— 荀子《劝学篇》 62、孩子:请高看自己一眼,你是最棒的! 63、路虽远行则将至,事虽难做则必成! 64、活鱼会逆水而上,死鱼才会随波逐流。 65、怕苦的人苦一辈子,不怕苦的人苦一阵子。 66、有价值的人不是看你能摆平多少人,而是看你能帮助多少人。 67、不可能的事是想出来的,可能的事是做出来的。 68、找不到路不是没有路,路在脚下。 69、幸福源自积德,福报来自行善。 70、盲目的恋爱以微笑开始,以泪滴告终。 71、真正值钱的是分文不用的甜甜的微笑。 72、前面是堵墙,用微笑面对,就变成一座桥。 73、自尊,伟大的人格力量;自爱,维护名誉的金盾。 74、今天学习不努力,明天努力找工作。 75、懂得回报爱,是迈向成熟的第一步。 76、读懂责任,读懂使命,读懂感恩方为懂事。 77、不要只会吃奶,要学会吃干粮,尤其是粗茶淡饭。 78、技艺创造价值,本领改变命运。 79、凭本领潇洒就业,靠技艺稳拿高薪。 80、为寻找出路走进校门,为创造生活奔向社会。
《12.1 全等三角形》 教学设计
《12.1 全等三角形》教学设计教材分析:本课是在学生已经学习了三角形、多边形及其相关概念的基础上,进一步研究图形之间的全等关系,全等形、全等三角形及其相关概念,全等三角形的性质.教学目标:【知识与能力目标】理解全等三角形及相关概念,能够从图形中寻找全等三角形.【过程与方法】1.了解并体会图形变换的思想,培养动态地研究几何图形的意识.2.探索并掌握全等三角形的性质,能够利用性质解决简单的问题.【情感态度与价值观】培养学生的识图能力、归纳总结能力和应用意识.教学重难点:【教学重点】全等三角形的有关概念和性质.【教学难点】理解全等三角形边、角之间的对应关系.课前准备:多媒体教学过程:问题1:(1)观察这些图片,你能看出形状、大小完全一样的几何图形吗?[追问]你能再举出生活中的一些类似例子吗?(2)操作并交流:将两张纸重叠在一起,剪出两张三角形,观察它们特征,你有何发现?[学生活动]先进行剪纸操作活动,然后观察思考,再与同学合作交流.[讨论交流]同学们,像上述这样“一模一样”的例子,生活还有许多,你能再举出一些例子吗?[学生活动]分组讨论交流.[教师点拨]像这种“一模一样”的两个图形,我们几何上称为全等形,本节课我们就来学习和研究全等形的有关知识.【设计意图】1.创设情境,激发学生兴趣,引出本节要讨论的内容.丰富的图形和问题容易引起学生的注意,使他们能很快地投入到学习的情境中.2.观察出示的图形,寻找形状、大小相同的图形,归纳全等形的概念,进而得出全等三角形的概念.问题2:(1)请同学用语言归纳出问题1 和问题2 中两个图形有何关系?[定义1]能够完全重合的两个图形叫做全等形.[定义2]能够完全重合的两个三角形叫做全等三角形.(2)【探究1】如图,△ABC与△DEF完全重合(电脑演示重合过程).这时,点A与点D重合.点B与点E重合,我们把这样互相重合的一对点叫做对应顶点;AB边与DE边重合,这样互相重合的边就叫做对应边;△A与△D重合,它们就是对应角.△ABC与△DEF全等,我们把它记作“△ABC△△DEF”.读作“△ABC全等于△DEF”.注意:记两个三角形全等时,通常把对应顶点的字母写在对应的位置上.(3)[练习]你能找出下列图形中的对应点、对应边和对应角吗?[师生活动]教师引导学生归纳在全等三角形中找对应元素的方法:(1)全等三角形对应角所对的边是对应边;两个对应角所夹的边也是对应边.(2)全等三角形对应边所对的角是对应角;两条对应边所夹的角也是对应角.【探究3】学生观察两个全等三角形,教师引导学生利用全等三角形的定义可得到下面性质:①全等三角形的对应边相等;②全等三角形的对应角相等;③全等三角形的周长、面积相等;④全等于同一个三角形的两个三角形全等.教师引导学生口述它们的推理格式.【设计意图】1.本活动主要是加深学生对全等三角形概念理解,以及动手操作能力培养.2.经过观察、操作可以发现,全等三角形可以经过平移、翻折、旋转得到,变化前后对应角、对应边不变.教师要组织学生观察、归纳,引导学生归纳全等三角形的性质:全等三角形的对应边相等,对应角相等.问题3:例1如图,△ABC≌△CDA,∠B=35°,∠BAC=102°,BC=18.(1)写出与△ABC和△CDA的对应边和对应角.(2)求△DAC的度数和边DA的长.例2大家经常折纸,取一张长方形纸片,用A,B,C,D表示它的四个顶点,将其折叠,使点B与点D重合,折痕为E,F,如图所示.观察图形并填空:(1)△BEF________△DEF;(2)若△AEB=70°,则△EDF=________,∠EFB=________.解:(1)由翻折可知:△BEF△△DEF.(2)△AD△BC,且△AEB=70°(已知),∴∠EBF=△AEB=70°(两直线平行,内错角相等).又△△BEF△△DEF(已证),∴∠EDF=△EBF=70°(全等三角形的对应角相等).∵∠AEB=70°(已知),且△AEB+△BED=180°(平角的定义),∴∠BED=180°-△AEB=180°-70°=110°(等式的性质).又△△BEF=△DEF(翻折的性质),∠BED=55°(等式的性质).∴∠BEF=△DEF=12又△AD△BC(已知),∴∠EFB=△DEF=55°(两直线平行,内错角相等).例3如图12-1-是一个等边三角形,你能利用折纸的方法把它分成两个全等的三角形吗?你能把它分成三个,四个全等的三角形吗?[学生活动设计]学生小组讨论,经过讨论交流自己的方法.可能有下列方法:【设计意图】1.要求学生注意解题格式.2.运用全等的性质解题,巩固全等的概念.3.使学生明确:计算一条边的长度或一个角的度数时,可以借助于三角形全等将其转化为它的等边或等角来计算.4.学生分组合作探究,每个小组讨论完成后,给出答案并进行展示,让学生上台说明,培养学生的总结能力以及大胆发言的良好习惯.问题4问题5 (1)课堂小结:a.同学们想一想,今天学习了哪些知识?b.为什么全等三角形的对应边相等、对应角相等?布置作业:课本P33中的习题12.1.(2)知识网络:【设计意图】引导学生回顾自己的学习过程,畅所欲言,进一步进行反思、提炼、归纳知识,并纳入自己的知识结构中.教学反思:1.本节课由于采用了图片展示、直观操作以及讨论交流等教学方法,从而有效地增强了学生的感性认识,提高了学生对新知识的理解与感悟,因而本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处:少数学生在分组活动时的积极性不高,有滥竽充数的现象,今后的教学中有待于进一步改进和完善学生的分组活动.教师要充分利用重合说明对应线段、对应角相等.2.通过具体练习让学生总结,并带领学生快速寻找对应元素,练习的设计采用由易到难的手法,符合学生的思维发展,突破了本节课的重点和难点.真正做到以生为本,突出效率教学.而在练习中,让学生使用数学推理的格式,使学生熟悉这种推理方法.3.教师要帮助学生总结:由于两个三角形的位置关系不同,在找对应边、对应角时,可以针对两个三角形不同的位置关系,寻找对应边、角的规律.学生回顾本节知识时,教师要注意组织学生谈个人收获,师生要共同交流.。
12.1全等三角形
F
C B
G
D
能够完全重合的两个图
形叫做全等形
观察下面两组图形,它们是不是 全等图形?为什么?
如果两个图形全等,它们的形状和 大小一定都相等 !
(1)
(2)
你能举出生活中的全等图形的例子吗?
片出 同 。的 一 同张 规底 格片 照洗
两张纸重合后的剪纸;
A
D
F B C E
全 等 形: 能够完全重合的两个图形; 定义 全等三角形: 能够完全重合的两个三角形。
拓展与应用
A D
2、全等三角形性质的运用
(2)将△ ABC 沿直线BC平移, 得到△ DEF,说出图中线段、角的 B 关系并说明理由。
E A
C
F
(3)△ABD≌△ACE,若∠B =25°,BD=6㎝,AD=4㎝, 你能得出△ACE中哪些角的大小, 哪些边的长度吗?为什么 ? B
E O
D
C
小结
交流:学会了什么?
B'
A'
C'
拓展与应用
1、全等对应元素的找法 A
O C B B D
A
D C
A
A
D
D
B
C
B
E
C
寻找对应元素的规律
(1)有公共边的,公共边是对应边; (2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边, 最小的边也是对应边; (5)两个全等三角形最大的角是对应角, 最小的角也是对应角;
能够完全重合的两个三角形,叫做____________. 全等三角形
A D
例 如
B
C
第十二章12.1全等三角形.1全等三角形课件ppt
A
B
D
A
D B
A
D
B
C
CLeabharlann C2、有公共角 、对顶角
D
A O
A
D
O
A
E
D
C B
C
B
C
B
让我们记住找对应边、对应角的方法
活动5:展示才华 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
A
填一填:
1、已知△ABC≌△ADE,
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
同一张底片洗出的照片
形状、大小相同的图形放在一起能够完全重合。 能够完全重合的两个图形叫做全等形.
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
F
全等三角形的性质: 1、全等三角形的对应边相等,
2、全等三角形的对应角相等。 ∵△ABC≌△DEF (已知)
∴ AB=DE,BC=EF,AC=DF(全等三角形的对应边相等)
∠A=∠D,∠B=∠E,∠C=∠F(全等三角形的对应角相等)
例1
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
C
D
A
B
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知3-讲
总结
知3-讲
在应用全等三角形性质时,要先确定两个条件: ①两个三角形全等;②找对应元素; 全等三角形的性质是证明线段、角相等的常用方法.
(来自《点拨》)
知3-练
1 如图,△OCA≌△OBD,点C和点B,点A和点D 是 对应顶点. 说出这两个三角形中相等的边和角.
(来自教材)
知3-练
解:相等的边:AC=DB,OA=OD,OC=OB; 相等的角:∠A=∠D,∠C=∠B, ∠AOC=∠DOB.
知2-讲
总结
对应元素的确定方法: (1)字母顺序确定法:根据书写规范,按照对应顶点确定对应边、
对应角,如△CAB≌△FDE,则AB与DE、AC与DF、BC 与EF是对应边,∠A和∠D、∠B和∠E、∠C和∠F是对应 角; (2)图形位置确定法:①公共边一定是对应边,②公共角一定是 对应角;③对顶角一定是对应角; (3)图形大小确定法:两个全等三角形的最大的边(角)是对应边 (角),最小的边(角)是对应边(角).
(来自《点拨》)
总结
知1-讲
(1)此题运用定义识别全等形,确定两个图形全等要 符合两个条件:①形状相同,②大小相等;是否 是全等形与位置无关.
(2)判断两个全等形还可以通过平移、旋转、翻折等 方法把两个图形叠合在一起,看它们能否完全重 合,即用叠合法判断.
(来பைடு நூலகம்《点拨》)
知1-练
1 下列四组图形中,是全等图形的一组是( D )
导引:在△ABD和△CDB中,∠ABD=∠CDB,则 ∠ABD,∠CDB所对的边AD与CB是对应边,公共 边BD与DB是对应边,余下的一对边AB与CD是对 应边.由对应边所对的角是对应角可确定其他两组 对应角.
知2-讲
解:BD与DB,AD与CB,AB与CD是对应边; ∠A与∠C,∠ABD与∠CDB,∠ADB与 ∠CBD是对应角.
(来自《点拨》)
导引:由全等三角形的性质知AB=FD,由等式的性 质可得AD=FB,所以要求FB的长,只需求 AD的长.
解:∵△ABC≌△FDE,∴ AB=FD. ∴ AB-DB=FD-DB,即AD=FB. ∵AB=8 cm,BD=6 cm,∴AD=AB-DB= 8-6= 2(cm). ∴FB=AD=2cm.
能够完全重合 的两个图形叫做全等形.
(来自《教材》)
知1-讲
例1 下列图中是全等形是 ①和⑨、②和③、④和⑧、⑪和⑫ .
导引:上述图形中,⑤和⑦形状相同,但大小不同,⑥和⑩大 小、形状都不同;①和⑨、②和③、⑪和⑫尽管方向不 同,但大小、形状完全相同,所以它们是全等形,④和 ⑧都是五角星,大小、形状都相同,是全等形.
图12.1-2
全等三角形的性质
全等三角形的对应边相等, 全等三角形的对应角相等。
知3-导
还具备:全等三角形对应边上的中线相等,对应边 上的高相等,对应角平分线相等;全等三角形的周 长相等、面积也相等.
知3-讲
例3 如图,已知点A,D,B,F在同一条直线上,
△ABC≌△FDE,AB=8 cm,BD=6 cm. 求FB的长.
(来自《点拨》)
知2-练
1 说出图12.1-2 (2)、图12.1-2 (3)中两个全等三角形 的 对应边、对应角.
(2)
(3)
图 12.1-2
(来自教材)
知2-练
解:在教材图12.1-2(2)中,AB和DB,BC和BC,AC和 DC是对应边;∠A和∠D,∠ABC和∠DBC, ∠ACB和∠DCB是对应角. 在教材图12.1-2(3)中,AB和AD,BC和DE,AC 和AE是对应边;∠BAC和∠DAE,∠B和∠D, ∠C和∠E是对应角.
(来自《典中点》)
知1-练
2 如图,有6个条形方格图,图中由实线围成的图形 中,全等形有:(1)与_____(_6_)_____;(2)与 __(_3_)__(5_)_____.
(来自《典中点》)
知1-练
3 下列说法:①两个图形全等,它们的形状相同;
②两个图形全等,它们的大小相同;③面积相
等的两个图形全等;④周长相等的两个图形全
等.其中正确的个数为( B )
A.1个
B.2个
C.3个
D.4个
(来自《典中点》)
知识点 2 全等三角形及对应元素
知2-导
能够完全重合的两个三角形,叫做_全__等__三__角__形___.
例 如
B
A CE
D F
记作:△ABC≌△DEF
读作 :△ABC全等于 △DEF
知2-讲
互相重合的顶点叫对应顶点. 互相重合的边叫对应边. 互相重合的角叫对应角.
知3-练
2 若△ABC与△DEF全等,点A和点E,点B和点D
分别是对应点,则下列结论错误的是( A )
A.BC=EF
B.∠B=∠D
C.∠C=∠F
D.AC=EF
(来自《典中点》)
观察这些图片,你能看出形状、大小完全一样 的几何图形吗?
追问 你能再举出生活中的一些类似例子吗?
知识点 1 全等形
知1-导
知1-导
知1-导
知1-导
知1-讲
一个图形经过平移,翻折,旋转后,位置变化了 ,但形_状__和大_小__都没有改变,即平移,翻 折,旋转前后的图形完_全__重__合______ . 定义 形状、大小相同的图形放在一起能够完全重合.
知2-练
2 如图,将△ABC沿BC所在的直线平移到△A′B′C′ 的位置,则△ABC____≌____△A′B′C′,图中∠A与 ___∠__A_′__ ,∠B与_∠__A__′B__′C_′,∠ACB与___∠__C_′__ 是对应角.
(来自《典中点》)
知识点 3 全等三角形的性质
知3-导
图12.1-2(中),△ABC≌△DEF,对应边有什么关系? 对应角有什么关系?
知2-讲
A
D
B
CE
F
点A 与点D、点B 与点E、点C 与点F 重合,称为对应顶点; 边AB 与DE、边BC 与EF、边AC 与DF 重合,称为对应边; ∠A 与∠D、∠B 与∠E、∠C 与∠F 重合,称为对应角.
例2 如图,已知△ABD≌△CDB,∠ABD=∠CDB, 写出其对应边和对应角.
知2-讲
