06级信号试卷B
西南科技大学信号与系统2006-20007学年第2学期B答案

参考答案及评分细则西南科技大学2006——2007学年第 2 学期《信号与系统X 》期末考试试卷(B 卷)一、填空题(每小题2分,共10分)1.1 。
2.-1。
3. ωj +31。
若为“ωj +-31”,得1分。
4. 0。
5.πω16000>s 。
若为“π16000>”,或“max 2ωω>s ”,或“max 2ω>”,得2分。
若为“π16000≥”,或“max 2ωω≥s ”,或“max 2ω≥”得1分。
二、判断题(每小题2分,共10分)1.╳2.╳3.√4.╳5.√三、证明题(5分)证明: )()(ωj X t x F−→←∴)()(**ωj X t x F -−→←,)()(ωj X t x F -−→←-,)()(**ωj X t x F−→←- --------(2分) 又 )(t x 为实偶信号,即:)()()()(*t x t x t x t x -=-==*--------(1分)∴)()()()(**ωωωωj X j X j X j X =-=-=即:)(ωj X 也为实偶信号。
--------(2分)备注:证明得出仅为偶信号或仅实信号,得3分。
写出FT 定义式,正确可得分。
用定义式或其它方法求解,根据步骤与答案情况,给分。
四、绘图题(每小题6分,共18分) 1.解:)1()1()(112-++=t y t y t y ---(2分)又 系统为线性时不变系统,∴)1()1()(112-++=t x t x t x ---(2分) )(2t x 波形如右图所示。
---(2分)备注:若直接给结果图,正确给满分。
用卷积法等,根据步骤与答案情况,给分。
2.解:输出)(*)()(t h t x t y =---(2分) )1()1()(*)]1()1([-++=-++=t h t h t h t t δδ---(2分) 波形如下图所示。
---(2分)备注:若直接给结果图,正确满分。
06信号与系统AB卷标准答案2

一、选择题(将唯一正确答案填入括号中,每题2分,共32分。
)1.积分dt t t e t )]()(['2δδ+⎰∞∞--等于:( D )(A )0 (B )1 (C )2 (D )3 2.序列和)2()4sin(-∑-∞=n n kn δπ等于:( C ) (A )1 (B )u(k) (C )u(k-2) (D ))2(-k δ3.已知某系统的单位样值响应)()5.1()(n u n h n =,则该系统的因果性和稳定性:( B )(A )因果,稳定 (B )因果,不稳定(C )非因果,稳定 (D )非因果,不稳定 4.dt t t t ejwt)]()([0--⎰∞∞--δδ 的结果为:( A ) (A )01jwt e -- (B )01jwt e -+ (C )01jwt e - (D )01jwt e + 5.序列卷积和)4()2()2()1(-*+--*+k k u k k u δδ等于:( B )(A ))(k δ (B ))1(-k δ (C ))1(-k u (D ))3(-k u 6.已知23)]([1-+=z z n x Z ,(2>z ),)3)(1()]([2++=z z zn x Z ,(3>z ),则)]()([21n x n x Z *为:( A )(A ))2)(1(-+z z z ,2>z (B ))2)(1(-+z z z,1>z(C ))2)(1(-+z z z ,6>z (D ))2)(1(-+z z z,3>z7.一LTI 无失真传输系统,它的幅度特性和相位特性要求为:( D )(A )幅度特性为常数,相位特性无要求 (B )幅度特性和相位特性均无要求(C )幅度特性无要求,相位特性的斜率为0t - (D )幅度特性为常数,相位特性的斜率为0t -8.若一LTI 系统输入)(1t e ,输出为)(1t r ,输入)(2t e ,输出为)(2t r ,则输入为dtt de t ae )()(21+,输出为:( C ) (A ))()(21t r t ar + (B ))()(21t r t r + (C )dt t dr t ar )()(21+(D )dtt dr t r )()(21+ 9.一理想低通滤波器的截止频率为c w ,下列信号经该滤波器滤波后信号不失真的是(cw w 32=):( B ) (A )cos2wt (B) coswt (C) coswt+cos2wt (D) cos3wt10.一LTI 系统响应的分解不对的是:( A )(A )强迫响应和瞬态响应 (B )零输入响应和零状态响应 (C )稳态响应和瞬态响应 (D )自由响应和强迫响应 11.已知一因果序列)(n f 的Z 变换式为)2)(1(12)(+++=z z z z z F ,则)(n f 的初值为:( B )(A ) 1 (B ) 0 (C )0.5 (D )2 12.若FE )()]([w F t f =,则FE )]([0t at f +为:( A )(A )a jwt e a w F a /0)(1 (B )0)(1jwt e a wF a- (C )0)(1jwt e a w F a(D )a jwt e a wF a /0)(1-13.已知1)]([2-=z zn x Z ,(1>z ),则)](3[n x Z n 为:( D ) (A )12-z z ,1>z (B )932-z z,1>z(C )12-z z ,3>z (D )932-z z,3>z14.若)()]([),()]([2211s F t f L s F t f L ==,则])()([222211dtt f d K dt t df K L +为:( C ) (A )]/)0(/)([]/)0(/)([22222111s f s s F K s f s s F K +++ (B ))]0(')0()([)]0()([22222111f sf s F s K f s sF K ++++ (C ))]0(')0()([)]0()([22222111f sf s F s K f s sF K --+-(D )]/)0(/)([]/)0(/)([22222111s f s s F K s f s s F K -+- 15.已知1)]([2-=z zn x Z ,(1>z ),则)]([2n x n Z 为:( B ) (A )2)1(2-z z (B )32)1(22-+z z z (C )32)1(-+z zz (D )12-z z 16.以下哪项陈述不是状态空间法分析系统的优点:( A )(A )特别适用于单输入单输出系统的分析 (B )特别适用于多输入多输出系统的分析(C )便于研究系统内部的一些物理量的变化规律 (D )适用于非线性时变系统的研究二、计算题17.求)12)(2(2)(2+++=s s s ss F 的拉氏逆变换。
自动化专业06级《现代控制理论》试卷答案精选全文完整版

自动化专业06级《现代控制理论》试卷答案一、(10分,每小题1分)试判断以下结论的正确性,若结论是正确的,则在其左边的括号里打√,反之打×。
( √ )1. 相比于经典控制理论,现代控制理论的一个显著优点是可以用时域法直接进行系统的分析和设计。
( √ )2. 传递函数的状态空间实现不唯一的一个主要原因是状态变量选取不唯一。
( × )3. 状态变量是用于完全描述系统动态行为的一组变量,因此都是具有物理意义。
( × )4. 输出变量是状态变量的部分信息,因此一个系统状态能控意味着系统输出能控。
( √ )5. 等价的状态空间模型具有相同的传递函数。
( × )6. 互为对偶的状态空间模型具有相同的能控性。
( × )7. 一个系统的平衡状态可能有多个,因此系统的李雅普诺夫稳定性与系统受扰前所处的平衡位置无关。
( √ )8. 若一线性定常系统的平衡状态是渐近稳定的,则从系统的任意一个状态出发的状态轨迹随着时间的推移都将收敛到该平衡状态。
( × )9. 反馈控制可改变系统的稳定性、动态性能,但不改变系统的能控性和能观性。
( × )10. 如果一个系统的李雅普诺夫函数确实不存在,那么我们就可以断定该系统是不稳定的。
二、(15分)建立一个合理的系统模型是进行系统分析和设计的基础。
已知一单输入单输出线性定常系统的微分方程为:)(8)(6)()(3)(4)(t u t u t u t y t y t y++=++&&&&&& (1)采用串联分解方式,给出其状态空间模型,并画出对应的状态变量图;(7分+3分) (2)归纳总结上述的实现过程,试简述由一个系统的n 阶微分方程建立系统状态空间模型的思路。
(5分) 解:(1)方法一:由微分方程可得345213486)(222++++=++++=s s s s s s s s G令352113452)(21++⋅+=+++=s s s s s s s G 每一个环节的状态空间模型分别为:⎩⎨⎧=+−=1111x y u x x & 和 ⎩⎨⎧+−=+−=1212223u x y u x x&又因为11y u =, 所以⎩⎨⎧−=+−=212113x x x u x x&&, 212x x y −= 因此,采用串联分解方式可得系统的状态空间模型为:u x x x x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡0131012121&& []u x x y +⎥⎦⎤⎢⎣⎡−=2112对应的状态变量图为:方法二: 由微分方程可得32143486)(22++⋅++=++++=s s s s s s s s s G 每一个环节的状态空间模型分别为:⎩⎨⎧+=+−=u x y u x x 11113& 和 ⎩⎨⎧+−=+−=121223u x y u x x&又因为11y u =, 所以⎩⎨⎧+−=+−=ux x x u x x2121133&&, u x x y +−=213 因此,采用串联分解方式可得系统的状态空间模型为:u x x x x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡1133012121&& []u x x y +⎥⎦⎤⎢⎣⎡−=2113对应的状态变量图为(2)单输入单输出线性时不变系统传递函数的一般形式是1110111)(a s a sa sb s b s b s b s G n n nn n n n +++++++=−−−−L L若,则通过长除法,传递函数总可以转化成0≠n b )(s G d s a s c d a s a s a s c s c s c s G n n n n n +=++++++++=−−−−)()()(01110111L L 将传递函数c (s )/a (s )分解成若干低阶(1阶)传递函数的乘积,然后根据能控标准型或能观标准型写出这些低阶传递函数的状态空间实现,最后利用串联关系,写出原来系统的状态空间模型。
北京邮电大学信号与系统2006年(B)卷答案
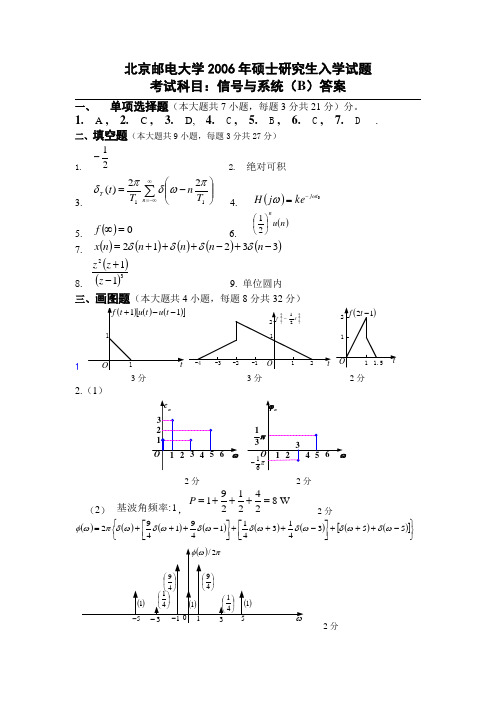
北京邮电大学2006年硕士研究生入学试题考试科目:信号与系统(B )答案一、 单项选择题(本大题共7小题,每题3分共21分)分。
1. A , 2. C , 3. D, 4. C , 5. B , 6. C , 7. D .二、填空题(本大题共9小题,每题3分共27分)1. 21-2. 绝对可积3. ∑∞-∞=⎪⎪⎭⎫⎝⎛-=n T T n T t 1122)(πωδπδ 4. ()0tj ke j H ωω-=5. ()0=∞f6. ()n u n⎪⎭⎫⎝⎛217. ()()()()()33212-+-+++=n n n n n x δδδδ8. ()()3211-+z z z 9. 单位圆内三、画图题(本大题共4小题,每题8分共32分)13分 3分 2分2.(1)2分 2分(2) 1:基波角频率,W 82421291=+++=P 2分()()()()()()()()[]⎭⎬⎫⎩⎨⎧-+++⎥⎦⎤⎢⎣⎡-+++⎥⎦⎤⎢⎣⎡-+++=553413411491492ωδωδωδωδωδωδωδπωφ2分3.()()()∑∞-∞=-=⇔nnFtfωδπω2,()()∑∞-∞=--⇔⋅nnttf1ωδπcos()()()()()()()[]111-+++=--⇔*⋅∑∞-∞=ωδωδωδπωπδωnnjHthttf cos3分3分分4.()()ωωωωωωsin.cos...551151150jeeejHjjj-+=+=+=-()ωωcos.+=2511jH高通1分2分3分2分四、计算题(本大题共7小题,共70分)1.(8分)()⎭⎬⎫⎩⎨⎧==↑47910631,,,nnx,,,2 . (8分)()()t ueeth tt2)(--∧-=()()()()t ueththth t-∧∧=+'=2 4分()t yzs=()()t ht f*=()()t uee tt321---4分3. (8分)(1)()()kskssH-+++=32324分(2)3<k 4分4. (15分)系统函数:()1114113112111----+⋅-=zzzzH5分差分方程:()()()()()131281143-+=-+--nxnxnynyny5分单位样值响应:()()n unhnn⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛-⎪⎭⎫⎝⎛=4137213105分5. (18分)(1)设()t g的傅立叶变换为()ωjG,则()t g经过()t cωcos调制后的频谱为()()[]c c G G ωωωω-++21,因此,A 点的频谱为()()()[]()ωωωωωωj 21j 1H G G R c c A -++= ()()()()c c c c u G u G ωωωωωωωω--+--+=2121 ……2分A 点的信号为()()()[]{}()()[]{}tj t j A c c e u F t g e u F t g t r ωωωω112121---⊗+-⊗= …1分()()ωωπδj 1+↔t u由对称性可得()()j t t u 12+↔-πδωπ即()()t j t u πδω221-↔- ()()t jt u πδω221+↔ …………1分 ∴()()()()()t j t j A c c e t j t t g e t j t t g t r ωωπδπδ⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡+⊗+⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-⊗=-2212122121 ()()[]()()[]t j t j c c e t g j t g e t gj t g ωωˆ41ˆ41++-=- ()()t t gt t g c c ωωsin ˆ21cos 21-= …. 1分 其中()t g ˆ是()t g 的希尔伯特变换 ()()()()t t t gt t g t t r t r c c c c A B ωωωωcos sin ˆ21cos 21cos 2-==∴ …………1分()()()()t t gt t g t g t r c c B ωω2sin ˆ412cos 4141-+=……… 1分通过一个理想低通滤波器,得C 点的信号()()()t Sa t g t r m C ω4141== ………… 1分对余弦信号作希尔伯特变换将变为正弦信号,因此,D 的信号为()()()()t t gt t t g t t r t r c c c c A D ωωωω2sin ˆ21cos sin 21sin -== …………1分()()()()t t g t gt t g t r c c D ωω2cos ˆ41ˆ412sin 41+-= …………1分 通过一个理想低通滤波器,得E 点的信号()()t g t r E ˆ41-= …………1分对E 点信号做希尔伯特变换,得到F 点的信号()()()t g t g t r F 41ˆˆ41=-=…………1分因此,G 点的信号为 ()()()()t g t r t r t r F C G 21=+= …………1分(2)由G 点的时域表达式可知,()t r 的能量是输入信号能力的41。
信号与系统2006试卷A参考答案

栏 姓名
息
班级
订
信
生
专业
考
学院 装
P5
P6
G (ω)
A
A/2
A/2
−3ωm −ω m ωm 3ωm
ω
(4分,没标注扣2分)
信息工程
学号 线
栏 姓名
得
五、限选题(每题 10 分)
分
1、给定系统流图如图所示,列写状态方程与输出方程。指出 A B C D 。
e1(t)
8
1/s
4 7 7 -3
3 r(t) [通信、电子专业必做]
课程名称
适用 学院、专业、
年级
备注
集美大学试卷纸
2007—2008 学年 第 2 学期
信号与系统
试卷 A
卷别
信息工程学院 2006 级 通信工程、电子信息工程、自动化
考试 闭卷 ■ 方式 开卷 □
参考答案及评分标准
5、已知系统函数
H (s)
=
(s
1 + 1)(s
+
2)
,起始条件为: y(0− )
= 1,
∴系统完全可控、完全可观的条件是a ≠ −1且b ≠ 0。
息
班级
订
信
生
专业
考
学院 装
信息工程
P7
P8
f
(t)
=
3cos t
+
sin
⎛ ⎜⎝
5t
+
π 6
⎞ ⎟⎠
+
2
cos
⎛ ⎜⎝
8t
+
π 3
⎞ ⎟⎠
1.画出单边幅度频谱和相位谱; 2.画出双边幅度谱和相位谱。
2006级操作系统期末试卷B卷及答案

漳州师范学院_计算机科学与工程_系_计算机科学与技术_专业_06_级《计算机操作系统》课程期末考试卷(B)(2007—2008学年度第一学期)班级_________学号____________姓名__________考试时间:一、单项选择题(每小题1分,共 20分)1.( c )不是操作系统设计目标。
A. 方便性B.有效性C.及时响应D.可扩充性和开放性2.下列进程状态的转换中,不正确的是(d )A.就绪到运行B.运行到就绪C.阻塞到就绪D.就绪到阻塞3.信号量S的初值为5,在S上执行了9次P操作,6次V操作后,S的值为( d)。
A.10B.8C.6D. 24.在下列那种情况下,可使进程从阻塞状态转换到就绪(b )。
A.时间片用完了B.等待的某事件已经发生C.分配到必要的资源并获得了处理机D.等待某事件5.作业调度的关键是( c)。
A.用户作业充分准备B.有较好的操作环境C. 选择恰当的作业调度算法D. 选择恰当的作业管理程序6.下面不是预防死锁方法的是(a )。
A.把资源的互斥访问改成可共享访问B.使进程运行前申请所需的资源和在等待时不占有资源C.占有一些资源的进程再申请新的资源而不能满足时,释放以前占有的资源D.对系统中的资源必须按照某种顺序申请。
7.把进程从就绪状态队列调出运行,是属于(a )。
A.低级调度B.中级调度C.高级调度D.作业调度8.下面那种调度算法可能引起长作业长期不能调度( b)。
A. FCFSB.SJFC.高响应比优先D.时间片轮转9.在程序的装入方式中,下面那种装入方式是在程序运行过程中把逻辑地址转换成物理地址(c)。
A. 绝对装入方式B.可重定位装入C.动态运行时装入方式D.装入时动态链接10.在请求分页存储管理系统中,凡未装入过的页都应从( B )调入主存。
A. 系统区B.文件区C. 对换区D.页面缓冲区11.在请求分页存储管理方式中,下面关于缺页中断描述不正确的是( d)A.只有进程所访问的页不在内存时才会产生缺页中断。
信号与系统 电力学院06年试题
,考试作弊将带来严重后果!华南理工大学期末考试2006年电力学院《信号与系统》试卷1. 考前请将密封线内填写清楚;2.答案写在试卷上;3. 考试形式:闭卷;附相关公式:τττd )()()()()(-=*=⎰∞∞-t h f t h t f t yt n n n C t f 0j =e )(ω∑∞-∞=,t t f T C TT n T n d e )(122t j 0⎰--=ωt t f F d e)()j (tj ⎰∞∞--=ωω,⎰∞∞-=ωωd e )j (π21)(j t ωF t f一、共 5 小题,40分。
(1)某线性时不变系统当初始状态y(0)=1时,零输入响应为yx (t)=2e-t ,t>=0;输入激励为f(t)时,零状态响应为y f (t)=2+e -t+2e -3t,t>=0。
当y(0)=5且激励为2f(t)时,求系统的完全响应y(t )(10分)。
(2)已知某连续LTI 系统的冲激响应h(t)=δ(t )-e -t u(t),求系统的频率响应H(jω)(5分)。
(3)已知信号f(t)=2u(t-1)-3u(t-2)+2u(t-3)-u(t-4),定性绘出信号f(t)和f(2-2t)的波形(10分)。
(4)f(t)及h(t)的波形如下图所示,计算卷积积分y(t)=f(t)*h(t)(10分)。
(5)写出下图所示连续时间系统的冲激响应h(t)的表达式(5分)。
二、已知周期矩形脉冲信号f(t)的波形如下图所示,其中τ=T/2,试计算信号f(t-T/4)的傅里叶级数展开式(15分)t三、(1)求下图非周期信号f(t)的频谱函数F(jω),(2)并求信号f1(t)的频谱函数F1(jω)(15分)。
tt四、计算以下R LC串联电路系统的频率响应(10分)。
Ry (t )Lﻬ五、已知某二阶线性时不变连续时间系统的动态方程y ’’(t)+3y ’(t)+2y(t)=6f’(t)+8f(t),t >0;f(t)=e -3tu(t),y(0-)=1,y ’(0-)=2,求系统的零输入响应、零状态响应和完全响应y (t)(20分)。
2007-2008学年度上学期06级11月份月考数学试卷(理B)
一.选择题(本大题共12小题,每小题5分,共60分 )1.在△ABC 中,3=AB ,1=AC ,∠A =30°,则△ABC 面积为 ( )A .23 B .43C .23或3 D .43 或23 2.已知ABC ∆中,a =5, b = 3 , C = 1200 ,则sinA 的值为 ( )A .1433B .1433- C.1435- D .14353.若两个等差数列{}n a ,{}n b 前n 项和分别为n A ,n B ,满足71()427n n A n n N B n ++=∈+,则1111a b 的值为 ( )A .74B .32C .43D .78714.若a 、b 为实数, 且a +b=2, 则3a +3b 的最小值为 ( )A .18B .6C .23D .2435.若不等式022>++bx ax 的解集⎭⎬⎫⎩⎨⎧<<-3121|x x 则a -b 值是 ( ) A 、-10 B 、-14 C 、10 D 、146.已知等比数列{}n a 的公比13q =-,则13572468a a a a a a a a ++++++等于 ( )A .13-B .3C .13D .3- 7.全称命题“所有被5整除的整数都是奇数”的否定是( )A .所有被5整除的整数都不是奇数B .所有奇数都不能被5整除C .存在一个被5整除的整数不是奇数D .存在一个奇数,不能被5整除8.抛物线2x y -=上的点到直线0834=-+y x 距离的最小值是 ( )A .34 B .57 C.58D.3 9.若”133“”3“,22表示双曲线方程是则=+-->∈k y k x k R k 的 ( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件10.已知抛物线x 2 = 4y 的焦点F 和点A (-1,8),P 为抛物线上一点,则 | P A|+ | PF| 的最小值是( ) A .6 B . 9 C.12 D.1611.已知双曲线的中心在原点,两个焦点F 1,F 2分别为)0,5()0,5(和-,点P 在双曲线上,PF 1⊥PF 2,且△PF 1F 2的面积为1,则双曲线的方程为 ( )A .13222=-y xB .12322=-y x C .1422=-y x D .1422=-y x12.已知双曲线)0,0(1122222222>>>=+=-b m a by m x b y a x 和椭圆的离心率互为倒数,那么以m b a ,,为边长的三角形是 ( ) A.锐角三角形 B.钝角三角形 C.直角三角形 D.锐或钝角三角形二.填空题(本大题共4小题,每小题4分,共16分) 13.已知的最大值是则4log 2log ,32,4,222y xxy y x ∙=>>________________ 14.已知1≤y x +≤3,2≤y x -2≤4,则y x z 3+=的最小值=______;最大值=_________.15.已知椭圆m x 2+ny 2=1与双曲线p x 2-q y 2=1(m ,n ,p ,q ∈R +)有共同的焦点F 1、F 2,P是椭圆和双曲线的一个交点,则|PF 1|·|PF 2|=_____________16.如果椭圆193622=+y x 的弦被点(4,2)平分,则这条弦所在的直线方程是 三.解答题(本大题共6小题,满分74分)17.在△ABC 中,BC =a ,AC =b ,a ,b 是方程02322=+-x x 的两个根,且()1cos 2=+B A .求:(1)角C 的度数; (2)AB 的长度.2007-2008学年度上学期06级11月份月考数学试卷(理B)满分:150分 时间:90分钟18.设,4,221==a a 数列}{n b 满足:,1n n n a a b -=+ 122n n b b +=+,(1) 求证:数列}2{+n b 是等比数列(要指出首项与公比), (2) 求数列}{n a 的通项公式.19.设函数]5)1(2)23lg[()(22+-++-=x m x m m x f : (1)如果函数)(x f 的定义域为R,求实数m 的取值范围; (2)如果函数)(x f 的值域为R,求实数m 的取值范围;20.已知抛物线x y 42=,焦点为F ,顶点为O ,点P 在抛物线上移动,Q 是OP 的中点,M 是FQ 的中点,求点M 的轨迹方程.(12分)21.求两条渐近线为02=±y x 且截直线03=--y x 所得弦长为338的双曲线方程。
06级数电考试试卷B(参考答案)
湘潭大学200 8 年 上 学期20 06 级《数字电子技术》课程期末考试(B 卷)适用专业 电子、通信、自动化、建筑智能学院 专业 班级 学号 姓名 考试时间 120 分钟 考试方式 闭卷 考试成绩一、填空题:(每空1分,共10分)1、数制转换:(10010111)B =( 227 )O =( 151 )D ;(101100.110011)B =( 2C. CC ) H =( 44.7968 )D 。
2、写出下列带符号位二进制数(最高位为符号位)的反码和补码。
(011011)2的补码( 011011 ),(111011)2的补码( 100101 )。
3、对于一个8位A/D 转换器,若最小输出电压增量为0.02V ,当输入代码为01101101B 时,输出电压V O 为( 2.18 )V ,若其分辨率用百分数表示,则应为( 0.39% )。
4、一个有2048个字的RAM ,每个字是8位,此存储器容量为( 16384bit ),有( 11 )根地址线。
二、将下列逻辑函数化简为最简“与或”式(每小题5分,共10分)(1)L(A,B,C,D)=AB ’(AC ’D+(AD+B ’C ’)’)(A ’+B)解:左边= AB ’ (A ’+B) (AC ’D+(AD+B ’C ’)’)=0(2) L(A,B,C,D,E)=(AB ’C ’D+AC ’DE+B ’DE ’+AC ’D ’E)’解:L ’= AB ’C ’D+AC ’DE+B ’DE ’+AC ’D ’E = AB ’C ’D+B ’DE ’ + (AC ’DE+ AC ’D ’E) = AB ’C ’D+B ’DE ’ +AC ’E = B ’DE ’ +AC ’EL= (B ’DE ’ +AC ’E)’=A ’B+A ’D ’+A ’E+BC+CD ’+CE+BE ’+D ’E ’三、说明下图中各门电路的输出是高电平还是低电平。
分别讨论门电路为TTL 和CMOS 两种情况。
哈尔滨理工大学2005-2006年第一学期信号与系统期末试卷B答案
2005-2006学年 第一学期考试试题答案 B 卷考试科目:信号处理 试卷总分100分一、填空题(本大题共12空,每空2分,总计24分)1、齐次性;可加性;微分特性;积分特性;频率保持性。
2、2π3、0t Ke ω- 4、0;25、0.5zz -;0.5z ≥ 6、12S mT f ≤二、画图题(本大题共2小题,每小题8分,总计16分) 1、2、三、简算题(本大题共3小题,每小题8分,总计24分)装订线班级:学号:姓名:2005年 12 月 15 日1、解:周期信号可以写成 ()1jn tnn f t Feω+∞•=-∞=∑ ()1221Tjn t n T F f t e dt T ω•--=⎰对其取傅氏变换得 ()()12nn F j F n ωπδωω+∞•=-∞=-∑则对应于()()T s n t t nT δδ+∞=-∞=-∑的()2211sss T jn t n T s sF t e dt T T ωδ•--==⎰则 ()()2T sn sF j n T πωδωω+∞=-∞=-∑2、解: 令()()f t t δ=,则()()y t h t =,特征方程为:2540λλ++=特征根为: 11λ=-, 24λ=-故 ()()()'25h t t x t δ=*()()()'4153t tt e e t δε--=*- ()420533t t e e t ε--⎛⎫=- ⎪⎝⎭ V3、解:对方程取z 变换得()()()2210.10.20.40.5z z z zz z z z ++==+--+ 由于()H z 得极点10.4z =,20.5z =-,均位于单位圆内,故该系统是稳定的。
四、综合应用题(本大题共3小题,每小题12分,总计36分) 1、解:由图知电流()i t 的微分方程为:()()()()"'566s i t i t i t i t ++=(1)ZIR : 令上式中()s i t =0,有齐次方程的特征方程为:2560λλ++=特征根为 12λ=-,23λ=-故ZIR 的形式为 ()2312tt zi i t Ae A e --=+ 由于 ()0i -=()0i +,()()00u u -+= 故 ()()002zi i i +-== A2005-2006学年 第一学期考试试题答案 B 卷()()()'10009/zi zi i Ri u A s L +++=-+=-⎡⎤⎣⎦ 则 ()1202zi i A A ++= A()'120239/zi i A A A s +=--=-解得 13A =-,25A =()()2335t t zi i t e e A --=-+ ()0t ≥(2)ZSR : ()4S i t A =, ()zs h p i t i i =+2312t th i B e B e --=+,p i I =代如方程 ()()()"'5624i t i t i t ++=得, 4p i A =故 ()23124tt zs i t B eB e --=++由于 ()()000zs i i +-== A()()()'10000zs zs i Ri u L+++=-+=⎡⎤⎣⎦ ()12040zs i B B +=++= ()'120230zs i B B +=--=解得 112B =-,28B =从而 ()()231284t t zs i t e e A --=-++ ()0t ≥ 系统得全响应 ()2323351284tt t t i t ee e e ----=-+-++3213154t te e --=-+2、解: 由于()22H j j ωω=+ 则求其反变换即为冲激响应 ()()22th t e t ε-=又知 ()()()S j H j F j ωωω=⋅ ()212j j πδωωω⎡⎤=⋅+⎢⎥+⎣⎦()112j j πδωωω=+-+ 则 ()()()()()221tt s t t et e t εεε--=-=-3、解:(1)在零状态下对方程取Z 变换2005年 12 月 15 日()()1113z Y z F z -⎛⎫-= ⎪⎝⎭故 ()()()1111133Y z zH z F z z z -===-- 所以 ()()13nh n n ε⎛⎫= ⎪⎝⎭(2)当()()11323n n y n n ε⎡⎤⎛⎫⎛⎫=-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦时,()133211112332zz z Y z z z z z =-=⎛⎫⎛⎫---- ⎪⎪⎝⎭⎝⎭ ()()()1212Y z F z H z z ==-反变换得: ()()112nf n n ε⎛⎫=- ⎪⎝⎭。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007-2008学年第二学期 《信号与系统》课程考试试卷(B 卷)
院系:电子信息学院 班级 姓名 __________ 序号 _____ 考试时间:120分钟 考试方式:闭卷笔试 考试日期:2008.7.7.
一、选择题(共13分)
(每题给出四个答案,其中一个是正确的,请将正确答案的标号写在横线上。
)
1.(2分) 因果系统的系统函数为)21)(1(1)(1121------++=z z z z z H ,则该系统是 。
(A)稳定的 (B)不稳定的 (C)临界稳定的 (D)不能确定 2.(3分) 设)(k f 和)(k y 分别表示离散时间系统的输入和输出序列,则 )1()2()(4)(+=-k f k y k y k y 所表示的系统是______的系统。
(A)线性时变非因果 (B)非线性时变非因果 (C)线性非时变因果 (D)非线性非时变因果
3.(2分) 已知系统的冲激响应)(5)(2t e t h t
ε-=, 则系统函数=)(s H ______。
(A)
25+s (B)s 5 (C)2
2+s (D)s 2
4.(3分) 某线性非时变系统的幅频响应2|)(|=ωj H ,相频响应如图所示。
当输入信号
t t t f 30cos 10cos )(+=时,则系统输出信号_______。
(A) 无失真; (B) 存在相位失真; (C) 存在幅度失真;
(D) 既有幅度失真又有相位失真。
5.(3分) 周期信号f (t )的傅立叶 级数中所含有的频率分量是 。
(A)余弦项的奇次谐波,无直流 (B)正弦项的偶次谐波,直流 (C)正弦和余弦项的偶次谐波,直流 (D)正弦和余弦的奇次谐波,无直流。
二、填空题(共18分)
(注:请将算得的正确答案写在横线上。
不必写求解过程。
) 6.(3分) 已知a z z F -=-1)(,则 =)(k f ______________。
7.(3分) 某线性非时变系统的单位阶跃响应为)()1()(2t e t g t ε-+=,则其系统函数
=)(s H __________。
8.(4分) 已知信号)()23()(t t t f ε-=,则)(t f 的拉普拉斯变换=)(s F 。
9.(4分) 已知信号)(1t f 是最高频率分量为2kHz 的带限信号,)(2t f 是最高频率分量为3kHz 的带限信号。
根据抽样定理,则信号)()(21t f t f *的奈奎斯特频率N f =__________。
10.(4分) 已知信号)()()(t Ae t e A t f t a t a --=-εε, 则它的傅里叶变换)(ωj F =
_________________。
三、作图题(共21分)
(注:请按题目要求绘出波形图或电路图等)
11.(6分) 若 )3()2()(1--+=k k k f εε,)5()5()(2-++=k k k f δδ, 试画出 )()()(21k f k f k f *= 的图形。
12.(10分) 画出如图所示中两信号的卷积)()()(21t f t f t f *=的波形。
t
13.(5分) 画出图中信号的一阶导数)(t f '的波形。
四、计算题(共48分)
(注:请按题目要求写出解题过程和详细步骤。
)
14.(12分) 一个数字滤波器的输入是()[1,0.5]f k ↑
=,响应是
()(1)2()(1)y k k k k δδδ=+---
(a) 求滤波器的系统函数()H z ; (b) 此滤波器是稳定的吗?是因果的吗?
15.(12分) 设系统在f 1(t )=sin2t ε(t )激励下的零状态响应为
)()2sin 21
2cos (52)(1t t t e t y t ε+-=-
求在)()(22t e t f t ε-=激励下的零状态响应)(2t y 。
16.(12分) 如图所示电路, 开关动作前电路已稳定。
t = 0时,断开开关K ,当0≥t 时,试求电路中的电流i (t )。
17.(12分) 如图所示系统,滤波器的频率响应为
⎩
⎨⎧≤≤-=-ωωωω其它,02
22)(3j e j H
求当t t f 2cos )(=时的系统响应)(t y 。
)
(t f )
(t y
Ω
V。
