高二数学 抛物线的定义-标准方程及几何性质(文) 人教实验B版
人教版高二数学课件抛物线及其标准方程

3.用坐标表示的焦半径公式 由教材中抛物线的定义可得抛物线的焦半径公式如下: 若点 M(x0,y0)是抛物线 y2=2px(p>0)上一点, 抛物线的焦点为 F,准线为 l,则线段 MF 叫作抛物 线的焦半径.如图所示,过点 M 作 l 的垂线段 MH, 由抛物线的定义可知|MF|=|MH|=x0+p2.
探究 3 一般方程标准化是基本的解题方法. 思考题 3 (1)抛物线 y=-16x2 的焦点坐标是________,准
线方程是________.
(2)已知抛物线的方程为 y2=ax(a≠0),求它的焦点坐标和准 线方程.
【思路分析】 由题设参数 a≠0,有两种情况 a>0 或 a<0, 需分别求解.
【解析】 ①当 a>0 时,∵2p=a,∴p=2a. ∴焦点坐标为 F4a,0,准线方程为 x=-4a. ②当 a<0 时,y2=-(-a)x, ∵2p=-a,∴p=-2a. ∴焦点坐标为 F4a,0,准线方程为 x=-4a. 综上所述,抛物线的焦点坐标为4a,0,准线方程为 x=-4a.
抛物线 y2=mx 的焦点为m4 ,0,准线为 x=-m4 ;抛物线 x2 =my(m≠0)的焦点为0,m4 ,准线为 y=-m4 .
小值为点 F 和点(0,2)之间的距离,即
122+(-2)2=
17 2.
题型三 抛物线的焦点和准线
互动 1 已知抛物线的标准方程,怎样确定抛物线的焦点位 置和开口方向?
【解析】 一次项变量为 x(或 y),则焦点在 x 轴(或 y 轴)上; 若系数为正,则焦点在正半轴上;若系数为负,则焦点在负半轴上.焦 点确定,开口方向也随之确定.
(2)已知点 M(-3,2)是坐标平面内一定点,若抛物线 y2=2x
的焦点为 F,点 Q 是该抛物线上的一动点,则|MQ|-|QF|的最小
高二数学2.4.1抛物线的定义与标准方程

高二数学2.4.1抛物线的定义与标准方程学习目标:1、理解抛物线的定义,并会应用定义解决一些简单问题;2、掌握抛物线的标准方程,并会应用标准方程解决一些简单问题;3、综合应用抛物线的定义与标准方程解决一些简单问题;重点与难点:1、重点:理解抛物线的定义,掌握抛物线的标准方程,并会应用它们解决一些简单问题;2、难点:综合应用抛物线的定义与标准方程解决一些简单问题;学习过程:提出问题:1、平面内与一个定点F和一条定直线l的距离相等的点的轨迹是什么样的图形?2、平面内到定点F(-a,0)与到定直线L:x=a的距离相等的点的轨迹方程是。
完成学习目标1:理解抛物线的定义,并会应用定义解决一些简单问题;1、抛物线定义:注:(1)定点F不在这条定直线l;(2)定点F在这条定直线l,则点的轨迹是什么?例1、平面内过点A(-2,0),且与直线x=2相切的动圆圆心的轨迹是什么样的图形? 完成学习目标2:掌握抛物线的标准方程,并会应用标准方程解决一些简单问题;2、推导抛物线的标准方程:例2、(1)已知抛物线标准方程是xy62=,求它的焦点坐标和准线方程(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程练2、求下列抛物线的焦点坐标和准线方程:(1)y2=20x(2)y=4x2 (3)2y2+5x=0 (4)082=+yx练3、根据下列条件写出抛物线的标准方程(1)焦点是F (-2,0)(2)准线方程是31y (3)焦点到准线的距离是4,焦点在y 轴上(4)焦点在直线x-y+1=0上。
(5)经过点A (6,-2)练4、抛物线的顶点是双曲线的中心,而焦点是双曲线的左顶点,求抛物线方程.练5、若抛物线上一点 到准线及对称轴的距离分别是10和6,求 的横坐标及抛物线方程.完成学习目标3:综合应用抛物线的定义与标准方程解决一些简单问题;例3、探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处.已知灯口圆的直径为,灯深,求抛物线的标准方程和焦点位置.练6、一条隧道的顶部是抛物拱形,拱高是m ,跨度是m ,求拱形的抛物线方程。
(人教课标版)普通高中课程标准实验教科书《数学》目录(B版)

(人教课标版)普通高中课程标准实验教科书《数学》目录(B版)(人教课标版)普通高中课程标准实验教科书《数学》目录(B版)必修一第一章集合1.1集合与集合的表示方法1.1.1集合的概念1.1.2集合的表示方法1.2集合之间的关系与运算1.2.1集合之间的关系1.2.2集合的运算本章小结阅读与欣赏聪明在于学习,天才由于积累第二章函数2.1函数2.1.1函数2.1.2函数的表示方法2.1.3函数的单调性2.1.4函数的奇偶性2.1.5用计算机作函数的图象(选学)2.2一次函数和二次函数2.2.1一次函数的性质与图象2.2.3待定系数法2.3函数的应用(Ⅰ)2.4函数与方程2.4.1函数的零点2.4.2求函数零点近似解的一种计算方法——二分法本章小结阅读与欣赏函数概念的形成与发展第三章基本初等函数(Ⅰ)3.1指数与指数函数3.1.1实数指数幂及其运算3.1.2指数函数3.2对数与对数函数3.2.1对数及其运算3.2.2对数函数3.2.3指数函数与对数函数的关系3.3幂函数3.4函数的应用(Ⅱ)本章小结阅读与欣赏对数的发明必修二第一章立体几何初步1.1空间几何体1.1.1构成空间几何体的基本元素1.1.2棱柱、棱锥和棱台的结构特征1.1.3圆柱、圆锥、圆台和球1.1.4投影与直观图1.1.5三视图1.1.6棱柱、棱锥、棱台和球的表面积1.1.7柱、锥、台和球的体积实习作业1.2点、线、面之间的位置关系1.2.1平面的基本性质与推论1.2.2空间中的平行关系1.2.3空间中的垂直关系本章小结阅读与欣赏散发着数学芳香的碑文第二章平面解析几何初步2.1平面直角坐标系中的基本公式2.1.1数轴上的基本公式2.1.2平面直角坐标系中的基本公式2.2直线的方程2.2.1直线方程的概念与直线的斜率2.2.2直线方程的几种形式2.2.3两条直线的位置关系2.2.4点到直线的距离2.3圆的方程2.3.1圆的标准方程2.3.2圆的一般方程2.3.3直线与圆的位置关系2.3.4圆与圆的位置关系2.4空间直角坐标系2.4.1空间直角坐标系2.4.2空间两点的距离公式本章小结阅读与欣赏笛卡儿必修三第一章算法初步1.1算法与程序框图1.1.1算法的概念1.1.2程序框图1.1.3算法的三种基本逻辑结构和框图表示1.2基本算法语句1.2.1赋值、输入和输出语句1.2.2条件语句1.2.3循环语句1.3中国古代数学中的算法案例本章小结阅读与欣赏我国古代数学家秦九韶附录1解三元一次方程组的算法、框图和程序附录2Scilab部分函数指令表第二章统计2.1随机抽样2.1.2系统抽样2.1.4数据的收集2.2用样本估计总体2.2.1用样本的频率分布估计总体的分布2.2.2用样本的数字特征估计总体的数字特征2.3变量的相关性2.3.1变量间的相关关系2.3.2两个变量的线性相关本章小结阅读与欣赏蚂蚁和大象谁的力气更大附录随机数表第三章概率3.1事件与概率3.1.1随机现象3.1.2事件与基本事件空间3.1.3频率与概率3.1.4概率的加法公式3.2古典概型3.2.1古典概型3.2.2概率的一般加法公式(选学)3.3随机数的含义与应用3.3.1几何概型3.3.2随机数的含义与应用3.4概率的应用本章小结阅读与欣赏概率论的起源必修四第一章基本初等函数(Ⅱ)1.1任意角的概念与弧度制1.1.1角的概念的推广1.1.2弧度制和弧度制与角度制的换算1.2任意角的三角函数1.2.1三角函数的定义1.2.2单位圆与三角函数线1.2.3同角三角函数的基本关系式1.2.4诱导公式1.3三角函数的图象与性质1.3.1正弦函数的图象与性质1.3.2余弦函数、正切函数的图象与性质1.3.3已知三角函数值求角教学建模活动本章小结阅读与欣赏三角学的发展第二章平面向量2.1向量的线性运算2.1.1向量的概念2.1.2向量的加法2.1.3向量的减法2.1.4数乘向量2.1.5向量共线的条件与轴上向量坐标运算2.2向量的分解与向量的坐标运算2.2.1平面向量基本定理2.2.2向量的正交分解与向量的直角坐标运算2.2.3用平面向量坐标表示向量共线条件2.3平面向量的数量积2.3.1向量数量积的物理背景与定义2.3.2向量数量积的运算律2.3.3向量数量积的坐标运算与度量公式2.4向量的应用2.4.1向量在几何中的应用2.4.2向量在物理中的应用本章小结阅读与欣赏向量概念的推广与应用第三章三角恒等变换3.1和角公式3.1.1两角和与差的余弦3.1.2两角和与差的正弦3.1.3两角和与差的正切3.2倍角公式和半角公式3.2.1倍角公式3.2.2半角的正弦、余弦和正切3.3三角函数的积化和差与和差化积本章小结阅读与欣赏和角公式与旋转对称必修五第一章解三角形1.1正弦定理和余弦定理1.1.1正弦定理1.1.2余弦定理1.2应用举例本章小结阅读与欣赏亚历山大时期的三角测量第二章数列2.1数列2.1.1数列2.1.2数列的递推公式(选学)2.2等差数列2.2.1等差数列2.2.2等差数列的前n项和2.3等比数列2.3.1等比数列2.3.2等比数列的前n项和本章小结阅读与欣赏级数趣题无穷与悖论第三章不等式3.1不等关系与不等式3.1.1不等关系与不等式3.1.2不等式的性质3.2均值不等式3.3一元二次不等式及其解法3.4不等式的实际应用3.5二元一次不等式(组)与简单的线性规划问题3.5.1二元一次不等式(组)所表示的平面区域3.5.2简单线性规划本章小结选修1-1第一章常用逻辑用语1.1命题与量词1.1.1命题1.1.2量词1.2基本逻辑联结词1.2.1“且”与“或”1.2.2“非”(否定)1.3充分条件、必要条件与命题的四种形式1.3.1推出与充分条件、必要条件1.3.2命题的四种形式本章小结阅读与欣赏什么是数理逻辑第二章圆锥曲线与方程2.1椭圆2.1.1椭圆及其标准方程2.1.2椭圆的几何性质2.2双曲线2.2.1双曲线及其标准方程2.2.2双曲线的几何性质2.3抛物线2.3.1抛物线级其标准方程2.3.2抛物线的几何性质本章小结阅读与欣赏圆锥面与圆锥曲线第三章导数及其应用3.1导数3.1.1函数的平均变化率3.1.2瞬时速度与导数3.1.3导数的几何意义3.2导数的运算3.2.1常数与幂函数的导数3.2.2导数公式表3.2.3导数的四则运算法则3.3导数的应用3.3.1利用导数判断函数的单调性3.3.2利用导数研究函数的极值3.3.3导数的实际应用本章小结阅读与欣赏微积分与极限思想选修1-2第一章统计案例1.1独立性检验1.2回归分析本章小结“回归”一词的由来附表相关性检验的临界值表第二章推理与证明2.1合情推理与演绎推理2.1.1合情推理2.1.2演绎推理2.2直接证明与间接证明2.2.1综合法与分析法2.2.2反证法本章小结阅读与欣赏《原本》与公理化思想数学证明的机械化——机器证明第三章数系的扩充与复数的引入3.1数系的扩充与复数的引入3.1.1实数系3.1.2复数的引入3.2复数的运算3.2.1复数的加法和减法3.2.2复数的乘法和除法本章小结复平面与高斯第四章框图4.1流程图4.2结构图本章小结阅读与欣赏冯·诺伊曼选修2-1第一章常用逻辑用语1.1命题与量词1.1.1命题1.1.2量词1.2基本逻辑联结词1.2.1“且”与“或”1.2.2“非”(否定)1.3充分条件、必要条件与命题的四种形式1.3.1推出与充分条件、必要条件本章小结阅读与欣赏什么是数理逻辑第二章圆锥曲线与方程2.1曲线与方程2.1.1曲线与方程的概念2.1.2由曲线求它的方程、由方程研究曲线的性质2.2椭圆2.2.1椭圆的标准方程2.2.2椭圆的几何性质2.3双曲线2.3.1双曲线的标准方程2.3.2双曲线的几何性质2.4抛物线2.4.1抛物线的标准方程2.4.2抛物线的几何性质2.5直线与圆锥曲线本章小结阅读与欣赏圆锥面与圆锥曲线第三章空间向量与立体几何3.1空间向量及其运算3.1.1空间向量的线性运算3.1.2空间向量的基本定理3.1.3两个向量的数量积3.1.4空间向量的直角坐标运算3.2空间向量在立体几何中的应用3.2.1直线的方向向量与直线的向量方程3.2.2平面的法向量与平面的向量表示3.2.3直线与平面的夹角3.2.4二面角及其度量3.2.5距离(选学)本章小结阅读与欣赏向量的叉积及其性质选修2-2第一章导数及其应用1.1导数1.1.1函数的平均变化率1.1.2瞬时速度与导数1.1.3导数的几何意义1.2导数的运算1.2.1常数函数与冥函数的导数1.2.2导数公式表及数学软件的应用1.2.3导数的四则运算法则1.3导数的应用1.3.1利用导数判断函数的单调性1.3.2利用导数研究函数的极值1.3.3导数的实际应用1.4定积分与微积分基本定理1.4.1曲边梯形面积与定积分1.4.2微积分基本定理本章小结阅读与欣赏微积分与极限思想第二章推理与证明2.1合情推理与演绎推理2.1.1合情推理2.1.2演绎推理2.2直接证明与间接证明2.2.1综合法与分析法2.2.2反证法2.3数学归纳法2.3.1数学归纳法2.3.2数学归纳法应用举例本意小结阅读与欣赏《原本》与公理化思想第三章数系的扩充与复数3.1数系的扩充与复数的概念3.1.1实数系3.1.2复数的概念3.1.3复数的几何意义3.2复数的运算3.2.1复数的加法与减法3.2.2复数的乘法3.2.3复数的除法本章小节阅读与欣赏复平面与高斯选修2-3第一章计数原理1.1基本计数原理1.2排列与组合1.2.1排列1.2.2组合1.3二项式定理1.3二项式定理1.3.2杨辉三角本章小结第二章概率2.1离散型随机变量及其分布列2.1.1离散型随机变量2.1.2离散型随机变量的分布列2.1.3超几何分布2.2条件概率与事件的独立性2.2.1条件概率2.2.2事件的独立性2.2.3独立重复试验与二项分布2.3随机变量的数字特征2.3.1离散型随机变量的数学期望2.3.2离散型随机变量的方差2.4正态分布本章小结阅读与欣赏关于“玛丽莲问题”的争论第三章统计案例3.1独立性检验3.2回归分析本章小结阅读与欣赏“回归”一词的由来附表选修3-1第一讲早期的算术与几何一古埃及的数学二两河流域的数学三丰富多彩的记数制度第二讲古希腊数学一希腊数学的先行者二毕达哥拉斯学派三欧几里得与《原本》四数学之神──阿基米德第三讲中国古代数学瑰宝一《周髀算经》与赵爽弦图二《九章算术》三大衍求一术四中国古代数学家第四讲平面解析几何的产生一坐标思想的早期萌芽二笛卡儿坐标系三费马的解析几何思想四解析几何的进一步发展第五讲微积分的诞生一微积分产生的历史背景二科学巨人牛顿的工作三莱布尼茨的“微积分”第六讲近代数学两巨星一分析的化身──欧拉二数学王子──高斯第七讲千古谜题一三次、四次方程求根公式的发现二高次方程可解性问题的解决三伽罗瓦与群论四古希腊三大几何问题的解决第八讲对无穷的深入思考一古代的无穷观念二无穷集合论的创立三集合论的进一步发展与完善第九讲中国现代数学的开拓与发展一中国现代数学发展概观二人民的数学家──华罗庚三当代几何大师──陈省身选修3-2暂缺选修3-3第一讲从欧氏几何看球面一平面与球面的位置关系二直线与球面的位置关系和球幂定理三球面的对称性第二讲球面上的距离和角一球面上的距离二球面上的角第三讲球面上的基本图形一极与赤道二球面二角形三球面三角形1.球面三角形2.三面角3.对顶三角形4.球极三角形第四讲球面三角形一球面三角形三边之间的关系二、球面“等腰”三角形三球面三角形的周长四球面三角形的内角和第五讲球面三角形的全等1.“边边边”(s.s.s)判定定理2.“边角边”(s.a.s.)判定定理3.“角边角”(a.s.a.)判定定理4.“角角角”(a.a.a.)判定定理第六讲球面多边形与欧拉公式一球面多边形及其内角和公式二简单多面体的欧拉公式三用球面多边形的内角和公式证明欧拉公式第七讲球面三角形的边角关系一球面上的正弦定理和余弦定理二用向量方法证明球面上的余弦定理1.向量的向量积2.球面上余弦定理的向量证明三从球面上的正弦定理看球面与平面四球面上余弦定理的应用──求地球上两城市间的距离第八讲欧氏几何与非欧几何一平面几何与球面几何的比较二欧氏平行公理与非欧几何模型──庞加莱模型三欧氏几何与非欧几何的意义阅读与思考非欧几何简史选修3-4第一讲平面图形的对称群一平面刚体运动1.平面刚体运动的定义2.平面刚体运动的性质二对称变换1.对称变换的定义2.正多边形的对称变换3.对称变换的合成4.对称变换的性质5.对称变换的逆变换三平面图形的对称群第二讲代数学中的对称与抽象群的概念一n元对称群Sn二多项式的对称变换三抽象群的概念1.群的一般概念2.直积第三讲对称与群的故事一带饰和面饰二化学分子的对称群三晶体的分类四伽罗瓦理论选修4-1第一讲相似三角形的判定及有关性质一平行线等分线段定理二平行线分线段成比例定理三相似三角形的判定及性质1.相似三角形的判定2.相似三角形的性质四直角三角形的射影定理第二讲直线与圆的位置关系一圆周角定理二圆内接四边形的性质与判定定理三圆的切线的性质及判定定理四弦切角的性质五与圆有关的比例线段第三讲圆锥曲线性质的探讨一平行摄影二平面与圆柱面的截线三平面与圆锥面的截线选修4-2引言第一讲线性变换与二阶矩阵一线性变换与二阶矩阵(一)几类特殊线性变换及其二阶矩阵1.旋转变换2.反射变换3.伸缩变换4.投影变换5.切变变换(二)变换、矩阵的相等二二阶矩阵与平面向量的乘法(二)一些重要线性变换对单位正方形区域的作用第二讲变换的复合与二阶矩阵的乘法一复合变换与二阶矩阵的乘法二矩阵乘法的性质第三讲逆变换与逆矩阵一逆变换与逆矩阵1.逆变换与逆矩阵2.逆矩阵的性质二二阶行列式与逆矩阵三逆矩阵与二元一次方程组1.二元一次方程组的矩阵形式2.逆矩阵与二元一次方程组第四讲变换的不变量与矩阵的特征向量一变换的不变量——矩阵的特征向量1.特征值与特征向量2.特征值与特征向量的计算二特征向量的应用1.Aa的简单表示2.特征向量在实际问题中的应用选修4-5第一章不等式的基本性质和证明的基本方法1.1 不等式的基本性质和一元二次不等式的解法1.2基本不等式1.3绝对值不等式的解法1.4绝对值的三角不等式1.5不等式证明的基本方法本章小结第二章柯西不等式与排序不等式及其应用2.1 柯西不等式2.2排序不等式2.3平均值不等式(选学)2.4最大值与最小值问题,优化的数学模型本章小结阅读与欣赏第三章数学归纳法与贝努利不等式3.1数学归纳法原理3.2用数学归纳法证明不等式,贝努利不等式本章小结阅读与欣赏附录部分中英文词汇对照表后记选修4-6引言第一讲整数的整除一整除1.整除的概念和性质2.带余除法3.素数及其判别法二最大公因数与最小公倍数1.最大公因数2.最小公倍数三算术基本定理第二讲同余与同余方程一同余1.同余的概念2.同余的性质二剩余类及其运算三费马小定理和欧拉定理四一次同余方程五拉格朗日插值法和孙子定理六弃九验算法第三讲一次不定方程一二元一次不定方程二二元一次不定方程的特解三多元一次不定方程第四讲数伦在密码中的应用一信息的加密与去密二大数分解和公开密钥学习总结报告附录一剩余系和欧拉函数附录二多项式的整除性选修4-7引言第一讲优选法一什么叫优选法二单峰函数三黄金分割法——0.618法1.黄金分割常数2.黄金分割法——0.618法阅读与思考黄金分割研究简史四分数法1.分数法阅读与思考斐波那契数列和黄金分割2.分数法的最优性五其他几种常用的优越法1.对分法2.盲人爬山法3.分批试验法4.多峰的情形六多因素方法1.纵横对折法和从好点出发法2.平行线法3.双因素盲人爬山法第二讲试验设计初步一正交试验设计法1.正交表2.正交试验设计3.试验结果的分析4.正交表的特性二正交试验的应用选修4-9引言第一讲风险与决策的基本概念一风险与决策的关系二风险与决策的基本概念1.风险(平均损失)2.平均收益3.损益矩阵4.风险型决策探究与发现风险相差不大时该如何决策第二讲决策树方法第三讲风险型决策的敏感性分析第四讲马尔可夫型决策简介一马尔可夫链简介1.马尔可夫性与马尔可夫链2.转移概率与转移概率矩阵二马尔可夫型决策简介三长期准则下的马尔可夫型决策理论1.马尔可夫链的平稳分布2.平稳分布与马尔可夫型决策的长期准则3.平稳准则的应用案例说明:A版适用于文件生使用,B版适用于理科生使用,B 版比A版略难。
抛物线及其标准方程 课件

思路分析先将所给方程转化为标准方程的形式,确定其开口方向,
求出p的值,再写出焦点坐标和准线方程.பைடு நூலகம்
解(1)由方程 y2=-12x 知,抛物线开口向左,焦点在 x 轴的负半
轴上,2p=12,所以 p=6,2=3,因此焦点坐标为(-3,0),准线方程为
解(1)因为点M(-8,4)在第二象限,所以抛物线焦点在y轴的正半轴
或x轴的负半轴上.
设抛物线方程为x2=2py(p>0)或y2=-2px(p>0).
将点M(-8,4)代入可得(-8)2=2p·4或42=-2p·(-8),
解得2p=16或2p=2,
故所求抛物线方程为x2=16y或y2=-2x.
(2)因为直线 x+4y+6=0 与坐标轴的交点为(-6,0),
轴还是y轴,是正半轴还是负半轴,从而设出相应的标准方程的形
式;“计算”就是指根据所给的已知条件求出方程中参数p的值,从而
得到抛物线的标准方程.
2.求抛物线的标准方程时需注意以下三个问题:
(1)注意开口方向与方程间的对应关系;
(2)当抛物线的类型没有确定时,可设方程为y2=mx或x2=my,这样
可以减少讨论情况的个数;
2 2 4
1
- ,0
4
,准线方程为
1
x= .
4
综上可知,当 a≠0 时,抛物线 x=-ay2 的焦点坐标为 1
线方程为 x=4.
1
,0
4
,准
纠错心得在解决抛物线问题时,必须注意抛物线方程的形式,若
不是标准方程,应首先转化为标准方程,其次要注意分类讨论思想
高二数学抛物线定义及其标准方程

已知抛物线的顶点在原点,焦点在 y轴,抛物线上一点M(m,-3)到焦 点的距离是5,求m的值及抛物线的
方程。
02
基本知识:抛物线的定 义、四种标准方程形式
及其对应关系。
01
小结:
03
思想方法:注重数形结 合。
思考:
01
02
一.抛物线标准方程与二 次函数 之间有什么区别与联 系?
二.抛物线标准方程与椭 圆、双曲 线的标准方程有什么 区别与联系?
练习:
一.求下列抛物线的焦点坐标和准线方程:
1. y2=20x
(2)x2+8y=0
2. y= -2x2
(4)x=ay2(a≠0)
根据下列条件,写出抛物线的标准方程:
(1)准线方程为y=0.5
(2)焦准
距为a(a>0),且焦点在x轴上。
01
02
03
例1.求满足下列条件 的抛物线的标准方程:
过点P(4,-2);
某隧道横断面由抛物线及矩形的三边组 成,尺寸如图,某卡车轻车时能通过此 隧道,现载一集装箱宽3米,车与箱共 高4.5米,问此车能否通过隧道?
如图,有一张长为8,宽为4的矩形纸 片ABCD,按图示方法进行折叠,使每 次折叠后点B都落在AD边上,此时将B 记为B1(EF为折痕,F也可落在CD上), 过点B1作B1T∥CD交EF于点T,求点T 的轨迹方程。
焦点在直线x-2y4=0上。
例2:已知点M与点F(4,0)的距离比它 到直线L:x+5=0的距离小1,求点M的 轨迹方程。
练习:1.已知点M与点F(1,0)的距离 比它到y轴的距离大1,求点M的轨迹方 程。
2.若点P(x,y)的坐标满足方程
5(x 1 )2 (y 2 )2 |3 x 4 y 1| 2 0
3.3.2抛物线的简单几何性质(第1课时)课件(人教版)

关于x轴
对称
( x, y )
O
•
F
(
p
,0)
2
若点(x,y)在抛物线上, 即满足y2 = 2px,
则 (-y)2 = 2px
即点(x,-y) 也在抛物线上,
故抛物线y2 = 2px(p>0)关于x轴对称.
x
3.顶点
定义:抛物线与它的对称轴的交
y
点叫做抛物线的顶点.
y2
= 2px (p>0)中,
叫做抛物线的焦半径.
y
焦半径公式:
p
MF x0
2
H
y2 = 2px
d
M (x0,y0)
O
•
F( p ,0) x
2
方程 y2 = 2px y2 = -2px x2 = 2py x2 = -2py
图
形
y
l
M
O F
M
x
F
y
y
l
O
F M
x
O
l
焦半
径
y
x
O
F
l
M x
p
p
p
p
MF x0
MF
例4.斜率为1的直线 l 经过抛物线
且与抛物线相交于A、B两点,求线段AB的长.
解:F(1,0),直线l:y=x-1
y x 1
由 2
消y得:x 2 6 x 1 0
y 4xyA来自oFB
法2:设A( x1 , y1 ), B( x2 , y2 )
x1 x2 6
x1 x2 1
由 2
y 4x
高中数学选修一第2章 2.7.2 抛物线的几何性质人教B版讲义
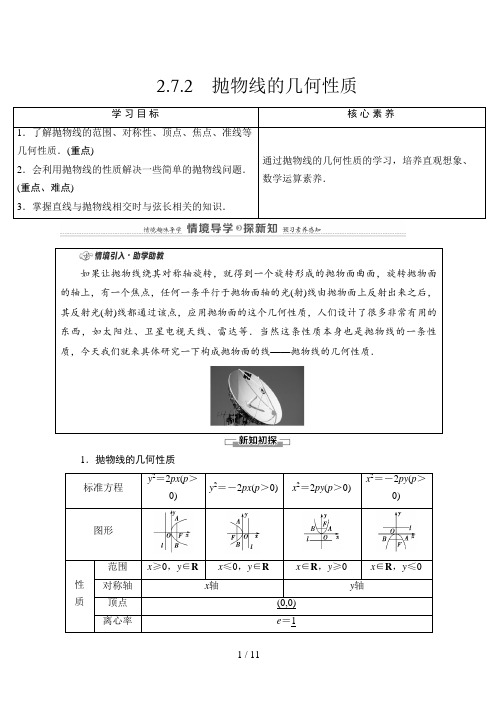
2.7.2 抛物线的几何性质学习目标核心素养1.了解抛物线的范围、对称性、顶点、焦点、准线等几何性质.(重点)2.会利用抛物线的性质解决一些简单的抛物线问题.(重点、难点)3.掌握直线与抛物线相交时与弦长相关的知识.通过抛物线的几何性质的学习,培养直观想象、数学运算素养.如果让抛物线绕其对称轴旋转,就得到一个旋转形成的抛物面曲面,旋转抛物面的轴上,有一个焦点,任何一条平行于抛物面轴的光(射)线由抛物面上反射出来之后,其反射光(射)线都通过该点,应用抛物面的这个几何性质,人们设计了很多非常有用的东西,如太阳灶、卫星电视天线、雷达等.当然这条性质本身也是抛物线的一条性质,今天我们就来具体研究一下构成抛物面的线——抛物线的几何性质.1.抛物线的几何性质标准方程y2=2px(p>0)y2=-2px(p>0) x2=2py(p>0)x2=-2py(p>0)图形性质范围x≥0,y∈R x≤0,y∈R x∈R,y≥0 x∈R,y≤0 对称轴x轴y轴顶点(0,0)离心率e=1思考1:抛物线x2=2py(p>0)有几条对称轴?[提示]有一条对称轴.思考2:抛物线的范围是x∈R,这种说法正确吗?[提示]抛物线的方程不同,其范围就不一样,如y2=2px(p>0)的范围是x≥0,y∈R,故此说法错误.思考3:参数p对抛物线开口大小有何影响?[提示]参数p(p>0)对抛物线开口大小有影响,因为过抛物线的焦点F且垂直于对称轴的弦的长度是2p,所以p越大,开口越大.2.焦点弦设过抛物线焦点的弦的端点为A(x1,y1),B(x2,y2),则y2=2px(p>0)|AB|=x1+x2+py2=-2px(p>0)|AB|=p-(x1+x2)x2=2py(p>0)|AB|=y1+y2+px2=-2py(p>0)|AB|=p-(y1+y2)1.思考辨析(正确的打“√”,错误的打“×”)(1)抛物线是中心对称图形.( )(2)抛物线的范围为x∈R.( )(3)抛物线关于顶点对称.( )(4)抛物线的标准方程虽然各不相同,但离心率都相同.( )[答案](1)×(2)×(3)×(4)√[提示](1)×在抛物线中,以-x代x,-y代y,方程发生了变化.(2)×抛物线的方程不同,其范围不同,y2=2px(p>0)中x≥0,y∈R.(3)×(4)√离心率都为1,正确.2.设抛物线y2=8x上一点P到y轴的距离是6,则点P到该抛物线焦点F的距离是( )A .8B .6C .4D .2 A [∵抛物线的方程为y 2=8x , ∴其准线l 的方程为x =-2, 设点P (x 0,y 0)到其准线的距离为d , 则d =|PF |,即|PF |=d =x 0-(-2)=x 0+2, ∵点P 到y 轴的距离是6, ∴x 0=6, ∴|PF |=6+2=8.]3.过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2),若x 1+x 2=6,则|AB |= .8 [∵y 2=4x ,∴2p =4,p =2.∵由抛物线定义知:|AF |=x 1+1,|BF |=x 2+1, ∴|AB |=x 1+x 2+p =6+2=8.]4.顶点在原点,对称轴是x 轴,并且顶点与焦点的距离等于6的抛物线方程是 .y 2=24x 或y 2=-24x [∵顶点与焦点距离为6,即p2=6,∴2p =24,又对称轴为x轴,∴抛物线方程为y 2=24x 或y 2=-24x .]由抛物线的几何性质求标准方程【】(1)平面直角坐标系xOy 中,有一定点A (2,1),若线段OA 的垂直平分线过抛物线y 2=2px (p >0)的焦点,则该抛物线的标准方程是 .(2)抛物线的顶点在原点,对称轴重合于椭圆9x 2+4y 2=36短轴所在的直线,抛物线焦点到顶点的距离为3,求抛物线的方程及抛物线的准线方程.(1)y 2=5x [线段OA 的垂直平分线为4x +2y -5=0,与x 轴的交点为⎝ ⎛⎭⎪⎫54,0,∴抛物线的焦点为⎝ ⎛⎭⎪⎫54,0,∴其标准方程是y 2=5x .](2)解:椭圆的方程可化为x24+y29=1,其短轴在x 轴上,∴抛物线的对称轴为x 轴,∴设抛物线的方程为y 2=2px 或y 2=-2px (p >0). ∵抛物线的焦点到顶点的距离为3, 即p2=3,∴p =6, ∴抛物线的标准方程为y 2=12x 或y 2=-12x , 其准线方程分别为x =-3和x =3.用待定系数法求抛物线方程的步骤提醒:求抛物线的方程时要注意抛物线的焦点位置.不同的焦点设出不同的方程.[跟进训练]1.已知抛物线关于x 轴对称,它的顶点在坐标原点,其上一点P 到准线及对称轴距离分别为10和6,求抛物线方程.[解] 设抛物线方程为y 2=2ax (a ≠0),点P (x 0,y 0). 因为点P 到对称轴距离为6,所以y 0=±6, 因为点P 到准线距离为10,所以⎪⎪⎪⎪⎪⎪x0+a 2=10.① 因为点P 在抛物线上,所以36=2ax 0.②由①②,得⎩⎨⎧a =2,x0=9或⎩⎨⎧a =18,x0=1或⎩⎨⎧a =-18,x0=-1或⎩⎨⎧a =-2,x0=-9.所以所求抛物线方程为y 2=±4x 或y 2=±36x .抛物线性质的应用【例2】(1)抛物线y 2=4x 的焦点为F ,准线为l ,点A 是抛物线上一点,且∠AFO =120°(O 为坐标原点),AK ⊥l ,垂足为K ,则△AKF 的面积是 .(2)已知正三角形AOB 的一个顶点O 位于坐标原点,另外两个顶点A ,B 在抛物线y 2=2px (p >0)上,求这个三角形的边长.(1)43 [如图,设A (x 0,y 0),过A 作AH ⊥x 轴于H , 在Rt △AFH 中,|FH |=x 0-1, 由∠AFO =120°,得∠AFH =60°, 故y 0=|AH |=3(x 0-1), 所以A 点的坐标为错误!,将点A 坐标代入抛物线方程可得3x 20-10x 0+3=0, 解得x 0=3或x 0=13(舍),故S △AKF =12×(3+1)×23=43.](2)解:如图所示,设正三角形OAB 的顶点A ,B 在抛物线上,且坐标分别为A (x 1,y 1),B (x 2,y 2),则y 21=2px 1,y 2=2px 2.又|OA |=|OB |,所以x 21+y 21=x 2+y 2, 即x 21-x 2+2px 1-2px 2=0, 整理得(x 1-x 2)(x 1+x 2+2p )=0. ∵x 1>0,x 2>0,2p >0, ∴x 1=x 2,由此可得|y 1|=|y 2|, 即线段AB 关于x 轴对称. 由此得∠AOx =30°, 所以y 1=33x 1,与y 21=2px 1联立, 解得y 1=23p .∴|AB |=2y 1=43p .利用抛物线的性质可以解决的问题(1)对称性:解决抛物线的内接三角形问题. (2)焦点、准线:解决与抛物线的定义有关的问题. (3)范围:解决与抛物线有关的最值问题. (4)焦点:解决焦点弦问题.提醒:解答本题时易忽略A ,B 关于x 轴对称而出错.[跟进训练] 2.已知双曲线x2a2-y2b2=1(a >0,b >0)的两条渐近线与抛物线y 2=2px (p >0)的准线分别交于A 、B 两点,O 为坐标原点,若双曲线的离心率为2,△AOB 的面积为3,求抛物线的标准方程.[解] 由已知得c a =2,所以a2+b2a2=4,解得ba=3.即渐近线方程为y =±3x ,而抛物线准线方程为x =-p 2,于是A ⎝ ⎛⎭⎪⎫-p 2,-32p ,B ⎝ ⎛⎭⎪⎫-p 2,32p ,从而△AOB 的面积为12·3p ·p 2=3.可得p =2,因此抛物线开口向右,所以标准方程为y 2=4x .焦点弦问题[探究问题]以抛物线y 2=2px (p >0)为例,回答下列问题: (1)过焦点F 的弦长|AB |如何表示?还能得到哪些结论? [提示] ①|AB |=2⎝ ⎛⎭⎪⎫x0+p 2(焦点弦长与中点关系).②|AB |=x 1+x 2+p =2psin2θ(θ为AB 的倾斜角).③A ,B 两点的横坐标之积、纵坐标之积为定值,即x 1·x 2=p24,y 1·y 2=-p 2.④S △AOB =p22sin θ.⑤1|AF|+1|BF|=2p(定值). (2)以AB 为直径的圆与直线l 具有怎样的位置关系?[提示] 如图,AB 是过抛物线y 2=2px (p >0)焦点F 的一条弦,设A (x 1,y 1),B (x 2,y 2),AB 的中点M (x 0,y 0),相应的准线为l .所以以AB 为直径的圆必与准线l 相切. (3)解决焦点弦问题需注意什么?[提示] 要注意抛物线定义在其中的应用,通过定义将焦点弦长度转化为端点的坐标问题,从而可借助根与系数的关系进行求解.【例3】已知抛物线方程为y 2=2px (p >0),过此抛物线的焦点的直线与抛物线交于A ,B 两点,且|AB |=52p ,求AB 所在直线的方程.[思路探究] 根据弦长求出直线斜率,进而求得直线方程. [解] ∵过焦点的弦长|AB |=52p ,∴弦所在的直线的斜率存在且不为零,设直线AB 的斜率为k ,且A (x 1,y 1),B (x 2,y 2). ∵y 2=2px 的焦点为F ⎝ ⎛⎭⎪⎫p 2,0.∴直线方程为y =k ⎝ ⎛⎭⎪⎫x -p 2.由⎩⎨⎧y =k ⎝ ⎛⎭⎪⎫x -p 2,y2=2px ,整理得k 2x 2-(k 2p +2p )x +14k 2p 2=0(k ≠0),∴x 1+x 2=k2p +2pk2,∴|AB |=x 1+x 2+p =k2p +2pk2+p , 又|AB |=52p ,∴k2p +2p k2+p =52p ,∴k =±2.∴所求直线方程为y =2⎝ ⎛⎭⎪⎫x -p 2或y =-2⎝⎛⎭⎪⎫x -p 2.1.(改变问法)本例条件不变,求弦AB 的中点M 到y 轴的距离. [解] 设AB 中点为M (x 0,y 0), 由例题解答可知2x 0=x 1+x 2=32p ,所以AB 的中点M 到y 轴的距离为34p .2.(变换条件)本例中,若A 、B 在其准线上的射影分别为A 1,B 1,求∠A 1FB 1. [解] 由例题解析可知AB 的方程为y =k ⎝⎛⎭⎪⎫x -p 2,即x =1k y +p2,代入y 2=2px 消x 可得y 2=2p k y +p 2,即y 2-2pky -p 2=0,∴y 1y 2=-p 2, 由A 1点的坐标为⎝ ⎛⎭⎪⎫-p 2,y1,B 1点的坐标为⎝ ⎛⎭⎪⎫-p 2,y2,得kA 1F =-y1p ,kB 1F =-y2p. ∴kA 1F ·kB 1F =y1y2p2=-1, ∴∠A 1FB 1=90°.解决过焦点的直线与抛物线相交有关的问题时,一是注意直线方程和抛物线方程联立得方程组,再结合根与系数的关系解题,二是注意焦点弦长、焦半径公式的应用.解题时注意整体代入思想的运用,简化运算.1.讨论抛物线的几何性质,一定要利用抛物线的标准方程;利用几何性质,也可以根据待定系数法求抛物线的方程.2.解决抛物线的轨迹问题,可以利用抛物线的标准方程,结合抛物线的定义. 3.抛物线y 2=±2px (p >0)的过焦点的弦长|AB |=x 1+x 2+p ,其中x 1,x 2分别是点A ,B 横坐标的绝对值;抛物线x 2=±2py (p >0)的过焦点的弦长|AB |=y 1+y 2+p ,其中y 1,y 2分别是点A ,B 纵坐标的绝对值.4.求抛物线的方程常用待定系数法和定义法;直线和抛物线的弦长问题、中点弦问题及垂直、对称等可利用判别式、根与系数的关系解决;抛物线的综合问题要深刻分析条件和结论,灵活选择解题策略,对题目进行转化.1.若抛物线y 2=2x 上有两点A 、B 且AB 垂直于x 轴,若|AB |=22,则抛物线的焦点到直线AB 的距离为( )A .12B .14C .16D .18A [线段AB 所在的直线方程为x =1,抛物线的焦点坐标为⎝ ⎛⎭⎪⎫12,0,则焦点到直线AB 的距离为1-12=12.]2.在抛物线y 2=16x 上到顶点与到焦点距离相等的点的坐标为( ) A .(42,±2) B .(±42,2) C .(±2,42)D .(2,±42)D [抛物线y 2=16x 的顶点O (0,0),焦点F (4,0),设P (x ,y )符合题意,则有错误!⇒错误!⇒错误!所以符合题意的点为(2,±42).]3.设O 为坐标原点,F 为抛物线y 2=4x 的焦点,A 是抛物线上一点,若OA →·AF→=-4,则点A 的坐标是( )A .(2,±22)B .(1,±2)C .(1,2)D .(2,22)B [由题意知F (1,0),设A ⎝ ⎛⎭⎪⎫y204,y0,则OA →=⎝ ⎛⎭⎪⎫y204,y0,AF →=⎝ ⎛⎭⎪⎫1-y204,-y0,由OA →·AF →=-4得y 0=±2,∴点A 的坐标为(1,±2),故选B .]4.已知AB 是过抛物线2x 2=y 的焦点的弦,若|AB |=4,则AB 的中点的纵坐标是 .158[设A (x 1,y 1),B (x 2,y 2),11 / 11 由抛物线2x 2=y ,可得p =14. ∵|AB |=y 1+y 2+p =4,∴y 1+y 2=4-14=154,故AB 的中点的纵坐标是y1+y22=158.] 5.已知点P (1,m )是抛物线C :y 2=2px 上的点,F 为抛物线的焦点,且|PF |=2,直线l :y =k (x -1)与抛物线C 相交于不同的两点A ,B .(1)求抛物线C 的方程;(2)若|AB |=8,求k 的值.[解] (1)抛物线C :y 2=2px 的准线为x =-p 2, 由|PF |=2得:1+p 2=2,得p =2. 所以抛物线的方程为y 2=4x .(2)设A (x 1,y 1),B (x 2,y 2),由错误!可得k 2x 2-(2k 2+4)x +k 2=0,Δ=16k 2+16>0,∴x 1+x 2=2k2+4k2. ∵直线l 经过抛物线C 的焦点F ,∴|AB |=x 1+x 2+p =2k2+4k2+2=8, 解得k =±1,所以k 的值为1或-1.。
高二数学人教B版选择性必修第一册 抛物线的几何性质PPT全文课件

2020-2021学年高二数学人教B版选择 性必修 第一册 抛物线的几何性质PPT全文课件【 完美课 件】 2020-2021学年高二数学人教B版选择 性必修 第一册 抛物线的几何性质PPT全文课件【 完美课 件】
2020-2021学年高二数学人教B版选择 性必修 第一册 抛物线的几何性质PPT全文课件【 完美课 件】
2020-2021学年高二数学人教B版选择 性必修 第一册 抛物线的几何性质PPT全文课件【 完美课 件】 2020-2021学年高二数学人教B版选择 性必修 第一册 抛物线的几何性质PPT全文课件【 完美课 件】
2020-2021学年高二数学人教B版选择 性必修 第一册 抛物线的几何性质PPT全文课件【 完美课 件】 2020-2021学年高二数学人教B版选择 性必修 第一册 抛物线的几何性质PPT全文课件【 完美课 件】
2020-2021学年高二数学人教B版选择 性必修 第一册 抛物线的几何性质PPT全文课件【 完美课 件】
尝试与发现
2020-2021学年高二数学人教B版选择 性必修 第一册 抛物线的几何性质PPT全文课件【 完美课 件】 2020-2021学年高二数学人教B版选择 性必修 第一册 抛物线的几何性质PPT全文课件【 完美课 件】
尝试与发现
2020-2021学年高二数学人教B版选择 性必修 第一册 抛物线的几何性质PPT全文课件【 完美课 件】
那么抛物线的范围(开口方向)、对称性、顶点、离心率中, 哪些与①所表示的抛物线是相同的? 哪些是有区别的?
答:可以看出,②③④所表示抛物线,顶点坐标、 离心率与①所表示的抛物线是相同的,但是:
抛物线的几何性质
高二年级 数学
知识概要
一、由抛物线的方程研究其具有的几何性质 二、应用抛物线的几何性质求解抛物线的相关问题 三、课堂小结
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学抛物线的定义;标准方程及几何性质(文)人教实验B版【本讲教育信息】一. 教学内容:抛物线的定义;标准方程及几何性质二. 本周学习目标掌握抛物线的定义,标准方程,能根据条件利用待定系数法求抛物线的方程,掌握抛物线的几何性质。
了解抛物线的参数方程,能根据方程讨论曲线的性质,掌握直线与抛物线的位置关系的判断方法,能够正确熟练地解决有关直线和抛物线的位置关系的一些问题。
三. 考点分析(一)抛物线的定义:平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫抛物线,定点F叫做抛物线的焦点,定直线l叫做抛物线的准线。
(二)2. 抛物线标准方程中p的几何意义是:焦点到准线的距离,故p>03. 抛物线的标准方程中,一次项的变量决定对称轴,一次项的符号决定开口方向。
4. 弦长公式:(1)过焦点F (2p,0)的弦长:x 1,x 2分别为弦AB 的端点的横坐标,y 1,y 2分别为弦AB 的端点的纵坐标,弦|AB|=x 1+x 2+p ,pBF AF 211=+,y 1y 2=-p 2 (2)一般的弦长公式:类似于椭圆,x 1,x 2分别为弦PQ 的横坐标,y 1,y 2分别为弦PQ 的纵坐标,弦PQ 所在的直线方程为y=kx+b,代入抛物线方程整理得Ax 2+Bx+C=0,则PQ =AACB kx x k 21122212-+=-+,若y 1,y 2分别为弦PQ 的纵坐标,则PQ =21211y y k-+5. 斜率为k 的弦的中点的轨迹方程是:y=kp,一条平行于x 轴且不包括端点在抛物线内部的射线。
6. 与焦点弦有关的一些几何图形的性质: (1)以过焦点的弦为直径的圆和准线相切(2)设AB 为焦点弦,端点在准线上的射影为A 1,B 1,M 为准线与x 轴的交点,则∠AMF =∠BMF(3)若P 为A 1B 1的中点,则PA ⊥PB(4)若AO 的延长线交准线于C ,则BC 平行于x 轴,反之,若过B 点平行于x 轴的直线交准线于C 点,则A ,O ,C 三点共线。
7. 过抛物线外一点总有三条直线和抛物线有且只有一个公共点:两条切线和一条平行于对称轴的直线。
【典型例题】例1. 指出抛物线的焦点坐标、准线方程. (1)(2)分析:(1)先根据抛物线方程确定抛物线是四种中的哪一种,求出p ,再写出焦点坐标和准线方程。
(2)先把方程化为标准方程形式,再对a 进行讨论,确定是哪一种后,求p 及焦点坐标与准线方程.解:(1),∴焦点坐标是(0,1),准线方程是:(2)原抛物线方程为: ,①当时,,抛物线开口向右,∴焦点坐标是 ,准线方程是:.②当时,,抛物线开口向左,∴焦点坐标是 ,准线方程是: .综合上述,当时,抛物线的焦点坐标为,准线方程是:.例2. 分别求满足下列条件的抛物线的方程。
过点B (-3,2); 焦点在直线240x y --=上解:(1)依题意,设所求抛物线的方程为2222(0)y px x py p =-=>或 ∵抛物线过点B (-3,2),代入22y px =-得23p = 代入22x py =得94p =∴所求抛物线的方程为224932y x x y =-=或 (2)令02x y ==-得, 令04y ==得x ∴抛物线的焦点坐标为(0,-2)或(4,0)当焦点坐标为(0,-2)时,抛物线的方程为28x y =- 当焦点坐标为(4,0)时,抛物线的方程为216y x =反思:抛物线的开口方向有四种,相应的标准方程的形式也就有四种,因此,在解题时要利用图形全面分析,防止遗漏符合题设条件的某个开口方向,从而防止遗漏符合题设条件的抛物线的标准方程。
例 3. 已知抛物线的顶点在原点,对称轴为轴,抛物线上的点到焦点的距离等于5,求抛物线的方程和的值。
解法一:设抛物线方程为,则焦点为,由题设可得:解得或故抛物线方程为的值为解法二:设抛物线方程为,则焦点为,准线方程为.根据抛物线定义, 到焦点的距离等于5,也就是 到准线的距离等于5,则因此抛物线方程为28y x =-.又点在抛物线上,于是点评:解法二利用抛物线的定义把到焦点的距离转化为到准线的距离,既快捷又方便,要善于转化。
例4. 斜率为1的直线经过抛物线x 4y 2=的焦点,与抛物线相交于两点A 、B ,求线段。
AB 的长。
由抛物线的标准方程可知,焦点为,准线方程为.由题设,直线的方程为:.代入抛物线方程,整理得:.解法一:解上述方程得: ,分别代入直线方程得:即坐标分别为、.解法二:设,,则:=84622=-⋅解法三:设、 ()22y ,x B . 由抛物线定义可知,等于点到准线的距离.即同理 1x |BF |2+=点拨:解法一利用传统的基本方法求出两点坐标,再利用两点间距离公式求出的长。
解法二没有直接求出A 、B 坐标。
而是利用韦达定理找到与的关系,利用直线截二次曲线的弦长公式求得,这是典型的设而不求的思想方法,比解法一先进,解法三充分利用抛物线的定义,把过焦点的这一特殊的弦分成两个半径的和,转化为准线的距离,这是思维产生质的飞跃的表现。
例5. 过抛物线2y x =的顶点O 作两条互相垂直的弦OA ,OB 。
求证:直线AB 过定点 求△AOB 面积的最小值解:(1)设A (11,x y )、B (22,x y ),则221122,y x y x ==若12,x x = 则由OA ⊥OB 得121x x ==,AB 过点M (1,0)若12,x x ≠则1212221212121y y y y k x x y y y y --===--+由OA ⊥OB 得0y y x x 2121=+,又212221x x y y =⋅∴121y y =-故AB 的方程为:11121()y y x x y y -=-+即2121121()y y y y y y x x +--=-化简得:12()1y y y x +=-,故直线AB 恒过定点M (1,0) (2) 直线AB :21x ty y x -==与联立,消去x 得方程:210y ty --=∴t y y 21=+,1y y 21-=⋅故2212()4y y t -=+∴4t 21|y y ||OM |21S 221AOB +=-⋅=△ ∴当t=0,即AB ⊥x 轴时AOB S ∆取最小值1反思:与弦有关的问题内容十分丰富,基本内容有弦长,弦终点,最值,轨迹等问题,但解题思想都一致,即由直线方程与圆锥曲线方程联立并消元,利用判别式、韦达定理使所求问题转化为方程的问题求解,或用点差法求解。
【模拟试题】(答题时间:60分钟)一、选择题(本大题共6小题,每小题5分,共30分)1. 以双曲线19y 16x 22=-的右焦点为顶点,左顶点为焦点的抛物线方程为( )A. )5x (18y 2--=B. )5x (4y 2--=C. )5x (36y 2--=D. )5x (36y 2+-=2. 若AB 为抛物线px 2y 2=(0p >)的焦点弦,l 是抛物线的准线,则以AB 为直径的圆与l 的公共点的个数是( )A. 0B. 1C. 2D. 0或1或23. 若抛物线01422=++--m y mx y 的准线与双曲线12322=-y x 的右准线重合,则m 的值为( )A. -2B. 4C. -8D. 24. 抛物线y px p 220=>()上一点的横坐标为6,这点的焦半径为10,则焦点到准线的距离为( ) A. 4B. 8C. 16D. 325. 已知定点A (4,3),抛物线y x 24=,F 为抛物线的焦点,B 是抛物线的动点,则BF AB+取最小值时的B 点的坐标为( )A. (2,3)B. (1,3)C. (4,4)D. (233,)6. 抛物线的顶点在原点,焦点在y 轴上,其上一点P (m ,1)到焦点的距离为5,则抛物线的方程为( )A. y 8x 2=B. y 8x 2-=C. y 16x 2=D. y 16x 2-=二、填空题(本题共4小题,每小题5分,共20分)7. 抛物线1x 2y :C 2+=向右平移21个单位得一曲线 C ,再把曲线 C 绕其焦点逆时针方向旋转︒90,则所得曲线的方程为_________。
8. 242_____.y x y x k k ==+=抛物线截直线所得弦长为则 9. AB 是过抛物线y px p 220=>()的焦点的弦,则AB 的最小值为_________10. 过抛物线焦点F 的直线与抛物线交于A 、B 两点,若A 、B 在抛物线准线上的射影分别为A B 11、,则∠A FB 11等于_________三、解答题(本大题共4题,共50分)11. 抛物线2x 21y -=与过点M (0,-1)的直线l 交于A 、B 两点,O 为坐标原点,若OA 与OB 的斜率之和为1,求直线l 的方程。
(12分)12. 如果抛物线1ax y 2-=上存在关于直线y x =+2对称的两个不同的点,求a 的取值范围。
(13分)13. 若抛物线y=ax 2-1上总存在关于直线 l :x+y=0的对称点,求a 的取值范围。
(12分) 14. 过抛物线x 4y 2=的焦点F 作弦AB ,且8|AB |≤,直线AB 与椭圆2y 2x 322=+相交于两个不同的点,求直线AB 的倾斜角的范围。
(13分)【试题答案】1. C2. BAB BB AA MM 21][21'''=+=,相切3. B)4()1(-=-x m y由4344=⇒=+-m m4. B 如图,设P 点是抛物线y px 22=上一点,且x P ==610,PF ,由抛物线定义,知P 到准线的距离为10,从而得y 轴到准线的距离为4,故F 到准线的距离为8。
5. D 如图,由抛物线定义BF BC =,∴+=+⊥BF AB AB BC BC l ,准线()当B 、C 、A 三点共线时,AB BC +最小,此时B 点的纵坐标与A 点的纵坐标相等,从而可确定()B 233,。
6. C提示:由点P (m ,1)所在的抛物线开口向上,又P 到焦点的距离为5,根据定义知P24=,从而216P = 7. ()()x y -=+122122 提示:C '方程为y x 22121=-+() 即y x 22=,顶点(0,0),焦点()120, 绕焦点逆时针方向旋转90︒,新顶点为1212,-⎛⎝ ⎫⎭⎪ 开口向上,而焦点到顶点的距离不变故得方程x y -⎛⎝ ⎫⎭⎪=+⎛⎝ ⎫⎭⎪1221228. k=-49. AB 的最小值即通径2p10. 如图,设∠==AA F AF AA 11α,则由,知∠=∠=AFA BB F 11αβ,设,则由 BF BB =1,知∠=BFB 1β又AA x BB 11////轴,∴∠=∠=A FK B FK 11αβ, ∴+=∠=︒∴+=︒∠=︒22180909011αβαβAFB A FB ,即11. 解:设A (x 1,y 1),B (x 2,y 2)x y x y 1212222122=-=-⎧⎨⎪⎩⎪()()y x y x x x 112212121+=-+=() ⇒+=-x x 122()()21-得:()()()x x x x y y 2121212+-=-- ⇒=k 1 ∴l :y x =-112. 解:设P (x y 11,),Q (x y 22,)是抛物线y ax =-21上关于直线y x =+2对称的两点,另设直线PQ 的方程为y x b =-+( PQ ⊥直线y x =+2) ()y x b y ax ax x b =-+=-⎧⎨⎩⇒+-+=22110 一方面,直线PQ 与抛物线有两个交点,则()∆=++>1410a b ……① 另一方面,由韦达定理,得:x x a121+=-,从而PQ 中点M 的横坐标为 x x x a012212=+=- M 在直线PQ 上,∴点M 的纵坐标为y x b ab 0012=-+=+ 又M 在直线y x =+2上,∴+=-+12122a b a……② 由①②,消去b ,可得:123014a a ->∴>, 13. 解:设A ,B 是抛物线y=ax 2-1上关于直线l :x+y=0的对称点,设A(x 1, y 1),B(x 2, y 2)b x y AB 1k l AB AB +==∴⊥的方程为,可设直线,用心 爱心 专心 11 y x b y ax ax x b =+=-⎧⎨⎩⇒--+=22110()直线与抛物线相交于两点AB∴=++>∆14101a b ()……()另外,,设的中点,则x x a AB M x y 12001+=(,)x xx a y x b a b 0120021212=+==+=+,而点在直线上,M x y x y x y (,)000000+=∴+= 即,……()1212012a a b b a ++==-()把()代入(),得,解得。
