fluent的一个实例(波浪管道的内部流动模拟).
fluent管道内气流两相冲刷模拟_图文(精)

与切应力(b分布
3.2烟气速度对冲刷磨损的影响
不同烟气速度时的磨损量见图4a。切应力见图4b。从图4a可以看出,随着烟气速度增加.管道的最大磨损量与平均磨损量都增加。最大磨损量随烟气流速增加反映了烟气流动紊乱程度的影响。湍动更加严重,增加了颗粒与壁面碰撞的几率:而平均磨损量的变化相对较小。这主要是由于烟气对管道的冲刷主要集中在入1:3处。对于整段管道而言,平均磨损量比最大磨损量小得多。从图4b可以看出。随着烟气速度的增加,固体颗粒对管道材料产生的最大切应力与平均切应力都增加。最大切应力的增加表明与腐蚀形成的耦合交互作用逐渐增大。当烟气速度介于5—25m/s时,最大切应力增加的速度恒定:当烟气速度介于25~30m/s时,最大切应力出现较显著变化。而在整个烟气速度范围内,平均切应力相对变化较小。
万方数据
万方数据
2011年第1期张义等:管道内气固两相流冲刷磨损特性数值模拟13
由于湍流对颗粒存在扩散作用,因此采用随机轨道模型。此时,式(1和式(2中的烟气速度按下式计算
U=U+U’(3式中i为流体的时均速度。Ut为流体的随机脉动速度。
采用随机游走模型确定U’.对Standard k-6模型有:
拈f俘(4式中k为湍流动能,f为服从正态分布的随机数。
k一
(upsincxo匹
×(叩一专u峰osma产(7
I J~
当口>Or0时
E:.rnp(u£cos2cx-C2(upsino为颗粒质量,C。、c2为与材料性质等有关的系数,比为冲刷磨损临界速度,痂为切削磨损模型的临界角度,岛、占D分别为材料表面产生单位切削和变形失重时吸收的能量。
运动颗粒和壁面碰撞过程中。存在能量损失和转化,因而反弹速度低于入射速度。不同性质材料的壁面碰转系数也不同。Forder等[101对AISI4130钢在固体颗粒冲击时的速度变化进行了研究,得到了恢复系数与颗粒冲击角的关系式:
fluent 案例教程-1圆管层流流动加有障碍通道内流动模拟

3.3 实验一:管内层流流动数值计算3.3.1 计算目的1、初步掌握软件的操作与边界条件设置方法;2、通过模拟计算了解圆管层流的入口段流动与充分发展段流动特点及边界层在入口处生长,然后,不断增加,直至两边相交于管中心线(管子足够长),管段进入充分发展段,在充分发展段形成抛物线分布等知识。
3.3.2 物理问题流体在水平圆管内流动,管径D =0.2 m 管长 L =8 m. 入流速度V in =1 m/ s 截面上速度认为一致,密度ρ=1 kg/ m 3, 粘性系数 µ= 2 x 10-3kg/(ms ). 雷诺数Re 100avg V D ρµ==,其中:V avg =1m/s 为入口平均速度, 应用Fluent 求解。
3.3.3 具体操作在GAMBIT 中创建如下物理模型。
首先,利用轴对称图形,我们创建四个节点。
然后连接各相邻节点,形成矩形。
再形成面。
运行GAMBIT ,选择求解器为Fluent5/6。
3.3.3.1 创建节点与面 (1)创建节点:((0,0.1进入界面:操作:> Vertex Command Button > Create Vertex进入界面:x=0;y=0;z=0,点击Apply. 便创建了vertex.1 (0,0,0)点。
重复操作,创建:V ertex 2: (0,0.1,0),Vertex 3: (8,0.1,0),Vertex 4: (8,0,0) 二维问题,Z轴省略默认为赋值为0。
操作:Global Control > Fit to Window Button可以查看整个图形,如下:(2)将节点连成线操作:> Edge Command Button > Create Edge选择矩形的两个点,点击Apply。
重复以上操作,可得4条线,得到一个矩形:(3)创建面操作:> Face Command Button > Form Face按下SHIFT键,鼠标点击每条边线,释放SHIFT键,则边线被选取,另外也可用以下方法进行操作:点击Edges右边的箭头:调入Edge List 窗口:点击ALL,选择所有边线,如下图。
FLUENT动网格-圆柱体在管道内运动模拟
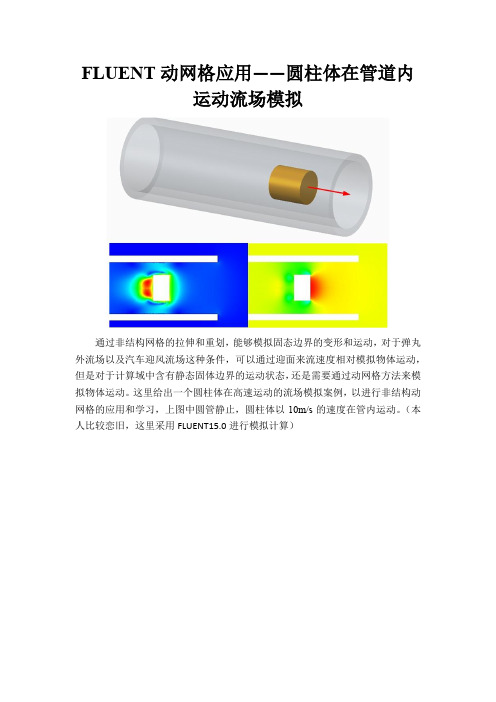
FLUENT动网格应用——圆柱体在管道内
运动流场模拟
通过非结构网格的拉伸和重划,能够模拟固态边界的变形和运动,对于弹丸外流场以及汽车迎风流场这种条件,可以通过迎面来流速度相对模拟物体运动,但是对于计算域中含有静态固体边界的运动状态,还是需要通过动网格方法来模拟物体运动。
这里给出一个圆柱体在高速运动的流场模拟案例,以进行非结构动网格的应用和学习,上图中圆管静止,圆柱体以10m/s的速度在管内运动。
(本人比较恋旧,这里采用FLUENT15.0进行模拟计算)。
fluent流体仿真实例

fluent流体仿真实例引言流体力学是研究物质的流动规律和力学性质的学科,而流体仿真则是在计算机环境下利用数值方法模拟流体力学过程的过程。
在流体力学研究和工程实践中,流体仿真已经成为一种非常重要的工具。
本文将探讨使用fluent软件进行流体仿真的实例,介绍其基本原理和应用。
什么是fluent?fluent是一种流体仿真计算软件,它被广泛应用于工业和学术研究领域。
fluent可以对不同类型的流体动力学问题进行建模和仿真,如空气动力学、燃烧和热传导等。
fluent是一款功能强大且易于使用的软件,能够提供准确可靠的流体力学仿真结果。
流体仿真的基本原理流体仿真建立在基本的流体力学原理之上,通过数值方法对流体的运动进行模拟和计算。
主要包括以下几个步骤:1. 建立几何模型在进行流体仿真之前,需要首先建立几何模型。
几何模型描述了流体领域的形状和结构,可以通过计算机辅助设计(CAD)软件进行建模。
常见的几何模型包括管道、汽车外形和飞机翼型等。
2. 网格划分网格划分是流体仿真中的关键步骤,它将流体区域分割为有限数量的小单元,称为网格。
不同的网格划分方式会对仿真结果产生影响,因此需要根据具体问题选择合适的网格划分方法。
3. 设置边界条件边界条件是仿真过程中的约束条件,描述了流场在模型边界上的行为。
根据具体问题,可以设置流体速度、压力和温度等边界条件。
4. 数值求解数值求解是流体仿真的核心步骤,通过数值方法对流体的运动进行模拟和计算。
常用的数值方法包括有限体积法和有限元法等。
5. 结果分析仿真计算完成后,需要对结果进行分析和后处理。
常见的后处理操作包括生成流线图、压力分布图和速度矢量图等。
一个fluent流体仿真实例为了更好地理解fluent的应用,我们以空气动力学为例进行一个流体仿真实例。
1. 几何模型建立假设我们要研究一辆汽车在高速行驶时的空气动力学性能。
首先需要在CAD软件中建立汽车外形的几何模型,包括汽车的车身、车轮和尾翼等。
FLUENT算例——TurbulentPipeFlow(LES)圆管湍流流动(大涡模拟)

FLUENT 算例——TurbulentPipeFlow (LES )圆管湍流流动(⼤涡模拟)Turbulent Pipe Flow (LES) 圆管湍流流动(⼤涡模拟)以ANSYS 17.0为例问题描述考虑通过圆形截⾯直管道的流动问题,圆管直径,长度。
管道进⼝处的平均流速为,假设流体密度为定值,,流体动⼒粘性系数。
那么基于圆管直径、平均流速、流体密度、动⼒粘性系数算得该问题的Reynold数(Re)为接下来咱们⽤ANSYS FLUENT中的LES⽅法来求解该流动问题,绘制在距离进⼝处下游截⾯上随着半径变化的平均速度和均⽅根速度,并⽐较由LES⽅法和⽅法模拟得到的平均速度。
1 预分析和准备⼯作预分析在⼤涡模拟中,瞬时速度被分解为滤波后的分量以及剩余的残差分量,滤波后的速度分量表征了⼤尺度的⾮定常运动。
在LES中,⼤尺度的湍流运动被直接表征,⽽⼩尺度的湍流运动则⽤模型近似。
关于滤波速度的滤波⽅程可以从Navier-Stokes⽅程推出,由于残差操作,动量⽅程中的⾮线性对流项引⼊了⼀个应⼒张量的残差项,该残差应⼒张量需要通过构造模型来完成⽅程组的封闭,⽽FLUENT中提供了从易到难的多种模型。
既然咱们要求解,那么LES就是个⾮定常的模拟过程,需要在时域内向前推进。
为了收集统计平均量,⽐如平均和均⽅根(root mean square(r.m.s.))速度,咱们需要⾸先达到统计上的稳定状态(然后再开展统计平均的处理)。
作为对⽐,模型求得的平均速度也⼀并给出。
关于LES的详细理论和⽅程可以再很多湍流的书籍中找到。
准备⼯作LES是三维⾮定常计算(只能适⽤于三维问题和⾮定常问题),那么计算域是全部的管道。
在打开ANSYS之前,先创建⼀个⽂件夹turbulent_pipe_LES,然后⾥⾯在创建⼀个ICEM⽂件夹和FLUENT⽂件夹,分别⽤来存放ICEM的建模和画⽹格⽂件,以及FLUENT的计算⽂件。
2 构建⼏何模型打开ICEM CFD 17.0软件,在其中完成建模⼯作,咱们计算域是圆管内部流道,也就是⼀个圆柱体,让圆柱体的轴线沿着⽅向,进⼝截⾯位于上,圆⼼位于坐标原点。
fluent流体仿真实例

fluent流体仿真实例Fluent是一种流体仿真软件,它广泛用于研究和优化各种流体系统。
本文将介绍Fluent的基本工作原理,并以一个实例为例说明如何使用Fluent进行流体仿真。
首先,Fluent采用有限体积法来解决流体问题。
这种方法将流体域划分为许多小的控制体积,并在每个体积中计算流体的平均速度、压力和温度。
然后,通过在体积之间应用质量和动量守恒方程以及其他物理方程来求解流体行为。
最后,Fluent通过计算流场中的速度、压力和温度分布来描绘流体的行为。
为了演示Fluent的用途,我们将以水的流动为例说明如何使用它进行流体仿真。
我们考虑一个具有弯曲管道的水流系统。
假设管道入口处是一个稳定的水流,出口处是一个自由表面,即水流向大气中自由流动。
我们想研究如何通过改变管道形状和入口速度来优化整个系统。
首先,我们需要使用CAD软件绘制出整个系统的几何形状,并将其导入到Fluent中。
然后,我们需要定义出入口处的水流速度和出口处自由表面的边界条件。
这些边界条件将告诉Fluent在哪里应该施加水流速度和处理自由表面的行为。
接下来,我们需要在Fluent中定义数值方法和物理模型。
对于数值方法,我们可以选择不同的离散化方法和求解器,以达到速度和精度的平衡。
对于物理模型,我们需要考虑水的流动特性,包括湍流、速度分布、压力分布等。
这将有助于我们更准确地预测水流的行为,并优化我们的设计。
最后,我们可以开始运行Fluent并分析结果。
Fluent将生成一个包括速度、压力和温度分布的二维或三维图像。
我们可以通过这些图像来研究水流的行为,并探索如何通过改变管道形状和入口速度来优化整个系统。
例如,我们可以通过改变管道半径和斜率来优化水流速度和压力分布。
总之,Fluent是一种广泛使用的流体仿真软件,它可以帮助我们更好地理解和优化各种流体系统。
通过使用Fluent,我们可以确定管道的最佳形状和入口速度,以确保流体系统的最佳性能。
FLUENT模拟泵内部流动的设置教程

FLUENT模拟泵内部流动的设置教程本教程以泵内定常流动数值模拟为例,详细讲述了如何应用FLUENT进行泵内流计算以及如何应用FLUENT进行简单的后处理。
基本步骤:1、启动FLUENT,选择3d求解器。
2、读入网格(×.msh);3、检查网格,确保最小体积为正,选择grid→check菜单;4、缩放网格;5、光顺/交换网格;6、求解器设置;7、设置计算模型;8、设置运行环境,对于离心泵数值模拟一般不考虑重力;9、设置转速单位;10、定义材料,也可以进行自定义材料;11、定义边界条件;12、设置交界面;13、设置求解参数;14、监视残差;15、初始化流场;16、保存case文件;17、开始迭代计算;18、FLUENT后处理。
1、启动FLUENT,选择3d求解器。
启动后FLUENT界面如下图所示:2、读入网格(×.msh),选择file→read→case菜单;3、检查网格,确保最小体积为正,选择grid→check菜单。
Check无误后才可以进行下面的操作。
4、缩放网格,选择grid→scale菜单,弹出下图的对话框,直接输入Scale Factors点击Scale即可,一般缩小1000倍到毫米。
由于FLUENT默认的单位是米,所以必须进行网格缩放。
5、光顺/交换网格,选择grid→smooth/swap菜单,进入下面的界面;先点击Smooth,然后点击Swap直至Number Swapped为0。
6、求解器设置,选择define→models→solver菜单,进入求解器设置界面,如下图所示。
一般定常求解设置为分离求解器、隐式算法、三维空间、稳态流动、绝对速度、压力梯度为单元压力梯度计算;7、设置计算模型,选择define→models→viscous菜单,弹出湍流模型选择对话框。
一般选用标准k-ε模型,进入k-ε模型设置界面,一般保持默认即可;8、设置运行环境,选择define→operating condition菜单,弹出下面的对话框。
管道的流体仿真教程

两相流管道仿真教程利用FLUENT对两相流管道内流场进行数值仿真,有如下步骤:1,利用Gambit软件,打开软件界面如下图:2,建立模型的几何文件:直接建体模型,如下图所示,管道圆柱形,长为5000mm,半径为500mm3,划分边界层网格:设置边界层首层厚度为2mm,其增长比率为1.2,层数为4,选择边界层施加面为face2,即为管道圆柱面4,划分体网格:对管道实体进行网格划分,可以直接对其进行体网格划分,选择管道实体volume.1,其他设置如下图所示,网格的Interval Size可以设置为10,点击Apply划分出的管道体网格以及边界层网格如上图所示5,设置入口边界条件,设置进口名称为Inlet ,类型为速度进口,面为Face.1,具体设置如下图所示:如下图所示:为face.2,如下所示:8,输出网格文件:如下图所示9,打开FLUENT软件,进行计算设置:首先设定单位为mm,如下图所示:10,设置操作环境,操作压强为101325帕,设置重力加速度为Y向为-9.8111,设置两相流模型:选取混合相模型,这里将固体颗粒相当做欧拉相进行研究,相数位2,如下图所示:12,选择湍流模型,根据管道模拟的实际情况,选取S-A湍流模型13,设置仿真材料,定义液相材料为水,参数为默认14,设置固体颗粒相计算材料,具体设置参数如下图所示:得到的材料栏的设置情况为15,对相进行设置,主相位水,选择材料为液态水,如下图所示:第二相为固体颗粒相,设置如下:16,设置两相之间的相互作用,采用默认设置,如下图所示:17,设置进口边界条件,如下图所示,类型为速度入口,此处也可以更改为其他的边界类型。
注意此处的相定义的是混合相设置速度入口边界如下,更改水力直径为1000mm,即为入口的直径值。
18,设置主相的进口边界如下,相改为水设置进口处主相水的速度矢量为0.5m/s,19,设置第二相的进口边界如下,相改为颗粒对颗粒相的速度进口进行设置,速度值设置与液相一致,也为0.5m/s,另外要设置进口处的颗粒相的体积分数,体积分数为0.6,体积分数设置如下图所示:20,出口边界条件设置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于FLUENT 的波浪管道热传递耦合模拟
CFD 可以对热传递耦合的流体流动进行模拟。
CFD 模拟可以观察到管道内部的流动行为和热传递,这样可以改进波浪壁面复杂通道几何形状中的热传递。
目的:
(1) 创建由足够数量的完整波浪组成的波浪管道,提供充分发展条件; (2) 应用周期性边界条件创建波浪通道的一部分; (3) 研究不同湍流模型以及壁面函数对求解的影响; (4) 采用固定表面温度以及固定表面热流量条件,确定雷诺数与热特性之间的
关系。
问题的描述:
通道由重复部分构成,每一部分由顶部的直面和底部的正弦曲面构成,如图。
图1 管道模型
空气的流动特性如下: 质量流量: m=0.816kg/s; 密度: ρ=1kg/m 3;
动力粘度:μ=0.0001kg/(m ·s); 流动温度: Tb=300K ;
流体其他热特性选择默认项。
流动初试条件:
x 方向的速度=0.816m/s ; 湍动能=1m 2/s 2;
湍流耗散率=1×105m 2/s 3。
所有湍流模型中均采用增强壁面处理。
操作过程:
一、 完整波浪管道模型的数值模拟
(1) 计算
Re=uH/v=0.816×1/ (0.0001/1) =8160 Cf/2=0.0359Re -0.2=0.0359× (8160)-0.2=0.0059259
0628.00059259.0816.02
=⨯==f t C u u
y +=u t y/v y=0.00159
(2)创建网格
本例为波浪形管道,管道壁面为我们所感兴趣的地方所以要局部细化。
入口和出口处的边界网格设置如图。
图2 边网格
生成面网格
图3 管道网格
(3)运用Fluent进行计算
本例涉及热传递耦合,所以在fluent中启动能量方程,如图。
图4 能量方程
设定条件,湍流模型选择标准k-e模型,近壁面处理选择增强壁面处理。
图5 湍流模型
设定材料,密度为1,动力粘度改为0.0001如图。
图6 材料设定
设定边界条件,入口速度为0.816,湍动能为1,湍流耗散率为100000。
出口为自由出口,壁面温度为固定温度分别为300k,500k。
图7 边界条件
初始化,并计算。
图8 残差
残差中的e和k并没有减小,没有达到10-3一下,并且由于网格很大,计算时间很长。
图9 压力分布图
随着流体流动,管道中压力分布趋于平稳,波浪管道中波谷的压力最低,在入口处的压力较高。
图10 速度分布图
从图中可以看出,在管道7-11个波浪处,流动已经充分发展,贴近上壁处速度最大,在波谷出的速度最小,甚至接近于零。
图11 温度分布图
贴近波浪壁面出的温度较高,流动充分发展后,由于换热作用,管道后部流体温度逐渐升高,在波峰与波谷之间的流体温度最高,如图。
图12 速度矢量图
可以看出,波浪壁面出流体出现反流,在波谷出反流的流体最多,速度在波谷出最小,接近于0,出现滞留区。
若要观察波峰、波谷处流体流动速度,需要在波峰、波谷处创建两条直线,观察直线上的速度。
因为管道7-11节处流动充分发展,所以在第十一节波峰、波谷处建立两条直线,如图。
图13 波峰、波谷
图14 波峰、波谷的速度
波峰贴近两侧壁面出的速度梯度很大,在管道中间速度随高度增加而增加,在0.7m左右达到最大。
波谷处靠近上壁面的速度梯度很大,但是由于有波谷存在,波谷处的速度梯度不大,在谷中速度先增大再减小,在0处左右达到最下,随后逐渐增加,在0.7m高度左右速度最大。
高度在0.5m处以上波峰波谷处的速度基本相等。
二、周期性波浪管道模型的数值模拟
图15 周期性网格
网格密度与完全管道网格相同。
在fluent中输入以下指令,创建周期性网格。
/grid> modify-zones
/grid/modify-zones> make-periodic
Periodic zone [()] inlet
Shadow zone [()] outlet
Rotational periodic? (if no, translational) [yes] no
Create periodic zones? [yes] yes
Auto detect translation vector? [yes] yes
computed translation deltas: 1.000000 0.000000
all 100 faces matched for zones 6 and 5.
zone 5 deleted
created periodic zones.
/grid/modify-zones>
边界条件中可以看到已经没有outlet,inlet也变成了periodic周期性的。
这里要设置周期性边界条件。
质量流量为0.816,其他设置与之前相同。
图16 边界条件
图17 残差
Energy并不收敛,反而随计算而发散。
其他参数都收敛。
计算量很小,计算速度明显提高。
图18 压力图
图18 压力图速度图温度图速度矢量图
管道中间压力最大并比较均匀,在波浪波谷出压力最低。
温度分布不太正确。
图19 波峰波谷速度图
波峰贴近两侧壁面出的速度梯度很大,与完全模型相似,波峰在管道中间速度随高度增加先增加在减小,但是变化不大,其他分布趋势与完全模型相似。
图20 周期模型与完全模型波峰速度图比较
周期性模型,管道中速度基本相等,没有呈现完全模型的变化趋势。
图21 周期模型与完全模型波谷速度图比较
两模型的波谷速度的变化趋势大致相同,在小于0.3m处,周期性模型速度大于完全模型,0.3m之后,周期性模型速度小于完全管道模型。
三、周期性波浪管道不同湍流模型的数值模拟
应用周期模型,再选分别应用RNG与Realizable湍流模型计算。
实验数据如图。
图21 RNG模型波峰波谷速度图
图22 Realizable模型波峰波谷速度图将之前的数据放在一起进行比较。
图23 不同湍流模型波峰速度图
图24 不同湍流模型波谷速度图
从图中可以看出realizable和标准k-e模型波峰的速度分布大致相同,RNG 模型与完全模型更接近,变化更大。
三种湍流模型波谷的速度分布与波峰分布特点相似。
四、整体模型壁面采用固定热流率的数值模拟
重新选用整体模型,只需改变波浪面即wall2的边界条件即可,改为热流率1000w/m2,其他条件不变。
图25 不同湍流模型波谷速度图
图26 固定壁面温度与固定热流率波峰速度图比较
图27 固定壁面温度与固定热流率波谷速度图比较
从图中可以看出固定壁面温度与固定热流率波峰与波谷的速度分布还是比较相似的,不同的是在0.6m处固定热流率波峰波谷速度比固定壁面温度的速度稍高,在0.6m之后固定热流率波峰波谷速度比固定壁面温度的速度稍低,在接近两壁面处基本相等。
图28 压力云图温度云图
从图中可以看出,固定壁面温度与固定热流率模型的压力分布基本相同,但是,固定热流率模型管道内流动充分发展后,靠近波浪壁面的温度比固定壁面温度模型温度要高,说明前者换热量比后者大。
