医学高等数学(第四版)(马建忠主编)思维导图
《实用外科学 第4版 全2册 》读书笔记思维导图PPT模板下载

实用外科学(第4版)上册
01
扉页
02
主编人合 影
03
《实用外 科学》 (第4版) 网络增值 服务
04
编者名单 (各专科 编者名单 按姓氏拼 音排序)
05
序
06
前言
第一篇 总 论 第二篇 普通外科
第三篇 血管外科 第四篇 神经外科
01
第一章 外科发展 的现代理 念及外科 医师的 成...
02
第二章 抗菌术和 灭菌术
04
第三十四 章 脾脏 疾病
06
第三十六 章 上消 化道出血
05
第三十五 章 急腹 症
01
第三十九 章 血管 外科的基 本问题
02
第四十章 血液透析 通路
03
第四十一 章 血管 损伤
04
第四十二 章 急性 肢体缺血
06
第四十四 章 下肢 动脉疾病
05
第四十三 章 颅外 脑血管疾 病
第四十五章 动脉 瘤
04
第五十五 章 颅脑 损伤和脊 髓损伤
05
第五十六 章 颅内 和椎管内 感染
06
第五十七 章 颅内 肿瘤
第五十八章 脊髓 肿瘤
第五十九章 颅内 血管性疾病
第六十章 脑神经 疾病
第六十一章 脑立 体定向手术
第六十三章 神 经介入放射治疗 的发展和应用
第六十二章 癫 痫的外科治疗
第六十四章 神 经外科新技术和
第二肠 疾病
02
第二十六 章 结肠、 直肠、肛 门疾病
03
第二十七 章 阑尾 疾病
04
第二十八 章 胃肠 胰神经内 分泌肿瘤
05
第二十九 章 胃肠 间质瘤
06
2023高等数学考试大纲思维导图,脑图
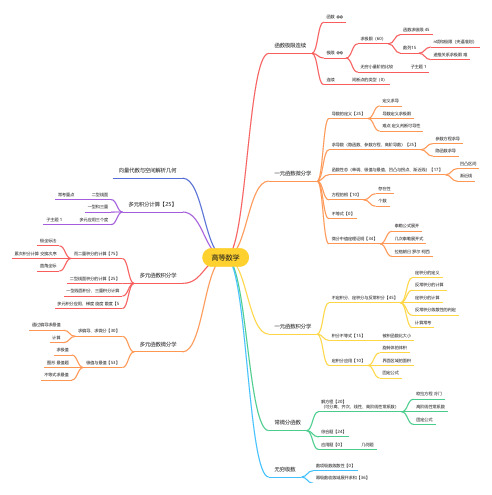
高等数学函数极限连续函数极限求极限(60)函数求极限 45数列15n项和极限(夹逼准则)递推关系求极限 难无穷小量阶的比较子主题 1连续间断点的类型(0)一元函数微分学导数的定义【25】定义求导导数定义求极限难点 定义判断可导性求导数(隐函数、参数方程、高阶导数)【25】参数方程求导隐函数求导函数性态(单调、极值与最值、凹凸与拐点、渐近线)【17】凹凸区间渐近线方程的根【10】存在性个数不等式【0】微分中值定理证明【34】泰勒公式展开几次泰勒展开式拉格朗日 罗尔 柯西一元函数积分学不定积分、定积分与反常积分【45】定积分的定义反常积分的计算定积分的计算反常积分敛散性的判定计算常考积分不等式【15】被积函数比大小定积分应用【10】旋转体的体积界面区域的面积固定公式常微分函数解方程【20】(可分离、齐次、线性、高阶线性常系数)欧拉方程 冷门高阶线性常系数固定公式综合题【24】应用题【0】几何题无穷级数数项级数敛散性【0】幂级数收敛域展开求和【36】向量代数与空间解析几何多元积分计算【25】二型线面常考重点一型和三重多元应用三个度子主题 1多元函数积分学而二重积分的计算【75】极坐标法累次积分计算 交换次序直角坐标二型线面积分的计算【25】一型线面积分、三重积分计算多元积分应用、梯度 旋度 散度【5多元函数微分学求偏导、求微分【30】通过偏导求最值计算极值与最值【53】求极值图形 最值题不等式求最值。
《高等数学(上册)》读书笔记思维导图PPT模板

0 1
第一节 导数的概 念及基本 求导公式
0 2
第二节 导数的计 算法则
0 3
第三节 微分的概 念与应用
0 4
第四节 微分中值 定理及其 应用
0 5
*第五节 泰勒中值 定理
0 6
第六节 函数的性 态与图形
第七节 微分学的 实际应用
本章小结
章节测试二 拓展阅读
第三章 一元函数积分学及其 应用
0 1
《高等数学(上册)》
PPT书籍导读
读书笔记模板
最
新
版
本
目录
01 第一章 函数、极限与 连续
03
第三章 一元函数积分 学及其应用
02
第二章 一元函数微分 学及其应用
04 第四章 微分方程来自本书是按照教育部大学数学教学指导委员会的基本要求,充分吸取当前高等数学教材的精华,并 结合数年 来的教学实践经验,针对当前学生的知识结构和习惯特点而编写的。全书分为上、下两册。本书 为上册,是一元 函数微积分部分,共四章,主要内容包括函数极限与连续,一元函数微分学及其应用,一 元函数积分学及其应用, 微分方程。每节前面配有课前导读,核心知识点配备微课,每章后面附有章节测 试和拓展阅读。 本书注重知识 点的引入方法,使之符合认知规律,更易于读者接受。同时,本书精炼了主要内容,适当 降低了学习难度,对部 分内容调整了顺序,使结构更加简洁,思路更加清晰。本书还注重知识的连贯性,例 题的多样性和习题的丰富性、 层次性,使读者在学习数学知识点的同时拓宽了视野,欣赏数学之美。 本书可作为高等院校理工科类各专业的教 材,也可作为社会从业人员的自学参考用书。
谢谢观看
读书笔记
最 新
版
本
第一章 函数、极限与连续
高等数学考研复习思维导图 脑图

高等数学函数特性:有界性、单调性、奇偶性、周期性反函数、复合函数、分段函数初等函数极限无穷小两个重要极限间断点连续零点定理、介值定理洛必达法则、泰勒公式导数和微分求导反函数求导复合函数求导高阶导数隐函数求导参数方程求导拐点、凹凸性最大值、最小值微分微分中值定理罗尔定理朗格拉日中值定理*柯西中值定理曲率、弧微分不定积分换元法分部积分法定积分反常积分微分方程可分离变量的微分方程齐次方程一阶线性微分方程齐次非齐次伯努利方程可降阶的高阶微分方程高/二阶线性微分方程解的结构常系数齐次线性微分方程常系数非齐次线性微分方程欧拉方程空间解析几何向量数量积向量积混合积曲面一次曲面二次曲面柱面圆柱面椭圆住吗抛物柱面椭圆锥面椭球面单叶双曲面双叶双曲面椭圆抛物面双曲抛物面(马鞍面)空间曲线空间曲线的一般方程空间曲线的参数方程空间曲线在坐标面上的投影平面及方程平面一般方程两平面夹角平面束方程空间直线及方程空间直线的一般方程空间直线的对称式方程空间直线的参数方程两直线夹角直线与平面的夹角多元函数微分法多元函数点集极限连续性偏导数全微分多元函数复合求导隐函数求导一个方程的情况方程组的情况几何应用一元向量值函数及导数空间曲线的切线和法平面曲面的切平面和法线(偏导数有关)方向导数和梯度(偏导数有关)多元函数的极值(偏导数有关)条件极值重积分二重积分性质极坐标计算二重积分三重积分柱面坐标计算三重积分球面坐标计算三重积分曲线积分对弧长的曲线积分(线密度)对坐标的曲线积分(力做功)两类曲线积分之间的关系格林公式路径无关原函数的一个全微分曲面积分对面积的曲面积分对坐标的曲面积分两类曲面积分之间的联系高斯公式无穷级数基本知识常数项级数、收敛、发散收敛级数的基本性质正项级数定义审敛比较审敛法比较审敛法的极限形式比值审敛法*根值审敛法(柯西审敛法)极限审敛法交错级数绝对收敛、条件收敛幂级数阿贝尔定理性质和运算收敛半径函数展开成幂级数傅立叶级数。
《生理学(第4版)(全国高等学历继续教育“十三五”(临床专科)》读书笔记PPT模板思维导图下载

《生理学(第4版)(全 国高等学历继续教育“十
三五”(临床专科)》
思维导图PPT模板
目录ห้องสมุดไป่ตู้
01 纸质版编者名单
全国高等学历继续教
02 育规划教材临床医学 专业...
全国高等学历继续教
03 育规划教材临床医学 专业...
第四届全国高等学历
04 继续教育规划教材评 审委...
02
第二节 下丘脑与 垂体的内 分泌
03
第三节 甲状腺的 内分泌
04
第四节 肾上腺的 内分泌
05
第五节 胰岛的内 分泌
06
第六节 调节钙、 磷代谢的 激素
学习小结
第七节 其他内 分泌腺的内分泌
复习参考题
第十二章 生 殖
第一节 男性 1
生殖
2
第二节 女性 生殖
3
第三节 妊娠 与分娩
4
学习小结
5
复习参考题
第四节 人体生理 功能的调 节
05
学习小结
06
复习参考 题
第二章 细胞的基本功能
01
第一节 细胞膜的 物质转运 功能
02
第二节 细胞的生 物电现象 及其产生 机制
03
第三节 细胞的跨 膜信号传 递功能
04
第四节 肌细胞的 收缩功能
06
复习参考 题
05
学习小结
第三章 血 液
第一节 血液的组 成及其理化特性
第二节 血浆及其 功能
第三节 血细胞及 其功能
第四节 血液凝固 与纤维蛋白溶解
学习小结
第五节 血量、 血型与输血原则
复习参考题
第四章 血 液 循 环
大学高数常微分方程思维导图_高等数学各章节知识点框架常微分方程.pdf

⼤学⾼数常微分⽅程思维导图_⾼等数学各章节知识点框架常微分⽅程.pdf【微信公众号:给⼒考研资料】免费分享常微分⽅程1.概念,2.⼀阶微分⽅程求解3.⾼阶微分⽅程求解4.应⽤题1.概念(7个概念,了解即可)微分⽅程—含有未知函数的导数或者微分的⽅程常微分⽅程—未知函数为⼀元函数的微分⽅程偏微分⽅程—未知函数为多元函数的微分⽅程微分⽅程的阶—未知函数的导数的最⾼阶数为⽅程的阶数微分⽅程的解—将函数代⼊⽅程,为恒等式,则该函数为解微分⽅程的通解与特解—通解—解中独⽴常数的个数等于⽅程的阶数,特解—解中没有任何常数初始条件(定解条件)—确定通解中的常数的条件2.⼀阶微分⽅程求解⼀阶⽅程(4个)1.可分离变量型(两边直接积分)2.可化成可分离变量型形如y'=f(ax+by+c)型 (令u=ax+by+c,相应对x求导,则化成可分离变量)⻬次型—形如y'=f(y/x) (令p=y/x,相应求导,则可化为分离变量型)Note :1.对于式⼦中出现lnu中u不知正负,则要带上绝对值,除过⼀阶线性2.对于⼀阶线性⽅程,不⽤带绝对值(18版18讲P217有分析)3.所求的通解可以不是全部解(线性:通解=全部解,⾮线性:通解不等于全部解)4.在求通解中,⼀定要带上对独⽴常数C的限定5.若出现不属于⼀阶⽅程四种类型,则考虑调换x ,y的地位6.能写成显⽰解就写要写成显⽰解3.⼀阶线性⽅程(要掌握推导解的公式,利⽤求导公式逆⽤法)—形如y'+p(x)y=q(x)4.伯努利⽅程(这⾥可以将其化成⼀阶线性,利⽤恒等变形中三种⽅法中换元)形如y'+p(x)y=q(x)yn(令y1-n=u ,相应求导,化成⼀阶线性)5.全微分⽅程利⽤积分与路径⽆关的性质,⽤折线法来求原函数=C⼆阶可降阶⽅程1.形如y''=f(x,y') 缺y型——将y斩草除根(令y'=u,y''=u',化成了⼀阶)2.形如y''=f(y,y')缺x型——将x斩尽杀绝(令y'=u,y'=udu/dy,化成⼀阶)要注意两种类型不同的处理⽅法Note :还有⼀种可降阶的n阶⽅程,连续求导即可3.⾼阶微分微分⽅程的求解(2~4阶)⼆阶线性微分⽅程的概念(详⻅18讲P218)1.⻬次与⾮⻬次2.变系数与常系数注意若真的出现了变系数⼆阶,要想到换元,化成⼆阶(或者是欧拉⽅程)解的结构与解的性质(各2个)(详⻅⾼数18讲P218)1.⼆阶常系数⻬次线性微分⽅程的通解结构(两个线性⽆关的解(通俗理解就是相除不为常数)可以构成起通解)2.⾮⻬次的解的结构——⻬次的特解+⾮⻬次的特解3.两个⾮⻬次的特解相加为⼀个全新⾮⻬次的特解(叠加原理)【微信公众号:给⼒考研资料】免费分享4.两个⾮⻬次的特解相减为其⻬次的⼀个解⼆阶常系数⻬次线性微分⽅程求解(背公式)⾮⻬次的特解(背公式)n阶常系数线性⻬次微分⽅程求解(背公式)注意特征⽅程的特征根各种情况(四种情况)4.欧拉⽅程(仅数⼀)(18讲259)形如x2y''+pxy'+qy=f(x)换元:当x⼤于0当x⼩于04.应⽤题:1.背景公平——信息给予2.翻译成数学表达式Note :注意⽐例系数应是正号,或负号,应根据题意主动添上。
