《超级画板》第五篇函数图像解析
怎样使用超级画板画函数图像

怎样使用超级画板画函数图像作者:李模云成华来源:《中国信息技术教育》2010年第12期当前中学函数图像教学现状函数及其图像,一直是中学数学课程的重要内容,也是学生较难理解的内容。
对于学生来说,函数的图像,函数的解析式,函数的性质之间怎样相互联系,一直是难以理解的问题;而对于教师来说,由于教学手段的限制,只能静态地画出特定参数下的函数图像,不仅不能准确反映出解析式、图像和表格三者之间的固有联系,而且占用了大量的课堂时间。
使用超级画板辅助中学函数图像教学的优点相比其他辅助教学工具,使用超级画板辅助函数图像教学有如下优点。
(1)功能强大超级画板和几何画板都具有动态几何作图的功能,但超级画板兼顾了几何与代数的教学,及编程开发的需求,提供了方便易用的编程环境,可以定义函数,对算法、函数以及概率统计的教与学提供更好的支持。
(2)操作简单超级画板独创的智能画笔,使几何作图操作类似于用粉笔画图,几乎不学就会,而几何画板图形处理比较复杂。
另外超级画板的操作直来直去,不像几何画板有很多技巧,容易入门,有利于师生双边互动和交流。
(3)编辑方便超级画板允许用户利用复制粘贴的数学表达式进行计算和作图,使曲线作图和表达式测量更为方便,几何画板则不允许。
超级画板还提供了用于标题的方便美观无级缩放的可变换文本,文本中插入公式更方便。
(4)演示功能完善超级画板提供了较完善的演示功能,能方便地全屏(按ESC)放大缩小图形、文本,修改文本、图形方便。
继承了集成软件的演示功能的优势,以及专业数学教学软件方便的作图功能,可以说是两者良好的结合,很适合中学数学教学。
使用超级画板作函数图像的主要过程用超级画板作函数图像时,只需要在程序区/文本作图区输入函数表达式及定义区间,就可以得到函数图像。
然后,打开图像的对象属性框,通过勾选/不勾选描点,显示组成函数图像的点;通过勾选/不勾选折线段可以控制图像的圆滑程度。
描点数也可以通过改变参数大小,任意调整。
函数图像绘制技巧与分析

函数图像绘制技巧与分析函数图像是数学中常见的一种形式,它能够直观地展现函数的性质和特点。
在学习和研究函数时,绘制函数图像是一种非常重要的方法。
本文将介绍一些函数图像绘制的技巧,并对函数图像进行一些分析。
一、函数图像绘制的基本步骤绘制函数图像的基本步骤包括确定函数的定义域、确定坐标轴范围、选择合适的点进行绘制、绘制曲线、标注关键点和分析曲线的性质。
首先,确定函数的定义域是绘制函数图像的基础。
函数的定义域是指函数能够取值的范围。
例如,对于函数y = 1/x,其定义域为x ≠ 0。
在确定定义域后,我们可以确定坐标轴的范围,使得函数图像能够在坐标系中完整地展示。
其次,选择合适的点进行绘制。
为了准确地绘制函数图像,我们需要选择一些关键的点来代表函数的特点。
一般来说,选择函数的零点、极值点、拐点等作为绘制的点是比较常见的方法。
通过计算函数在这些点的取值,我们可以得到这些点的坐标,从而绘制出函数图像。
然后,绘制曲线。
通过连接选择的点,我们可以绘制出函数的曲线。
在绘制曲线时,可以使用直线段和曲线段相结合的方式,使得曲线更加平滑和自然。
接下来,标注关键点。
在绘制完曲线后,我们可以通过标注关键点的方式来更好地展示函数的性质。
例如,在函数图像上标注函数的零点、极值点等,有助于读者更加直观地理解函数的特点。
最后,分析曲线的性质。
通过观察函数图像,我们可以分析函数的增减性、奇偶性、周期性等特点。
例如,如果函数图像在某个区间上是递增的,那么我们可以得出函数在该区间上是增函数的结论。
通过对函数图像的分析,我们可以更深入地理解函数的性质。
二、函数图像绘制的技巧在绘制函数图像时,有一些技巧可以帮助我们更加准确和高效地完成任务。
首先,利用对称性。
许多函数具有对称性,例如偶函数和奇函数。
对于偶函数,其函数图像关于y轴对称;对于奇函数,其函数图像关于原点对称。
通过利用对称性,我们可以只绘制函数图像的一部分,然后通过对称性得到整个函数图像。
2024.9.12函数的图象
补充练习:
4.已知函数 y f (2x 1) 是偶函数,则函数 y f (2x) 的图象一定关于 直线_x _1__对称.
5.偶函数 f2( x) 满足 f ( x 1) f ( x 1) ,且当 x 0,1 时, f ( x) x ,
∴ f ( x) 是周期函数,且周期为 4. 画出 y f ( x) 的图象易知与直线 y 1 有四个交点,且四个交点横坐标之和
2
为 2+10=12.
补充练习:
12.已知定义在区间 (0, 2) 上的函数 y f ( x) 的图象如图所示,则 y f (2 x)
的图象为( B )
13.(多选)某学习小组在研究函数 f ( x) 1 的性质时,得出如下结论,其中正确的是( )
x 2
BCD
(A)函数 f ( x) 的图象关于点 (2,0) 中心对称 (B)函数 f ( x) 在 (2,0) 上单调递增
(C)函数 f ( x) 在0, 2 的最大值为 1
(D)方程 f ( x) x 0 有 2 个不同实根
2
14.已知函数
f (x)
x 1 ( x ≤ 0) ,若函数
例
1.已知函数
f
(x)
log4 x
x2
10
x
(0 < 25
x ≤ 4) , a、b、c、d ( x > 4)
是互不相
同的正数,且 f (a)=f (b)=f (c)=f (d),则 abcd 的取值范围是(_2_4_, 2_5.)
例 2.定义在 R 上的函数 f(x)满足 f ( x 1) 1 f ( x), 且当 x 0,1 时,
用超级画板探究圆锥曲线切线性质

2
程 中Z F与 AP BP F不相等, 但是笔者意外发 现无论 P点在何处, 始终有 P FA = PF B,
故可得到上述类似 的命题: 命题 3 如 图4 设抛物线的焦点为 F, , 过抛 物线外任一点P作抛物线的两条切线, 切点分别
上运动, P作椭 圆 的两条切线 P 过 、PB, 且
与椭圆 分 别相切于 、B两点, 则 P 2= F
ZB PF1 .
为 一 =i—) :zx 双 曲线 分别相切于 、B两点,则 ZAPF2= : 嚣= ( , = 一i = 即 = ・ x p 詈
同理过点 B的切线方 程为 : 2 一 . x 联立
又 由斜率公式得: 直线 PF 的斜率 k F 1 p x=
,
直线 PF 的斜率 F : 2 2
.
由到角公式可得 tI a1 BP 1 - l F F = k  ̄ k- p
’2 一o
Y o
1一 Xo — C —
数学教 学
1 0 =) 0 ( _c一
《 数学教 学》2 1 年第 3 01 期刊登 “ 破解 网上
‘ 赏’ 有感” J 悬 题 【 一文.该文 称:网上 一道数学
s ( i B+P)i n s nP .s (— s ( i a P)i B+P n n )
snA snO i i L
s nA i i sn
。
’
既然上述结论在双 曲线 中成立, 又抛物线和 椭 圆、双 曲线的几何性质有很多相 同的地方, 那 么该结论在抛物 线中是否也成立呢? 同样借助 超级画板探究了一下, 结果发现在 P点的移动过
:
用超级画板画一次函数图像实验研究

用超级画板画一次函数图像实验研究进入21世纪以来,信息技术迅猛发展,信息技术全方位渗透到人们生活的各个层面,教育也不例外。
在这样一个大背景下,张景中院士团队开发的超级画板作为在信息时代计算机辅助中学数学教学的软件,深受广东省广州市景中实验中学(以下简称我校)数学教师和广大学生的重视和青睐。
它如同一块展现动态图形的黑板,打破了传统的教学方法的局限,为创新教学模式注入了无限的活力,已成为我校数学教育品牌。
很多一线教师都在运用超级画板进行数学教学和数学教学的研究。
作图方便准确、色彩鲜艳、富有动感,超级画板的这些优势让课堂高潮迭起、妙趣横生,从根本上改变了数学学科枯燥、乏味的特点,极大激发了学生学习数学的热情。
文章作者用超级画板画一次函数图像时融入了音乐、舞蹈,美妙的音乐、优美的舞姿伴着优美的曲线,数学如诗一般美丽。
标签:超级画板;一次函数图像;研究以前课堂上基本是这样进行的:复习旧知识→引入新课→学习新概念和定理→例题讲解→学生模仿性解题→教师点评、总结。
这种教学模式下如画一次函数y=-x+2图像的步骤是:1.列表2.描点(-1,-3)(0,2)(1,1)(2,0)3.连线教师在黑板上建立坐标系,描点连线。
一次函数图像为什么是直的?很显然,从始至终学生对画出的一次函数图像是一条直线持怀疑态度。
这种教学模式下学生的发展还是基本上以教师为中心,教师讲学生听,没有使课堂真正成为数学活动的教学。
新课标的数学大纲明确规定:教师应该帮助学生在自主探索和合作交流中真正理解和掌握基本的数学知识与技能、数学思想和方法,获得广泛的数学活动经验。
二、超级画板的应用点的运动问题是动态几何问题,它是以几何图形为背景讨论点的运动变化,探索其中隐含的规律。
利用超级画板能够帮助学生很好地理解并解决这类问题。
1.用超级画板画一次函数y=-x+2图像函数及图像对初一的孩子们而言难于理解,为了展示图像对函数关系的动态反应,把抽象变为具体,在学校数学实验室,每个孩子都能打开电脑里的超级画板,建立平面直角坐标系。
如何用几何画板画函数图像?
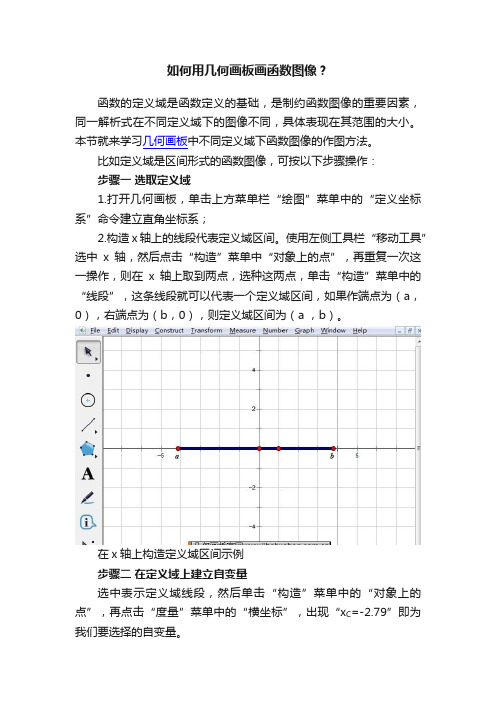
如何用几何画板画函数图像?函数的定义域是函数定义的基础,是制约函数图像的重要因素,同一解析式在不同定义域下的图像不同,具体表现在其范围的大小。
本节就来学习几何画板中不同定义域下函数图像的作图方法。
比如定义域是区间形式的函数图像,可按以下步骤操作:步骤一选取定义域1.打开几何画板,单击上方菜单栏“绘图”菜单中的“定义坐标系”命令建立直角坐标系;2.构造x轴上的线段代表定义域区间。
使用左侧工具栏“移动工具”选中x轴,然后点击“构造”菜单中“对象上的点”,再重复一次这一操作,则在x轴上取到两点,选种这两点,单击“构造”菜单中的“线段”,这条线段就可以代表一个定义域区间,如果作端点为(a,0),右端点为(b,0),则定义域区间为(a ,b)。
在x轴上构造定义域区间示例步骤二在定义域上建立自变量选中表示定义域线段,然后单击“构造”菜单中的“对象上的点”,再点击“度量”菜单中的“横坐标”,出现“x C=-2.79”即为我们要选择的自变量。
构造线段上的点作为自变量示例步骤三计算自变量的函数值单击“度量”菜单中的“计算”命令,在弹出的对话框利用“x C=-2.79”计算出如下图所示的函数值。
利用计算命令计算函数值示例步骤四构造函数图像上的点使用移动工具选中上面得到的自变量值和函数值,然后单击“绘图”菜单中的“绘制(x,y)”命令,就可以构造出函数图像上的点P。
构造函数图像上的点P示例步骤五绘制函数图像使用移动工具选中上面图像上的点P和定义域上C点,单击上方菜单栏“构造”菜单中“轨迹”命令,就可以画出如下图所示的函数图像。
构造轨迹绘制函数图像示例步骤六任意调整函数的定义域区间用移动工具选中“a”和“b”点任意拖动,可以看到函数图像随a、b的变化而变化的情形,比如如下图所示的效果。
调整函数的定义域观看图像变化示例看了以上教程,就掌握了用几何画板画指定定义域函数图像的方法,主要运用了几何画板构造轨迹功能,通过拖动线段上的“a”和“b”点,就可以改变定义域,观察函数图像的不同。
_超级画板_帮你教函数_1_

图 1
单 击【曲 线 】前 面 的
“+ ”,使之展开 ,点击第一
个 Function 函 数 , 依 次 输
入 y = x + 1 , - 3 ,0 ,5. 其
中 ,第 1 项是函数表达式 ,
后面的 - 3 和 0 是 x 的范
图 2
围 ,最后的 5 是描点作图时取点的个数 ,同理
我们可输入“Function ( y = cos( x ) ,0 ,pi ,20) ;
析数据的变化 ,需要进一步将表转化为图.
例 4 下表是某校高一 (1) 三名同学在 高一学年度六次数学测试的成绩及班级平均 分表.
图 7
打开【对象】|【文本作图】,弹出【文本命 令作图对话框】,输入“Stat (5 ,7 ,70 ,50) ;”后 点击运行则会生成一个 5 行 7 列的统计表 格 ,然后我们按图 7 所示输入内容. 就这样 , 我们得到了一个与图 7 一模一样的统计表 格. 作好表格之后 ,单击右键 ,然后将表格属 性改为【折线图】即可 (图 7) . 根据需要 ,我们 还可以将表格类型设置成【条形图】和【饼型 图】.
解析法略.
图象法 :我们根据需要 ,首先对坐标系进
行设置. 打开【对象工作区】,单击[ 4 ]对象组 :
12
数 学 通 讯 2007 年第 3 期
坐标系 ,使之展开 ,右键单击[ 0 ]直角坐标系 ,
弹出对话框 ,选中【显示刻度】,将其下方的刻
度比改为 1 :5 去掉【等单位】前面的勾选 ;再
设置 ,这就需要大家自己
图 4
花时间去摸索了. 譬如说 ,有断点的函数如 y
= floor ( x ) 和 y = sign ( x ,0) ,描点数目要足
《Z+Z超级画板》中“文本作图”的函数

《Z+Z超级画板》中“文本作图”的函数一.点Point(x,y[,Text]);//自由点Point(x,y,xDrag,yDrag[,"right"("polar")[,Text]]);//坐标点Midpoint(A,B[,Text);//线段AB中点PointOnLine(line[,Text]);//直线上的点PointOnPLine(A,line[,Text]);//平行线上的点PointOnVLine(A,line[,Text]);//垂直线上的点PointOnPolygon(A,B,C,…[,Text);//多边形上的点Foot(A,line[,Text]);//点在直线上的垂足IsosTriangle(A,B[,Text]);//线段AB中垂线上的点EqTriangle(A,B[,Text[);//ABC是等边三角形IsocelesEchelon(A,B,C[,Text]);//ABCD是等腰梯形Parallelogram(A,B,C,Text]);//ABCD是平行四边形Square(A,B[,Text]);//AB=BC,AB⊥BCSymmetricPoint(A,B[,Text]);//A关于点B的对称点PointOfAngleBisector(A,B,C[,Text]);//∠ABC的平分线DivisionPoint(A,B,nValue[,Text]);//定比分点IntersectionOfLine(line1,line2[,Text]);//两直线的交点IntersectionOfLinePLine(line1,A,line2[,Text]);//直线和平行线的交点IntersectionOfLineVLine(line1,A,line2[,Text]);//直线和垂直线的交点IntersectionOfPLinePLine(A,line1,B,line2[,Text]);//平行线和平行线的交点IntersectionOfPLineVLine(A,line1,B,line2[,Text]);//平行线和垂直直线的交点IntersectionOfVLineVLine(A,line1,B,line2[,Text]);//垂直直线和垂直直线的交点Centroid(A,B,C[,Text]);//三角形ABC重心Orthocenter(A,B,C[,Text]);三角形垂心Circumcenter(A,B,C[,Text]);三角形外心Incenter(A,B,C[,Text]);三角形外心RatioPoint(P0,P1,P2,nValue[,Text]);//p0p平行p1p2 |p0p|=|u*|p1p2|| RatioPoint(P0,P1,P2,p3,nValue[,Text]);//p0,p1p共线,|p0p|=|u*|p2p3|| PointFlexRotate(P,A,nTime,nAngle[,Text]);//P绕A放缩旋转点ConicLeftFocus(Conic[,Text]);//左焦点ConicRightFocus(Conic[,Text]);//右焦点ConicLeftVertex(Conic[,Text]);//左顶点ConicRightVertex(Conic[,Text]);//右顶点ConicLowerVertex(Conic[,Text]);//下顶点ConicUpperVertex(Conic[,Text]);//上顶点PointOnConic(Conic[,Text]);//圆锥曲线上的点PointOnCircle(Circle[,Text]);//圆上的点CircleCentre(Circle[,Text]);//圆心ConicCentre(Conic[,text]);//圆锥曲线的中心IntersectionOfCircle(Circle1,Circle2,nType=1(2)[,Text]);//两圆的交点IntersectionOfLineConic(line,Conic,nType=1(2)[,Text]);//直线和圆锥曲线的交点VertexOfPolygon(A,B,n,k[,Text]);//正多边形的顶点VertexOfCircle(Circle,A,n,k[,Text]);//内接正多边形的顶点VertexOfCircleEx(Circle,A,n,k[,Text]);//外接正多边形的顶点二、直线Segment(A,B[,Text]);//线段Vector(A,B[,Text]);//向量Radial(A,B[,Text]);//射线Line(A,B[,Text]);//直线ParallelLine(A,Line[,Text]);//过点平行于已知直线VerticalLine(A,Line[,Text]);//过点垂直于已知直线AngleBisector(A,B,C[,Txet]);//∠ABC的平分线LineOfPointSlope(A,slope[,Text] );//点和斜率LineOfPointAngle(B,Angle[,Text] );//点和倾斜角LineOfPointXIntercept(A,xIntercept[,Text] );//点和x-截距LineOfPointYIntercept(A,yIntercept[,Text]);//点和y-截距LineOfIntercept(xIntercept, yIntercept[,Text] );//截距式LineOfSlopeIntercept(slope,intercept[,Text]);//斜截式LineOfEquation(a*x+b*y+c=0[,Text] );//一般式CommonTangent(cricle1,cricle2,nType[,Text] );//两圆的共切线Tangent(A,conic,nType[,Text] );//圆锥曲线的切线Directrix(conic,nType[,Text]);//圆锥曲线的准线Asymptote(Hyperbola,nType[,Text] );//双曲线的渐近线三、圆和圆弧Circle(O,A[,Text] );//圆心和圆上一点CircleOfTPRadius(O,A,B[,Text] );//圆心和半径CircleOfRadius(O,r[,Text] );//圆心和半径CircleOf3Point(A,B,C[,Text] );//过三点的圆Circle(O,line[,Text]);//圆心和圆的切线AngleArc(A,B,C[,Text]);//无心圆弧ABCThreePointArc(A,B,C[,Text]);//过三点的圆弧ABCArcOnCircle(A,B,cricle[,Text] );//圆上的圆弧四、圆锥曲线NormalEllipse(O,a(b c e)=expr1,b(a c e)=expr2 ,x(y)[, sText] );//标准椭圆EllipseOfFocusPoint(F1,F2,P[, sText]);//两焦点和椭圆上一点EllipseOfFocusAxis(F1,F2,a[, sText] );//两焦点和椭圆半轴长NormalHyperbola((O,a(b c e)=expr1,b(a c e)=expr2 ,x(y)[, sText] );//标准双曲线HyperbolaOfFocusPoint(F1,F2,P[, sText]);//两焦点和双曲线上一点HyperbolaOfFocusAxis(F1,F2,a[, sText] );//两焦点和双曲线实轴长NormalParabola(V,P,"upper"("lower" "left" "right")[, sText] );//标准抛物线Parabola(F,A,P[, sText]);//焦点,对称轴上一点并过定点的抛物线Parabola(V,F[, sText]);//顶点和焦点的抛物线ParabolaOfVertexDirectrix(V,line [, sText]);//顶点和准线的抛物线ConicOfEquation(sEpuation[, sText]);//二次曲线ConicOfFivePoint(A,B,C,D,E[, sText] );//过五点作二次曲线ConicOfUniform(F,line,sEcc[, sText]);//统一定义二次曲线五、曲线Function(y=f(x)[x=f(y) rho=f(thet)],nMin,nMax,nCount, );//显式函数Function(x(t), y(t), t, nMin, nMax, nCount, );//参数方程DiscreteDataCurve(x1,y1,x2,y2,x3,y3,x4,y4, …[, sText] );//离散数据DiscretePointCurve(A,B,C,D, …[, sText] );//离散数据Polygon(A,B, C, D,…[, sText] );//离散数据LabelAngle(A,B,C[, sText] );//标注角MediaFile(Type,x,y,nWidth,nHeight,sPath,bDocpath[, sText]);//媒体对象六、图形变换Symmetric(Drawobj,Line[, sText] );//关于直线对称Translate(Drawobj,P1,P2[, sText]);//向量平移Rotate(Drawobj,P,nAngle[, sText]);//旋转TranslateRotate(Drawobj,p1, p2, P,nAngle[, sText] );//平移旋转Transform(Drawobj,a1,b1,x0,a2,b2,y0[, sText]);//仿射变换AffineTriangle(Drawobj,A,B,C,D,E,F[, sText]);//仿射变换:ABC-->DEF 七、对象组Group(obj1, obj2,…, objn[, sText] );//对象组八、文本Text([, sText]);//文本Text(x, y[, sText] );//文本TransformText([, sText]);//可变换文本TransformText(x,y[, sText]);//可变换文本Variable(sVar[, sText]);//变量Variable(sVar,nMin ,nMax [, sText] );//变量TextWarp(tText,np1 ,np2 ,np3 ,np4 );//弯曲字体Grid(nRow, nColumn, nwidth, nheighr[, sText] );//网格Grid(nCurve, nRow, nColumn, nwidth, nheighr[, sText] );//网格Stat(nRow, nColumn, nwidth, nheighr[, sText] );//统计Stat(nCurve, nRow, nColumn, nwidth, nheighr[, sText] );//统计九.测量MeasureVariable(sVar);//测量变量MeasureRightCoor(A);//测量直角坐标MeasurePolarCoor(A);//测量极坐标MeasureXCoor(A);//测量x坐标MeasureYCoor(A);//测量y坐标MeasureVector(A,B);//测量向量MeasureProduct(A,B,C,D);//测量向量内积MeasureAngle(A,B,C);//测量角MeasureAngleLineToLine(line1,line2);//测量直线到直线的角MeasureAngleBetweenLines(line1,line2);//直线与直线的夹角MeasureAngleOfVector(A,B);//向量的角MeasureLength(A,B);//向量或线段的长度MeasureDistance(A,line);//点到直线的距离MeasureArea(A,B,C,…);//凸多边形的面积IntPointIn(nGraph);//封闭图形内的整点个数IntPointOn(nGraph);//封闭图形边界上的整点个数MeasureAngleOfInclination(nline);//测量直线的倾斜角MeasureSlope(nline);//测量直线的斜率MeasureXIntercept(nline);//测量直线的x-截距MeasureYIntercept(nline);//测量直线的y-截距MeasureSlopeInterceptForm(nline);//测量直线的斜截式方程MeasureInterceptForm(nline);//测量直线的截距式方程MeasureGeneralForm(nline);//测量直线的一般方程MeasureRadius(nCricle);//测量圆的半径MeasurePerimeter(nCricle);//测量圆的周长MeasureAreaOfCircle(nCricle);//测量圆的面积MeasureCentreOfCircle(nCricle);//测量圆心坐标MeasureNormalOfCircle(nCricle);//测量圆的标准方程MeasureGeneralOfCircle(nCricle);//测量圆的一般方程MeasureArcLenght(nArc);//测量圆弧的弧长MeasureArcRadius(nArc);//测量圆弧的半径MeasureSectorArea(nArc);//测量扇形的面积MeasureArchArea(nArc);//测量弓形的面积MeasureCentreOfConic(nConic);//测量二次曲线的中心坐标MeasureLeftFocus(nConic);//测量二次曲线的左下焦点坐标MeasureRightFocus(nConic);//测量二次曲线的右上焦点坐标MeasureLeftVertex(nConic);//测量二次曲线的左顶点坐标MeasureRightVertex(nConic);//测量二次曲线的右顶点坐标MeasureLowerVertex(nConic);//测量二次曲线的下顶点坐标MeasureUpperVertex(nConic);//测量二次曲线的上顶点坐标MeasureSemiMajorAxis((nConic);//测量二次曲线的长实半轴的长度MeasureSemiMinorAxis(nConic);//测量二次曲线的短虚半轴的长度MeasureSemiFocus(nConic);//测量二次曲线的半焦距的长度MeasureEccentricity(nConic);//测量二次曲线的离心率MeasureLeftDirectrix(nConic);//测量二次曲线的左下准线方程MeasureRightDirectrix(nConic);//测量二次曲线的右上准线方程MeasureUpperAsymptote(nConic);//测量二次曲线的上渐近线方程MeasureLowerAsymptote(nConic);//测量二次曲线的下渐近线方程MeasureNormalOfConic(nConic);//测量二次曲线的标准方程MeasureGeneralOfConic(nConic);//测量二次曲线的一般方程MeasureTransform(nConic);//测量二次曲线的坐标变换公式十、动画、轨迹与跟踪AnimationVar(Var[,Text]);//动画Animation(A, );//动画Animation(A,B[,Text]);//动画Animation(A,B,C[,Text]);//动画Locus(A, B,C ,D ,…,L , Text);//轨迹Trace(obj, Text);//跟踪十一.对象属性Button(sTitle);//按钮Button(button1,button2 ,…,sTitle);//按钮Hide(obj1,obj2 ,obj3 ,…);//隐藏对象HideAll();//隐藏所有对象Show(obj1,obj2 ,obj3 ,…);//显示对象ShowAll();//显示所有对象Move(obj1,obj2 ,obj3 ,…);//开始动画Play(obj1,obj2 ,obj3 ,…);//开始播放Flash和MovieWink(obj1,obj2 ,obj3 ,…);//开始闪烁Stop(obj1,obj2 ,obj3 ,…);//停止闪烁、动画、Flash和Movie PointSize(piont1,piont2,piont3,…,nsize);//设置点的大小SetVarValue(sVar1,nValue1 , sVar2,nValue2, …);//设置变量的值AnimationSpeed(obj1,obj2,obj3,…,nspeed);//设置动画的运动类型AnimationType(obj1,obj2,obj3,…,nType);//设置动画的运动类型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《超级画板》第五篇函数图像函数及其图像,是中学数学课程的重要内容。
《超级画板》提供了制作动态函数图像的丰富的功能,并具有辅助教学和学习的一些附加的功能,例如在函数曲线上取点,作函数曲线的切线,列出函数值的表格,对曲线和x轴之间的面积填充或作细分,等等。
另外,还有许多办法作出教学所需要的特殊效果,那就要了解更多的操作方法了。
一函数图像配合函数表函数通常有三种表示方法:解析表达式、图像和表格。
用《超级画板》可以把三种表示方法紧密结合起来。
输入解析表达式,画出图像,再让图像和表格关联,以显示出函数值的表格。
请看本书配套资源中的文件5-1图像和列表.zjz,如图5-1。
图5-1这个课件有如下的功能:(1)显示曲线所对应的函数的表达式当鼠标指着左边对象工作区中编号为[5]的曲线条目时,旁边会显示出函数的表达式。
从图中看到,y是x的平方根。
(2)呈现函数的定义域所画的函数曲线,函数的定义域为[a,b]。
在左上部的两个测量数据文本中显示出,a的当前值为0,b的当前值为9。
(3)显示描点画线时所取的点和对应的函数值表函数曲线上,连同两端点共有19个点,把自变量x的范围[0,9]均匀分为18份。
曲线就是根据这19个点描出来的。
这19个点所对应的自变量x和函数y(x的平方根)的值可以在右上方的函数表里查出来。
(4)用一个按钮控制着函数表的显示或隐藏。
(5)改变描点的数目和对应的函数表描点的数目并非固定是19。
拖动下方参数n的变量尺上的滑钮,可以改变描点的数目。
点的数目越多,曲线就画得越准确。
当点的数目变化时,函数表也就随着改变。
例如,当描点的数目减少到5时,函数表里也就只有5组数据了。
(6)可以显示或不显示曲线上所取的点在函数曲线的属性对话框里,如图4-23,可以在左下角勾选或不勾选画点。
即使不把点显示出来,曲线仍然是根据这些点的位置而画出来的。
(7)可以选择用曲线或线段来组成图像曲线的画法有两种方案:一种是用曲线来连接这些点,一种是用线段来连接这些点。
当前是用曲线来连接的。
如图在属性对话框的右部可以勾选或不勾选“折线段”。
若勾选“折线段”,就是用线段来连接这些点了。
(8)在曲线上有一个样例点曲线上有一个红点A。
这个点的坐标,可以在属性对话框里查出来,是u000和u000^(1/2)。
当u000变化时,点A的轨迹或踪迹比较准确地显示出曲线的样子。
在图上,我们用x来标示A的横坐标,用f(x) 来标示A的纵坐标。
图中看到,点A的横坐标和纵坐标都被测量出来了,从测量数据中可以对更多的自变量x的值查出对应的函数值,准确到10位小数。
(9)可以准确地设置函数定义域和样例点为了更准确地控制参数a、b和u000, 我们制作了3个动画按钮和参数k的变量尺,并测量出floor(k),但测量数据命名为k。
打开动画按钮的属性对话框,可以查出动画的设置:动画的参数范围是floor(k)到pi*floor(k);频率小于10;类型是一次运动且为逆向运动。
例如,若用变量尺把k的值调整到2至3之间,这时测量数据显示k=2。
若单击a的动画按钮的主钮,则a的值变为2;单击a的动画按钮的副钮时,则a的值变为2π。
同样方法可以把b或u000的值准确地设置为整数或π的整数倍。
如果想要a、b和u000准确地取其它数值,可以在动画按钮属性对话框里设置。
(10)可以改变函数的表达式,一图百变单击“显示或隐藏说明”按钮,出现如图5-2所示的说明。
按说明操作,可以变换函数的表达式。
图5-2回忆学过的操作,可知上述功能除作函数表外都不难实现。
而作函数表的功能,可以用文本作图命令中“文本”类倒3行的函数命令Grid(5,10,10,70, 20, ); 其中第1个参数5是函数曲线的编号;第2,3两个参数11和8是表格的行列数目;第4,5两个参数70和20是表格中一格的宽度和高度的像素数目。
注意,表格的宽度和高度可以用鼠标拖动调整,行列的数目可以在属性对话框里修改。
这命令也适用于参数曲线、极坐标曲线和点的轨迹。
你也可以把这个文件当作模板使用,只要把函数表达式和点A的坐标改一下,就能作出你所要的带有函数表的函数的图像了。
例如,上述文件的第2页(如图5-3),呈现出在[0, 2π]上的函数y=sinx 的图像和函数表,就是从第一页修改得到的。
这里重要的是两点修改:在曲线的属性对话框里把函数的表达式改成sin(x);在点A的属性对话框里把“y-参数”(即A的y坐标)改为sin(u000)。
此外,还要把定义域调整为[0, 2π]。
方法是先用变量尺把k调到2和3之间,再单击b 的动画按钮的副钮。
当描点个数n=9时,得到图5-3所示曲线。
图5-3虽然只取了9个点,图像已相当准确了。
拖动点A检查一下,便知分晓。
如果减少到只用4个点,误差就大了。
图5-4显示出用4个点描出的曲线和对点A的跟踪的对比。
图5-4用折线代替曲线,在描点数很多时效果相当好,在描点数很少的情形,误差比曲线大得多。
图5-5是取6点用线段连接的情形。
若用曲线,要好得多。
你不妨试试。
图5-5[习题5-1] 复制上述文件,利用它作为模板,分别作出适当的定义域上的二次函数,余弦函数以及对数函数的图像和函数表。
[习题5-2] 上述文件中只能把参数a、b和u000准确地调为整数或π的整数倍。
请你设计变量尺和动画按钮,使操作者能够方便地把这些参数准确地调为分数或π的分数倍。
(分子分母不超过100)。
二基本的初等函数族在中学课程中,有几族函数特别重要。
这包括二次函数族y=ax2+bx+c, 指数函数族y=a x, 对数函数族y=log a x,幂函数族y=x k以及正弦函数族y=Asin(ωx+φ)这些函数族都带有可变的参数。
用超级画板作出函数图像和有关的参数尺,拖动参数尺上的滑钮,跟踪曲线的变化,可以对函数形态和参数的关系,有非常直观地了解。
打开本书配套资源中的文件5-2二次函数.zjz,如图5-6。
图5-6用文本作图函数命令Function(y=a*x^2+b*x+c, -6, 6,500 , ); 可以作出图中的函数曲线;用文本作图函数命令Point(a, -2, a, , , a);Point(b, -3, b, , , b);和Point(c, -4, c, , ,c );可以作出可以拖动的坐标点a、b、c,用以控制参数a,b和c;曲线和x 轴的交点x1和x2以及顶点D,也都是可以用文本作图函数命令作出的坐标点;有关的坐标可以根据课本上的公式写出来,你也可以从点的属性对话框里查出来。
还可以用文本作图函数命令Variable(k, );作出一个参数k的变量尺,测量出k的整数部分floor(k)并将测量得到数据命名为k。
这是为了用动画按钮驱动系数a、b、c取到整数值。
这样的办法,在上一节已经用过,以后还会常用。
曲线方程中的系数是动态的,可以随a、b、c的变化而变化。
在文本中嵌入动态的数据,在前一章已经用过。
这次算是复习吧。
如果忘了是如何操作的,可以双击方程的文本,使它进入编辑状态,就能看到原来的输入是:y=$bl{a,21}x^2+$bl{b,21}x+$bl{c,21}这就明白了。
再作3个动画按钮,用来分别驱动a、b、c 在一定范围变化,以便对曲线跟踪观察。
例如,当a在-5到5之间变化时,对曲线的跟踪情形如图5-7。
图5-7图中还测量了判别式b2-4ac的值。
当判别式为负时,曲线和x轴没有交点。
此外,这里的标题是漂亮的“可变换文本”,可以用文本作图的“文本”类函数命令TransformText(二次函数的图像);来实现。
用可变化文本制作的文字,可以填充,可以选择后拖动角上的“把手”来改变其长宽。
当我们选择了曲线并对它跟踪时,有时可能希望停止跟踪,或又恢复跟踪。
在对象工作区单击该“跟踪”条目前的小方框,可以在停止跟踪和恢复跟踪之间切换。
若不想在对象工作区操作,可以作一个按钮来实现跟踪的显示和隐藏,方法是使用“动态alpha”功能和变量动画。
在前一章也介绍过了。
总之,制作动态的函数图像的所有操作都是前面讲过的。
这里是复习。
类似的方法,在文件5-3指数函数族.zjz中,可以看出函数y=a x的图像当a变化时的变化情形,如图5-8.图5-8而文件5-4指数函数和对数函数.zjz 则将指数函数和对数函数做了对比,如图5-9。
图5-9至于幂函数,它的情形要复杂一些。
随着幂指数k的不同,幂函数y=x k 的定义域是不同的。
当k取一般实数值时,其定义域为(0,+∞);而当k为整数时,其定义域为(-∞,+∞)。
文件5-5幂函数族的图像.zjz 的第一页,显示了k取一般实数值的情形。
用动画按钮驱动k并对图像跟踪,如图5-10。
该文件的第2页和第3页,则对应于k为偶数或奇数的情形。
图5-10在三角函数中,最有用的是一般正弦波函数y=A sin(ωx+φ);作出随3个参数改变而变化的这样的图像的方法,在不少资料中有所讨论。
用超级画板作这样的图像,不过是一个简单的常规操作。
见文件5-6一般正弦波.zjz的第一页,如图5-11。
图5-11注意这里的3个参数A、ω、φ,在输入函数表达式、建立变量尺以及制作动画按钮时,实际用的参数是a、b、c。
用动画按钮驱动a、b、c,可以得到指定的正弦曲线。
如何通过参数的变化把基本的正弦函数y=sin x的曲线变为某种特定的正弦曲线,是中学数学教材的传统内容之一。
上述文件的第2页,提供了实现这种转化的具体操作,如图5-12。
图5-12在图5-12中,有5条曲线。
4条虚曲线是固定不动的,它们的表达式用同色的文本框分别标出在右上角。
一条实曲线是可以变化的, 表达式在上方,就是y=a sin(bx+c)。
自上而下顺次单击3个动画按钮的主钮,驱动3个参数a、b、c 分别变化,则红色的实曲线通过向左平移、沿x轴压缩、沿y轴放大由一条曲线顺次变为另外3条;再自下而上顺次单击3个动画按钮的副钮,则曲线通过沿y 轴压缩,沿x轴放大,向右平移而复原。
从属性对话框中,可以查到这些曲线的方程和定义域。
注意,可变化的实曲线,它的定义域是可变化的参数。
[习题5-3] 观察下面的一列文本作图函数命令,这些命令运行时将作出那些对象?命令中的数字有何意义?其中哪些命令可以用智能画笔和菜单操作实现(这些命令文本见文件“5-2二次函数.zjz”第2页)?Function(y=a*x^2+b*x+c, -6, 6, 200, );Point(a, -2, a, , , a);Point(b, -3, b, , , b);Point(c, -4, c, , , c);Point((-b-(b^2-4*a*c)^(1/2))/(2*a), 0, , , , x_1);Point((-b+(b^2-4*a*c)^(1/2))/(2*a), 0, , , , x_2);Point(-b/(2*a), (4*a*c-b^2)/(4*a), , , , D);Variable(k, 0, 20, );TransformText(二次函数的曲线);Foot(6, 3, );Foot(7, 3, );Foot(8, 3, );Segment(6, 14, );Segment(7, 15, );Segment(8, 16, );MeasureExpress(floor(k),k);MeasureExpress(b^2-4*a*c, b^2-4ac);Text(y=$bl{a,21}x^2+$bl{b,21}x+$bl{c,21});Trace(5, );AnimationVar(a, a: a->5);AnimationVar(b, b: b->5);AnimationVar(c, c: c->5);AnimationVar(a, a: -k->k);AnimationVar(b, b: -k->k);AnimationVar(c, c: -k->k);请把这些命令复制到文本作图的对话框的适当的栏里运行一遍,以证实自己的结论。
