数字信号处理第9章答案讲解
数字信号处理教程课后习题及答案

6.试判断:
是否是线性系统?并判断(2),(3)是否是移不变系统?
分析:利用定义来证明线性:满足可加性和比例性, T [a1 x1 (n ) + a 2 x2 (n )] = a1T [ x1 (n )] + a2T [ x2 (n )] 移不变性:输入与输出的移位应相同 T[x(n-m)]=y(n-m)。
,
(2)x(n) = R3(n)
,
(3)x(n) = δ (n − 2) ,
(4)x(n) = 2n u(−n − 1) ,
h(n) = R5(n) h(n) = R4 (n) h(n) = 0.5n R3(n) h(n) = 0.5n u(n)
分析:
①如果是因果序列 y (n ) 可表示成 y (n ) ={ y (0) , y(1) , y(2) ……},例如小题(2)为
y1 (1) = ay1 (0) + x1 (1) = 0 y1 (2) = ay1 (1) + x1 (2) = 0
┇
8
y1(n) = ay1(n − 1) + x1(n) = 0 ∴ y1 (n) = 0 , n ≥ 0 ii) 向 n < 0 处递推,将原方程加以变换
y1(n + 1) = ay1(n) + x1(n + 1)
结果 y (n ) 中变量是 n ,
∞
∞
∑ ∑ y (n ) =
x ( m )h (n − m ) =
h(m)x(n − m) ;
m = −∞
m = −∞
②分为四步 (1)翻褶( -m ),(2)移位( n ),(3)相乘,
《数字信号处理》第三版课后答案(完整版)

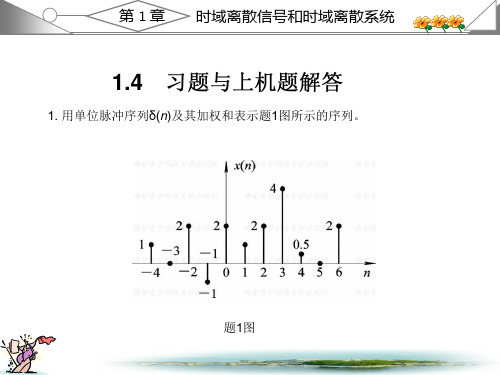
西安电子 ( 高西全丁美玉第三版 ) 数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列 (n) 及其加权和表示 题 1 图所示的序列。
解:x( n)(n4) 2 (n 2) ( n 1)2 (n)(n 1) 2 (n 2) 4 ( n 3)0.5(n 4)2 (n 6)2n 5, 4 n 12. 给定信号: x( n)6,0n 40, 其它(1)画出 x( n) 序列的波形,标上各序列的值; (2)试用延迟单位脉冲序列及其加权和表示 x(n) 序列;(3)令 x 1( n) 2x(n 2) ,试画出 x 1( n) 波形;(4)令 x 2 (n) 2x(n 2) ,试画出 x 2 (n) 波形;(5)令 x 3 (n) 2x(2 n) ,试画出 x 3 (n) 波形。
解:( 1) x(n) 的波形如 题 2 解图(一) 所示。
( 2)x(n)3 ( n 4)(n 3) (n 2) 3 ( n 1) 6 (n) 6 (n 1)6 ( n 2)6(n 3) 6 (n 4)( 3) x 1 (n) 的波形是 x(n) 的波形右移 2 位,在乘以 2,画出图形如 题 2 解图(二) 所示。
( 4) x 2 (n) 的波形是 x(n) 的波形左移 2 位,在乘以 2,画出图形如 题 2 解图(三) 所示。
( 5)画 x 3 (n) 时,先画 x(-n) 的波形,然后再右移2 位, x3 ( n) 波形如 题 2 解图(四) 所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1) x( n)Acos(3n) ,A 是常数;78(2)x(n)j ( 1n)e 8。
解:(1)w 3214T=14 ;7,,这是有理数,因此是周期序列,周期是w3(2)w 1 , 216 ,这是无理数,因此是非周期序列。
8w5. 设系统分别用下面的差分方程描述,x(n) 与 y(n) 分别表示系统输入和输出,判断系统是否是线性非时变的。
数字信号处理(第三版)-课后习题答案全-(原题+答案+图)
将x(n)的表示式代入上式, 得到 1 y(n)=-2δ(n+2)-δ(n+1)-0.5δ(2n)+2δ(n-1)+δ(n-2)
+4.5δ(n-3)+2δ(n-4)+δ(n-5)
第 1 章 时域离散信号和时域离散系统
8. 设线性时不变系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况,
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
(5)y(n)=x2(n)
(6)y(n)=x(n2)
(7)y(n)=
n
(8)y(n)=x(n)sin(ωxn(m) )
m0
解: (1) 令输入为
输出为
x(n-n0)
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2)
x(m)h(n-m)
m
第 1 章 时域离散信号和时域离散系统
题7图
第 1 章 时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
数字信号处理DSP9-2

p
E e n R e n 1
2 p 1 p p 1 2
E e n p
E e n 1 R e n
2 p 1 p p 1 2
优化条件
2 2 E e p n E e p n 0 R p
一维卡尔曼滤波
设含有噪声的信号测量值与信号估计值分 别采用以下模型表达:
xn c sn wn sn a sn 1 vn 1
a, c 为与时间无关的常数; w, v 为方差不随时间变化的白噪声。
一维卡尔曼滤波
建立一维卡尔曼方程如下:
sn an sn 1 bn xn
格型滤波
例:3阶系统
1 0.5 z 1 0.5 z 2 z 3 H z 1 1.8 z 1 1.4 z 2 0.4 z 3
c3 b3 3 1 c2 b3 2 c3a3 1 1.3 c1 b3 1 c2 a2 1 c3a3 2 1 c0 b3 0 c1a1 1 c2 a2 2 c3a3 3 0.8
k 1 p 1
格型滤波
P阶后向预测
P阶前向预测
格型滤波
误差递推关系与格型滤波结构
e n e 1 n R p e 1 n Fra bibliotek 1 p p p
e n e 1 n 1 R p e 1 n p p p
格型滤波
最小均方优化设计: 选择反射系数使前后向均方误差之和为最小 前向均方误差 后向均方误差
n p p 1 2 p 1 2 N 1
R p N 1
n p
e n e n 1
格型滤波
《数字信号处理》第三版课后习题答案

《数字信号处理》第三版课后习题答案数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-??=≤≤其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列;(3)令1()2(2)x n x n =-,试画出1()x n 波形;(4)令2()2(2)x n x n =+,试画出2()x n 波形;(5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14;(2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
数字信号处理习题及答案解析

==============================绪论==============================1. A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统==================1.①写出图示序列的表达式答:3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用δ(n) 表示y (n )={2,7,19,28,29,15}2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的; 若是周期的, 确定其周期。
(1)A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= (2))81(j e )(π-=n n x 解: (1) 因为ω=73π, 所以314π2=ω, 这是有理数, 因此是周期序列, 周期T =14。
(2) 因为ω=81, 所以ωπ2=16π, 这是无理数, 因此是非周期序列。
③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。
3.加法乘法序列{2,3,2,1}与序列{2,3,5,2,1}相加为__{4,6,7,3,1}__,相乘为___{4,9,10,2} 。
移位翻转:①已知x(n)波形,画出x(-n)的波形图。
②尺度变换:已知x(n)波形,画出x(2n)及x(n/2)波形图。
卷积和:①h(n)*求x(n),其他02n 0n 3,h(n)其他03n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤= }23,4,7,4,23{0,h(n)*答案:x(n)=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5},则h (-m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15}③(n)x *(n)x 3),求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案:x(n)=4.如果输入信号为,求下述系统的输出信号。
数字信号处理英文版课后答案 (9)

0 0.0 0
/8 –2.9 –68
/4 3/8 –16.9 –14.5 –135 –12
/2 –16.9 –90
5/8 –20.5 23
|H()|
()
100
50
0
-50
-100
-150 0 0.5 1 1.5 2 2.5 3
(b) In the pass band, which lies within the first “bump” of the magnitude spectrum, the phase spectrum follows a straight line. This means the phase is linear in this region, which in turn means that no distortion will occur. 9.4 (a)
h 1 [n ]
The sample values are given in the table. Note that at n = 0, it is easiest to evaluate h1[n] if it is re-expressed as
h 1 [n ] 0.5n sin 0.5n 0.5 sinc0.5n ) n 0.5n
y[n ]
The difference equation for a three-term moving average filter is
1 x[n] x[n 1] x[n 2] 3
The filter finds the average of each group of three input samples. The first sixteen outputs are: n y[n] n y[n] 0 3.33 8 1.00 1 3.67 9 1.00 2 4.00 10 1.00 3 1.00 11 4.00 4 1.00 12 4.00 5 1.00 13 4.00 6 1.00 14 1.00 7 1.00 15 1.00
《数字信号处理》第三版答案(非常详细完整)

答案很详细,考试前或者平时作业的时候可以好好研究,祝各位考试成功!!电子科技大学微电子与固体电子学陈钢教授著数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列; (3)令1()2(2)x n x n =-,试画出1()x n 波形; (4)令2()2(2)x n x n =+,试画出2()x n 波形; (5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如 5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
(1)()()2(1)3(2)y n x n x n x n =+-+-; (3)0()()y n x n n =-,0n 为整常数; (5)2()()y n x n =; (7)0()()nm y n x m ==∑。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9章 自 测 题 题9图
第9章 自 测 题
9.4 自 测 题 (四)
1.
设
X
(z)
(1
0.19 0.9z)(1
0.9z 1 )
试求与X(z)对应的所有可能的序列x(n)。
(该题12分)
2. 假设x(n)=R8(n), h(n)=R4(n) (1)令y(n)=x(n)*h(n), 求y(n)。 要求写出y(n)的表达式,
9.1 自 测 题
1. 判断下列各题的结论是否正确, 你认为正确就在括
弧中画“√”, 否则画“×”
(1) 如果X(k)=DFT[x(n)] k=0, 1, 2, 3, …, 7
y(n)=x((n+5))8R8(n) Y(k)=DFT[y(n)]
k=0, 1, 2, 3, …, 7
则
|Y(k)|=|X(k)| k=0, 1, 2, 3, …, 7 ( )
题2图
第9章 自 测 题
(4) 画出下面系统函数的直接型和级联型结构图: H (z) 4z3 2.83z 2 z (z 2 1.4z 1)(z 0.7)
(该题25分, (1)4分 , (2)7分, (3)7分, (4)7分) 3. 对x(t)进行理想采样, 采样间隔T=0.25 s, 得到 xˆ(t) ,
第9章 自 测 题 9. 已知RC模拟滤波网络如题9 (1)试利用双线性变换法将该模拟滤波器转换成数字滤 波器, 求出该数字滤波器的系统函数, 并画出它的结构图。 最后分析该数字滤波器的频率特性相对原模拟滤波器的频率特
(2) 能否用脉冲响应不变法将该模拟滤波器转换成数字 滤波器? 为什么?
(该题21分, (1)15分, (2)6 (自测时间2.5~3小时, 满分100分)
如将H(z)中的z用z4代替, 形成新的网络系统函数, H1(z)=H(z4)。 试画出|H1(ejω)|~ω曲线, 并求出它的峰值点频
(该题10 8. 设网络的单位脉冲响应h(n)以及输入信号x(n)的波形 如题8图所示, 试用圆卷积作图法画出该网络的输出y(n)波 形(要求画出作图过程)。
第9章 自 测 题 题8图
(该题7分)
第9章 自 测 题
3. 如果FIR网络用下面差分方程描述:
y(n)
6
1 3k
x(n k)
k0 2
(1)画出直接型结构图, 要求使用的乘法器最少; (2)判断该滤波器是否具有线性相位特性, 如果具 有线性相位特性, 写出相位特性公式。 (该题11分, (1)6分, (2)5分)
第9章 自 测 题
第9章 自 测 题
9.1 自测题(一) 9.2 自测题(二) 9.3 自测题(三) 9.4 自测题(四) 9.5 自测题(五) 9.6 自测题(一)参考答案 9.7 自测题(二)参考答案 9.8 自测题(三)参考答案 9.9 自测题(四)参考答案 9.10 自测题(五)参考答案
第9章 自 测 题
(1)试画出直接型结构(要求用的乘法器个数最少); (2)试画出频率采样型结构, 采样点数为N=5; 为简单 起见, 结构中可以使用复数乘法器; 要求写出每个乘法器系
(3) 该滤波器是否具有线性相位特性, (该题21分, 每小题7分)
第9章 自 测 题
5. 已知归一化二阶巴特沃斯低通滤波器的传输函数为
5. 已知x(n)的N点DFT为
X (k)
N
2 N
2
(1
(1 0
j) j)
k m
k N m 其它k
式中, m 、 N是正的整常数, 0<m<N/2 。
第9章 自 测 题
(1) 求出x(n); (2)用xe(n)和xo(n)分别表示x(n)的共轭对称序列和共轭 反对称序列, 分别求DFT[xe(n)]和DFT[xo(n) (3) 求X(k)的共轭对称序列Xe(k)和共轭反对称序列Xo(k)。 (该题16分, (1)4分, (2)6分, (3)4分) 6. 用窗口法设计第一类线性相位高通滤波器, 用理想高 通滤波器作为逼近滤波器, 截止频率为ωc, 选用矩形窗 w(n)=RN(n), 长度N=31。 (1)求出理想高通滤波器的单位脉冲响应hd(n); (2)求出所设计的滤波器的单位脉冲响应h(n) (该题8分, 每小题4分)
(3) 画出数字滤波器的直接型结构图。
(该题15分, (1) 5分, (2) 5分, (3) 5
(自测时间2.5~3小时, 满分100分)
第9章 自 测 题
9.2 自 测 题(二)
1. 假设x(n)=δ(n)+δ(n-1), 完成下列各题: (1)求出x(n)的傅里叶变换X(ejω), 并画出它的幅频特性 曲线; (2) 求出x(n)的离散傅里叶变换X(k), 变换区间的长度 N=4, 并画出|X(k)|~k曲线;
第9章 自 测 题
(2) 用窗函数法设计FIR数字滤波器时, 加大窗函数 的
长度可以同时加大阻带衰减和减少过渡带的宽度。 ( )
(3)如果系统函数用下式表示:
H (z)
(1
1 0.5z 1 )(1
0.5z)
可以通过选择适当的收敛域使该系统因果稳定。
(4)令x(n)=a|n| 0<|a|<1, -∞≤n≤∞
第9章 自 测 题
6. 设H(ejω)是因果线性时不变系统的传输函数, 它的单 位脉冲响应是实序列。 已知H(ejω)的实部为
5
H R (e j ) 0, 5n cosn n0
求系统的单位脉冲响应h(n) (该题8分)
第9章 自 测 题
7. 假设网络系统函数为
H
(
z
)
1
1
z 1 0.9z 1
x(n)分别用下式表示: h(n)=R8(n), x(n)=0.5nR8(n)
(1) 计算并图示该系统的输出信号y(n);
第9章 自 测 题
(2) 如果对x(n)和 h(n)分别进行16点DFT, 得到X(k)和 H(k), 令
Y1(k)=H(k)X(k) k=0, 1, 2, 3, …, 15 y1(n)=IDFT[Y(k)] n, k=0, 1, 2, 3, …, 15 画出y1(n)的波形。 (3)画出用快速卷积法计算该系统输出y(n)的计算框图 (FFT计算作为一个框图), 并注明FFT的最小计算区间N 等于多少。 (该题22分, (1) 7分, (2) 7分, (3) 8分)
H (k) H (z) zejk
k
2π k; N
k 0,1,2,3,, N 1
hN(n)=IDFT[H(k)] n, k=0, 1, 2, 3, …, N-1
第9章 自 测 题
则
h(n)=hN(n) (该题24分, 每小题4
()
2. 完成下列各题:
(1)已知
3z 1 H(z)
(该题10分)
第9章 自 测 题
4. 已知
1 x(n) 0
n≤ 3 其它n
(1)求出该信号的傅里叶变换; (2)利用x(n)求出该信号的DFT, X(k)=DFT[x(n)], 区间为8。 (提示: 注意x(n)的区间不符合DFT要求的区间。) (该题8分, 每小题4分)
第9章 自 测 题
Ha (s)
s2
1 2s 1
要求用双线性变换法设计一个二阶巴特沃斯数字低通滤波器,
该滤波器的3 dB截止频率 间隔T=2 s。
rcad,π3 为简单起见, 设采样
第9章 自 测 题
(1)求出该数字低通滤波器的系统函数H(z) (2 (3)设:
H (k) H (z) zexp[j2π k]
再让 xˆ(t) 通过理想低通滤波器G(jΩ), Gj(Ω)用下式表示:
G(
j
)
0.25 0
≤ 4π
4π
第9章 自 测 题
设 x(t)=cos(2πt)+cos(5πt)
要求: (1) 写出 xˆ(t) 的表达式; (2) 求出理想低通滤波器的输出信号y(t)
(该题14分 , (1)6分, (2)8 4. 假设线性非时变系统的单位脉冲响应h(n)和输入信号
15
k 0,1,2,3,,14
h15(n)=IDFT[H(k)] n=0, 1, 2, 3, …, 14 h(n)=IZT[H(z)
试写出h15(n)与h(n) (该题21分, 每小题7 (自测时间2.5~3小时, 满分100分)
第9章 自 测 题
9.3 自 测 题 (三)
1. 设
X (z)
试写出y(n)与x(n)之间的关系式, 并画出y(n) (该题14分)
第9章 自 测 题
5. 已知x(n)是实序列, 其8点DFT的前5点值为: {0.25, 0.125-j0.3, 0, 0.125-j0.06, 0.5}
(1) 写出x(n)8点DFT的后3 (2) 如果x1(n)=x((n+2))8R8(n), 求出x1(n)的8点DFT值。 (该题14分, 每小题7
第9章 自 测 题 3. 数字滤波器的结构如题3 (1 (2 (3)按照零极点分布定性画出其幅频特性曲线, 并近似 求出幅频特性的峰值点频率(计算时保留4位小数)。 (该题18分, 每小题6分)
题3图
第9章 自 测 题
4. 设FIR数字滤波器的单位脉冲响应为 h(n)=2δ(n)+δ(n-1)+δ(n-3)+2δ(n-4)
(3) 将x(n)以4为周期进行延拓, 得到周期序列 ~x (n) , 求出~x (n)的离散傅里叶级数系数X~ (k ), 并画出 X~(k) ~ k 曲线;
