比例尺导学案
六年级下册数学导学案-2.3比例尺 北师大版

六年级下册数学导学案-2.3比例尺北师大版一、教学目标1.能够定义比例的概念,并能够根据比例求解问题;2.能够理解比例尺的概念,并能够根据比例尺求解问题。
二、知识准备在学习比例尺之前,我们需要对比例有一定的了解。
比例是两个比较大小相等的量之间的比值。
例如,将小明和小芳的身高进行比较,如果小明身高是1.5米,小芳身高是1.2米,我们就可以用比例表示为1.5∶1.2,也可以简化为5∶4。
三、新知预习1. 比例尺的定义比例尺是地图上的两个量之间的比例。
例如,在1∶1000的比例尺下,一厘米的长度代表实际上的1000厘米。
比例尺通常用于展示地图上的距离、长度或面积等。
2. 比例尺的计算方法在计算比例尺时,需要将地图上的长度或面积与实际长度或面积进行比较。
假设在1∶500的比例尺下,地图上一条直线的长度为6厘米,那么实际上这条直线的长度应该是多少呢?我们只需要将6乘以500,也就是6×500=3000(厘米),即这条直线的实际长度为3000厘米。
3. 比例尺的应用比例尺经常被用于表示不同距离之间的比例关系,例如,地图上的两个城市之间的距离。
在1∶1000的比例尺下,两个城市之间的距离为5厘米,那么实际距离应该是多少呢?我们只需要将5乘以1000,也就是5×1000=5000(米),即这两个城市之间的实际距离为5000米。
四、课堂练习1. 比例的练习题假设小明的身高是1.5米,小芳的身高是1.2米,那么请回答以下两个问题:1.小明的身高与小芳的身高之比是多少?2.如果小芳的身高是1.6米,那么请计算小明的身高应该是多少?2. 比例尺的练习题假设在1∶1000的比例尺下,地图上两个城市之间的距离为5厘米,请计算这两个城市之间的实际距离。
五、课后作业1.小明的体重是35千克,小芳的体重是28千克,那么小明的体重与小芳的体重之比是多少?2.在1∶500的比例尺下,地图上一条路的长度为8厘米,请计算这条路的实际长度是多少?六、知识总结本节课程我们学习了比例尺的概念、计算方法和应用,还学习了比例的概念以及如何求解比例问题。
人教版数学六年级下册第20课比例尺导学案(精推3篇)

人教版数学六年级下册第20课比例尺导学案(精推3篇)〖人教版数学六年级下册第20课比例尺导学案第【1】篇〗【教学内容】北师大版数学六年级下册30页——比例尺【教材分析】教材从学生比较熟悉的房屋平面图入手,引导学生认识比例尺,初步感受比例尺在生活中的应用。
出示平面图后,借助图形放缩的经验和其他学习经验,了解比例尺的含义。
【学情分析】本节课内容是学生在学习了化简比的基础上学习的,因此不会感到陌生。
但学生对比例尺的意义可能不好理解,这部分知识相对来说比较抽象,在具体计算上可能存在一定困难。
【教学目标】1、结合具体情境,认识比例尺;能根据图上距离、实际距离、比例尺中的两个量求第三个量。
2、运用比例尺的有关知识,通过测量、绘图、估算、计算等活动,学会解决生活中的一些实际问题。
3、能积极参与数学学习活动,进一步体会数学与日常生活的密切联系。
【教学重点】结合具体情境理解比例尺的意义。
【教学难点】应用比例尺的知识解决实际问题。
【教学准备】多媒体课件,直尺,中国地图【教学流程】一、谈话导入,激起兴趣1、如果要绘制我们教室的平面图,需要多大的纸?如果要绘制中国地图呢?(学生自由回答。
得出结论。
)2、聪明的人想出了一个办法,把物体实际的长度按一定比例缩小再画在图纸上,这就是我们这节课要研究的内容。
【设计意图:先抓住学生急于认知的心理,从生活中熟悉的事物出发,真切感受到在绘制平面图的时候,不可能按照实际的长度来操作,需要有一个科学的方法,从而引入本节课内容。
】二、创设情境,探究新知活动一:(课件出示)六.一儿童节快要到了,学校要举办一个大型的篝火晚会,想让同学们设计一个舞台。
在平面图上如果用10厘米表示地面上10米的距离,那么图上距离与实际距离的比是多少呢?【设计意图:用学生喜欢的活动引起浓厚的兴趣,用亲身经验走近数学,探索其中的奥秘。
】(1)读懂题目中的信息。
(学生汇报已知条件和所求问题。
)(2)根据题目的要求,引导学生得出10厘米:10米,并用学生已有的学习经验化简比。
比例尺导学案

比例尺导学案比例尺导学案(2篇)比例尺导学案篇1尚美课堂教学模式——数学“五段”教学导学案年级六年级备课教师教学课题比例尺教学内容教科书第88~89页例1、例2,课堂活动第1~3题,练习十九第1、3题教学目标1.在操作、观察、思考、归纳等学习活动中理解比例尺的意义,正确计算比例尺,了解比例尺在实际生活中的各种用途。
2.在实践活动中体验生活中需要的比例尺,能读懂不同形式的比例尺。
3.体验数学与生活的联系,培养学生用数学眼光观察生活的习惯。
教学重点理解比例尺的意义,正确运用比例尺的意义解决实际问题。
教学难点理解比例尺的意义,正确运用比例尺的意义解决实际问题。
教学过程教师活动学生活动问题呈现情境导入创设情境,揭示课题1.创设情境,激趣设疑。
课件出示:一幅中国地图和国旗的平面图。
再依次点击,出现一组大小不同的地图平面图和国旗平面图。
教师:通过观察,你发现了什么?什么变了?什么没变?教师:我们可以把地图和国旗画在纸上,同样也可以把我们的住房缩小后画在纸上,这是几天前,我在售房中心看房时,一位售楼先生给我了两套住房(课件出示),可是他只给看了一下图纸,我买房的标准是想要面积大一些,我想请同学们帮帮我这个忙,好吗?学生1:建议购买第二套。
学生2:建议购买第一套。
学生3:我也同意购买第一套,第一套的住房前面标有比例尺,而且它的比例尺大。
学生4:不同意,第二套大,应该购买第二套。
2.揭示课题。
教师:看来同学们的意见不统一了,目前还不能帮老师确定到底购买那一套住房。
那么,住房平面图与实际的房屋之间有什么关系呢?这就是我们今天要学习的内容。
(板书:比例尺)1、学生观看主题图:一幅中国地图和国旗的平面图,再依次点击,出现一组大小不同的地图平面图和国旗平面图。
2、学生观察发现了什么?什么变了?什么没变?3、学生讨论,说说想法学生1:建议购买第二套。
学生2:建议购买第一套。
学生3:我也同意购买第一套,第一套的住房前面标有比例尺,而且它的比例尺大。
小学六年级数学《比例尺》导学案设计
课 题
比例尺
学 科
数学
课 型
新授
年 级
六年
时 间
主备人
执教人
学习
目标
1、进一步理解比例尺的含义; 2、能熟练地求比例尺、图上距离和实际距离,并综合运用比例尺的有关知识解决实际问题; 3、经历应用知识的过程,体验数学知识的应用价值。
学习重点
熟练地求图上距离和实际距离。
1、在一张1:500的设计图纸上,量得一正方形建筑的边长是20cm,这个建筑物的实际占地面积是多少平方米?
2、
课件出示,集体交流
板书设计
比例方法解:
解:设地铁1号线的实际长度是X厘米。
根据: X=10×500000 (问:根据什么?)
X=5000000 根据比例的基本性质。
5000000㎝=50㎞
答:地铁1号线路的实际长度是50千米。
则怎样求图上距离和实际距离呢?
预习质疑自主探究
(1) 打开课文观察例题及插图。
(2) 说一说从中你得到哪些信息。
(3)你认为可以用什么方法解决问题?
教师巡视课堂,了解解答情况,并对个别学生进行指导,帮助他们找到解决问题的方法。
合作交流
体验快乐
方程解:
解:设地铁1号线的实际长度是X厘米。
X=10×500000 X=5000000 5000000㎝=50㎞
2、对于感到疑惑、困难或有不同看法的问题要做出标记,便于交流时提出。
精读点拨
深化理解
(1)无论是计算比例尺、计算实际距离,还是计算图上距离,都要统一成最小的长度单位。这样方便一些。
(2)计算实际距离和计算图上距离时,比例尺最好写成分数形式,这样可以把比例尺当作一个分数。
比例尺的导学案
比例尺的导学案一、学习目标1、理解比例尺的含义。
2、知道比例尺的分类。
3、掌握比例尺的计算。
二、探究新知探究一:比例尺及其分类看书第 48 面,完成下列问题 (自主学习+合作交流+小组展示 时间:3分+3分+4分) 1、一幅图的 ____ 和 ____ 比,叫做这幅图的比例尺。
2、比例尺= _______: ______ 或比例尺=________.3、 1:100000000是_____比例尺,有时写成———— 表示_____________________________;或表示________________________。
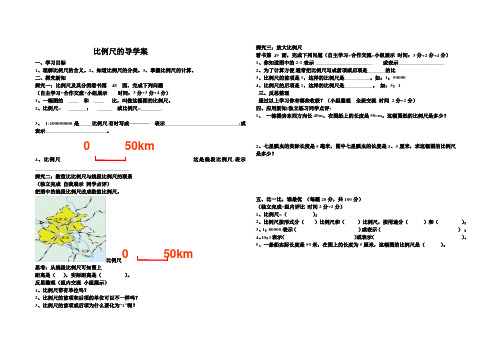
4、比例尺这是线段比例尺,表示_____________________________________探究二:数值比比例尺与线段比例尺的联系 (独立完成 自我展示 同学点评) 把图中的线段比例尺改成数值比例尺。
比例尺思考:从线段比例尺可知图上距离是( ),实际距离是( )。
反思整理(组内交流 小组展示)1、比例尺带有单位吗?2、比例尺的前项和后项的单位可以不一样吗?3、比例尺的前项或后项为什么要化为“1”呢?探究三:放大比例尺看书第 49 面,完成下列问题(自主学习+合作交流+小组展示 时间:3分+2分+4分) 1、你知道图中的2:1表示 ______________________ 或表示__________________ 2、为了计算方便,通常把比例尺写成前项或后项是_______的比 3、比例尺的前项是1,这样的比例尺是__________。
如:1:50000 4、比例尺的后项是1,这样的比例尺是___________。
如:5:1 三、反思整理通过以上学习你有哪些收获?(小组整理 全班交流 时间 2分+2分) 四、应用新知(独立练习同学点评)1、 一栋楼房东西方向长40m ,在图纸上的长度是50cm 。
这幅图纸的比例尺是多少?2、七星瓢虫的实际长度是5毫米,图中七星瓢虫的长度是2、5厘米,求这幅图的比例尺 是多少?五、比一比,谁最优 (每题20分,共100分)(独立完成+组内评比 时间2分+2分) 1、比例尺=( );2、比例尺按形式分( )比例尺和( )比例尺,按用途分( )和( );3、1:80000表示( )或表示( ) ;4、10:1表示( )或表示( )。
《比例尺》 导学案

《比例尺》导学案一、学习目标1、理解比例尺的概念,知道比例尺的种类。
2、能根据比例尺的定义计算实际距离和图上距离。
3、能够运用比例尺解决实际生活中的问题,如绘制地图、设计建筑图纸等。
二、学习重难点1、重点(1)理解比例尺的含义,掌握比例尺的计算方法。
(2)能正确运用比例尺解决实际问题。
2、难点(1)理解比例尺的本质,即图上距离与实际距离的比。
(2)根据不同的比例尺和实际距离,准确计算图上距离或实际距离。
三、知识链接在日常生活中,我们常常会看到各种各样的地图,比如世界地图、中国地图、城市地图等。
这些地图是怎么绘制出来的呢?为什么地图上的距离和实际的距离不一样呢?这就需要用到我们今天要学习的知识——比例尺。
四、学习过程(一)比例尺的概念1、观察下面两张地图,思考它们有什么不同?(展示两张比例尺不同的地图)2、引导得出比例尺的定义:比例尺是表示图上一条线段的长度与地面相应线段的实际长度之比。
公式表示为:比例尺=图上距离 ÷实际距离3、比例尺的表示方法(1)数值比例尺:如 1:1000,表示图上 1 厘米代表实际距离 1000 厘米。
(2)线段比例尺:如,表示图上 1 厘米代表实际距离 50 千米。
(二)比例尺的计算1、已知图上距离和比例尺,求实际距离例 1:在一幅比例尺为 1:50000 的地图上,量得学校到图书馆的图上距离为 4 厘米。
请问学校到图书馆的实际距离是多少米?解:实际距离=图上距离 ÷比例尺= 4 ÷ 1/50000= 4 × 50000= 200000(厘米)= 2000(米)2、已知实际距离和比例尺,求图上距离例 2:实际距离为 800 米,比例尺为 1:20000,求图上距离。
解:图上距离=实际距离 ×比例尺800 米= 80000 厘米图上距离= 80000 × 1/20000 = 4(厘米)(三)比例尺的应用1、绘制地图假设要绘制学校的平面图,我们首先需要测量学校各个建筑物之间的实际距离,然后根据选定的比例尺,计算出图上距离,最后进行绘制。
六年级上册数学导学案-6.2 认识比例尺|冀教

六年级上册数学导学案-6.2 认识比例尺 | 冀教一、导入1.1 问题导入小明拿到一张地图,他发现地图上写着:“比例尺1:50 000”,小明不懂这是什么意思,请问老师这张地图的含义是什么?1.2 学习目标•了解比例尺的概念和表示方法•掌握应用比例尺进行实际测量和计算的方法二、概念解释2.1 什么是比例尺?在地图、平面图、工程图、建筑图等图形中,由于图形比较复杂,不易在真实大小下显示,因此必须将图形按一定比例缩小,以便能在较小的空间内方便地观察和测量。
用来表示缩小比例的尺度叫做比例尺。
2.2 如何表示比例尺?比例尺常用分数或比例的方法来表示。
例如:比例尺1:5000表示每1厘米对应5000cm,1:5 000表示每1cm对应5 000cm。
这种两数比较的方式在各种图形中都十分常见。
比例尺等于1/n,表示实际长度与图上长度的比值。
例如1:50,即表示实际长度是图上长度的50倍。
三、练习3.1 单项选择题1.在比例尺1:2 000 000中,地图上两地之间距离是2mm,那么实际距离是多少千米?A. 1 000 kmB. 2 000 kmC. 4 000 kmD. 8 000 km答案:C。
2.将一个区域缩小5 000倍,则实际面积是图上面积的多少倍?A. 1/5000B. 1/25 000 000C. 5000D. 25 000 000答案:B。
3.2 计算题1.某区域的面积是75 000km²,用1:40 000的比例尺画成地图,请问这张地图的面积是多少平方厘米?解:1:40 000表示实际长度1厘米表示4 000厘米。
因此,实际面积是75 000km²×(1 000m/1km)×(100cm/1m)×(1cm/4 000cm)²=23.44 cm²。
所以这张地图的面积是23.44 cm²。
2.某城市距离广州的直线距离为800km,一张地图上两地之间距离是4cm,这张地图的比例尺是多少?解:比例尺等于实际长度与图上长度的比值,因此比例尺为800 km÷(4cm÷1 000 000cm/km)=200 000 : 1。
比例尺的应用全册导学案设计.docx

1、完成教材54页 “做一做”。
2、完成教材57页8题。
3、出示练习题:在 比例尺是1:10000000的地图 上,量得甲、乙两城 之间的路程是10 COlo一辆汽车以每 小时100 km的速度
1、独立完成,汇报交 流。
2、填写后,说出求图上 距离和实际距离的方 法。
3、分析题中的数量关 系后,独立解答并汇 报。
(2)指名试做。
1、(D分析题意,明确:图上距离_.. ,ttl根据实际距离一比例 尺,可以用解比例的方 法求出实际长度。
(2)尝试解决。
解:设从苹果园站至四 惠东站的实际长度大 约是Xcmo
7.81
* ^400000
2、解决问题。
(1)一幅地图 的比例尺是1:1700000,量得图上3 cm可以表示 实际多少「 米?
课前准
备
教师准备PPT课件
教学过程
教学环
节
教师指导
学生活动
效果检测
一、复习
导入。(5分钟)
引导学生思考:
(1)什么叫做比例 尺?
(2)比例尺有什么 特点?
(3)怎样求比例 尺?
思考后回答:
(1)一幅图的图上距离 和实际距离的比,叫做 这幅图的比例尺。
(2)比例尺的特点:比 例尺是一个比,不是 尺,不带单位名称。
2、关注学生解决问题能力的培养。
《数学课程标准》强调:要让学生学习有用的数学,并 能主动运用所学的数学知识解决现实生活中的实际问题。为 此,应引导学生从数学的角度去看待和解决生活中的实际问 题,形成解决问题的一些基本策略,体验解决问题策略的多 样性,从而提高解决问题的能力。在教学中,要有效地利用教 材提供的素材,恰当补充例题,引导学生进行小组合作交流、 探究用比例尺的知识解决相关问题的方法,使学生在理解多 种解题策略的同时,实现解题策略的优化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级下册数学总复习《比例尺》导学案
编者:泉湖小学张红莲
复习目标:1、进一步理解、掌握比例尺的意义;
2、能够运用比例尺知识解决有关设计问题。
复习过程:
一、回顾与交流
1.什么叫比例尺?比例尺有几种类型?举例说说它的意思?(重点是线段比例尺)
2.举例说说怎样求图上距离?怎样求实际距离。
二、达成目标
(一)填空。
1.在比例尺是1:4000000的地图上,图上距离1厘米表示实际距离()千米。
也就是图上距离是实际距离的,实际距离是图上距离的()倍。
2.一种微型零件的长5毫米,画在图纸上长20厘米,这幅图的比例尺是()。
3.判断下列各题中两种量是否成比例?成什么比例?
(1)路程一定,车轮的周长和车轮滚动的圈数。
()
(2)长方形的长一定,宽和面积。
()
(3)大米的总量一定,吃掉的质量和剩下的质量。
()
(4)圆的半径和周长。
()
(5)分数的分子一定,分数值和分母。
()
(6)铺地面积一定,方砖的边长和所需块数。
()
(7)铺地面积一定,方砖面积和所需块数。
()
(8)除数一定,被除数和商。
()
4.A、B 、C 三种量的关系是: A×B = C
(1)如果 A一定,那么 B和 C成()比例;
(2)如果 B一定,那么 A和C 成()比例;
(3)如果 C一定,那么 A和 B成()比例.
5.4X=Y,X和Y成()比例。
4÷X=Y ,X和Y成()比例。
(二)判断
1.一项工程,甲队40天可以完成,乙队50天可以完成。
甲乙两队的工作效率比是4:5。
()
2.圆柱体与圆锥体的体积比是3:1,则圆柱体与圆锥体一定等底等高。
()
3.甲数与乙数的比是3:4,甲数就是乙数的。
()
4.比的前项和后项同时乘以同一个数,比值不变。
()
5.总价一定,单价和数量成反比例。
()
6.实际距离一定,图上距离与比例尺成正比例。
()
7.正方体体积一定,底面积和高成反比例。
()
(三)解决问题
1.一块直角三角形钢板用1:200的比例尺画在图上,两条直角边共长5.4厘米,它们的比是5:4.这块钢板的实际面积是多少?
2. 甲乙两地在比例尺是1:20000000的地图上长4厘米,乙丙两地相距500千米,画在这幅地图上,应画多长?一辆汽车以每小时200千米的速度从甲地经过乙地,去丙地需要多少小时?
补充:用比例解
(1)一条公路全长600米,前3天已经修了120千米,如果按照这样的进程,还需要几天修完?
(2)工厂里要加工一批服装,原来每天加工250套,需要40天完工。
现在每天多加工50套,现在几天可以完工?
【
能力有限,实属抱歉,望海涵!。
