电子科大讲义课堂信号与系统考卷-资料
杭州电子科技大学信号与系统真题2000-2009
7. 已 知 线 性 时 不 变 系 统 的 输 入 — 输 出 方 程 为
r (t ) = ∫ e −(t −τ ) e(τ )dτ 则其冲击响应 h(t)为________
−∞
8.
e −αt u (t ) * sin tu (t ) = ________
9. 已知某连续系统的零点为 1;极点为 0,-3;冲激响应的终
要求:1 画出其信号流图; 2 写出其状态方程。(12 分)
某些地方难免出错,敬请见谅。 其中2001年真题以及历年答案本人没有找到, 如果谁有可以跟我联系。 做出一份比较完整的考研试卷帮助大家Q:305942916
7/26
杭州电子工业学院 2003 年攻读硕士学位研究生入学考试 《信号与系统》 (共九大题)
e − t u (t ) * sin t u (t ) =_______
3 £ [(1 + 2t )e −t ] = ________ 4 £ −1 ⎢
⎤ s+3 ⎥ =________ 3 ⎣ ( s + 1) ( s + 2) ⎦ ⎡
5 若 F [ f (t )] = F ( w) ,则 F[(1-t)f(1-t)]=_________ 6 已 知 系 统 函 数 H(s)= r(t)=_________
五. (8 分)系统如图所示,试画出其流图表示,并求转移函数 H(s) =
Y (s) 。 X ( s)
六. (10 分)信号的频谱如图所示,若此信号通过下图系统,试绘出 A、B、C、D 各点信号的频谱图形,设理想滤波器截止频率均为 W 0 ,
2/26
通带内传输值为 1,相移为零,且 W 0 >>W c .
值为-10,则该系统函数为 H(S)=________
信号与系统试卷电科专业
哈尔滨理工大学2006-2007学年第二学期考试试题 A 卷考试科目: 信号与系统 考试时间:120分钟 试卷总分100分一、选择题(在每个小题四个备选答案中选出一个正确答案,填在题末的括号中)(本大题共5小题,每小题2分,总计10分)1、已知()f t ,为求0()f t at -应按下列哪种运算求得正确结果(式中0t 和a 都为正值)? (A )()f at -左移0t ; (B )()f at 左移0t ; (C )()f at -左移0t a; (D )()f at 左移t a; 2、连续时间系统输出()r t 和输入()e t 满足()5()tr t e d ττ-∞=⎰,则该系统是( )(A )线性、时变、非因果 (B )线性、时不变、因果 (C )非线性、时变、非因果 (D )非线性、时不变、非因果 3.连续时间系统输出()r t 和输入()e t 满足()()de t r t dt=,则该系统是( ) (A )线性、时变、非因果 (B )线性、时不变、因果 (C )非线性、时变、非因果 (D )非线性、时不变、非因果4、已知信号()f t 的傅里叶变换为()F j ω,则信号()()2t f t -的傅里叶变换:(A )()()2dFj F j d ωωω-+; (B )()()2dF j F j d ωωω+;(C )()()2dF j F jd ωωω--; (D )()()2dF j F j d ωωω--;5、已知信号()f t 的傅里叶变换为()F j ω,则信号()2tf t 的傅里叶变换:(A )122dF j d ωω⎛⎫ ⎪⎝⎭-; (B )122dF j d ωω⎛⎫ ⎪⎝⎭; (C )()()2dF j F jd ωωω--; (D )()()2dF j F j d ωωω--; 6、连续周期信号的频谱具有( )(A )连续性、周期性 (B )连续性、收敛性 (C )离散性、周期性 (D )离散性、收敛性 7、连续非周期信号的频谱具有( )(A )连续性、周期性 (B )连续性、收敛性 (C )离散性、周期性 (D )离散性、收敛性 8、系统()()2r t e t =是(A )稳定系统、可逆系统 (B )稳定系统、非可逆系统 (C )非稳定系统、可逆系统 (D )非稳定系统、非可逆系统 9、系统()()5r t e t =-是(A )稳定系统、可逆系统 (B )稳定系统、非可逆系统 (C )非稳定系统、可逆系统 (D )非稳定系统、非可逆系统 二、填空题(每空2分,共20分) 1、()()0j t e t t t dt ωδδ∞--∞--⎡⎤⎣⎦⎰= ;2、()sin 6t t t dt πδ∞-∞⎛⎫+- ⎪⎝⎭⎰= ;3、确定信号()()210060Sa t Sa t +的最低抽样率 ,奈奎斯特间隔 ;4、确定信号()()210080Sa t Sa t +的最低抽样率 ,奈奎斯特间隔 ;哈尔滨理工大学2006-2007学年第二学期考试试题 A 卷5、确定信号()()1T n t t nT δδ∞=-∞=-∑的傅里叶变换 。
电子科技大学信号与系统-信号与系统考题
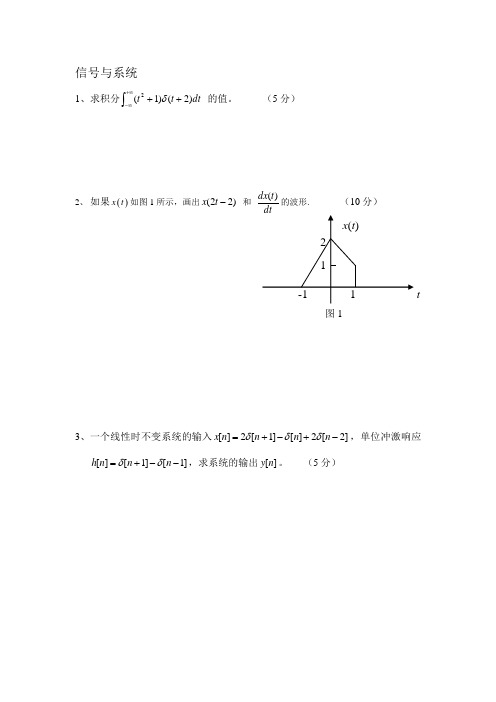
信号与系统1、求积分⎰+∞∞-++dt t t )2()1(2δ 的值。
(5分)2、 如果()x t 如图1所示,画出)22(-t x 和t dx )(的波形. (10分)图13、一个线性时不变系统的输入]2[2][]1[2][-+-+=n n n n x δδδ,单位冲激响应]1[]1[][--+=n n n h δδ,求系统的输出][n y 。
(5分)t4、一个线性时不变系统的输入为)(1tx时,输出为)(1ty。
若输出信号为)(2tx,求输出信号)(2ty。
各信号如图2所示。
(5分)图25、已知)1()()(--=tututx,)2/()(txth=,求)(*)()(thtxty=。
(5分)6、一个线性时不变系统的单位冲激响应为 )2sin 8(sin 1)(t t tt h πππ-=, 如果输入信号为 t t t x ππ6sin 4cos 1)(++=, 求输出信号()y t .(10分)7、 设 ()x t 是一个带限信号,()x t 的频谱满足()0 for 100X j ωωπ=>。
现对)()(2t x t y =冲激串采样,得到()()()p n y t y nT t nT δ+∞=-∞=-∑求采样间隔 T 的范围使得 ()t y 能由信号()t y p 恢复。
(10分)8、(15分)一个稳定的线性时不变系统,其微分方程如下)()()(6)(5)(22t x dtt dx t y dtt dy dtt y d +=++1) 求系统函数H(S),决定H(S)的收敛域。
2)求系统的单位冲激响应()h t ,判定系统是否因果。
3)画出系统的模拟方框图。
第九章考题电子科技大学信号与系统858期末复习

Solution
5. H (S)
S
,3 Re{S} 2
(S 3)(S 2)
6. Consider a stable LTI systemwith rational systemfunction H (S)
for whichthe pole - zero plot is shownin Figure.
is this systemcausal? c).Determni e the output y(t) with theinput x(t) e2tu(t) . d).Determine the output y(t) with theinput x(t) 1.
x(t)
+
1/s
1/s
y(t)
is this systemcausal? c).Determni e the output y(t) with theinput x(t) e2t .
1/(s+2)
x(t)
+
1/s
+
y(t)
-3
Solution
11. H (S) 2S 5 , Re{S} 2 (S 3)(S 2)
Chapter 9
Determine x(t)
1. Determine thefunctionof time, x(t), for theLT transform
X (S) and its associatedregions of convergence :
X
(S)
es
1 es
Re{s} 0.
Solution
4. H (S) S 3 ,4 Re{S} 1 (S 4)TI systemwith systemfunction
电子科技大学2014-2015 学年第 1 学期信号与系统期 末 考试 A 卷

电子科技大学2014-2015 学年第 1 学期期末考试A 卷课程名称:信号与系统考试形式:一页纸开卷考试日期:20 15年 1 月 15 日考试时长: 120 分钟课程成绩构成:平时 10 %,半期考试 20 %,实验 10 %,期末 60 %本试卷试题由二部分构成,共 5 页。
题号一二合计1234得分得分一、选择填空题(共30分,共 6问,每问5分)1.Consider two signals and , as shown in Figure 1. The Fourier transform of is . Then the Fourier transform ofshould be().(a)(b)(c)(d)Figure 1 The waveforms of and2. The convolution sum ( ).(a) (b) (c) (d) not existed3. Consider a stable discrete-time system, whose system function is a rational function and has only two poles:. The positions of zeros are unknown. The impulse response of the system must be ( ).(a) finite duration (b) right-sided (c) left-sided (d) two sided4.The relation between the input and the output of a causal continuous-time LTI system is described by the differential equation . The system is ().(a) Low-pass filter (b) Band-pass filter (c) High-pass filter (d) Band-stop filter5.The Fourier transform of the signal is shown in Figure 2.The signal may beFigure 2(a) real and even (b) real and odd(c) pure imaginary and odd (d) pure imaginary and even6. The Laplace Transform of is ().(a) , (b) ,(c) , (d) ,二、计算题(共70分)得分1.(15 points)Suppose and are both band-limited signals, where.Impulse-train sampling is performed on to obtain , as shown inFigure 3 where .Deduce the value of so that for .Specify the range ofvalues for the sampling period T which ensures that =.32.( 18 points ) Consider an LTI system with unit impulseresponse .The input signal ,where is the unit stepfunction.得分(a) Sketch. (b) Determine the magnitude and phase responseof this system. (c) Determine the output .3(17分)A causal continuous-time LTI system is given in Figure 4.(a)Determine the range of the constant K toensure that the system is stable.(b)If K=2, determine the unit step response.1/S-31/S-2KFigure 44(20 分)Suppose that we are given the following information about a causal discrete-time LTI system:(1)If the input is ,then the output is .(2)The value of the unit impulse response at n=0 is .Solve the following problems:(a) Determine the system function ,and indicate its ROC.(b) Draw a block diagram representation of this system.(c) Determine the unit impulse response .(d) Suppose. Determine the range of real numberso that is the unit impulse response of a stable system.。
电子科大信号与系统习题解答1

信号与系统习题解答11.1 用代数式表达下列复数:已知形式为θj re ,要求表达形式为jy x +,采用公式:θcos r x =,θsin r y =。
解: 2121-=πj e 2121-=-πj ej e j =2π j e j -=-2πj ej=25πj ej+=124π j ej+=1249πj ej -=-1249π j ej-=-124π1.2 用极式表达下列复数:已知形式为jy x +,要求表达形式为θj re ,采用公式:22y x r +=,()πθπθ≤<-=-xytg 1。
解:055j e = πj e 22=- 233πjej -=-()2242221ππjj e e j --=⎪⎪⎭⎫ ⎝⎛=- ()442221πππjjje eej j =⋅=--2442211πππjjje ee jj ==-+-1234223122πππjj je e ej j -==++1.54 (a )证明表达式 ⎪⎩⎪⎨⎧≠--==∑-=111110αααααN N n nN证: 因为 1=α 时,1=n α (n 为任意值时)所以,1=α 时,N N n n =∑-=10α因为 ()()NN ααααα-=++++--1 (111)2所以,当1≠α时,()ααααα--=++++-11 (11)2NN 原式得证。
(b) 证明:1<α时,αα-=∑∞=110n n 证:因为 1<α时,0lim ==∞→NN α所以:αααα-=--=∞→∞=∑1111lim 0N N n n(c )证明:1<α时,()21ααα-=∑∞=n nn 证:令()αααf n n=-=∑∞=11为α的连续函数对上式进行微分运算可得:()()2111αααα-==∑∞=-n n n d df 同时乘以α就可以得到:()21αααααα-==∑∞=n nn d df (d )当1<α时,计算?=∑∞=kn nα解: 因为∑∑∑∞=-=∞=+=kn nk n n n n ααα100所以:αααααααα-=----=-=∑∑∑-=∞=∞=1111110kk k n nn nk n n1.55 计算下列和式,采用代数式表达。
电子科大信号与系统期中考试试卷及答案11-12学年

………密………封………线………以………内………答………题………无………效……电子科技大学二零 一 一 至二零 一 二 学年第 一 学期期 中 考试SIGNALS AND SYSTEMS 课程考试题 卷 ( 120 分钟) 考试形式: 闭卷 考试日期 20 11 年 月 日课程成绩构成:平时 10 分, 期中 20 分, 实验 10 分, 期末 60 分1(56points).Each of the following questions may have one or two right answers, justify your answers and write it in the blank. (1)()cos 221πδ+∞-∞-=⎰t t dt ( d ).(a) 1 (b) -1 (c) 0.5 (d) -0.5(2) The fundamental period of the signal []23cos sin 32ππ⎡⎤⎡⎤=-⎢⎥⎢⎥⎣⎦⎣⎦x n n n is ( a ). (a) 12N = (b) 6N = (c) 8N = (d) 24N = (3) Let ()1tx t e -= and ()()()14k x t x t t k δ+∞=-∞=*-∑. The Fourier series coefficients of ()x t may be ( a ).(a) {} and Im 0-==k k k a a a (b) {} and Im 0-=-=k k k a a a (c) {} and Re 0-==k k k a a a (d) {} and Re 0k k k a a a -=-=(4) Consider an LTI system with unit impulse response ()h t illustrated in Figure 1, if the input is ()()d t x t dtδ=, the output () 0.5t y t =- is( b ).(a) -1 (b) 1 (c) -0.5 (d) 0.5(5) The convolution integral ()222t te e u t -*=( c ).(a) 2 (b)214te (c)212te (d)()212te u t(6) Which of the following systems is an linear system ( a ). In each example, []y n denotes the system output and []x n is the systeminput.(a) [][][]cos y n n x n = (b) [][]{}cos 3y n x n = (c) [][]()ln y n x n = (d) [][]2y n x n =(7) Which of the following systems are causal and stable system ( ad ). In each example, ()h t denotes the impulse response of thefollowing systems.(a) ()()()13h t t t δδ=-+- (b) ()()()0.5cos 2t h t t e u t =- (c) ()()()13h t t t δδ=+++ (d) ()()()cos 2t h t t e u t -=-(8) Determine the following signals which have finite total energy ( bc ). (a) []()[]1x n n u n =+ (b) ()()23tx t eu t -=+(c) []()[]1cos /32nx n n u n π⎛⎫= ⎪⎝⎭(d) () , tx t e t =-∞<<+∞tFigure 1………密………封………线………以………内………答………题………无………效……(9) Consider a continuous-time LTI system whose frequency response is ()()sin /2Hj ωωω=. If we know the output ()y t to some periodicinput signals are ()0y t =. The fundamental period of the input signal may be ( ac ). (a) 1T = (b) 2T = (c) 0.5T = (d) 3T =2(12points). A continuous-time signal ()32-+x t is illustrated in Figure 2.(a) Determine the signal ()x t . (b) Sketch and label carefully ()x t .3(10 points).Consider an LTI system whose response to the signal ()t x 1 in Figure 3 is the signal ()t y 1 illustrated in Figure 4. Determine the response of the system to the input ()t x 2 depicted in Figure 5 .4(12 points). Consider a continuous-time LTI system whose frequency response ()H j ω is illustrated in Figure 6. If the input signal()1cos 3sin 6ππ=++x t t t , determine the output of the system.12Figure 3ωFigure 6tFigure 2………密………封………线………以………内………答………题………无………效……14(10points). Consider an LTI system whose input []x n and unit impulse response []h n are given by []{}1,0,1,1,0,1x n n =-=-,[]{}2,1,3,2,2,3,4,5h n n ==. Determine the output [][][]n h n x n y *= of this system.《信号与系统》半期考试评分标准说明1.填空题(56分)⑴. (d) ⑵ (a) ⑶ (a) ⑷ (b) ⑸ (c) ⑹ (a) ⑺ (ad) ⑻ (bc) ⑼ (ac) ⑽ (ab) 本部分评分规则:1) 选择题共14个正确答案,1-6题为单选,7-10题为双选; 2) 若只填写了1个答案,正确得4分,错误得0分;3) 若填写了2个答案,2个正确得8分,1个正确、1个错误得4分,2个错误得0分;4) 若填写了3个答案,2个正确、1个错误得4分,1个正确、2个错误得2分,3个错误得0分; 5) 若填写了4个答案,得0分。
电子科大《信号与系统》考卷汇总

x t
cos 4 t
2
w t
H ( j )
2
w t
5 4
1
4
5
0
1
y t
H ( j )
X j
1
4
0
Figure 2 5
0
y t
5 4
Figure 1
0
信号与系统试卷
2004年7月
2. (
10points来自G j 15 X j for 0 ,
x t
h 1 t
r1 t
r2 t
H 2 j
y t
p t
Figure 2
信号与系统试卷
4. (15 points) The system function of an LTI system is
2
(a)Specify the range of values for the sampling period T which ensures that r1 t is recoverable from
r2 t .
(b) If T
1 second, sketch the spectrum of r1 t and r2 t . 20
Attention: You must answer the following questions in English.
信号与系统试卷 2005 1.( 12 points)The spectrum X j of the signal x t is depicted in Figure 1.
the output y t 1 . (a) Determine the system function H s , then indicate the ROC of H s . (b) Determine the unit impulse response h t of this system, is this system causal? (c) For the input x t te u t , compute the output y t .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
h n 1, 0, 2 , n 0,1, 2
5.
(20
points)
Consider
h t
sin 2 t t
cos 7 t
,
if
the
an
LTI
system
input is
x t n
with
unit
impulse
response
t n , determine the output
.
t 2
x t u t , and
h t
is illustrated in Figure 4. Please
h t
1
0
1
2
3
t
Figure 4
4. (10 points) Compute the convolution y n x n h n , where
x n 3,1, 5 , n 1, 2, 3
t n ,
determine
the
output
y t . 6. (20 points) Consider an LTI system with input
x t
t e3t u t and output
y t et u t .
(a) Determine the system function H s , then indicate the ROC of
H s .
(b) Determine the unit impulse response
y t .
2.
( 10 points ) Consider a continous-time system with input
x t
and output
y t
related by
(a)
Linear? Stable?
(b)
y t x 2t 1
, is this system
Time-invariant?
x n 3,1, 5 , n 1, 2, 3
h n 1, 0, 2 , n 0,1, 2
5.
(20
points)
Consider
h t sin 2 t
t cos 7
t,
if
the
an
LTI
input is
system
x t
n
with
unit
impulse
response
t n , determine the output
y t .
6. (20 points) Consider an LTI system with input
x t
t e3t u t and output
y t et u t .
(a) Determine the system function H s , then indicate the ROC of
y t related by
y t x 2t 1 , is this system
(a) Linear? Stable?
(b) Time-invariant?
(c) Memoryless?
(d) Causal?
(e)
3. (10 points) If we know
determine x t h t
2.
( 10 points ) Consider a continous-time system with input
x t
and output
y t
related by
(a) Linear? Stable?
(b)
y t x 2t 1
, is this system
Time-invariant?
H s .
(b) Determine the unit impulse response
h t
of this system, is this system
causal and stable?
Hale Waihona Puke (c) For the input
x t 2 , compute the output
y t .
(d) Determine the differential equation of this system.
(c)
Memoryless?
(d)
Causal?
(e)
3. (10 points) If we know
determine
x t h t
.
t 2
x t u t , and
h t
is illustrated in Figure 4. Please
h t
1
0
1
2
3
t
Figure 4
4. (10 points) Compute the convolution y n x n h n , where
x1 (t ) 1
y1 (t ) 1
0
1
t
Figure 1
0
1
2
t
Figure 2
x2 t depicted in Figure 3.
x2 (t ) 1
0
1
2
3
t
Figure 3
2.
( 10 points ) Consider a continous-time system with input x t and output
x n 3,1, 5 , n 1, 2, 3
h n 1, 0, 2 , n 0,1, 2
5.
(20
points)
Consider
h t sin 2 t
t cos 7
t,
if
the
an
LTI
input is
system
x t n
with
unit
impulse
response
1. (10 points) Consider an LTI system whose response to the signal x1 t in
Figure 1 is the signal
y1 t illustrated in Figure 2. Determine and sketch
carefully the response of the system to the input
(c)
Memoryless?
(d)
Causal?
(e)
3. (10 points) If we know
determine
x t h t
.
t 2
x t u t , and
h t
is
illustrated
h t
in
Figure
4.
Please
1
0
1
2
3
t
Figure 4
4. (10 points) Compute the convolution y n x n h n , where
