信号与系统实验指导书版
信号与系统实验指导书070119
实验一信号波形的观察和测试一、实验目的1．学习示波器、函数发生器和万用电表的使用方法。
2．学会用示波器测量信号的周期和频率。
3．学会用示波器测量, 直流信号, 正弦交流信号的叠加。
二、实验原理1．直流, 正弦交流, 三角波，方波是常用的电信号, 可由直流稳压电源, 函数发生器提供, 如下图1-1所示, 这些波形都能用示波器进行观察。
图1-1 用示波器观察波形2．直流电的主要参数是幅度V或I, 用万用表测试最方便，但直流电压的幅度也可用示波器测量。
当需要测定信号中直流分量时, 可将输入耦合方式开关置“DC”, 这时仅显示信号中的直流分量波形,从示波器Y轴就能读出直流分量的幅度。
正弦交流电的主要参数是振幅(V m,I m), 周期T, 频率f和初相角, 它们都可以用示波器进行测定, 从示波器Y轴(垂直)刻度尺可读得被测波形的幅度, 从X轴(水平)刻度尺可读得被测波形的周期。
测试信号幅度的常用仪器有万用表, 晶体管毫伏表和示波器。
应注意用万用表和毫伏表测交流电时, 读书都是有效值,它们的测量对象, 仅限于正弦交流电, 测量误差会受到信号的频率和波形失真程度的影响。
因此不要用万用表和毫伏表去测量方波, 三角波的幅度.除非对读数进行必要的修正。
万用毫伏表示波器测试正弦家六电压的性能比较如表2-10-1所示。
三、实验内容1、信号的观察及幅度的测定：按图1-2方式连接函数信号发生器, 示波器, 晶体管毫伏表和万用表。
图1-2 信号的测量a．信号发生器产生100HZ, 1500Hz, 5kHz三种不同频率的正弦信号, 幅度自定。
要求调节示波器在荧光屏上观察到一个或若干个完整波形, 务必使图形清晰和稳定。
从Y轴刻度读出被测信号幅度, 并与万用电表读数相比较。
结果填表1-1。
表1-1b．信号发生器产生400Hz正弦信号，方波和三角波, 调节示波器使波形稳定, 从Y轴刻度读出被测信号幅度, 并与万用电表读数相比较。
结果填表1-2。
信号与系统实验指导书
信号与系统
实验教学
(8) 函数信号发生器
本信号发生器由单片集成函数信号发生 器ICL8038及外围电路、功率放大电路等组 合而成。其输出频率范围为2Hz～150KHz， 由“频段选择”开关(粗调分五档)和“频率 调节”旋钮(细调)进行调节。输出幅度峰峰 值为0～16Vp-p，由“幅度调节”旋钮进行 细调。使用时，只要开启函数信号发生器分 开关，信号源即进入工作状态。
信号与系统
实验教学
信号与系统实验 指导书
湖南文理学院电信学院
信号与系统
教材及参考资料
教材：
《信号与系统》曾喆昭、倪振文 编著 湖南大学出版社
参考资料：
《信号与系统》刘树棠 译 西安交通大学出版社出版
《自动控制理论》孙扬声 编著 中国电力出版社出版
《通信原理》樊昌信、张甫翊 等编著 西安电子科技大学出版社
输出波形分正弦波、方波和三角波三种， 由“波形选择”开关选择，输出阻抗为50Ω， 当负载电阻为50Ω时，输出幅值为开路输出 值的一半。
信号与系统
实验教学
(9) 频率计
本频率计是由单片机89C51和六位共阴极LED 数码管设计而成的，具有输入阻抗大和灵敏度 高的优点。其分辨率为1Hz，测频范围为1Hz～ 10MHz，灵敏度为100mV，输入阻抗1MΩ，闸门 时间1秒。
信号与系统
实验教学
（5）直流稳压电源
提供四路±5V，0.5A和±15V，0.5A直流稳 压电源，每路均有短路保护自恢复功能，只 要开启电源总开关，就有相应的电压输出， 并有响应发光二极管指示。
（6）非正弦多波形信号发生器
提供50Hz半波、全波、方波、矩形波、三 角波共五种波形,半波由交流电半波整流得到， 全波由交流电全波整流得到，方波、矩形波 由运放加外围器件构成，三角波是在方波的 基础上加了一个由运放和电容构成的积分环 节而得到。
信号与系统实验指导书
信号与系统实验指导书庞勇倪育德韩萍编中国民航学院空管学院通信工程系目录实验一常用信号的分类与观察 (1)实验二零输入响应与零状态响应 (6)实验三离散时间信号卷积和 (8)实验四连续时间卷积的数值近似 (11)实验五信号的分解与合成 (13)实验六连续时间周期信号的傅立叶级数表示与综合 (18)实验七连续时间信号的时域采样与恢复 (20)实验八连续系统的频率响应 (24)实验九无失真传输系统 (30)实验十连续时间系统分析 (34)实验一 常用信号的分类与观察一、实验目的1、观察常用信号的波形特点及产生方法。
2、学会使用示波器对常用波形参数的测量。
二、实验内容1、信号的种类相当的多，这里列出了几种典型的信号，便于观察。
2、这些信号可以应用到后面的“基本运算单元”和“无失真传输系统分析”中。
三、实验仪器1、信号与系统实验箱一台（主板）。
2、20MHz 双踪示波器一台。
四、实验原理对于一个系统特性的研究，其中重要的一个方面是研究它的输入输出关系，即在一特定的输入信号下，系统对应的输出响应信号。
因而对信号的研究是对系统研究的出发点，是对系统特性观察的基本手段与方法。
在本实验中，将对常用信号和特性进行分析、研究。
信号可以表示为一个或多个变量的函数，在这里仅对一维信号进行研究，自变量为时间。
常用信号有：指数信号、正弦信号、指数衰减正弦信号、抽样信号、钟形信号、脉冲信号等。
1、正弦信号：其表达式为)sin()(θω+=t K t f ，其信号的参数：振幅K 、角频率ω、与初始相位θ。
其波形如图1.1所示。
图 1.1 正弦信号2、指数信号：指数信号可表示为atKe t f =)(。
对于不同的a 取值，其波形表现为不同的形式，如图1.2所示。
图 1.2 指数信号3、指数衰减正弦信号：其表达式为 ⎪⎩⎪⎨⎧><=-)0()sin()0(0)(t t Ke t t f at ω其波形如图1.3所示。
图 1.3 指数衰减正弦信号4、抽样信号：其表达式为： sin ()tSa t t=。
信号与系统实验指导书
实验一 滤波器一 实验目的1 了解无源和有源滤波器的种类、基本结构及其特性；2 对比并研究无源滤波器和有源滤波器的滤波特性； 二 原理说明1．滤波器的作用是对输入信号的频率具有选择性。
滤波器的种类很多，但总的来说，可分为两大类，即经典滤波器和现代滤波器。
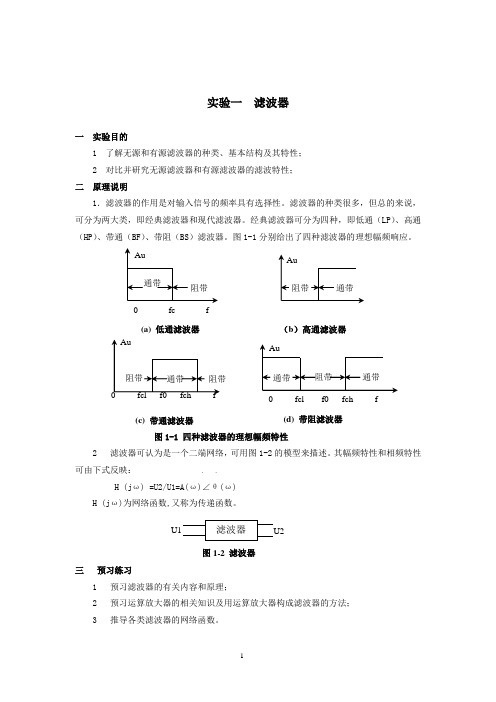
经典滤波器可分为四种，即低通（LP ）、高通（HP ）、带通（BF ）、带阻（BS ）滤波器。
图1-1分别给出了四种滤波器的理想幅频响应。
图1-1 四种滤波器的理想幅频特性2 滤波器可认为是一个二端网络，可用图1-2的模型来描述。
其幅频特性和相频特性可由下式反映： . .H (j ω) =U2/U1=A(ω)∠θ(ω)H (j ω)为网络函数,又称为传递函数。
三 预习练习1预习滤波器的有关内容和原理；2 预习运算放大器的相关知识及用运算放大器构成滤波器的方法；3 推导各类滤波器的网络函数。
（b ）高通滤波器(c) 带通滤波器(a) 低通滤波器0 fc f(d) 带阻滤波器0 fcl f0 fch f图1-2 滤波器四实验步骤及内容1 用实验导线按图1-3构造滤波器：(a) 无源低通滤波器 (b) 有源低通滤波器(c) 无源高通滤波器 (d) 有源高通滤波器(e) 无源带通滤波器 (f) 有源带通滤波器（g）无源带阻滤波器（h）有源带阻滤波器图1-3 各种滤波器的实验电路图2 测试各无源和有源滤波器的幅频特性：例1：测试RC无源低通滤波器的幅频特性。
实验电路如图1-3（a）所示。
实验时，打开函数信号发生器，使其输出幅度为1V的正弦信号，将此信号加到滤波器的输入端，在保持正弦信号输出幅度不变的情况下，逐渐改变其频率，用交流电压表测量滤波器输出端的电压U2。
每当改变信号源频率时，例2：测试RC有源低通滤波器的幅频特性。
实验电路如图1-3（b）所示。
放大系数K=1。
实验时，打开函数信号发生器，使其输出幅度为1V的正弦信号，将此信号加到滤波器的输入端，在保持正弦信号输出幅度不变的情况下，逐渐改变其频率，用交流电压表测量滤波器输出端的电压U2。
信号与系统实验指导书
信号与线性系统分析实验指导书山东理工大学电气与电子工程学院目录实验一、50Hz非正弦周期信号的分解与合成 (2)实验二、三无源和有源滤波器 (6)实验四、抽样定理 (11)实验一、50Hz非正弦周期信号的分解与合成一、试验目的1、用同时分析法观测50Hz非正弦周期信号的频谱，并与其傅立叶级数各项的频率与系数作比较。
2、观测基波和其谐波的合成。
二、实验设备1、信号与系统实验箱TKSS-A型或TKSS-B型或TKSS-C型。
2、双踪示波器三、原理说明1、一个非正弦周期函数可以用一系列频率成整数倍的正弦函数来表示，其中与非正弦具有相同频率的成分称为基波或一次谐波，其它成分则根据其频率为基波频率的2、3、4…、n等倍数分别称为二次、三次、四次…、n次谐波，其幅度将随谐波次数的增加而减少，直至无穷小。
2、不同频率的谐波可以合成一个非正弦周期波，反过来，一个非正弦周期波也可以分解为无限个不同频率的谐波成分。
3、一个非正弦周期函数可用傅立叶级数来表示，级数各项系数之间的关系可用各个频谱来表示，不同的非正弦周期函数具有不同的频谱图，各种不同波形及其傅氏级数表达式见表1-1，方波频谱图如图1-1表示。
图1-1 方波频谱图表1-1 各种不同波形的傅立叶级数表达式1、方波⎪⎭⎫⎝⎛ΩΩ+Ω+Ω+Ω=t n n t t t t u t u m sin 17sin 715sin 513sin 31sin 4)( π 2、三角波⎪⎭⎫⎝⎛+Ω+Ω-Ω=t t t u t u m 5sin 2513sin 91sin 8)(2π 3、半波⎪⎭⎫⎝⎛+Ω-Ω-Ω+=t t t u t u m 4cos 151cos 31sin 4212)(ππ 4、全波⎪⎭⎫ ⎝⎛+Ω-Ω-Ω-=t t t u t u m 6cos 3514cos 1512cos 31214)(π 5矩形波⎪⎭⎫⎝⎛+Ω+Ω+Ω+=t T u t T u t T u u Tu t u m m m m m3cos 3sin 312cos 2sin 21cos sin2)(τττπτ 实验装置的结构如图1-2所示图1-2 信号分解与合成实验装置结构框图图中LPF 为低通滤波器，可分解出非正弦周期函数的直流分量。
信号与系统实验指导书-学生
第一章功能模块操作说明实验一函数信号发生器一、实验目的1、了解函数信号发生器的操作方法。
2、了解单片多功能集成电路函数信号发生器的功能及特点。
3、熟悉信号与系统实验箱信号产生的方法。
二、实验内容1、用示波器观察输出的三种波形。
2、调其中电位器、拨位开关，观察三种波形的变化，了解其中的一些极限值。
三、实验原理1、MAX038的原理MAX038是单片精密函数信号产生器,它用±5V电源工作，基本的振荡器是一个交变地以恒流向电容器充电和放电的驰张振荡器, 同时产生一个三角波和矩形波。
通过改变COSC 引脚的外接电容和流入IIN引脚的充放电电流的大小来控制输出信号频率,频率范围为0.1Hz～20MHz。
流入IIN 的电流由加到FADJ 和DADJ 引脚上的电压来调制, 通过此两引脚可用外接电压信号调整频率和占空比。
MAX038 内部有一个正弦波形成电路把振荡器的三角波转变成一个具有等幅的低失真的正弦波。
三角波、正弦波和矩形波输入一个多路器。
两根地址线A0和A1从这三个波形中选出一个, 从OUT引脚输出2V(峰锋值)振幅的信号。
三角波又被送到产生高速矩形波的比较器 (由SYNC 引脚输出)，它可以用于其它的振荡器, SYNC 电路具有单独的电源引线因而可被禁止。
另外, PDI、PDO 引脚分别是相位检波器的输入和输出端, 本信号源没有使用。
2、MAX038的管脚图及管脚功能图1-1-2 MAX038的管脚图3、实验电路如图1-1-3所示：图1-1-3 MAX038实验电原理图四、实验步骤1、接上电源线，按下船形开关、电源开关及该模块电源开关S1201、S1202，使其“输出”为方波，通过调整电位器“占空比调节”，使方波的占空比达到50%（当MAX038的第7脚电压DADJ为0V时，方波的占空比为50%）。
(注：“波形选择”开关K1201和K1202用于选择“方波”、“三角波”、“正弦波”，当K1201和K1202拨到左边时，输出方波，当K1201拨到右边且K1202拨到左边时，输出三角波；当K1201和K1202拨到右边时，输出正弦波。
信号与系统实验指导书
信号与系统实验指导书目录实验1非正弦信号的谐波分解 (1)实验2波形的合成 (6)实验3无源和有源滤波器 (8)实验4开关电容滤波器 (12)实验5抽样定理 (16)实验一非正弦信号的谐波分解一、实验目的1、掌握利用傅氏级数进行谐波分析的方法。
2、学习和掌握不同频率的正弦波相位差的鉴别与测试方法，并复习李沙育图形的使用方法。
3、掌握带通滤波器的有关测试。
二、预习要求1、阅读实验指导书的相关内容。
2、复习教材中非正弦交流电章、节的相关内容。
3、复习高等数学中傅里叶三角级数的原理，以及它在谐波分析中的应用、测量方法。
4、复习带通滤波器的原理及实验方法。
三、实验仪器1、双踪示波器2、TPE—SS1型或SS2型实验箱（1型还需频率计和交流毫伏表）四、实验原理1、在电力电子系统中最常用的是正弦交流信号，对电路的分析中均以之作为基础。
然而，电子技术领域中常遇到另一类交流电，虽是周期波，却不是正弦量，统称为非正弦周期信号，常见的有方波、锯齿波等等。
它们对电路产生的影响比单频率的正弦波复杂得多，即使在最简单的线性电路中，也无法使用相量模型或复频域分析法，而必须去解形式复杂的微积分方程，十分麻烦。
为求简化，是否可将其转化成正弦波呢？高等数学的傅里叶解析给了肯定的答案。
2、傅里叶解析认为任意一个逐段光滑的周期函数()x f均可分解出相应的f，在每一个间断点收敛于函三角级数，且其级数在每一连续点收敛于()x数()x f 的左右极限的平均值。
反映到电子技术领域中，就是说任意一个非正弦交流电都可以被分解成一系列频率与它成整数倍的正弦分量。
也就是说我们在实际工作中所遇到的各种波形的周期波，都可以由有限或无限个不同频率的正弦波组成。
3、一个非正弦周期波可以用一系列频率与之成整数倍的正弦波来表示。
反过来说，也就是不同频率的正弦波可以合成一个非正弦周期波。
这些正弦波叫做非正弦波的谐波分量，其中频率与之相同的成分称为基波或一次谐波。
信号与系统实验指导书新
实验要求 (2)概述 (3)实验一常用信号的分类与观察 (9)实验二信号的基本运算单元 (13)实验三信号的合成 (17)实验四线性时不变系统 (20)实验五信号的抽样与恢复（ＰＡＭ） (23)实验要求1．实验前必须充分预习，完成指定的预习任务。
预习要求如下：1）认真阅读实验指导书，分析、掌握实验电路的工作原理。
2）完成各实验“预备知识”中指定的内容。
3）熟悉实验任务。
4）复习实验中所用各仪器的使用方法及注意事项。
5）每次实验前写好实验预习报告。
2．使用仪器和实验箱前必须了解其性能、操作方法及注意事项，在使用时应严格遵守。
3．实验时接线要认真，相互仔细检查，确定无误才能接通电源。
4．实验时应注意观察，若发现有破坏性异常现象（例如有元件冒烟、发烫或有异味）应立即关断电源，保持现场，报告指导教师。
找出原因、排除故障，经指导教师同意再继续实验。
5．实验过程中需要改接线时，应关断电源后才能拆、接线。
6．实验过程中应仔细观察实验现象，认真记录实验结果(数据、波形、现象) 。
所记录的实验结果经指导教师审阅签字后再拆除实验线路。
7．实验结束后，必须关断电源、拔出电源插头，将仪器、设备、工具、导线等按规定整理，并将凳子摆放整齐。
8．实验后每个同学必须按要求独立完成实验报告。
概述1.1 电路组成概述在ZH5004“信号与系统”实验箱中，主要由以下功能模块组成：1、基本运算单元；2、信号的合成；3、线性时不变系统；4、零输入响应与零状态响应；5、二阶串联谐振、二阶并联谐振；6、有源与无源滤波器；7、PAM传输系统8、FDM传输系统；9、PAM抽样定理；10、二阶网络状态矢量；11、RC振荡器12、一阶网络13、二阶网络；14、反馈系统应用15、二次开发16、信号产生模块在“信号与系统”实验箱中，电源插座与电源开关在机箱的后面，电源模块在实验平台电路板的下面，它主要完成交流 220V到+5V、+12V、-12V的直流变换，给整个硬件平台供电。
信号与系统实验指导书DOC
实验一 零输入响应零状态响应一、实验目的1、掌握电路的零输入响应。
2、掌握电路的零状态响应。
3、学会电路的零状态响应与零输入响应的观察方法。
二、实验内容1、观察零输入响应的过程。
2、观察零状态响应的过程。
三、实验仪器1、信号与系统实验箱一台（主板）。
2、系统时域与频域分析模块一块。
3、20MHz 示波器一台。
四、实验原理1、零输入响应与零状态响应： 零输入响应：没有外加激励的作用，只有起始状态（起始时刻系统储能）所产生的响应。
零状态响应：不考虑起始时刻系统储能的作用（起始状态等于零）。
2、典型电路分析：电路的响应一般可分解为零输入响应和零状态响应。
首先考察一个实例：在下图中由RC 组成一电路，电容两端有起始电压Vc(0-),激励源为e(t)。
图2-1-1 RC 电路则系统响应－电容两端电压：1()01()(0)()ttt RCRCC c V t eV e e d RC -τ=-+ττ⎰ 上式中第一项称之为零输入响应，与输入激励无关，零输入响应(0)t RCc eV -是以初始电压值开始，以指数规律进行衰减。
第二项与起始储能无关，只与输入激励有关，被称为零状态响应。
在不同的输入信号下，电路会表征出不同的响应。
五、实验步骤1、把系统时域与频域分析模块插在主板上，用导线接通此模块“电源接入”和主板上的电源（看清标识，防止接错，带保护电路），并打开此模块的电源开关。
2、系统的零输入响应特性观察（1）接通主板上的电源，同时按下此模块上两个电源开关，将“时域抽样定理”模块中的抽样脉冲信号（SK1000用于选择频段，“频率调节”用于在频段内的频率调节，“脉宽调节”用于脉冲宽度的调节，以下实验都可改变以上的参数进行相关的操作），通过导线引入到“零输入零状态响应”的输入端。
（2）用示波器的两个探头，一个接输入脉冲信号作同步，一个用于观察输出信号的波形，当脉冲进入低电平阶段时，相当于此时激励去掉，即在低电平时所观察到的波形即为零输入信号。
学生用信号与系统实验指导书教材
信号与系统实验指导书电子信息工程系信号与系统综合实验指导书目录信号与系统实验箱简介 (2)实验一信号源实验 (5)实验二周期矩形脉冲信号的分解 (7)实验三周期矩形脉冲信号的合成 (12)实验四相位对波形合成的影响 (15)实验五抽样定理与信号恢复 (17)1信号与系统综合实验指导书2 信号与系统实验箱简介一、信号与系统模块组成介绍实验箱自带实验所需的电源、信号发生器、扫频信号源、数字交流毫伏表、数字频率计，其中数字交流毫伏表和数字频率计均采用自行设计电路，而不是像传统实验箱那样采用通用的表头，让仪表部分充分与本实验系统相配合。
实验箱采用了DSP 数字信号处理新技术，将模拟电路难以实现或实验结果不理想的“信号分解与合成”、“信号卷积”等实验得以准确地演示，并能生动地验证理论结果；可系统地了解并比较无源、有源、数字滤波器的性能及特性，学会数字滤波器的设计与实现。
该实验系统由以下模块组成：1、 电源输入模块2、信号源模块3、毫伏表4、频率计5、主机接口与二次开发区6、CPLD 可编程和数字信号处理器模块2、 一阶电路暂态响应模块8、二阶电路传输特性模块9、二阶网络状态轨迹模块信号与系统综合实验指导书10、阶跃响应与冲激响应模块11、抽样定理模块12、模拟滤波器模块13、基本运算单元与连续系统的模拟模块14、信号分解与合成和信号卷积实验模块15、无失真传输模块16、二阶网络的系统模拟模块17、系统相平面分析模块（选配）18、极点对频响特性的影响模块（选配）19、频分复用模块（选配）二、相关实验模块介绍3、电源输入模块此模块位于实验平台的右上角部分，分别提供+12v、+5v、-12 v、-5 v的电源输出。
４组电源对应４个发光二极管，电源输出正常时对应的发光二极管则亮。
4、信号源模块（见实验一）5、毫伏表毫伏表可测量交直流信号的峰峰值，测量幅度范围为０－20Ｖ。
S201：选择测量交流信号或直流信号。
S202：选择被测量的对象是信号源单元的正弦波、方波或外部输入信号。
信号与系统实验指导手册_控制学院
信号与系统实验指导手册山东大学控制科学与工程学院2005-1-26目录实验一 信号的产生与运算-------------------------------------------2 实验二 离散线性不变系统分析---------------------------------------8 实验三 周期信号的傅立叶级数表示----------------------------------11 实验四 离散时间傅立叶变换----------------------------------------12 实验五 连续时间系统分析------------------------------------------16 实验六 采样与重建------------------------------------------------17实验一 信号的产生与运算一、 信号的产生1.内容：产生并画出以下信号：a、单位冲击函数b、单位阶跃函数c、正弦波d、周期三角波和锯齿波e、周期方波程序：a、 subplot(2,3,1); %将图片分为2行3列6部分，在第一部分显示stem(0,1); %在零点画离散信号，幅度为一title('单位冲激信号')b、 subplot(2,3,2);x=-10:0.01:10; %x范围为-10到10，步长为0.01y=(x>=0);plot(x,y) ; %按上述程序要求画出连续信号坐标为（x,y）axis([-10,10,0,2]); %显示坐标范围为横坐标-10至10，纵坐标0至2title('单位阶跃信号')c、subplot(2,3,3);x=-pi:pi/20:pi;plot(x,sin(x));title('正弦波')d、subplot(2,3,4);x=-2*pi:0.01:2*pi;plot(x,sawtooth(x,0.5));title('周期三角波')e、subplot(2,3,5);x=-2*pi:0.01:2*pi;plot(x,sawtooth(x,1));title('周期锯齿波')f、subplot(2,3,6);x=-3*pi:0.01:3*pi;plot(x,square(x));axis([-10,10,0,2]);title('周期方波')图像：-10100.20.40.60.81单单单单单单-1001000.511.52单单单单单单-505-1-0.500.51正正正-1-0.500.51周周周周正-1-0.500.51周周周周正00.511.52周周周正2．内容：产生并画出以下离散序列：a 、离散正余弦序列：100),5.0sin(2)3/1.0cos(3)(≤≤++=n n n n x πππb 、单位采样序列⎩⎨⎧≠==−3,03,1)3(n n n δ c 、单位阶跃序列⎩⎨⎧<≥=−3,03,1)3(n n n ud 、实数指数序列100,)9.0()(≤≤=n n x n程序：function[x]=impseq(n0,n1,n2)%产生单位采样序列 n=[n1:n2]; x=[(n-n0)==0];function[x,n]=stepseq(n0,n1,n2)%产生单位阶跃序列 n=[n1:n2]; x=[(n-n0)>=0];a. subplot(2,2,1);n=[0:10];x=3*cos(0.1*pi*n+pi/3)+2*sin(0.5*pi*n); stem(n,x) grid ontitle('离散余弦序列')b. subplot(2,2,2);x=impseq(3,0,10); stem(n,x); grid on;title('单位采样序列')c. subplot(2,2,3);x= stepseq(3,0,10); stem(n,x); grid on;title('单位阶跃序列')d. subplot(2,2,4);n=[0:10];x=(0.9).^n;stem(n,x) grid ontitle('实数指数序列')图像：510离离离正离离单单单单离离单单单单离离实实实实离离4．内容：产生复数值信号：1010,)()3.01.0(≤≤−=+−n e n x n j在四个子图中画出其幅度、相位、实部和虚部的波形。
信号与系统实验指导书
信号与系统实验指导书实验一：信号与系统实验指导书实验目的：本实验旨在通过对信号与系统的实际应用，加深对信号与系统理论知识的理解和掌握程度。
具体实验目标如下：1. 学习使用示波器和信号发生器进行信号的产生与观测；2. 熟悉信号与系统实验中常用的信号类型，如正弦信号、方波信号等；3. 掌握信号的频谱分析方法，如傅里叶变换和功率谱估计；4. 理解系统的时域和频域特性，如冲激响应、单位脉冲响应和传递函数。
实验器材：1. 示波器（型号：XXXX）2. 信号发生器（型号：XXXX）3. 实验信号源（型号：XXXX）4. 电缆、连接线等实验辅助器材实验步骤：注意：在进行实验之前，请确保所有仪器设备连接正确，且电源线接地良好。
第一步：信号发生与观测1. 将信号发生器的输出端与示波器的输入端连接，在信号发生器上选择合适的信号类型和频率进行输出。
2. 调节示波器的触发模式和水平控制，使得信号在示波器屏幕上显示清晰。
3. 改变信号发生器的输出参数，观察示波器上信号的变化，并记录观测结果。
第二步：信号频谱分析1. 使用信号发生器产生一个频率为f的正弦信号，并将信号输入示波器。
2. 切换示波器的测量模式为频谱分析模式，选择傅里叶变换作为频谱分析方法。
3. 记录示波器上显示的频谱图像，并分析频谱图像中各谐波分量的相对强度和频率。
第三步：系统时域特性测量1. 使用信号发生器产生一个单位冲激信号，并将信号输入系统。
2. 通过示波器观测系统的响应信号，并记录系统对单位冲激信号的响应情况。
3. 切换示波器的触发模式，选择单次触发模式，以便更好地观察系统的响应。
第四步：系统频域特性测量1. 使用信号发生器产生一个频率为f的正弦信号，并将信号输入系统。
2. 通过示波器观测系统的输出信号，并记录观测结果。
3. 将示波器的触发模式设置为频谱分析模式，进行系统输出信号的频谱分析。
4. 根据频谱分析结果，分析系统在不同频率下的增益特性和相位特性。
信号与系统实验指导书
2、系统二全通
3、系统三低通
4、系统一的幅度响应和频率响应的实部是关于w的偶函数；相位响应和频率响应的虚部是关于原点对称的奇函数；系统二的幅值响应是关于w一值的一条直线，相位响应、频率响应的实部虚部没有对称关系；系统三的幅度响应和频率响应的实部没有一定的对称关系，而相位响应，频率响应的虚部在低频是关于w一值的奇函数。
3、 最好频率是100HZ，恰当，因为大于2f
4、 是的，频率越高，频率混叠越小。
1. 若 f (t) 是实函数，实函数的傅里叶变换的幅度谱为偶函数，而相位谱为奇函数。
2. 若 f (t)= jg (t) 是虚函数，虚函数的傅里叶变换的幅度谱仍为偶函数，相位谱仍为奇函数。 3. 实偶函数的傅里叶变换仍为实偶函数。
4不会。因为系统一、系统三分别是带通和低通滤波器，他们的相位频率响应不是线性的，那么群延时就不一样，所以会产生相位失真。系统二的相位频率响应是线性的，那么它的群延时是一个常数，不会产生相位失真。
试验四
1、 信号的采样要符合奈奎斯特采样定律，就是采样频率要高一点，被采信号最高频率的2
被，这样才能保证频率不会混叠，也就是采样出来的数字信号包含了被采信号的所有信息，而且没有引入刚绕。这就是信号的时域采样。
2、 是带限信号，可以选择一个抽样频率消除已抽样信号的频率混叠，但是不能完全消除。
信号与系统实验指导书(新)
信号与系统实验讲义吴光永编重庆文理学院电子电气学院二○○九年十月实验一 函数信号发生器一、实验目的1、了解函数信号发生器的操作方法。
2、了解单片多功能集成电路函数信号发生器的功能及特点。
3、熟悉信号与系统实验箱信号产生的方法。
二、实验内容1、用示波器观察输出的三种波形。
2、调其中电位器、拨位开关，观察三种波形的变化，了解其中的一些极限值。
3、熟悉其中的极限值，便于后面的实验，因为信号源是后面用的最多的。
三、预备知识阅读原理说明部分有关ICL8038的资料，熟悉管脚的排列及其功能。
四、实验仪器1、20M 双踪示波器一台。
2、信号与系统实验箱一台。
五、实验原理1、ICL8038是单片集成函数信号发生器，其内部框图如图1-1－1所示。
它由恒流源1I 和2I 、电压比较器A 和B 、触发器、缓冲器和三角波变正弦波电路等组成。
外接电容C 由两个恒流源充电和放电，电压比较器A 、B 的阀值分别为电源电压(指EE cc U U +)的2/3和1/3。
恒流源1I 和2I 的大小可通过外接电阻调节，但必须12I I >。
当触发器的输出为低电平时，恒流源2I 断开，恒流源1I 给C 充电，它的两端电压UC 随时间线性上升，当UC 达到电源电压的2/3时，电压比较器A 的输出电压发生跳变，使触发器输出由低电平变为高电平，恒流源C 接通，由于12I I > (设122I I =)，恒流源2I 将电流21I 加到C 上反充电，相当于C 由一个净电流I 放电，C 两端的电压UC 又转为直线下降。
当它下降到电源电压的1/3时，电压比较器B 的输出电压发生跳变，使触发器的输出由高电平跳变为原来的低电平，恒流源2I 断开，1I 再给C 充电，…如此周而复始，产生振荡。
若调整电路，使122I I =，则触发器输出为方波，经反相缓冲器由管脚⑨输出方波信号。
C 上的电压C U 上升与下降时间相等时为三角波，经电压跟随器从管脚③输出三角波信号。
信号与系统实验指导书(信丽萍)
信号和系统实验指导书北方民族大学2012年3月目录第一部分信号和系统实验箱简介 (3)第二部分：实验内容 (4)实验一、信号的时域、频域分析及测试 (4)实验二、信号合成 (6)实验三、无源滤波器和有源滤波器 (8)实验四、信号采样及恢复 (11)实验五、连续时间系统模拟 (14)第一部分信号和系统实验箱简介信号系统实验箱电路板如下图：图2-1-11该实验箱为信号系统实验配置了较为全面的实验电路，主要有无源和有源滤波器；串联谐振网络；并联谐振网络；基本运算单元；连续时间系统模拟；以及信号抽样单元。
多种有无源滤波器可以级联使用。
实验箱上有源电路的电源通过一个三芯插座和外电源相连。
基本电源电压为+12V和-12V。
电源如正常，红、绿两发光二极管应正常发光，否则应检查原因。
8、实际操作1、用示波器测量正弦波的Vpp和Vrms，并估算其周期。
2、用示波器观察调幅信号。
3、用I ST-B分别进行电压测量频率测量、频率测量、频谱测量以及失真度测量等。
第二部分：实验内容实验一信号的时域、频域分析及测试1-1实验目的:1．熟悉掌握电信号的时域观察方法和参数测量方法。
2．学习信号频谱的测量的方法，加深信号频谱的概念。
1-2实验仪器：1．I ST-B 智能信号测试仪2．双踪示波器3．信号系统实验箱1-3 实验原理周期信号的频谱是以基频ω1 为间隔的离散谱线。
下图示出了方波的振幅频谱图，特点是随着谐波次数的增加幅度是下降的。
基波幅度A 1 = 4/π，n 次谐波幅度为A n = A 1 /n (n= 1,3,5…)。
方波只有奇次谐波。
图1-1-1 对称方波及其频谱 如果对此频谱进行归一化处理，即A n /A 1,则其归一化频谱为A n =1/n。
对于下图所示的幅度为1、周期为T 、宽度为τ的矩形脉冲，其n 次谐波的幅度A n 为：下图画出了τ/ T = 1/4 时的振幅频谱图：图1-1-2 矩形脉冲及其频谱 1) 频谱包络线的零点为2n π/τ，τ越小，零点频率越高，当τ=T/2时，即为方波。
信号与系统实验指导书
实验一常用信号分类与观察一、实验目的1、观察常用信号的波形，了解其特点及产生方法。
2、学会用示波器测量常用波形的基本参数，了解信号及信号的特性。
二、实验内容1、了解几种常用典型信号的解析式及时域波形。
2、观察这些信号的波形，思考可以从那几个角度观察分析这些信号的参数。
三、实验仪器1、信号与系统实验箱一台（主板）。
2、20MHz双踪示波器一台。
四、实验原理信号可以表示为一个或多个变量的函数，在这里仅对一维信号进行研究，自变量为时间。
常用信号有：指数信号、正弦信号、指数衰减正弦信号、抽样信号、钟形信号、脉冲信号等。
1、指数信号：指数信号可表示为()atf t Ke。
对于不同的a取值，其波形表现为不同的形式，如图1-1所示：图1-1 指数信号2、指数衰减正弦信号：其表达式为(0)()sin()(0)att f t Ket t ω-<⎧=⎨>⎩，其波形如图1-2所示：图1-2 指数衰减正弦信号3、抽样信号：其表达式为：sin ()a t S t t=。
()a S t 是一个偶函数，t =±π,±2π,…,±n π时，函数值为零。
该函数在很多应用场合具有独特的运用。
其信号如图1-3所示：图1-3 抽样信号4、钟形信号（高斯函数）：其表达式为：()2t f t Eeτ⎛⎫- ⎪⎝⎭=，其信号如图1-4所示：图1-4钟形信号5、脉冲信号：其表达式为)()()(T t u t u t f --=，其中)(t u 为单位阶跃函数。
6、方波信号：信号周期为T ，前2T 期间信号为正电平信号，后2T期间信号为负电平信号。
五、实验步骤常规信号是由DSP 产生，并经过D/A 后输出，按以下步骤，分别观察各信号。
预备工作：将开关S401——S408置为OFF （on 为闭合，off 为断开）。
将拨号开关SW601置为“0001”（开关拨上为1，拨下为0）, 打开实验箱电源，按下复位键S601。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《信号与系统》实验指导书中南大学信息科学与工程学院2014年3月目录实验一基本信号的生成 (1)实验二信号的基本运算 (8)实验三系统的时域分析 (13)实验四周期信号的频域分析 (20)实验一 基本信号的生成1．实验目的● 学会使用MATLAB 产生各种常见的连续时间信号与离散时间信号； ● 通过MATLAB 中的绘图工具对产生的信号进行观察，加深对常用信号的理解；● 熟悉MATLAB 的基本操作，以及一些基本函数的使用，为以后的实验奠定基础。
2．实验原理⑴ 连续信号的MATLAB 表示① 指数信号指数信号at Ae 在MATLAB 中可用exp 函数表示，其调用形式为exp()y A a t =**【例1】 单边衰减指数信号的MATLAB 表示如下：（取1,0.4A a ==-） % program exa_1.m, decaying exponentialA=1;a=-0.4;t=0:0.001:10;ft=A*exp(a*t);plot(t,ft)② 正弦信号正弦信号0cos()A t ωφ+和0sin()A t ωφ+分别用MATLAB 的内部函数cos 和sin 表示，其调用形式为cos(0phi)sin(0phi)A w t A w t **+**+ 【例2】 正弦信号的MATLAB 表示如下：（取01,2,/6A ωπφπ===）% program exa_2.m, sinusoidal signalA=1;w0=2*pi;phi=pi/6;t=0:0.001:8;ft=A*sin(w0*t+phi);plot(t,ft)③ 抽样函数抽样函数()Sa t 在MATLAB 中用sinc 函数表示，定义为sinc()sin()/()t t t ππ=其调用形式为y=sinc()t【例3】 抽样函数的MATLAB 表示如下：（取33t ππ=-:）% program exa_3.m, sample functiont=-3*pi:pi/100:3*pi;ft=sinc(t/pi);plot(t,ft)④矩形脉冲信号矩形脉冲信号在MATLAB中用rectpuls函数表示，其调用形式为ty=rectpuls(,width)用以产生一个幅度为1，宽度为width以0t=为对称的矩形波。
width的默认值为1。
【例4】以2=为对称中心的矩形脉冲信号的MATLAB表示如下：（取1t TT=）% program exa_4.m, rectpulst=0:0.001:4;T=1;ft=rectpuls(t-2*T,2*T);plot(t,ft)⑤三角波脉冲信号三角波脉冲信号在MATLAB中用tripuls函数表示，其调用形式为y=tripuls(,width,skew)t用以产生一个最大幅度为1，宽度为width的三角波。
函数值的非零范围为-≤≤+；当skew0 (width/2,width/2)-；参数skew的取值范围为(1skew1)=时，产生标准正三角波。
【例5】三角波脉冲信号的MATLAB表示如下：（取33,4,0.5)=-==:）t width skew% program exa_5.m, tripulst=-3:0.001:3;ft=tripuls(t,4,0.5);plot(t,ft)⑵ 离散信号的MATLAB 表示① 指数序列指数序列k Aa 可用MATLAB 中的数组幂运算.a k ∧实现。
【例6】 衰减指数序列的MATLAB 表示如下：（取1,0.6A a ==-）% program exa_6.m, exponential sequencek=0:10;A=1;a=-0.6;fk=A*a.^k;stem(k,fk)② 正弦序列正弦序列的MATLAB 表示与连续信号相同，只是用stem(k,f)画出序列的波形。
【例7】 正弦序列0sin()k Ω的MATLAB 实现如下：（取0/6πΩ=）% program exa_7.m, discrete-time sinusoidal signal k=0:39;fk=sin(pi/6*k);stem(k,fk)③ 单位脉冲序列单位脉冲序列可借助MATLAB 中的零矩阵函数zeros 表示。
函数zeros(1,N)产生一个由N 个零组成的列向量。
【例8】 有限区间的单位脉冲序列[]k δ的MATLAB 实现如下：（取区间：1010-:）% program exa_8.m, delta sequencek=-10:10;delta=[zeros(1,10),1,zeros(1,10)];% 或者： delta=[(k-0)==0];stem(k,delta)④ 单位阶跃序列单位阶跃序列可借助MATLAB 中的单位矩阵函数ones 表示。
函数ones(1,N)产生一个由N 个1组成的列向量。
【例9】 有限区间的单位阶跃序列[]u k 的MATLAB 实现如下：（取区间：1010-:）% program exa_9.m, unit step sequencek=-10:10;uk=[zeros(1,10),ones(1,11)];% 或者： uk=[k>=0];stem(k,uk)3．实验内容⑴ 运行以上九个例子程序，掌握一些常用基本信号的特点及其MATLAB 实现方法；改变有关参数，进一步观察信号波形的变化。
⑵ 在 k [10:10]=- 范围内产生并画出以下信号：a) 1f [k][k]δ=；b) 2f [k][k+2]δ=；c) 3f [k][k-4]δ=；d) 4f [k]2[k+2][k-4]δδ=-。
⑶ 在 k [0:31]=范围内产生并画出以下信号：a) ()()k k 144f [k]sin cos ππ=；b) ()2k 24f [k]cos π=；c) ()()k k 348f [k]sin cos ππ=。
请问这三个信号的基波周期分别是多少？实验二 信号的基本运算1．实验目的● 学会使用MATLAB 完成信号的一些基本运算；● 了解复杂信号由基本信号通过尺度变换、翻转、平移、相加、相乘、差分、求和、微分及积分等运算来表达的方法；● 进一步熟悉MATLAB 的基本操作与编程，掌握其在信号分析中的运用特点与使用方式。
2．实验原理⑴ 信号的尺度变换、翻转、平移信号的尺度变换、翻转、平移运算，实际上是函数自变量的运算。
在信号的尺度变换()f at 和[]f Mk 中，函数的自变量乘以一个常数，在MATLAB 中可用算术运算符“﹡”来实现。
在信号翻转()f t -和[]f k -运算中，函数的自变量乘以一个负号，在MATLAB 中可以直接用负号“－”写出。
翻转运算在MATLAB 中还可以利用fliplr(f )函数实现，而翻转后信号的坐标则可由fliplr(k)-得到。
在信号时移0()f t t ±和0[]f k k ±运算中，函数自变量加、减一个常数，在MATLAB 中可用算术运算符“＋”或“－”来实现。
【例10】 对图示三角波()f t ，试利用MATLAB 画出(2)f t 和(22)f t -的波形。
解：实现(2)f t 和(22)f t -的MATLAB 程序如下：% program exa_10.m, Changed triangular pulse signal t=-3:0.001:3;ft1=tripuls(2*t,4,0.5);subplot(2,1,1)plot(t,ft1)title('f(2t)')ft2=tripuls((2-2*t),4,0.5);subplot(2,1,2)plot(t,ft2)title('f(2-2t)')程序运行结果如下图所示。
⑵ 离散序列的差分与求和离散序列的差分[][][1]f k f k f k ∇=--，在MATLAB 中用diff 函数来实现，其调用格式为：diff()y f = 离散序列的求和21[]k k k f k =∑与信号相加运算不同，求和运算是把1k 和2k 之间的所有样本[]f k 加起来，在MATLAB 中用sum 函数来实现，其调用格式为：f(2t)f(2-2t)sum((1:2))y f k k =【例11】 用MATLAB 计算指数信号(0.6)[]k u k -的能量。
解：离散信号的能量定义为： 2lim []NN k NE f k →∞=-=∑其MATLAB 程序实现如下：% program exa_11.m, the energy of exponential sequence k=0:10;A=1;a=-0.6; fk=A*a.^k;W=sum(abs(fk).^2) 程序运行结果为：W =1.5625⑶ 连续信号的微分与积分连续信号的微分也可以用上述diff 函数来近似计算。
例如，22sin()2cos()y x x x '==可由下列MATLAB 语句来近似实现：h=.001;x=0:h:pi;y=diff(sin(x.^2))/h;连续信号的定积分可由MATLAB 中quad 函数或quad8函数来实现。
其调用格式为：quad ('function_name',a,b)其中function_name 为被积函数名（.m 文件名），a 和b 为指定的积分区间。
【例12】 用对图示三角波()f t ，试利用MATLAB 画出()d f t dt和()t f d ττ-∞⎰的波形。
解：为了便于利用quad函数来计算信号的积分，将图示三角波()f t写成MATLAB 函数，函数名为functri（相应的.m文件名为functri.m），程序如下：function yt=functri(t)yt=tripuls(t,4,0.5);然后利用diff和quad函数，并调用自编函数functri即可实现三角波信号()f t 的微分和积分，源程序如下：% program exa_12_1.m, differentiationh=0.001;t=-3:h:3;y1=diff(functri(t))*1/h;plot(t(1:length(t)-1),y1)title('df(t)/dt')程序运行结果如图所示：Array% program exa_12_2.m, integrationt=-3:0.1:3;for x=1:length(t)y2(x)=quad('functri',-3,t(x));endplot(t,y2)title('integral of f(t)')程序运行结果如图所示：3．实验内容⑴ 运行以上三个例题程序，掌握信号基本运算的MATLAB 实现方法；改变有关参数，考察相应信号运算结果的变化特点与规律。