材料力学2005年
南京航空航天大学 材料力学 考研历年真题详解
南京航空航天大学2005年硕士研究生入学考试试题考试科目：材料力学说明：答案一律写在答题纸上，写在答卷上无效。
_____________________________________________________________________________ 一、图示受扭作用的实心圆轴的横截面，直径150mm,该横截面上的最大扭转切应力 τ=90Mpa(小于扭转比例极限)。
图中AB是平均直径为100mm.宽度0.25mm的圆max环的一部分，求该区域所承担的扭矩。
（15分）二、图示结构中，杆AB和杆AC,且每根杆均为两部分胶结而成，胶结面与杆的轴线方向成p。
（15[σ]=20Mpa,[τ]=15Mpa,求结构所能承受最大载荷max三、已知载荷q及尺寸a,试作图示外伸梁的剪力图和弯矩图。
（10四、图示悬梁在C 截面作用向上集中力p，在BC 段作用向下均布载荷q。
在A 截的顶部测得沿轴向线应变为2ε=300×610−材料的弹性模量E=200Gpa,泊松系数μ=0.3。
试求载荷p 及q 的大小。
（15分）五、已知图示应力单元体的σ=τ=50Mpa,E=200Gpa,μ=0.3。
（1） 画该点的应力圆。
（2）求该点的三个主应力.第三主应变和最大剪应力。
六、等截面圆杆左端固支如图所示，设材料的弹性模量为平面内与x轴p力和θ角。
（15分）七、平面刚架EI等于常数，自由端C受一水平力及一竖直力p的共同作用。
试AB和BC 的长度分别为ι和α。
（15分）八、一刚架如示。
试绘制此刚架的弯矩图。
两杆的抗弯刚度EI九、结构如图，重物Q从高为H为矩形截面梁，宽b=50mm,高h=10mm,BC 为圆截面杆，直径d=2mm,Q=20N,ι=0.5m,α=0.4m,H=100mm。
试校核结构的强度。
（15分）十、图示桁架由五根圆杆接而成，各杆编号如图所示。
已知ι=1m,各杆直径为d=30mm 弹性模量为E=200Gpa,许用应力[σ]=200Mpa,比例极限p σ=200Mpa,稳定安全系数st n=3试求此结构的许可载荷。
2005级材料力学期末统考试卷80学时B卷(06-07第二学期)
诚信应考,考试作弊将带来严重后果！华南理工大学期末考试《材料力学》试卷（2005级 B 卷）注意事项：1. 考前请将密封线内填写清楚； 2. 所有答案请直接答在试卷上； 3．考试形式：闭卷；4. 本试卷共 六 大题，满分100分， 考试时间120分钟。
题 号 一 二 三 四 五 六 总 分 得 分 评卷人一、简单计算题（共30分）1． 重量为Q 的重物自由下落冲击梁的B 点，梁的抗弯刚度EI 为常量，若Q 、EI 、l 、h 均已知，试推出B 的转角θB 的表达式。
（6分）2．试求图示交变应力的循环特征r 、应力幅值a σ。
（4分）3．图示为某构件内危险点的应力状态（图中应力单位为MPa ），试分别求其第二、第四强度理论的相当应力2r σ、4r σ（3.0=ν）。
（6分）_____________ ________姓名 学号学院 专业 座位号( 密 封 线 内 不 答 题 ) …………………………密………………………………………………封………………………………………线……………………………………4． 直径为d 的圆柱放在直径为D =3d 、厚为t 的圆形基座上，地基对基座的支反力为均匀分布，圆柱承受轴向压力P ，试求基座剪切面的剪力Q 。
（6分）5. 试求图示悬臂梁自由端B 的挠度。
（4分）6．如下结构中，OA 为刚性杆，杆2的长度短了 ，现强行将三杆装配，试写出变形协调方程。
（4分）P DdtlmxBAEIyaC二、已知q 、a ，试作梁的剪力图和弯矩图。
（12分）三、平面刚架如图所示，EI 为常量，试用能量法求出A 、C 处的约束力。
（16分）四、横截面为b ×h 的矩形截面梁如图所示，已知：h ＝2b ＝5.2cm ，F ＝1kN ，q ＝1kN/m ，材料的许用应力为[σ]＝140MPa 。
试校核该梁的正应力强度。
（10分）21 CBAO D a alδ4mF =1kN 1mC BAhq =1kN/m五、圆截面杆，受横向外力F 和绕轴线的外力偶0m 作用。
《材料力学》课程参考资_2005.12_
《材料力学》课程参考资料一、教材类参考资料1、孙训方，方孝淑，关来泰编，孙训方，胡增强修订，材料力学（I，II），第四版，北京：高等教育出版社，2002（★★）2、范钦珊主编，材料力学，北京：高等教育出版社，2000（■）3、李庆华主编，材料力学（第二版），西南交通大学出版社，2000（■）4、干光瑜等编，材料力学（建筑力学第二分册），第三版，北京：高等教育出版社，2000（★）5、单辉祖主编，材料力学（I,II），第四版，北京：高等教育出版社，20036、刘鸿文主编，材料力学（I,II），第四版，北京：高等教育出版社，20007、蒋智翔编，材料力学（上、下册），北京：清华大学出版社，19858、宋子康，蔡文安编，材料力学，上海：同济大学出版社，19979、蒋平编著，工程力学基础(I)，北京：高等教育出版社，200310、吴代华主编，材料力学，武汉：武汉工业大学出版社，198811、王燮山著，奇异函数及其在力学中的应用，北京：科学出版社，199312、刘鸿文主编，高等材料力学，北京：高等教育出版社，1985（■）我院曾选用的教材；（★）我院选用的教材（少学时和专科）（56学时的理论授课学时）（★★）我院选用的教材（多学时）（80学时的理论授课学时）二、学习指导书和习题集1、胡增强编，材料力学学习指导（配合主教材孙训方等编《材料力学》（第四版）（I，II））,北京：高等教育出版社，20032、老亮，赵福滨，郝松林，吴荣礼合编，材料力学思考题集，北京：高等教育出版社，20053、胡增强编，材料力学习题解析,北京：中国农业机械出版社，19834、苏翼林主编，材料力学难题分析，北京：高等教育出版社，19885、奚绍中编，材料力学精讲，成都：西南交通大学出版社，19936、苟文选，材料力学典型题解析及自测习题，西安：西北工业大学出版社，20007、陈乃立，陈倩编，材料力学学习指导（配合主教材孙训方等编《材料力学》（第四版）（I，II）），北京：高等教育出版社，20048、江苏省力学学会科普委员会编著，理论力学、材料力学考研与竞赛试题精解，徐州：中国矿业大学出版社，20019、Gross G. ,Schnell W., Ehlers W., Wriggers P 等合著，工程力学公式与习题（第I册（任文敏，曹致玉译）），（第II册（姚振汉，王宝玺译），（第III册，陆明万译）），清华大学出版社，Springer, 200210、沃国纬编，工程力学题典，上海：上海交通大学出版社，200111、刘达主编，材料力学常见题型解析及模拟题，西安：西北工业大学出版社，199712、顾志荣，吴永生编，材料力学学习方法及解题指导，第二版，同济大学出版社，200013、皮萨连科 Γ.C.，亚科符列夫Α. Π.，马特维也夫 Β.Β.编著，范钦珊，朱祖成译，材料力学手册，中国建筑工业出版社，198514、蔡乾煌，任文敏，崔玉玺，殷雅俊编，材料力学精要与典型例题讲解，清华大学出版社，Springer,200415、清华大学材料力学教研室编，材料力学解题指导及习题集，(第二版)，北京：高等教育出版社，198816、黄一红编，材料力学考研全真试题与解答，西安：西安电子科技大学出版社，200117、高云峰，蒋持平，吴鹤华，殷金生编，力学小问题及全国大学生力学竞赛试题，北京：清华大学出版社，Springer，200318、范磷编著，材料力学习题精选精解，上海：同济大学出版社，200119、陈平主编，材料力学辅导和习题精解，（配合刘鸿文主编《材料力学（I、II）》(第四版)），陕西师范大学出版社，200420、H.H. 缪勒，K.马格努斯著，张维等译，工程力学基础习题详解，高等教育出版社，2001三、相关力学网站1、中国力学学会：2、北京工业大学《材料力学》精品课程：http://211.71.86.13:8081/web/jp-cl.htmhttp://211.71.86.13:8081/web/jp/05sb/cllx/index.htm3、哈尔滨工业大学《材料力学》精品课程：/cllx/cllx.htm4、合肥工业大学《材料力学》精品课程：/2004/cllx/5、哈尔滨工程大学《材料力学》精品课程：http://210.46.96.21/jpsystem/properview.asp?lessonid=4666、天津大学《材料力学》精品课程：http://202.113.13.85/webclass/cllx/7、山东大学《材料力学》精品课程：/Get/016/8、中北大学《材料力学》精品课程：/kjjd/cllx/9、西北工业大学《材料力学》精品课程：http://202.117.80.9/jp2005/27/10、长安大学《材料力学》精品课程：/2004/cllx/11、长安大学《材料力学》精品课程：/2004/cllx/12、中国国家图书馆/四、英文参考资料1、Timoshenko S.P. and Gere J.M. Mechanics of materials. V on NostrandReinhold Company, New York, 19722、Gere J.M. Mechanics of materials. (5th Edition),Chinese Machine Press.20013、Budynas R. G. Advanced strength and applied stress analysis. (2ndEdition) McGraw-Hill and Tsinghua University Press, 20014、Olson G A. Elements of Mechanics of Materials.(4th Edition),Prentice-Hall, New Jersy,19825、Oden J.T. Mechanics of Elastic Structures. McGraw Hill BookCompany, New York, 19676、Nash W.A. Theory and problems of strength of materials. (4th Edition),Tsinghua University Press, 1998五、其他参考资料1、老亮，材料力学史漫话—从胡克定律的优先权讲起，北京：高等教育出版社，19932、徐秉业主编，身边的力学，北京：北京大学出版社，19973、Timoshenko S P. History of strength of materials. Dover PublicationsISBN: 04866118764、范钦珊的投入积累与创新文章、5、International Journal of Engineering Education(力学专刊)5、American Society for Engineering Education6、Global Journal of Engineering Education7、European Journal of Engineering Education8、新西兰University of Auckland9、材料力学动画10、Micro- and Nanoscale Mechanics11、Mechanics of Materials12、Negative Poisson Ratio13、Mechanics of material ,Finite element method(M. Vable/ MichiganTechnological University)14、Dilbert's Theorem on Salary（Iowa State University）15、The electronic Journal of Engineering TechnologyTable of Contents for History of Strength of Materials PrefaceIntroductionI.THE STRENGTH OF MATERIALS IN THE SEVENTEENTH CENTURY1.Galileo2.Galileo's work on strength of materialsanization of the national academies of science4.Robert Hooke5.MariotteII.ELASTIC CURVES6.The mathematicians Bernoulli7.Euler8.Euler's contribution to strength of materialsgrangeIII.STRENGTH OF MATERIALS IN THE EIGHTEENTH CENTURY10.Engineering applications of strength of materials11.Parent12.Coulomb13.Experimental study of the mechanical properties of structual materials in the eighteenth century14.Theory of retaining walls in the eighteenth century15.Theory of arches in the eighteenth centuryIV.STRENGTH OF MATERIALS BETWEEN 1800 AND 183316.L'Ecole Polytechnique17.Navier18.Navier's book on strength of materials19.The experimental work of French engineers between 1800 and 183320.The theories of arches and suspension bridges between 1800 and 183321.Poncelet22.Thomas Young23.Strength of materials in England between 1800 and 183324.Other notable European contributions to strength of materialsV.THE BEGINNING OF THE MATHEMATICAL THEORY OF ELASTICITY25.Equations of equilibrium in the theory of elasticity26.Cauchy27.Poisson28.G. Lamé and B. P. E. Clapeyron29.The theory of platesVI.STRENGTH OF MATERIALS BETWEEN 1833 AND 186730.Fairbairn and Hodgkinson31.The growth of German engineering schools32.Saint-Venant's contributions to the theory of bending of beams33.Jourawski's analysis of shearing stresses in beams34.Continuous beams35.Bresse36. E. WinklerVII.STRENGTH OF MATERIALS IN THE EVOLUTION OF RAILWAY ENGINEERING37.Tubular bridges38.Early investigations on fatigue of metals39.The work of Wöhler40.Moving loads41.Impact42.The early stages in the theory of trusses43.K. Culmann44.W. J. Macquorn Rankine45.J. C. Maxwell's contributions to the theory of structures46.Problems of elastc stability. Column formulas47.Theory of retaining walls and arches between 1833 and 1867VIII.THE MATHEMATICAL THEORY OF ELASTICITY BETWEEN 1833 AND 186748."The physical elasticity and "the elastic constant controversy"49.Early work in elasticity at Cambridge University50.Stokes50a.Barré de Saint-Venant51.The semi-inverse method52.The later work of Saint-Venant53.Duhamel and Phillips54.Franz Neumann55.G. R. Kirchoff56. A. Clebsch57.Lord Kelvin58.James Clerk MaxwellIX.STRENGTH OF MATERIALS IN THE PERIOD 1867-190059.Mechanical Testing Laboratories60.The work of O. Mohr61.Strain energy and Castigliano's theorem62.Elastic stability problems63.August FöpplX.THEORY OF STRUCTURES IN THE PERIOD 1867-190064.Statistically determinate trusses65.Deflection of trusses66.Statically indeterminate trusses67.Arches and retaining wallsXI.THEORY OF ELASTICITY BETWEEN 1867 AND 190068.The work of Saint-Venant's pupils69.Lord Rayleigh70.Theory of elasticity in England between 1867 and 190071.Theory of elasticity in Germany between 1867 and 190071a.Solutions of two-dimensional problems between 1867 and 1900XII.PROGRESS IN STRENGTH OF MATERIALS DURING THETWENTIETH CENTURY72.Properties of materials within the elastic limit73.Fracture of brittle materials74.Testing of ductile materials75.Strength theories76.Creep of metals at elevated temperatures77.Fatigue of metals78.Experimental stress analysisXIII.THEORY OF ELASTICITY DURING THE PERIOD 1900-195079.Felix Klein80.Ludwig Prandtl81.Approximate methods of solving elasticity problems82.Three-dimensional problems of elasticity83.Two-dimensional problems of elasticity84.Bending of plates and shells85.Elastic stability86.Vibrations and impactXIV.THEORY OF STRUCTURES DURING THE PERIOD 1900-195087.New methods of solving statically indeterminate systems88.Arches and suspension bridges89.Stresses in railway tracks90.Theory of ship structuresName Index Subject Index。
《材料力学》试卷(2005级A)答案
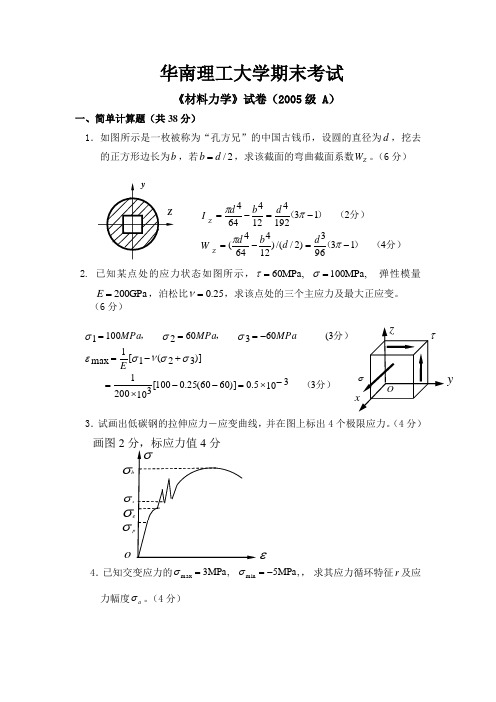
华南理工大学期末考试《材料力学》试卷（2005级 A ）一、简单计算题（共38分）1．如图所示是一枚被称为“孔方兄”的中国古钱币，设圆的直径为d ，挖去的正方形边长为b ，若2/d b =，求该截面的弯曲截面系数Z W 。
（6分）分）（）（分）（）（413963)2//()124644(2131924124644-=-=-=-=ππππdd b d Wd b d IZZ2. 已知某点处的应力状态如图所示，,MPa 100,MPa 60==στ弹性模量GPa 200=E ，泊松比25.0=ν，求该点处的三个主应力及最大正应变。
（6分）分）（分），，31035.0)]6060(25.0100[1032001)]32(1[1max 3(6036021001-⨯=--⨯=+-=-===σσνσεσσσE MPaMPa MPa3．试画出低碳钢的拉伸应力－应变曲线，并在图上标出4个极限应力。
（4分）画图24．已知交变应力的,MPa 5,MPa 3min max -==σσ， 求其应力循环特征r 及应力幅度a σ。
（4分）yoεσbσsσσ分）分）3(42)5(32min max 3(6.053minmax MPar a =--=-=-=-==σσσσσ 5．如图所示为矩形截面悬臂梁，在梁的自由端突然加一个重为Q 的物块，求梁的最大弯曲动应力。
（4分） 分）分）分）1(2123(262(2max max max bhQLbhQLW M K d zd ====σσ 6．如图所示为两根材料相同的简支梁，求两梁中点的挠度之比b a ωω/。
（4分）812)2(22/2==EI L P k EI L kP ba ωω7．两块相同的钢板用5个铆钉连接如图所示，已知道铆钉直径d ，钢板厚度t ，宽度b ，求铆钉所受的最大切应力，并画出上钢板的轴力图。
（6分）dPd P AQ ππτ2544/25/max ===（3分）QhbLL)(b 2/L 2/L )(a P 5/2P 5/3P P8．超静定结构如图所示，所有杆件不计自重，AB为刚性杆，试写出变形协调方程。
青岛科技大学2005-2006年研究生入学考试材料力学试卷
青岛科技大学2006年研究生入学考试试卷考试科目： 材料力学 （答案全部写在答题纸上）一．判断对错（每小题3分，共30分）1． 变截面杆受轴向集中力F 作用，如图。
设11-σ、22-σ、33-σ分别表示杆中截面1-1，2-2，3-3上的全应力的数值，则可能有11-σ<33-σ<22-σ。
1 2 32．应变为无量纲量，若物体内各点的应变均为零，则物体无位移。
3．当低碳钢试件的试验应力s σσ≥时，试件将发生断裂。
4．低碳钢拉伸经过冷作硬化后，其强度极限将得到提高。
5．切应力互等定理，既适用于平面应力状态，而不论有无正应力作用，又适用于空间任意应力状态。
6．图示，由惯性矩的平行依轴公式，34312bh I I Z Z +=。
P2h q 2h 2h 2题6图 题7图 7．梁的受力如图，在B 截面处：Q 图有突变，M 图连续光滑。
8．在线弹性和小变形的条件下，计算应力、变形和应变能都可以应用叠加法。
9．一梁在力F 作用下应变能为U ，若将F 改为2F ，其它条件不变，则应变能为4U 。
10．求位移的图乘法不能用于桁架、变截面梁和曲杆。
二．填空题（每小题5分，共40分）1．扭转应力、变形公式P I T /ρτ=、⎰=APGITdx /φ的应用条件是 。
2．图示长度为l 等直梁承受均布载荷q 。
为使梁横截面内最大弯矩达到最小值，则对称放置的两支座的间距=a 。
qal3．两根梁尺寸、受力和支承情况完全相同，但材料不同，弹性模量分别为21217E E E E =，且和，则两根梁的挠度之比21:f f 为 。
4．图示梁，欲使跨度中点挠度为零，则P 与q 的关系为 。
q5．在线弹性结构中，外力F 在相应的位移Δ上所作的功，当 时，W=21F Δ；当 时，W=F Δ。
6．抗弯刚度为EI 的简支梁如图。
当梁只受1=F 作用时，截面A 的转角为EI L 16/2；当梁只受1=m 作用时，其跨度中点C 的挠度为 。
FXQ-材料力学-第7章
TSINGHUA UNIVERSITY
无裂纹体
含裂纹体
7
强度失效判据与设计准则概述
屈服准则 最大切应力准则 形状改变比能准则 断裂准则 无裂纹体的断裂准则—最大拉应力准则 应用举例
TSINGHUA UNIVERSITY
7
屈服准则
最大切应力准则
TSINGHUA UNIVERSITY
刚度失效
7
构件失效概念与失效分类
失效分类
TSINGHUA UNIVERSITY
屈曲失效 —由于平衡构形的突然转 变而引起的失效.
7
构件失效概念与失效分类
TSINGHUA UNIVERSITY
构件失效概念与失效分类
7
失效分类
TSINGHUA UNIVERSITY
7
第7章 强度失效分析与设计准则
构件失效概念与失效分类 强度失效判据与设计准则概述
屈服准则
TSINGHUA UNIVERSITY
断裂准则
强度失效判据与设计准则的应用 结论与讨论
7
第7章 强度失效分析与设计准则
TSINGHUA UNIVERSITY
构件失效概念与失效分类
返回总目录
返回
7
失效—由于材料的力学行为而使 构件丧失正常功能的现象.
TSINGHUA UNIVERSITY
7
强度失效
TSINGHUA UNIVERSITY
1989年，前苏联乌拉尔山，输气管爆裂，死伤 1024人
7
构件失效概念与失效分类
失效—由于材料的力学行为而使
构件丧失正常功能的现象.
7
构件失效概念与失效分类
材料力学05级习题册07-3-1
第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( ) 1.2 内力只作用在杆件截面的形心处。
( ) 1.3 杆件某截面上的内力是该截面上应力的代数和。
( ) 1.4 确定截面内力的截面法，适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ) 1.5 根据各向同性假设，可认为材料的弹性常数在各方向都相同。
( ) 1.6 根据均匀性假设，可认为构件的弹性常数在各点处都相同。
( ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。
( ) 1.8 同一截面上各点的正应力σ必定大小相等，方向相同。
( ) 1.9 同一截面上各点的切应力τ必相互平行。
( ) 1.10 应变分为正应变ε和切应变γ。
( ) 1.11 应变为无量纲量。
( ) 1.12 若物体各部分均无变形，则物体内各点的应变均为零。
( ) 1.13 若物体内各点的应变均为零，则物体无位移。
( ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。
( )1.15 题1.15图所示结构中，AD 杆发生的变形为弯曲与压缩的组合变形。
( ) 1.16 题1.16图所示结构中，AB 杆将发生弯曲与压缩的组合变形。
( )二、填空题1.1 材料力学主要研究 受力后发生的 ，以及由此产生的 。
1.2 拉伸或压缩的受力特征是 ，变形特征是 。
1.3 剪切的受力特征是 ，变形特征是 。
1.4 扭转的受力特征是 ，变形特征是 。
1.5 弯曲的受力特征是 ，变形特征是 。
B题1.15图题1.16图1.6 组合受力与变形是指 。
1.7 构件的承载能力包括 ， 和 三个方面。
1.8 所谓 ，是指材料或构件抵抗破坏的能力。
所谓 ，是指构件抵抗变形的能力。
所谓 ，是指材料或构件保持其原有平衡形式的能力。
1.9 根据固体材料的性能作如下三个基本假设 ， ， 。
材料力学试卷试题(附参考答案)
一、简单计算题（共38分）1．如图所示是一枚被称为“孔方兄”的中国古钱币，设圆的直径为d ，挖去的正方形边长为b ，若2/d b =，求该截面的弯曲截面系数Z W 。
（6分）2. 已知某点处的应力状态如图所示，,MPa 100,MPa 60==στ弹性模量GPa 200=E ，泊松比25.0=ν，求该点处的三个主应力及最大正应变。
（6分）3．试画出低碳钢的拉伸应力－应变曲线，并在图上标出4个极限应力。
（4分）y4．已知交变应力的,MPa 5,MPa 3min max -==σσ， 求其应力循环特征r 及应力幅度a σ。
（4分）5．如图所示为矩形截面悬臂梁，在梁的自由端突然加一个重为Q 的物块，求梁的最大弯曲动应力。
（4分）Qhb6．如图所示为两根材料相同的简支梁，求两梁中点的挠度之比b a w w /。
（4分）7．两块相同的钢板用5个铆钉连接如图所示，已知铆钉直径d ，钢板厚度t ，宽度b ，求铆钉所受的最大切应力，并画出上钢板的轴力图。
（6分）)(b2/L 2/L )(a P8．超静定结构如图所示，所有杆件不计自重，AB为刚性杆，试写出变形协调方程。
（4分）Pa a a 2/AF二、作图示梁的剪力图与弯矩图。
（10分）三、不计剪力的影响，已知EI ，试用能量法求图示悬臂梁自由端的挠度A w 。
（12分）四、铸铁梁的载荷及截面尺寸如图所示，其中4cm 5.6012,mm 5.157==Z C I y 。
2A C已知许用拉应力MPa 40][=t σ，许用压应力MPa 160][=C σ。
试按正应力条件校核梁的强度。
若载荷不变，但将截面倒置，问是否合理？为什么？ （14分）五、圆截面直角弯杆ABC 放置于图示的水平位置，已知cm 50=L ，水平力（单位：mm ）200kN 40=F ，铅垂均布载荷m /kN 28=q ，材料的许用应力MPa 160][=σ，试用第三强度理论设计杆的直径d 。
注册结构工程师一级基础考试上午(材料力学)历年真题试卷汇编2
注册结构工程师一级基础考试上午（材料力学）历年真题试卷汇编2(总分：82.00，做题时间：90分钟)1.(2005年)图5—35所示梁，剪力等于零的截面位置X之值为( )（分数：2.00）√解析：解析：首先求支反力，设F A向上，取整体平衡：∑M B =0，F A .3a+qa.a=3qa. 所以由F s (x)=F A—qx=0，得2.(2005年)梁的横截面形状如图5—36所示，则截面对z轴的抗弯截面模量W z为( )。
（分数：2.00）√3.(2006年)矩形截面梁横力弯曲时，在横截面的中性轴处( )。
（分数：2.00）A.正应力最大，剪应力为零B.正应力为零，剪应力最大√C.正应力和剪应力均最大D.正应力和剪应力均为零解析：解析：矩形截面梁横力弯曲时，横截面上的正应力σ沿截面高度线性分布，如图5—37(a)所示。
在上下边缘σ最大，在中性轴上正应力为零。
横截面上的剪应力τ沿截面高度呈抛物线分布，如图5—37(b)所示。
在上下边缘τ4.(2006年)一跨度为l的简支架，若仅承受一个集中力P，当P在梁上任意移动时，梁内产生的最大剪力Q max和最大弯矩M max分别满足( )。
（分数：2.00）A.Q max≤P，M max =Pl／4 √B.Q max≤P／2，M max≤Pl／4C.Q max≤P，M max≤Pl／4D.Q max≤P／2，M max =Pl／2解析：解析：经分析可知，移动荷载作用在跨中处时，有最大弯矩5—38(a)所示。
当移动荷载作用在支座附近、无限接近支座时，有最大剪力Q max趋近于P值。
[]5.(2005年)就正应力强度而言，题图所示的梁，以下列哪个图所示的加载方式最好? ( )（分数：2.00）√解析：解析：题图所示四个梁，其支反力和弯矩图如下(D为主梁弯矩图)：就梁的正应力强度条件而言，，M max越小σmax越小，梁就越安全。
上述四个弯矩图中显然(D)图M max最小。
材料力学试卷
攀枝花学院考试试卷2005 ～2006 学年度第一学期《材料力学》试卷（A卷）适用专业年级：2004级土木工程考试形式：开（）、闭（√）卷注：学生在答题前，请将密封线内各项内容准确填写清楚，涂改及模糊不清者、试卷作废。
A、构件不发生断裂破坏；B、构件原有形式下的平衡是稳定的；C、构件具有足够的抵抗变形的能力；D、构件具有足够的强度、刚度和稳定性。
2、下列关于平面弯曲正应力公式的应用范围的说法，哪种是正确的：A、细长梁、弹性范围内加载；B、弹性范围内加载、载荷加在对称面或主轴平面内；C、细长梁、弹性范围内加载、载荷加在对称面或主轴平面内；D、细长梁、载荷加在对称面或主轴平面内。
3、外径为D，内径为d的空心圆截面，其抗扭截面系数等于；A、316PDWπ=B、331616PD dWππ=-C、344116PD dWDπ⎛⎫=-⎪⎝⎭D、344132PD dWDπ⎛⎫=-⎪⎝⎭4、正多边形截面有多少根形心主惯性轴：A、一根B、无穷多根C、一对D、三对5、细长压杆，常用普通碳素钢制造，而不用高强度优质钢制造，这是应为：A、普通碳素钢的强度极限高；B、钢强度优质钢的比例极限低。
C、普通碳素钢便宜；D、普通碳素钢价格便宜，而弹性模量和高强度优质钢差不多；6、在连接件挤压实用计算的强度条件[]Pcc ccFAσσ=≤中，A C是指连接件的：A、横截面面积；B、有效挤压面积；C 、实际挤压部分面积；D 、最大挤压力所在的横截面面积。
7、图示应力状态，用第三强度理论校核时，其相当应力为： A 、3r σ= B 、 3r στ=C、3r σ= D 、 32r στ=8、有A 、B 两种不同材质的杆件，受到相同的轴向拉力，若两杆的抗拉刚度相同，长度一样，则两杆内各点：A 、应力不同，但应变相同；B 、应力不同，应变也不一样；C 、应力相同，应变不相同；D 、应力相同，应变也一样。
9、两根圆轴，一为实心轴，一为空心轴，若它们的长度、横截面面积、、所用材料及所受扭矩均相同，则有结论： A 、ϕϕ=空实； B 、ϕϕ>空实；C 、ϕϕ<空实； D 、有待具体计算，才能作出ϕϕ空实与的比较。
江苏大学-材料力学2005
H
A
C
L/2
L/2
b
(2) 抗弯刚度同为ＥＩ的ＡＣ梁 和Ａ1Ｃ1 梁，左端固定，右端用刚性 连杆ＣＣ1 铰接（见图）。当梁中点 Ｂ点受到自由落体冲击时,已知落体 的重量Ｑ，高度Ｈ，长度ａ和抗弯 刚度ＥＩ。试求冲击时ＡＣ梁内的最 大动应力（σd）max。 A1 a B1 a C1 b h
共4页,第4页
第三题 ( 6 分)
直径为Ｄ的实心圆轴，两端受扭转力偶作用，最大许可力偶矩为ｍ。若将轴的横截面面积增 加一倍，则其最大许可力偶矩为ｍ的多少倍？（按强度条件考虑）。
y
=40MPa σy=40 Pa
第四题 ( 8 分)
某点应力状态如图示， 若已知σ1＝１２０MPa。 试求该点的τxy 、σ2 、 σ3 和τmax 之值。 x
σx=100MPa
τxy
z
共4页,第1页
第五题 ( 6 分)
三杆的刚度和杆长相等， 受力如图 （a）、（b）、（c） 所示。 若已知（a）、（b）杆 的变形能分别为Ｕa 和Ｕb，Ｂ端位移分别为Δa 和Δb。则（c）杆的变形能Ｕc＝＿＿＿＿＿＿； Ｕ Ｕ Δ Δ Ｕ （c）杆的Ｂ端位移Δc＝＿＿＿＿＿＿＿。
ψ
A
C d
D
B
ξ
ζ
P1
150 300
P2
150
第十题 ( 20 分)
图示刚架ＡＢＣ，各段的抗弯刚度 均为ＥＩ。略去轴力及剪力对变形的影 响。求Ｃ端的铅垂位移Δcy 及转角θc。 A a B a
P
第十一题 ( 20 分)
2 4
CHale Waihona Puke 4某连杆如图所示,截面为工字形,其面积和惯性矩为 A=64.7cm , Iy=407cm , Iz=1776cm 。连杆 的材料为 Q235 钢,其 E=200GPa ,σs=235 MPa , σP =200 MPa 。该连杆所受的最大轴向压力为 465 kN 。连杆在摆动平面(xy 平面)内发生弯曲时,两端可认为铰支，而在与摆动平面相垂直的 xz 平面内发生弯曲时,两端可认为是固定支座。计算中柔度压杆临界力的直线公式为 σ = a − bλ ， 其中的材料常数 a=304MPa, b=1.12MPa。试求该连杆的临界压力 Fcr 和该连杆的稳定工作安全因 数n 。
2005南航材力试题
2005年南京航空航天大学硕士研究生入学考试试题科目：材料力学一、图示受扭矩作用的实心圆轴的横截面，直径150mm，该横截面上的最大扭转切应力τmax=90MPa（小于扭转比例极限）。
图中AB是平均直径为100mm、宽度0.25mm的圆环的一部分，求该区域所承担的扭矩。
（15分）二、图示结构中，杆AB和杆AC的两端均为铰接，两杆的横截面面积为200mm2，且每根杆均为两部分胶结而成，胶结面与杆的轴线方向均成45°角。
设胶结面的[σ]=20MPa，[τ]=15MPa，求结构所能承受的最大载荷P max。
（15分）题一图题二图三、已知载荷q及尺寸a，试作图示外伸梁的剪力图和弯矩图。
（10分）四、图示悬臂梁在C截面作用向上集中力P，在BC段作用向下均布载荷q。
在A截面的顶部测得沿轴向线应变ε1=500×10-6，在中性层与轴线成45°方向的线应变为ε2=300×10-6。
材料的弹性模量E=200GPa，泊松系数μ=0.3。
试求载荷P及q的大小。
（15分）题三图题四图五、已知图示应力单元体的σ=τ=50MPa，E=200GPa，μ=0.3。
求：（1）画该点的应力圆（2）求该点的三个主应力、第三主应变和最大剪应力。
（15分）六、等截面圆杆左端固支如图所示，设材料的弹性模量为E，泊松比为μ。
自由端受到O xy平面内与x轴成θ角的P力作用，测出距自由端距离为a的截面上、下表面x方向线应变εA和εB。
试求：P力和θ角。
（15分）题五图题六图七、平面刚架EI等于常数，自由端C受一水平力P及一竖直力P的共同作用。
试用能量法求自由端C的竖直位移，设AB和BC的长度分别为l和a。
（15分）八、一刚架如图所示。
试绘制此刚架的弯矩图。
两杆的抗弯刚度EI相同。
（20分）题七图题八图九、结构如图，重物Q从高为H的位置落下。
若已知：[σ]=200MPa，E=200GPa，AB 为矩形截面梁，宽b=50mm，高h=10mm，BC为圆截面杆，直径d=2mm，Q=20N，l=0.5m，a=0.4m，H=100mm。
河海大学材料力学真题汇总
= 88mm ，横截面对中性轴的惯性矩为 I z = 764 × 10−8 m4 。试求梁的容许均布荷载 q 的大小
2007 年第 3 大题 图示钢杆，弹性模量 E
= 200GPa ，截面面积为 2500mm 2 ，受力之前， B 端与刚性墙间的间隙为 δ = 0.3mm ，现于 C 点作
2004 年第 2 部分第 6 大题 图示结构中， AC 梁为矩形截面， CD 杆为圆截面，均由 Q 235 钢制成， C 、 D 两处均为球铰，已知 d
= 20mm ， b = 100mm ，
h = 180mm ， E = 200GPa ，σ s = 235MPa ，σ b = 400MPa ，强度安全因素 n = 2.0 ，稳定安全因素 nst = 3.0 。试确定
30
o
= 143.3 × 10 −6 ，
Fd /10 ， d = 100mm ， E = 200GPa ，ν = 0.3 。试求荷载 F 和 Me 。若许用应力 [σ ] = 160 MPa ，试用第三
2007 年第 7 大题 图示结构 AB 为矩形截面梁，Wz
= 105 mm3 ； CD 为圆截面杆，直径 d = 20mm ，两端铰支，可视为细长杆。弹性模量均为
E = 200GPa ，容许应力 [σ ] = 160 MPa ， L = 0.8m ，稳定安全系数 nst = 2 ，现在 B 端作用一力偶 M = 10 KN ⋅ m ，试校
= 200GPa ）
2006 年第 2 大题 由空心圆管 B 和实心圆杆 A 牢固地粘结在一起组成的轴（横截面如图） ，它们的切变弹模分别为 G A 和 GB ，且 G A （1）画出横截面上切应力分布规律（以任一半径） （2）求出扭矩为 M x 时， A 、 B 材料内的最大切应力
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
北京化工大学2005年材料力学考研专业课试卷
注意事项：
⒈答案（包括有关图）必须写在答题纸上，写在试题上均不给分。
⒉答题时可不抄题，但必须写清题号。
⒊答题时用蓝、黑墨水笔或圆珠笔，用红色笔或铅笔均不给分。
一、（共15分）
1.用大于或小于号将以下值排列起来1 b σs σ e σp σcr P
强度极限，屈服极限，弹性极限，比例极限。
2两端铰支，矩形截面的细长压杆，杨氏模量E，其临界压力= ；挠曲线位于面内。
3.当交变应力的不超过材料的持久极限时，试件可经历无限多次应力循环。
A 最大应力
B 最小应力
C 平均应力
D 应力幅
4. 重量Q的物体自高度h处落在梁上D截面处，梁上截面C处的动应力为，其中st d K σσ= , 应取梁在静载荷作用下st ? 的挠度。
北京化工大学研究生考试试题纸第2页共4页
二、作下面外伸梁的剪力图和弯矩图。
（15分）
三、矩形截面简支梁受均布载荷q,为使其最大正应力减少到原有的二分之一，在梁的中心部分上下各“焊接”一片同宽（b）的板材，试求板材的厚度t与宽度a.。
（15分）
四、等截面曲杆如图所示（EI已知），试求B点的水平位移。
（15分）
2北京化工大学研究生考试试题纸第3页共4页
五、圆形截面直角拐，端部受铅直向下的力P，截面直径d , 弹性模量E，泊松比μ为已知，求A点位移。
（15分）
六、求图示简支梁的挠曲线方程及中点挠度。
（EI=常数）（15分）
七、求A-A截面的最大正应力并画出A-A面上的应力分布图。
（15分）
3北京化工大学研究生考试试题纸第4页共4页
八、平均半径为R的细圆环，截面为圆形，直径为d，P力垂直于圆环中面所在的平面，求：1. 画出B及C危险点的应力状态；2.求出上两点用第三强度理论表示的相当应力并确定危险截面。
（15分）
九、如图所示铁道路标的圆信号板装在直径d=50mm的圆柱上，a=600mm,l=800mm，D=600mm。
若信号板上作用的最大风载的压强p=2kPa,圆柱的许用应力[σ]=60Mpa,试按第四强度理论校核该圆柱的强度。
（15分）
十、作图示静不定梁的弯矩图。
（15分）。