材料力学讲解作业(2)
材料力学——精选推荐
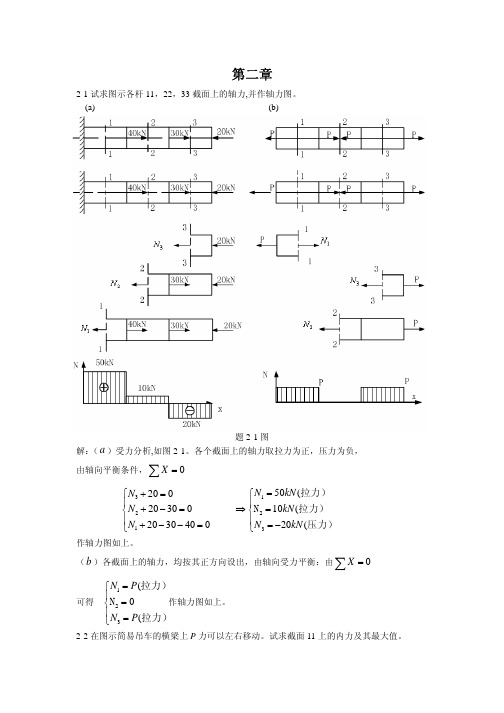
第二章2-1试求图示各杆11,22,33截面上的轴力,并作轴力图。
(a)(b)题2-1图解:()受力分析,如图2-1。
各个截面上的轴力取拉力为正,压力为负, a 由轴向平衡条件,0X =∑321200203002030400N N N +=⎧⎪+−=⎨⎪+−−=⎩ ⇒1350(10(20(N kN kN N kN =⎧⎪=⎨⎪=−⎩2拉力)N 拉力)压力)作轴力图如上。
(b )各截面上的轴力,均按其正方向设出,由轴向受力平衡:由0X =∑可得 作轴力图如上。
13(0(N P N P =⎧⎪=⎨⎪=⎩2拉力)N 拉力)2-2在图示简易吊车的横梁上P 力可以左右移动。
试求截面11上的内力及其最大值。
解:如图所示,题2-2图构件在1截面处“断开”,以下方的部分为研究对象,轴力和力作用在研究对象上,由平衡条件:1−1N P 0AM=∑1(sin )P x N l 0α⋅+−⋅= 11()sin P xN N x l α⋅==(P l α、、均为常数)1N 最大值为 1,max1()sin sin P l PN N l l αα⋅===⋅ 2-3图示为简易起重机。
已知钢丝绳子AC 的横截面积24AC A cm =,吊杆AB 的横截左面积26AB A cm =,当起重量P=20KN 时,求钢丝绳子AC 和吊杆AB 的正应力。
题2-3图解:先假设吊杆AB 、均受拉力作用,则对AC A 点进行受力分析可知,两杆对A 的作用力如图示方向。
AB AC T T 、由受力平衡得:0AB AC P T T ++=J G JJJ G JJJ GX Y ⎧=⎪⎨=⎪⎩∑∑ cos30cos 450cos 45cos600AC AB AB AB T T P T T ⋅°+⋅°=⎧⇒⎨+⋅°+⋅°=⎩20P k =N N =⎧⎨=−⎩54.6466.93AC AB N kNN kN=⎧⎨=−⎩ ⇒54.6466.93AC AB T k T kN 可见,杆受拉,而AC AB 杆实际受压。
材料力学教案 第2章 拉伸、压缩与剪切

第2章拉伸压缩与剪切教学目的:了解材料的力学性质;掌握轴向拉伸、压缩、剪切和挤压的概念;掌握轴向拉压时构件的内力、应力、变形的计算;熟练掌握剪切应力及挤压应力的计算方法并进行强度校核;掌握拉压杆的超静定问题。
教学重点:建立弹性杆件横截面上内力、内力分量的概念;运用截面法画轴力图;掌握低碳钢的力学性质;掌握轴向拉伸和压缩时横截面上正应力计算公式及其适用条件;掌握拉压杆的强度计算;熟练掌握剪切和挤压的实用计算。
教学难点:低碳钢类塑性材料在拉伸过程中反映出的性质;许用应力的确定和使用安全系数的原因;强度计算问题;剪切面和挤压面的确定;剪切和挤压的实用计算;拉压杆超的静定计算。
教具:多媒体。
教学方法:采用启发式教学,通过提问,引导学生思考,让学生回答问题。
举例掌握轴向拉伸、压缩和剪切变形概念,通过例题、作业,加强辅导熟练运用截面法,掌握轴力图的画法;建立变形、弹性变形、应变、胡克定律和抗拉压刚度的概念;教学内容:轴向拉伸和压缩的概念;强度计算;材料的力学性能及应力应变图;许用应力与安全系数;超静定的计算;剪切概念;剪切实用计算;挤压实用计算。
教学学时:8学时。
教学提纲:2.1 轴向拉伸与压缩的概念和实例1.实例(1)液压传动中的活塞杆(2)内燃机的连杆(3)起吊重物用的钢索(4)千斤顶的螺杆(5)桁架的杆件2.概念及简图这些杆件虽然外形各异,受力方式不同,但是它们有共同的特点:(1)受力特点:作用在杆件上的外力合力的作用线与杆件轴线重合,杆件变形是沿轴线方向的伸长或缩短。
(如果两个F 力是一对离开端截面的力,则将使杆发生纵向伸长,这样的力称为轴向拉力; 如果是一对指向端截面的力,则将使杆发生纵向缩短,称为轴向压力)。
(2)变形特点:主要变形是纵向伸长或缩短。
(3)拉(压)杆的受力简图:(4)说明:本章所讲的变形是指受压杆没有被压弯的情况下,不涉及稳定性问题。
2.2 轴向拉伸或压缩时横截面上的内力和应力1.截面法求内力(1)假想沿m-m 横截面将杆切开(2)留下左半段或右半段(3)将弃去部分对留下部分的作用用内力代替(4)对留下部分写平衡方程,求出内力(即轴力)的值。
《材料力学》第2章 轴向拉(压)变形 习题解讲解

第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(b)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(c)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(d)解:(1)求指定截面上的轴力(2)作轴力图中间段的轴力方程为:轴力图如图所示。
[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EC横截面上的应力。
解:(1)求支座反力由结构的对称性可知:(2)求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断,取左部分为研究对象,其受力图如图所示。
由平衡条件可知:②以C节点为研究对象,其受力图如图所示。
由平平衡条件可得:(3)求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为:[习题2-5] 石砌桥墩的墩身高,其横截面面尺寸如图所示。
荷载,材料的密度,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:墩身底面积:因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
[习题2-6]图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当时各斜截面上的正应力和切应力,并用图表示其方向。
解:斜截面上的正应力与切应力的公式为:式中,,把的数值代入以上二式得:轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。
材料力学扭转详细讲解和题目,非常好
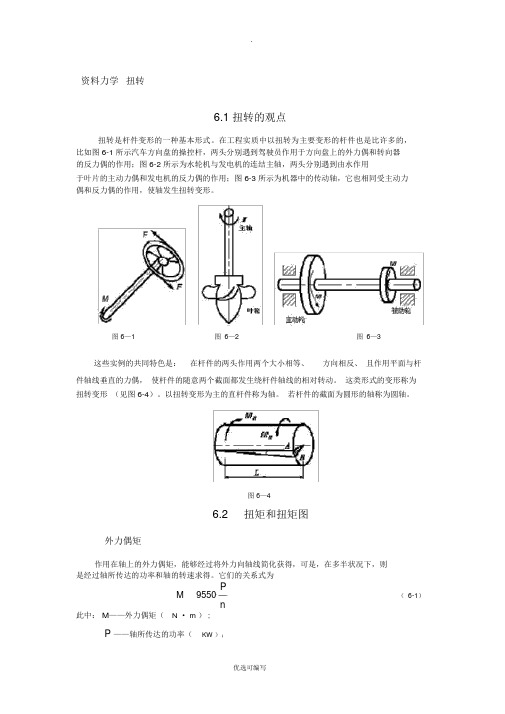
.资料力学扭转6.1扭转的观点扭转是杆件变形的一种基本形式。
在工程实质中以扭转为主要变形的杆件也是比许多的,比如图 6-1 所示汽车方向盘的操控杆,两头分别遇到驾驶员作用于方向盘上的外力偶和转向器的反力偶的作用;图 6-2 所示为水轮机与发电机的连结主轴,两头分别遇到由水作用于叶片的主动力偶和发电机的反力偶的作用;图 6-3 所示为机器中的传动轴,它也相同受主动力偶和反力偶的作用,使轴发生扭转变形。
图 6—1图6—2图6—3这些实例的共同特色是:在杆件的两头作用两个大小相等、方向相反、且作用平面与杆件轴线垂直的力偶,使杆件的随意两个截面都发生绕杆件轴线的相对转动。
这类形式的变形称为扭转变形(见图 6-4)。
以扭转变形为主的直杆件称为轴。
若杆件的截面为圆形的轴称为圆轴。
图 6—46.2扭矩和扭矩图外力偶矩作用在轴上的外力偶矩,能够经过将外力向轴线简化获得,可是,在多半状况下,则是经过轴所传达的功率和轴的转速求得。
它们的关系式为PM 9550(6-1)n此中: M——外力偶矩(N · m ) ;P ——轴所传达的功率(KW );n ——轴的转速(r/ min )。
外力偶的方向可依据以下原则确立:输入的力偶矩若为主动力矩则与轴的转动方向相同;输入的力偶矩若为被动力矩则与轴的转动方向相反。
扭矩圆轴在外力偶的作用下,其横截面大将产生连续散布内力。
依据截面法,这一散布内力应构成一作用在横截面内的协力偶,进而与作用在垂直于轴线平面内的外力偶相均衡。
由分布内力构成的协力偶的力偶矩,称为扭矩,用 M n表示。
扭矩的量纲和外力偶矩的量纲相同,均为 N·m或 kN· m。
看作用在轴上的外力偶矩确立以后,应用截面法能够很方便地求得轴上的各横截面内的扭矩。
如图6-5( a)所示的杆,在其两头有一对大小相等、转向相反,其矩为M 的外力偶作用。
为求杆任一截面 m-m 的扭矩,可设想地将杆沿截面 m-m 切开分红两段,观察此中任一部分的均衡,比如图 6-5( b)中所示的左端。
工程力学--材料力学(第五、六章)经典例题及讲解
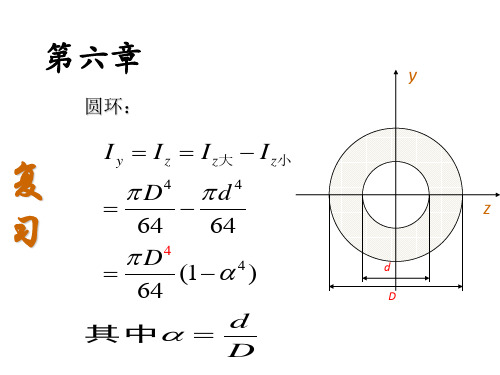
P
A
0.5 m
C D
0.4 m 1m
B
20
40
解:C点的应力 σ C = E ε = 200 × 10 3 × 6 × 10 − 4
= 120M Pa
C截面的弯矩
M C = σ C W z = 640 N ⋅ m
由 M C = 0.5 R A = 0.5 × 0.4 P = 0.2 P = 640 N ⋅ m 得 P = 3.2kN
度减小一半时,从正应力强度条件考虑, 该梁的承载能力将是原来的多少倍? 解: 由公式
σ max
M max M max = = 2 Wz bh 6
可以看出:该梁的承载能力将是原来的2 可以看出:该梁的承载能力将是原来的2倍。
例4:主梁AB,跨度为l,采用加副梁CD AB,跨度为l 采用加副梁CD
的方法提高承载能力, 的方法提高承载能力,若主梁和副梁材料 相同,截面尺寸相同, 相同,截面尺寸相同,则副梁的最佳长度 a为多少? 为多少?
2 2
2
bh b( d − b ) Wz = = 6 6
2 2 2
∂ Wz d 2 b 2 = − =0 ∂b 6 2
d 由此得 b = 3
d
2 2
h
h = d −b =
h = 2 ≈3:2 b
2 d 3
b
例12:跨长l =2m的铸铁梁受力如图示,已知材料许用拉、 12:跨长l =2m的铸铁梁受力如图示 已知材料许用拉、 的铸铁梁受力如图示,
10 kN / m
200 2m 4m 100
10 kN / m
200
2m
Fs( kN ) 25 Fs(
45 kN
4m
100
材料力学讲解作业

材料力学讲解作业Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】作下图所示梁的剪力图和弯矩图。
2m1m1mm1kN 2kN2kN 2kNA BCD梁分三段,AB 、BC 为空荷载段,CD 段为均布荷载段,均布荷载q=2kN/2m=1kN/m 。
A ,B ,D 三处剪力有突变,说明有集中力作用,在A 截面有向上集中力2kN ,在B 截面有向下集中力2kN ,在D 截面有向上集中力2kN 。
荷载图如图 (b)。
根据荷载图作弯矩图,如图 (c)所示。
如下图所示机构中,1,2两杆的横截面直径分别为cm d 101= ,cm d 202= ,P=10kN 。
横梁ABC ,CD 视为刚体。
求两杆内的应力。
p DCBA122m2m1.5m1m1mCD 杆的D 支座不受力,CD 杆内也不受力,所以p 可视为作用于ABC 杆的C 端。
取ABC 为受力体,受力图如图(b)所示。
MPaMPa A N MPaMPa A N kN N kN N 7.6310204103203.12710104101020210162222623111=⨯⨯⨯⨯===⨯⨯⨯⨯====--πσπσ,如图所示的阶梯形圆轴,直径分别为cm d 41=,cm d 72=。
轮上三个皮带轮,输入功率为kW N 171=,kW N 132=,kW N 303=。
轴的转速为n=200r/min ,材料的许用剪应力[τ]=60MPa 。
试校核其强度。
1计算各轮处的扭转外力偶矩。
mkN m kN m m kN m kN n N m m kN m kN n N m ⋅=⋅⨯=⋅=⋅⨯=⋅=⋅⨯==433.12003055.9621.02001355.9255.9812.02001755.9155.9321(c)(b)kN m 31图3 传动轴可简化为图3(b),⑦扭矩图如图3(c)。
AD 段的最大剪应力为[]τπτ>=⨯⨯⨯==-MPa Pa W M T TAD 6.64104168126311max BC 段的最大剪应力为[]τπτ>=⨯⨯⨯==-MPa Pa W M T TBC 3.211071614326322max AD 段的单位长度扭转角为[]θπθ>=⨯⨯⨯⨯⨯⨯==-m mGI M p TAD /1.23/104108018032812842911BC 段的单位长度扭转角为[]θπθ<=⨯⨯⨯⨯⨯⨯==-m m GIp MINC/44.0/1074108018032143222829由此可知轴的强度与刚度都不够。
材料力学作业解答

材料力学作业解答1.弹簧的力学行为弹簧是一种具有弹性的材料,它可以在受力时发生弹性形变,并且能够恢复到原始形状。
弹簧的力学行为可以通过胡克定律来描述。
根据胡克定律,弹簧的形变与施加在它上面的力成正比,即F=k*x,其中F是施加在弹簧上的力,k是弹簧的弹性系数,x是弹簧的形变量。
2.弹簧的应变能和弹性势能当弹簧被拉伸或压缩时,它会储存一定量的应变能。
弹簧的应变能可以通过下式计算:U=(1/2)*k*x^2,其中U是弹簧储存的应变能,k是弹簧的弹性系数,x是弹簧的形变量。
3.伸长弹簧的应变能假设一个弹簧的弹性系数为k,它被拉伸或压缩x长度。
根据胡克定律,施加在弹簧上的力可以通过F = k * x计算得到。
通过积分力在形变路径上的关系,可以得到弹簧的应变能。
假设初始长度为L,拉伸后的长度为L+x,则弹簧的伸长应变能可以计算如下:U = ∫[0, L+x] F(x)dx = ∫[0, x] k * x dx = (1/2) k * x^24.剪切应力和剪切应变剪切应力是作用于物体上的横截面内的剪切力与该横截面上的面积之比。
剪切应变是物体在受到剪切应力时产生的形变。
剪切应力和剪切应变之间的关系可以通过剪切弹性模量来描述。
剪切弹性模量G可以通过下式计算:G=τ/γ,其中τ是剪切应力,γ是剪切应变。
5.弯曲应力和弯曲应变弯曲应力是作用于物体上的弯曲力与该物体的横截面想对距离之比。
弯曲应变是物体在受到弯曲应力时产生的形变。
弯曲应力和弯曲应变之间的关系可以通过弯曲弹性模量来描述。
弯曲弹性模量E可以通过下式计算:E=σ/ε,其中σ是弯曲应力,ε是弯曲应变。
6.斯特拉因准则斯特拉因准则描述了材料在达到破坏点之前的应力和应变行为。
根据斯特拉因准则,当材料达到其屈服点时,应力和应变之间的关系可以通过单一的线性方程来描述。
这个线性方程表明了在屈服点之前,应力与应变之间的比例关系。
7.杨氏模量和泊松比杨氏模量是一种描述材料刚度的量度,它可以表示应力与应变之间的比例关系。
德州学院,材料力学,期末试题7章习题讲解

德州学院,材料⼒学,期末试题7章习题讲解第七章⼒和应变分析强度理论 §7.1应⼒状态概述1.过受⼒构件内⼀点,取截⾯的不同⽅位,这⼀点在各个⾯上的(D ). (A )正应⼒相同,切应⼒不同;(B )正应⼒不同,切应⼒相同;(C )正应⼒和切应⼒都相同;(D )正应⼒和切应⼒都不同。
2.关于单元体的描述,下列正确的是A(A )单元体的三维尺⼨必须是微⼩的;(B )单元体是平⾏六⾯体;(C )单元体必须是正⽅体;。
(D )单元体必须有⼀对横截⾯。
3.对于图⽰承受轴向拉伸的锥形杆上的A 点,哪⼀种应⼒状态是正确的Dxτxx4.在单元体的主平⾯上()。
(A )正应⼒⼀定最⼤;(B )正应⼒⼀定为零;(C)切应⼒⼀定最⼩;(D )切应⼒⼀定为零。
§7.2⼆向应⼒状态实例1. Q235钢制成的薄壁圆筒形蒸汽锅炉,壁厚δ,内径D ,蒸汽压⼒p ,试计算锅炉壁内任意⼀点处的三个主应⼒。
注:薄壁圆筒受⼒均匀,因此,任意点的应⼒状态均相同。
1.求⽔平⽅向上的正应⼒σx2.求竖直⽅向上的正应⼒σy3.求垂直于纸⾯⽅向上的正应⼒σz 薄壁圆筒与纸⾯垂直⽅向上的σz 为零.总结:薄壁圆筒的三个主应⼒为:薄壁圆筒为两向应⼒状态注意事项:1.注意单位配套使⽤;2. 纵向截⾯上正应⼒是横截⾯正应⼒的两倍;3.按规定排列正应⼒。
课本215页例7.1如下由Q235钢制成的蒸汽锅炉,壁厚δ=10mm,内径D=1m,蒸汽压⼒p=3MPa,试计算锅炉壁内任意⼀点处的三个主应⼒。
经分析,薄壁圆筒为两向应⼒状态2. 圆球形容器的壁厚为δ,内径为D,内压为p,求容器内任意⼀点的应⼒。
注:薄壁圆球受⼒均匀,因此,任意点的应⼒状态均相同。
1.求⽔平⽅向上的正应⼒σx2.求竖直⽅向上的正应⼒σy3.求垂直于纸⾯⽅向上的正应⼒σz薄壁圆筒与纸⾯垂直⽅向上的σz为零.球形薄壁容器的三个主应⼒为:受内压的球形薄壁容器为⼆向应⼒状态§7.3 ⼆向应⼒状态分析——解析法⼆向应⼒状态下,单元体各⾯上应⼒分量皆为已知,如下图所⽰:求垂直于xy平⾯的任意斜截⾯ef上的应⼒及主应⼒和主平⾯⼀.符号规定1.正应⼒正负号规定2.切应⼒正负号规定使微元或其局部顺时针⽅向转动为正;反之为负。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、 轴向拉伸的等直杆,杆任一点处最大剪应力的方向与轴线成___________。
2、一空心圆截面直杆,其、外径之比为α=0.8,两端承受轴向拉力作用,如将、外径增加一倍,则其抗拉刚度将是原来的________倍。
3、 在减速箱中,转速低的轴的直径比转速高的轴_____________。
4、 若梁上某段的弯矩值全为零,则该段的剪力值为_____________。
5、梁的截面为对称的空心矩形,如图1所示,这时,梁的抗弯截面模量W 为_______________。
6、 在梁的变形中挠度和转角之间的关系是____________。
7、减小梁变形的主要途径有:_______________ 、__________________ 、_________________。
8、二向应力状态(已知x σ,y σ ,xy τ)的应力圆圆心的横坐标值为_____________________,圆的半径为_____________。
9、与图2所示应力圆对应的单元体是____________向应力状态。
图1 图210、 将圆截面压杆改成面积相等的圆环截面压杆,其它条件不变,其柔度将________,临界应力将________。
工程上通常把延伸率δ>________的材料称为塑性材料。
低碳钢经过冷作硬化处理后,它的_________极限得到了明显的提高。
bbh h12图1正方形单元体ABCD ,变形后成为AB `C`D`。
单元体的剪应变为_________。
简支梁全梁上受均布荷载作用,当跨长增加一倍时,最大剪力增加一倍,最大弯矩增加了_______________倍。
如图2所示截面的抗弯截面模量Wz =_________________。
运用叠加原理求梁的变形时应满足的条件是:___________________________。
已知梁的挠曲线方程为)3(6)(2x l EIPx x y -= ,则该梁的弯矩方程是______________________。
图1 图2单向受拉杆,若横截面上的正应力为σ0,则杆任一点的最大正应力为_______,最大剪应力为____________。
图3应力圆,它对应的单元体属______________________应力状态。
细长杆的临界力与材料的____________________有关, 为提高低碳钢压杆的稳定性,改用高强刚不经济,原因是 _______________________________。
图3zhbdτσ下列结论中正确的是( )。
A.外力是指作用于物体外部的力B.自重是外力C.支座约束反力不属于外力D. 惯性力不属于外力 2、碳钢制成的圆轴在扭转变形时,单位长度扭转角θ超过了许用值。
为使轴的刚度满足安全,以下方案中最有效的是( )。
A. 改用合金钢B. 改用铸铁C. 减少轴的长度D. 增加轴的直径 3、对剪力与弯矩的关系,下列说确的是( )。
A. 同一段梁上,剪力为正,弯矩也必为正B. 同一段梁上,剪力为正,弯矩必为负C. 同一段梁上,弯矩的正负不能由剪力唯一确定D. 剪力为零处,弯矩也必为零4、简支梁受集中力偶0M 作用,如图3所示。
以下结论中错误的是( )。
A.b=0时,弯矩图为三角形 B.a=0时,弯矩图为三角形C.无论C 在何处,最大弯矩必为0MD.无论C 在何处,最大弯矩总在C 处 图3 5、当矩形截面梁剪切弯曲时,在横截面的中性轴处( )。
A.正应力最大,剪应力为零B.正应力为零,剪应力最大C.正应力和剪应力均最大D.正应力和剪应力均为零 6、图4示简支梁受集中力作用,其最大挠度ƒ发生在(A.集中力作用处B.跨中截面C.转角为零处D.转角最大处 7、在单元体的主平面上( )。
A.正应力一定最大B.正应力一定为零 图4C.剪应力一定最大D.剪应力一定为零8、脆性材料的单元体和塑性材料的单元体,均在相同的三向等压应力状态下,若发生破坏, 其破坏方式()。
A.分别为脆性断裂和塑性屈服B.分别为塑性屈服和脆性断裂C.都为脆性断裂D. 都为塑性屈服9、如果细长压杆有局部削弱,削弱部分对压杆的影响有四种答案,其中正确答案是()。
A.对稳定性和强度都有影响B. 对稳定性和强度都没有影响C.对稳定性有影响,对强度没有影响D. 对稳定性没有影响,对强度有影响10、当一根理想压杆承受的轴向力等于欧拉临界压力时,杆件保持直线平衡状态,但其受到一个微小横向干扰力后发生弯曲变形。
若此时解除干扰力,则有关压杆变形的正确答案为()。
A. 弯曲变形消失,恢复直线形状B.弯曲变形减少,不能恢复直线形状C.弯曲变形状态不变D.弯曲变形继续增大下列结论中正确的是()。
A.影响材料强度的是正应力和剪应力的大小B.影响材料强度的是力的大小C.同一截面上的正应力必定是均匀分布的D. 同一截面上的剪应力必定是均匀分布的2、剪应力互等定理与剪切胡克定律的正确适用围是()。
A.都只是在比例极限围成立B.超过比例极限时都成立C.剪应力互等定理在比例极限围成立,剪切胡克定律不受比例极限限制D.剪切胡克定律在比例极限围成立,剪应力互等定理不受比例极限限制3、用力方程计算剪力和弯矩时,横向外力与外力矩的正负判别正确的是()。
A. 横面左边梁向上的横向外力计算的剪力及其对截面形心计算的弯矩都为正B. 横面右边梁向上的横向外力计算的剪力及其对截面形心计算的弯矩都为正C. 横面左边梁向上的横向外力计算的剪力为正,向下的横向外力对截面形心计算的弯矩为正D. 横面右边梁向下的横向外力计算的剪力为正,该力对截面形心计算的弯矩也为正4、以下说确的是()。
A.集中力作用处,剪力和弯矩值都有突变B.集中力作用处,剪力有突变,弯矩图不光滑C.集中力偶作用处,剪力和弯矩值都有突变D.集中力偶作用处,剪力图不光滑,弯矩值有突变如图4所示的四种截面梁,材料和横截面面积相等。
从强度观点考虑,图()所示的截面梁在铅直面所能够承担的弯矩最大。
A B C D图46、挠曲线方程中的积分常量主要反映了()A.对近似微分方程误差的修正B.剪力对变形的影响C.约束条件对变形的影响D.梁的轴向位移对变形的影响7、图5悬臂梁给出了1,2,3,4点的应力状态单元体,其中错误的为图()DCA3图58、在下列论述中,正确的是()A.强度理论只适用于复杂应力状态B.第一、第二强度理论只适用于脆性材料C.第三、第四强度理论只适用于塑性材料D. 第三、第四强度理论只适用于屈服失效9、压杆的柔度λ集中反映了哪些因素对临界应力的影响( )A.压杆长度、约束条件、横截面尺寸和形状B.压杆材料、长度和约束条件C.压杆材料、约束条件、横截面尺寸和形状D.压杆材料、长度、横截面尺寸和形状10、两根细长杆,截面、支承均相同,但材料不同,且212E E =,两杆临界应力的关系的正确答案是( )。
A. 21)()(cr cr σσ=B. 21)(2)(cr cr σσ=C. 2)()(21cr cr σσ=D. 21)(3)(cr cr σσ= 1、o45 2、4 3、粗 4、零5、)2//()12/12/(3113h h b bh - 6、)()('x x θω=7、合理安排受力,减小M;减小1;加大EI 8、2/)(y x oc σσ+= 22)2(xyx r τσσ++= 9、二向应力状态 10、减小;增大二、选择题。
1、B2、D3、C4、C5、B6、C7、D8、D9、D 10、A1、5%。
2、比例。
3、α2。
4、3。
5、⎪⎪⎭⎫⎝⎛-632134bh d d π。
6、小变形及材料为线弹性。
7、)()(x l P x M -=。
8、2max 0max στσσ==,。
9、单向压缩应力状态。
10、弹性模量,不同强度钢材的弹性模量差别很小。
二、选择题。
1、A2、D3、A4、B5、D6、C7、D8、D9、A 10、B1.材料的失效模式 。
A 只与材料本身有关,而与应力状态无关;B 与材料本身、应力状态均有关;C 只与应力状态有关,而与材料本身无关;D 与材料本身、应力状态均无关。
2.下面有关强度理论知识的几个论述,正确的是 。
A 需模拟实际构件应力状态逐一进行试验,确定极限应力;B 无需进行试验,只需关于材料破坏原因的假说;C 需要进行某些简单试验,无需关于材料破坏原因的假说;D 假设材料破坏的共同原因,同时,需要简单试验结果。
3、 轴向拉伸细长杆件如图所示,_______。
A .1-1、2-2面上应力皆均匀分布;B .1-1面上应力非均匀分布,2-2面上应力均匀分布;C.1-1面上应力均匀分布,2-2面上应力非均匀分布;D.1-1、2-2面上应力皆非均匀分布。
4、塑性材料试件拉伸试验时,在强化阶段______。
A.只发生弹性变形;B.只发生塑性变形;C.只发生线弹性变形;D.弹性变形与塑性变形同时发生。
5、比较脆性材料的抗拉、抗剪、抗压性能:_______。
A.抗拉性能>抗剪性能<抗压性能;B.抗拉性能<抗剪性能<抗压性能;C.抗拉性能>抗剪性能>抗压性能;D.没有可比性。
6、水平面放置的薄壁圆环平均直径为d,横截面面积为A。
当其绕过圆心的轴在水平面匀角速度旋转时,与圆环的初始尺寸相比______。
A.d增大,A减小;B.A增大,d减小;C.A、d均增大;D.A、d均减小。
7、如右图所示,在平板和受拉螺栓之间垫上一个垫圈,可以提高______。
A.螺栓的拉伸强度;B.螺栓的挤压强度;C.螺栓的剪切强度;D.平板的挤压强度。
8、图中应力圆a、b、c表示的应力状态分别为A 二向应力状态、纯剪切应力状态、三向应力状态;B 单向拉应力状态、单向压应力状态、三向应力状态;C 单向压应力状态、纯剪切应力状态、单向拉应力状态;D 单向拉应力状态、单向压应力状态、纯剪切应力状态。
正确答案是。
9.压杆临界力的大小,A 与压杆所承受的轴向压力大小有关;B 与压杆的柔度大小有关;C 与压杆的长度大小无关;D 与压杆的柔度大小无关。
正确答案是。
10.一点的应力状态如下图所示,则其主应力1σ、2σ、3σ分别为A 30MPa、100 MPa、50 MPaB 50 MPa、30MPa、-50MPaC 50 MPa、0、-50MPaD -50 MPa、30MPa、50MPa正确答案是。
1 B2 D3 B4 D5 B 6A 7 D 8 C 9 B 10 B。
为保证工程结构或机械的正常工作,构件应满足三个要求,即。
2. 四种基本变形是 。
3.为了求解静不定问题,必须研究构件的 ,从而寻找出 。
4.材料力学中求力的基本方法是 。
5.矩形截面梁的弯曲剪力为F S ,横截面积为A ,则梁上的最大切应力为 。
