刚体绕定轴转动 力矩共17页文档
合集下载
力矩 刚体绕定轴转动定律-精品文档
力矩 刚体绕定轴转动定律
一、刚体绕定轴转动的力矩
z
F//
F
F对点O转动的力矩:
MO
O
Mz
y
x
r
P
F
F对定轴z转动的力矩:
M r F O r F r F //
M r F z
二、定轴转动定律
M β z J
M J Fr 2 M Fr 39 . 2 [ rad /s ]
mg T ma
Tr J
J
r
O
T
F
mg
(2)
ar
21 . 8 [ rad /s]
2
例: 均匀细直棒m 、l ，可绕轴 O 在竖直平面内转动 初始时它在水平位置 m l O 求: 它由此下摆 角时的
转动惯量与转轴有关
例: 求圆环绕中心轴旋转的转动惯量
2 解: dm 转动惯量 d JR d m
2 J R d m R d m mR 2 2 0 0 L L
dl R o
m
例: 求圆盘绕中心轴旋转的转动惯量 m 2 mr m d S 解: d 2 2πrdr 2 dr πR R dm 转动惯量 d J r2d m
M r d f df 的力矩 d
R
2 d M mgR 圆盘摩擦力矩 M 0 2 1 2d 3 mgR mR
d M
d 3 转动定律 MJ dt 3R0 t 0 3 R t d t d 0 4g g 04
2
d t
例: 一均质棒，长度为 l，现有一水平打 击力F 作用于距轴 l 处。 求: l =? 时, 轴对棒作用力的水平分量为 0。
一、刚体绕定轴转动的力矩
z
F//
F
F对点O转动的力矩:
MO
O
Mz
y
x
r
P
F
F对定轴z转动的力矩:
M r F O r F r F //
M r F z
二、定轴转动定律
M β z J
M J Fr 2 M Fr 39 . 2 [ rad /s ]
mg T ma
Tr J
J
r
O
T
F
mg
(2)
ar
21 . 8 [ rad /s]
2
例: 均匀细直棒m 、l ，可绕轴 O 在竖直平面内转动 初始时它在水平位置 m l O 求: 它由此下摆 角时的
转动惯量与转轴有关
例: 求圆环绕中心轴旋转的转动惯量
2 解: dm 转动惯量 d JR d m
2 J R d m R d m mR 2 2 0 0 L L
dl R o
m
例: 求圆盘绕中心轴旋转的转动惯量 m 2 mr m d S 解: d 2 2πrdr 2 dr πR R dm 转动惯量 d J r2d m
M r d f df 的力矩 d
R
2 d M mgR 圆盘摩擦力矩 M 0 2 1 2d 3 mgR mR
d M
d 3 转动定律 MJ dt 3R0 t 0 3 R t d t d 0 4g g 04
2
d t
例: 一均质棒，长度为 l，现有一水平打 击力F 作用于距轴 l 处。 求: l =? 时, 轴对棒作用力的水平分量为 0。
一,刚体的定轴转动(运动)二,力矩,刚体定轴转动的转动定律,转动惯量
二、刚体定轴转动的转动定律
～利用力矩定义＋牛顿第二定律，研究刚体作定 轴转动的动力学规律。 设：oz为定轴， 为 P 刚体中任一质点 i ，其 质量为 ∆ m i。质点 iv ur 受外力 F i ，内力 F i ′ 的作用，均在与 O z 轴 相垂直的同一平面内。 ①牛顿第二定律： ur r v F i + Fi ′ = ∆ m i a i 建立自然坐标：切向、法向；
三、转动惯量 J 1.转动惯量的物理意义： 当以相同的力矩分别作用于两个绕定轴转动的不同 刚体时，它们所获得的角加速度一般是不一样的，转 动惯量大的刚体所获得的角加速度小，即角速度改变 得慢，也就是保持原有转动状态的惯性大；反之，转 动惯量小的刚体所获得的角加速度大，即角速度改变 得快，也就是保持原有转动状态的惯性小。因此，转 动惯量是描述刚体在转动中的惯性大小的物理量。 2.与转动惯量有关的因素：①刚体的质量；②转轴的 位置；③刚体的形状。 实质与转动惯量有关的只有前两个因素。形状即质量 分布，与转轴的位置结合决定转轴到每个质元的矢径。
R 3
例3、求长为L、质量为m的均匀细棒对图中不同轴的 转动惯量。 B 解：取如图坐标，dm=λdx A
J
A
=
∫
∫
L
0
x 2 λ dx = mL 2 / 3
A
x λ dx = mL
2 2
JC =
L 2 L − 2
L C L/2 L/2
X B X
/ 12
例4. 求质量 m ,半径 R 的球壳对直径的转动惯量 解：取离轴线距离相等的点的 集合为积分元
F i t ri + F i t′ ri = ∆ m i ri 2 α
外力矩 内力矩
③对所有质元的同样的式子求和：
第4章刚体转动
16
长江大学物理教程
M1
外力在转动平面上对转
轴的力矩使刚体发生转动
F2
j2
F 2
F 1
r2 O r1
P2 d2 d1
P1
F1 力矩 M1 = r1 × F1 j1 大小 M1 = r1 F1 sin j1
= F1 d1 =F 1 r1
方向 MM2 = r2 × F2
M2
大小 M 2 = r2F2 sin j 2
定轴转动刚体在某时刻t 的瞬时角速度为 ，瞬
时角加速度 ， 刚体中一质点P至转轴的距离为r
瞬时线速度
质点P 瞬时切向加速度 瞬时法向加速度
的大小
2019/10/31
这是定轴转动中线量与角量的基本关系
11
长江大学物理教程
质点直线运动或刚体平动 位移 速度 加速度
匀速直线运动 匀变速直线运动
刚体的定轴转动 角位移 角速度 角加速度 匀角速定轴转动 匀变角速定轴转动
2019/10/31
12
长江大学物理教程
例1 在高速旋转的微型电动机里，有一 圆柱形转子可绕垂直其横截面并通过中心的 转轴旋转．开始起动时，角速度为零．起动
后式其中转m速随5时40间r变 s化1，关系为2.：0s ．求m (：1 et / )
(1)t=6 s时电动机的转速．(2)起动后，电动 机在 t=6 s时间内转过的圈数．(3)角加速度 随时间变化的规律．
优秀精品课件文档资料
长江大学物理教程
长江大学物理科学与技术学院
第四章 刚体的转动
主讲教师：喻秋山
2010～2011年第一学期
4-0 教学基本要求
一 理解描写刚体定轴转动角速度和 角加速度的物理意义，并掌握角量与线量 的关系．
力矩刚体绕定轴转动定律
3g cos
2l
d d dt d
d
3g cos d
0
0 2l
2 3g sin / l
例: 圆盘以 0 在桌面上转动,受摩擦力而静止
求: 到圆盘静止所需时间。
解: 取宽为dr的细圆环 其质量为
dm
σdS
π
m R2
2π
rdr
dm 摩擦力 df gdm
dr r
df
df 的力矩 dM rdf
圆盘摩擦力矩 M
R
dM
2
mgR
0
3
转动定律 M J d
dM
2 mgR 1 mR2 d
3
2 dt
dt
t
0
dt
0
0
3R d 4g
t 3R0 4g
例: 一均质棒，长度为 l，现有一水平打
击力F 作用于距轴 l 处。
求: l =? 时, 轴对棒作用力的水平分量为 0。
解: 设轴对棒的水平分力为 Nx
rO
T
mg
例: 均匀细直棒m 、l ，可绕轴 O 在竖直平面内转动
初始时它在水平位置
求: 它由此下摆 角时的
解: dm 质元 dm m dx l
O
ml
dm 重力矩 dM gdm x cos
x
M
dM
1 2
mgl cos
gdm
重力对棒的合力矩等于重力全部集中于质心所产生的力矩
M
J
J 1 ml2 3
在绳端施以 F = 98 N 的拉力，不计摩擦力
求 (1) 滑轮的角加速度；
(2) 如以重量P = 98 N 的物体挂在绳端，计算滑轮 的角加速度
力矩作功与刚体绕定轴转动的动能定理
Ek0 0
1 mgl 1 J 2 0
2
2
m,l
o
J 1 ml 2
3
3g
mg
l
练习2、一质量 M、半径 R 圆盘绕一无摩檫 轴转动，盘上绕有轻绳，下端挂物体 m。 求：当 m 由静止下落h时速度 v ？
解：
刚体 M
N T
o
对m：
G
TP
m
v 2 mgh h
M 2m
注意和前面的方法比较！
练习3、一匀质细棒长l ，质量m，可绕通过 其端点O水平轴转动。当棒从水平位置自由释
放后，它在竖直位置上与放在地面上的物体
相撞。该物体的质量也为m ，地面的摩擦系 数为 。撞后物体沿地面滑行s后而停止。求 相撞后棒的质心C 离地面的最大高度h，并说
明棒在碰撞后将向重力外，其余内力与外力都 O
（3）
由匀减速直线运动的公式得
亦即
（4）
由（1）（2）与（4）联合求解，即得
（5）
当 >0 则棒向左摆条件： 亦即L>6s；
当0，则棒向右摆条件：
亦即L <6s
由机械能守恒定律，棒上升的最大高度：
(6)
把（5）代入上式，求得：
练习4：工程上，两飞轮常用摩擦啮合器使它们
以相同的转速一起转动。如图所示，A和B两飞
动量守恒；
动量不守恒；
角动量守恒；
角动量守恒；
机械能不守恒 .
机械能不守恒 .
圆锥摆系统 动量不守恒； 角动量守恒； 机械能守恒 .
直线运动与定轴转动规律对照
质点的直线运动
刚体的定轴转动
P126书例2 一长为 l , 质
量为m 的竿可绕支点O自由转 动．一质量为m’、速率为v
力矩 刚体定轴转动的转动定律
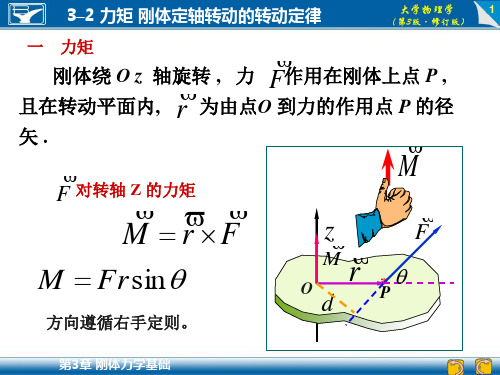
dJ R dm
2
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
12
考虑到所有质元到转轴的距离均为R，所以细圆环对 中心轴的转动惯量为
J dJ R dm R
2 m
2
m
dm mR
2
(2)求质量为m，半径为R的圆盘对中心轴的转动惯量
m 如图 dS 2 rdr , , dm dS 2 rdr 2 R
l 2
o
P
d d d d dt d dt d
代入初始条件积分 得
第3章 刚体力学基础
3g d sin d 2l 3g (1 cos ) l
1 2 J x dx ml 0 3
l 2
由此看出，同一均匀细棒，转轴位置不同，转动惯 量不同.
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
11
例3.2 设质量为m，半径为R的细圆环和均匀圆盘分 别绕通过各自中心并与圆面垂直的轴转动，求圆环和 圆盘的转动惯量. 解 (1) 在环上任 取一质元，其质量 为dm，距离为R， 则该质元对转轴的 转动惯量为
解 (1)转轴通过棒的中心并与棒垂直
m l
dm dx
dJ x 2dm x 2dx
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
10
整个棒对中心轴的转动惯量为
J dJ
l 2 l 2
1 x dx ml 2 12
2
(2)转轴通过棒一端并与棒垂直时，整个棒对该轴的 转动惯量为
解 (1) M k 2 ，故由转动定律有
k k J 即 J 2 1 k0 0 3 9J
2.91刚体的定轴转动力矩 转动定律 转动惯量
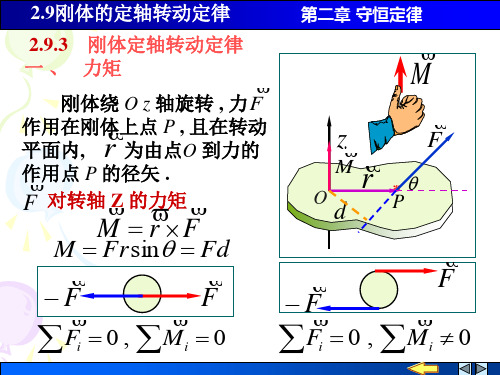
Fi 0 , M i 0
M r F
d
P
F
F
Fi 0 , M i 0
F
F
2.9刚体的定轴转动定律
讨论
第二章 守恒定律
1）若力 F 不在转动平面内，把力分解为平行和垂
直于转轴方向的两个分量 其中 Fz 对转轴的力 矩为零，故 F 对转轴的 力矩
代入初始条件积分 得
3g d sind 2l
3g (1 cos ) l
考虑到
7lg 12 v0 dr g cost cos( t) dt 2 24 v0 7l
t
2.9刚体的定轴转动定律
第二章 守恒定律
例4 一长为 l 质量为 m 匀质细杆竖直放置，其 下端与一固定铰链 O 相接，并可绕其转动 . 由于此 竖直放置的细杆处于非稳定平衡状态，当其受到微小 扰动时，细杆将在重力作用下由静止开始绕铰链O 转 动 .试计算细杆转动到与竖直线成 角时的角加速度 和角速度 .
刚体定轴转动的角动量定理
第二章 守恒定律
t2
t1
Mdt J 2 J1
3 刚体定轴转动的角动量守恒定律 若M 讨论 若 J 不变， 不变；若 J 变， 也变，但 L 内力矩不改变系统的角动量.
守 恒条件
0 ，则 L J 常量
M 0
J 不变.
在冲击等问题中
L mi ri vi (
i
2 mi ri )
L J
i
ri
mi
z
2 刚体定轴转动的角动量定理 dL d( J ) M dt dt
O
vi
t1
M r F
d
P
F
F
Fi 0 , M i 0
F
F
2.9刚体的定轴转动定律
讨论
第二章 守恒定律
1）若力 F 不在转动平面内，把力分解为平行和垂
直于转轴方向的两个分量 其中 Fz 对转轴的力 矩为零，故 F 对转轴的 力矩
代入初始条件积分 得
3g d sind 2l
3g (1 cos ) l
考虑到
7lg 12 v0 dr g cost cos( t) dt 2 24 v0 7l
t
2.9刚体的定轴转动定律
第二章 守恒定律
例4 一长为 l 质量为 m 匀质细杆竖直放置，其 下端与一固定铰链 O 相接，并可绕其转动 . 由于此 竖直放置的细杆处于非稳定平衡状态，当其受到微小 扰动时，细杆将在重力作用下由静止开始绕铰链O 转 动 .试计算细杆转动到与竖直线成 角时的角加速度 和角速度 .
刚体定轴转动的角动量定理
第二章 守恒定律
t2
t1
Mdt J 2 J1
3 刚体定轴转动的角动量守恒定律 若M 讨论 若 J 不变， 不变；若 J 变， 也变，但 L 内力矩不改变系统的角动量.
守 恒条件
0 ，则 L J 常量
M 0
J 不变.
在冲击等问题中
L mi ri vi (
i
2 mi ri )
L J
i
ri
mi
z
2 刚体定轴转动的角动量定理 dL d( J ) M dt dt
O
vi
t1
5.2 力矩 刚体绕定轴转动微分方程
M J 、 ma F M F , J m, a
两个定律在形式上对应, 都是反映瞬时效 应的。 d dv M J J F ma m dt dt (2) m反映质点的平动惯性，J 则反映刚 体的转动惯性。
大学物理 第三次修订本
7
第5章 刚体力学基础 动量矩
三、转动惯量 刚体质量不连续分布 刚体质量连续分布
O .
大小
F
方向由右螺旋法则确定。
r
θ
2
大学物理 第三次修订本
第5章 刚体力学基础 动量矩
力对定轴力矩的矢量形式
z
F//
M Z r F
方向由右螺旋法则确定。
F
r
A
F
大学物理 第三次修订本
3
第5章 刚体力学基础 动量矩
二、刚体绕定轴转动微分方程 作用在 mk上的外力 Fk ，内力 f k dvk mk Fk f k dt 在圆规迹切线方向
2
J z' 刚体绕任意轴的转动惯量；
J z 刚体绕通过质心的轴的转动惯量；
L
两轴间垂直距离。
大学物理 第三次修订本
13
第5章 刚体力学基础 动量矩
5. J 的计算 （1）按定义计算
例1求长为L质量为m 的均匀细棒对图 中不同轴的转动惯量。
解: 取如图坐标，dm = dx
A
dm B
x
L
J A x dx mL / 3
15
2
第5章 刚体力学基础 动量矩
求图所示刚体对经过棒端且与棒垂直的轴的 转动惯量如何计算？(棒长为L、圆盘半径为R）
J L1
1 2 J o mo R 2
力矩刚体绕定轴转动定律课件
03
力矩刚体绕定轴转动的实际应用
日常生活中的应用实例
自行车轮转动
方向盘控制
当我们在骑自行车时，脚踏板施加的 力量通过链条传递到车轮上，使车轮 发生转动。
在驾驶汽车时，我们通过转动方向盘 来控制车辆的方向，方向盘的转动就 是力矩刚体绕定轴转动的实例。
门把手转动
当我们握住门把手转动时，门被推开 或关闭，这是由于门把手施加的力矩 使门发生转动。
力矩的大小决定了刚体转动的速度，力矩 越大，刚体的角速度越快。
刚体转动惯量的概念
01
02
03
转动惯量定义
转动惯量是描述刚体转动 惯性大小的物理量，与刚 体的质量分布和转动轴的 位置有关。
计算公式
对于质量均匀分布的刚体 ，转动惯量I = (1/2) * m * r^2，其中m是质量，r 是到转动轴的距离。
实验结果分析和结论
实验结果分析
通过实验数据，分析角速度与力矩之间的关系，验证力矩刚体绕定轴转动定律 。同时，比较不同转动惯量下刚体的角速度变化，加深对转动惯量影响的理解 。
实验结论
通过实验验证，可以得出力矩刚体绕定轴转动定律的正确性。同时，实验结果 也表明转动惯量对刚体的角速度有影响，转动惯量越大，相同力矩作用下刚体 的角速度越小。
05
力矩刚体绕定轴转动定律的深入探讨
力矩刚体转动过程中的能量转换
机械能转换
力矩作用在刚体上，使刚体从静 止或匀速转动状态变为加速转动 状态，在此过程中，刚体的动能 增加，而势能保持不变。
能量守恒
力矩刚体转动过程中的能量转换 符合能量守恒定律，即输入的力 矩能量等于刚体动能的变化量。
力矩刚体转动过程中的动量守恒
工业生产中的应用实例
刚体定轴转动的转动定律
R
M
h
Hale Waihona Puke 解法一 用牛顿第二运动 定律及转动定律求解.分 析受力如图所示. 对物体m用牛顿第二 运动定律得 mg T ma 对匀质圆盘形滑轮用 转动定律有 TR J 物体下降的加速度的 大小就是转动时滑轮边缘 上切向加速度，所以
o R M
T
h
a
G
a R 物体m 落下h 高度时的速率为
2
3.试求质量为m 、半径为R 的匀质圆环 对垂直于平面且过中心轴的转动惯量. 解 作示意图如右,由于质 量连续分布，所以由转动 惯量的定义得
J R 2dm
m
dm
o
R
2R 0
m R dl 2R
2
mR 2
4.试求质量为m 、半径为R 的匀质圆盘 对垂直于平面且过中心轴的转动惯量. dr 解 如图所示, 由于质 量连续分布，设圆盘的 R l o r 厚度为l，则圆盘的质量 密度为 m 2 R l
r近日 r远日
v近日
解 彗星受太阳引力的作用，而引力通过了 太阳，所以对太阳的力矩为零，故彗星在运 行的过程中角动量守恒. 于是有 r近日 v近日 r远日 v远日 因为 r近日 v近日 ，r远日 v远日
r近日v近日 所以 r远日 v远日
代入数据可, 得
J r 2dm
m
R 0
1 1 4 r 2r ldr R l mR 2 2 2
2
5. 如图所示，一质 量为M 、半径为R 的匀 质圆盘形滑轮，可绕一 无摩擦的水平轴转动. 圆盘上绕有质量可不计 绳子，绳子一端固定在 滑轮上，另一端悬挂一 质量为m 的物体，问物 体由静止落下h 高度时, 物体的速率为多少？
刚体定轴转动的转动定律力矩PPT
求 θ角及着陆滑行时的速度多大？
解 引力场（有心力）
v0
系统的机械能守恒
质点的动量矩守恒
m r0
v R
OM
m 1 2m v v 0 r 00 2s iGπ n r0 M) ( 1 2 m m m vv 2 R GRMm vv0r0R sin4v0sin
sin14123RGv0M 21/2
1/2
LZ Δmiviri Δmiri2 JZ
i
i
LZJZ(所有质元对 Z 轴的动量矩之和)
2. 刚体定轴转动的动量矩定理
对定轴转动刚体，Jz 为常量。
dLZ dt
JZ
d
dt
dLZ dt
Mz
M zd t d L z d J
动量矩定理 微分形式
t1 t2M zd t 1 2d JJ2 J1（动量矩定理积分形式）
0tm1m 1m 2m 21 2 gmtr
3.2.2 刚体定轴转动的动能定理
1. 刚体定轴转动的动能
Δ m 1 ,Δ m 2 ,,Δ m k ,,Δ m N r 1 ,r 2 ,,r k ,,r N v 1 , v 2 , , v k , , v N
Δmk 的动能为
Ek 12Δmkvk212Δmkrk22
F FF Fn
2)力对点的力矩
Mo
M O r F
F
大小 M OrF sin
O . r
指向由右螺旋法则确定 力对定轴力矩的矢量形式
z
F//
F
M Z r F
（力对轴的力矩只有两个指向）
r
A
FF
2. 刚体定轴转动的转动定律
第 k个质元 F k f k m k a k
4-4 力矩的功 刚体绕定轴转动的动能定理
物理学
第五版
4-4
力矩的功 刚体绕定轴转动的动能定理
M 4 µg α= = 作匀加速转动） （作匀加速转动） J 3R 3ωR 由 ω = ω0 + αt 可求得 t = 4 µg 2 2 (3) 由 ω = ω0 + 2αθ 可得在 0 到 t ) 2 的时间内， 的时间内，转过的角度为 θ = 3ω R 8µg 1 驱动力矩做的功为 W = Mθ = mR 2ω 2 4
第四章 刚体的转动
13
物理学
第五版
4-4
力矩的功 刚体绕定轴转动的动能定理
解 (1) 如图取面 ) 积元ds 积元 = drdl，该面元 ， 所受的摩擦力为
df
df =
µ mg
πR
2
o
r
dl dr
drdl
R
此力对点o的力矩为
rdf =
µmg
πR
2
rd r d l
刚体的转动
14
第四章
物理学
第五版
4-4
O
G
N
θ
A
l dA = mg cosθdθ 2
π
ω
A′ G
l l 2 A = ∫ dA = ∫0 mg cosθdθ = mg 2 2
第四章 刚体的转动
11
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理 按力矩的功和转动动能增量的关系式得
由此得
l 1 2 mg = Jω 2 2 mgl ω= J
例， 留声机的转盘绕通过盘心垂直盘 作匀速转动． 面的轴以角速率 ω 作匀速转动．放上唱片 后，唱片将在摩擦力作用下随转盘一起转 设唱片的半径为R，质量为m， 动．设唱片的半径为 ，质量为 ，它与转 盘间的摩擦系数为 µ ，求：(1)唱片与转盘 ) 间的摩擦力矩； ) 间的摩擦力矩； (2)唱片达到角速度 ω时需 要多长时间；(3)在这段时间内，转盘的驱 要多长时间； )在这段时间内， 动力矩做了多少功？ 动力矩做了多少功？
刚体定轴转动的转动定律力矩-文档资料
讨论 (1) 合力矩的功 2 2 2 A M d ( M )d M d A i i i 1 1 1 i i i (2) 力矩的功就是力的功。
Δmk 的动能为 1 2 1 2 2 E Δ m v Δ m r k k k k k 2 2
刚体的总动能
z
O
rk
P
vk
• Δ mk
1 2 2 1 2 2 1 2 E E Δ m r Δ m r J k kk kk 2 2 2 结论 绕定轴转动刚体的动能等于刚体对转轴的转动惯量与其 角速度平方乘积的一半
r
A
（力对轴的力矩只有两个指向）
F F
2. 刚体定轴转动的转动定律 k k
rk
fk
Fk
F f m a k k k k
在上式两边同乘以 rk 对所有质元求和
F r f r m a r m r r k k k k k k k k k k
求 (1) 飞轮的角加速度 (2) 如以重量P =98 N的物体挂在绳
端，试计算飞轮的角加速 解 (1) Fr J
Fr 98 0 . 2 2 39 . 2 rad/s J 0 . 5
mgr 2 J mr
两者区别
rO
T F
T ma (2) mg
Tr J
kk kk 2 k k
F r f r ( m r )
内力矩之和为0 转动惯量 J
刚体绕定轴转动微分方程（刚体的转动定律）
M J
与牛顿第二定律比较： M F , J m , a
3. 转动惯量 定义
刚体定轴转动定律
于 180°的夹角 θ 转向 F 时，拇指所指的方向就是力矩的方向。
可见，力矩的方向与转轴的方向平行，只有两个可能的方向，因此，可用 M 的正负表示力矩的方向。 一般可按力矩的作用来判断其正负：由转轴 Oz 正向俯视，若力矩的作用使刚体逆时针转动，则力矩为 正，否则为负。
刚体定轴转动定律 1.1 力矩
可加性
• 对同一转轴而言，刚体各部分转动惯量之 和等于整个刚体的转动惯量。
平行轴定理
• 设有两个彼此平行的转轴，一个通过刚体 的质心，另一个不通过质心。两平行轴之 间的距离为d，刚体的质量为m。
如果此刚体对通过质心转轴的转动惯量为 Jc ，则对另一 转轴的转动惯量 J 为 J Jc md 2
刚体定轴转动定律
刚体定轴转动定律Βιβλιοθήκη ， ，，，
例题讲解 2
如图所示，一轻绳跨过一轴承光滑的定滑轮。绳两边分别悬有质量为 m1 和 m2 的两个物体 A，B。已知 m1
小于 m2 ，滑轮可看作质量均匀分布的等厚圆盘，其质量为 m，半径为 r，设绳与滑轮间无相对滑动。求：① 物
体的加速度；② 滑轮的角加速度；③ 绳的张力。
i 1
n
用 M 表示，即 M (Δmiri2 ) β
i 1
n
n
式中的 (Δmiri2 ) 称为转动惯量，用 J 表示，即 J (Δmiri2 )
i 1
i 1
于是，式可写为 M Jβ
刚体定轴转动定律 1.2 转动定律
转动定律：刚体定轴转动时，刚体的角加速度与刚体所受的合外力矩成正比，与刚体的转动惯量 成反比。
r 2 dm
Ω
式中 r ——质元 dm 到转轴的距离（m）。 在国际单位制中，转动惯量的单位为 kg m2 。
可见，力矩的方向与转轴的方向平行，只有两个可能的方向，因此，可用 M 的正负表示力矩的方向。 一般可按力矩的作用来判断其正负：由转轴 Oz 正向俯视，若力矩的作用使刚体逆时针转动，则力矩为 正，否则为负。
刚体定轴转动定律 1.1 力矩
可加性
• 对同一转轴而言，刚体各部分转动惯量之 和等于整个刚体的转动惯量。
平行轴定理
• 设有两个彼此平行的转轴，一个通过刚体 的质心，另一个不通过质心。两平行轴之 间的距离为d，刚体的质量为m。
如果此刚体对通过质心转轴的转动惯量为 Jc ，则对另一 转轴的转动惯量 J 为 J Jc md 2
刚体定轴转动定律
刚体定轴转动定律Βιβλιοθήκη ， ，，，
例题讲解 2
如图所示，一轻绳跨过一轴承光滑的定滑轮。绳两边分别悬有质量为 m1 和 m2 的两个物体 A，B。已知 m1
小于 m2 ，滑轮可看作质量均匀分布的等厚圆盘，其质量为 m，半径为 r，设绳与滑轮间无相对滑动。求：① 物
体的加速度；② 滑轮的角加速度；③ 绳的张力。
i 1
n
用 M 表示，即 M (Δmiri2 ) β
i 1
n
n
式中的 (Δmiri2 ) 称为转动惯量，用 J 表示，即 J (Δmiri2 )
i 1
i 1
于是，式可写为 M Jβ
刚体定轴转动定律 1.2 转动定律
转动定律：刚体定轴转动时，刚体的角加速度与刚体所受的合外力矩成正比，与刚体的转动惯量 成反比。
r 2 dm
Ω
式中 r ——质元 dm 到转轴的距离（m）。 在国际单位制中，转动惯量的单位为 kg m2 。
7-31 刚体定轴转动的力矩 转动定律 转动惯量
1 2 I A ml 3
A
C l 2 l 2
m
1 2 I c ml 12
另外一些参见P224表7.1。
3、计算 I 的几条规律:
1）对同一轴 I 具有可叠加性
JC C d J m 2）平行轴定理 平行
I Ii
I Ic md
2
d --两平行轴距离
2） 平行轴定理 质量为 m 的刚体，如果对 其质心轴的转动惯量为 J C ，则 对任一与该轴平行，相距为 d 的转轴的转动惯量
3、绕一端轴，杆的转动惯量
x dx
例2、均质细圆环的转动惯量 任取线元dl ， dm=dl，距离轴 r
ω m r
I r dm r
2
2
dm m r
2
例3、质量为m，半径为R 的均质圆盘的转动惯量 可看作由半径不同的圆环构成，盘面 m 单位面积的质量为
ω
R
3
0
R2
任取面元ds（离r 远处dr 宽细环）
Note: 绳中张力
例： 已知: 圆盘转动惯量I，初角速度0 阻力矩M= -k (k为正的常量) 求: 从0变为0/2所需的时间
解：转动定律： -k = Id /dt
k d 2 dt 0 0 I I ln 2 t k
t
0
[思考] 从任意值变为其一半值所需的时间？
例:
有一均质细直杆在一个粗糙的水平面上可绕一条通过其一端 的竖直轴旋转，它与平面之间的摩擦系数为m 。设杆子质量为m, 长度为 l ，其初始转速为ω 0 。试求当它的转速为原来的一半时 所用的时间。 m 解：
o
dm
l
o
´
x
dx
A
C l 2 l 2
m
1 2 I c ml 12
另外一些参见P224表7.1。
3、计算 I 的几条规律:
1）对同一轴 I 具有可叠加性
JC C d J m 2）平行轴定理 平行
I Ii
I Ic md
2
d --两平行轴距离
2） 平行轴定理 质量为 m 的刚体，如果对 其质心轴的转动惯量为 J C ，则 对任一与该轴平行，相距为 d 的转轴的转动惯量
3、绕一端轴，杆的转动惯量
x dx
例2、均质细圆环的转动惯量 任取线元dl ， dm=dl，距离轴 r
ω m r
I r dm r
2
2
dm m r
2
例3、质量为m，半径为R 的均质圆盘的转动惯量 可看作由半径不同的圆环构成，盘面 m 单位面积的质量为
ω
R
3
0
R2
任取面元ds（离r 远处dr 宽细环）
Note: 绳中张力
例： 已知: 圆盘转动惯量I，初角速度0 阻力矩M= -k (k为正的常量) 求: 从0变为0/2所需的时间
解：转动定律： -k = Id /dt
k d 2 dt 0 0 I I ln 2 t k
t
0
[思考] 从任意值变为其一半值所需的时间？
例:
有一均质细直杆在一个粗糙的水平面上可绕一条通过其一端 的竖直轴旋转，它与平面之间的摩擦系数为m 。设杆子质量为m, 长度为 l ，其初始转速为ω 0 。试求当它的转速为原来的一半时 所用的时间。 m 解：
o
dm
l
o
´
x
dx
4-4 力矩的功 刚体绕定轴转动的动能定理
轴以角速率ω 作匀速转动．放上唱片后，唱片将 在摩擦力作用下随转盘一起转动．设唱片的半径 为R，质量为m，它与转盘间的摩擦系数为 ，求： (1)唱片与转盘间的摩擦力矩； (2)唱片达到角速 度 时需要多长时间； (3)在这段时间内，转盘的 ω 驱动力矩做了多少功？
4-4 力矩的功 刚体绕定轴转动的动能定理
作的总功为 二、力矩的功率
4-4 力矩的功 刚体绕定轴转动的动能定理
刚体中任一质元 的速率 该质元的动能
对所有质元的动能求和
∑
∑
转动惯量 J
得
J
4-4 力矩的功 刚体绕定轴转动的动能定理
四、刚体绕定轴转动的动能定理
回忆质点的动能定理
刚体转动的动能定理
由 力矩的元功 转动定律 则
合外力矩的功
称为
转动动能的增量
L J
2、角动量定理.
dL M dt
2015-7-12
微分形式
积分形式
t1 M dt L2 L1 t2 冲量矩 M dt
t2
t1
17
3、角动量守恒定律.
若作用于物体的合外力矩 M 0 ,则角动量守恒: L 恒矢量
对质点有: 对刚体有:
4-4 力矩的功 刚体绕定轴转动的动能定理
第一节
4-4 力矩的功 刚体绕定轴转动的动能定理
力的空间累积效应： 力的功、动能、动能定理．
力矩的空间累积效应： 力矩的功、转动动能、动能定理．
一 力矩作功
4-4 力矩的功 刚体绕定轴转动的动能定理
力
的元功
力对转动刚体所作的功用力矩的功来计算
若在某变力矩 的作用下，刚体由 转到 ，
o
x
dx x
4-4 力矩的功 刚体绕定轴转动的动能定理
作的总功为 二、力矩的功率
4-4 力矩的功 刚体绕定轴转动的动能定理
刚体中任一质元 的速率 该质元的动能
对所有质元的动能求和
∑
∑
转动惯量 J
得
J
4-4 力矩的功 刚体绕定轴转动的动能定理
四、刚体绕定轴转动的动能定理
回忆质点的动能定理
刚体转动的动能定理
由 力矩的元功 转动定律 则
合外力矩的功
称为
转动动能的增量
L J
2、角动量定理.
dL M dt
2015-7-12
微分形式
积分形式
t1 M dt L2 L1 t2 冲量矩 M dt
t2
t1
17
3、角动量守恒定律.
若作用于物体的合外力矩 M 0 ,则角动量守恒: L 恒矢量
对质点有: 对刚体有:
4-4 力矩的功 刚体绕定轴转动的动能定理
第一节
4-4 力矩的功 刚体绕定轴转动的动能定理
力的空间累积效应： 力的功、动能、动能定理．
力矩的空间累积效应： 力矩的功、转动动能、动能定理．
一 力矩作功
4-4 力矩的功 刚体绕定轴转动的动能定理
力
的元功
力对转动刚体所作的功用力矩的功来计算
若在某变力矩 的作用下，刚体由 转到 ，
o
x
dx x
相关主题