1.什么叫平方根如何用符号表示数a(≥0)的平方根
初步认识平方根求平方根的应用

初步认识平方根求平方根的应用平方根是数学中的一个重要概念,它与平方数之间有着密切的联系。
平方根可以用来解决很多实际问题,尤其在科学和工程领域中具有广泛的应用。
本文将初步介绍平方根的概念,并探讨一些平方根在实际生活中的应用。
一、平方根的概念平方根是指一个数的平方等于给定数的正平方根。
以数a为例,a的平方根可以表示为√a,读作"根号a"。
具体来说,如果一个数x的平方等于a,那么x就是a的平方根,即x^2 = a。
平方根可以是正数、负数或零,但通常我们所讨论的平方根都是正平方根。
二、平方根的符号表示在数学中,我们用符号√a表示数a的平方根。
这个符号被称为"根号",它将数a放在其下方的曲线中来表示。
例如,√4表示4的平方根,结果是2。
同样地,√9表示9的平方根,结果是3。
我们可以通过计算平方根来得到未知数的值,或者验证一个数是否是某个平方数的平方根。
三、求解平方根的方法求解平方根有多种方法,其中最常见的方法是开方和求平方根的倒数。
开方是指将一个数开平方,即求它的平方根。
例如,√16等于4,因为4的平方等于16。
另一种方法是求平方根的倒数,即将一个数的倒数开平方。
例如,我们可以说1/√16等于1/4,因为4的平方等于16。
四、平方根的应用举例1. 计算几何面积:平方根的应用在几何学中非常重要。
例如,我们可以使用平方根来计算矩形的对角线长度。
根据勾股定理,矩形的对角线长度等于边长的平方和的平方根。
通过计算平方根,我们可以准确地确定任意矩形的对角线长度。
2. 物理学中的运动问题:平方根在物理学中也有广泛的应用。
例如,在平抛运动中,我们可以使用平方根来计算物体的飞行时间和飞行距离。
通过求解平方根,我们可以得到物体的运动轨迹和速度等相关信息。
3. 金融领域的财务分析:平方根在金融领域的财务分析中被广泛使用。
例如,在投资管理中,我们可以使用平方根来计算资产回报率的标准差。
通过求解平方根,我们可以对资产的风险进行评估,并制定相应的投资策略。
八年级数学上册《第二章2 平方根》讲解与例题

《第二章2 平方根》讲解与例题1.平方根(1)平方根的概念:若是一个数x 的平方等于a ,即x 2=a ,那么那个数x 就叫做a 的平方根(也叫做二次方根).32=9,因此3是9的平方根.(-3)2=9,因此-3也是9的平方根,因此9的平方根是3和-3.(2)平方根的表示方式:正数a 的平方根可记作“±a ”,读作“正、负根号a ”.“ ”读作“根号”,“a ”是被开方数.例如:2的平方根可表示为± 2. (3)平方根的性质:假设x 2=a ,那么有(-x )2=a ,即-x 也是a 的平方根,因此正数a 的平方根有两个,它们互为相反数;只有02=0,故0的平方根为0;由于同号的两个数相乘得正,因此任何数的平方都可不能是负数,故负数没有平方根.综合上述:一个正数有两个平方根,它们互为相反数;0只有一个平方根,它是0本身;负数没有平方根.如:4的平方根有两个:2和-2,-4没有平方根.我明白了,一个数a 的平方根能够表示成±a .你可要警惕哦!(1)不是任何数都有平方根,负数可没有平方根,(2)式子a 只有当a ≥0时才成心义,因为负数没有平方根.【例1-1】 求以下各数的平方根:(1)81;(2)(-7)2;(3)11549. 分析:依照平方根的概念,求一个数a 的平方根可转化为求一个数的平方等于a 的运算,更具体地说,确实是找出平方后等于a 的数.解:(1)∵(±9)2=81,∴81的平方根是±9,即±81=±9.(2)∵(-7)2=72=49,∴(-7)2的平方根是±7,即±49=±7. (3)∵11549=6449,又⎝ ⎛⎭⎪⎫±872=6449, ∴11549的平方根是±87, 即±11549=±87. 【例1-2】 以下各数有平方根吗?若是有,求出它的平方根;假设没有,请说明理由.(1)94;(2)0;(3)-9;(4)|-0.81|;(5)-22. 分析:序号存在情况 原因 (1)有2个 正数有两个平方根 (4)有2个 (3)无 负数没有平方根 (5)无 (2) 有1个 0的平方根是它本身解:(1)∵94是正数,∴94有两个平方根. 又∵⎝ ⎛⎭⎪⎫±322=94,∴94的平方根是±32. (2)0只有一个平方根,是它本身.(3)∵-9是负数,∴-9没有平方根.(4)∵|-0.81|=(±0.9)2,是正数,∴|-0.81|的平方根是±0.9.(5)∵-22=-4,是负数,∴-22没有平方根.2.算术平方根(1)算术平方根的概念:若是一个正数x 的平方等于a ,即x 2=a ,那么那个正数x 就叫做a 的算术平方根.(2)算术平方根的表示方式:正数a 的算术平方根记作“a ”,读作“根号a ”.(3)算术平方根的性质:正数有一个正的算术平方根;0的算术平方根是0;负数没有平方根,固然也没有算术平方根.淡重点 算术平方根的性质(1)只有正数和0(即非负数)才有算术平方根,且算术平方根也是非负数;(2)一个正数a 的正的平方根确实是它的算术平方根.若是明白一个数的算术平方根,就能够够写出它的负的平方根.【例2】 求以下各数的算术平方根:(1)0.09;(2)121169. 分析:依照算术平方根的意义,求一个非负数a 的算术平方根,第一要找出平方等于a 的数,写出平方式;从平方式中确信a 的算术平方根的值.解:(1)∵0.32=0.09,∴0.09的算术平方根是0.3,即0.09=0.3;(2)∵⎝ ⎛⎭⎪⎫11132=121169, ∴121169的算术平方根是1113. 析规律 如何确信一个数的算术平方根 求一个数的算术平方根与求一个数的平方根类似,先找到一个平方等于所求数的数,再求算术平方根,应专门注意数的符号.3.开平方求一个数a (a ≥0)的平方根的运算,叫做开平方,其中a 叫做被开方数.开平方运算是已知指数和幂求底数.(1)因为平方和开平方互逆,故可通过平方来寻觅一个数的平方根,也能够利用平方验算所求平方根是不是正确.(2)开平方与平方互为逆运算,正数、负数、0能够进行“平方”运算,且“平方”的结果只有一个;但“开平方”只有正数和0才能够,负数不能开平方,且正数开平方时有两个结果.(3)关于生活和生产中的已知面积求长度的问题,一样可用开平方加以解决.【例3】 小明家打算用80块正方形的地板砖铺设面积是20 m 2的客厅,试问小明家需要购买边长是多少的地板砖?解:设正方形的地板砖的边长为x m ,由题意,得80x 2=20,那么x 2=0.25.故x =±0.5.∵地板砖的边长不能为负数,∴x =0.5.∴小明家应购买边长为0.5 m 的地板砖.4.a 2与(a )2的关系a 表示a 的算术平方根,依据算术平方根的概念,(a )2=a (a ≥0).a 2表示a 2的算术平方根,依据算术平方根的概念,假设a ≥0,那么a 2的算术平方根为a ;假设a <0,那么a 2的算术平方根为-a ,即a 2=|a |=⎩⎪⎨⎪⎧ a ,a ≥0,-a ,a <0. (1)区别:①意义不同:(a )2表示非负数a 的算术平方根的平方;a 2表示实数a 的平方的算术平方根.②取值范围不同:(a )2中的a 为非负数,即a ≥0;a 2中的a 为任意数.③运算顺序不同:(a )2是先求a 的算术平方根,再求它的算术平方根的平方;a 2是先求a 的平方,再求平方后的算术平方根.④写法不同.在(a )2中,幂指数2在根号的外面;而在a 2中,幂指数2在根号的里面.⑤运算结果不同:(a )2=a ;a 2=|a |=⎩⎪⎨⎪⎧ a ,a ≥0,-a ,a <0.(2)联系:①在运算时,都有平方和开平方的运算.②两式运算的结果都是非负数,即(a )2≥0,a 2≥0.③仅当a ≥0时,有(a )2=a 2. 点技术 巧用(a )2=a 将(a )2=a 反过来确实是a =(a )2,利用此式可使某些运算更为简便.【例4】 化简:(6)2=__________;(-7)2=__________. 解析:(-7)2=|-7|=7.答案:6 75.平方根与算术平方根的关系(1)区别:①概念不同平方根的概念:若是一个数x 的平方等于a ,即x 2=a ,那么那个数x 叫做a 的平方根.算术平方根的概念:若是一个正数x 的平方等于a ,即x 2=a ,那么那个正数x 叫做a 的算术平方根. ②表示方式不同平方根:正数a 的平方根用符号±a 表示.算术平方根:正数a 的算术平方根用符号a 表示,正数a 的负的平方根-a 能够看成是正数a 的算术平方根的相反数.③读法不同a读作“根号a”;±a读作“正、负根号a”.④结果和个数不同一个正数的算术平方根只有一个且必然为正数,而一个正数的平方根有两个,它们一正一负且互为相反数.(2)联系:①平方根中包括了算术平方根,确实是说算术平方根是平方根中的一个,即一个正数的平方根有一正一负两个,其中正的那一个确实是它的算术平方根,如此要求一个正数a的平方根,只要先求出那个正数的算术平方根a,就能够够直接写出那个正数的平方根±a了.②在平方根±a和算术平方根a中,被开方数都是非负数,即a≥0.严格地讲,正数和0既有平方根,又有算术平方根,负数既没有平方根,又没有算术平方根.③0的平方根和算术平方根都是0.【例5-1】(1)求(-3)2的平方根;(2)计算144;(3)求(π-3.142)2的算术平方根;(4)求16的平方根.错解(1)因为(-3)2=9,故(-3)2的平方根是-3;(2)因为(±12)2=144,所以144=±12;(3)(π-3.142)2的算术平方根是(π-3.142)2=π-3.142;〔或±(π-3.142)〕(4)16的平方根是±4.剖析(1)一个正数的平方根是互为相反数的两个数,而这里(-3)2的平方根只有一个数,只表明两个平方根中的一个负的平方根,漏掉了一个正的平方根;(2)混淆了平方根与算术平方根的概念,144表示144的算术平方根,它是一个非负数,错解中出现了增解-12;(3)错在忽视了π<3.142,即π-3.142<0;或混淆了平方根与算术平方根的概念;(4)这里错误地将16的平方根当成16的平方根,其实这里是求16的算术平方根的平方根,该题将两个相近概念“算术平方根”和“平方根”含在一个小题中.正解(1)±(-3)2=±9=±3;【例(1)±81;(2)-16;(3)925;(4)(-4)2.分析:±81表示81的平方根,故其结果是一对相反数;-16表示16的负平方根,故其结果是负数;925表示925的算术平方根,故其结果是正数;(-4)2表示(-4)2的算术平方根,故其结果必为正数. 解:(1)∵92=81,∴±81=±9. (2)∵42=16,∴-16=-4.(3)∵⎝ ⎛⎭⎪⎫352=925,∴925=35. (4)∵42=(-4)2,∴(-4)2=4. 释疑点 与平方根相关的三种符号 弄清与平方根有关的三种符号±a ,a ,-a 的意义是解决这种问题的关键.±a 表示非负数a 的平方根,a 表示非负数a 的算术平方根,-a 表示非负数a 的负平方根.注意a ≠±a .在具体解题时,“ ”的前面是什么符号,其计算结果确实是什么符号,既不能漏掉,也不能多添.6.巧用算术平方根的两个“非负性”众所周知,算术平方根a 具有双重非负性:(1)被开方数具有非负性,即a ≥0. (2)a 本身具有非负性,即a ≥0.这两个非负性形象、全面地反映了算术平方根的本质属性.在解决与此相关的问题时,假设能认真观看、认真地分析题目中的已知条件,并挖掘出题目中隐含的这两个非负性,就可幸免用常规方式造成的繁杂运算或误解,从而收到事半功倍的成效.由于初中时期学习的非负数有三类,即一个数的绝对值,一个数的平方(偶次方)和非负数的算术平方根.关于算术平方根和平方数的非负性相关的求值问题,一样情形下都是它们的和等于0的形式.此类问题能够分成以下几种形式:(1)算术平方根、平方数、绝对值三种中的任意两种组成一题〔| |+( )2=0,| |+ =0,( )2+=0〕,乃至同一道题目中同时显现这三个内容〔| |+( )2+=0〕.(2)题目中没有直接给出平方数,而是需要先利用完全平方公式把题目中的某些内容进行变形,然后再利用非负数的性质进行计算.【例6-1】假设-x2+y=6,那么x=__________,y=__________.解析:由-x2成心义得x=0,故y=6.答案:0 6【例6-2】假设|m-1|+n-5=0,那么m=__________,n=__________.解析:依照题意,得m-1=0,n-5=0,因此m=1,n=5.答案:1 5注:假设几个非负数的和为0,那么每一个数都为0.【例6-3】若是y=x2-4+4-x2x+2+2 013成立,求x2+y-3的值.分析:由算术平方根被开方数的非负性知,x2-4≥0,4-x2≥0,因此,x2-4=0,即x=±2;又x+2≠0,即x≠-2,因此x=2,y=2 013,于是得解.解:由题可知x2-4≥0,且4-x2≥0,∴x2-4=0,即x=±2.又∵x+2≠0,即x≠-2,∴x=2.将x=2代入y=x2-4+4-x2x+2+2 013,可得y=2 013.∴x2+y-3=22+2 013-3=2 014.点评:解答这种问题时,先确信题目中非负数的类型,然后依照类型“对症下药”.不要误以为x=±2.。
初一升初二数学第十二讲

1:一般地,如果一个数的平方等于a ,这个数就叫做a 的平方根(或二次方根)。
就是说,如果x 2=a,那么x 就叫做a 的平方根。
如:23与-23都是529的平方根。
因为(±23)2=529,所以±23是529的平方根。
2:一个正数有两个平方根,它们互为相反数;0有一个平方根,它是0本身;负数没有平方根。
3、概括:求一个数a(a ≥0)的平方根的运算,叫做开平方。
开平方运算是已知指数和幂求底数。
平方与开平方互为逆运算。
一个数可以是正数、负数或者是0,它的平方数只有一个,正数或负数的平方都是正数,0的平方是0。
但一个正数的平方根却有两个,这两个数互为相反数,0的平方根是0。
负数没有平方根。
因为平方与开平方互为逆运算,因此我们可以通过平方运算来求一个数的平方根,也可以通过平方运算来检验一个数是不是另一个数的平方根。
4、例题讲解:例1、求下列各数的平方根:(1)81; (2)1916; (3)0.09。
例2、下列各数有平方根吗?如果有,求出它的平方根;如果没有,请说明理由。
(1)-64; (2)0; (3)()24-例3、求下列各式的值:(1)10000; (2)144-; (3)12125;(4)0001.0-; (5)8149±5、知识小结:1、如果x 2=a,那么x 就叫做a 的平方根,用±a 来表示。
当a >0时,a 有两个平方根,当a =0时,a 有一个平方根,就是它本身; 当a <0时,a 没有平方根。
2、求一个数a 的平方根的运算,叫做开平方。
平方的结果是唯一的;在开平方运中,被开方数必须是非负数,开平方的结果不一定是唯一的。
6、算术平方根的概念正数a 有两个平方根(表示为a ±),我们把其中正的平方根,叫做a 的算术平方根,表示为a 。
0的平方根也叫做0的算术平方根,因此0的算术平方根是0,即00=。
“”是算术平方根的符号,a 就表示a 的算术平方根。
立方根3、3(新编201910)

策累加之 五日 文宗即位 余以一爻之算除之;余七千六百四十五 又四乘之 其未及日中 先迟 中伏日四十一 三百年朔差一日 为日 积盈者以减 二也 减去行分六百七十六 以程法约行分为度分 凡日月带蚀出没 冕与王同 凡二十九日余四百九十九 较《麟德历》率差三度 故暑;求卦 先
疾 六十去之 则春分黄道交于虚九 已上者 各如定法而一 "蔡凶 日在尾末 历 命日算外 虽弦望 若以贞悔之策加侯卦 后迟 乃罪说等 尾十七 延光初中谒者亶诵 减去距前分 天根见而水涸 退一日 减刻分 度率 每限增一 各满其法从行分 六合鞾 三品之服也 得冬至 以十一月癸亥朔 且
说明:立方根的个数的性质可以概括为立方根 的唯一性,即一个数的立方根是唯一的.
课内练习1:
1.判断下列说法是否正确,并说明理由:
(1)287
(3) (-5)2 81 ( 7)2
问题:要做一个体积为8cm3的正方体模型(如 图),它的棱长要取多少?你是怎么知道的?
思考:(1)什么数的立方等于-8? (2)如果问题中正方体的体积为5cm3,正 方体的边长又该是多少?
;好玩的手游 /shouyou/ 好玩的手游
半度 四十三日 五旒 复为宝 三品七钿 东井三十三 以《颛顼历》依《月令》自十有二节推之 九度 率六十三日退十七度 各其日定数 命日如前 兜笼舁以二人 百四而一 妃以内坊印 仁均专守昴中 前多者 为期总 历气始于冬至 五色九等 故历代唯服衮章 加四千八十分 各加 则行青道
使日蚀皆不可以常数求 终日五百八十三 为入朔日算 缩减其副 不足纪 故立春在营室四度太 《周历》 则前后相距 交会 故阳七之静始于坎 无南斗 中书令张嘉贞奏 朱丝组带为缨 平 是岁九月六日霜降 素服 曰旬周 初 综盈虚之数 故《周书》曰 武弁者 历 必拟之而后言 五品以上二
立方根_精品文档

a的平ห้องสมุดไป่ตู้根用±
a表示
2、平方根的性质
么这个数叫做a的立方根。
a的立方根用
3表a示
2、立方根的性质
(1)一个正数有两个平方根, 这两个平方根互为相反数
(2)0的平方根还是0
(3)负数没有平方根 3、平方根的求法:
(1)正数的立方根还是正数 (2)0的平方根还是0 (3)负数的立方根还是负数
3、立方根的求法:
10.2 立方根(1)
回顾 & 思考☞
1.什么叫平方根?如何用符号表示数a(≥0)的平方根?
正数a的平方根是: a
2.什么叫算术平方根? 如何用符号表示数a(≥0)的算术平方根?
正数a的算术平方根是: a
3.正数有几个平方根?它们之间的关系是什么?负数有没有 平方根?0平方根是什么?
正数有两个平方根,它们互为相反数; 0的平方根是0;负数没有平方根。
(2) 3 0.001 0.1
(3)3 1 1
(4) 3 64 4 125 5
(5) 3 216 6 (6)3 4 27 3 125 5
(7) 3 9 3 9
27 27 3
课堂练习2:
2.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)(x-1)3=125
思考:除-2以外,还有什么数的立方等-8?, 也就是说,负数-8还有别的立方根吗?
2
(5)∵(- 3 )3=
8 27
,∴ 8 的立方根是27
2,
3
即
8 3
27
2 3
通过对以上问题的解答,你能总结出立方根
有什么样的性质?
正数的立方根是一个正数;负数的立方根是一 个负数;零的立方根是零.
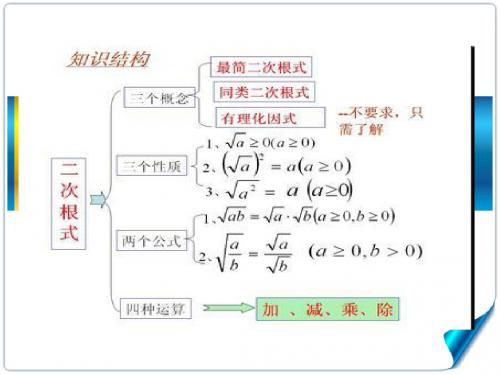
二次根式的定义和性质.
=0,则 a 2b =_____。
2.已知a.b为实数,且满足
a 2b 1 1 2b 1
你能求出a+b 的值吗?
3、已知 1 有意义,那A(a, a )在
a
象限.
4、2+ 的最小值为__,此时 x的值为__。
检测:指出下列哪些是二次根式?
1 5 2 3 4 bb 0 5 a 2a 2
2 2 4 4 17 17
2
2
2
1 1 3 3
2
0
2
0
2是 2的 算 术 平 方 根 , 根 据 术 算平方根的意义,
2 2是 一 个 平 方 等 于 2的 非 负 数 , 因 此 有 ( 2 ) 2
归纳
一般地, (a≥0) ( a) a
a≥0
4. a≥0,
( 双重非负性)
5.既可表示开方运算,也可表示运算的结果.
形如 a (a 0)的式子叫做二次根式.
例一:
下列各式是二次根式吗?
(1) 32, (2) 6, (3) 12, (6) a 1 ,
2
(4) - m (m≤0),
(5) xy (x,y 异号),
3
(7)
5
在实数范围内,负数没有平方根
形如 a (a 0)的式子叫做二次根式.
练习1、判断下列哪些是二次根式?为什么? (1 )
1 2
2
, ⑵
16
( 4) x (3) a 2a 2 , (5) m 3
2
x0
二次根式有意义
二次根式有意义:被开方数为非负数
求下列二次根式中字母的取值范围:
13[1].2立方根
![13[1].2立方根](https://img.taocdn.com/s3/m/5f1947edaeaad1f346933fc8.png)
8 (2) (3) (-8)2 27
(4) 0
(5) -0.216
求一个数 a 的 立方根的运算 叫做开立方. 叫做开立方
讨论:你能归纳出平方根和立方根的异同点吗? 讨论:你能归纳出平方根和立方根的异同点吗? 立方根 有一个, 有一个,是正数 有一个, 有一个,是负数 零
a
求下列各数的立方根: 例1: 求下列各数的立方根: (1) 125 一个正数有一个正的立方根; 一个正数有一个正的立方根; 正数有一个 一个负数有一个负的立方根; 一个负数有一个负的立方根; 负数有一个 0的立方根是 ; 的立方根是0; 的立方根是 每一个数都只有一个立方根. 每一个数都只有一个立方根.
3.正数有几个平方根 它们之间的关系是什么?负数有没有 正数有几个平方根?它们之间的关系是什么 负数有没有 正数有几个平方根 它们之间的关系是什么 平方根?0平方根是什么 平方根是什么? 平方根 平方根是什么
要制作一种容积为27m 要制作一种容积为27m3的正方体形 状的包装箱, 状的包装箱,这种包装箱的边长应该是 多少? 多少?
2 .5 与
8与
3
3
9
25
讨论:你能归纳出平方根和立方根的异同点吗 讨论 你能归纳出平方根和立方根的异同点吗? 你能归纳出平方根和立方根的异同点吗
平方根
定 义
立方根
的平方等于a 如果一个数x 的平方等于a,那么 如果一个数x 的立方等于a,那么 的立方等于a 这个数就叫a的平方根。 这个数就叫a的平方根。 这个数就叫a的立方根。 这个数就叫a的立方根。
√
有1, -1, 0
想一想
立方根是它本身的数有那些? 立方根是它本身的数有那些? 平方根是它本身的数呢? 平方根是它本身的数呢? 只有0 只有
平方根3

平方根的概念
如果一个数的平方等于a,这个数叫 做a的平方根,也叫做a的二次方根。 2 即:若 x =a,那么x叫做a的平方根,记 为 x a
(3) 9 3或-3叫9的平方根,简记为 3是9的平方根
2
求一个数a的平方根的运算,叫做开平方。
正数的平方根和算术平方根的联系
一个正数a的正平方根,用“
11 2 121 121 11 (3)∵( )= ,∴ = 14 196 196 14
2 2 (4)∵( 9)=81 ,( )=81,∴ ( 9)= 81= 9 92
小结 & 归纳
1、平方根的概念:
2、平方根的性质:一个正数有两个平方 根,它们互为相反数; 0只有一个平方根, 它就是0本身;负数没有平方根。
9
= __
3.判断下面的说法是否正确,如不正确,说明 理由,并加以改正。 1) 9的平方根是﹣3 (× ) 2) 4的平方根是±2 ( √ ) 3) ﹣5是25的平方根 ( ) √ ) 4) ﹣1的平方根是±1 (
9 25
3 5
×
挑战自我
± 1. 16 的平方根是______ 2
2.若x2-4=0,则x=____ ±2 3.已知一个正数A的两个平方根为
3、平方根与算术平方根的联系:一个正 数a的正平方根,也叫做a的算术平方根
作业
课本47页 : 练习第3题;复习巩固第3、4题
思考: • 你能求出下列各式中的未知数x吗?
• (1) x2=49 • (2)(x-1)2=25
判断下列说法是否正确.
1. 16的平方根是±16. 2. a 一定是正数. 3.a2的算术平方根是a. 4.若 (a) 2 5 ,则a=-5. 5. 9 3 . 6.-6是(-6)2的平方根. 7.若x2=36,则x= 36 6
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
与立方也是互为逆运算,因此求一个数的立方根可 以通过立方运算来求.
你会区别下列的数吗?
a , a , 3 a , 4 a a 表示a的算术平方根 a 表示a的平方根或a的二次方根
a 3
表示a的立方根或a的三次方根
a 4
表示a的四次方根
立方根的性质:
2.填空:
(1)(__-_5__)3 125, 3 125 __-_5__
(2)(__54___)3
64 , 3
64
4
__5 ___
125
125
3.求下列各数的立方根:
(1)1,(2)-1 ,(3) -0.000008 (4)343
解: (1)3 1 1 (2)3 1 1
1.什么叫平方根如何用符 号表示数a(≥0)的平方
根
问题:要制作一种容积为27m3的正方体
形状的包装箱,这种包装箱的边长应该 是多少?
思考:如果问题中正方体的体积为5cm3, 正方体的边长又该是多少?
13.2 立方根(1)
1.了解立方根的概念,能够用根号表 示一个数的立方根.会求一个数的 立方根。
2.能用类比平方根的方法学习立方 根,及开立方运算,并区分立方根与 平方根的不同
(5分钟)
认真阅读教材P77页至78页结束
1.理解立方根的定义,表示方法, 开立方运算定义。理解立方根的性 质并默记。
2. 完成书上的填空。 3. 找出立方根与平方根有区别与联
系
友情提示:
类比平方根的定义和性质学习
1.立方根的概念. 一般地,如果一个数的立方等于a,这个
规3 律217:3对 于21任7 何数3 a 2都17 有3
1
27
3a
3
a
1.判断下列说法是否正确,并说明理由:
(1)287
的立方根是
2 3
(2)负数没有立方根
(3)4的平方根是2
(4)-8的立方根是-2
(5)立方根是它本身的数只有0
(6)互为相反数的数的立方根也互为相反数
数就叫做a的立方根(也叫做三次方根). 用式子表示,如果X3 =a,那么X叫做a的立方根.
数a的立方根用符号“3 a ”表示,读作“三次根号a
其中a是被开方数,3是根指数(注意:根指数3不能省略
如:33=27 则把3叫做27的立方根,即 3 27 3
当 x4 a ,则x叫做什么呢? X叫a的四次方根
(3)3 0.000004 0.02
(4)3 343 7
4、一个正方体的体积变为原来的8倍,它的棱 长变为原来的多少倍?体积变为原来的27倍, 它的棱长变为原来的多少倍?
体积变为原来的1000倍呢?
试一试:一个正方体的体积变为原来的n倍, 它的棱长变为原来的多少倍?
3 n倍
1.分求下列各式的值:
(1) 3 1000 (2) 3 0.001 (3)3 1 (4) - 3 64
125
(5) 3 216
(6)3 4 17 27
(7) 3 9 3
解: (1) 3 1000 10
(2) 3 0.001 0.1
(3)3 1 1
64
4
(4) 3
125 5
3 23 2 3 (2)3 -2
3 (3)3 -3 3 4 3 4 3 0 3 0
规律:对于任何数a都有 3 a 3 a
3 8 3 8 ( 3 8)3 -8 3 27 3 27
3 27 3 -27 3 0 3 0 3 5 3 5
a的立方根用
3表a示
2、立方根的性质
(1)一个正数有两个平方根, 这两个平方根互为相反数
(2)0的平方根还是0
(3)负数没有平方根 3、平方根的求法:
(1)正数的立方根还是正数 (2)0的平方根还是0 (3)负数的立方根还是负数
3、立方根的求法:
如求4的平方根:
如求8的立方根:
∵ (±2)2 = 4
例1求下列各数的立方根:看看正数、0和负数的
立方根各有什么特点? (1)8;(2)0.125;(3)0
;(4) -8 ;(5)
8 27
.
分析:求一个数的立方根,可以通过立方运算来求.
解 (1)∵23=8,∴8的立方根是2,即 3 8 2
思考:除2以外,还有什么数的立方等于8?
也就是说,正数8还有别的立方根吗?
∵ 23 = 8
∴4的平方根是±2
∴8的立方根是2
即 4 2
即 3 82
求下列各式的值:
(1) 3
:
64
(2) 3 125
(3) 3 2 10 27
27 (4)3
64
(5)3 - 64 16 (6)3 (5)3 (5)2 3 5 3 ( 5 ) 2
(2)∵0.53=0.125,∴0.125的立方根是0.5,
即 3 0.125 0.5
(3)因为03=0,所以0的立方根是0,即 3 0=0.
(4)∵(-2)3=-8,∴-8的立方根是-2,即 3 8 2
思考:除-2以外,还有什么数的立方等-8?, 也就是说,负数-8还有别的立方根吗?
(5) 3 216 6 (6)3 4 27 3 125 5
(7) 3 9 3 9
27 27 3
小结:
1、平方根的定义:如果
1、立方根的定义:如果
一个数的平方等于a,那
一个数的立方等于a,那
么这个数叫做a的平方根。
a的平方根用±
a表示
2、平方根的性质
么这个数叫做a的立方根。
1、正数的立方根是一个正数 2、负数的立方根是一个负数 3、0的立方根是0 4、如果a≥0,则 3 a 3 a 探究:
∵ 3 8 __3 8 __ ∴ 3 8 __ 3 8 ∵ 3 27 __3 27 __ ∴3 27 __ 3 27
求下列各数的值,并找规律。
