数据分布特征的统计描述习题
第五章数据分布特征习题

第五章数据分布特征的描述练习题一、填空题1.常用的数值平均数有和以及。
2.权数对算术平均数的影响作用不决定于权数的大小,而决定于权数的的大小。
3.计算算术平均数的基本公式。
4.当标志值较大而次数较多时,平均数接近于标志值较的一方;当标志值较小而次数较多时,平均数靠近于标志值较的一方。
5.加权算术平均数等于简单算术平均数的前提条件是。
6.利用组距数列计算算术平均数,应首先计算各组的。
7.统计中的变量数列是以为中心而左右波动,所以平均数反映了总体分布的。
8.中位数是位于变量数列的那个标志值,众数是在总体中出现次数的那个标志值。
中位数和众数也可以称为平均数。
9.调和平均数是平均数的一种,它是的算术平均数的。
10.现象的是计算或应用平均数的原则。
11.当变量数列中算术平均数大于众数时,这种变量数列的分布呈分布;反之算术平均数小于众数时,变量数列的分布则呈分布。
12.较常使用的离中趋势指标有、、、、。
13.极差是总体单位的与之差,在组距分组资料中,其近似值是。
14.是非标志的平均数为、标准差为。
15.标准差系数是与之比。
16.已知某数列的平均数是200,标准差系数是30%,则该数列的方差是。
17.标准差用的方法解决了离差之和为0而不能求平均离差的问题,因此它在数学处理上优于,因此应用范围更为广泛。
18.对某村6户居民家庭共30人进行调查,所得的结果是,人均收入400元,其离差平方和为5100000,则标准差是,标准差系数是。
19.测定峰度,往往以为基础。
依据经验,当β=3时,次数分配曲线为;当β<3时,为曲线;当β>3时,为曲线。
20.在对称分配的情况下,平均数、中位数与众数是的。
在偏态分配的情况下,平均数、中位数与众数是的。
如果众数在左边、平均数在右边,称为偏态。
如果众数在右边、平均数在左边,则称为偏态。
二、单选题1.下列属于平均指标的是( )。
A某县平均每亩粮食产量B全员劳动生产率C某县平均每人占有耕地D某县平均每户拥有小汽车的数量2,平均数反映了( )。
数据分布特征练习-应用统计学 习题@北工大
习题3.教材 版 习题 教材3版P.109第4.3题 教材 第 题 习题4. 教材3版 习题 (教材 版P.110第4.5题)甲乙两企业 第 题 三种规格产品成本资料如下: 三种规格产品成本资料如下:
单位成本 产品规格 (元/件 ) A B C 15 20 30 总成本( 总成本(元) 甲企业 乙企业 2100 3255 3000 1500 1500 1500
要求:比较哪个企业的总平均单位成本高, 要求:比较哪个企业的总平均单位成本高,并 分析其原因。 分析其原教材3版P.81第3.9题)某地区某年 第 题 某地区某年12000
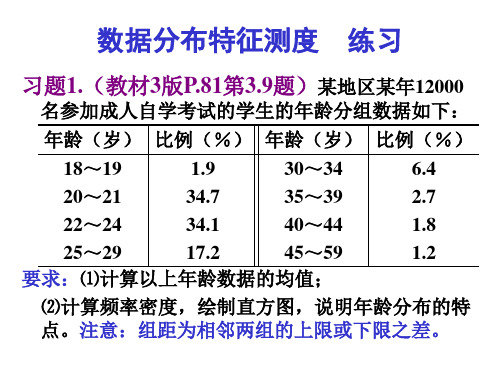
名参加成人自学考试的学生的年龄分组数据如下: 名参加成人自学考试的学生的年龄分组数据如下: 年龄( 比例(%) 年龄( 比例(%) 年龄(岁) 比例(%) 年龄(岁) 比例(%) 1.9 6.4 18~19 30~34 ~ ~ 34.7 2.7 20~21 35~39 ~ ~ 34.1 1.8 22~24 40~44 ~ ~ 17.2 1.2 25~29 45~59 ~ ~ 要求: 计算以上年龄数据的均值; 要求:⑴计算以上年龄数据的均值; 计算频率密度,绘制直方图, ⑵计算频率密度,绘制直方图,说明年龄分布的特 注意:组距为相邻两组的上限或下限之差。 点。注意:组距为相邻两组的上限或下限之差。
习题2. 已知甲公司20名雇员年龄如下 名雇员年龄如下: 习题 已知甲公司 名雇员年龄如下:
55 23 42 30 37 48 59 27 34 30 28 35 52 45 41 37 26 42 37 32 要求: 要求: 计算年龄数据的众数、中位数、四分位数、均值、 ⑴计算年龄数据的众数、中位数、四分位数、均值、 极差、四分位差、标准差; 极差、四分位差、标准差; 又知乙公司雇员平均年龄为36岁 标准差9.5岁 ⑵又知乙公司雇员平均年龄为 岁,标准差 岁,比 较说明哪个公司雇员年龄差异大; 较说明哪个公司雇员年龄差异大; 对上述年龄数据进行组距分组(组距为10, ⑶对上述年龄数据进行组距分组(组距为 ,如20~ ~ 30,30~40……),编制频数分布表; ),编制频数分布表 , ~ ),编制频数分布表; 利用组距分组数据计算众数(用公式计算 用公式计算)、 ⑷利用组距分组数据计算众数 用公式计算 、中位数 (用公式计算 、均值、标准差(例出计算表),对 用公式计算) 均值、标准差(例出计算表), ),对 用公式计算 比分组前后的计算结果, 比分组前后的计算结果,说明同名指标数值差异的 原因。 原因。
统计学 第4章 综合指标和数据分布特征的描述

G 0.95 0.92 0.90 0.85 0.80
5
0.5349 88.24%
5
例2 加权几何平均数
投资银行某笔投资的年利率是按复利计算的,25年的 年利率分配是:有1年为3%,有4年为5%,有8年为8%, 有10年为10%,有2年为15%,求平均年利率。 年本利率(%) X 年数 f
三、调和平均数 (一)基本公式
例4-1-7:某蔬菜批发市场三种蔬菜的日成交 数据如表,计算三种蔬菜该日的平均批发价格
某日三种蔬菜的批发成交数据 蔬菜 名称
批发价格 (元)
成交额(元) 成交量(公斤)
xi
1.20 0.50 0.80 —
mi
18000 12500 6400 36900
Fi
甲 乙 丙 合计
平均完成计划程度
m 1,100 110% 1 1,000 m X
2.由相对数计算平均数时加权平均数法的应用:
例
某公司有四个工厂,已知其计划完成程度(%)及计划产值资料如下: 工厂 计划完成程度(%) X 90 100 计划产值 (万元) F 100 200
甲 乙
丙
丁 合计
平均完成计划程度
5000-6000
6000以上
200
180
解: 众数组为第四组
1 d M 0 = XL+ 1 2
= 4000 +
950 320 1000 (950 320) (950 200)
•加权算术平均数: •证明:
(X X ) f
0
Xf f Xf Xf 0 ( X X ) f Xf X f Xf f
习题及参考答案

习题及参考答案第三章数据分布特征的描述⼀、单项选择题 1、经验表明,当数据分布近似于正态分布时,则有95%的数据位于区间() A 、σ±X B 、σ2X ± C 、σ3X ± D 、σ4X ± 2、实际中应⽤最⼴泛的离散程度测度值是()A 、极差和平均差B 、平均差和四分位差C 、⽅差和标准差D 、异众⽐率和四分位差3、集中趋势的测度值中,最主要的是()A 、众数B 、中位数C 、均值D 、⼏何平均数4、有10个数据,它们对数据6的离差分别为:-3,-2,-2,-2,0,0,4,4,5,5。
由此可知这10个数据的()A 、均值为0B 、均值为1 B 、均值为6C 、均值为5、某⽣产⼩组由36名⼯⼈,每⼈⽣产的产量数量相同,其中有14⼈⽣产每件产品耗时8分钟;16⼈⽣产每件产品耗时10分钟;6⼈⽣产每件产品耗时5分钟,计算该⽣产⼩组⽣产每件产品的平均耗时应采⽤()A 、简单算术均值B 、简单调和算术均值C 、加权算术均值 D.、加权调和均值6、某敬⽼院⾥有9位百岁⽼⼈的岁数分别为101、102、103、104、108、102、105、110、102 ,据此计算的结果是()A 、均值=中位数=众数B 、均值>中位数>众数C 、众数>中位数>均值D 、中位数>均值>中数 7、⼏何均值主要适合于()A 、具有等差关系的数列B 、变量值为偶数的数列C 、变量值的连乘积等于总⽐率或总速度的数列D 、变量值之和等于总⽐率或总速度的数列 8、加权算术均值不但受变量值⼤⼩的影响,也受变量之出现的次数多少的影响,因此下列情况中对均值不发⽣影响的是()A 、变量值出现次数相等时B 、变量值较⼩、次数较多时C 、变量值较⼤、次数较少时D 、变量值较⼤、次数较多时9、⼀组数据的均值为350,众数为200,则()A 、中位数为275,数据呈右偏分布B 、中位数为275,数据呈左偏分布C 、中位数为300,数据呈左偏分布D 、中位数为300,数据呈右偏分布10、⼀组数据的均值为5,中位数为3,则()A 、数据呈右偏分布B 、数据呈对称分布C 、数据呈左偏分布D 、数据呈正态分布11、经验表明,当数据分布近似于正态分布时,则变量值落在区间σ±X 的概率为()A、95%B、68%C、%D、%12、当众数(Mo)中位数(Me)和均值(X)三者的关系表现为:Mo=Me=X,则()A、数据有极⼩值B、数具有极⼤值C、数据是对称分布D、数据是左偏分布E、数据右偏分布13、在单项式数列中,假定标志值所对应的权数都缩⼩1/10,则算术平均数()A、不变B、⽆法判断C、缩⼩1/100D、扩⼤10倍14、若单项式数列的所有标志值都减少⼀倍,⽽权数都增加⼀倍,则其算术平均数()A、增加⼀倍B、减少⼀倍C、不变D、⽆法判断15、各变量值与其算术平均数的离差之和()A、等于各变量值之和的平均数B、等于最⼤值C、等于零D、等于最⼩值16、各变量值与其算术平均数的离差平⽅之和()A、等于各变量值之和的平均数B、等于最⼤值C、等于零D、等于最⼩值⼆、多项选择题1、当众数(Mo)、中位数(Me)和均值(X)三者的关系表现为:X<Me<Mo,则()A、数据是左偏分布B、数据是右偏分布C、数据是对称分布D、数据存在极⼩值E、数据存在极⼤值2、当众数(Mo)、中位数(Me)和均值(X)三者的关系表现为:Mo<Me<X,则()A、数据是右偏分布B、数据是对称分布C、数据是左偏分布D、数据有极⼤值E、数据有极⼩值3、数据分布的两个重要特征是()A、正态分布B、集中趋势C、t分布D、 2分布E、离散程度4、利⽤组距分组数据计算众数时,有⼀些基本假定,即()A、假定数据分布具有明显的离中趋势B、既定数据分布具有明显的集中趋势C、假定众数组的频数在该组内是正态分布D、假定众数组的频数在该组内是均匀分布E、假定众数组的频数在该组内是⼆项分布5、众数()A、是⼀组数据分布的最⾼峰点所对应的数值B、可以不存在C、也可以有多个D、是位置代表值E、不受数据中极端值的影响。
曾五一《统计学导论》配套题库【课后习题】第三章 数据分布特征的描述 【圣才出品】

2 / 16
圣才电子书 十万种考研考证电子书、题库视频学习平台
映了全部数据的信息。众数、中位数和四分位数都是根据数据分布的特定位置所确定的集中 趋势测度值。算术平均数只能用于定量(数值型)数据,中位数、四分位数适用于定序数据 和定量数据,众数对所有形式的数据(定性数据和定量数据)都适用。本题中测验成绩的记 录结果为定性数据,所以 B 项正确。
答 : 可 计 算 出 总 体 标 准 差 =100 × 10 % =10 , 总 体 方 差 为 100 , 于 是 峰 度 系 数 K=34800/10000=3.48,可以认为总体呈现非正态分布。
4 / 16
圣才电子书 十万种考研考证电子书、题库视频学习平台
峰度系数 K
5.一组数据呈微偏分布,且知其均值为 510,中位数为 516,则可推算众数为( )。 A.528 B.526 C.513 D.512 【答案】A
【解析】英国统计学家皮尔逊( K.Pearson )提出了一个经验公式:在数据分布呈轻
微偏态时,算术平均数和众数、中位数三者之间存在如下的近似关系:
,由此可得众数 M0 528 。
2.你正在筹划一次聚会,想知道该准备多少瓶饮料,你最希望得到所有客人需要饮料 数量的( )。
A.均值 B.中位数 C.众数 D.四分位数 【答案】A 【解析】算术平均数是数值平均数,即它是利用全部数据加总来计算的平均数,综合反
1 / 16
圣才电子书 十万种考研考证电子书、题库视频学习平台
曲线的陡峭(或平坦)的程度。对峰度的度量通常以正态分布曲线为比较标准,一般将峰度
统计第三章练习题

第三章 数据分布特征的描述(一)单项选择题(在下列备选答案中,只有一个是正确的,请将其顺序号填入括号内)1.平均指标反映了( )。
①总体变量值分布的集中趋势 ②总体分布的离散特征 ③总体单位的集中趋势 ④总体变动趋势 2.加权算术平均数的大小( )。
①受各组标志值的影响最大 ②受各组次数的影响最大③受各组权数系数的影响最大 ④受各组标志值和各组次数的共同影响3.在变量数列中,如果变量值较小的一组权数较大,则计算出来的算术平均数( )。
①接近于变量值大的一方 ②接近于变量值小的一方 ③不受权数的影响 ④无法判断4.权数对于平均数的影响作用取决于( )。
①总体单位总量 ②各组的次数多少 ③各组标志值的大小 ④各组次数在总体单位总量中的比重 5.由组距变量数列计算算术平均数时,用组中值代表组内标志值的一般水平,有一个假定条件,即( )。
①各组的次数必须相等 ②各组标志值必须相等 ③各组标志值在本组内呈均匀分布 ④各组必须是封闭组 6.如果次数分布中,各个标志值扩大为原来的2倍,各组次数都减小为原来的1/2,则算术平均数( )。
①增加到原来的21 ②稳定不变 ③减少到原来的21④扩大为原来的2倍 7.已知某市场某种蔬菜早市、午市、晚市的每公斤价格,在早市、午市、晚市的销售额基本相同的情况下,计算平均价格可采取的平均数形式是( )。
①简单算术平均数 ②加权算术平均数③简单调和平均数 ④加权调和平均数8.凡是变量值的连乘积等于总比率或总速度的现象,要计算其平均比率或平均速度都可以采用( )。
①算术平均法 ②调和平均法 ③几何平均法 ④中位数法 9.四分位差排除了数列两端各( )单位标志值的影响。
①10% ②15% ③25% ④ 35% 10.如果一组变量值中有一项为零,则不能计算( )。
①算术平均数 ②调和平均数 ③众数 ④中位数11.在掌握了各组单位成本和各组产量资料时,计算平均单位成本所使用的方法应是( )。
描述统计部分练习题
描述统计练习题及参考答案单选题1.某考生在一项测验中得分6060,,经换算百分等级为7070,这表明在所有考生中,得分低于该,这表明在所有考生中,得分低于该考生的人数占总人数的A .30 A .30%% B.40 B.40%% C C..6060%% D D..7070%%2.用于描述两个变量之间相关关系的统计图是A .直方图.直方图B B B.线形图.线形图.线形图C C C.条形图.条形图.条形图D D D.散点图.散点图3.将Z 分数转换成T 分数时,需要进行A .正态化转换.正态化转换B B B.非正态化转换.非正态化转换.非正态化转换C C C.线性转换.线性转换.线性转换D D D.非线性转换.非线性转换4. 4. 已知某次学业成就测验的平均分数是已知某次学业成就测验的平均分数是8080,标准差为,标准差为4。
如果某考生得分为9292,则该分数,则该分数转换为标准分后是A .1B 1 B..2C 2 C..3D 3 D..45.现有一列数据,它们是4,4,5,3,5,5,2。
这列数据的平均数、众数和全距依次是A .4,4,2 B. 42 B. 4,,5,3 C 3 C..5,4,4 D 4 D..5,5,16.一组数据的平均数是100100,标准差是,标准差是2525,这组数据的变异系数是(,这组数据的变异系数是() A A..4% B B..2525%% C C..4 D 4 D..257.有一组数据:.有一组数据:33,6,2,7,3232,,4,8,6,5。
要描述这组数据的特征,受极端数据值影响的统计量是()A A.平均数.平均数.平均数B B B.中数.中数.中数C C C.四分位数.四分位数.四分位数D D D.众数.众数8.在某次考试中,小明的语文、数学成绩均为8080,英语成绩为,英语成绩为7575。
已知全班三科平均成绩。
已知全班三科平均成绩都为6565,语文标准差为,语文标准差为1010,数学标准差为,数学标准差为1515,英语标准差为,英语标准差为5。
2数据描述练习题
第二章数据描述练习题一、单项选择题1、频数分布表中落在某一特定类别的数据个数称为()A、组数B、频数C、众数D、中位数2 、饼图是利用圆形及圆内扇形的()来表示数值大小。
A、面积B、弧线长度C、角度D、颜色3 、条形图是利用宽度相同的条形的()来表述数据多少的图形。
A、面积B、高度或者长度C、频数D、类别4、若需要比较不同变量不同的结构差异,可采用的图形为()。
A、频数分布图B、条形图C、饼图D、环形图5、生成定量数据的频数分布表时,首先要对数据()。
A、分类B、确定组距C、分组D、确定组频数6、组距是指每一个组变量值中的()。
A、最大值与最小值之差B、组中值与最小值之差C、最大值与组中值之差D、组中值与众数之差7、可用来表述定性数据的统计图形()。
A、饼图B、直方图C、折线图D、散点图8、某组数据的集中趋势是指()。
A、该组数据的数值向其中心值的靠拢程度B、该组数据的数值远离其中心值的趋势和程度C、该组数据的数值向其中位数的靠拢程度D、该组数据的数值远离其中位值的趋势和程度9、某组数据的离散程度是指()。
A、该组数据的数值向其中心值的靠拢程度B、该组数据的数值远离其中心值的趋势和程度C、该组数据的数值向其中位数的靠拢程度D、该组数据的数值远离其中位值的趋势和程度10、下列指标中不能反映定性数据的集中趋势是的()。
A、百分比B、中位数C、平均数D、众数11、下列指标中不能反映定量数据的集中趋势的是()。
A、平均数B、中位数C、众数D、标准差12、某连续变量分为五组,第一组为40-50,第二组为50-60,第三组为60-70,第四组为70-80,第五组80 以上,依据规定()。
A 、50 在第一组,70 在第四组B 、60 在第二组,80 在第五组C 、70 在第四组,80 在第五组D 、80 在第四组,50 在第二组13 、对于一组数据:10 、25 、36 、40 、53 、69,中位数为()。
统计学习题第四章数据分布特征的描述习题答案
第四章 静态指标分析法(一)一、填空题1、数据分布集中趋势的测度值(指标)主要有、和。
其中和用于测度品质数据集中趋势的分布特征,用于测度数值型数据集中趋势的分布特征。
2、标准差是反映的最主要指标(测度值)。
3、几何平均数是计算和的比较适用的一种方法。
4、当两组数据的平均数不等时,要比较其数据的差异程度大小,需要计算。
5、在测定数据分布特征时,如果M M e X 0==,则认为数据呈分布。
6、当一组工人的月平均工资悬殊较大时,用他们工资的比其算术平均数更能代表全部工人工资的总体水平。
二.选择题单选题:1.反映的时间状况不同,总量指标可分为( )A 总量指标和时点总量指标B 时点总量指标和时期总量指标C 时期总量指标和时间指标D 实物量指标和价值量指标2、某厂1999年完成产值200万元,2000年计划增长10%,实际完成了231万元,超额完成( )A 5.5%B 5%C 115.5%D 15.5%3、在同一变量数列中,当标志值(变量值)比较大的次数较多时,计算出来的平均数( )A 接近标志值小的一方B 接近标志值大的一方C 接近次数少的一方D 接近哪一方无法判断4、在计算平均数时,权数的意义和作用是不变的,而权数的具体表现( )A 可变的B 总是各组单位数C 总是各组标志总量D 总是各组标志值 5、1998年某厂甲车间工人的月平均工资为520元,乙车间工人的月平均工资为540元,1999年各车间的工资水平不变,但甲车间的工人占全部工人的比重由原来的40%提高到了60%,则1999年两车间工人的总平均工资比1998年( )A 提高B 不变C 降低D 不能做结论 6、在变异指标(离散程度测度值)中,其数值越小,则( )A 说明变量值越分散,平均数代表性越低B 说明变量值越集中,平均数代表性越高C 说明变量值越分散,平均数代表性越高D 说明变量值越集中,平均数代表性越低7、有甲、乙两数列,已知甲数列:07.7,70==甲甲σX ;乙数列:41.3,7==乙乙σX 根据以上资料可直接判断( )A 甲数列的平均数代表性大B 乙数列的平均数代表性大C 两数列的平均数代表性相同D 不能直接判别8、杭州地区每百人手机拥有量为90部,这个指标是 ( )A 、比例相对指标B 、比较相对指标C 、结构相对指标D 、强度相对指标 9、某组数据呈正态分布,计算出算术平均数为5,中位数为7,则该数据分布为 ( ) A 、左偏分布 B 、右偏分布 C 、对称分布 D 、无法判断10、加权算术平均数的大小 ( )A 主要受各组标志值大小的影响,与各组次数多少无关;B 主要受各组次数多少的影响,与各组标志值大小无关;C 既与各组标志值大小无关,也与各组次数多少无关;D 既与各组标志值大小有关,也受各组次数多少的影响11、已知一分配数列,最小组限为30元,最大组限为200元,不可能是平均数的为 ( ) A 、50元 B 、80元 C 、120元 D 、210元12、比较两个单位的资料,甲的标准差小于乙的标准差,则 ( ) A 两个单位的平均数代表性相同 B 甲单位平均数代表性大于乙单位C 乙单位平均数代表性大于甲单位D 不能确定哪个单位的平均数代表性大 13、若单项数列的所有标志值都增加常数9,而次数都减少三分之一,则其算术平均数 ( ) A 、增加9 B 、增加6C 、减少三分之一 D 、增加三分之二 14、如果数据分布很不均匀,则应编制( )A 开口组B 闭口组C 等距数列D 异距数列 15、计算总量指标的基本原则是:( ) A 总体性B 全面性C 同质性D 可比性16、某企业的职工工资分为四组:800元以下;800-1000元;1000—1500元;1500以上,则1500元以上这组组中值应近似为()A1500元 B 1600元 C 1750元D 2000元 17、统计分组的首要问题是( )A 选择分组变量和确定组限B 按品质标志分组C 运用多个标志进行分组,形成一个分组体系D 善于运用复合分组18、某连续变量数列,其末组为开口组,下限为200,又知其邻组的组中值为170,则末组组中值为( )A 230B 260C 185D 215 19、分配数列中,靠近中间的变量值分布的次数少,靠近两端的变量值分布的次数多,这种分布的类型是( )A 钟型分布B U 型分布C J 型分布D 倒J 型分布 20、要了解上海市居民家庭的开支情况,最合适的调查方式是:() A 普查B 抽样调查C 典型调查D 重点调查21、已知两个同类企业的职工平均工资的标准差分别为5元和6元,而平均工资分别为3000元,3500元则两企业的工资离散程度为 ( )A 甲大于乙B 乙大于甲C 一样的D 无法判断 22、加权算术平均数的大小取决于( )A 变量值B 频数C 变量值和频数D 频率23、如果所有标志值的频数都减少为原来的1/5,而标志值仍然不变.那么算术平均数( ) A 不变 B 扩大到5倍 C 减少为原来的1/5 D 不能预测其变化 24、 计算平均比率最好用 ( )A 算术平均数B 调和平均数C 几何平均数D 中位数25、若两数列的标准差相等而平均数不同,在比较两数列的离散程度大小时,应采用() A 全距 B 平均差 C 标准差 D 标准差系数26、若n=20,∑∑==2080,2002x x ,标准差为( )A 2B 4C 1.5D 327、已知某总体3215,3256==eMM,则数据的分布形态为( )A左偏分布B正态分布 C 右偏分布DU型分布28、一次小型出口商品洽谈会,所有厂商的平均成交额的方差为156.25万元,标准差系数为14.2%,则平均成交额为( )万元A11 B 177.5 C 22.19 D 8826、欲粗略了解我国钢铁生产的基本情况,调查了上钢、鞍钢等十几个大型的钢铁企业,这是()A普查B重点调查C典型调查D抽样调查多选题:1.某企业计划2000年成本降低率为8%,实际降低了10%。
统计学课后习题与答案 郑贵华、颜泳红主编 湘潭大学出版:第四章 数据分布特征的度量
第四章思考与习题一、思考题1.什么是集中趋势?测度集中趋势常用指标有哪些?2.算术均值.众数和中位数有何关系?3.什么是几何平均数?其适用场合是什么?4.什么叫离散趋势?测度离散趋势常用指标有哪些?5.为什么要计算离散系数?二、练习题(一)填空题1.统计数据分布的特征,可以从三个方面进行测度和描述:一是分布的__________,反映所有数据向其中心值靠拢或聚集的程度;二是分布的__________,反映各数据远离其中心值的趋势;三是分布的__________,反映数据分布的形状。
2.在某城市随机抽取13个家庭,调查得到每个家庭的人均月收入数据如下:1080.750.1080.850.960.2000.1050.1080.760.1080.950.1080.660,则其众数为,中位数为。
3.算术均值有两个重要数学性质:各变量值与其算术均值的__________等于零;各变量值与其算术均值的__________等于最小值。
4.简单算术均值是__________的特例。
4.几何均值主要用于计算__________的平均。
5.在一组数据分布中,当算术均值大于中位数大于众数时属于________分布;当算术均值小于中位数小于众数时属于________分布。
6.__________是各变量值与其均值离差平方的平均数,是测度数值型数据__________最主要的方法。
7.为了比较人数不等的两个班级学生的学习成绩的优劣,需要计算__________;而为了说明哪个班级学生的学习成绩比较整齐,则需要计算________。
8.偏态是对数据分布__________或__________的测度;而峰度是对数据分布_________的测度。
(二)判断题1.众数的大小只取决于众数组与相邻组次数的多少。
()2.当总体单位数n为奇数时,中位数=(n+1)/2。
()3.根据组距分组数据计算的均值是一个近似值。
()4.若已知甲企业工资的标准差小于乙企业,则可断言:甲企业平均工资的代表性好于乙企业。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 数据分布特征的统计描述思考与练习一、选择题1.有n 辆汽车在同一距离的公路上行驶的速度资料,确定汽车平均每小时行驶速度的平均数公式是:( C )A .n x∑ B .∑∑fxf C .∑x n 1 D .∑∑xm m2.权数对加权算术平均数的影响,取决于( B )A. 权数所在组标志值的大小;B. 权数的大小;C. 各组单位数的多少;D. 总体单位数的多少 3.是非标志不存在变异时,意味着:( B ,C )A. 各标志值遇到同样的成数;B. 所有单位都只具有某种属性C. 所计算的方差为0;D. 所计算的方差为0.254.能够综合反映总体各个单位标志值的差异,对总体标志变异程度作全面客观评定的指标有( A ,C )A.方差B.算术平均数C.标准差D.全距二、判断题1.甲乙两地,汽车去程时速20公里,回程时速30公里,其平均速度为25公里。
[答]错。
本题应采用调和平均法计算平均速度。
2.权数起作用的前提是各组的变量必须互有差异。
[答]对。
3.变量同减某个数再同除于另一数然后求其方差,其方差等于原方差乘于除数的平方。
[答]对。
4.与平均数相比,中位数比较不受极端值的影响。
[答]对。
三、计算题1.甲乙两企业生产三种产品的单位成本和总成本资料如下表,试比较哪个企业的平均成本高,并分析其原因。
产品 单位成本(元) 总成本(元) 甲企业 乙企业 A B C15 20 302100 3000 1500 3255 1500 1500[解]甲企业的平均成本210030001500660019.4118210030001500340152030++===++乙企业的平均成本325515001500625518.2895 325515001500342152030++===++由上面的计算得知,甲企业的平均成本高于乙企业。
因为乙企业单位成本低的A产品生产的数量多,占总成本一半以上,即成本低的产品相对权数大,而甲企业生产单位成本低的A产品数量少,仅占总成本的31.8%(=2100/6600)。
由于权数的作用,乙企业的平均成本低于甲企业。
2.甲、乙两市场农产品价格及成交量资料如下表,试比较哪个市场的平均价格高,并分析其原因。
品种价格(元/公斤) 甲市场成交额(万元) 乙市场成交量(万公斤)甲乙丙1.21.41.51.22.81.5211合计-- 5.5 4 [解]甲市场的平均价格1.22.8 1.5 5.51.375 1.22.8 1.541.2 1.4 1.5++===++乙市场的平均价格1.22 1.41 1.51 5.31.32544⨯+⨯+⨯===由上面的计算得知,甲市场农产品的平均价格高高于乙市场。
因为价格低的甲产品在甲市场成交额少,仅占21.8%(=1.2/5.5);而在乙市场的成交额大,占45.3%(=2.4/5.3),由于权数的作用,甲市场的平均价格高于乙市场。
3.某企业工人平均月工资为1440元,月收入少于1280元的占一半,试估计众数,并对该企业工人工资的分布情况做一简要说明。
[解] 由题中可知,企业工人月工资的中位数=1280所以众数≈1440-3×(1440-1280)=960所以众数<中位数<平均数,则该企业的月工资分布为右(正)偏,说明该企业工人的月工资分布中出现极大值,即出现有人拿到高额的工资,导致月工资分布呈右偏。
4.某城市对3000户居民户均月消费支出进行调查,得到下表资料。
居民户月均支出(元) 户数比重(%)200以下200~ 300 300~ 400 400~ 500 500~ 600 600~ 700 700~ 800 800~ 900301804506001 050300180120161520351064900~1 000 1000以上60 30 2 13 000100.00要求:(1)计算居民户总平均月支出;(2)计算居民户月均支出标准差和变异系数; (3)计算居民月均支出中位数和众数;(4)分析平均数、中位数和众数之间的数量联系,并阐明分布的特征。
[解](1)居民总平均月支出52501.0105002.095004.085006.07501.065035.05502.045015.035006.025001.0150=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=(2)居民月均支出标准差()()()()7492.93888125052510505253505252505251502222≈=-++-+-+-(3)居民户数数列向上累计频数为2310,占总户数一半以上,中位数处于在这一组,即月均支出数列500~600中。
用下限公式计算:8571.5228571.2250010010501260150050021=+≈⨯-+=⨯-+=-∑e ee e M M M M e df S fL M用上限公式计算:8571.5221429.776001001050690150060021=-≈⨯--=⨯--=+∑e ee e M M M M e df S fU M频数最高的(户数最多)组就是众数所在之组,众数应处于居民月均支出分组500~600这一组,用下限公式计算:()()5.537100300105060010506001050500)()(111=⨯-+--+=⨯-+--+=+--oo o o o o o o M M M M M M M M o d f f f f f f L M用上限公式计算:()()5.537100300105060010503001050600)()(111=⨯-+---=⨯-+---=+-+oo o o o o o o M M M M M M M M o d f f f f f f U M5.某生产班组11个工人日生产零件数为:15,17,19,20,22,22,23,23,25,26,30。
要求:(1)计算平均数和方差;(2)按照15~19、20~24、24以上分成三组,计算组内方差和组间方差;(3)验证总方差等于组间方差与组内方差平均数之和。
[解](1)总平均数2211301715=+++=x ,总方差()()()11178112230221722152222=-++-+-=σ(2)组一(15~19):15,17,19 ;171=x 组内方差:3821=σ 组二(20~24):20,22,22,23,23 ;222=x ; 组内方差:5622=σ 组三:(24以上):25,26,30 ;273=x ; 组内方差:31423=σ ∴组间方差()()()11150113222752222322172222=⨯-+⨯-+⨯-=δ(3)证明:总方差216.18σ=,组间方差213.64δ=组内方差的平均值11281133145563382=⨯+⨯+⨯=i σ 22211281115011178i σδσ+=+==∴总方差=组间方差+组内方差的平均值。
原命题得证。
6.某管理局下属8家企业的产品销售数据如下表所示:.试比较其产品销售额和销售利润的离散程度。
企业产品销售额(X 1) (万元)销售利润(X 2) 1 2 3170 220 3908.1 12.5 18.04 5 6 7 8430 480 650 950 1 00022.0 26.5 40.0 64.0 69.0[解] 产品销售额的平均数=536.25,标准差=289.2204;∴其标准差系数5393.025.5362204.289≈=销售利润的平均数=32.5125,标准差=21.6004∴其标准差系数6644.05125.326004.21≈=根据标准差系数的计算结果,产品销售额的标准差系数较小,说明产品销售额离散程度较小,分布比较均匀。
7.某高校学生参加英语四级考试的优秀率和合格率分别为15%和90%,试计算优秀率和合格率分布的方差和标准差。
[解] 该题属于求0-1分布的方差和标准差 由题意得优秀率P 1=15%,合格率P 2=90% ∴优秀率的方差和标准差21111(1)0.150.850.12750.3571P P σσ=-=⨯== ∴合格率的方差和标准差22222(1)0.90.10.090.3P P σσ=-=⨯==8.某粮食作物的产量和播种面积资料如下,试测定其偏度和峰度。
亩产量x 400~500 500~600 600~700 700~800 800~900 900~1 000 合计播种面积f630 50 60 40 14 200[解]亩 产(百斤) 组中值i xi fi i f x x x - ()f x x 2- ()f x x 3- ()f x x 4-1 4~5 4.5 6 27 -2.7 43.74 -118.098 318.86462 5~6 5.5 30 165 -1.7 86.7 -147.39 250.563 3 6~7 6.5 50 325 -0.7 24.5 -17.15 12.0054 7~8 7.5 60 450 0.3 5.4 1.62 0.486 5 8~9 8.5 40 340 1.3 67.6 87.88114.24469~109.5141332.374.06170.338 391.77742.72001440===∑∑fxf x (百斤),2288.151.1200302===σ; 偏度00614.02288.12008.22333<-=-==σνα 峰度06143.033857.2320030220094.10873244<-=-=-⎪⎭⎫⎝⎛=-=σνβ负偏;低峰态。
2001440302-22.81087.94。
