【课件】高中数学课件《独立重复实验与二项分布》PPT
合集下载
独立重复试验与二项分布 课件

k_=__0_,1_,_2_,·_··_,__n________.
此时称随机变量X服从_二__项__分__布_,记作__X_~__B_(_n_,__p_) ,并 称p为__成__功____概率.
例如:某射手射击1次,击中目标的概率是0.9,他射击4 次恰好击中3次的概率是
_P_(_X_=__3__)=__C__340_._9_3_(1_-___0_.9_)_4_-_3=__0_._2_9_1_6_.____________________
所求概率为 P=C35×353×1-352=261265.
(3)该射手射击了 5 次,其中恰有 3 次连续击中目标,而 其他两次没有击中目标,应用排列组合知识,把 3 次连续击 中目标看成一个整体可得共有 C13种情况.
故所求概率为 P=C13·353·1-352=3312245.
二项分布
将一枚均匀硬币随机掷100次,求正好出现50次正 面的概率.
点评:独立重复试验是同一试验的n次重复,每次试验结
果的概率不受其他次结果的概率的影响,每次试验有两个可
能结果:成功和失败,n次试验中A恰好发生了k次的概率为
C
k n
pk(1-p)n-k,这k次是n次中的任意k次.若是指定的k次,则概 率为pk(1-p)n-k.
解析:(1)该射手射击了 5 次,其中只在第一、三、五次 击中目标,是在确定的情况下击中目标 3 次,也就是在第二、 四次没有击中目标,所以只有一种情况,又因为各次射击的
结果互不影响,故所求概率为 P=35×1-35×35×1-35×35= 108 3125.
(2)该射手射击了 5 次,其中恰有 3 次击中目标.根据排 列组合知识,5 次当中选 3 次,共有 C35种情况,因为各次射 击的结果互不影响,所以符合 n 次独立重复试验概率模型.故
此时称随机变量X服从_二__项__分__布_,记作__X_~__B_(_n_,__p_) ,并 称p为__成__功____概率.
例如:某射手射击1次,击中目标的概率是0.9,他射击4 次恰好击中3次的概率是
_P_(_X_=__3__)=__C__340_._9_3_(1_-___0_.9_)_4_-_3=__0_._2_9_1_6_.____________________
所求概率为 P=C35×353×1-352=261265.
(3)该射手射击了 5 次,其中恰有 3 次连续击中目标,而 其他两次没有击中目标,应用排列组合知识,把 3 次连续击 中目标看成一个整体可得共有 C13种情况.
故所求概率为 P=C13·353·1-352=3312245.
二项分布
将一枚均匀硬币随机掷100次,求正好出现50次正 面的概率.
点评:独立重复试验是同一试验的n次重复,每次试验结
果的概率不受其他次结果的概率的影响,每次试验有两个可
能结果:成功和失败,n次试验中A恰好发生了k次的概率为
C
k n
pk(1-p)n-k,这k次是n次中的任意k次.若是指定的k次,则概 率为pk(1-p)n-k.
解析:(1)该射手射击了 5 次,其中只在第一、三、五次 击中目标,是在确定的情况下击中目标 3 次,也就是在第二、 四次没有击中目标,所以只有一种情况,又因为各次射击的
结果互不影响,故所求概率为 P=35×1-35×35×1-35×35= 108 3125.
(2)该射手射击了 5 次,其中恰有 3 次击中目标.根据排 列组合知识,5 次当中选 3 次,共有 C35种情况,因为各次射 击的结果互不影响,所以符合 n 次独立重复试验概率模型.故
独立重复试验与二项分布课件(人教A选修2-3)(

独立重复试验与二项分布课件
contents
目录
• 独立重复试验 • 二项分布 • 二项分布的应用 • 独立重复试验与二项分布的关系 • 实例分析 • 总结与思考
01
独立重复试验
定义与特点
独立重复试验是指在相同的条件下,独立地重复进行n次试验 ,每次试验只有两种可能结果(成功或失败),并且每次试 验中成功的概率为p,失败的概率为q=1-p。
概率密度函数
二项分布的概率密度函数可以用 于描述在n次独立重复试验中成功 的次数,从而帮助我们理解随机 事件的分布情况。
决策制定
决策依据
在风险决策中,二项分布可以用于评 估不同决策的风险和收益,帮助我们 做出最优决策。
风险评估
通过二项分布,我们可以评估不同决 策的风险,从而选择风险较小的方案 。
数据分析与预测
二项分布的期望是np,方差是np(1-p)。
二项分布的期望是np,其中n是试验次数,p是每次试验成功的概率;方差是np(1-p),表示实际观测值与期望值之间的偏离 程度。
03
二项分布的应用
概率计算
概率计算
二项分布可以用于计算在独立重 复试验中成功的概率。例如,在 抛硬币试验中,可以计算连续出 现三次正面的概率。
二项分布的性质
二项分布具有可加性、独立性、对称性和均匀性等性质。
二项分布具有可加性,即如果将两个独立的二项分布相加,结果仍然服从二项分 布;独立性,即各次试验是独立的;对称性,即成功的次数和失败的次数是对称 的;均匀性,即随着试验次数的增加,成功次数和失败次数的概率趋于相等。
二项分布的期望与方差
06
总结与思考
独立重复试验与二项分布在生活中的意义
概率思维
预测未来
contents
目录
• 独立重复试验 • 二项分布 • 二项分布的应用 • 独立重复试验与二项分布的关系 • 实例分析 • 总结与思考
01
独立重复试验
定义与特点
独立重复试验是指在相同的条件下,独立地重复进行n次试验 ,每次试验只有两种可能结果(成功或失败),并且每次试 验中成功的概率为p,失败的概率为q=1-p。
概率密度函数
二项分布的概率密度函数可以用 于描述在n次独立重复试验中成功 的次数,从而帮助我们理解随机 事件的分布情况。
决策制定
决策依据
在风险决策中,二项分布可以用于评 估不同决策的风险和收益,帮助我们 做出最优决策。
风险评估
通过二项分布,我们可以评估不同决 策的风险,从而选择风险较小的方案 。
数据分析与预测
二项分布的期望是np,方差是np(1-p)。
二项分布的期望是np,其中n是试验次数,p是每次试验成功的概率;方差是np(1-p),表示实际观测值与期望值之间的偏离 程度。
03
二项分布的应用
概率计算
概率计算
二项分布可以用于计算在独立重 复试验中成功的概率。例如,在 抛硬币试验中,可以计算连续出 现三次正面的概率。
二项分布的性质
二项分布具有可加性、独立性、对称性和均匀性等性质。
二项分布具有可加性,即如果将两个独立的二项分布相加,结果仍然服从二项分 布;独立性,即各次试验是独立的;对称性,即成功的次数和失败的次数是对称 的;均匀性,即随着试验次数的增加,成功次数和失败次数的概率趋于相等。
二项分布的期望与方差
06
总结与思考
独立重复试验与二项分布在生活中的意义
概率思维
预测未来
人教A版高中数学选修23.3独立重复试验与二项分布PPT课件
人 教A版高 中数学 选修23 .3独立 重复试 验与二 项分布 PPT课 件
人 教A版高 中数学 选修23 .3独立 重复试 验与二 项分布 PPT课 件
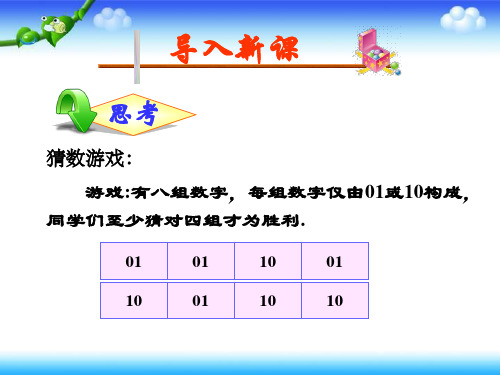
思考
课开始时的游戏是否可以看成是独立重复 试验?
游戏中,我们用X表示猜对的组数,下面 分组探讨X的取值和相应的概率,完成下表.
对每组数 猜对的概率均为p= _____; 猜错的概率为q=1-p=________.
(2)按比赛规则甲获胜的概率.
人 教A版高 中数学 选修23 .3独立 重复试 验与二 项分布 PPT课 件
解:
甲、乙两队实力相等,所以每局比赛甲获胜 的概率为0.5,乙获胜的概率为0.5.
记A事件=“甲打完3局才能取胜”,
记B事件=“甲打完4局才能取胜”,
记C事件=“甲打完5局才能取胜”.
①甲打完3局取胜,相当于进行3次独立重复 试验,且每局比赛甲均取胜.
√ A. 0.192 B. 0.288 C. 0.648 D. 0.254
3.解答题
(1)十层电梯从低层到顶层停不少于3次的概 率是多少?停几次概率最大?
解:
依题意,从低层到顶层停不少于3次,应包括 停3次,停4次,停5次,……,直到停9次.
∴从低层到顶层停不少于3次的概率:
P
=
C93
(
1 2
)3
教学目标
知识目标
(1)在了解条件概率和相互独立事件概念 的前提下,理解n次独立重复试验的模型及二 项分布,并能解决一些简单的实际问题;
(2)渗透由特殊到一般,由具体到抽象的 数学思想方法.
能力目标
(1)培养学生的自主学习能力; (2)培养学生的数学建模能力; (3)培养学生的应用数学知识解决实际问 题的能力.
人 教A版高 中数学 选修23 .3独立 重复试 验与二 项分布 PPT课 件
思考
课开始时的游戏是否可以看成是独立重复 试验?
游戏中,我们用X表示猜对的组数,下面 分组探讨X的取值和相应的概率,完成下表.
对每组数 猜对的概率均为p= _____; 猜错的概率为q=1-p=________.
(2)按比赛规则甲获胜的概率.
人 教A版高 中数学 选修23 .3独立 重复试 验与二 项分布 PPT课 件
解:
甲、乙两队实力相等,所以每局比赛甲获胜 的概率为0.5,乙获胜的概率为0.5.
记A事件=“甲打完3局才能取胜”,
记B事件=“甲打完4局才能取胜”,
记C事件=“甲打完5局才能取胜”.
①甲打完3局取胜,相当于进行3次独立重复 试验,且每局比赛甲均取胜.
√ A. 0.192 B. 0.288 C. 0.648 D. 0.254
3.解答题
(1)十层电梯从低层到顶层停不少于3次的概 率是多少?停几次概率最大?
解:
依题意,从低层到顶层停不少于3次,应包括 停3次,停4次,停5次,……,直到停9次.
∴从低层到顶层停不少于3次的概率:
P
=
C93
(
1 2
)3
教学目标
知识目标
(1)在了解条件概率和相互独立事件概念 的前提下,理解n次独立重复试验的模型及二 项分布,并能解决一些简单的实际问题;
(2)渗透由特殊到一般,由具体到抽象的 数学思想方法.
能力目标
(1)培养学生的自主学习能力; (2)培养学生的数学建模能力; (3)培养学生的应用数学知识解决实际问 题的能力.
独立重复试验与二项分布 课件

件分拆成若干个互斥事件的和,其次要将分拆后的每个事件再分拆
为若干个相互独立事件的乘积.这两个步骤做好了,问题的思路就
清晰了,接下来就是按照相关的概率值进行计算的问题了.如果某
(1)3 台都未报警的概率为
P(X=0)= C30 × 0.90 × 0.13 = 0.001;
(2)恰有 1 台报警的概率为
P(X=1)= C31 × 0.91 × 0.12 = 0.027;
(3)恰有 2 台报警的概率为
P(X=2)= C32 × 0.92 × 0.1 = 0.243;
(4)3 台都报警的概率为
发生k次的概率为 P(X=k)=C pk(1-p)n-k,k=0,1,2,…,n,此时称随机变
量X服从二项分布,简记为X~B(n,p),并称p为成功概率.
知识拓展 1.在 n 次试验中,有些试验结果为 A,有些试验结果为,
所以总结果是几个 A 同几个的一种搭配,要求总结果中事件 A 恰好
发生 k 次,就是 k 个 A 同 n-k 个的一种搭配,搭配种类为C ;其次,每
1
分布,故该空填C32
20
C25 C195
答案:(1)
C3100
2 19 1
20
.
1
(2)C32
20
2
19 1
20
【示例2】 某厂生产的电子元件,其次品率为5%,现从一批产品
中任意连续地抽取2件,其中次品数ξ的概率分布列为
ξ
P
,请完成此表.
0
1
2
解析:由于本题中工厂生产的电子元件数量很大,从中抽取2件时,
(X=1)或不发生(X=0);二项分布是指在n次独立重复试验中事件A发
生的次数X的分布列,试验次数为n(每次试验的结果也只有两种:事
为若干个相互独立事件的乘积.这两个步骤做好了,问题的思路就
清晰了,接下来就是按照相关的概率值进行计算的问题了.如果某
(1)3 台都未报警的概率为
P(X=0)= C30 × 0.90 × 0.13 = 0.001;
(2)恰有 1 台报警的概率为
P(X=1)= C31 × 0.91 × 0.12 = 0.027;
(3)恰有 2 台报警的概率为
P(X=2)= C32 × 0.92 × 0.1 = 0.243;
(4)3 台都报警的概率为
发生k次的概率为 P(X=k)=C pk(1-p)n-k,k=0,1,2,…,n,此时称随机变
量X服从二项分布,简记为X~B(n,p),并称p为成功概率.
知识拓展 1.在 n 次试验中,有些试验结果为 A,有些试验结果为,
所以总结果是几个 A 同几个的一种搭配,要求总结果中事件 A 恰好
发生 k 次,就是 k 个 A 同 n-k 个的一种搭配,搭配种类为C ;其次,每
1
分布,故该空填C32
20
C25 C195
答案:(1)
C3100
2 19 1
20
.
1
(2)C32
20
2
19 1
20
【示例2】 某厂生产的电子元件,其次品率为5%,现从一批产品
中任意连续地抽取2件,其中次品数ξ的概率分布列为
ξ
P
,请完成此表.
0
1
2
解析:由于本题中工厂生产的电子元件数量很大,从中抽取2件时,
(X=1)或不发生(X=0);二项分布是指在n次独立重复试验中事件A发
生的次数X的分布列,试验次数为n(每次试验的结果也只有两种:事
独立重复试验与二项分布(上课用)课件

二项分布的偏态和峰态描述了概率分布的不对称性和 尖锐程度。
偏态(Skewness)和峰态(Kurtosis)是描述概率分 布形态的两个重要统计量。偏态用于衡量概率分布的 不对称性,峰态则用于描述概率分布的尖锐程度。在 二项分布中,偏态和峰态的计算公式分别为 Skewness=(3(p-0.5))/(np) 和 Kurtosis=3(p0.5)^2/(n*p*(1-p))。通过计算偏态和峰态,可以进 一步了解二项分布的概率分布特征。
独立重复试验与二项 分布课件
目 录
• 独立重复试验 • 二项分布 • 独立重复试验与二项分布的关系 • 实例分析 • 总结与思考
CHAPTER 01
独立重复试验
பைடு நூலகம்
定义与特点
定义
独立重复试验是指在每次试验中 ,事件发生的概率都不受其他试 验结果影响,每次试验都是独立 的。
特点
每次试验都有两个可能的结果, 互不影响,多次独立重复同一试 验。
风险评估
通过二项分布,我们可以评估一系列独立事 件的风险,从而制定有效的风险管理策略。 例如,在金融领域,二项分布被用于评估股 票价格涨跌的概率。
对未来的展望
扩展应用领域
随着科技的发展和研究的深入,独立重复试 验和二项分布在各个领域的应用将更加广泛 。例如,在人工智能、大数据分析、生物信 息学等领域,二项分布的应用前景非常广阔 。
在二项分布中,期望(E)和方差(Var)是两个重要的统计量,用于描述随机事件发生的概率。期望值是随机变量取值的平 均数,而方差则描述了随机变量取值分散的程度。在二项分布中,期望和方差的计算公式分别为 E=np 和 Var=np(1-p),其 中 n 是试验次数,p 是事件发生的概率。
独立重复试验与二项分布 课件

独立重复试验与二项分布
1.n 次独立重复试验 一般地,在 相同 条件下重复做的 n 次试验称为 n 次独立重 复试验.
2.二项分布 前提
X 字母事件 A 发生的次数
每次试验中事件 A 发生的概率 P(X=k)=Cpk(1-p)n-k,k= 0,1,2,…,n
8 729
解决二项分布问题的两个关注点 (1)对于公式 P(X=k)=Cknpk(1-p)n-k(k=0,1,2,…,n)必须 在满足“独立重复试验”时才能运用,否则不能应用该公式. (2)判断一个随机变量是否服从二项分布,关键有两点:一是对 立性,即一次试验中,事件发生与否两者必有其一;二是重复 性,即试验是独立重复地进行了 n 次.
Y01 2
P
77 15 15
1 15
二项分布实际应用问题的解题策略 (1)根据题意设出随机变量. (2)分析出随机变量服从二项分布. (3)找到参数 n(试验的次数)和 p(事件发生的概率). (4)写出二项分布的分布列.
另一枚的点数为点 P 的纵坐标,求连续抛掷这两枚骰子三次, 点 P 在圆 x2+y2=16 内的次数 X 的分布列. 【解】 由题意可知,点 P 的坐标共有 6×6=36(种)情况,其 中在圆 x2+y2=16 内的有点(1,1),(1,2),(1,3),(2,1), (2,2),(2,3),(3,1),(3,2)共 8 种,则点 P 在圆 x2+y2= 16 内的概率为386=29.
结论 记法
随机变量 X 服从二项分布 记作 X~B(n,p) ,并称 p 为
成功概率
探究点 1 独立重复试验的概率 甲、乙两人各射击一次,击中目标的概率分别是23和34,
假设每次射击是否击中目标,相互之间没有影响.(结果须用分 数作答) (1)求甲射击 3 次,至少 1 次未击中目标的概率; (2)求两人各射击 2 次,甲恰好击中目标 2 次且乙恰好击中目标 1 次的概率.
1.n 次独立重复试验 一般地,在 相同 条件下重复做的 n 次试验称为 n 次独立重 复试验.
2.二项分布 前提
X 字母事件 A 发生的次数
每次试验中事件 A 发生的概率 P(X=k)=Cpk(1-p)n-k,k= 0,1,2,…,n
8 729
解决二项分布问题的两个关注点 (1)对于公式 P(X=k)=Cknpk(1-p)n-k(k=0,1,2,…,n)必须 在满足“独立重复试验”时才能运用,否则不能应用该公式. (2)判断一个随机变量是否服从二项分布,关键有两点:一是对 立性,即一次试验中,事件发生与否两者必有其一;二是重复 性,即试验是独立重复地进行了 n 次.
Y01 2
P
77 15 15
1 15
二项分布实际应用问题的解题策略 (1)根据题意设出随机变量. (2)分析出随机变量服从二项分布. (3)找到参数 n(试验的次数)和 p(事件发生的概率). (4)写出二项分布的分布列.
另一枚的点数为点 P 的纵坐标,求连续抛掷这两枚骰子三次, 点 P 在圆 x2+y2=16 内的次数 X 的分布列. 【解】 由题意可知,点 P 的坐标共有 6×6=36(种)情况,其 中在圆 x2+y2=16 内的有点(1,1),(1,2),(1,3),(2,1), (2,2),(2,3),(3,1),(3,2)共 8 种,则点 P 在圆 x2+y2= 16 内的概率为386=29.
结论 记法
随机变量 X 服从二项分布 记作 X~B(n,p) ,并称 p 为
成功概率
探究点 1 独立重复试验的概率 甲、乙两人各射击一次,击中目标的概率分别是23和34,
假设每次射击是否击中目标,相互之间没有影响.(结果须用分 数作答) (1)求甲射击 3 次,至少 1 次未击中目标的概率; (2)求两人各射击 2 次,甲恰好击中目标 2 次且乙恰好击中目标 1 次的概率.
独立重复试验与二项分布 课件

独立重复试验与二项分布
1.n 次独立重复试验:一般地,在 相同 条件下重复做的 n 次试验称为 n 次独立重复试验.
2.在 n 次独立重复试验中,“在相同的条件下”等价于 各次试验的结果不会受其他试验的 影响 ,即 P(A1A2…An)=
P(A1)P(A2)…P(An).其中 Ai(i=1,2,…,n)是第 i 次试验的结 果.
则 P(A)=0.7,P(B)=0.6,P(C)=0.8. 所以从甲、乙、丙三台机床加工的零件中各取一件检验, 至少有一件一等品的概率为 P1=1-P(-A )P(-B )P(-C )=1-0.3×0.4×0.2=0.976. (2)将甲、乙、丙三台机床加工的零件混合到一起,从中任 意地抽取一件检验,它是一等品的概率为 P2=2×0.7+40.6+0.8=0.7.
4 243
1 729
[点评] 解此类题首先判断随机变量 X 服从二项分布,即 X~B(n,p),然后求出 P(X=k)=Cknpk(1-p)n-k(k=0,1,2,…,n), 最后列出二项分布列.
二项分布的应用
甲、乙、丙三台机床各自独立地加工同一种零 件,已知甲、乙、丙三台机床加工的零件是一等品的概率分别 为 0.7、0.6、0.8,乙、丙两台机床加工的零件数相等,甲机床 加工的零件数是乙机床加工的零件数的 2 倍.
4.Cknpk(1-p)n-k 是[p+(1-p)]n 的二项展开式中的第 k+1 项.
独立重复试验概率的求法
某人射击 5 次,每次中靶的概率均为 0.9,求他至 少有 2 次中靶的概率.
[分析] 至少有 2 次中靶包括恰好有 2 次中靶,恰好有 3 次 中靶,恰好有 4 次中靶和恰好有 5 次中靶四种情况,这些事件 是彼此互斥的,而每次射击中靶的概率均相等,并且相互之间 没有影响,所以每次射击又是相互独立事件,因而射击 5 次是 进行 5 次独立重复试验.
1.n 次独立重复试验:一般地,在 相同 条件下重复做的 n 次试验称为 n 次独立重复试验.
2.在 n 次独立重复试验中,“在相同的条件下”等价于 各次试验的结果不会受其他试验的 影响 ,即 P(A1A2…An)=
P(A1)P(A2)…P(An).其中 Ai(i=1,2,…,n)是第 i 次试验的结 果.
则 P(A)=0.7,P(B)=0.6,P(C)=0.8. 所以从甲、乙、丙三台机床加工的零件中各取一件检验, 至少有一件一等品的概率为 P1=1-P(-A )P(-B )P(-C )=1-0.3×0.4×0.2=0.976. (2)将甲、乙、丙三台机床加工的零件混合到一起,从中任 意地抽取一件检验,它是一等品的概率为 P2=2×0.7+40.6+0.8=0.7.
4 243
1 729
[点评] 解此类题首先判断随机变量 X 服从二项分布,即 X~B(n,p),然后求出 P(X=k)=Cknpk(1-p)n-k(k=0,1,2,…,n), 最后列出二项分布列.
二项分布的应用
甲、乙、丙三台机床各自独立地加工同一种零 件,已知甲、乙、丙三台机床加工的零件是一等品的概率分别 为 0.7、0.6、0.8,乙、丙两台机床加工的零件数相等,甲机床 加工的零件数是乙机床加工的零件数的 2 倍.
4.Cknpk(1-p)n-k 是[p+(1-p)]n 的二项展开式中的第 k+1 项.
独立重复试验概率的求法
某人射击 5 次,每次中靶的概率均为 0.9,求他至 少有 2 次中靶的概率.
[分析] 至少有 2 次中靶包括恰好有 2 次中靶,恰好有 3 次 中靶,恰好有 4 次中靶和恰好有 5 次中靶四种情况,这些事件 是彼此互斥的,而每次射击中靶的概率均相等,并且相互之间 没有影响,所以每次射击又是相互独立事件,因而射击 5 次是 进行 5 次独立重复试验.
独立重复试验与二项分布 课件

1
4
4
k k
11 4 7 4
7 4
k
11 4
k 2.
P2 (2)
C
2 10
( 1 )2 4
(3)8 4
0.28
例2.有译电员若干员,每人独立 破到译 译密 出码密的码概 的率 概均 率为 为013.9,若9,至要少达 要配备多少人?
(lg2=0.3010,lg3=0.4771)
袋中有12个球,其中白球4个,
则:C13P(1 P)2 C23P(2 1 P) C33P3 19 27
3P(1 P)2 3P(2 1 P) P3 19 27
P3 3P(1 P) 19 , P 1
27
3
例2.甲、乙两个篮球运动员投篮 命中率为0.7及0.6,若每人各投3次, 试求甲至少胜乙2个进球的概率
P(甲胜3个球) (0.7)(3 1 0.6)3 0.021952
P( 3) P( 0) 1 3 3 3 3 5 5 25
例4.有10道单项选择题,每题有4个选支,某人随机选定 每题中其中一个答案,求答对多少题的概率最大?并求 出此种情况下概率的大小.
解:设“答对k题”的事件为A,用P1(0 k)表示其概率,由
P10 (k )
P10 (k 1)
可以发现
P(Bk ) C3k pkq3k,k=0,1,2,3
一般地,在n次独立重复试验中,设事件A发生的次数 为X,在每次试验中事件A发生的概率是P,那么在n次 独立重复试验中,这个事件恰好发生k次的概率
A
P( X k) Cnk pk (1 p)nk,k 0,1,2,, n
此时称随机变量X服从二项分布,记作X~B(n,p), 并称p为成功概率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Cnk Pk (1 P)nk 是(1 P) Pn 展开式的第k 1项.
共同特点是:
1)多次重复的做同一试验; 2)每次试验是在同样条件下进行; 3)每次试验中的某个事件只有两种结果, 要么发生,要么不发生;
4)各次试验中的事件是相互独立的。
二、新课讲授
1、n次独立重复试验:
一般地,在相同条件下重复做的n次试验
仔细观察事件的概率和出现针尖向上的次数之间的规律:
P(Bk ) C3k pkq3k , k 0,1, 2,3.
思考?
二项分布与两点分布有何区别联系?
两点分布是特殊的二项分布,二项分 布是两点分布的一般情形;
三、运用二项分布概率模型解题
例1(试验2) 某射手每次射击击中目标的概
率是0.8. 求这名射手在10次射击中: (1)恰有8次击中目标的概率; (2)至少有8次击中目标的概率。
诚朴、健美、笃学、奋进
独立重复实验与二项分布
一、新课引入
分析下面的试验,他们有什么共同特点?
(1)投掷一枚图钉3次; (2)某人射击1次,击中目标的概率是0.8, 他射击10次; (3)一个盒子中装有5个形状大小完全相同的 小球,(3个红球和2个白球),有放回的依次 从中抽取5个球;
共同特点是:
C8 10
0.88
(1
0.82)
C9 10
0.89
(1
0.8)1
C10 10
0.810
0.68.
练习1(试验3)
一个盒子中装有5个形状大小完全相同 的小球(3个红球和2个白球),有放回的依 次从中抽取5个球;
1)求恰有3个是红球的概率;
2)求至少有3个是红球的概率;
例2 实力相等的甲、乙两队参加乒乓球团体比
(结果保留两个有效数字)
解:设X为击中目标的次数,则X~B 10, 0.8 .
1 在10次射击中,恰有8次击中目标的概率为
PX
8
=C8 10
0.88
(1
0.8)2
0.30.
2 在10次射击中,至少有8次击中目标的概率为
P (X 8) P X 8 P X 9 P X 10
而A1 A2 A3,A1A2 A3和A1 A2 A3彼此互斥,则
P(B1) P( A1 A2 A3 ) P( A1A2 A3 ) P( A1 A2 A3 )
q2 p q2 p q2 p 3q2 p C31 p1q2.
思考?
上面我们利用掷1次图钉,针尖向上的概率为p,求 出了连续掷3次图钉,仅出现1次针尖向上的概率。类
2、二项分布:
一般地,在n次独立重复试验中,设事 件A发生的次数为X,在每次试验中事件A发生 的概率为p,那么在n次独立重复试验中,
事件A恰好发生k次的概率为
Pn ( X k) Cnk pk qnk,(k=0,1,2,n,q=1-p).
此时称随机变量X服从二项分布,记作X B(n, p), 并称p为成功概率。
赛,规定5局3胜制(即5局内谁先赢3局就算胜 出并停止比赛). ⑴试求甲打完4、5局才能取胜的概率. ⑵按比赛规则甲获胜的概率.
错解:(1)甲、乙两队实力相等,所以每局比赛甲获胜
的概率为 1 ,乙获胜的概率为 1.
2
2
记事件A为“甲打完3局才能取胜”,记事件B为“甲打完4局 才能取胜”,记事件C为“甲打完5局才能取胜”,
才能取胜”,记事件C为“甲打完5局才能取胜”,
①甲打完4局才能取胜,相当于进行4次独立重复试验,
且甲第4局比赛取胜,前3局为2胜1负
甲打完4局才能取胜的概率为P(B)Biblioteka C32(1)2 2
1 2
称为n次独立重复试验.
独立重复试验的特点: 1)每次试验是在同样条件下进行; 2)各次试验中的事件是相互独立的; 3)每次试验中的某个事件只有两种结果,要么发生,要 么不发生;
在 n 次独立重复试验中,记 Ai 是“第 i 次试验 的结果”,显然:
P( A1A2 An ) P( A1)P( A2 ) P( An )
似地,连续掷3次图钉,出现 k(0 k 3,k Z ) 次针尖向上的概率是多少? 你能发现其中的规律吗?
P(B0 ) P( A1 A2 A3 ) q3 C30 p0q3, P(B1) P( A1 A2 A3 ) P( A1A2 A3 ) P( A1 A2 A3 ) 3q2 p C31 p1q2 , P(B2 ) P( A1A2 A3 ) P( A1A2 A3 ) P( A1 A2 A3 ) 3qp2 C32 p2q1, P(B3 ) P( A1A2 A3 ) p3 C33 p3q0 ,
1)多次重复的做同一试验; 2)每次试验是在同样条件下进行; 3)每次试验中的某个事件只有两种结果, 要么发生,要么不发生;
4)各次试验中的事件是相互独立的。
相互独立事件:
设A、B为两个事件,如果P(AB)=P(A)P(B), 则称事件A与事件B相互独立。
1)若A与B是相互独立事件,则A与B,A与B,A与B也相互独立; 2)一般地,如果事件A1, A2, , An相互独立,那么这n个事件 同时发生的概率,等于每个事件发生的概率的积,即 P( A1 A2 An ) P( A1) P( A2 ) P( An )
①甲打完4局才能取胜的概率为P(B)
C43
(1)3 2
1 2
1. 4
②甲打完5局才能取胜的概率为P(C)
C53
(1)3 2
( 1 )2 2
5. 16
错在哪里?
正解:甲、乙两队实力相等,所以每局比赛甲获胜的概
率为 1 ,乙获胜的概率为 1.
2
2
记事件A为“甲打完3局才能取胜”,记事件B为“甲打完4局
探究
(试验1)投掷一枚图钉,设针尖向上的概率为p, 则针尖向下的概率为q=1-p.连续掷一枚图钉3次,仅 出现1次针尖向上的概率是多少?
连续掷一枚图钉3次,就是做3次独立重复试验。
用A i
表示第i次掷得针尖向上的事件,用B1表示“仅
出现一次针尖向上”的事件,则
B1 ( A1 A2 A3 ) ( A1A2 A3 ) ( A1 A2 A3 )
共同特点是:
1)多次重复的做同一试验; 2)每次试验是在同样条件下进行; 3)每次试验中的某个事件只有两种结果, 要么发生,要么不发生;
4)各次试验中的事件是相互独立的。
二、新课讲授
1、n次独立重复试验:
一般地,在相同条件下重复做的n次试验
仔细观察事件的概率和出现针尖向上的次数之间的规律:
P(Bk ) C3k pkq3k , k 0,1, 2,3.
思考?
二项分布与两点分布有何区别联系?
两点分布是特殊的二项分布,二项分 布是两点分布的一般情形;
三、运用二项分布概率模型解题
例1(试验2) 某射手每次射击击中目标的概
率是0.8. 求这名射手在10次射击中: (1)恰有8次击中目标的概率; (2)至少有8次击中目标的概率。
诚朴、健美、笃学、奋进
独立重复实验与二项分布
一、新课引入
分析下面的试验,他们有什么共同特点?
(1)投掷一枚图钉3次; (2)某人射击1次,击中目标的概率是0.8, 他射击10次; (3)一个盒子中装有5个形状大小完全相同的 小球,(3个红球和2个白球),有放回的依次 从中抽取5个球;
共同特点是:
C8 10
0.88
(1
0.82)
C9 10
0.89
(1
0.8)1
C10 10
0.810
0.68.
练习1(试验3)
一个盒子中装有5个形状大小完全相同 的小球(3个红球和2个白球),有放回的依 次从中抽取5个球;
1)求恰有3个是红球的概率;
2)求至少有3个是红球的概率;
例2 实力相等的甲、乙两队参加乒乓球团体比
(结果保留两个有效数字)
解:设X为击中目标的次数,则X~B 10, 0.8 .
1 在10次射击中,恰有8次击中目标的概率为
PX
8
=C8 10
0.88
(1
0.8)2
0.30.
2 在10次射击中,至少有8次击中目标的概率为
P (X 8) P X 8 P X 9 P X 10
而A1 A2 A3,A1A2 A3和A1 A2 A3彼此互斥,则
P(B1) P( A1 A2 A3 ) P( A1A2 A3 ) P( A1 A2 A3 )
q2 p q2 p q2 p 3q2 p C31 p1q2.
思考?
上面我们利用掷1次图钉,针尖向上的概率为p,求 出了连续掷3次图钉,仅出现1次针尖向上的概率。类
2、二项分布:
一般地,在n次独立重复试验中,设事 件A发生的次数为X,在每次试验中事件A发生 的概率为p,那么在n次独立重复试验中,
事件A恰好发生k次的概率为
Pn ( X k) Cnk pk qnk,(k=0,1,2,n,q=1-p).
此时称随机变量X服从二项分布,记作X B(n, p), 并称p为成功概率。
赛,规定5局3胜制(即5局内谁先赢3局就算胜 出并停止比赛). ⑴试求甲打完4、5局才能取胜的概率. ⑵按比赛规则甲获胜的概率.
错解:(1)甲、乙两队实力相等,所以每局比赛甲获胜
的概率为 1 ,乙获胜的概率为 1.
2
2
记事件A为“甲打完3局才能取胜”,记事件B为“甲打完4局 才能取胜”,记事件C为“甲打完5局才能取胜”,
才能取胜”,记事件C为“甲打完5局才能取胜”,
①甲打完4局才能取胜,相当于进行4次独立重复试验,
且甲第4局比赛取胜,前3局为2胜1负
甲打完4局才能取胜的概率为P(B)Biblioteka C32(1)2 2
1 2
称为n次独立重复试验.
独立重复试验的特点: 1)每次试验是在同样条件下进行; 2)各次试验中的事件是相互独立的; 3)每次试验中的某个事件只有两种结果,要么发生,要 么不发生;
在 n 次独立重复试验中,记 Ai 是“第 i 次试验 的结果”,显然:
P( A1A2 An ) P( A1)P( A2 ) P( An )
似地,连续掷3次图钉,出现 k(0 k 3,k Z ) 次针尖向上的概率是多少? 你能发现其中的规律吗?
P(B0 ) P( A1 A2 A3 ) q3 C30 p0q3, P(B1) P( A1 A2 A3 ) P( A1A2 A3 ) P( A1 A2 A3 ) 3q2 p C31 p1q2 , P(B2 ) P( A1A2 A3 ) P( A1A2 A3 ) P( A1 A2 A3 ) 3qp2 C32 p2q1, P(B3 ) P( A1A2 A3 ) p3 C33 p3q0 ,
1)多次重复的做同一试验; 2)每次试验是在同样条件下进行; 3)每次试验中的某个事件只有两种结果, 要么发生,要么不发生;
4)各次试验中的事件是相互独立的。
相互独立事件:
设A、B为两个事件,如果P(AB)=P(A)P(B), 则称事件A与事件B相互独立。
1)若A与B是相互独立事件,则A与B,A与B,A与B也相互独立; 2)一般地,如果事件A1, A2, , An相互独立,那么这n个事件 同时发生的概率,等于每个事件发生的概率的积,即 P( A1 A2 An ) P( A1) P( A2 ) P( An )
①甲打完4局才能取胜的概率为P(B)
C43
(1)3 2
1 2
1. 4
②甲打完5局才能取胜的概率为P(C)
C53
(1)3 2
( 1 )2 2
5. 16
错在哪里?
正解:甲、乙两队实力相等,所以每局比赛甲获胜的概
率为 1 ,乙获胜的概率为 1.
2
2
记事件A为“甲打完3局才能取胜”,记事件B为“甲打完4局
探究
(试验1)投掷一枚图钉,设针尖向上的概率为p, 则针尖向下的概率为q=1-p.连续掷一枚图钉3次,仅 出现1次针尖向上的概率是多少?
连续掷一枚图钉3次,就是做3次独立重复试验。
用A i
表示第i次掷得针尖向上的事件,用B1表示“仅
出现一次针尖向上”的事件,则
B1 ( A1 A2 A3 ) ( A1A2 A3 ) ( A1 A2 A3 )
