欧拉方程推导
欧拉公式的推导

03
欧拉公式的证明
利用三角函数的性质进行证明
总结词
利用三角函数的周期性和对称性,通 过一系列的等式变换,推导出欧拉公 式。
详细描述
首先,利用三角函数的周期性和对称 性,将角函数转化为指数形式。然 后,通过一系列的等式变换,将指数 形式转化为欧拉公式。
利用复数的性质进行证明
总结词
利用复数的共轭和模的性质,通过代数运算 和等式变换,推导出欧拉公式。
快速傅里叶变换(FFT)
欧拉公式在快速傅里叶变换算法中有重要应用, 该算法用于信号处理和频谱分析等领域。
加密算法的实现
欧拉公式可以用于实现一些加密算法,例如 RSA公钥加密算法。
并行计算中的向量旋转
在并行计算中,欧拉公式可以用于实现向量的旋转操作,提高计算效率。
THANKS
感谢观看
欧拉公式的应用场景
01
在物理学中,欧拉公式被广泛应用于波动方程、电磁学、量子 力学等领域。
02
在工程学中,欧拉公式被用于信号处理、控制系统等领域。
在金融学中,欧拉公式被用于计算复利、评估风险等。
03
02
欧拉公式的推导过程
利用三角函数的性质进行推导
总结词
利用三角函数的周期性和对称性,通过一系列的恒等变换,推导出欧拉公式。
04
欧拉公式的变种和推广
欧拉恒等式
总结词
欧拉恒等式是数学中一个重要的恒等式,它 表示三角函数和指数函数之间的关系。
详细描述
欧拉恒等式是数学中一个重要的恒等式,它 表示三角函数和指数函数之间的关系。这个 恒等式在数学分析、复变函数、微分方程等 领域有着广泛的应用。通过欧拉恒等式,我 们可以将三角函数转化为指数函数,从而简
欧拉公式的推导

欧拉公式的推导
欧拉公式是由瑞士数学家拉斐尔·欧拉提出的一个有关多边形面积与边数的公式,是一个
显示复杂性的表达式,被用在多边形计算中。
拉斐尔·欧拉公式可用来快速计算多边形面积。
它主要用于几何图形和多边形概念的研究,从而确定图形的大小和形状。
拉斐尔·欧拉发现,多边形面积可以表示为多边形边数乘以一半周长,减去多边形内部夹
角的和,这种观点形成拉斐尔·欧拉公式,公式的原理是由钝角三角形的面积来派生出来的。
拉斐尔·欧拉定理的数学表达式如下:
S=1/2 (n x c) - ( Σ θ )
其中,S代表多边形的面积,n代表多边形的边数,c代表多边形的周长,θ表示多边形内部所有夹角的和。
拉斐尔·欧拉公式是一个非线性的计算公式,以方便和简单的方式计算任意多边形的面积,包括三角形,四边形,五边形等等,这是一个重要的数学原理,有助于理解多边形的几何
学计算。
经过拉斐尔·欧拉的费力调查和发现,他终于得出了多边形面积与边数之间的关系,并利
用这一关系表示出欧拉公式。
拉斐尔·欧拉公式一直被许多数学家们转化为新的数学表达
式使用,用以表示多边形的面积运算。
拉斐尔·欧拉公式‘被应用于从小学到大学,从总体
分析到详细测量,甚至是机器人多边形数学分析等方面。
拉斐尔·欧拉公式可以更有效地解决几何问题,是几何测量的一个重要工具、这也被应用
到各种工程领域中,它能够用最简洁的方式表达多边形的面积计算。
拉斐尔•欧拉的贡献
也帮助人们用数学的方式去研究多边形,几何学,他的贡献也为人类几何学的发展增添了浓厚的历史气息。
欧拉方程推导全过程

欧拉方程推导全过程嘿,数学爱好者们!今天我要带大家走进一个超级有趣的数学世界,那就是欧拉方程的推导。
这可不像在公园散步那么简单,但也绝不是无法攀登的高山,只要跟着我一步一步来,保准你能搞明白。
咱先来说说什么是欧拉方程。
想象一下,在数学这个大王国里,有一个神秘的方程式,就像一颗璀璨的明珠,它把指数函数、三角函数这些看似不太相关的家伙巧妙地联系在了一起。
这就是欧拉方程,$e^{ix} = \cos x + i\sin x$,其中$e$是自然常数,$i$是虚数单位,$x$是一个实数。
这个方程就像一把魔法钥匙,能打开很多数学难题的大门呢。
那咱们怎么推导这个神奇的方程呢?咱们得从泰勒级数这个有力的工具开始。
泰勒级数就像是一个超级放大镜,可以把一个函数展开成无穷项的多项式。
对于指数函数$e^x$,它的泰勒级数展开式是:$e^x = 1 + x + \frac{x^2}{2!}+ \frac{x^3}{3!}+ \frac{x^4}{4!}+ \cdots$。
这个式子看起来有点吓人,但是别怕,咱们一点点分析。
这里的$n!$就是$n$的阶乘,也就是从$1$乘到$n$。
再来看三角函数$\cos x$和$\sin x$的泰勒级数展开式。
$\cos x = 1 - \frac{x^2}{2!}+ \frac{x^4}{4!}- \frac{x^6}{6!}+ \cdots$,$\sin x = x - \frac{x^3}{3!}+ \frac{x^5}{5!}- \frac{x^7}{7!}+ \cdots$。
现在咱们把$x$换成$ix$代入到$e^x$的泰勒级数展开式中。
$e^{ix} = 1 + ix + \frac{(ix)^2}{2!}+ \frac{(ix)^3}{3!}+ \frac{(ix)^4}{4!}+ \cdots$。
那这个式子要怎么化简呢?咱们来仔细瞧瞧。
$(ix)^2 = -x^2$,$(ix)^3 = -ix^3$,$(ix)^4 = x^4$等等。
欧拉公式推导
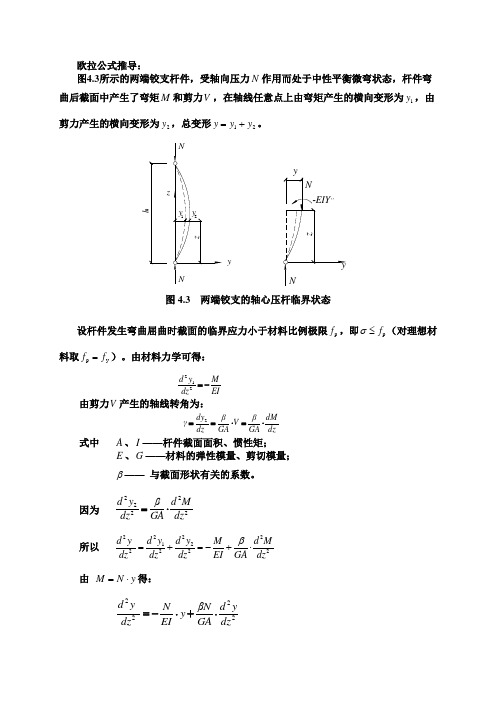
欧拉公式推导:图4.3所示的两端铰支杆件,受轴向压力N 作用而处于中性平衡微弯状态,杆件弯曲后截面中产生了弯矩M 和剪力V ,在轴线任意点上由弯矩产生的横向变形为1y ,由剪力产生的横向变形为2y ,总变形21y y y +=。
y图4.3 两端铰支的轴心压杆临界状态设杆件发生弯曲屈曲时截面的临界应力小于材料比例极限p f ,即p f ≤σ(对理想材料取y p f f =)。
由材料力学可得:EI M dz y d -=212 由剪力V 产生的轴线转角为:dz dM GA V GA dzdy ⋅=⋅==ββγ2 式中 A 、I ——杆件截面面积、惯性矩;E 、G ——材料的弹性模量、剪切模量; β—— 与截面形状有关的系数。
因为 22222dz M d GA dz y d ⋅=β 所以 2222122222d y d y d y M d M dz dz dz EI GA dzβ=+=-+⋅ 由 y N M ⋅=得:2222dzy d GA N y EI N dz yd ⋅+⋅-=β01=⋅+⎪⎭⎫ ⎝⎛-''y EIN GA N y β 令 ⎪⎭⎫ ⎝⎛-=GA N EI Nk β12得常系数线性二阶齐次方程 20y k y ''+=其通解为:sin cos y A kz B kz =+由边界条件:;0,0==y z 0=B ,kz A y sin =。
再由0,==y l z 得:0sin =kl A上式成立的条件是0=A 或0sin =kl ,其中0=A 表示杆件不出现任何变形,与杆件微弯的假设不符。
由0sin =kl ,得πn kl =(=n 1,2,3…),取最小值=n 1,得π=kl ,即2221N k N l EI GA πβ==⎛⎫- ⎪⎝⎭由此式解出N ,即为中性平衡的临界力cr N12222222211Ι11γππβππ⋅+⋅=⋅+⋅=lΕΙl ΕGA l ΕΙl ΕΙN cr (4.6) 临界状态时杆件截面的平均应力称为临界应力cr σ1222211γλπλπσ⋅+⋅==ΕΑΕA N cr cr (4.7)式中 1γ——单位剪力时杆件的轴线转角,)/(1GA βγ=;l ——两端铰支杆得长度;λ——杆件的长细比,i l /=λ;i ——杆件截面对应于屈曲轴的回转半径,A I i /=。
欧拉动力学方程推导

欧拉动力学方程推导欧拉动力学方程推导作为物理学必修的内容,欧拉动力学方程常常被各类研究者所关注。
欧拉动力学方程是描述物体在运动过程中受到各个力作用所导致的运动变化规律。
下面,我们将进行欧拉动力学方程的详细推导,以便让读者更加深入了解物理学的这部分内容。
1. 初步摆放对于欧拉动力学方程的推导,第一步是明确出力的平衡关系,也就是万有引力定律。
万有引力定律的核心是万有引力定律公式,即F=Gm_1m_2/r^2。
其中,F表示两个物体之间的力,G是万有引力常数,m_1和m_2分别是两个物体的质量,r是两个物体距离的距离。
2. 重心位置计算另外,需要求出物体的重心位置,以便在计算过程中进行更加精准的计算。
重心位置是物体的质量分布情况的简化结果。
具体的求解过程可以从物体几何结构上出发进行计算。
3. 动能定理应用在具备力的平衡关系和物体重心位置的计算结果后,我们还需要应用动能定理进行计算。
动能定理描述的是物体在做功时能量的变化规律。
物体在运动过程中由于受到外力的作用而发生的速度变化,同时产生的动能变化会导致物体做功。
4. 应用欧拉动力学方程最后,我们需要应用欧拉动力学方程,进行力的平衡关系的进一步推导。
欧拉动力学方程的核心是对所受到的力进行平衡分析,从而得出物体的加速度变化规律。
在欧拉动力学方程的具体应用中,需要注意对不同物体所受到的力进行区分,并且进行相应的求解。
总之,欧拉动力学方程的推导需要对力的平衡关系、重心位置计算、动能定理和欧拉动力学方程等各个方面进行分析。
通过深入研究这些内容,读者将会对欧拉动力学方程和物理学的各个细节问题有更加深入的认识和理解。
牛顿-欧拉方程向量法推导

牛顿-欧拉方程向量法推导
欧拉方程(Euler equations),是欧拉运动定律的定量描述,该定律为:
)]([1b
b b b b b I M I Ω⨯Ω-=Ω-& 其中b Ω为体坐标系下的角速度,b I 为体坐标系下的转动惯量,b M 为体坐标系下的外力矩。
欧拉方程通常与牛顿的平移运动方程被一起写出,称为牛顿-欧拉方程(Newton-Euler equations),此处只推导欧拉方程。
在不考虑外力矩时,约束条件为惯性坐标系的角动量守恒(非体坐标系的角动量守恒),即有:
0/)(=Ωdt RI d b b
其中R 为旋转矩阵。
拆解有:
0=Ω+Ωb
b b b RI I R && 0)(=Ω+Ω⨯Ωb
b b b b I I & 最后可得:
b
b b b b I I /)(Ω⨯Ω-=Ω& 加入外力矩后可得完整的欧拉方程:
)]([1b
b b b b b I M I Ω⨯Ω-=Ω-&。
因式分解欧拉公式推导

因式分解欧拉公式推导因式分解可是数学里的一个有趣“魔法”,而欧拉公式更是数学世界中的一颗璀璨明珠。
今天咱们就来聊聊因式分解欧拉公式的推导,准备好和我一起走进这个神奇的数学世界了吗?先来说说什么是因式分解。
就好比把一个大蛋糕切成小块,因式分解就是把一个复杂的多项式,分解成几个简单的式子相乘的形式。
比如说,$x^2 - 1$ 就可以分解成 $(x + 1)(x - 1)$ 。
那欧拉公式是啥呢?它长这样:$e^{ix} = \cos x + i\sin x$ 。
这里的$e$ 是自然常数,约等于 2.718 ,$i$ 是虚数单位,满足 $i^2 = -1$ 。
咱们开始推导啦!假设我们有一个复数 $z = \cos x + i\sin x$ ,对它求导,可得:$z^\prime = -\sin x + i\cos x$然后,我们把 $i$ 乘到 $z$ 上,得到:$iz = i\cos x - \sin x$嘿,您瞧瞧,这 $iz$ 不就正好是 $z^\prime$ 嘛!这就说明 $z$ 满足一个微分方程:$z^\prime = iz$ 。
解这个微分方程,您猜怎么着?它的解就是 $z = e^{ix}$ 。
所以,我们就得到了欧拉公式:$e^{ix} = \cos x + i\sin x$ 。
这推导过程是不是还挺神奇的?我想起之前给学生们讲这部分内容的时候,有个学生瞪着大眼睛,一脸迷茫地问我:“老师,这欧拉公式到底有啥用啊?”我笑着跟他说:“孩子,就好比你有一把神奇的钥匙,这欧拉公式就是能打开很多数学难题大门的那把钥匙。
”比如说,在计算一些复杂的积分时,欧拉公式就能大显身手。
还有在研究波动现象,像声波、光波的时候,欧拉公式也能帮我们更好地理解和分析。
数学的世界就是这样,一个公式的推导,可能看起来复杂,但当您真正理解了它,就会发现其中的美妙和乐趣。
就像探索一个神秘的宝藏,每一步的发现都让人兴奋不已。
希望通过这次的讲解,能让您对因式分解欧拉公式的推导有更清晰的认识,感受到数学的魅力。
【数学科普】欧拉公式的推导

【数学科普】欧拉公式的推导
欧拉公式是数学中一个非常重要的公式,它连接了三角函数和复数。
以下是欧拉公式的推导过程:
第一步,我们设z=x+yi,其中x 和y 是实数,i 是虚数单位,满足i2=−1。
第二步,根据复数的三角形式,我们可以将z 写
成ρ(cosθ+isinθ)的形式,其中ρ=x2+y2,
θ是z 在复平面上的辐角。
第三步,根据三角函数的加法公式,我们有:
cos(A+B)=cosAcosB−sinAsinB
sin(A+B)=sinAcosB+cosAsinB
第四步,令A=θ,B=2nπ(其中n 是整数),则:cos(A+B)=cos(θ+2nπ)=cosθ
sin(A+B)=sin(θ+2nπ)=sinθ
第五步,由于ρ和θ是z 的极坐标表示中的两个变量,我们可以将ρ和θ分别替换
为r 和t,其中r=∣z∣。
第六步,根据第五步的替换,我们可以得到:
z=r(cost+isint)
第七步,根据复数的模长和辐角,我们有:
r=∣z∣=x2+y2
t=arctan(xy)
第八步,将第七步中的r 和t 代入第六步中的公式,得到:
z=r(cost+isint)
综上,我们得到了欧拉公式:
z=x+yi=r(cost+isint)。
