M序列产生及其特性仿真实验报告
智能控制 M序列的产生
做一个M 序列一、实验内容:利用MATLAB 语言产生一个M 序列m 序列是最长线性反馈移位寄存器序列的简称,m 序列是由带线性反馈的移位寄存器产生的.由n 级串联的移位寄存器和和反馈逻辑线路可组成动态移位寄存器,如果反馈逻辑线路只由模2和构成,则称为线性反馈移位寄存器。
带线性反馈逻辑的移位寄存器设定初始状态后,在时钟触发下,每次移位后各级寄存器会发生变化。
其中任何一级寄存器的输出,随着时钟节拍的推移都会产生一个序列,该序列称为移位寄存器序列。
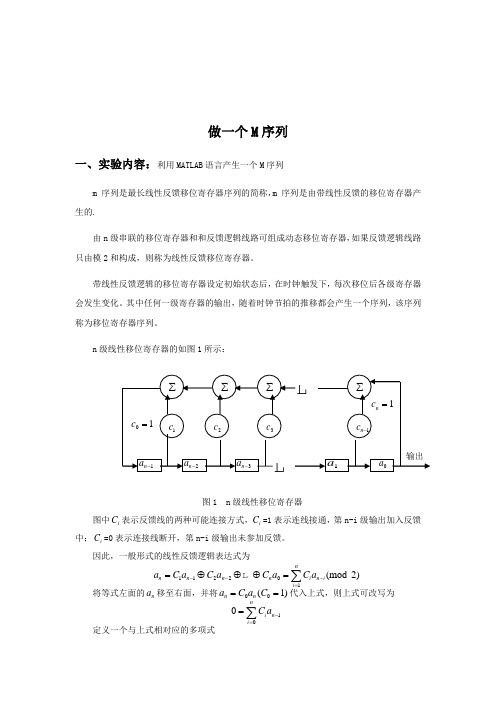
n 级线性移位寄存器的如图1所示:图1 n 级线性移位寄存器图中i C 表示反馈线的两种可能连接方式,i C =1表示连线接通,第n-i 级输出加入反馈中;i C =0表示连接线断开,第n-i 级输出未参加反馈。
因此,一般形式的线性反馈逻辑表达式为112201(mod 2)nn n n n i n i i a C a C a C a C a ---==⊕⊕⊕=∑将等式左面的n a 移至右面,并将00(1)n n a C a C ==代入上式,则上式可改写为100ni n i C a -==∑定义一个与上式相对应的多项式1n a -2n a -3n a -∑∑∑∑1c 2c 3c 1n c -01c =1n c =0a 1a 输出()ni i i F x C x ==∑其中x 的幂次表示元素的相应位置。
式称为线性反馈移位寄存器的特征多项式,特征多项式与输出序列的周期有密切关系.当F(x)满足下列三个条件时,就一定能产生m 序列:(1) F(x)是不可约的,即不能再分解多项式; (2) F(x)可整除1px +,这里21n p =-; (3) F(x)不能整除1q x +,这里q<p.满足上述条件的多项式称为本原多项式.这样产生m 序列的充要条件就变成了如何寻找本原多项式.根据m 序列的特征方程:20120()nn i n i i f x c c x c x c x c x ==++++=∑并根据其联接多项式编写Matlab 程序.二、源程序如下:%m 序列发生器及其自相关 mseq.m clear all; close all; g=19;%G=10011; state=8;%state=1000 L=1000; %m 序列产生 N=15;mq=mgen(g,state,L); %m 序列自相关ms=conv(1-2*mq,1-2*mq(15:-1:1))/N;figure(1)%subplot(222)stem(ms(15:end));axis([0 63 -0.3 1.2]);title('m序列自相关序列') figure(2)%m序列构成的信号(矩形脉冲)N_sample=8;Tc=1;dt=Tc/N_sample;t=0:dt:Tc*L-dt;gt=ones(1,N_sample);mt=sigexpand(1-2*mq,N_sample);mt=conv(mt,gt);figure(2)%subplot(221);plot(t,mt(1:length(t)));axis([0 63 -0.3 1.2]);title('m序列矩形成形信号') st=sigexpand(1-2*mq(1:15),N_sample);s=conv(st,gt);st=s(1:length(st));rt1=conv(mt,st(end:-1:1))/(N*N_sample);figure(3)%subplot(223)plot(t,rt1(length(st):length(st)+length(t)-1));axis([0 63 -0.3 1.2]);title('m序列矩形成形信号的自相关');xlabel('t');Tc=1;dt=Tc/N_sample;t=-20:dt:20;gt=sinc(t/Tc);mt=sigexpand(1-2*mq,N_sample);mt=conv(mt,gt);st2=sigexpand(1-2*mq(1:15),N_sample);s2=conv(st2,gt);st2=s2;rt2=conv(mt,st2(end:-1:1))/(N*N_sample);figure(4)%subplot(224);t1=-55+dt:dt:Tc*L-dt;plot(t,mt(1:length(t)));plot(t1,rt2(1:length(t1)));axis([0 63 -0.5 1.2]);title('m序列since成形信号的自相关');xlabel('t') 调用的子程序如下:(1)mgen.m:function [out] = mgen(g,state,N)%输入 g:m序列生成多项式(10进制输入)%state:寄存器初始状态(10进制输入)%N:输出序列长度% test g=11;state=3;N=15;gen = dec2bin(g)-48;M = length(gen);curState = dec2bin(state,M-1) - 48;for k =1:Nout(k) = curState(M-1);a = rem(sum( gen(2:end).*curState),2); curState = [a curState(1:M-2)];end(2)mseq.m%m序列发生器及其自相关 mseq.mclear all;close all;g=19;%G=10011;state=8;%state=1000L=1000;(3)sigexpand.m:function [out] = sigexpand(d,M)N = length(d);out = zeros(M,N);out(1,:)=d;out = reshape(out,1,M*N);四、仿真波形:测试结果:图2 m序列自相关序列图3 m序列矩形成形信号图4 m序列矩形成形信号的自相关图5 m序列since成形信号的自相关。
m序列实验报告
3
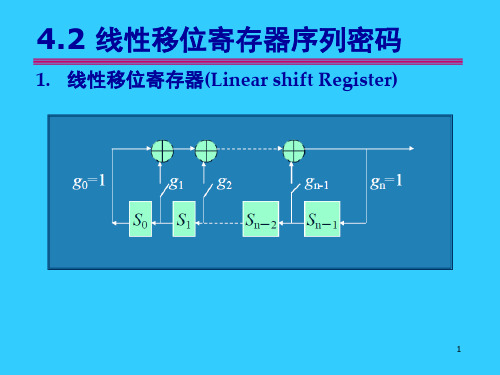
4.2 线性移位寄存器序列密码
1. 线性移位寄存器
举例:设g(x)=x4+x+1,g(x)为本原多项
式,以其为连接多项式的线性移位寄存 器的输出序列为100110101111000…, 周期为24-1=15的m序列。
0001 0010 0100 1001 0011 0110 1101 1010 0101 1011 0111 1111 1110 1100 4 1000
仅当连接多项式g(x)为本原多项式时,其线性移位 寄存器的输出为m序列。
设f(x)为GF(2)上的多项式,使f(x)|xp-1的最小正整
数p称为f(x)的周期。如果f(x)的次数为n,且其周期 2n-1,则称f(x)为本原多项式。
可以证明:对于任意的 n 级线性移位寄存器,至少
存在一种连接方式使其输出序列为m序列。
5
m <= m_data[0]; m_data[0] <= m_data[1]; m_data[1] <= m_data[2]; m_data[2] <= m_data[3]; m_data[3] <= m_data[3]^m_data[0];
6
Байду номын сангаас
4.2 线性移位寄存器序列密码
1. 线性移位寄存器(Linear shift Register)
1
4.2 线性移位寄存器序列密码
1. 线性移位寄存器(Linear shift Register)
n级线性移位寄存器最多有2n个不同的状态。
若其初始状态为零,则其后续状态恒为零;若其初 始状态不为零,则其后续状态也不为零。因此,n
级线性移位寄存器的状态周期≤2n-1,其输出序列的 周期≤2n-1。
M序列的产生和性能分析

M序列的产生和性能分析本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.MarchM序列的产生和性能分析摘要在扩频函数中,伪随机信号不但要求具有尖锐的互相关函数,互相关函数应接近于零,而且具有足够长的码周期,以确保抗侦破、抗干扰的要求;由足够多的独立地址数,以实现码分多址的要求。
M序列是伪随机序列的一种,可由m序列添加全0状态而得到。
m序列与M序列对比得出在同级移位寄存器下M序列的数量远远大于m序列数量,其可供选择序列数多,在作跳频和加密码具有极强的抗侦破能力。
本文在matlab中的Simulink下用移位寄存器建立了4级、5级、6级M序列的仿真模型,进行了仿真,画出其时域图、频谱图、互相关性图。
通过时域图和频域图可看出,经过扩频后的信号频带明显的被扩展;由M 序列互相关性图,得出M序列有较小的互相关性,较强的自相关性,但相关性略差于m序列。
最后,本文又将M序列应用于CDMA扩频通信仿真系统中,得到下列结论:当使用与扩频时相同的M序列做解扩操作与用其他序列做解扩的输出有巨大的差别。
使用相同的序列进行解扩时系统输出值很大,而使用其他序列解扩时输出值在零附近变化。
这就是扩频通信的基础。
关键词:伪随机编码, 扩频通信自相关函数,互相关函数M SEQUENCE GENERATION AND PERFORMANCE ANALYSISABSTRACTIn spread-spectrum communication, pseudo-random sequence must have high autocorrelation value, low cross correlation, long code period and lots of dependent address to satisfy code division mul tipleaccess(CDMA). M sequence is one kind of the pseudo-random sequences. It can be may obtained through adding entire 0 states to m sequence. The number of M sequence is greater than the m-sequence under the same level shift register. It may supply the more choice. The M-sequence is often applied to the frequency hopping and adds the password to have greatly strengthened anti- solves the ability.At first, M sequences which has n=4、5、7 levels of shift registers are produced under Simulink of Matlab. The t ime domain chart, the spectrograph, the mutual correlation chart are plotted. Through the time domain chart and the spectrograph, we could see how the bandwidth of the information signal is expanded. The pseudo-random symbol speed rate higher noise signal frequency spectrum is proliferated widely, the output power spectrum scope is lower. This can explain the spread-spectrum communication system principle from the frequency range. Through the M sequence’s auto correlation chart we can see that the auto correlation of M-sequence is quite good but is inferior to the m sequence. Finally, the M sequence is applied to the code division multiple access (CDMA) communication system. This is the spread-spectrum communication foundation.KEY WORDS:Pseudo-random code, auto-correlation, cross-correlation目录前言 ......................................................... 错误!未定义书签。
m序列实验报告

实验报告--m序列的产生及其特性实验班级:XXXXXX学号:XXXXX姓名:XXXXXM序列的产生及其特性实验一、实验目的掌握m序列的特性、产生方法及运用二、实验内容(1)编写MATLAB程序生成并观察m序列,识别其特征(2)观察m序列的相关特性三、实验原理m序列是有n级线性移位寄存器产生的周期为2n −1的码序列,是最长线性移位寄存器序列的简称。
码分多址系统主要采用两种长度的m序列:一种是周期为215 −1的m序列,又称短PN序列;另一种是周期为242 −1的m序列,又称为长PN码序列。
m序列主要有两个功能:①扩展调制信号的带宽到更大的传输带宽,即所谓的扩展频谱;②区分通过多址接入方式使用同一传输频带的不同用户的信号。
四、实验分析在实验中我选择的是n=6的级数,选择了103、147、155这三个反馈系数1:当反馈系数会Ci=(103)8=(1000011)2原理框图2: 当反馈系数会Ci=(147)8=(1100111)2原理框图3: 当反馈系数会Ci=(155)8=(1101101)2原理框图五、实验程序clearclose all;clcG=127;%使用多项式(103)8=(1000011)2产生第一个m序列sd1=[0 0 0 0 0 1];%寄存器的初始状态PN1=[];%第一个序列for j=1:GPN1=[PN1 sd1(1)];if sd1(1)==sd1(2)temp1=0;else temp1=1;endsd1(1)=sd1(2);sd1(2)=sd1(3);sd1(3)=sd1(4);sd1(4)=sd1(5);sd1(5)=sd1(6);sd1(6)=temp1;endsubplot(3,1,1)stem(PN1)title('使用生成多项式(103)8=(1000011)2产生第一个m序列')%使用生成多项式(147)8=(1100111)2产生第二个m序列sd2=[0 0 0 0 0 1];%寄存器的初始状态PN2=[];%第一个序列for j=1:GPN2=[PN2 sd2(1)];if sd2(1)==sd2(2)temp1=0;else temp1=1;endif sd2(5)==temp1temp2=0;else temp2=1;endif sd2(6)==temp2temp3=0;else temp3=1;endsd2(1)=sd2(2);sd2(2)=sd2(3);sd2(3)=sd2(4);sd2(4)=sd2(5);sd2(5)=sd2(6);sd2(6)=temp3;endsubplot(3,1,2)stem(PN2)title('使用生成多项式(147)8=(1100111)2产生第二个m序列')%使用生成多项式(155)8=(1101101)2产生第三个m序列sd3=[0 0 0 0 0 1];%寄存器的初始状态PN3=[];%第一个序列for j=1:GPN3=[PN3 sd3(1)];if sd3(1)==sd3(2)temp1=0;else temp1=1;endif sd3(4)==temp1temp2=0;else temp2=1;endif sd3(5)==temp2temp3=0;else temp3=1;endsd3(1)=sd3(2);sd3(2)=sd3(3);sd3(3)=sd3(4);sd3(4)=sd3(5);sd3(5)=sd3(6);sd3(6)=temp3;endsubplot(3,1,3)stem(PN3)title('使用生成多项式(155)8=(1101101)2产生第三个m序列')六、实验结果七、m序列的相关性质PN1 =0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 1 1 0 1 0 0 0 1 1 1 0 0 1 0 0 1 0 1 1 0 1 1 1 0 1 1 0 0 1 1 0 1 0 1 0 1 1 1 1 1 1PN2 =0 0 0 0 0 1 1 0 1 1 1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 1 1 1 1 1 0 1 1 0 1 0 0 0 1 0 0 0 0 1 0 1 1 0 0 1 0 1 0 1 0 0 1 0 0 1 1 1 1PN3 =0 0 0 0 0 1 0 1 1 1 1 1 1 0 0 1 0 1 0 1 0 0 0 1 1 0 0 1 1 1 1 0 1 1 1 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 0 0 1 0 0 1 0 0 0 0 1 1 11)均衡性在m序列的一个周期中,0和1的数目基本相等,1的数目比0的数目多一个,由PN1可知总共有32个1和31个0.2)游程分布M序列中取值相同的那些相继的元素合称为一个“游程”。
南昌大学M序列信号发生器实验报告

南昌大学信息工程学院M序列信号发生器课程设计班级:姓名:学号:基于MULTISIM的序列信号发生器实验目的实验要求实验元件实验原理MLTISIM知识简介MLTISIM中仿真仪器实验设计仿真分析仿真电路示波器显示输出波形实验结果实验结论实验感想一、实验目的:1、掌握M序列信号产生的基本方法2、利用MULTISIM产生M序列信号,设计电路做成M序列信号发生器3、掌握M序列 0 状态消除的基本手段二、实验要求:在MULTISIM中采用移存器自启动电路设计仿真M=31序列信号发生器电路,采用虚拟逻辑分析仪观察波形输出。
要求自制时钟脉冲信号,并能清楚地观察到M序列稳定的波形。
采用EDA进行图形仿真,硬件电路来实现。
三、实验元件函数发生器,双端输入示波器,74LS30,74LS164,74LS005V直流电源四、实验原理1、MULTISIM 软件的简介在众多的 EDA 设计和仿真软件中,MULTISIM 软件以其强大的仿真设计应用功能,在各高校电信类专业电子电路的仿真和设计中得到了较广泛的应用。
软件及其相关库包的应用对提高学生的仿真设计能力,MULTISIM更新设计理念有较大的好处。
MULTISIM(电子工作平台)软件,最突出的特点是用户界面好,各类器件和集成芯片丰富,尤其是其直观的虚拟仪表是 MULTISIM 软件的一大特色。
它采用直观的图形界面创建电路:在计算机屏幕上模仿真实实验室的工作台,绘制电路图需要的元器件、电路仿真需要的测试仪器均可直接从屏幕上选取。
MULTISIM 软件所包含的虚拟仪表有:示波器,万用表,函数发生器,波特图图示仪,失真度分析仪,频谱分析仪,逻辑分析仪,网络分析仪等。
这些仪器的使用使仿真分析的操作更符合平时实验的习惯。
电子设计自动化(EDA)技术,使得电子线路的设计人员能在计算机上完成电路的功能设计、逻辑设计、性能分析、时序测试直至印刷电路板的自动设计。
是在计算机辅助设计EDA(CAD)技术的基础上发展起来的计算机设计软件系统。
m序列产生实验

m序列产生实验一、实验目的1、m序列产生的基本方法;2、m序列0状态消除的基本手段;二、实验仪器1、JH5001型通信原理实验箱一台;2、MaxplusII开发环境一台;3、JTAG下载电缆一根;4、CPLD下载板一块;5、微机一台;6、示波器一台;三、实验原理m序列产生电路在通信电路设计中十分重要,它广泛使用在扩频通信、信号产生、仪器仪表等等电路中。
m序列有时也称伪噪声(PN)或伪随机序列,在一段周期内其自相关性类似于随机二进制序列。
尽管伪噪声序列是确定的,但其具有很多类似随机二进制序列的性质,例如0和1的数目大致相同,将序列平移后和原序列的相关性很小。
PN序列通常由序列逻辑电路产生,一般是由一系列的两状态存储器和反馈逻辑电路构成。
二进制序列在时钟脉冲的作用下在移位寄存器中移动,不同状态的输出逻辑组合起来并反馈回第一级寄存器作为输入。
当反馈由独立的“异或”门组成(通常是这种情况),此时移位寄存器称为线性PN序列发生器。
如果线性移位寄存器在某些时刻到达零状态,它会永远保持零状态不变,因此输出相应地变为全零序列。
因为n阶反馈移位寄存器只有2n-1个非零状态,所以由n阶线性寄存器生成的PN序列不会超过2n-1个。
周期为2n-1的线性反馈寄存器产生的序列称为最大长度(ML)序列——m序列。
m 序列发生器的一般组成m 序列发生器一般组成如上图所示,它用n 级移位寄存器作为主支路,用若干级模2加法器作为各级移位寄存器的抽头形成线性反馈支路。
各抽头的系数hi 称为反馈系数,它必须按照某一个n 次本原多项式:∑==ni i i x h x h 0)(中的二进制系数来取值。
在伪序列发生模块中,可以根据本原多项式的系数,…..h 8、h 7、h 6、h 5、h 4、h 3、h 2、h 1、h 0产生m 序列,这些系数可表示8进制数(1代表相连抽头进入反馈回路,0代表该抽头不进入反馈回路),如:13、23、103、203四、 课题设计要求在输入时钟256KHz 的时钟作用下,可在外部跳线器的控制下改变产生不同的m 序列,在程序中定义的几个变量为:输入: Main_CLK :输入 256KHz 主时钟 M_Sel[1..0]:选择输出不同的m 序列当 Mode[]=0:本原多项式为13(8进制表示); 当 Mode[]=1:本原多项式为23(8进制表示); 当 Mode[]=2:本原多项式为103(8进制表示); 当 Mode[]=3:本原多项式为203(8进制表示);输出: M_Out :m 序列输出 说明:1、 M_Sel[1..0]与复接模块的m_sel0、m_sel1相连; M_Out 在测试点TPB01输出;五、 实验步骤1、将JH5001二次开发光盘内的基本程序m.tdf 及其它相关程序(在光盘的“2th\student_m ”子目录下)拷入机器内。
m序列产生及其特性实验

3G移动通信实验报告实验名称:扩频码仿真学生姓名:学生学号:学生班级:所学专业:实验日期:1.实验目的1.掌握m序列的特性、产生方法及应用。
2.. 掌握Gold序列的特性、产生方法及应用。
3. 掌握Gold序列与m序列的区别。
4. 掌握Walsh码的产生原理及特性。
5. 了解它们在3G系统中的应用。
2.实验内容找一个127长度的m序列,验证其特性自相关性之+互相关性质m+m=goldwalsh 128位长度求 2个互相关自相关m+walsh 互相关自相关3.实验代码clear all;A1=[0 0 0 0 0 1 1];A1=A1';D1=[0 0 0 0 0 0 1];Dm1=zeros(1,127);A2=[0 0 0 1 0 0 1];A2=A2';D2=[0 0 0 0 0 0 1];Dm2=zeros(1,127);for i=1:127;Dm1(1,i)=D1(1,7);Dm2(1,i)=D2(1,7);Dr1=mod(D1*A1,2);Dr2=mod(D2*A2,2);for n=7:-1:2D1(1,n)=D1(1,n-1);D2(1,n)=D2(1,n-1);endD1(1,1)=Dr1;D2(1,1)=Dr2;end%m序列自相关特性验证Dm11=zeros(1,127)Dm12=zeros(1,127)Dm1n=[Dm1,Dm1,Dm1];p1=zeros(1,253);Dm11=Dm1n(1,128:254);for i=-126:1:126n1=i+128;Dm12=Dm1n(1,n1:1:(n1+126));Dm1s=mod(Dm11+Dm12,2);sum0=0;sum1=0;for i1=1:127if Dm1s(1,i1)==0 sum0=sum0+1; else sum1=sum1+1;endendp1(1,i+127)=(sum0-sum1)/127;endsubplot(4,2,1);plot(-126:1:126,p1);title('m序列自相关特性');%m序列互相关特性验证Dm21=zeros(1,127)Dm22=zeros(1,127)Dm2n=[Dm2,Dm2,Dm2];p2=zeros(1,253);pmax=0;pmax_n1=0;pmin=0;pmin_n1=0;Dm21=Dm2n(1,128:254);for i=-126:1:126n1=i+128;Dm22=Dm1n(1,n1:1:(n1+126));Dm2s=mod(Dm21+Dm22,2);sum0=0;sum1=0;for i1=1:127if Dm2s(1,i1)==0 sum0=sum0+1; else sum1=sum1+1;endendp=(sum0-sum1)/127;if p>pmaxpmax=p;pmax_n1=n1;endif p>pminpmin=p;pmin_n1=n1;endp2(1,i+127)=p;endsubplot(4,2,2);plot(-126:1:126,p2);title('m序列互相关特性');%gold序列的自相关特性Dmg11=Dm21;Dmg12=Dm1n(1,pmax_n1:1:(pmax_n1+126)); Dmg1=mod(Dmg11+Dmg12,2);Dmg1n=[Dmg1,Dmg1,Dmg1];pg1=zeros(1,253);Dmg11=Dmg1n(1,128:254);for i=-126:1:126n1=i+128;Dmg12=Dmg1n(1,n1:1:(n1+126));Dmg1s=mod(Dmg11+Dmg12,2);sum0=0;sum1=0;for i1=1:127if Dmg1s(1,i1)==0 sum0=sum0+1; else sum1=sum1+1;endendpg1(1,i+127)=(sum0-sum1)/127;endsubplot(4,2,3);plot(-126:1:126,pg1);title('gold序列自相关特性');%gold序列的互相关特性Dmg21=Dm21;Dmg22=Dm1n(1,pmin_n1:1:(pmin_n1+126)); Dmg2=mod(Dmg21+Dmg22,2);Dmg2n=[Dmg2,Dmg2,Dmg2];pg2=zeros(1,253);for i=-126:1:126n1=i+128;Dmg22=Dmg2n(1,n1:1:(n1+126));Dmg2s=mod(Dmg1+Dmg22,2);sum0=0;sum1=0;for i1=1:127if Dmg2s(1,i1)==0 sum0=sum0+1; else sum1=sum1+1;endendpg2(1,i+127)=(sum0-sum1)/127;;endsubplot(4,2,4);plot(-126:1:126,pg2);title('gold序列自相关特性');%walsh序列产生H1=0;H2=[H1,H1;H1,H1*(-1)+1];H4=[H2,H2;H2,H2*(-1)+1];H8=[H4,H4;H4,H4*(-1)+1];H16=[H8,H8;H8,H8*(-1)+1];H32=[H16,H16;H16,H16*(-1)+1];H64=[H32,H32;H32,H32*(-1)+1];H128=[H64,H64;H64,H64*(-1)+1];%walsh序列的自相关特性W11=H128(2,1:128);W1n=[W11,W11,W11]pw1=zeros(1,253);for i=-126:1:126n1=i+128;W12=W1n(1,n1:1:(n1+127));W1s=mod(W11+W12,2);sum0=0;sum1=0;for i1=1:128if W1s(1,i1)==0 sum0=sum0+1; else sum1=sum1+1;endendpw1(1,i+127)=(sum0-sum1)/128;endsubplot(4,2,5);plot(-126:1:126,pw1);title('walsh序列自相关特性');%walsh序列的互相关特性W21=W11;W22=H128(8,1:128);W2n=[W22,W22,W22];pw2=zeros(1,253);for i=-126:1:126n1=i+128;W22=W1n(1,n1:1:(n1+127));W2s=mod(W21+W22,2);sum0=0;sum1=0;for i1=1:128if W2s(1,i1)==0 sum0=sum0+1; else sum1=sum1+1;endendpw2(1,i+127)=(sum0-sum1)/128;endsubplot(4,2,6);plot(-126:1:126,pw2);title('walsh序列互相关特性');%m+walsh序列产生mw1=mod([Dm1,0]+H128(2,1:128),2);mw2=mod([Dm2,0]+H128(8,1:128),2);%mw序列的自相关特性mwa1=mw1;mwan=[mwa1,mwa1,mwa1];pmwa=zeros(1,253);for i=-126:1:126n1=i+128;mwa2=mwan(1,n1:1:(n1+127));mwas=mod(mwa1+mwa2,2);sum0=0;sum1=0;for i1=1:128if mwas(1,i1)==0 sum0=sum0+1; else sum1=sum1+1;endendpmwa(1,i+127)=(sum0-sum1)/128; endsubplot(4,2,7);plot(-126:1:126,pmwa);title('m+walsh序列自相关特性');%mw序列的互相关特性mwb1=mw1;mwb2=mw2;mwbn=[mwb2,mwb2,mwb2];pmwb=zeros(1,253);for i=-126:1:126n1=i+128;mwb2=mwbn(1,n1:1:(n1+127));mwbs=mod(mwb1+mwb2,2);sum0=0;sum1=0;for i1=1:128if mwbs(1,i1)==0 sum0=sum0+1;else sum1=sum1+1;endendpmwb(1,i+127)=(sum0-sum1)/128;endsubplot(4,2,8);plot(-126:1:126,pmwb);title('m+walsh序列互相关特性'); 4.实验结果。
m序列实验报告

实验报告--m序列的产生及其特性实验班级:XXXXXX学号:XXXXX姓名:XXXXXM序列的产生及其特性实验一、实验目的掌握m序列的特性、产生方法及运用二、实验内容(1)编写MATLAB程序生成并观察m序列,识别其特征(2)观察m序列的相关特性三、实验原理m序列是有n级线性移位寄存器产生的周期为2n −1的码序列,是最长线性移位寄存器序列的简称。
码分多址系统主要采用两种长度的m序列:一种是周期为215 −1的m序列,又称短PN序列;另一种是周期为242 −1的m序列,又称为长PN码序列。
m序列主要有两个功能:①扩展调制信号的带宽到更大的传输带宽,即所谓的扩展频谱;②区分通过多址接入方式使用同一传输频带的不同用户的信号。
四、实验分析在实验中我选择的是n=6的级数,选择了103、147、155这三个反馈系数1:当反馈系数会Ci=(103)8=(1000011)2原理框图2: 当反馈系数会Ci=(147)8=(1100111)2原理框图3: 当反馈系数会Ci=(155)8=(1101101)2原理框图五、实验程序clearclose all;clcG=127;%使用多项式(103)8=(1000011)2产生第一个m序列sd1=[0 0 0 0 0 1];%寄存器的初始状态PN1=[];%第一个序列for j=1:GPN1=[PN1 sd1(1)];if sd1(1)==sd1(2)temp1=0;else temp1=1;endsd1(1)=sd1(2);sd1(2)=sd1(3);sd1(3)=sd1(4);sd1(4)=sd1(5);sd1(5)=sd1(6);sd1(6)=temp1;endsubplot(3,1,1)stem(PN1)title('使用生成多项式(103)8=(1000011)2产生第一个m序列')%使用生成多项式(147)8=(1100111)2产生第二个m序列sd2=[0 0 0 0 0 1];%寄存器的初始状态PN2=[];%第一个序列for j=1:GPN2=[PN2 sd2(1)];if sd2(1)==sd2(2)temp1=0;else temp1=1;endif sd2(5)==temp1temp2=0;else temp2=1;endif sd2(6)==temp2temp3=0;else temp3=1;endsd2(1)=sd2(2);sd2(2)=sd2(3);sd2(3)=sd2(4);sd2(4)=sd2(5);sd2(5)=sd2(6);sd2(6)=temp3;endsubplot(3,1,2)stem(PN2)title('使用生成多项式(147)8=(1100111)2产生第二个m序列')%使用生成多项式(155)8=(1101101)2产生第三个m序列sd3=[0 0 0 0 0 1];%寄存器的初始状态PN3=[];%第一个序列for j=1:GPN3=[PN3 sd3(1)];if sd3(1)==sd3(2)temp1=0;else temp1=1;endif sd3(4)==temp1temp2=0;else temp2=1;endif sd3(5)==temp2temp3=0;else temp3=1;endsd3(1)=sd3(2);sd3(2)=sd3(3);sd3(3)=sd3(4);sd3(4)=sd3(5);sd3(5)=sd3(6);sd3(6)=temp3;endsubplot(3,1,3)stem(PN3)title('使用生成多项式(155)8=(1101101)2产生第三个m序列')六、实验结果七、m序列的相关性质PN1 =0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 1 1 0 1 0 0 0 1 1 1 0 0 1 0 0 1 0 1 1 0 1 1 1 0 1 1 0 0 1 1 0 1 0 1 0 1 1 1 1 1 1PN2 =0 0 0 0 0 1 1 0 1 1 1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 1 1 1 1 1 0 1 1 0 1 0 0 0 1 0 0 0 0 1 0 1 1 0 0 1 0 1 0 1 0 0 1 0 0 1 1 1 1PN3 =0 0 0 0 0 1 0 1 1 1 1 1 1 0 0 1 0 1 0 1 0 0 0 1 1 0 0 1 1 1 1 0 1 1 1 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 0 0 1 0 0 1 0 0 0 0 1 1 11)均衡性在m序列的一个周期中,0和1的数目基本相等,1的数目比0的数目多一个,由PN1可知总共有32个1和31个0.2)游程分布M序列中取值相同的那些相继的元素合称为一个“游程”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M序列产生及其特性仿真实验报告一、三种扩频码序列简介1.1 m序列它是由多级移位寄存器或其他延迟元件通过线性反馈产生的最长的码序列。
m序列的特性1、最长周期序列:N=2n-12、功率平衡性:‘1’的个数比‘0’的个数多13、‘0’、‘1’随机分布:近似高斯噪声4、相移不变性:任意循环移位仍是m序列,仅初相不同5、离散自相关函数:‘0’->+1,‘1’->-11.2 Gold序列Gold序列是两个等长m序列模二加的复合序列两个m序列应是“优选对”特点:1、包括两个优选对m序列,一个Gold序列族中共有2n+1个Gold序列2、Gold序列族中任一个序列的自相关旁瓣及任意两个序列的互相关峰值均不超过两个m序列优选对的互相关峰值1.3OVSF序列又叫正交可变扩频因子,系统根据扩频因子的大小给用户分配资源,数值越大,提供的带宽越小,是一个实现码分多址(CDMA)信号传输的代码,它由Walsh函数生成,OVSF码互相关为零,相互完全正交。
OVSF序列的特点1、序列之间完全正交2、极适合用于同步码分多址系统3、序列长度可变,不影响正交性,是可变速率码分系统的首选多址扩频码4、自相关性很差,需与伪随机扰码组合使用二、三种扩频码序列产生仿真一、M序列的产生代码:X1=1;X2=0;X3=1;X4=0; %移位寄存器输入Xi初T态(0101), Yi为移位寄存器各级输出m=60; %置M序列总长度for i=1:m %1#Y4=X4; Y3=X3; Y2=X2; Y1=X1;X4=Y3; X3=Y2; X2=Y1;X1=xor(Y3,Y4); %异或运算if Y4==0U(i)=-1;elseU(i)=Y4;endendM=U%绘图i1=ik=1:1:i1;plot(k,U,k,U,'rx')xlabel('k')ylabel('M序列')title('移位寄存器产生的M序列')用阶梯图产生表示:X1=1;X2=0;X3=1;X4=0; %移位寄存器输入Xi初T态(0101),Yi为移位寄存器各级输出m=60; %置M序列总长度for i=1:m %1#Y4=X4; Y3=X3; Y2=X2; Y1=X1;X4=Y3; X3=Y2; X2=Y1;X1=xor(Y3,Y4); %异或运算if Y4==0U(i)=-1;elseU(i)=Y4;endendM=U%绘图stairs(M);二、GOLD序列的产生:M序列A的生成:X1=1;X2=0;X3=1;X4=0; %移位寄存器输入Xi初T态(1010), Yi为移位寄存器各级输出m=60; %置M序列总长度for i=1:m %1#Y4=X4; Y3=X3; Y2=X2; Y1=X1;X4=Y3; X3=Y2; X2=Y1;X1=xor(Y3,Y4); %异或运算if Y4==0A(i)=0;elseA(i)=Y4;endendM=A%绘图i1=ik=1:1:i1;plot(k,A,k,A,'rx')xlabel('k')ylabel('M序列')title('移位寄存器产生的M序列')M序列B的生成:X1=0;X2=1;X3=0;X4=1; %移位寄存器输入Xi初T态(0101), Yi为移位寄存器各级输出m=60; %置M序列总长度for i=1:m %1#Y4=X4; Y3=X3; Y2=X2; Y1=X1;X4=Y3; X3=Y2; X2=Y1;X1=xor(Y3,Y4); %异或运算if Y4==0B(i)=0;elseB(i)=Y4;endendN=B%绘图i1=ik=1:1:i1;plot(k,B,k,B,'rx')xlabel('k')ylabel('M序列')title('移位寄存器产生的M序列') 生成gold序列:c=xor(A,B);stairs(c);三、OVSF序列的产生:%Function [OVSF_Codes]=OVSF_Generator(Spread_Fator,Code_Number)%Code_Number=-1 表示生成所有扩频因子=Spread_Factor的ovsf码Code_Number=-1;Spread_Fator=8;OVSF_Codes=1;if Spread_Fator==1return;endfor i=1:1:log2(Spread_Fator)Temp=OVSF_Codes;for j=1:1:size(OVSF_Codes,1)if j==1OVSF_Codes=[Temp(j,:),Temp(j,:) Temp(j,:),(-1)*Temp(j,:)];elseOVSF_Codes=[OVSF_Codes Temp(j,:),Temp(j,:) Temp(j,:),(-1)*Temp(j,:)];endendend%if Code_Number>-1% OVSF_Codes=OVSF_Codes((Code_Number+1),:);%endfigure(3)[b4,t4]=stairs([1:length(OVSF_Codes)],OVSF_Codes); plot(b4,t4);axis([0 130 -1.1 1.1]);title('OVSF序列')三、三种扩频码序列特性仿真(一)M序列自相关函数X1=1;X2=0;X3=1;X4=0; %移位寄存器输入Xi初T态(0101), Yi为移位寄存器各级输出m=2^8-1; %置M序列总长度for i=1:m %1#Y4=X4; Y3=X3; Y2=X2; Y1=X1;X4=Y3; X3=Y2; X2=Y1;X1=xor(Y3,Y4); %异或运算if Y4==0U(i)=-1;elseU(i)=Y4;y = xcorr(U);stairs(y);end互相关函数:输入两个m序列clcclear allclose allm1 = [0 1 0 0 1 1 0 0 1 0 1 0 1 0 0 1 1 0 1 1 0 0 0 1] m2 = [1 0 1 0 1 1 1 0 0 1 1 1 0 0 1 0 1 0 0 1 1 1 0 1]y = xcorr(m1,m2,'unbiased');stairs(y)(二)Gold码的自相关函数x2=[(2*c)-1];%将运行结果Gold序列c从单极性序列变为双极性序列y1=xcorr(x2,'unbiased');%求自相关性stairs(y1);gridxlabel('t')ylabel('相关性')title('移位寄存器产生的Gold序列的相关性')互相关性gold序列和m序列的互相关性y1=xcorr(c,m1,'unbiased'); stairs(y1);(三)ovsf码的互相关和自相关a=[1 -1 1 1 -1 1 -1 -1];b=[1 -1 -1 1 1 -1 -1 1];P=length(a);%求序列a的自相关函数Ra(1)=sum(a.*a);for k=1:P-1Ra(k+1)=sum(a.*circshift(a,[0,k])); end%求序列b的自相关函数Rb(1)=sum(b.*b);for k=1:P-1Rb(k+1)=sum(b.*circshift(b,[0,k])); end%求序列a和b的互相关函数Rab(1)=sum(a.*b);for k=1:P-1Rab(k+1)=sum(a.*circshift(b,[0,k])); endx=[0:P-1];figure(9)subplot(3,1,1);stem(x,Rab);ylabel('a和b的互相关函数');axis([0 P-1 -10 12]);grid;xlabel('偏移量');subplot(3,1,2);stem(x,Ra);ylabel('a自相关函数');xlabel('偏移量');%axis([0 P-1 -5 30]);subplot(3,1,3);stem(x,Rb);%plot(x,Rb)xlabel('偏移量');ylabel('b的自相关函数');四、总结一、M序列自相关函数近似于冲激函数的形状,不同序列间的互相关特性一致性不好。
二、Gold序列的自相关特性略差于m序列,但互相关特性优于m序列三、OVSF序列之间完全正交,即互相关性很好,因此极适合用于同步码分多址系统,但自相关性很差。
