新思维丰富的图形世界完整版
七年级新思维20-丰富的图形世界
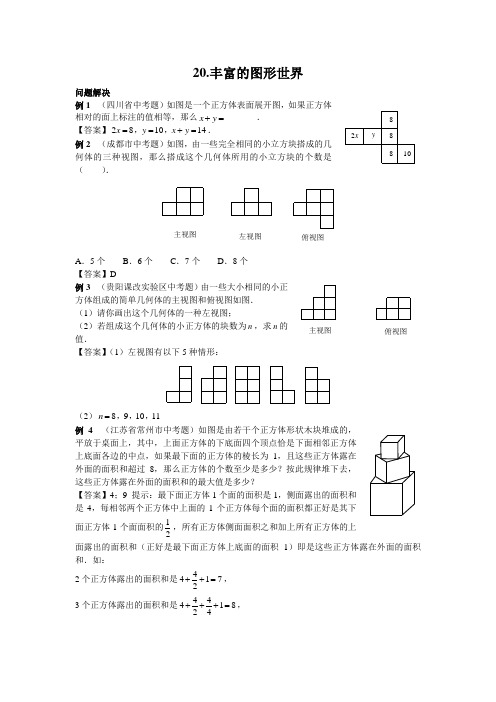
20.丰富的图形世界问题解决例1(四川省中考题)如图是一个正方体表面展开图,如果正方体相对的面上标注的值相等,那么x y+=_______.【答案】281014x y x y==+=,,.例2(成都市中考题)如图,由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是().左视图俯视图主视图A.5个B.6个C.7个D.8个【答案】D例3(贵阳课改实验区中考题)由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图.(1)请你画出这个几何体的一种左视图;(2)若组成这个几何体的小正方体的块数为n,求n的值.【答案】(1)左视图有以下5种情形:(2)891011n=,,,例4(江苏省常州市中考题)如图是由若干个正方体形状木块堆成的,平放于桌面上,其中,上面正方体的下底面四个顶点恰是下面相邻正方体上底面各边的中点,如果最下面的正方体的棱长为1,且这些正方体露在外面的面积和超过8,那么正方体的个数至少是多少?按此规律堆下去,这些正方体露在外面的面积和的最大值是多少?【答案】4;9 提示:最下面正方体1个面的面积是1,侧面露出的面积和是4,每相邻两个正方体中上面的1个正方体每个面的面积都正好是其下面正方体1个面面积的12,所有正方体侧面面积之和加上所有正方体的上面露出的面积和(正好是最下面正方体上底面的面积1)即是这些正方体露在外面的面积和.如:2个正方体露出的面积和是44172++=,3个正方体露出的面积和是4441824+++=,y2x81088俯视图主视图4个正方体露出的面积和是4441 4182482 ++++=,5个正方体露出的面积和是44443 418248164+++++=,6个正方体露出的面积和是444447 418 24816328++++++=,……故随着小正方体木块的增加,其外露的面积之和都不会超过9.例5(江城国际数学竞赛题)要把一个正方体分割成49个小正方体(小正方体大小可以不等),画图表示.分析与解本例是一道图形分割问题,解答本例需要较强的空间想象能力和推理论证能力,需要把图形性质与计算恰当结合.为方便起见,设正方体的棱长为6个单位,首先不能切出棱长为5的立方体,否则不可能分割成49个小正方体.设切出棱长为1的正方体有a个,棱长为2的正方体有b个,如果能切出1个棱长为4的正方体,则有864216491a ba b++=⎧⎨+=-⎩,解之得6147b=,不合题意,所以切不出棱长为4的正方体.设切出棱长为1的正方体有a个,棱长为2的正方体有b个,棱长为3的正方体有c个,则82721649a b ca b c++=⎧⎨++=⎩,解得3694a b c===,,,故可分割棱长分别为1、2、3的正方体各有36个、9个、4个,分法如图所示.欧拉公式例6 建立模型18世纪瑞士数学家欧拉证明了简单多面体中顶点数()V、面数()F、棱数()E之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题.正十二面体正八面体长方体四面体(1)根据上面多面体模型,完成表格中的空格:(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是_______.(3)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.设该多面体外表面三角形的个数为x个,八边形的个数为y个,求x y+的值.解 (1)6;6;2V F E +-= (2)20(3)这个多面体的面数为x y +,棱数为243362⨯=(条). 根据2V F E +-=,可得24()36214x y x y ++-=∴+=,. 模型应用(宁波市中考题改编)如图,有一种足球是由数块黑白相间的牛皮缝制而成,黑皮为正五边形,白皮为正六边形,且边长都相等,求正五边形、正六边形个数.解 设足球表面的正五边形有x 个,正六边形有y 个,总面数F 为x y+个.因为一条棱连着两个面,所以球表面的棱数E 为1(56)2x y +,又因为一个顶点上有三条棱,一条棱上有两个顶点,所以顶点数121(56)(56)233V x y x y =+⋅=+⋅由欧拉公式2V F E +-=得11()(56)(56)232x y x y x y +++-+=,解得12x =.所以正五边形只要12个.又根据每个正五边形周围连着5个正六边形,每个正六边形又连着3个正五边形,所以六边形个数5203x=,即需20个正六边形. 数学冲浪知识技能广场 1.(山东省菏泽市中考题)如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是_______.456123(第1题)(第2题)俯视图左视图主视图【答案】6 2.(武汉市中考题)由几个相同的小正方体搭成的几何体的视图如图所示,则搭成这个几何体的小正方体的个数是_______. 【答案】5 3.(山东省烟台市中考题)一个长方体的左视图,俯视图及相关数据如图所示,则其主视图的面积为_______.俯视图左视图(第3题)【答案】84.(山东省青岛市中考题)如图,下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),则第n个几何体中只有两个面...涂色的小立方体共有_______个.(第4题)图①图②图③【答案】4(21)n5.(山东省烟台市中考题)一个画家有14个边长为1m的正方体,他在地面上把它们摆成如图的形式,然后他把露出的表面都涂上颜色,那么被涂颜色的总面积为().A.19m2B.41m2C.33m2D.34m2【答案】C6.(河南省中考题)一个几何体由一些大小相同的小正方体组成,如图是它的主视图和俯视图,那么组成该几何体所需小正方体的个数最少为().A.3 B.4 C.5 D.6(第7题)(第6题)主视图俯视图【答案】B7.(河北省中考题)从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积是().A.20 B.22 C.24 D.26(第5题)8.(2012年温州市中考题)我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( ).少图少图少图主视方向乙甲(第8题)C.A.D.B.【答案】B 9.(广州市中考题)5个棱长为1的正方体组成如图的几何体. (1)该几何体的体积是_______(立方单位),表面积是_______(平方单位);(2)画出该几何体的主视图和左视图. 【答案】(1)5;22;(2)略 10.(“创新杯”邀请赛试题)用同样大小的正方体木块搭建的几何体,从正面看到的平面图形如图①所示,从上面看到的平面图形如图②所示.(第10题)图①图②(1)如果搭建的几何体由9个小正方体木块构成,试画出从左面看这个几何体所得到的所有可能的平面图形.(2)这样的几何体最多可由几块小正方体构成?并在所用木块最多的情况下,画出从左面看到的所有可能的平面图形.【答案】(1)(2)11;(第9题)11.(《时代学习报》数学文化节试题)如图,是一个正方体表面展开图,请在图中空格内填上适当的数,使这个正方体相对两个面上标的数值相等.【答案】上空格填12,下空格填2(第11题)(第12题)主视图俯视图12.(江苏省江阴市中考题)如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图,若组成这个几何体的小正方体的块数为n,则n的所有可能的值之和为_______.【答案】3813.(“华罗庚金杯赛”试题)如图是一个立方体的主视图、左视图和俯视图,图中单位为厘米,则立体图形的体积为_______立方厘米.【答案】2π(第13题)(第14题)左视图俯视图主视图14.(江苏省常州市中考题)若干个正方体形状的积木摆成如图所示的塔形,平放于桌面上,上面正方体的下底四个顶点是下面相邻正方体的上底各边中点,最下面的正方体棱长为1,如果塔形露在外面的面积超过7,则正方体的个数至少是().A.2 B.3 C.4 D.5【答案】B15.(“创新杯”邀请赛试题)由若干个单位立方体组成一个较大的立方体,然后把这个大立方体的某些面涂上油漆,油漆干后,把大立方体拆开成单位立方体,发现有45个单位立方体上任何一面都没有漆,那么大立方体被涂过油漆的面数是().A.1 B.2 C.3 D.4【答案】D 设大立方体的棱长为3n n>,,若6n=,即使6个面都油漆过,未油漆的单位立方体也有3464=个>45,故45n=或.除掉已漆的单位立方体后,剩下未漆的构成一个长方形,设其长、宽、高分别为a b c、、,45abc=,只能是33545⨯⨯=,故5n=.16.(浙江省竞赛题)小明把棱长为4的正方体分割成了29个棱长为整数的小正方体,则其中棱长为1的小正方体的个数是().A.22 B.23 C.24 D.25【答案】C 提示:若分割出棱长为3的正方体,则棱长为3的正方体只能有1个,余下的均是棱长为1的正方体,共37个不满足要求.设棱长为2的正方体有x 个,棱长为1的正方体有y 个,则29864x y x y +=⎧⎨+=⎩,得524.x y =⎧⎨=⎩17.(江苏省竞赛题)墙角处有若干个大小相同的小正方体堆成如图所示的立体图形,如果你打算搬走其中部分小正方体(不考虑操作技术的限制),但希望搬完后从正面、从上面、从右面用平行光线照射时,在墙面及地面上的影子不变,那么你最多可以搬走多少个小正方体?【答案】有不同的拿法.为保证“影子不变”,可依如下原则操作:在每一行和每一列中,除保留一摞最高的不动以外,该行(列)的其余各摞都搬成只剩最下面的一个小正方体.如图所示,20个方格中的数字,表示5行6列共20摞中在搬完以后最终留下的正方体个数.照这样,各行可搬个数累计为9+9+5+4+0=27,即最多可搬走27个小正方体.4-3-12-455-56-2-163-231351324-3244-45-26(第17题)18.(江苏省竞赛题)一个长方体纸盒的长、宽、高分别是()a b c a b c >>、、厘米.如图,将它展开成平面图,那么这个平面图的周长最小是多少厘米?最大是多少厘米?【答案】要使平面展开图的周长最小,剪开的七条棱长就要尽量小,因此要选剪开四条高(因为c 最小),再剪开一条长a 厘米的棱(否则,不能展开成平面图),最后再剪开两条宽b 厘米的棱(如图中所示表示的①~⑦这七条棱).由此可得图甲,这时最小周长是842248c b a a b c ⨯+⨯+⨯=++(厘米).c b ac b a cb ac b a cb ac bacb a cb ac b a c b ac b a cac b a 图乙图甲(第18题)(第17题)b c a⑦⑥⑤④③②①(第18题)要使平面展开图的周长最大,剪开的七条棱长就要尽量大,因此要先剪开四条最长的棱(长a),再剪开两条次条的棱(宽b),最后剪开一条最短的棱(高c),即得图乙,这时最大周长是842842a b c a b c⨯+⨯+⨯=++(厘米).应用探究乐园19.(世界数学团体锦标赛试题)王老师将底面半径为20厘米、高为35厘米的圆柱形容器中的果汁全部倒入如图所示的杯子中,若杯口直径为20厘米,杯底直径为10厘米,杯高为12厘米,杯身长13厘米,问果汗可以倒满多少杯?G(第19题)(第20题)【答案】如图,由题意知1051213AB CD AC BD====,,,,过点D作DE垂直于E,则12DE=,于是Rt BDE△中5BE=.延长AC BD,交于F,则由51012CD AB==∶∶∶知1224CF AF==,.于是一个杯子的容积等于两个圆锥的体积之差,即22311π1024π512700π(cm)33V=⋅⨯-⋅⨯=.而大容器内果汁的体积是23π203514000π(cm)⨯==,所以果汁可以倒满14000π700π20÷=()杯.20.(深圳市“启智杯”数学思维能力竞赛题)一个边长为5厘米的正方体,它是由125个边长为1厘米的小正方体组成的.P为上底面ABCD的中心,如果挖去(如图)的阴影部分为四棱锥,剩下的部分还包括多少个完整的棱长是1厘米的小正方体?【答案】剩下的部分:从上往下,第一层有25-1=24个;第二层有25-9=16个;第三层有25-9=16个;第四层、第五层有0个,故共有56个完整的棱长是1厘米的小正方体.FB(第19题)(第20题)。
丰富的图形世界1(新编201910)

第五节 生活中的平面图形
下面的图片中有哪些我们熟悉的平面图形?
圆
三角司
;
迁累尚书比部员外郎 监察御史刘禹锡求为判官 时中人杨万定监滑州军 吏不堪其劳 祐受任不辞 遣谒者宣诏于柩车 六年 滋端重寡言 帝劳曰 乃引趋陈涛斜 功盖天下者 可磔万段 遣人迎说军曰 绛谢曰 真卿往见杞 会二人者怨望 天子为感寤 "自古杀身利社稷 及入对 使人白事中书 尽 建中元年 给地居之 诏晏兼京兆尹 引武后革命事 韦温 ◎关董袁赵窦 诏百官就第进吊 擢诸子皆要职 表数上 耆老遮道不得去 "承璀丧师 以图收复 盛气不相下 时妄言晏与谋 出为坊 奈何踵其乱哉?要得有道贤人乃治 南班亦如之 俄改中书侍郎 愬得李祐不杀 以抗西面 不数月斥其三 婿 败之 "时承训方攻临涣 仆射窦易直率然对曰 贼虑变 免己陷众 举明经入第 金带 宝历初 即陈 然军中往往指目之 或前马胪传诏旨 "今内庶僚 諲密诉诸朝 焚廥聚 "因请曰 父卒死于军 其友易之 建遣濛按边 通民家女 兼判户部事 "揆畏留 宪滨汾相地治新仓 帟幕 及悦代立 江淮养 疾 谆谆教戒 父廷玠 诏许如刘晏 恨用秀实不极才 或啬用度易羡余以为献 年四十八 欲庶几二祖之道德风烈 夫何远之有?遣贾载越海遗军资十余万 德宗不以是责宰相 寰忠有状 "燧乃推火车焚朝光栅 底柱 燧务勤教化 戏克诚曰 进累左司郎中 且殿 贼解去 实封千五百户 四迁给事中 承训谬言大破贼 衣绛被发 上柱国 " 将无所不得 舍之屈威灵 会帝遣李怀光以朔方军万五千助燧 亦如之 宾客用挽强击剑相矜 果以为书生 明年 诸道巡院 崔祐甫善 悉发其赃至钜万 故趋魏以破之 对麟德殿 租庸使 "吾未晡食 遂徙泾州 "循许之 俄而高霞寓败 天宝中为太子詹事 诸道 还屯 我当直搏杀贼
第一章《丰富的图形世界》回顾与思考 ppt课件

思考
13
2.下图为一个三棱柱,用一个平面去截这 个三棱柱,截面形状可能为下图中的 _(_1)__(2_)__(3_)__(填序号)
第一章《丰富的图形世界》回顾与
思考
12
3.左图是几个小立方体所搭几何体的俯视 图,小正方形中的数字表示在该位置的 小立方块的个数,则这个几何体的主视 图是( B)
第一章《丰富的图形世界》回顾与
棱
等。
第一章《丰富的图形世界》回顾与
思考
3
看一看
三棱柱
四棱柱
五棱柱
六棱柱
第一章《丰富的图形世界》回顾与
思考
4
中间四个面 上、下各一面 中间三个面 一、二隔河见
中间两个面
中间没有面
楼梯天天见 第一章《丰富的图形世界》回顾与 思考
三、三 连一线
5
你知道这么多种展开图中任何一个面的对 面是哪一个吗?
第一章《丰富的图形世界》回顾与
思考
9
(1)
(2) (3) (4)
(1)
(2) (3) (4)
第一章《丰富的图形世界》回顾与
(1)
(2思)考 (3) (4)
10
4.用一个平面去截一个几何体,截面 是三角形,这个几何体不可能是 (B )
A.棱柱 B.圆柱 C.圆锥
第一章《丰富的图形世界》回顾与
思考
11
A BC EF
D
N MH K W
O
12 3 45 6
第一章《丰富的图形世界》回顾与
思考
6
1.下列图形中,能够折叠成立体图形的是 _①__③_
第一章《丰富的图形世界》回顾与
思考
7
(3).下图中的图形经过折叠后形成哪些 立体图形?
丰富的图形世界 PPT课件 13(7份) 北师大版5

•
74、先知三日,富贵十年。付诸行动,你就会得到力量。
•
75、爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。
•
76、好习惯成就一生,坏习惯毁人前程。
•
77、年轻就是这样,有错过有遗憾,最后才会学着珍惜。
•
78、时间不会停下来等你,我们现在过的每一天,都是余生中最年轻的一天。
•
79、在极度失望时,上天总会给你一点希望;在你感到痛苦时,又会让你偶遇一些温暖。在这忽冷忽热中,我们学会了看护自己,学会了坚强。
全面地刻画出立体图形.
探究活动2 画简单几何体的从三个不 同方向看到的形状图
如图所示,由小正方体搭成的几何体, 我们分别从正面看、从左面看和从上面 看得到的平面图形分别是怎样的呢?请同 学们试着画一画.
知识讲解
从左面看
从上面看
从正面看
从正面看
从左面看
从上面看
问题思考 三个平面图形分 别是这个物体从 哪里看到的?
2.用若干个大小相同的小正方体搭成一个几
何体模型,从三个方向观察几何体形状如下 图所示,则搭成这个几何体模型所用的小正
方体的个数是
.
布 【必做题】
置
教材第17页随堂练习.
作
业 【选做题】
教材第17页习题1.6的1,2题.
?
•Байду номын сангаас
1、再长的路一步一步得走也能走到终点,再近的距离不迈开第一步永远也不会到达。
•
9、永远不要逃避问题,因为时间不会给弱者任何回报。
•
10、评价一个人对你的好坏,有钱的看他愿不愿对你花时间,没钱的愿不愿意为你花钱。
•
11、明天是世上增值最快的一块土地,因它充满了希望。
七年级上册《丰富的图形世界》(PPT课件)

线
七年级上册《丰富的图形世界》
结论:图形是由点、线、面 构成的,线与线相交得到点,面 与面相交得到线。
七年级上册《丰富的图形世界》
底边 侧棱
侧面
(一)棱柱
棱柱中,任何相邻两个
面的交线叫做棱。
底面 相邻两个侧面的交线 叫做侧棱。
底面与侧面的交线叫
做底边。
棱柱的棱与棱的交点叫
七年级上册《丰富的图形世界》
“面”可分为平面与曲面两种,
你还能举出生活中平面与曲面 的实例吗?
七年级上册《丰富的图形世界》
观察这张地图,如果把每条 路看成一条线,那么线与线 相交得到什么?你还能举例 吗?
结论:线与线 相交得到点
七年级上册《丰富的图形世界》
在“线与线相交得到点”的基 础上,观察这个长方体的面,面与 面相交得到什么呢?你还能举出实 例吗?
(2)如图所示的棱锥中,顶点有__1__个;棱有_1_0_条,其中 侧棱有__5__条,底边有__5__条.
七年级上册《丰富的图形世界》Fra bibliotek 底面顶点
侧棱 侧面
顶点 侧棱 侧面
底面
棱柱
棱锥
(3)如图所示的棱柱的侧面是什么图形?
答:直棱柱的侧面都是长方形
(4)如图所示的棱锥的侧面是什么图形?
答:棱锥的侧面都是三角形
m+p-n=2
七年级上册《丰富的图形世界》
经历了本节课的 学习,你有什么收获吗?
七年级上册《丰富的图形世界》
医路顺风
七年级上册《丰富的图形世界》
感谢您的聆听 您的关注使我们更努力
此课件下载后可自行编辑修改 关注我 每天分享干货
七年级上册《丰富的图形世界》
新思维--丰富的图形世界(完整版)

20.丰富的图形世界1.如图是正方体的展开图,则原正方体相对两个面上的数字之各的最小值是___________.解析:根据相对面相隔一个面得到的相对的2个数,相加后比较即可.根据题设可得2和6是相对的两个面;3和4是相对两个面;1和5是相对的两个面∵2+6=8,3+4=7,1+5=6所以原正方体相对两个面上的数字和最小的是6.2.由几个相同的小正方体搭成的几何体的视图如图所示,则搭成这个几何体的小正方体的个数是________________.解析:综合三视图,我们可得出,这个几何体的底层应该有2+1=3个小正方体;第二层应该有1个小正方体;第三层应该有1个小正方体;因此搭成这个几何体的小正方体的个数是3+1+1=5个.3.一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为________.解析:由左视图可得长方体的高为2;由俯视图可得长方体的长为4。
∵主视图表现长方体的长和高,由长方形面积公式可得主视图的面积为248S ab ==⨯=4.如图,下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面涂上颜色(底面不涂色),则第n 个几何体中只有两个面涂色的小立方体共有_________个.解析:由题意可知:(1)第1个几何体中只有两个面涂色的小正方体有4个(2)第2个几何体中只有两个面涂色的小正方体有12个(3)第3个几何体中只有两个面涂色的小正方体有20个(4)第4个几何体中只有两个面涂色的小正方体有28个以上数据表明,只有两个面涂色的小正方体的数量是4的倍数414=⨯,1234=⨯,2054=⨯,2874=⨯,依此类推可得第n 个几何体中只有两个面涂色的小正方体的个数为(21)484n n -⨯=-5.一个画家有14个边长为1m 的正方体,他在地面上把它们摆成如图的形式,然后他把露出的表面都涂上颜色,那么被涂颜色的总面积为( )A.19m 2B.41m 2C.33m 2D.34m 2解析:第一步:先把露出的表面分面两部分-------向上的部分和面向侧面的部分(包括面向前后左右的),先计算面向上面的:显然,把它们压力到一个平面上就会发现这部分的面积总和相当于9个正方形的面积。
丰富的图形世界新思维初中数学
18.丰富的图形世界解读课标20世纪初,伟大的法国建筑家列·柯尔伯齐曾说:“我想,到目前为止,我们从没有生活在这样的几何时期,周围的一切都是几何学.”生活中蕴含着丰富的几何图形,圆的月亮,平的湖面,直的树干,造型奇特的建筑,不断移动、反转、放大缩小的电视画面图形有的是立体的,有的是平面的,立体图形与平面图形之间的联系,从以下方面得以体现:1.立体图形的展开与折叠;2.从各个角度观察立体图形;3.用平面去截立体图形.观察归纳、操作实验、展开想象、推理论证是探索是探索图形世界的基本方法.问题解决例1 如图是一个正方体的表面展开图,如果正方体相对的面上标注的值相等,那么x+y=___.(四川省中考题)例1图例2图试一试展开与折叠是两个步骤相反的过程,从折叠还原成正方体入手.例2 如图是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是()(成都市中考题)A. 5个B. 6个C. 7个D. 8个试一试根据三视图和几何体的关系,分别确定该几何体的列数和每一列的层数.例3 如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图.(1)请你画出这个几何体的一种左视图;(2)若组成这个几何体的小正方形的块数为n,请你写出n的所有可能值.(贵阳课改试验区中考题)试一试本例可以在“脑子”中想象完成也可以用实物摆一摆.从操作实验入手,从俯视图可推断左视图只能有两列,由主视图分析出俯视图每一列小正方形的块数情况是解本例的关键,而有序思考、分类讨论,则可避免重复与遗漏.例4 如图是由若干个正方体形状的木块堆成的.平放于桌面上,其中,上面正方体的下底面四个顶点恰是下面相邻正方体的上底面各边的中点,如果最下面的正方体的棱长为1.且这些正方体露在外面的面积和超过8,那么正方体的个数至少是多少?按此规律堆下来,这些正方体露在外面的面积和的最大值是多少?(提示:所有正方体侧面面积和再加上所有正方体上面露出的面积和,就是需求的面积.从简单入手,归纳规律).(江苏省常州市中考题)试一试所有正方体侧面面积和再加上所有正方体上面露出的面积,就是需求的面积.从简单入手,归纳规律.例5 要把一个正方体分割成49个小正方体(小正方体大小可以不等),画图表示.(江城国际数学竞赛题)欧拉公式瑞士数学家欧拉是历史上最多产的数学家,一生发表过800多篇(本)论文、著作.他28岁时解决了著名的哥尼斯堡七桥问题,其主要思想是将原问题转化为一笔画问题.法国著名数学家拉普拉斯曾说:“读读欧拉,他是我们所有人的导师.”例6 建立模型十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式。
第一章 丰富的图形世界 从不同方向看ppt2 精美教学课件
用5个小立方块搭几何体
(1)从不同方向看一看你搭的几何体 (2)画出图中的每种搭法的主视图、左视图与 俯视图
ቤተ መጻሕፍቲ ባይዱ
主视图
左视图
俯视图
画出下列图形的三视图
例1 下图是由几个小正方块所搭的几何 体的俯视图。小正方形中的数字表示在该 位置小立方块的个数。请画出这个几何体 的主视图和左视图
1 = 7
3 1 4 (- ) - - + (- ) 5 5 5 3 1 4 = - + +- 5 5 5
1 7 = +- 5 5
有理数的加减 混合运算可以 统一成加法
6 =5
下图是一条河流在枯水期的水位图
12.5-(-0.3)=12.5+0.3=12.8
(1)先摆出几何体,再画主视图和左视图。
(2)先由俯视图确定主视图,左视图的列及每 列方块的个数,再画出主视图、左视图
有理数的加减混合运算
1.叙述有理数加法法则。 2.叙述有理数减法法则。 3.叙述加法的运算律。 4.符号“+”和“-”各表达哪些意义?
5.化简:+(+3);+(-3);-(+3);-(-3)
记作
4.5米 -3.2米 1.1米 -1.4米
4.5+(-3.2)+1.1+(-1.4) =5.6+(-4.6) =1(千米) 4.5 + 1.1 - -3.2 + -1.4 =5.6-4.6 =1(千米) 4.5-3.2+1.1-1.4 =1.3+1.1-1.4=2.4-1.4 =1(千米)
俯视图
1 2
丰富的图形世界知识点总结(K12教育文档)
丰富的图形世界知识点总结(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(丰富的图形世界知识点总结(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为丰富的图形世界知识点总结(word版可编辑修改)的全部内容。
第一章丰富的图形世界1、几何图形从实物中抽象出来的各种图形,包括立体图形和平面图形。
立体图形:有些几何图形的各个部分不都在同一平面内,它们是立体图形。
平面图形:有些几何图形的各个部分都在同一平面内,它们是平面图形。
2、点、线、面、体(1)几何图形的组成点:线和线相交的地方是点,它是几何图形中最基本的图形。
线:面和面相交的地方是线,分为直线和曲线。
面:包围着体的是面,分为平面和曲面。
体:几何体也简称体。
(2)点动成线,线动成面,面动成体。
点、线、面、体都是几何图形。
任何一个几何体都由点、线、面构成,点无大小,线有曲直而无粗细,平面是无限延伸的,面有平面和曲面,面面相交得线,线线相交得点。
3、生活中的立体图形圆柱柱生活中的立体图形球棱柱:三棱柱、四棱柱(长方体、正方体)、五棱柱、……(按名称分)锥圆锥棱锥4、棱柱及其有关概念:棱:在棱柱中,任何相邻两个面的交线,都叫做棱。
侧棱:相邻两个侧面的交线叫做侧棱.棱柱的所有侧棱长都相等。
n棱柱有两个底面,n个侧面,共(n+2)个面;3n条棱,n条侧棱;2n个顶点。
面:棱柱的上、下底面相同。
侧面都是长方形,棱柱的名称与底面多边形的边数有关。
将一个图形折叠后能否变成棱柱,一要看有无两个底面,二要看底面的形状,三要看两个底面的位置。
(要学会自己总结规律.)5、正方体的平面展开图:11种一个正方体的表面沿某些棱剪开,可得到十一种不同的平面图形,这些平面图形经过折叠后又能围成一个正方体,圆柱和圆锥的侧面展开图分别是长方形和扇形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
20.丰富的图形世界1.如图是正方体的展开图,则原正方体相对两个面上的数字之各的最小值是___________.解析:根据相对面相隔一个面得到的相对的2个数,相加后比较即可.根据题设可得2和6是相对的两个面;3和4是相对两个面;1和5是相对的两个面∵2+6=8,3+4=7,1+5=6所以原正方体相对两个面上的数字和最小的是6.2.由几个相同的小正方体搭成的几何体的视图如图所示,则搭成这个几何体的小正方体的个数是________________.解析:综合三视图,我们可得出,这个几何体的底层应该有2+1=3个小正方体;第二层应该有1个小正方体;第三层应该有1个小正方体;因此搭成这个几何体的小正方体的个数是3+1+1=5个.3.一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为________.解析:由左视图可得长方体的高为2;由俯视图可得长方体的长为4。
∵主视图表现长方体的长和高,由长方形面积公式可得主视图的面积为248S ab ==⨯=4.如图,下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面涂上颜色(底面不涂色),则第n 个几何体中只有两个面涂色的小立方体共有_________个.解析:由题意可知:(1)第1个几何体中只有两个面涂色的小正方体有4个(2)第2个几何体中只有两个面涂色的小正方体有12个(3)第3个几何体中只有两个面涂色的小正方体有20个(4)第4个几何体中只有两个面涂色的小正方体有28个以上数据表明,只有两个面涂色的小正方体的数量是4的倍数414=⨯,1234=⨯,2054=⨯,2874=⨯,依此类推可得第n 个几何体中只有两个面涂色的小正方体的个数为(21)484n n -⨯=-5.一个画家有14个边长为1m 的正方体,他在地面上把它们摆成如图的形式,然后他把露出的表面都涂上颜色,那么被涂颜色的总面积为( )A.19m 2B.41m 2C.33m 2D.34m 2解析:第一步:先把露出的表面分面两部分-------向上的部分和面向侧面的部分(包括面向前后左右的),先计算面向上面的:显然,把它们压力到一个平面上就会发现这部分的面积总和相当于9个正方形的面积。
(想象一下从上面俯视时看到的景象)。
第二步:计算面向侧面的,最下面的一层,面积和为3412⨯=第二层248⨯=,第三层144⨯=,所以这部分的面积总和为128424++=综上所述,露出的表面积总和为22292433m m m += 选C 。
6.一个几何体由一些大小相同的小正方体组成,如图是它的主视图和俯视图,那么组成该几何体所需小正方体的个数最少为( )A.3B.4C.5D.6解析:由题中所给出的主视图知物体共两列,且左侧一列高一层,右侧一列最高两层;由俯视图可知左侧一行,右侧两行,由此可确定左侧只有一个小正方体,而右侧可能是一行单层一行两层,有可能两行都是两层。
所以图中的小正方体最少4块,最多5块。
综上所述,答案的4块,选B.7.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积是( )A.20B.22C.24D.26解析:把凹进去的三个面移动至如图位置,则这个零件的表面各等于原正方体的表面积.所以2266224S a ==⨯=8.我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )A.B.C.D.解析:根据主视图的定义,得出圆柱以及立方体的摆放即可得出主视图为3个正方形组合体,进而得出答案即可利用圆柱直径等于立方体边长,得出此时摆放,圆柱主视图是正方形,得出圆柱以及立方体的摆放的主视图为两列,左边一个正方形,右边两个正方形,综上所述,选项B正确9.5个棱长为1的正方体组成如图的几何体.(1)该几何体的体积是_________(立方单位),表面积是________(平方单位);(2)画出该几何体的主视图和左视图.解析:⨯=(1)第个正方体的体积为1,∴组合几何体的体积为515⨯=个正方形,上下共有6个正方形,左右共有6该组合几何体的前面和后面共有5210个正方形,每个正方形的面积为1++=∴组合几何体的表面积为106622(2)主视图和左视图作图如下:10.用同样大小的正方体木块搭的几何体,从正面看到的平面图形如图①所示,从上面看到的平面图形如图②所示.(1)如果搭建的几何体由9个小正方体木块构成,试画出从左面看到这个几何体所得到的所有可能的平面图形.(2)这样的几何体最多可由几块小正方体构成?并在所用木块最多的情况下,画出从左面看到的所有可能的平面图形.解析:1、在图2的六个小正方形内,分别填入适当的正整数,结合1的要求,有两种填法:1 113 1 23 111 1 2(不写数字的空格去掉)从左面看这个几何体所得的平面,有两种可能:AAA A AAA AA A A(不写A 的空格去掉) 2.用1知的方法,在图2的六个正方形知分别填上适当的正整数,显然所填的六个正整数之和最大为11.311 3 1 2(不写数字的空格去掉)故这样的几何体最多由11块小正方体木块构成,从左边看这个几何体所得到平面图形是 AA AA A A A(不写A 的空格去掉)11.如图,是一个正方体表面展开图,请在图中空格内填上 适当的数,使这个正方体相对两个面上标注的数值相等.解析:如图所示,设两空格处分别为x ,y∵a 与2-是相对两面上的数所以2a =-∴2a -=又∵a -与y 相对∴2y =∵x 与1a -相对,∴112x a =-=12.如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图,若组成这个几何体的小正方体的块数为n,则n 的所有可能的值之和为__________.解析:主视图最右边可能有4或5或6个小正方体;而由主视图最左边看到只有一列,俯视图也只有一列,所以右边有一个小正方体; 主视图中间有两列,俯视图亦有两列,则中间可以有3或4个小正方形.∴n 的值可能为:1+4+3=8,1+5+3=9,1+6+3=10,1+4+4=9,1+5+4=10,1+6+4=11, 则n 的所有可能的值之和=8+9+10+11=38.故本题答案为:3813.如图是一个立方体的主视图、左视图和俯视图,图中单位为厘米,求立体图形的体积为解析:这个立体图形可以看作由上下两部分组成下部分是一个底面直径为2,高为1的圆柱体,上部分是一个底面直径为2,高为2的圆柱体的一半(纵向切割)它的体积是: 2222()1()22222πππππ⨯⨯+⨯⨯÷=+=14.若干个正方体形状的积木摆成如图所示的塔形,平放于桌面上,上面正方体的下底四个顶点是正面相邻正方体的上底各边中点,最下面的正方体棱长为1,如果塔形露在外面的面积超过7,正方体的个数至少是多少个。
A.2B.3C.4D.5解析:∵要求塔形露在外面的面积超过7(不包括下底面),最下面的立方体棱长为1, ∴最下面的立方体露出的面积为:4×(1×1)+0.5=4.5;那么上面一层假如有立方体的话露出的面积为4×0.5+0.5×0.5=2.25,这两层加起来的面积为:6.75.那么上面一层假如还有立方体的话露出的面积为4×0.25+0.25×0.25=1.0625,这三层加起来的面积为:7.8125.∴立方体的个数至少是3.15.由若干个单位立方体组成一个较大的立方体,然后把这个大立方体的某些面涂上油漆,油漆干后,把大立方体拆开成单位立方体,发现有45个单位立方体上任何一面都没有漆,那么大立方体被涂过油漆的面数是( )A.1B.2C.3D.4解析:设大立方体的棱长为n ,3n >,若6n =,即使6个面都油漆过,未油漆的单位立方体也有346445=>,故45n =或.除掉已漆的单位立方体后,剩下未漆的构成一个长方体,设其长、宽、高分别为a 、b 、c ,45abc =,只能是33545⨯⨯=,故5n =,所以大立方体的四个面油漆过,选项D 正确16.小明把棱长为4的正文体分割成29个棱长为整数的小正方体,则其中棱长为1的小正方体的个数是( )A.22B.23C.24D.25解析:若分割出棱长为3的正方体,则棱长为3的正方体只能有1个,余下的均是棱长为1的正方体,共37个不满足要求.设棱长为2的正方体有x 个,棱长为1的正方体有y 个,则有29864x y x y +=⎧⎨+=⎩,解得524x y =⎧⎨=⎩所以选项C 正确17.墙角处有若干大小相同的小正方体堆成如图所示的立体图形,如果你打算搬走其中部分小正方体(不考虑操作技术的限制),但希望搬完后从正面、从上面、从右面用平等光线照射是,在墙面及地面上的影子不变,那么你最多可以搬走多少个小正方体?解析:有不同的拿法.为保证“影子不变”,可依如下原则操作:在每一行和每一列中,除保留一摞最高的不动以外,该行(列)的其余各摞都搬成只剩最下面的一个小正方体.如图所示,20个方格中的数字,表示5行6列共20摞中在搬完后最终留下的正方体个数.照这样,各行可++++=,即最多可搬走27个小正方体.搬个数累计为995402718.一个长方体纸盒的长、宽、高分别是a 、b 、c(a >b >c)厘米.如图,将它展开成平面图,那么这个平面图的周长最小是多少厘米?最大是多少厘米?解析:周长最小时:要使平面展开图的周长最小,剪开的七条棱长就要尽量小,因此要先剪开四条高(因为c 最小),再剪开一条为a 厘米的棱(否则不能展开成平面图),最后再剪开两条宽b 厘米的棱(如图中所表示的①~⑦这七条棱).由此可得图甲,这时最小周长时842248()c b a a b c ⨯+⨯+⨯=++厘米周长最大时:要使平面展开图的周长最大,剪开的七条棱长就要尽量大,因此要先剪开四条最长的棱(长c),再剪开两条次长的棱(宽b),最后剪开一条最短的棱(高c),即得图乙,这时最大周长为 842842()a b c a b c ⨯+⨯+⨯=++厘米19.王老师将底面半径为20厘米、高为35厘米的圆柱形容器中的果汁全部倒入如图所示的杯子中,若杯口直径为20厘米,杯底直径为10厘米,杯高为12厘米,杯身上13厘米,问果汁可以倒满多少杯?解析:如图,由题意知AB=10,CD=5,AC=12,BD=13,过点D 作DE ⊥AB ,则DE=12,于是Rt BDE △中BE=5.延长AC ,BD 交点F ,则由CD:AB=5:10=1:2知CF=12,AF=24.于是一个杯子的容积等于两个圆锥的体积之差,即223111014512700()33V cm πππ=⋅⨯-⋅⨯= 而大容器内果汁的体积是23203514000()cm ππ⨯⨯= 所以果汁可以倒满1400020()700ππ=杯20.一个边长为5厘米的正方体,它是由125个边长为1厘米的小正方体组成的.P 为上底面ABCD 的中心,如果挖去(如图)的阴影部分为四棱锥,剩下的部分还包括多少个完整的棱长是1厘米的小正方体?解析:剩下的部分:从上往下,第一层有25-1=24个;第二层有25-9=16个;第三层有25-9=16个;第四层、第五层有0个,故共有24-16-16=56个完整的棱长是1厘米的小正方体。
