1第5章刚体的定轴转动和转动定律
合集下载
大学物理 第5章刚体定轴转动

赵 承 均
转动平面 某质点所在的圆周平面,称为转动平面。
参考线
转心 矢径
转动平面内任一过转轴的直线,如选 x 轴。
某质点所在的轨迹圆的圆心,称为转心。 某质点对其转心的位矢,称为该质点的矢径。
第一篇
力学
重 大 数 理 学 院
显然:转动刚体内所有点有相同的角量,故用角量描述刚体 的转动更方便,只需确定转动平面内任一点的角量即可。 1.角坐标— 描写刚体转动位臵的物理量。 角坐标 转动平面内刚体上任一点 P 到转轴 O 点的连线与 参考线间的夹角 。
赵 承 均
第二类问题:已知J和力矩M:求出运动情况和 b及 F 。
第三类问题:已知运动情况和力矩M,求刚体转动惯量 J 。
第一篇
力学
重 大 数 理 学 院
第一类问题:已知运动情况和 J ,确定运动学和动力学的联 系 例 :长为 l,质量为 m 的细杆,初始时的角速 度为 ωo ,由于细杆与 桌面的摩擦,经过时间 t 后杆静止,求摩擦力 矩 Mf 。
Fi cos i Fi cos i mi ain mi ri 2 法向:
e i
第一篇
力学
重 大 数 理 学 院
由于法向力的作用线穿过转轴,其力矩为零。可在切向 方程两边乘以 ri ,得到:
Fi e ri sin i Fi i r i sin i mi ri 2
4.角加速度— 描写角速度变化快慢和方向的物理量。 ⑴ 平均角加速度 t
即:刚体的角速度变化与发生变化所用的时间之比。
赵 承 均
⑵ 角加速度 ①用平均角加速度代替变化的角加速度; ②令 t 0 取极限;
d d lim 2 t 0 t dt dt
5.2 刚体定轴转动定律
因为各质元角动量方向相同, 因为各质元角动量方向相同, 所以合矢量的大小就是分矢量 大小的直接相加 因为 L = L = rmυ S
mi
α r P
r
i
i i
υi = riω
L = ω(∑ mi ri2 )
i
定义刚体对定轴 定义刚体对定轴 J = 的转动惯量
3
∑m r
i
2
i i
r r L = Jω
对于转轴z,
r ri α
A
r F τ
r r r M z = ri × F⊥
不产生对z轴的力矩
α
Fn
r r F ⊥
M z = ri F⊥ sin α = F⊥ h
F ——平行于z轴 平行于 //
在转动平面内 F ——在转动平面内 产生对z轴的力矩 ⊥
r rz
O
r r
α
r F ⊥
y
x
力对任意点的力矩, 力对任意点的力矩,在通过该点的任一轴上的投影 等于该力对该轴的力矩
2 第5章 刚体的定轴转动
质点对定点 的动量矩 角动量) 质点对定点o的动量矩 角动量 定点 的动量矩(角动量
r r r r r L = r × P = r × mv = Lx x + Ly y + Lz z
2. 任一质量元的定轴角动量大小为
对z轴的 轴的 动量矩
r LO
Liz = ri miυi
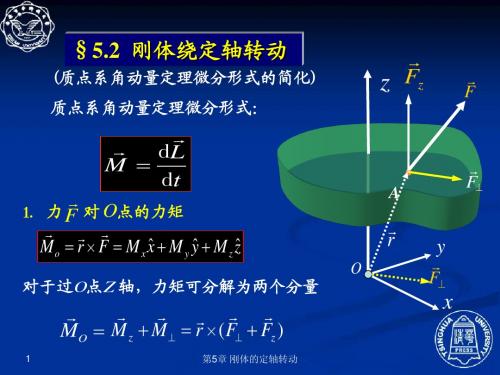
§5.2 刚体绕定轴转动
(质点系角动量定理微分形式的简化) 质点系角动量定理微分形式的简化) 质点系角动量定理微分形式: 质点系角动量定理微分形式:
r z Fz
r F
r r dL M = dt
r 1. 力 F 对 O点的力矩
mi
α r P
r
i
i i
υi = riω
L = ω(∑ mi ri2 )
i
定义刚体对定轴 定义刚体对定轴 J = 的转动惯量
3
∑m r
i
2
i i
r r L = Jω
对于转轴z,
r ri α
A
r F τ
r r r M z = ri × F⊥
不产生对z轴的力矩
α
Fn
r r F ⊥
M z = ri F⊥ sin α = F⊥ h
F ——平行于z轴 平行于 //
在转动平面内 F ——在转动平面内 产生对z轴的力矩 ⊥
r rz
O
r r
α
r F ⊥
y
x
力对任意点的力矩, 力对任意点的力矩,在通过该点的任一轴上的投影 等于该力对该轴的力矩
2 第5章 刚体的定轴转动
质点对定点 的动量矩 角动量) 质点对定点o的动量矩 角动量 定点 的动量矩(角动量
r r r r r L = r × P = r × mv = Lx x + Ly y + Lz z
2. 任一质量元的定轴角动量大小为
对z轴的 轴的 动量矩
r LO
Liz = ri miυi
§5.2 刚体绕定轴转动
(质点系角动量定理微分形式的简化) 质点系角动量定理微分形式的简化) 质点系角动量定理微分形式: 质点系角动量定理微分形式:
r z Fz
r F
r r dL M = dt
r 1. 力 F 对 O点的力矩
第5章 刚体的定轴转动

(1) 式中n表示转动方向,ω表示角速度的大小。 2、角加速度矢量
角加速度矢量定义为
(2) 显然,若角加速度矢量的方向与角速度矢量的方向相同,见下图 (a),则角速度在增加;反之,若角加速度与角速度的方向相反,见 下图(b),则角速度在减小。从图(a)、(b)中不难验证,角加速 度矢量的方向与直观转动的加速方向也构成右手螺旋关系。既当四个手 指指向直观的加速方向时,大姆指所指向的方向即为角加速度矢量的方 向。
(4) 其中
为各分力的力矩,证毕。 由于作用力和反作用力是成对出现的,所以它们的力矩也成对出
现。由于作用力与反用力的大小相等,方向相反且在同一直线上因而有 相同的力臂,见下图,所以作用力矩和反作用力矩也是大小相等,方向 相反,其和为零。
(5)
作用力矩和反作用力矩 二、刚体对定轴的角动量
在刚体的定轴转动中,刚体对定轴的角动量是一个很重要的物理 量,在很多问题的分析中都要用到这个概念,下面我们来讨论这个问 题。 刚体绕定轴转动时,它的每一个质点都在与轴垂直的平面上运动。下面 我们先分析质点对定轴的角动量,而且只考虑质点在轴的垂面上运动的 情况。如下图所示,有一质点在z轴的垂面M内运动,质点的质量为m, 对z轴(即对质点转心)的矢径为r,速度为v,动量p=mv。如同在角动 量知识点中讨论的一样,我们定义质点对定轴的角动量为
第5章 刚体的定轴转动 ◆ 本章学习目标 理解:刚体、刚体转动、转动惯量的概念;刚体定轴转动定律及角动量守
恒定律。 掌握:转动惯量,转动中的功和能的计算;用刚体定轴转动定律及角动量
守恒定律求解定轴转动问题的基本方法。 ◆ 本章教学内容
1.刚体的运动 2.刚体定轴转动定律 3.转动惯量的计算 4.刚体定轴转动定律的应用 5.转动中的功和能 6.对定轴的角动量守恒 ◆ 本章重点 刚体转动惯量的物理意义以及常见刚体绕常见轴的转动惯量; 力矩计算、转动定律的应用; 刚体转动动能、转动时的角动量的计算。 ◆ 本章难点 力矩计算、刚体转动过程中守恒的判断及其准确计算。
角加速度矢量定义为
(2) 显然,若角加速度矢量的方向与角速度矢量的方向相同,见下图 (a),则角速度在增加;反之,若角加速度与角速度的方向相反,见 下图(b),则角速度在减小。从图(a)、(b)中不难验证,角加速 度矢量的方向与直观转动的加速方向也构成右手螺旋关系。既当四个手 指指向直观的加速方向时,大姆指所指向的方向即为角加速度矢量的方 向。
(4) 其中
为各分力的力矩,证毕。 由于作用力和反作用力是成对出现的,所以它们的力矩也成对出
现。由于作用力与反用力的大小相等,方向相反且在同一直线上因而有 相同的力臂,见下图,所以作用力矩和反作用力矩也是大小相等,方向 相反,其和为零。
(5)
作用力矩和反作用力矩 二、刚体对定轴的角动量
在刚体的定轴转动中,刚体对定轴的角动量是一个很重要的物理 量,在很多问题的分析中都要用到这个概念,下面我们来讨论这个问 题。 刚体绕定轴转动时,它的每一个质点都在与轴垂直的平面上运动。下面 我们先分析质点对定轴的角动量,而且只考虑质点在轴的垂面上运动的 情况。如下图所示,有一质点在z轴的垂面M内运动,质点的质量为m, 对z轴(即对质点转心)的矢径为r,速度为v,动量p=mv。如同在角动 量知识点中讨论的一样,我们定义质点对定轴的角动量为
第5章 刚体的定轴转动 ◆ 本章学习目标 理解:刚体、刚体转动、转动惯量的概念;刚体定轴转动定律及角动量守
恒定律。 掌握:转动惯量,转动中的功和能的计算;用刚体定轴转动定律及角动量
守恒定律求解定轴转动问题的基本方法。 ◆ 本章教学内容
1.刚体的运动 2.刚体定轴转动定律 3.转动惯量的计算 4.刚体定轴转动定律的应用 5.转动中的功和能 6.对定轴的角动量守恒 ◆ 本章重点 刚体转动惯量的物理意义以及常见刚体绕常见轴的转动惯量; 力矩计算、转动定律的应用; 刚体转动动能、转动时的角动量的计算。 ◆ 本章难点 力矩计算、刚体转动过程中守恒的判断及其准确计算。
大学物理第5章刚体的定轴转动

d ctdt
对上式两边积分得
d c td t
0 0
t
1 2 ct 2
2 2 600π π 3 rad s 由给定条件, c 2 t 300 2 75
d π 2 由角速度的定义,则任意 t 时刻的角速度可写为: d t 150
得到: 转子转数:
A M d E K
a b
动能定理
动量定理
A F ds E K
动能定理 角动量定理 角动量 守恒
t 0Fdt P
t
动量守恒
F 0, P 0
t 0 M z dt Lz
t
M 0, L 0
§5.1 刚体、刚体运动
一、一般运动 二、刚体的定轴转动 三、解决刚体动力学问题的一般方法
基本方法: 加
质点系运动定理 刚体特性 平动:动量定理
刚体定轴转动的 动能定理 角动量定理
F mac
可以解决刚体的一般运动(平动加转动)
一、一般运动
1. 刚体 特殊的质点系, 形状和体积不变化 —— 理想化模型 在力作用下,组成物体的所有质点间的距离始终保持不变 2. 自由度 确定物体的位置所需要的独立坐标数 —— 物体的自由度数 z
刚体平面运动可看做刚体的平动与定轴转动的合成。 例如:车轮的滚动可以看成车轮随轮 轴的平动与绕轮轴的转动的组合。 描述刚体平面运动的自由度:3个
定点转动 刚体运动时,刚体上的一点固定不动,刚体绕过定点的一 瞬时转轴的转动,称作定点转动。
描述定点转动的自由度:3个
刚体的一般运动 质心的平动
+
绕质心的转动
z
描述刚体绕定轴转动的角量: 角坐标
[理学]第5章-刚体的定轴转动
![[理学]第5章-刚体的定轴转动](https://img.taocdn.com/s3/m/9cd5eb80c0c708a1284ac850ad02de80d5d8065b.png)
(2)刚体可以看作是由许多质点组成,每一个 质点叫做刚体的一个质元,刚体这个质点系 的特点是,在外力作用下各质元之间的相对 位置保持不变。
质元
Δmi
Δmj rij
2. 刚体的运动形式:
⑴平动: 在描述刚体的平动时,可以用一点的运动
来代表,通常就用刚体的质心的运动来代 表整个刚体的平动。
转轴
⑵转动: 转动是刚体的基本运动形式之一。 刚体转动时各质元均做圆周运动,而且各
列方程
mg-T2 = ma2 T1-mg = ma1
T2 (2r)-T1r = 9mr2 / 2 2r = a2 r = a1
2r T2 T2 a2 m mg
r m 2m T1
T1 m a1
mg
解联立方程,得: 2g
19r
练习1:如图所示,有两个质量分别为 M1 、M2 ,对转轴的转动惯
量分别为
Z’ Z
C d
J = Jc+ m d 2
例: 如图一质量为M 长为l的匀质细杆,中间和右端各有一 质量皆为m的刚性小球,该系统可绕其左端且与杆垂直 的水平轴转动,若将该杆置于水平位置后由静止释放, 求:杆转到与水平方向成θ角时,杆的角加速度是多少?
解:设转轴垂直向里为正,系统对该转轴的转动惯量为
J
第五章 刚体的定轴转动
转轴
复习
一、力矩
M rF
1. 大小:M = rFsinθ
Z F// F
O r F⊥ p
2.方向:由右手螺旋定则确定。
注意:上式中F指的是与转轴垂直平面(转动平面)上的力,
若F不再该平面上,可将F分解为垂直于转轴和平行于转
轴的两个分力,力矩是指的是在转动平面内力F⊥(平行
大学物理第5章刚体的定轴转动

Jz Jx Jy
Jc J mC
质心
d
yi
xi
ri
y
x
Δmi
1 2
mR
2
R
1 4
mR
2
6
第六页,编辑于星期六:二十一点 四十五分。
常用的转动惯量
细杆:
J过中点垂直于杆
1 12
mL2
J过一端垂直于杆
1 3
mL2
圆柱体:
J对称轴
1 2
mR 2
薄球壳:
J 直径
2 3
mR
2
球体:
J 直径
2 5
mR
2
7
第七页,编辑于星期六:二十一点 四十五分。
d L Lsin dΘ M d t
旋进角速度: Ω dΘ
dt
Ω d
dL
Lsin L
Ω M M
Lsin J sin
O
当 90 时 ,Ω M J
Ω
1
,
Ω
演示 车轮旋进(KL023) TV 旋进防止炮弹翻转(注2)
M外z 0 ,则 J z const .
大小不变 正、负不变
对刚体系, M外z = 0 时, Jizi const.,
此时角动量可在系统内部各刚体间传递,
而却保持刚体系对转轴的总角动量不变。
演示 角动量守恒:茹科夫斯基转椅(KL016)
转台车轮 (KL017)
陀螺仪(KL029)
30
第三十页,编辑于星期六:二十一点 四十五分。
5、车轮进动
2
第二页,编辑于星期六:二十一点 四十五分。
§5.1 刚体的定轴转动定律
z
Mz
dLz dt
第五章 刚体的定轴转动

单位: 单位:rad / s 角速度
刚体定轴转动
ω
v 的方向按右手螺旋法则确定. 的方向按右手螺旋法则确定.
在定轴转动中, 在定轴转动中,角速度的方向 沿转轴方向. 沿转轴方向.
角加速度α 角加速度
v ω
2
ω dω d θ = = 2 α = lim t →0 t dt dt
单位: 单位:rad /s 2 角加速度也是矢量, 角加速度也是矢量,方向与角速度增量 的极限方向相同,在定轴转动中, 与 同向 的极限方向相同,在定轴转动中,α与ω同向 或反向. 或反向. 刚体的转动其转轴是可以改变的, 刚体的转动其转轴是可以改变的,为反映瞬时轴的方 向及其变化情况,引入角速度矢量和角加速度矢量. 向及其变化情况,引入角速度矢量和角加速度矢量. 注意 退化为代数量. :定轴转动时, ω,α退化为代数量. 定轴转动时, 退化为代数量
刚体的一般运动都可认为是平动和转动的结合. 刚体的一般运动都可认为是平动和转动的结合.
1. 用角量描述转动 (1) 角位移 θ : ) 时间内刚体转动角度. 在 t 时间内刚体转动角度. 单位: 单位:rad (2)角速度 ω : )
z θ
B A
θ dθ ω = lim = t →0 t dt
●
r2
转动惯量的定义: 转动惯量的定义:
J = ∑mi ri
2
对质量连续分布的刚体, 对质量连续分布的刚体,上式可写成积分形式
J = ∫ r dm
2
dm—质元的质量 质元的质量 r—质元到转轴的距离 质元到转轴的距离
线分布 dm = λdx 面分布 dm = σds 体分布 dm = ρdV
λ 是质量的线密度
F iz
ri = roi sinθ
刚体定轴转动
ω
v 的方向按右手螺旋法则确定. 的方向按右手螺旋法则确定.
在定轴转动中, 在定轴转动中,角速度的方向 沿转轴方向. 沿转轴方向.
角加速度α 角加速度
v ω
2
ω dω d θ = = 2 α = lim t →0 t dt dt
单位: 单位:rad /s 2 角加速度也是矢量, 角加速度也是矢量,方向与角速度增量 的极限方向相同,在定轴转动中, 与 同向 的极限方向相同,在定轴转动中,α与ω同向 或反向. 或反向. 刚体的转动其转轴是可以改变的, 刚体的转动其转轴是可以改变的,为反映瞬时轴的方 向及其变化情况,引入角速度矢量和角加速度矢量. 向及其变化情况,引入角速度矢量和角加速度矢量. 注意 退化为代数量. :定轴转动时, ω,α退化为代数量. 定轴转动时, 退化为代数量
刚体的一般运动都可认为是平动和转动的结合. 刚体的一般运动都可认为是平动和转动的结合.
1. 用角量描述转动 (1) 角位移 θ : ) 时间内刚体转动角度. 在 t 时间内刚体转动角度. 单位: 单位:rad (2)角速度 ω : )
z θ
B A
θ dθ ω = lim = t →0 t dt
●
r2
转动惯量的定义: 转动惯量的定义:
J = ∑mi ri
2
对质量连续分布的刚体, 对质量连续分布的刚体,上式可写成积分形式
J = ∫ r dm
2
dm—质元的质量 质元的质量 r—质元到转轴的距离 质元到转轴的距离
线分布 dm = λdx 面分布 dm = σds 体分布 dm = ρdV
λ 是质量的线密度
F iz
ri = roi sinθ
第5章 刚体的定轴转动

m J 1 mR 2 2 2 pR l
可见,转动惯量与l无关。所以,实心圆柱对其轴的 转动惯量也是mR2/2。
例3、求质量为m,长为L的均匀细棒对下面三 种转轴的转动惯量: 转轴通过棒的中心O并与棒垂直
转轴通过棒的一端B并与棒垂直 转轴通过棒上距质心为h的一点A并与棒垂直 A h
如图建立坐标,以物体初始位置为势能零 点。根据机械能守恒:
y
1 J w 2 1 mv2 mg h 0 2 2
滑轮转动动能 物体动能
物体势能
mg
O
1 MR2 , w v 代入可解得: 将J 2 R
物体的速度:
滑轮角速度:
4mgh v 2m M
v 4mgh R w 2m M R
力矩的功反映力矩对空间的积累作用,力矩越大,在 空间转过的角度越大,作的功就越大。这种力矩对空 间的积累作用的规律是什么呢?
2、定轴转动的动能定理
质点系动能定理 A外 A EKB EKA 也适用于刚体。 内 由于刚体内质点的间距不变,一切内力作的功都为零。 而对于定轴转动而言,外力作的功总表现为外力矩作 的功,故有: 1 2 1 2
dA Md
力对转动刚体作的元功 等于相应的力矩和角位 移的乘积。
在一微小过程中 力矩作的功
dA Md (1)
在考虑一个有限过程,设 在力矩作用下,刚体的角 位置由 1 2 则力矩的 功:
2 1
X X
1
w2 w1
O
2
M
M
A dA Md (2)
B
O质
B
A
h L
O质
dm
X
x
dx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
得到:
F r sin φ (Δm r
i 1 i i i i 1
N
N
2
i i
)α
上式左端为刚体所受外力的合外力矩,以M 表 示;右端求和符号内的量与转动状态无关,称为刚 体转动惯量,以J 表示。于是得到
转动定律
dω M Jα J dt
刚体定轴转动的角加速度与它所受的合外力矩成 正比 ,与刚体的转动惯量成反比 .
第5章 刚体力学基础 动量矩
A
mA FN F T1 mA O x PA FT1 FC
PC
FT1
C
mC FT2
FT2
mB B
O
解 (1)隔离物体分 别对物体A、B 及滑轮作 受力分析,取坐标如图, 运用牛顿第二定律 、转 动定律列方程 .
FT1 mA a
第5章 刚体力学基础
结构框图
刚体转动
刚体动力学 力矩 牛顿定律 角动量 角动量 变化率 角动量 定理 刚体运动学 角量 角速度、 角加速度 角量与线 量关系 角动量守 恒定律
刚体定轴转动定律
转动 惯量
力矩 作功
动能 定理
转动 动能
第5章 刚体力学基础 动量矩
一、刚体的基本运动
1.刚体概念(rigid body ) 在外力作用下,形状和大小都不发生变化的物体 . (任意两质点间距离保持不变的特殊质点组) 说明: ①刚体是一个物体,可视为由许多质点组成;因此 研究质点系的方法和得出的一般结论均适合刚体。 ②刚体是物理学中的一个理想模型,绝对的刚体是 不存在的。
该点的切向加速度和法向加速度
an rω 0.2 (4 π) m s 31.6 m s
π 2 2 aτ rα 0.2 ( )m s 0.105 m s 6 2 2 2 2
第5章 刚体力学基础 动量矩
二、力矩
F
转动定律
a
?
α
1、力矩( torque)
第5章 刚体力学基础 动量矩
2、刚体的基本运动
刚体的运动形式:平动、转动 . 平动:若刚体中所有点的 运动轨迹都保持完全相同, 或者说刚体内任意两点间 的连线总是平行于它们的 初始位置间的连线 .
刚体平动
质点运动
vB vA
d vB d v A a A aB dt dt
第5章 刚体力学基础 动量矩
r
1 3 J 2 r dr l 0 12 1 ml 2 12
l/2 2
如转轴过端点垂直于棒
J
l 2 0 r dr
1 2 ml 3
第5章 刚体力学基础 动量矩
例3 一质量为 m 、半径为 R 的均匀圆盘,求通 过盘中心 O 并与盘面垂直的轴的转动惯量 .
解 设圆盘面密度为 , 在盘上取半径为 ,宽为 dr 的圆环
质量连续分布刚体的转动惯量
i
J Δmi ri r dm
2 2
dm
:质量元
在(SI)中,J 的单位:kgm2
i
第5章 刚体力学基础 动量矩
质量连续分布刚体的转动惯量
J Δmi ri r dm
2 2 i
dm
:质量元
对质量线分布的刚体: dm
dl
:质量线密度
大小: M 注意: 1)同一个力对空间不 同参考点的力矩不同。力平行 于轴或者通过轴时,力矩为零。
M
M
O
z
r
F
*
2)多个力作用在刚体上时,合 外力矩为外力矩的和,而不是合 外力的矩。
d
P
Fi 0 , Mi 0
F
F
Fi 0 , Mi 0
d
C
m
O
J O J C md
2
1 圆盘对P 轴 J P mR 2 mR 2 的转动惯量 2
P
R O m
第5章 刚体力学基础 动量矩
例4 质量为 mA 的物体 A 静止在光滑水平面上, 和一质量不计的绳索相连接,绳索跨过一半径为 R、质 量为 mC 的圆柱形滑轮 C,并系在另一质量为 mB 的物 体 B 上. 滑轮与绳索间没有滑动,且滑轮与轴承间的摩擦 力可略去不计. 问1)两物体的线加速度为多少? 水平 和竖直两段绳索的张力各为多少? 2)物体 B 从 静止落下距离 y 时, C A mA 其速率是多少?(3) mC 若滑轮与轴承间的摩 擦力不能忽略,并设 它们间的摩擦力矩为 M f 再求线加速度及 mB B 绳的张力.
2
v v0 at
x x0 v0t at
1 2
2 2 0
0 t 2 1 0 0t 2a( x x0 ) 2 ( 0 )
第5章 刚体力学基础 动量矩
5 、角量与线量的关系 2 d d d 2 dt dt dt
r
圆环质量
dm 2 π r dr
2 3
R R
O
r dr
圆环对轴的转动惯量
dJ r dm 2π r dr R 3 4 J 2π r dr π R 0
2
而
m π R
2
所以
1 2 J mR 2
第5章 刚体力学基础 动量矩
4、平行轴定理 质量为 m 的刚体,如果对 其质心轴的转动惯量为 J C ,则 对任一与该轴平行,相距为 d 的转轴的转动惯量
m反映质点的平动惯性,J反映刚体的转动惯性
第5章 刚体力学基础 动量矩
3、 转动惯量
J Δmi ri2 , J r 2dm
i
物理意义:转动惯性的量度 . 转动惯性的计算方法 质量离散分布刚体的转动惯量
J Δmi ri m r m r
2 2 11 2 2 2
Fi sin φi f i sin θ i Δ m i a iτ Δ m i ri α
physics
用
ri 乘以上式左右两端: 2 Fi ri sin φi f i ri sin θ i Δ m i ri α
N N
第5章第 刚体力学基础 动量矩 1章 质点运动学
设刚体由N 个点构成,对每个质点可写出上述 类似方程,将N 个方程左右相加,得:
F
F
第5章 刚体力学基础 动量矩
1)若力 F 不在转动平面内,把力分解为平行和垂 直于转轴方向的两个分量 z F Fz F F 其中 Fz 对转轴的力 k Fz
矩为零,故 F 对转轴的 力矩
讨论
M z k r F M z rF sin
F
质点的角加速度与质点所受的力矩成正比
第5章 刚体力学基础 动量矩
2)刚体 把刚体看成是由许多质点所组成的 对刚体中任一质量元 mi
Fi
z
O
-外力
fi -内力
应用牛顿第二定律,可得:
Δm ri
i
i
Fi
fi
Fi f i mi a i
采用自然坐标系,上式切向分量式为:
dω 讨论: M Jα J dt α (1) M 一定,J
转动惯量是转动
惯性大小的量度; (2)M 的符号:使刚体向规定的转动正方向加速 的力矩为正; (3)转动惯量的大小取决于三个因素:
刚体的质量、转轴的位置及质量对轴的分布。
(4)转动定律是解决刚体定轴转动问题的基本方程。
M J 与 F =ma 地位相当
τ Δs rΔθ v rωτ aτ rα 2 a rατ rω n tgφ aτ α 2 2 a rω
n
an r
a
τ v a
唯一
an
ω
注意:、是矢量,由于在定轴转动中轴的方位不变,故用正负 表示其方向。整个刚体只有一个和一个,转动刚体上各点速度 和加速度的大小都与该点到转轴的距离成正比。
1 0. 5 π rad s , t = 30 s 时, 解 ( 1) 0 设 t = 0 s 时, 0 0 .飞轮做匀减速运动 0 0 5π π 1 2 rad s rad s t 30 6
飞轮 30 s 内转过的角度
2 2 0 (5 π ) 2 75π rad 2 2 (π 6)
转动:刚体中所有的点都绕同一直线做圆周运动. 转动又分定轴转动和非定轴转动 .
刚体的平面运动 .
第5章 刚体力学基础 动量矩
3、 刚体定轴转动的角速度和角加速度 角坐标 (t ) 约定 沿逆时针方向转动 r 角位移
z
(t )
>0 r 沿顺时针方向转动 < 0
参考平面
mB g FT2 mBa
RFT2 RFT1 J
刚体绕 O z 轴旋转 , 力 F
M
O
M
z
作用在刚体上点 P , 且在转动 平面内, r 为由点O 到力的 作用点 P 的矢径 . Z 的力矩 F 对转轴 单位:N m 牛顿米
M r F
r
F
*
d
P
第5章 刚体力学基础 动量矩
Fr sin Fd 方向:右手螺旋法则 d : 力臂
O
r
F
M M1 M 2 M 3
2)合力矩等于各分力矩的矢量和
M= Mi
第5章 刚体力学基础 动量矩
3) 刚体内作用力和反作用力的力矩互相抵消
M ij
O
M ji
