线性代数5 PPT课件
合集下载
线性代数ppt 第五章 二次型

a11 a 21 a n1
a12 a 22 an2
a1n a2n , a nn
x =
x1 x2 , xn
则 二 次 型 可 记 作 f = xT Ax, 其 中 A为 对 称 矩 阵 .
(3)
此时A 此时A称为二次型 f 的矩阵, f 称为对称矩阵A 的矩阵, 称为对称矩阵A 对应的二次型. 对应的二次型. 对矩阵A的秩叫做二次型 的秩 二次型f的秩 二次型 的秩. f(x1,x2)=3x12+3x22+2x1x2 )=3x +3x +2x
k1 0 TAP = P … 0
0 k2 … 0
… … … …
0 0 … kn
第五章 二次型
§5.1 二次型及其矩阵表示
三. 矩阵的合同 可逆矩阵P, 使得PTAP = B. 记为: A B. 可逆矩阵 使得P 矩阵P 记为: 矩阵间的合同关系也是一种等价关系. 矩阵间的合同关系也是一种等价关系. An与Bn合同(congruent): 合同(congruent):
(1) 反身性: A A; 反身性: A; (2) 对称性: A B B A; 对称性: (3) 传递性: A B, B C A C. 传递性:
定理5.1. 实对称矩阵与对角矩阵合同. 定理5.1. 实对称矩阵与对角矩阵合同.
作业 P151 1. (B) 1(1), (3); 2
本章主要内容 (1) 二次型矩阵表示 (2) 标准二次型,规范二次型 标准二次型, 二次型 (3) 将二次型化为标准形 (4)二次型的正定型的判定—主要是利用顺序 (4)二次型的正定型的判定 主要是利用顺序 二次型的正定型的判定— 主子式判定 主子式判定 作业: 作业: P152 7(1); 20(1)
线性代数第五章 正交性

b = (-1, -1, 2, 2),
中每一个正交.
c = (3, 2, 5, 4),
20
练 习:
设 q1=
1 2
(1,1,1,1)T, q2=
1 2
(1,1,1,
1)T,
用两种方法将它们扩充成 4的一组规范正交基.
作业:
5.1节练习: 1. 2.
5.4节练习: 1. 2.
5.6节练习: 8.
课后练习:
在欧氏空间 4里找出两个单位向量,使它们同时与向量
a = (2, 1, -4, 0),
v2 ||v2||
正 交
基
vn=
xn
xn, v1,
v1 v1
v1
xn, v2,
v2 v2
v2
…
xn, vn1 vn1, vn1
vn1
un
=
vn ||vn||
Span(x1, x2, . . . , xn ) = Span(v1, v2, . . . , vn )
例5
设V = span(x1, x2, x3, x4),求 V的一组规范正交基. 其中x1= (1,−1, 1,−1)T, x2 = (1, 1, 3,−1) T , x3= (2,0, 4,−2)T , x4 = (3, 7, 1, 3)T .
||x|| ||y||
定 理 1 | xTy | ||x|| ||y|| 柯西-施瓦兹不等式 定 理 2 x y xT y = 0 称 x 和 y 正交 .
推广至更一般 向量空间 V
3
内积(P213 5.4 内积空间)
定 义 在向量空间V上定义一种运算,在这种运算下,V 中任意 一对向量 x 和 y,都对应一个实数,记作 x, y,若还满足: 对任意的 x, y, z ∈ V 及 s, t ∈ R,成立 (1) x, x 0 , 取等号当且仅当 x = 0 .
线性代数同济大学第五版课件5-3

正整数, f(x) = a0xm + a1xkB 相似, Am 与 Bm 相似, AT 与 BT 相似,
f(A) 与 f(B) 相似.
上页 下页
三、矩阵的对角化
对于 n 阶方阵 A , 若存在可逆矩阵 P , 使 P-1AP = ( 为对角矩阵),则称 A 能对角化.
以这些向量为列构造矩阵 P = ( p1 , p2 , · , pn ), · · 则 P 可逆, 且 AP = P , 其中 =diag (1 , 2 , · , n ) , · · 即 推论 P-1AP = .
证毕
如果n阶矩阵A的n个特征值互不相等,
则A与对角阵相似.
上页 下页
0 0 1 1 1 x , 问 x 为 何 值 时 , 例11 设 A 1 0 0 矩 阵A能 对 角 化 ?
第 三 节
主要内容
相似矩阵
相似矩阵的概念 相似矩阵的性质 矩阵对角化的充要条件
上页
下页
一、相似矩阵的概念
定义 7 设 A , B 为 n 阶方阵, 若有可逆矩阵P,
使 P-1AP = B , 则称矩阵 A 相似于矩阵 B. 对 A 进行运算
P-1AP 称为对 A 进行相似变换,可逆矩阵 P 称 为把 A 变成 B 的相似变换矩阵.
上页 下页
可. 推论 A与 阶方阵 A 与对角矩阵 由于 若 n B 相似, 所以, 必有可逆矩阵 P
由相似的定义和定理3,有下列 结论:
1. 若矩阵 A 与 矩阵 B 相似, 若矩阵 A
可逆, 则矩阵 B 也可逆, 且 A-1 与 B-1 相似.
2.若矩阵 A 与 B 相似, k 是常数, m 是
1 , 2 , · , n 的特征向量. · ·
f(A) 与 f(B) 相似.
上页 下页
三、矩阵的对角化
对于 n 阶方阵 A , 若存在可逆矩阵 P , 使 P-1AP = ( 为对角矩阵),则称 A 能对角化.
以这些向量为列构造矩阵 P = ( p1 , p2 , · , pn ), · · 则 P 可逆, 且 AP = P , 其中 =diag (1 , 2 , · , n ) , · · 即 推论 P-1AP = .
证毕
如果n阶矩阵A的n个特征值互不相等,
则A与对角阵相似.
上页 下页
0 0 1 1 1 x , 问 x 为 何 值 时 , 例11 设 A 1 0 0 矩 阵A能 对 角 化 ?
第 三 节
主要内容
相似矩阵
相似矩阵的概念 相似矩阵的性质 矩阵对角化的充要条件
上页
下页
一、相似矩阵的概念
定义 7 设 A , B 为 n 阶方阵, 若有可逆矩阵P,
使 P-1AP = B , 则称矩阵 A 相似于矩阵 B. 对 A 进行运算
P-1AP 称为对 A 进行相似变换,可逆矩阵 P 称 为把 A 变成 B 的相似变换矩阵.
上页 下页
可. 推论 A与 阶方阵 A 与对角矩阵 由于 若 n B 相似, 所以, 必有可逆矩阵 P
由相似的定义和定理3,有下列 结论:
1. 若矩阵 A 与 矩阵 B 相似, 若矩阵 A
可逆, 则矩阵 B 也可逆, 且 A-1 与 B-1 相似.
2.若矩阵 A 与 B 相似, k 是常数, m 是
1 , 2 , · , n 的特征向量. · ·
线性代数-线性空间与线性变换PPT课件

例1
次数不超过
n
的多项式的全体,记作
P
x
,
n
即
P x n p x anx n a1x a0 an, ,a1,a0 ,
对于通常的多项式加法、数乘多项式的乘法构成线性空间.
这是因为:通常的多项式加法、数乘多项式的乘法两种运算显然满足线性运算规律,
故只要验证
P
x
对运算封闭.
n
一、线性空间的定义
1
0 ,
E 22
0
1
线性无关,所以 E11, E12 , E21, E22 是 M2
的一个基,向量
A
a11 a21
a12 a22
在这个基下的
坐标就是 a11, a12, a21, a22 T .
二、基变换与坐标变换
设1,2, ,n 与 1, 2, , n 是线性空间Vn 中的两个基,且
第5章 线性空间与线性变换 20
目录/Contents
第5章 线性空间与线性变换 21
5.2 维数、基与坐标
一、线性空间的基、维数与坐标 二、基变换与坐标变换
一、线性空间的基、维数与坐标
第5章 线性空间与线性变换 22
定义 1 在线性空间V 中,如果存在n 个元素1,2, ,n 满足
(i) 1,2, ,n 线性无关; (ii) V 中任一元素 总可由1,2, ,n 线性表示,
x1, x2, , xn ,使
x11 x22 xnn ,
x1, x2, , xn 这组有序数就称为元素 在基1,2, ,n 下的坐标,并记作
x1, x2,
,xn
T
.
一、线性空间的基、维数与坐标
第5章 线性空间与线性变换 25
线性代数课件--05矩阵的初等变换与初等矩阵-PPT精品文档

课件 7
Go
由此可知,方程组的三种同解变换很自然地要引 入到矩阵上,导出矩阵矩阵的三种初等行变换. 同时,必须注意,原方程组能同解变换成什么样 的最简单方程组,就是相当于增广矩阵在初等行 变换下能变成什么样的最简单矩阵(行最简形矩 阵). 就本例来说,四个未知数划分为自由未知数 x 3 和 非自由未知数 x 1, x 2, x 4.
《线 性 代 数》
电子教案之五
课件
1
主要内容
第 矩阵的初等变换的概念; 五 阶梯形矩阵的概念; 讲
矩 阵 的 初 等 变 换 与 初 等 矩 阵 矩阵等价的概念; 三种初等矩阵,初等矩阵与初等变换的联系.
基本要求
熟悉掌握用初等行变换把矩阵化成行阶梯形矩 阵,知道矩阵等价的概念; 知道初等矩阵,了解初等矩阵与初等变换的联 系,掌握用初等变换求可逆矩阵的逆阵的方法.
1 2 3 4
Байду номын сангаас
( B2 )
x x 2 x x 4 , 1 2 3 4 2 12 x x x 0 , 2 3 4 2 x 6 , 3 52 4 4 32 x 3 . 4
课件
( B3 )
4
2
1 2
3 52 4 32 3
1 2
4 3 0 . 3
课件
6
说明
求解线性方程组可分为消元与回代两过程。消元 过程的实质,就是通过一系列方程组的同解变换 找到一个形式上较简单的方程组,然后进行回代, 这里方程组的同解变换是指下列三种变换: 对调两个方程; 以不为零的数乘某一个方程; 把一个方程的倍数加到另一个方程上. 从原方程组 ( 1 ) 同解变换到方程组( B 5 ) 的过程可见, 除去代表未知数的文字外,矩阵与方程组是一一 对应的.换言之,方程组有没有解,有什么样解完 全由各方程组的系数和常数项连同它们相互位置 所成数表,即增广矩阵所决定.而且,对方程组作 同解变换,相当于对它的增广矩阵作相应的变换.
Go
由此可知,方程组的三种同解变换很自然地要引 入到矩阵上,导出矩阵矩阵的三种初等行变换. 同时,必须注意,原方程组能同解变换成什么样 的最简单方程组,就是相当于增广矩阵在初等行 变换下能变成什么样的最简单矩阵(行最简形矩 阵). 就本例来说,四个未知数划分为自由未知数 x 3 和 非自由未知数 x 1, x 2, x 4.
《线 性 代 数》
电子教案之五
课件
1
主要内容
第 矩阵的初等变换的概念; 五 阶梯形矩阵的概念; 讲
矩 阵 的 初 等 变 换 与 初 等 矩 阵 矩阵等价的概念; 三种初等矩阵,初等矩阵与初等变换的联系.
基本要求
熟悉掌握用初等行变换把矩阵化成行阶梯形矩 阵,知道矩阵等价的概念; 知道初等矩阵,了解初等矩阵与初等变换的联 系,掌握用初等变换求可逆矩阵的逆阵的方法.
1 2 3 4
Байду номын сангаас
( B2 )
x x 2 x x 4 , 1 2 3 4 2 12 x x x 0 , 2 3 4 2 x 6 , 3 52 4 4 32 x 3 . 4
课件
( B3 )
4
2
1 2
3 52 4 32 3
1 2
4 3 0 . 3
课件
6
说明
求解线性方程组可分为消元与回代两过程。消元 过程的实质,就是通过一系列方程组的同解变换 找到一个形式上较简单的方程组,然后进行回代, 这里方程组的同解变换是指下列三种变换: 对调两个方程; 以不为零的数乘某一个方程; 把一个方程的倍数加到另一个方程上. 从原方程组 ( 1 ) 同解变换到方程组( B 5 ) 的过程可见, 除去代表未知数的文字外,矩阵与方程组是一一 对应的.换言之,方程组有没有解,有什么样解完 全由各方程组的系数和常数项连同它们相互位置 所成数表,即增广矩阵所决定.而且,对方程组作 同解变换,相当于对它的增广矩阵作相应的变换.
线性代数课件-05矩阵的初等变换与初等矩阵

THANKS FOR WATCHING
感谢您的观看
练习题与答案
题目
设矩阵$A = begin{bmatrix} -2 & -3 -4 & -6 end{bmatrix}$,求$A^{-1}$。
答案
首先,对矩阵$A$进行初等行变换,将第一 行乘以-2加到第二行,得到矩阵$B = begin{bmatrix} -2 & -3 0 & -3 end{bmatrix}$。然后,对矩阵$B$进行初 等列变换,将第一列乘以-3加到第二列,得 到单位矩阵$I = begin{bmatrix} -2 & -3 0 & 1 end{bmatrix}$。因此,矩阵$A^{-1} = begin{bmatrix} -2 & -3 0 & 1 end{bmatrix}$。
具体操作为将第j列的每一个 元素都乘以k。
数学表达为$A_{.j} times k$ 。
用常数乘以矩阵的每一个元素
将矩阵的每一个元素都乘以常数k,记作$k times A$。 具体操作为将矩阵的每一个元素都乘以k。 数学表达为$k times A_{ij}$。
02 初等矩阵
单位矩阵
定义
单位矩阵是n阶方阵,其主对角线上的元素都是1,其余元素都是0。记作I 或E。
练习题与答案
题目
设矩阵$A = begin{bmatrix} 2 & -3 4 & -6 end{bmatrix}$,求$A^{-1}$。
VS
答案
首先,对矩阵$A$进行初等行变换,将第 二行乘以-2加到第一行,得到矩阵$B = begin{bmatrix} -2 & 3 4 & -6 end{bmatrix}$。然后,对矩阵$B$进行 初等列变换,将第一列乘以-4加到第二列 ,得到单位矩阵$I = begin{bmatrix} -2 & 3 0 & -6 end{bmatrix}$。因此,矩 阵$A^{-1} = begin{bmatrix} -2 & 3 0 & -6 end{bmatrix}$。
线性代数课件5-2相似矩阵与二次型

23
解得x2 2 x1 ,
所以,对应的特征向量可取为p2
1 2 .
2
3对应的全部特征向量为k2
p2
k2
1
2
,
(k2
0).
9
2 1 1
例2
求矩阵A
0
2 0 的特征值和特征向量。
4 1 3
解 特征多项式为 f ( ) A E
2 1 1
2 1
0
2
0
(2 )
4
3
4 1 3
20
于是,得到关于 x1, x2 , , xm 的m个方程 从而,满足下面的方程组:
x1 p1 x2 p2 xm pm 0
1 x1 p1 2 x2 p2 m xm pm 0
1m1
x1
p1
m1 2
x2
p2
m1 m
xm
pm
0
下求该齐次方程组的解
1 1
1
2
1 x1 p1 0
2xx21
x3 x3
,
令x3 1,
基础解系为p1
1 2
1
.
故对应于1 1的全体特征向量为 1
k1 p1
(k1 0).
当2 3 2时, 齐次方程为
1
2
1 2
2 2
1
A
2
2
1 2 2
1 2 2
r3
r1 (1) r2 , r2
2r1
1 0 0
1 x1 0
则有
(1) 1 2 n a11 a22 ann; (2) 12 n A .
5.对应特征向量 i的特征值即是 齐次方程( A i E)x 0的解pi .
解得x2 2 x1 ,
所以,对应的特征向量可取为p2
1 2 .
2
3对应的全部特征向量为k2
p2
k2
1
2
,
(k2
0).
9
2 1 1
例2
求矩阵A
0
2 0 的特征值和特征向量。
4 1 3
解 特征多项式为 f ( ) A E
2 1 1
2 1
0
2
0
(2 )
4
3
4 1 3
20
于是,得到关于 x1, x2 , , xm 的m个方程 从而,满足下面的方程组:
x1 p1 x2 p2 xm pm 0
1 x1 p1 2 x2 p2 m xm pm 0
1m1
x1
p1
m1 2
x2
p2
m1 m
xm
pm
0
下求该齐次方程组的解
1 1
1
2
1 x1 p1 0
2xx21
x3 x3
,
令x3 1,
基础解系为p1
1 2
1
.
故对应于1 1的全体特征向量为 1
k1 p1
(k1 0).
当2 3 2时, 齐次方程为
1
2
1 2
2 2
1
A
2
2
1 2 2
1 2 2
r3
r1 (1) r2 , r2
2r1
1 0 0
1 x1 0
则有
(1) 1 2 n a11 a22 ann; (2) 12 n A .
5.对应特征向量 i的特征值即是 齐次方程( A i E)x 0的解pi .
广东工业大学《线性代数》课件 PPT 5.2线性相关和线性无关
例 已知向量组a1 a2 a3线性无关 b1a1a2 b2a2a3 b3a3a1 试证向量组b1 b2 b3线性无关
证法二 利用矩阵秩 把已知的三个向量等式写成一个矩阵等式
1 0 1
(b1
,
b2
,
b3
)
(a1
,
a2
,
a3
)
1
1
0
0 1 1
记作BAK 因为 |K|20 知K可逆 所以 r(B)r(A)
的数 k1, k2 , , km ,使得
k11 k22 kmm 0 () 则称向量组1,2 , ,m 线性相关, 否则称它们线性无关.
依据前面的分析可得如下重要结论
向量组
A:a1, a2, …, am 线性相关(无关)
m 元齐次线性方程 Ax = 0
有非零解(零解)
r(A) < m (r(A) = m )
其中向量的个数就是齐次线性方程组的未知数的个数.
以上结果,显示了Rn的向量之线性相关性与齐 次方程组的解及矩阵秩三者之间的联系. 注 给定向量组 A,不是线性相关,就是线性无关,两者必
居其一; 对于单个向量,当且仅当是零向量时,线性相关;否则
线性无关. 两个非零向量a1 a2线性相关 a1ka2(对应分量成比例)
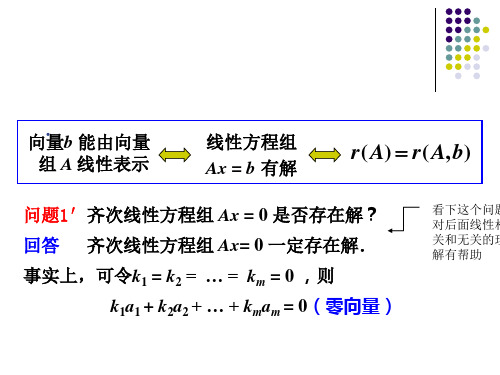
看下这个问题 对后面线性相 关和无关的理 解有帮助
向.量b 能由向量 组 A 线性表示
线性方程组 Ax = b 有解
r( A) r( A,b)
问题2′齐次线性方程组 Ax = 0 是否存在非零解? 回答 齐次线性方程组不一定有非零解,从而线性组合 的系数不一定全等于零.
1、线性相关性的概念
定义 设1,2 , ,m 为同维向量, 若存在不全为零
