金版学案高中物理人教版必修2配套课件：5.6《向心力》
合集下载
新人教版高中物理必修二：5.6向心力2 课件 (共28张PPT)
• 物体半径越大-------向心力越 大
1．探究向心力F与角速度ω的关系 m、r相同，长短槽上小球角速度比为1
比2。
长槽端 角速度1
短槽端 角速度2
在m、r一定时，F向与____________比
向心力演示器 实验步骤： 2．探究向心力F与质量m的关系 r、ω相同，长短槽上小球质量比为1比2。
• 10、人的志向通常和他们的能力成正比例。2021/3/182021/3/182021/3/183/18/2021 11:12:03 AM • 11、夫学须志也，才须学也，非学无以广才，非志无以成学。2021/3/182021/3/182021/3/18Mar-2118-Mar-21 • 12、越是无能的人，越喜欢挑剔别人的错儿。2021/3/182021/3/182021/3/18Thursday, March 18, 2021 • 13、志不立，天下无可成之事。2021/3/182021/3/182021/3/182021/3/183/18/2021
问题二、谁担当向心力
圆锥摆
O’
圆锥摆
T
O
G
向心力不是物体另外受到的一个力 向心力按效果命名 重力，拉力，弹力等
是按性质命名的力 O’
O
一、向心力特点： 1、向心力指向圆心，方向不断变化。 2、向心力的作用效果——只改变运
动物体的速度方向， 不改变速度大小。
3．向心力是根据效果命名的力
4．向心力的来源：可以是各种性质的 单个力，也可以是几个力的合力或某个 力的分力。
M=1 ω=1 r=2 V=2
四
M=1 ω=1 r=1 V=1
M=2 ω=2 r=2 V=4
五
M=2 ω=2 r=1
六 V=2
1．探究向心力F与角速度ω的关系 m、r相同，长短槽上小球角速度比为1
比2。
长槽端 角速度1
短槽端 角速度2
在m、r一定时，F向与____________比
向心力演示器 实验步骤： 2．探究向心力F与质量m的关系 r、ω相同，长短槽上小球质量比为1比2。
• 10、人的志向通常和他们的能力成正比例。2021/3/182021/3/182021/3/183/18/2021 11:12:03 AM • 11、夫学须志也，才须学也，非学无以广才，非志无以成学。2021/3/182021/3/182021/3/18Mar-2118-Mar-21 • 12、越是无能的人，越喜欢挑剔别人的错儿。2021/3/182021/3/182021/3/18Thursday, March 18, 2021 • 13、志不立，天下无可成之事。2021/3/182021/3/182021/3/182021/3/183/18/2021
问题二、谁担当向心力
圆锥摆
O’
圆锥摆
T
O
G
向心力不是物体另外受到的一个力 向心力按效果命名 重力，拉力，弹力等
是按性质命名的力 O’
O
一、向心力特点： 1、向心力指向圆心，方向不断变化。 2、向心力的作用效果——只改变运
动物体的速度方向， 不改变速度大小。
3．向心力是根据效果命名的力
4．向心力的来源：可以是各种性质的 单个力，也可以是几个力的合力或某个 力的分力。
M=1 ω=1 r=2 V=2
四
M=1 ω=1 r=1 V=1
M=2 ω=2 r=2 V=4
五
M=2 ω=2 r=1
六 V=2
新人教版高中物理必修二课件：5.6向心力 (共17张PPT)
r2 r1
做一做:实验体会感受向心力F与m、r、 ω的关系 想一想:研究多个变量之间的关系应用什么方法？ 控制变量法
操作一:手握绳绳结A,使沙袋在水 平方向做匀速圆周运动,每秒转1周, 体会此时绳子拉力的大小F
操作二:手握绳绳结B,仍使沙袋在水 平方向上每秒运动1周,体会此时绳 子拉力的大小2F.
θ
F
F合O r
4.把一个小球放在漏斗中,晃动漏斗,可以使小球沿光滑漏
斗壁在某一平面内做匀速圆周运动, 小球的向心力是什么
力提供的?若小球转动的角速度为ω,如图倾角为α,试求小
球做圆周运动的半径.
F
解析:小球受力分析如图,向心力是重力
G和支持力F的合力提供的.也可以认为
是支持力F在水平方向的分力提供的
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other fam ous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
变速圆周运动F向 F合F向是F合的指向圆心方向的分力Fn
2.处理一般曲线运动的方法：
把一般曲线分割为许多极短的小段，每一 段都可以看作为一小段圆弧，而这些圆弧的弯 曲程度不一样，表明它们具有不同的曲率半径。 在注意到这点区别之后，分析质点经过曲线上 某位置的运动时，就可以采用圆周运动的分析 方法对一般曲线运动进行处理了。
做一做:实验体会感受向心力F与m、r、 ω的关系 想一想:研究多个变量之间的关系应用什么方法？ 控制变量法
操作一:手握绳绳结A,使沙袋在水 平方向做匀速圆周运动,每秒转1周, 体会此时绳子拉力的大小F
操作二:手握绳绳结B,仍使沙袋在水 平方向上每秒运动1周,体会此时绳 子拉力的大小2F.
θ
F
F合O r
4.把一个小球放在漏斗中,晃动漏斗,可以使小球沿光滑漏
斗壁在某一平面内做匀速圆周运动, 小球的向心力是什么
力提供的?若小球转动的角速度为ω,如图倾角为α,试求小
球做圆周运动的半径.
F
解析:小球受力分析如图,向心力是重力
G和支持力F的合力提供的.也可以认为
是支持力F在水平方向的分力提供的
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other fam ous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
变速圆周运动F向 F合F向是F合的指向圆心方向的分力Fn
2.处理一般曲线运动的方法：
把一般曲线分割为许多极短的小段，每一 段都可以看作为一小段圆弧，而这些圆弧的弯 曲程度不一样，表明它们具有不同的曲率半径。 在注意到这点区别之后，分析质点经过曲线上 某位置的运动时，就可以采用圆周运动的分析 方法对一般曲线运动进行处理了。
人教版高中物理必修二5.6 向心力公开课教学课件共24张PPT
= m v2 = mω2r r
2、做变速圆周运动的物体，其合外力指向圆心的分力提
供了改变运动方向所需要的向心力，跟圆周相切的分力改
变速度的大小。
Fn = ma n
F合
=
v2 m
=
mr ω 2
r
Ft mat
学习与探究
归纳与总结
实践与练习
实践与练习
作业：问题与练习：1、3、4
谢谢各位老师和同学!
学习与探究
归纳与总结
实践与练习
归纳与总结
1、做匀速圆周运动的物体受到的合外力时刻指向圆心， 提供了改变运动方向所需要的向心力。
F合 = Fn = ma n = m v2 = mω2r
r
学习与探究
归纳与总结
实践与练习
学习与探究 实验探究：用圆锥摆粗略验证向心力的表达式
FT F
G
摆球所需向心力和 需要测量 比较计算
F合
v2 Fnmnamr
mr2
Ft mat
Ft v
F合
Fn
做变速圆周运动的物体是否需要向心力？向心力又 是如何提供的呢？
学习与探究
归纳与总结
实践与练习
归纳与总结
1、做匀速圆周运动的物体受到的合外力时刻指向圆心，
提供了改变运动方向所需要的向心力。
F合 = Fn = ma n
= m v2 = mω2r r
2、做变速圆周运动的物体，其合外力指向圆心的分力提
供了改变运动方向所需要的向心力，跟圆周相切的分力改
变速度的大小。
Fn = ma n
F合
=
v2 m
=
mr ω 2
r
Ft mat
学习与探究
新人教版高中物理必修二课件：5.6《向心力》 (共12张PPT)
(1)切线方向的分力改变速度的大小
(2)法向(指向圆心方向)的合力改 变速度的方向，这个方向的合 力才是向心力
2.变速率圆周运动的合外力并 不指向圆心，即不是向心力；而 沿半径指向圆心方向的合力才是 向心力。
（四）关于向心力的说明：
(1)任何一个曲线运动的法向加速都 可以看成是向心加速度 (2)法向合力仍满足向心力公式， 就是半径为该点的曲线半径。
•
（三）向心力表达式的验证（传感器）：
v2 Fn m r 1.实验目的：
Fn mr2
① 验证向心力与速度平方成正比
② 验证向心力与角速度平方成正比
③ 验证在线速度一定的情况下，半径越大 需要的向心力越小
④ 验证在角速度一定的情况下，半径越大 需要的向心力越大
2.实验原理：
① 如果在控制质量与半 径不变，测定在不同速 度下的向心力，画出Fn 与v2的图象，如果是通过 原点的直线，则向心力 正比于速度的平方。
3.实验结果：
① 向心力与速度的平方成正比； ② 向心力与角速度的平方成正比； ③ 在线速度不变的情况下半径越大，
需要的向心力越小； ④ 在角速度不变的情况下，半径越大，
需要的向心力越大。
（四）关于向心力的说明：
Fn
Fn
1.向心力可能是某一个力，也 可能是几个力的合力，也可以是 某个力的分力。
（四）关于向心力的说明：
3.任何曲线运动的一小段均可以近 似为一小段圆弧，但在不同地方曲线 半径可能不同。因此，曲线运动也可 以用圆周运动来处理。
（一）观察与思考
（一）观察与思考
（二）向心力的大小
匀速圆周运动
向心加速度
根据牛顿第二定律
指向圆心的合力
向心力
(2)法向(指向圆心方向)的合力改 变速度的方向，这个方向的合 力才是向心力
2.变速率圆周运动的合外力并 不指向圆心，即不是向心力；而 沿半径指向圆心方向的合力才是 向心力。
（四）关于向心力的说明：
(1)任何一个曲线运动的法向加速都 可以看成是向心加速度 (2)法向合力仍满足向心力公式， 就是半径为该点的曲线半径。
•
（三）向心力表达式的验证（传感器）：
v2 Fn m r 1.实验目的：
Fn mr2
① 验证向心力与速度平方成正比
② 验证向心力与角速度平方成正比
③ 验证在线速度一定的情况下，半径越大 需要的向心力越小
④ 验证在角速度一定的情况下，半径越大 需要的向心力越大
2.实验原理：
① 如果在控制质量与半 径不变，测定在不同速 度下的向心力，画出Fn 与v2的图象，如果是通过 原点的直线，则向心力 正比于速度的平方。
3.实验结果：
① 向心力与速度的平方成正比； ② 向心力与角速度的平方成正比； ③ 在线速度不变的情况下半径越大，
需要的向心力越小； ④ 在角速度不变的情况下，半径越大，
需要的向心力越大。
（四）关于向心力的说明：
Fn
Fn
1.向心力可能是某一个力，也 可能是几个力的合力，也可以是 某个力的分力。
（四）关于向心力的说明：
3.任何曲线运动的一小段均可以近 似为一小段圆弧，但在不同地方曲线 半径可能不同。因此，曲线运动也可 以用圆周运动来处理。
（一）观察与思考
（一）观察与思考
（二）向心力的大小
匀速圆周运动
向心加速度
根据牛顿第二定律
指向圆心的合力
向心力
新人教 必修二高中物理5.6 向心力 课件(共16张PPT)
6 向心力
回顾与思考
（1）做匀速圆周运动的物体的加速
度有什么特点？写出向心加速度的公
式。
an
v2 r
rω2
4π 2r T2
vω
（2）做匀速圆周运动的物体的受力有
什么特点？
观察与思考：
小球受到哪些力作用？
N F
G
做匀速圆周运动的物体所受的力或合外力指向圆心。
一、向心力
1、定义： 做匀速圆周运动的物体受到的合外力指
向圆心的，这个力叫做向心力。 2、方向：总指向圆心，与速度垂直，方向
不断变化。 二、向心力的大小
只改变速度的方向，不达式
θ
Fh
F合O r
小球受到哪些力的作用？ 向心力由什么力提供？
G
分析得出: 向心力由拉力F和重力G的合力 提供。
F F mg tan
r
r
2
1
小结
匀速圆周运动：
F向
F合
v2 m
r
mw 2r
向心力的来源：可以是重力、弹力、摩擦力等各种性质 的力，也可以是几个力的合力，还可以是某个力的分力。
物体做匀速圆周运动时，由合力提供向心力。
非匀速圆周运动：
F向 F合
F F F 向是 合的指向圆心方向的分力 n
随堂练习
1
关于向心力说法中正确的是（ B）
A.1∶4 B.2∶3
C.4∶9 D.9∶16
❖ 9、春去春又回，新桃换旧符。在那桃花盛开的地方，在这醉人芬芳的季节，愿你生活像春天一样阳光，心情像桃花一样美丽，日子像桃子一样甜蜜。2 1.3.1621.3.16Tuesday, March 16, 2021
❖ 10、人的志向通常和他们的能力成正比例。14:23:2614:23:2614:233/16/2021 2:23:26 PM ❖ 11、夫学须志也，才须学也，非学无以广才，非志无以成学。21.3.1614:23:2614:23Mar-2116-Mar-21 ❖ 12、越是无能的人，越喜欢挑剔别人的错儿。14:23:2614:23:2614:23Tuesday, March 16, 2021 ❖ 13、志不立，天下无可成之事。21.3.1621.3.1614:23:2614:23:26March 16, 2021
回顾与思考
（1）做匀速圆周运动的物体的加速
度有什么特点？写出向心加速度的公
式。
an
v2 r
rω2
4π 2r T2
vω
（2）做匀速圆周运动的物体的受力有
什么特点？
观察与思考：
小球受到哪些力作用？
N F
G
做匀速圆周运动的物体所受的力或合外力指向圆心。
一、向心力
1、定义： 做匀速圆周运动的物体受到的合外力指
向圆心的，这个力叫做向心力。 2、方向：总指向圆心，与速度垂直，方向
不断变化。 二、向心力的大小
只改变速度的方向，不达式
θ
Fh
F合O r
小球受到哪些力的作用？ 向心力由什么力提供？
G
分析得出: 向心力由拉力F和重力G的合力 提供。
F F mg tan
r
r
2
1
小结
匀速圆周运动：
F向
F合
v2 m
r
mw 2r
向心力的来源：可以是重力、弹力、摩擦力等各种性质 的力，也可以是几个力的合力，还可以是某个力的分力。
物体做匀速圆周运动时，由合力提供向心力。
非匀速圆周运动：
F向 F合
F F F 向是 合的指向圆心方向的分力 n
随堂练习
1
关于向心力说法中正确的是（ B）
A.1∶4 B.2∶3
C.4∶9 D.9∶16
❖ 9、春去春又回，新桃换旧符。在那桃花盛开的地方，在这醉人芬芳的季节，愿你生活像春天一样阳光，心情像桃花一样美丽，日子像桃子一样甜蜜。2 1.3.1621.3.16Tuesday, March 16, 2021
❖ 10、人的志向通常和他们的能力成正比例。14:23:2614:23:2614:233/16/2021 2:23:26 PM ❖ 11、夫学须志也，才须学也，非学无以广才，非志无以成学。21.3.1614:23:2614:23Mar-2116-Mar-21 ❖ 12、越是无能的人，越喜欢挑剔别人的错儿。14:23:2614:23:2614:23Tuesday, March 16, 2021 ❖ 13、志不立，天下无可成之事。21.3.1621.3.1614:23:2614:23:26March 16, 2021
人教版高中物理必修二 5.6向心力(共28张PPT)
7、向心力的大小
根据牛顿第二定律： F ma
n
n
Fn
m v2 r
m 2 r
mvFn
m
4
T
2 2
r
例1.用细线拴一球做匀速圆周运动，下列说法中正 确的是
A 在线速度一定情况下，线越长越易断
B 在线速度一定情况下，线越短越易断 C 在角速度一定情况下，线越长越易断
D 在角速度一定情况下，线越短越易断
向心力
【思维引导】 由牛顿运动定律知：物体做圆周运动，必然要 受到外力的作用。
那么，是怎样的力使物体做圆周运动呢？
【实验探究】 在下列圆周运动中，感受……
一、向心力
1、定义： 做匀速圆周运动的物体一定受到一 个指向圆心的合力，这个合力叫做向心力。
2、方向：总是沿着半径指向圆心.方向时刻改变, 因此向心力是变力。
②滚筒洗衣机衣服跟着滚筒转动。
物块做匀速圆周运动时，
ω
Ff
合力提供向心力，即桶对
物块的支持力。
FN G
F向= F合= FN
③小球在水平面内做匀速圆周运动(圆锥摆)
θ
T
F
图2
G
小球重力和绳拉力的合力提供向心力
分
析 ④物体相对转盘静止，随盘做匀速圆周运动
向
心
力
ω FN
的
来
源
O Ff
F向= F合= Ff
3、作用：只改变速度方向，不改变速度大小。
物体做匀速圆周运动的条件：物体做圆周运 动，合力大小不变，方向始终指向圆心。
4、匀速圆周运动的实例分析—向心力来源
下列物体做匀速圆周运动时，向心力分别 由什么力提供？
①人造地球卫星绕地球运动时；
新人教版高中物理必修二：5.6_向心力(共25张PPT)
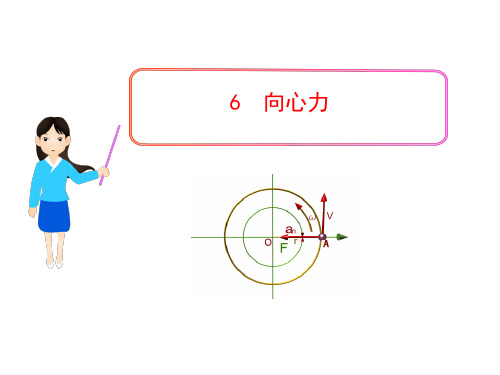
Fsinmg Fcos F向
F
Fcos F向
G
用圆锥摆粗略验证向心力的表达式
1.实验器材有哪些？ 2.简述实验原理（怎样达到验证的目的） 3.实验过程中要注意什么？需测量哪些物理量（记录哪 些数据）？ 4.实验过程中产生误差的原因主要有哪些？
m(kg) d1(m) d2(m) d=d1-d2(m) T(s) r(m) Fn=4mπ2r/T2 F合=mgtanθ 注：d1指悬挂点到纸面的距离,d2指球心到纸面的距离， d指悬挂点到球心的距离。
。2021年3月18日星期四2021/3/182021/3/182021/3/18
• 15、会当凌绝顶，一览众山小。2021年3月2021/3/182021/3/182021/3/183/18/2021
• 16、如果一个人不知道他要驶向哪头，那么任何风都不是顺风。2021/3/182021/3/18March 18, 2021
6 向心力
1.知道什么是向心力，理解它是一种效果力。 2.知道向心力大小与哪些因素有关。理解公式的确切含 义，并能用来进行计算。
3.结合向心力,理解向心加速度。 4.理解变速圆周运动中，合外力与向心力的关系。
什么是匀速圆周运动？“匀速”的含义是什么？ 匀速圆周运动是_变__速曲线运动 运动状态改变
3.在光滑的水平桌面上，用细线系一个小球，球在桌面上 做匀速圆周运动，当系球的线突然断了，关于球的运动， 下列说法中正确的是（ C） A．向圆心运动 B．背离圆心沿半径向外运动 C．沿切线方向匀速运动 D．做半径逐渐变大的曲线运动
4.一个小球在竖直放置的光滑圆环的内侧槽内做圆周运动， 如图所示，则关于小球加速度的方向的说法中正确的 是（ A ） A．一定指向圆心 B．一定不指向圆心 C．只有在最高点和最低点时指向圆心 D．不能确定是否指向圆心
人教版高中物理必修二5.6 向心力(共22张PPT)优质课件
θ
r m θ F合 O
ω mg
竖直方向：FT cosθ＝mg
水平方向：F合=mω2l sinθ
竖直方向：F升 cosθ＝mg
水平方向：F合=mω2r
☞ 练习：
质量为m的球用长为L的细线悬于天花板的O点， 并使之在水平面内做匀速圆周运动，细线 与竖直方向成θ角，则以下说法正确的是 θ A、摆球受重力、拉力和向心力的作用
产生向心加速度，改变速度的方向
变速圆周运动和一般的曲线运动
r2
一般曲线运动
各个地方的弯
r1
曲程度不一样， 如何研究？
把一般曲线分割为许多极短的小段，每一段都可以看 作一小段圆弧。这些圆弧的弯曲程度不一样，表明它 们具有不同的曲率半径。在分析质点经过曲线上某位 置的运动时可以采用圆周运动的分析方法进行处理。
例6：质量为m的小球，用长为L的线悬挂在O点，在 O点正下方处有一光滑的钉子O′，把小球拉到右侧某 一位置释放，当小球第一次通过最低点P时：
A、小球速率突然减小 B、小球角速度突然增大 C、小球向心加速度突然增大 D、摆线上的张力突然增大
例7：如图所示，MN为水平放置的光滑圆盘，半径 为1.0m，其中心O处有一个小孔，穿过小孔的细绳两 端各系一小球A和B，A、B两球的质量相等。圆盘上 的小球A作匀速圆周运动。问：
B、摆球只受重力、拉力的作用
C、摆球做匀速圆周运动的向心力为
D、摆球做匀速圆周运动的周期为
➢ 4、合外力提供向心力
FN
θ
m
r F合O
θω
mg
竖直方向：FN cosθ＝mg
水平方向：F合=mω2 R sinθ
竖直方向：FN cosθ＝mg
水平方向：F合=mω2r
r m θ F合 O
ω mg
竖直方向：FT cosθ＝mg
水平方向：F合=mω2l sinθ
竖直方向：F升 cosθ＝mg
水平方向：F合=mω2r
☞ 练习：
质量为m的球用长为L的细线悬于天花板的O点， 并使之在水平面内做匀速圆周运动，细线 与竖直方向成θ角，则以下说法正确的是 θ A、摆球受重力、拉力和向心力的作用
产生向心加速度，改变速度的方向
变速圆周运动和一般的曲线运动
r2
一般曲线运动
各个地方的弯
r1
曲程度不一样， 如何研究？
把一般曲线分割为许多极短的小段，每一段都可以看 作一小段圆弧。这些圆弧的弯曲程度不一样，表明它 们具有不同的曲率半径。在分析质点经过曲线上某位 置的运动时可以采用圆周运动的分析方法进行处理。
例6：质量为m的小球，用长为L的线悬挂在O点，在 O点正下方处有一光滑的钉子O′，把小球拉到右侧某 一位置释放，当小球第一次通过最低点P时：
A、小球速率突然减小 B、小球角速度突然增大 C、小球向心加速度突然增大 D、摆线上的张力突然增大
例7：如图所示，MN为水平放置的光滑圆盘，半径 为1.0m，其中心O处有一个小孔，穿过小孔的细绳两 端各系一小球A和B，A、B两球的质量相等。圆盘上 的小球A作匀速圆周运动。问：
B、摆球只受重力、拉力的作用
C、摆球做匀速圆周运动的向心力为
D、摆球做匀速圆周运动的周期为
➢ 4、合外力提供向心力
FN
θ
m
r F合O
θω
mg
竖直方向：FN cosθ＝mg
水平方向：F合=mω2 R sinθ
竖直方向：FN cosθ＝mg
水平方向：F合=mω2r
人教版高中物理必修二第五章第六节《向心力》课件(共70张PPT)
速转动时，下列说法正确的是 (
)
A．两小球速率必相等 B．两小球角速度必相等 C．两小球加速度必相等 D．两小球到转轴距离与其质量成反比
练 习
在光滑的横杆上穿着两质量不同的两 个小球，小球用细线连接起来，当转台匀
速转动时，下列说法正确的是 ( BD )
A．两小球速率必相等
B．两小球角速度必相等
C．两小球加速度必相等
(C)
A. 1∶4 C. 4∶9
B. 2∶3 D. 9∶16
小 结 1、向心力的方向：指向圆心
2、向心力的作用效果：改变速度的方向 3、向心力的大小
4、向心力的来源
小 结 1、向心力的方向：指向圆心
2、向心力的作用效果：改变速度的方向
3、向心力的大小
Fn=m
v2 r
Fn=m rω2
4、向心力的来源
几
种
常
见 的
r
O
圆
ω
周
运
动
几
种
常
见 的
m
r
O
圆
θω
周
运
动
几
种
常
见 的
m
r
O
圆 周
mgθ ω
运
动
几
种
常
FN
见
的
m
r
O
圆 周
mgθ ω
运
动
几
种
常
FN
见
的
m
r F合O
圆 周
mgθ ω
运
动
几
种
常
FN
见
θ
的
m
r F合O
圆 周
mgθ ω
物理必修2人教版 5.6向心力 (共29张PPT)[优秀课件资料]
![物理必修2人教版 5.6向心力 (共29张PPT)[优秀课件资料]](https://img.taocdn.com/s3/m/4cede73a1711cc7930b7163a.png)
随盘做匀速圆周运动的角速度ω=2rad/s,
如果物体到转盘圆心的距离为R=0.5m,求
物体受到的静摩擦力大小.
ω
FN
O
F静
2N G
五、一般曲线运动：
运动轨迹既不是直线也不是圆周的曲线
运动，可以称为一般曲线运动。
r2 rr11
问题讨论:一 般曲线运动各 个地方的弯曲 程度不一样， 如何研究？
处理方法----把曲线分割为许多极短的小段,每小 段都看作一小段圆弧.它们具有不同的曲率半径. 在分析质点在某位置的运动时可采用分析圆周运 动的方法进行处理.即向心力的公式仍然适用。
圆心方向的合力即向心力
二、变速圆周运动和一般的曲线运动
1.回顾
只加速
v
a
只减速
a
v
v
an
只改变速度方向
2.思考
为什么变速速圆周运动的速度大小时刻改变， 速度方向时刻改变？
Ft
F
Fn
O
Fn
an 改变速度的方向
a起着改变速
度大小、方
Ft
at
改变速度的大小
向的作用
随堂练习
1、用细线拴柱一球做匀速圆周运动，下列说法中 正确的是（ ） A.在线速度一定情况下，线越长越易断 B.在线速度一定情况下，线越短越易断 C.在角速度一定情况下，线越长越易断 D.在角速度一定情况下，线越短越易断
5.7 向心力
向心加速度
知识回顾
1. 向心加速度：作圆周运动的物体具有的总 是沿半径指向圆心的加速度叫做向心加速度。
2. 向心加速度的方向：指向圆心，时刻变化。
3. 向心加速度大小：
a r 2 或
a v2 r
人教版高中物理必修二5.6《向心力》ppt课件
解决圆周运动的一般步骤：
(1)确定做圆周运动的物体为研究对象．明确圆周运动的轨
道平面、圆心位置和半径．
(2)对研究对象进行受力分析，画出受力示意图．运用平行
四边形定则或正交分解法求出外界提供的向心力Fn.
(3)抓住所给的已知条件，是线速度 v、角速度 ω、还是周
期
T，根据向心力公式
FN＝mvr2＝mω2r＝m4Tπ2
【例2】如图5－6－1所示，一圆盘可绕过圆盘
的中心O且垂直于盘面的竖直轴转动，在圆
盘上放一小木块A，它随圆盘一起运动——
做匀速圆周运动，则关于木块A的受力，下
列说法中正确的是
()
A．木块A受重力、支持力和向心力
B．木块A受重力、支持力和静摩擦力，摩 图5－6－1
擦力的方向与木块运动方向相反
C．木块A受重力、支持力和静摩擦力，摩擦力的方向指
② 根据自己预习时理解过的逻辑结构抓住老师的思路。老师讲课在多数情况下是根据教材本身的知识结构展开的，若把自己预习时所理解过的知识 逻辑结构与老师的讲解过程进行比较，便可以抓住老师的思路。
③ 根据老师的提示抓住老师的思路。老师在教学中经常有一些提示用语，如“请注意”、“我再重复一遍”、“这个问题的关键是····”等等，这些 用语往往体现了老师的思路。来自：学习方法网
图5－6－4
答案 (1)
gtan θ r＋Lsin θ
mg (2)cos θ
解析 (1)对座椅受力分析，如图所示．转盘转动
的角速度为ω时，钢绳与竖直方向的夹角为θ，则
座椅到转轴的距离即座椅做圆周运动的半径为R
＝r＋Lsin θ
①
根据牛顿第二定律：
mgtan θ＝mω2R
②
人教版高中物理必修二5.6向心力课件+(共12张PPT)
问题3：小车受到的力向什么方向？
实例分析1
模型建立
小球受力分析：
FN
F
OO
G
FN与G平衡，合力为F， F即提供向心力
实例分析2
FN
OO f
G
•1、“手和脑在一块干是创造教育的开始，手脑双全是创造教育的目的。” •2、一切真理要由学生自己获得，或由他们重新发现，至少由他们重建。 •3、反思自我时展示了勇气，自我反思是一切思想的源泉。 •4、好的教师是让学生发现真理，而不只是传授知识。 •5、数学教学要“淡化形式，注重实质.
6 向心力
温故知新
1．匀速圆周运动的运动性质 变速曲线运动
2．向心加速度的定义、方向、大小及r
2r
( 2 )2 r
T
物理意义：描述速度方向改变的快慢
3．牛顿第二定律的内容及表达式 F=ma
合作探究
问题1： 在实验中小车做什么运动？
问题2： 在小车运动过程中，弹簧秤的示数有何变化？
大小：
二、变速圆周运动和一般曲线运动
思考与讨论1 1.小球在最高点和最低点哪个位置的速度大？ 2.小球在运动过程中受哪些力，有何特点？
思考与讨论2 阅读课本，怎样研究一般的曲线运动？
课堂小结
一、向心力
定义：做圆周运动的物体受到的指向圆心的合力 方向：总是指向圆心，与速度方向垂直 特点：是变力，可以是重力、弹力、摩擦力等性质力，
也可以是它们的合力或某一个力的分力 作用效果：只改变速度的方向，不改变速度的大小
•8、普通的教师告诉学生做什么，称职的教师向学生解释怎么做，出色的教师示范给学生，最优秀的教师激励学生。 2021/11/162021/11/162021/11/162021/11/16
实例分析1
模型建立
小球受力分析：
FN
F
OO
G
FN与G平衡，合力为F， F即提供向心力
实例分析2
FN
OO f
G
•1、“手和脑在一块干是创造教育的开始，手脑双全是创造教育的目的。” •2、一切真理要由学生自己获得，或由他们重新发现，至少由他们重建。 •3、反思自我时展示了勇气，自我反思是一切思想的源泉。 •4、好的教师是让学生发现真理，而不只是传授知识。 •5、数学教学要“淡化形式，注重实质.
6 向心力
温故知新
1．匀速圆周运动的运动性质 变速曲线运动
2．向心加速度的定义、方向、大小及r
2r
( 2 )2 r
T
物理意义：描述速度方向改变的快慢
3．牛顿第二定律的内容及表达式 F=ma
合作探究
问题1： 在实验中小车做什么运动？
问题2： 在小车运动过程中，弹簧秤的示数有何变化？
大小：
二、变速圆周运动和一般曲线运动
思考与讨论1 1.小球在最高点和最低点哪个位置的速度大？ 2.小球在运动过程中受哪些力，有何特点？
思考与讨论2 阅读课本，怎样研究一般的曲线运动？
课堂小结
一、向心力
定义：做圆周运动的物体受到的指向圆心的合力 方向：总是指向圆心，与速度方向垂直 特点：是变力，可以是重力、弹力、摩擦力等性质力，
也可以是它们的合力或某一个力的分力 作用效果：只改变速度的方向，不改变速度的大小
•8、普通的教师告诉学生做什么，称职的教师向学生解释怎么做，出色的教师示范给学生，最优秀的教师激励学生。 2021/11/162021/11/162021/11/162021/11/16
新人教版物理必修二5.6向心力 课件 (共23张PPT)
FN=mω2r
解以上各式得： ＝
g
r
Ff FN
G
9、春去春又回，新桃换旧符。在那桃花盛开的地方，在这醉人芬芳的季节，愿你生活像春天一样阳光，心情像桃花一样美丽，日子像桃子一样甜蜜。 2021/3/62021/3/6Saturday, March 06, 2021
10、人的志向通常和他们的能力成正比例。2021/3/62021/3/62021/3/63/6/2021 3:48:57 PM 11、夫学须志也，才须学也，非学无以广才，非志无以成学。2021/3/62021/3/62021/3/6Mar-216-Mar-21 12、越是无能的人，越喜欢挑剔别人的错儿。2021/3/62021/3/62021/3/6Saturday, March 06, 2021 13、志不立，天下无可成之事。2021/3/62021/3/62021/3/62021/3/63/6/2021
向心力不是物体真实受到的一个力，不能 说物体受到向心力的作用 ，只能说某个力或 某几个力提供了向心力。
变速圆周运动和一般曲线运动
⑴ 变速圆周运动的合外力也指向圆心吗？ 变速圆周运动的速度大小是怎么改变的？
⑵ 怎么分析研究一般的曲线运动？
做变速圆周运动的物体所受的力
变速圆周
Ft
F Fn
Ft 切向分力，它产生切向加速度，改变速度的大小. Fn 向心分力，它产生向心加速度，改变速度的方向.
小球受力分析：
FN F
O
G
向心力由小球受到的桌面支持力FN、小球的重力G、绳子 的拉力的合力提供。
F向= F合= F
匀速圆周运动实例分析——向心力的来源
物体相对转盘静止，随盘做匀速圆周运动
ω FN Ff
人教版高中物理必修二第五章第六节向心力课件 (共59张PPT)
【典例 3】 一般的曲线运动可以分成很多小段，每 小段都可以看成圆周运动的一部分，即把整条曲线用一 系列不同半径的小圆弧来代替．如图甲所示，曲线上 A 点的曲率圆定义为：通过 A 点和曲线上紧邻 A 点两侧的 两点作一圆，在极限情况下，这个圆就叫作 A 点的曲率 圆，其半径 ρ 叫作 A 点的曲率半径．现将一物体沿与水 平面成 α 角的方向以速度 v0 抛出，如图乙所示．则在其 轨迹最高点 P 处的曲率半径是( )
1．有一个惊险的杂技节目叫“飞车走壁”，杂技演 员骑摩托车先在如图所示的大型圆筒底部 做速度较小、半径较小的圆周运动，通过 逐步加速，圆周运动的半径逐步增大，最后 能以较大的速度在竖直的壁上做匀速圆周运 动，这时使车子和人整体做匀速圆周运动的向心力是 ( )
A．圆筒壁对车的静摩擦力 B．筒壁对车的弹力 C．摩托车本身的动力 D．重力和摩擦力的合力
提示： 钢球在水平面内做圆周运动， 其受力如图所示， 重力 mg 和拉力 FT 的合力提供向心力，Fn＝mgtan θ.
1．向心力的特点． (1)方向：方向时刻在变化，始终指向圆心，与线速 度的方向垂直．
2 v2 4 π (2)大小：Fn＝m r ＝mrω2＝mωv＝m 2 r，在匀速圆 T
周运动中，向心力大小不变；在非匀速圆周运动中，其 大小随速率 v 的变化而变化．
v22 g2＋ R v22 2 － g R
v2 B．m R D．mg
解析： 飞机的受力情况如图所示． 飞机受到重力 mg、 空气对飞机的作用力 F，两力的合力 F 合提供向心力，方 向沿水平方向指向圆心，重力 mg 与 F
合垂直，故
F＝
2 v （mg）2＋F2 合，又 F 合＝m ，则 F＝m R
绳与竖直方向的夹角小，选项 C 错误；
