7. 弯曲应力材料力学第7章
合集下载
材料力学第7章应力状态

y
2
2 xy
m m
ax in
m
ax
2
m
in
极值切应力等于极值正应力差的一半。
§7.2 平面应力状态分析的解析法
三、极值切应力和主平面夹角
注意到 则 所以
tan
2 0
2 xy x
y
tan
21
x 2 xy
y
tan
20
1
tan 21
§7.2 平面应力状态分析的解析法
7.2.3 极值切应力及其作用面 一、极值切应力方位角
d 0 d
( x y ) cos 2 2 xy sin 2 0
得
tan
21
x 2 xy
y
二、最大、最小切应力
m m
ax
in
x
2
x
y
2
sin 2
xy cos 2
§7.2 平面应力状态分析的解析法
7.2.2 主应力 主方向 一、主应力
正应力是求极值
d d
x
y
2
(2sin 2 ) xy(2cos2 ) 0
得极值条件为
x
2
y
sin
2
xy
cos
2
0
(1) 极值正应力所在的斜面,恰好是切应力等于零的
平面,即主平面。
(2) 极值正应力就是主应力。
§7.2 平面应力状态分析的解析法
秦飞编著《材料力学》第7章 弯曲应力

危险点发 生在什么 位置?
秦飞 编著《材料力学》 第7章 弯曲应力
14
7.1 弯曲正应力
弯曲正应力公式
各种型钢的Iz、Wz值均可以从附录的型钢规格表中查到。
常用截面:矩形截面
bh 3 Iz 12
y max
h 2
bh 2 Wz 6
h
b
对于直径为D的实心圆形截面
πD Iz 64
4
ymax
C
拉
z
M
z
C
压
拉 y y
秦飞 编著《材料力学》 第7章 弯曲应力 8
7.1 弯曲正应力
纯弯曲时梁横截面上的正应力
(2)静力平衡关系 由平面假设,横截面上只有正应力σ。纯弯曲情况下,梁横 截面上的内力只有Mz=M,轴力和 My等其他内力均为零,则
dA 0
A
中性轴
z dA 0
A
由这3个静力平衡方
y
与y成正比,沿截面高
度线性变化。
秦飞 编著《材料力学》 第7章 弯曲应力
ρ为中性层曲率半径
10
7.1 弯曲正应力
纯弯曲时梁横截面上的正应力
(4)物性关系
y 将 代入物性关系,得: y E E
可见,梁横截面上的弯曲正应力 (normal stress in bending) 与y成正比, 即 (1)沿截面高度线性分布; (2)在中性层处为零,在上、下表面 处最大。
My Iz
—弯曲正应力公式
此公式适用于所有横截面具有纵向对称轴的梁,如圆形截 面、工字形截面和T形截面。 由公式: 正比于y。 沿高度线性分布。 中性轴处=0。
秦飞 编著《材料力学》 第7章 弯曲应力 13
秦飞 编著《材料力学》 第7章 弯曲应力
14
7.1 弯曲正应力
弯曲正应力公式
各种型钢的Iz、Wz值均可以从附录的型钢规格表中查到。
常用截面:矩形截面
bh 3 Iz 12
y max
h 2
bh 2 Wz 6
h
b
对于直径为D的实心圆形截面
πD Iz 64
4
ymax
C
拉
z
M
z
C
压
拉 y y
秦飞 编著《材料力学》 第7章 弯曲应力 8
7.1 弯曲正应力
纯弯曲时梁横截面上的正应力
(2)静力平衡关系 由平面假设,横截面上只有正应力σ。纯弯曲情况下,梁横 截面上的内力只有Mz=M,轴力和 My等其他内力均为零,则
dA 0
A
中性轴
z dA 0
A
由这3个静力平衡方
y
与y成正比,沿截面高
度线性变化。
秦飞 编著《材料力学》 第7章 弯曲应力
ρ为中性层曲率半径
10
7.1 弯曲正应力
纯弯曲时梁横截面上的正应力
(4)物性关系
y 将 代入物性关系,得: y E E
可见,梁横截面上的弯曲正应力 (normal stress in bending) 与y成正比, 即 (1)沿截面高度线性分布; (2)在中性层处为零,在上、下表面 处最大。
My Iz
—弯曲正应力公式
此公式适用于所有横截面具有纵向对称轴的梁,如圆形截 面、工字形截面和T形截面。 由公式: 正比于y。 沿高度线性分布。 中性轴处=0。
秦飞 编著《材料力学》 第7章 弯曲应力 13
工程力学---材料力学(第七章- 梁弯曲时位移计算与刚度设计)经典例题及详解

得: D 0
Pl 2 得: C 16
AC段梁的转角方程和挠曲线方程分别为:
P 2 2 (4 x l ) 16 EI Px y (4 x 2 3 l 2 ) 48 EI
y
P
B
A
x
l 2
C
l 2
x
最大转角和最大挠度分别为:
max A B
ymax y
q 7qa 8k 384 EI
3
q/2
B C
q/2
A B C
顺时针
q/2
例16:图示梁B处为弹性支座,弹簧刚 度
EI k 求C端挠度fC。 2a 3
q
A
EI k
B
C
2a
a
解:(1)梁不变形,仅弹簧变形引起的C点挠度为 4 3 qa 3qa B处反力=qa fC 1 2 k EI
q
B
x
l
由边界条件: x 0时,y 0
x l时,y 0
得:
ql 3 C , D0 24
梁的转角方程和挠曲线方程分别为:
y
q 2 3 3 (6lx 4 x l ) 24 EI
q
x
A qx y (2lx 2 x 3 l 3 ) 24 EI
ql 3 24 EI
A a a
q
B C
a
qa 12 EI
顺时针
3 3
P=qa
A B
P=qa
m=qɑ²/2
qa qa C B 6 EI 4 EI
4
顺时针
B
q
C
qa 5qa fC B a 8EI 24 EI
工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析,都需要求出应力的极值, 无论是强度分析还是刚度分析,都需要求出应力的极值,为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向, 到构件内最大应力的位置和方向,需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合,称为一点的 受力构件内一点处所有方位截面上应力的集合,称为一点的 研究一点的应力状态时, 应力状态 。研究一点的应力状态时,往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定: 主应力符号按代数值的大小规定:
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0
材料力学课件第七章变曲应力(土木专业)

3
46470 10 8 m 4
a
y
z
138.6 106 Pa =138.6 MPa
第七章
弯曲应力
[例2] 试求图示 T 形截面梁的最大拉应力和最大压应力。已知
Iz = 7.64×106 mm4、 y1 = 52 mm、y2 = 88 mm。
解: 1)画弯矩图
梁的最大正弯矩发生
在截面 C 上,最大负弯 矩发生在截面 B 上,分
对称弯曲
对称截面梁,在纵向对称面承受横向 外力时的受力与变形形式-对称弯曲
第七章
弯曲应力
弯 曲 试 验
第七章
试验现象
弯曲应力
(纯弯与正弯矩作用)
横线为直线, 仍与纵线正交 靠顶部纵线缩短, 靠底部纵 线伸长 纵线伸长区,截面宽度减小 纵线缩短区, 截面宽度增大 弯曲假设 横截面变形后保持平面,仍与纵线正交-弯曲平面假设 各纵向“纤维”处于单向受力状态-单向受力假设
第七章
7.1 概 述
弯曲应力
F
C
a
F
D
a
B
弯曲正应力只与弯矩有关,故 通过纯弯曲梁来研究弯曲正应力.
FS
A
纯弯曲: 梁的剪力恒为零, 弯矩为常量。
F
x
F
x
M
Fa
第七章
弯曲应力
纯弯曲
第七章
弯曲应力
.2 弯曲应力
弯曲正应力
弯曲应力
梁弯曲时横截面上的
弯曲切应力
梁弯曲时横截面上的
A ydA M
yC ydA A 0 A
(c)
(a)(b)
A ydA 0
E
中性轴通过横截面形心
(a)(c)
46470 10 8 m 4
a
y
z
138.6 106 Pa =138.6 MPa
第七章
弯曲应力
[例2] 试求图示 T 形截面梁的最大拉应力和最大压应力。已知
Iz = 7.64×106 mm4、 y1 = 52 mm、y2 = 88 mm。
解: 1)画弯矩图
梁的最大正弯矩发生
在截面 C 上,最大负弯 矩发生在截面 B 上,分
对称弯曲
对称截面梁,在纵向对称面承受横向 外力时的受力与变形形式-对称弯曲
第七章
弯曲应力
弯 曲 试 验
第七章
试验现象
弯曲应力
(纯弯与正弯矩作用)
横线为直线, 仍与纵线正交 靠顶部纵线缩短, 靠底部纵 线伸长 纵线伸长区,截面宽度减小 纵线缩短区, 截面宽度增大 弯曲假设 横截面变形后保持平面,仍与纵线正交-弯曲平面假设 各纵向“纤维”处于单向受力状态-单向受力假设
第七章
7.1 概 述
弯曲应力
F
C
a
F
D
a
B
弯曲正应力只与弯矩有关,故 通过纯弯曲梁来研究弯曲正应力.
FS
A
纯弯曲: 梁的剪力恒为零, 弯矩为常量。
F
x
F
x
M
Fa
第七章
弯曲应力
纯弯曲
第七章
弯曲应力
.2 弯曲应力
弯曲正应力
弯曲应力
梁弯曲时横截面上的
弯曲切应力
梁弯曲时横截面上的
A ydA M
yC ydA A 0 A
(c)
(a)(b)
A ydA 0
E
中性轴通过横截面形心
(a)(c)
材料力学第七章弯曲剪应力
腹板负担了截面上的绝大部分剪力,翼缘负担了 截面上的大部分弯矩。
对于标准工字钢梁:
t max
*
F SS zmax Izb
FS
b
Iz
/
S* Z max
在翼板上:
FN I
A* sⅠdA
My dA
I A* z
FN
M Iz
ydA
A*
M Iz
Sz*
FN II
A* (s Ⅱ)dA
(M dM )
即:M
dM Iz
S
* z
M Iz
S
* z
tbdx
t
S
* z
dM
Izb dx
结论:
t
FS
S
* z
Izb
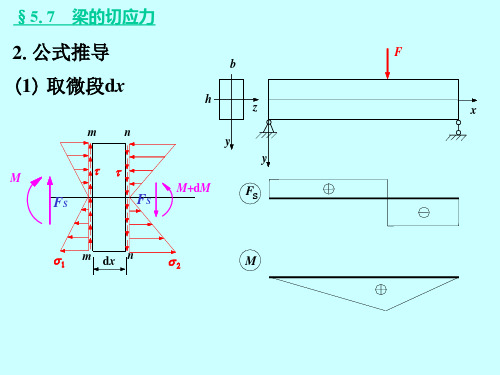
§5.7 梁的切应力
3.切应力分布规律
t
FS
S
* z
FS
h2 (
y2)
I zb 2I z 4
6FS bh3
h 2 4
y2
S* z
A*
y* C
b
h
y
y
h 2
y
2
2
b 2
h2 4
y2
用剪应力为[τ],求螺栓的最小直径?
解:叠梁承载时,每
F
梁都有自己的中性层
L
FS
F
-FL
M
h 2
1.梁的最大正应力:
h 2
b
s max
1 2
M
max
W
其中:
W
b( h )2 2
bh2
6 24
s max
M max 2W
12FL bh2
对于标准工字钢梁:
t max
*
F SS zmax Izb
FS
b
Iz
/
S* Z max
在翼板上:
FN I
A* sⅠdA
My dA
I A* z
FN
M Iz
ydA
A*
M Iz
Sz*
FN II
A* (s Ⅱ)dA
(M dM )
即:M
dM Iz
S
* z
M Iz
S
* z
tbdx
t
S
* z
dM
Izb dx
结论:
t
FS
S
* z
Izb
§5.7 梁的切应力
3.切应力分布规律
t
FS
S
* z
FS
h2 (
y2)
I zb 2I z 4
6FS bh3
h 2 4
y2
S* z
A*
y* C
b
h
y
y
h 2
y
2
2
b 2
h2 4
y2
用剪应力为[τ],求螺栓的最小直径?
解:叠梁承载时,每
F
梁都有自己的中性层
L
FS
F
-FL
M
h 2
1.梁的最大正应力:
h 2
b
s max
1 2
M
max
W
其中:
W
b( h )2 2
bh2
6 24
s max
M max 2W
12FL bh2
材料力学第七章 应力状态

主平面的方位:
tan
2a0
2 xy x
y
主应力与主平面的对应关系: max 与切应力的交点同象限
例题:一点处的平面应力状态如图所示。
已知 x 60MPa, xy 30MPa, y 40MPa, a 30。
试求(1)a 斜面上的应力; (2)主应力、主平面; (3)绘出主应力单元体。
x y cos 2a
2
x sin 2a
x
a
x y sin 2a
2
x cos 2a
300
10 30 2
10 30 cos 60020sin 600
2
2.32 MPa
300
10 30 sin 600 2
20cos 600
1.33 MPa
a
20 MPa
c
30 MPa
b
n1
y xy
a x
解:(1)a 斜面上的应力
y xy
a
x
2
y
x
2
y
cos 2a
xy
sin 2a
60 40 60 40 cos(60 ) 30sin(60 )
2
2
a x 9.02MPa
a
x
y
2
sin
2a
xy
cos
2a
60 40 sin(60 ) 30cos(60 ) 2
58.3MPa
2
1.33 MPa
300 600 x y 40 MPa
在二向应力状态下,任意两个垂直面上,其σ的和为一常数。
在二向应力状态下,任意两个垂直面上,其σ 的和为
一常数。
证明: a
x y
材料力学-7-应力状态分析

7.1 应力状态的基本概念
y
y
1 1 4
z
4
Mz
x
x
l
S FP
2
3
Mx
z
3
a
第7章 应力状态分析
7.2 平面应力状态任意方向面上的应力 ——解析法
7.2 平面应力状态任意方向面上的应力 ——解析法
一、方向角与应力分量的正负号约定
x
正应力
x
x
拉为正
压为负
x
7.2 平面应力状态任意方向面上的应力 ——解析法
?
第7章 应力状态分析 7.1 应力状态的基本概念
7.2 平面应力状态任意方向面上的应力 ——解析法 7.3 主应力、主平面与面内最大切应力 ——解析法 7.4 应力圆及其应用——图解法
7.5 三向应力状态的特例分析
7.6 广义胡克定律
7.7 应变能密度
第7章 应力状态分析
tan 2q p=- 2 τ
xy
x y
主平面(principal plane):切应力q=0的方向面,用 qp表示。 主应力(principal stress):主平面上的正应力。 主方向(principal directions):主平面法线方向,用方 向角qp表示。
7.3 主应力、主平面与面内最大切应力 ——解析法
第7章 应力状态分析
第7章 应力状态分析
1
3
2
max
max
拉压、弯曲正应力 扭转、弯曲切应力
这些强度问题的共同特点是:
1、危险截面上的危险点只承受正应力 或切应力; 2、都是通过实验直接确定失效时的极限应力,并以此为依据建立强度 设计准则。 复杂受力:危险截面上危险点同时承受正 应力和切应力,或者危险点的其他面上同 时承受正应力或切应力。 → 强度条件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FN2 FN1 τ'bdx 0
τ' dM S*z dx Izb
由 τ' τ
和
dM dx
FQ
τ FQS*z Izb
FQ━━横截面上的剪力,
(7-5)
为横截面对中性轴的惯性矩,
b ━━截面宽度
S*z ━━横截面上部分面积对中性轴的静矩
(7-5)
工程力学系
第七章 弯曲应力
S*Z A1 y1dA yh/2by1dy1
工程力学系
第七章 弯曲应力
第七章 弯曲应力
7.1 引言 7.2 弯曲正应力 7.37-1弯引曲言切应力 7.4 弯曲强度计算 7.5 提高弯曲强度的一些措施 7.6 开口薄壁杆件的弯曲中心
工程力学系
第七章 弯曲应力
本章任务:
7.1 引言
1)梁的弯曲应力计算 2)梁的弯曲强度计算
横截面上的内力━━剪力 FQ 和弯矩 M
Pa
28.8M Pa
拉压强度条件均满足
工程力学系
第七章 弯曲应力
7.5 提高弯曲强度的一些措施
7.5.1 合理安排梁的支座和载荷
M max
1 8
ql 2
M max
1 ql 2 40
适当地调整梁的支座位置,可以降低最大弯矩值
工程力学系
第七章 弯曲应力
M max
1 Fl 4
1
M max
Fl 8
M max
τy
FQS*z 2tI z
环形截面的最大切应力计算:
先求半圆环对中性轴的静矩
(7-15)
S*Z A1 ydA 20/ 2 R cos θtRdθ 2R 2t
及环形截面对中性轴的惯性矩
I z A y2dA 202 R 2 cos2 θtRdθ R3t
得到
tmax
FQ (2R 2t) 2tR 3t
Pa 10.5MPa
b点
S*z
Ab
yb
40
( 70 2
15) 106
[15
1 2
(70 2
15)]103 m3
2 105 m3
tb
FQ1S*z Izb
40 103 2 105 1.143106 40 10
3
Pa
17.5MPa
工程力学系
7.3.2 工字形截面梁的切应力 7.1 引言
第七章 弯曲应力
c
d
b
工程力学系
第七章 弯曲应力
解: 1)求 Iz
解: 1.求 Iz
2)求s
Iz
(D4 d 4 ) 64
π(504 254 ) (103)4 m4 64
2.88107 m4
a点
sa
M Iz
ya
1103 .88 107
25 103 Pa
86.8MPa(压应力)
b点
sb
c点
M Iz
yb
1103 .88 107
工程力学系
7.3.3 圆形截面梁的切应力
第七章 弯曲应力
τy
FQS*z Izb
式中b为弦线长度 , b 2 R2 y2
(7-13)
工程力学系
圆形截面梁的最大切应力为
t max
4 3
FQ R 2
7.3.4 环形截面梁的切应力
第七章 弯曲应力
(7-14)
工程力学系
第七章 弯曲应力
环形截面梁切应力的计算公式
52mm,试校核梁的强度。
例7-4 T形截面铸铁梁的载荷和截面尺寸如图所示,
[sc ] 30MPa,[st ] 140MPa,Iz 763cm4, y1 52mm
试校核梁的强度。
工程力学系
第七章 弯曲应力
解 FA 2.5kN, FB 10.5kN
MC 2.5kN.m, M B 4kN.m
1.横截面上各点切应力的方向均与剪
力FQ的方向平行。 2.切应力沿截面宽度均匀分布。
工程力学系
第七章 弯曲应力
FN2
A1σ nsdA
M
A1
dM Iz
y1dA
M
dM Iz
A1
y1dA
M
dM Iz
S*z
FN1
M Iz
S*z
工程力学系
第七章 弯曲应力
考虑截出部分mnsr的平衡,见图(c).由 Fx 0 得
计算公式仍然是适用的,其结果能够 满足工程精度要求.
工程力学系
第七章 弯曲应力
例7-2 槽形截面梁如图(a)所示,试求梁横截面上的最大拉应力。
解: 绘M图,得B、C两截面的弯矩
MB 10kN.m MC 7.5kN.m
如图(b)所示
工程力学系
第七章 弯曲应力
求截面的形心及对形心轴的惯性矩,取参考坐标z1Oy,
横截面上的应力——正应力 s 和切应力t
横截面上内力与应力的关系:
FQ ~ t M ~ s
横截面上的弯矩只与该截面上的正应力有关 横截面上的剪力只与该截面上的切应力有
工程力学系
第七章 弯曲应力
7.2 弯曲正应力
7.2.1 纯弯曲梁的正应力应力
纯弯曲━━梁的各横截面上只有弯矩,而剪力为零 横力弯曲━━梁的各横截面上,同时存在着剪力和弯矩
1.工字形截面腹板部分的切应力
考虑图(b)的mnsr部分的平衡,可得腹板的切应力
计算公式
τ FQS*z Izd
(7-9)
工程力学系
第七章 弯曲应力
由于
S*z
1 (H 22
h)b( H 22
h) 2
1 (h 22
y)d ( h 2
y)
t
FQ
[b(H
2
h2)
h2 4d (
y 2 )]
8I z d
4
第七章 弯曲应力
b'b' ( y)d
bb OO O'O' d
变形前
变形后
b'b'bb ( y)d d y
bb
d
(a)
工程力学系
第七章 弯曲应力
物理方面 s E E y
(b)
纯弯曲时的正应力在y方向按线性规律变化 静力学方面
工程力学系
平衡条件
第七章 弯曲应力
Fx 0
,
5 Fl 36
使集中载荷适当分散和使集载荷尽 可能靠近支座均能降低最大弯矩
工程力学系
7.5.2 采用合理的截面形状
第七章 弯曲应力
值越大,截面越趋于合理
bh 2 Wz 6 h A bh 6
b2h Wz 6 b A bh 6
Wz 值越大,截面越趋于合理 A
工程力学系
第七章 弯曲应力
M max y1
BC段:纯弯曲
AB 和 CD段:横力弯曲
工程力学系
第七章 弯曲应力
纯弯曲梁横截面上正应力的分析方法: 变形方面、物理方面和静力学方面 实验和观察
变形前
变形后
梁内部的变形的基本假设:
(1)平面假设 (2) 单向受力假设
工程力学系
第七章 弯曲应力
概念和术语: 对称轴,中性轴,中性层
工程力学系
变形方面
对于矩形截面
Wz
bh3 /12 h/2
bh 2 6
(7-3) (7-4)
对于圆形截面
Wz
D4 / 64 D/2
πD3 32
工程力学系
第七章 弯曲应力
例7-1 受纯弯曲的空心圆截面梁如图(a)所示。
已知:弯矩M= l kN.m,外径D=50mm,内径d=25mm。 试求横截面上a、b、c及d四点的应力,并绘过a、b两点的 直径线及过c、d两点弦线上各点的应力分布图。
{ 1 12
350
5003
350 500
(317
250) 2
[ 1 250 4003 250 300 (317 200)2 ]}mm4 12
1728106 mm4
工程力学系
第七章 弯曲应力
B截面的最大拉应力为
s Bt
MB Iz
ymax
B截面1的0最大拉1应0力3为 (500 317) 103 1728 106 (103 )4
b ( h2 y2) 24
t FQ ( h2 y 2 ) 2Iz 4
(7-6)
t max
FQh2 8Iz
t max
3FQ 2bh
(7-7)
t
G
FQ ( h2 y 2 ) (7-8)
2GIz 4
最大切应力发生在中性轴上, 上、下边缘线上各点的切应力为零,
切应力沿截面高度按抛物线规律变化
工程力学系
第七章 弯曲应力
例7-3 矩形截面梁的横截面尺寸如图(b)所示。集中力F=88kN,
试求1-1截面上的最大切应力以及a、b两点的切应力。
解: 支反力FA、FB分别为
FA=40kN,FB=48kN
1-1截面上的剪力 FQ1=FA=40kN
Iz
40 703 12
(103 )4 m4
1.143106 m4
σt
M B y1 Iz
4 103 52 103
Pa 27.2MPa
763 (10 ) 2 4 解 由静力平衡方程求出梁的支反力为
σc
MBy2 Iz
40 103 (120 20 52) 103 Pa 46.2MPa 763 (102 )4
σt
MC
y 2
Iz
2.5 103
(120 20 52) 103 763 (102 )4
Pa
1.06MPa
C截面的最大拉应力为
sCt
