半导体物理第六、七章习题答案
半导体物理第七章参考答案
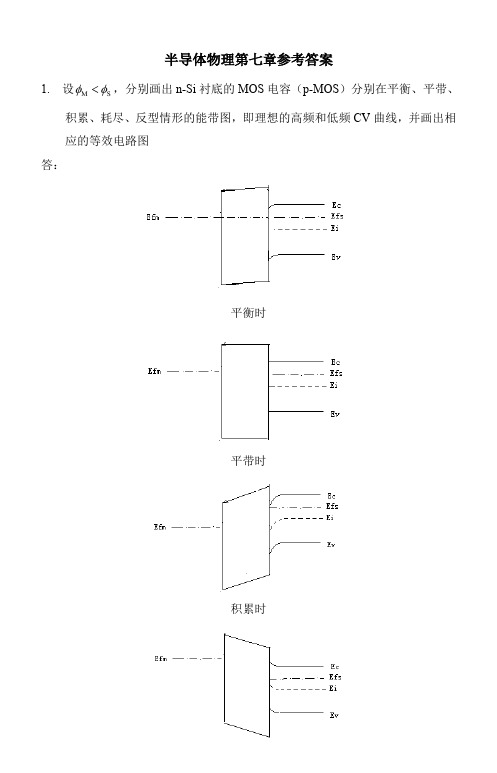
半导体物理第七章参考答案1. 设M S φφ<,分别画出n-Si 衬底的MOS 电容(p-MOS )分别在平衡、平带、积累、耗尽、反型情形的能带图,即理想的高频和低频CV 曲线,并画出相应的等效电路图 答:平衡时平带时积累时耗尽时弱反时强反时理想的高频和低频CV曲线等效电路图2. 设氧化层厚度为1μm 的Si MOS 结构的p 型衬底的掺杂浓度分别为N =1015/cm 3和1016/cm 3,比较这两种结构的耗尽层电容和MOS 电容的极小值。
答:1) 耗尽层电容由耗尽层厚度决定,而耗尽层厚度与Si 表面势有关,根据耗尽层厚度、表面势,可求得耗尽层电容为:()d Sid sdd Q C d W εψ-==又由MOS 电容为氧化层电容与耗尽层电容串联而成:dox C C C 111+= 以及栅压方程:g fb s oxV V ψ-=消去表面势s ψ,可得:C =显然,相同氧化层厚度,即相同氧化层电容,相同栅压下,衬底掺杂浓度高的MOS 结构耗尽层电容大。
2) 由C =MOS 电容的极小值出现在强反型时,此时耗尽层厚度最大,表面势为2B φ:max d W ==min maxSid d C W ε==则:1minmin 11ox d C C C -⎛⎫=+ ⎪⎝⎭当N =1015/cm 3时,12min min 1126.7ox d C F m C C μ-⎛⎫=+= ⎪⎝⎭当N =1016/cm 3时,12min min 1131.3ox d C F m C C μ-⎛⎫=+= ⎪⎝⎭3. 从物理上说明F B i C C 随氧化层厚度及掺杂浓度的变化趋势,并计算315/10cm N =,nm t ox 10=的Si MOS 结构的FB i C C 值和德拜长度。
答:由公式:11ox D FB i Si ox t L C C εε=+=+有:11FB D i iSi C L C C ε==+ 其中oxi oxC t ε=。
半导体物理学(刘恩科)第七版-完整课后题答案)

半导体物理学(刘恩科)第七版-完整课后题答案)第⼀章习题1.设晶格常数为a 的⼀维晶格,导带极⼩值附近能量(k)和价带极⼤值附近能量(k)分别为:220122*********)(,)(3m k h m k h k E m k k h m k h V -=-+ 0m 。
试求:为电⼦惯性质量,nm a ak 314.0,1==π(1)禁带宽度;(2)导带底电⼦有效质量; (3)价带顶电⼦有效质量;(4)价带顶电⼦跃迁到导带底时准动量的变化解:(1)eV m k E k E E E k m dk E d k m kdk dE Ec k k m m m dk E d k k m k k m k V C g V V V c 64.012)0()43(0,060064338232430)(2320212102220202020222101202==-==<-===-==>=+===-+ηηηηηηηη因此:取极⼤值处,所以⼜因为得价带:取极⼩值处,所以:在⼜因为:得:由导带:043222*83)2(1m dk E d mk k C nC===η sN k k k p k p m dk E d mk k k k V nV/1095.7043)()()4(6)3(25104300222*11-===?=-=-=?=-==ηηηηη所以:准动量的定义:2. 晶格常数为0.25的⼀维晶格,当外加102,107的电场时,试分别计算电⼦⾃能带底运动到能带顶所需的时间。
解:根据:t khqE f== 得qE k t -?=?ηsat sat 137192821911027.810106.1)0(1027.810106.1)0(----?=??--==--=ππηη补充题1分别计算(100),(110),(111)⾯每平⽅厘⽶内的原⼦个数,即原⼦⾯密度(提⽰:先画出各晶⾯内原⼦的位置和分布图)在(100),(110)和(111)⾯上的原⼦分布如图1所⽰:(a )(100)晶⾯(b )(110)晶⾯(c )(111)晶⾯补充题2214221422142822/1083.7342232212414111/1059.92422124142110/1078.6)1043.5(224141100cmatom a a a cm atom a a a cm atom a a ?==?+?+??==??+?+?=?==?+-):():():(⼀维晶体的电⼦能带可写为)2cos 81cos 87()22ka ka ma k E +-=η(,式中a 为晶格常数,试求(1)布⾥渊区边界;(2)能带宽度;(3)电⼦在波⽮k 状态时的速度;(4)能带底部电⼦的有效质量*n m ;(5)能带顶部空⽳的有效质量*p m 解:(1)由0)(=dk k dE 得 an k π=(0,1,2…)进⼀步分析an k π)12(+= ,E (k )有极⼤值,222)ma k E MAXη=(ank π2=时,E (k )有极⼩值所以布⾥渊区边界为an k π)12(+= (2)能带宽度为222)()ma k E k E MINMAXη=-((3)电⼦在波⽮k 状态的速度)2sin 41(sin 1ka ka ma dk dE v -==ηη(4)电⼦的有效质量)2cos 21(cos 222*ka ka m dkEd m n-==η能带底部 an k π2=所以m m n 2*=(5)能带顶部 an k π)12(+=,且**n p m m -=,所以能带顶部空⽳的有效质量32*mm p=半导体物理第2章习题1. 实际半导体与理想半导体间的主要区别是什么?答:(1)理想半导体:假设晶格原⼦严格按周期性排列并静⽌在格点位置上,实际半导体中原⼦不是静⽌的,⽽是在其平衡位置附近振动。
半导体物理学第七版完整答案修订版

半导体物理学第七版完整答案修订版IBMT standardization office【IBMT5AB-IBMT08-IBMT2C-ZZT18】第一章习题1.设晶格常数为a 的一维晶格,导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为:E C (K )=0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ (1)禁带宽度;(2)导带底电子有效质量;(3)价带顶电子有效质量;(4)价带顶电子跃迁到导带底时准动量的变化解:(1)2. 晶格常数为0.25nm 的一维晶格,当外加102V/m ,107 V/m 的电场时,试分别计算电子自能带底运动到能带顶所需的时间。
解:根据:tkhqE f ∆∆== 得qE k t -∆=∆补充题1分别计算Si (100),(110),(111)面每平方厘米内的原子个数,即原子面密度(提示:先画出各晶面内原子的位置和分布图)Si 在(100),(110)和(111)面上的原子分布如图1所示:(a )(100)晶面 (b )(110)晶面(c )(111)晶面补充题2一维晶体的电子能带可写为)2cos 81cos 87()22ka ka ma k E +-=(, 式中a 为 晶格常数,试求(1)布里渊区边界;(2)能带宽度;(3)电子在波矢k 状态时的速度;(4)能带底部电子的有效质量*n m ;(5)能带顶部空穴的有效质量*p m解:(1)由0)(=dk k dE 得 an k π= (n=0,?1,?2…)进一步分析an k π)12(+= ,E (k )有极大值,ank π2=时,E (k )有极小值所以布里渊区边界为an k π)12(+=(2)能带宽度为222)()mak E k E MINMAX =-( (3)电子在波矢k 状态的速度)2sin 41(sin 1ka ka ma dk dE v -==(4)电子的有效质量能带底部 an k π2=所以m m n2*= (5)能带顶部 an k π)12(+=, 且**n p m m -=,所以能带顶部空穴的有效质量32*mm p =半导体物理第2章习题1. 实际半导体与理想半导体间的主要区别是什么答:(1)理想半导体:假设晶格原子严格按周期性排列并静止在格点位置上,实际半导体中原子不是静止的,而是在其平衡位置附近振动。
半导体物理习题第六章第七章答案

第6章 p-n 结1、一个Ge 突变结的p 区和n 区掺杂浓度分别为N A =1017cm -3和N D =5⨯1015cm -3,求该pn 结室温下的自建电势。
解:pn 结的自建电势 2(ln )D A D iN N kTV q n =已知室温下,0.026kT =eV ,Ge 的本征载流子密度1332.410 cm i n -=⨯代入后算得:1517132510100.026ln 0.36(2.410)D V V ⨯⨯=⨯=⨯ 4.证明反向饱和电流公式(6-35)可改写为20211()(1)i s n n p pb k T J b q L L σσσ=++ 式中npb μμ=,n σ和p σ分别为n 型和p 型半导体电导率,i σ为本征半导体电导率。
证明:将爱因斯坦关系式p p kT D q μ=和n n kT D qμ=代入式(6-35)得 0000()p n pnS p n n p npn pp nn p J kTn kTp kT L L L L μμμμμμ=+=+因为002i p p n n p =,02i n n n p n =,上式可进一步改写为221111()()S n p i n p i n p p p n n n pp nJ kT n qkT n L p L n L L μμμμμμσσ=+=+又因为()i i n p n q σμμ=+22222222()(1)i i n p i p n q n q b σμμμ=+=+即22222222()(1)i i i n p p n q q b σσμμμ==++ 将此结果代入原式即得证2222221111()()(1)(1)n p i i S p n p p n n p p nqkT b kT J q b L L q b L L μμσσμσσσσ=+=⋅⋅+++ 注:严格说,迁移率与杂质浓度有关,因而同种载流子的迁移率在掺杂浓度不同的p 区和n区中并不完全相同,因而所证关系只能说是一种近似。
半导体物理学(刘恩科)第六第七版第1234578章完整课后题答案

第一章习题1.设晶格常数为a 的一维晶格,导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为:E C(K )=0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ 0m 。
试求:为电子惯性质量,nm a ak 314.0,1==π(1)禁带宽度;(2)导带底电子有效质量; (3)价带顶电子有效质量;(4)价带顶电子跃迁到导带底时准动量的变化 解:(1)eVm k E k E E E k m dk E d k m kdk dE Ec k k m m m dk E d k k m k k m k V C g V V V c 64.012)0()43(0,060064338232430)(2320212102220202020222101202==-==<-===-==>=+===-+ 因此:取极大值处,所以又因为得价带:取极小值处,所以:在又因为:得:由导带:043222*83)2(1m dk E d mk k C nC===sN k k k p k p m dk E d mk k k k V nV/1095.7043)()()4(6)3(25104300222*11-===⨯=-=-=∆=-== 所以:准动量的定义:2. 晶格常数为0.25nm 的一维晶格,当外加102V/m ,107 V/m 的电场时,试分别计算电子自能带底运动到能带顶所需的时间。
解:根据:tkhqE f ∆∆== 得qE k t -∆=∆sat sat 137192821911027.810106.1)0(1027.810106.1)0(----⨯=⨯⨯--=∆⨯=⨯⨯--=∆ππ补充题1分别计算Si (100),(110),(111)面每平方厘米的原子个数,即原子面密度(提示:先画出各晶面原子的位置和分布图)Si 在(100),(110)和(111)面上的原子分布如图1所示:(a )(100)晶面 (b )(110)晶面(c )(111)晶面补充题2一维晶体的电子能带可写为)2cos 81cos 87()22ka ka ma k E +-= (, 式中a 为 晶格常数,试求(1)布里渊区边界; (2)能带宽度;(3)电子在波矢k 状态时的速度; (4)能带底部电子的有效质量*n m ;(5)能带顶部空穴的有效质量*p m 解:(1)由0)(=dk k dE 得 an k π= (n=0,±1,±2…) 进一步分析an k π)12(+= ,E (k )有极大值,214221422142822/1083.7342232212414111/1059.92422124142110/1078.6)1043.5(224141100cm atom a a a cm atom a a a cm atom a a ⨯==⨯+⨯+⨯⨯==⨯⨯+⨯+⨯=⨯==⨯+-):():():(222)mak E MAX=( ank π2=时,E (k )有极小值所以布里渊区边界为an k π)12(+=(2)能带宽度为222)()ma k E k E MIN MAX =-( (3)电子在波矢k 状态的速度)2sin 41(sin 1ka ka ma dk dE v -== (4)电子的有效质量)2cos 21(cos 222*ka ka mdkEd m n-==能带底部 an k π2=所以m m n 2*= (5)能带顶部 an k π)12(+=, 且**n p m m -=,所以能带顶部空穴的有效质量32*mm p =半导体物理第2章习题1. 实际半导体与理想半导体间的主要区别是什么?答:(1)理想半导体:假设晶格原子严格按周期性排列并静止在格点位置上,实际半导体中原子不是静止的,而是在其平衡位置附近振动。
半导体物理学刘恩科习题答案权威修订版

半导体物理学 刘恩科第七版习题答案---------课后习题解答一些有错误的地方经过了改正和修订!第一章 半导体中的电子状态1.设晶格常数为a 的一维晶格,导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为:220122021202236)(,)(3Ec m k m k k E m k k m k V0m 。
试求:为电子惯性质量,nm a ak 314.0,1(1)禁带宽度;(2)导带底电子有效质量; (3)价带顶电子有效质量;(4)价带顶电子跃迁到导带底时准动量的变化 解:10911010314.0=ak (1)J m k m k m k E k E E m k k E E k m dk E d k m kdk dE J m k Ec k k m m m dk E d k k m k k m k dk dE V C g V V V V c C 17312103402120122021210122022202173121034021210202022210120210*02.110108.912)1010054.1(1264)0()43(6)(0,0600610*05.310108.94)1010054.1(4Ec 43038232430)(232因此:取极大值处,所以又因为得价带:取极小值处,所以:在又因为:得:由导带:043222*83)2(1m dk E d mk k C nCs N k k k p k p m dk E d mk k k k V nV/1095.71010054.14310314.0210625.643043)()()4(6)3(251034934104300222*11所以:准动量的定义:2. 晶格常数为0.25nm 的一维晶格,当外加102V/m ,107V/m 的电场时,试分别计算电子自能带底运动到能带顶所需的时间。
解:根据:tkqE f得qE k ts a t s a t 137192821993421911028.810106.1)0(1028.810106.11025.0210625.610106.1)0(第二章 半导体中杂质和缺陷能级7. 锑化铟的禁带宽度Eg=0.18eV ,相对介电常数 r =17,电子的有效质量*n m =0.015m 0, m 0为电子的惯性质量,求①施主杂质的电离能,②施主的弱束缚电子基态轨道半径。
半导体物理学(刘恩科第七版)课后答案(完整版)-阳光大学生网
1000 3L3
欢迎光临阳光大学生网,提供最全面的大学生课后习题答案和复习试题免费下载,/
2. 试证明实际硅、锗中导带底附近状态密度公式为式(3-6) 。
2.证明:si、Ge 半导体的E(IC) ~ K关系为
2 2 h 2 k x k y k z2 E( EC ( ) C k) 2 mt ml ' 令k x ( 1 ma m 1 m 1 ' ) 2 kx , ky ( a ) 2 k y , k z' ( a ) 2 k z mt mt ml
2 8 mn l
1 Z0 V 4 (
Ec
100 h 2
2 8 mn l
EC * n
g ( E )dE
3 2
EC
2
4 (
1 * 3 2m n 2 2 ) ( E E ) dE C 2 h
2m ) h2
2 ( E EC ) 3
3
Ec Ec
100h 2 2 8mn L
欢迎光临阳光大学生网,提供最全面的大学生课后习题答案和复习试题免费下载,/
第三章习题
1. 计算能量在 E=Ec 到 E E C 解:
100h 2 之间单位体积中的量子态数。 2 8m * nL
1 * 3 2m n 2 g ( E ) 4 ( 2 ) ( E EC ) 2 V h dZ g ( E )dE dZ 单位体积内的量子态数Z 0 V Ec 100 h 2
所以布里渊区边界为 k ( 2n 1)
a 2 2 ma 2
(2)能带宽度为 E(k ) MAX E ( k ) MIN (3)电子在波矢 k 状态的速度 v (4)电子的有效质量
半导体物理学习题答案(有目录)
半导体物理学习题答案(有目录)半导体物理习题解答目录1-1.(P32)设晶格常数为a的一维晶格,导带极小值附近能量E c(k)和价带极大值附近能量E v(k)分别为: (2)1-2.(P33)晶格常数为0.25nm的一维晶格,当外加102V/m,107V/m的电场时,试分别计算电子自能带底运动到能带顶所需的时间。
(3)3-7.(P81)①在室温下,锗的有效状态密度Nc=1.05×1019cm-3,Nv=5.7×1018cm-3,试求锗的载流子有效质量mn*和mp*。
(3)3-8.(P82)利用题7所给的Nc和Nv数值及Eg=0.67eV,求温度为300k和500k时,含施主浓度ND=5×1015cm-3,受主浓度NA=2×109cm-3的锗中电子及空穴浓度为多少? (4)3-11.(P82)若锗中杂质电离能△ED=0.01eV,施主杂质浓度分别为ND=1014cm-3及1017cm-3,计算(1)99%电离,(2)90%电离,(3)50%电离时温度各为多少? (5)3-14.(P82)计算含有施主杂质浓度ND=9×1015cm-3及受主杂质浓度为1.1×1016cm-3的硅在300k 时的电子和空穴浓度以及费米能级的位置。
(6)3-18.(P82)掺磷的n型硅,已知磷的电离能为0.04eV,求室温下杂质一般电离时费米能级的位置和磷的浓度。
(7)3-19.(P82)求室温下掺锑的n型硅,使EF=(EC+ED)/2时的锑的浓度。
已知锑的电离能为0.039eV。
(7)3-20.(P82)制造晶体管一般是在高杂质浓度的n型衬底上外延一层n型的外延层,再在外延层中扩散硼、磷而成。
①设n型硅单晶衬底是掺锑的,锑的电离能为0.039eV,300k时的EF位于导带底下面0.026eV处,计算锑的浓度和导带中电子浓度。
(8)4-1.(P113)300K时,Ge的本征电阻率为47Ω.cm,如电子和空穴迁移率分别为3900cm2/V.S和1900cm2/V.S,试求本征Ge的载流子浓度。
半导体物理课后习题(保密)
解: 须先求出本征载流子浓度ni,即
代入数据得,ni=1.86 ×1013cm-3 根据电中性条件有 p0+ND+=n0+NA-
ni
q( n p )
i
1 i ( n p )
联立 载流子浓度公式
n0p0=ni2
可求解得 n0=3.89 ×1013cm-3, p0=8.89 ×1012cm-3 所以样品的电导率为:
解: 由图3-7查得T=500k时,Si的本征载流子浓度ni=3.5×1014cm-3 联立方程
p0=ni2/n0
解得, ND=3.5×1014cm-3时,n0≈4.3×1014cm-3, p0=2.8×1014cm-3 —— n0,p0差别不显著,杂质导电特性不很明显 ND=1012cm-3时,n0≈ni=3.5×1014cm-3, p0=3.5×1014cm-3,即n0=p0. —— 进入本征 半导体材料在某一温度下所处的区域与杂质浓度相关 或 杂质浓度不同,材料进入同一区域所需要的温度不一样。
m0为电子惯性质量,k1=1/2a; a=0.314nm。试求: (1)禁带宽度; (2)导带底电子有效质量; (3)价带顶电子有效质量; (4)价带顶电子跃迁到导带底时准动量的变化。
练习2-课后习题2
第一章 半导体中的电子状态
2.晶格常数为0.25nm的一维晶格,当外加102V/m和107V/m 的电 场时,试分别计算电子自能带底运动到能带顶所需的时间。
作业-课后习题14
第三章 半导体中载流子的统计分布
计算含有施主杂质浓度ND=9×1015cm-3与受主杂质浓度为1.1×1016cm-3 的硅在室温时的电子和空穴浓度以及费米能级的位置。
刘恩科半导体物理第六章课后习题最全答案
d 2V x 0 2 dx dV x x c dx
令 V 0 0 ,则 A 0 ,V x cx
E(x) c<0 0 V(x) x c>0 c>0
dV x V x dx x dx cx A dx
2 11.6 8.85 10 14 0.94 19 16 1.6 10 10
1 2
12.2 10
1 10 2
3.5 105 cm
(2) 画出 x 和 V x 的图线
+ + + + + + + + V + + + + + + + +
kT n , p kT p ,Ln Dn n , 又 Dn D q q L p D p p
Jp Jn D p N A Ln Dn N D L p
p N A Dn n n N D D p p
p N A n n n N D p p
1.56 10 x 3.47 10
9
5
V
cm
2
2 x
dV x dx
2
qN D x n
1.56 109 x 3.47 109 V cm2
V1 x qN A x 2 r 0
8 2 p
r 0
J s 400 6 10 1.6 10 5 J s 300 1.5 10 10
12 2
解法二:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章课后习题解析1.一个Ge 突变结的p 区n 区掺杂浓度分别为N A =1017cm -3和N D =5⨯1015cm -3,该pn 结室温下的自建电势。
解:pn 结的自建电势 2(ln )D A D iN N kTV q n =已知室温下,0.026kT =eV ,Ge 的本征载流子密度1332.410 cm i n -=⨯代入后算得:1517132510100.026ln 0.36(2.410)D V V ⨯⨯=⨯=⨯ 4.证明反向饱和电流公式(6-35)可改写为20211()(1)i s n n p pb k T J b q L L σσσ=++ 式中npb μμ=,n σ和p σ分别为n 型和p 型半导体电导率,i σ为本征半导体电导率。
证明:将爱因斯坦关系式p p kT D q μ=和n n kT D qμ=代入式(6-35)得 0000()p n pnS p n n p npn pp nn p J kTn kTp kT L L L L μμμμμμ=+=+因为002i p p n n p =,002i n n n p n =,上式可进一步改写为221111()()S n p i n p i n p p p n n n pp nJ kT n qkT n L p L n L L μμμμμμσσ=+=+又因为()i i n p n q σμμ=+22222222()(1)i i n p i p n q n q b σμμμ=+=+即22222222()(1)i i i n p p n q q b σσμμμ==++ 将此结果代入原式即得证2222221111()()(1)(1)n p i i S p n p p n n p p nqkT b kT J q b L L q b L L μμσσμσσσσ=+=⋅⋅+++注:严格说,迁移率与杂质浓度有关,因而同种载流子的迁移率在掺杂浓度不同的p区和n 区中并不完全相同,因而所证关系只能说是一种近似。
2.试分析小注入时,电子(空穴)在5个区域中的运动情况(分析漂移和扩散的方向及相对大小)答:正向小注入下,P区接电源正极,N区接电源负极,势垒高度降低,P区空穴注入N区,N区电子注入P区。
注入电子在P区与势垒区交界处堆积,浓度高于P区平衡空穴浓度,形成流向中性P区的扩散流,扩散过程中不断与中性P区漂移过来的空穴复合,经过若干扩散长度后,全部复合。
注入空穴在N区与势垒区交界处堆积,浓度比N区平衡电子浓度高,形成浓度梯度,产生流向中性N区的空穴扩散流,扩散过程中不断与中性N区漂移过来的电子复合,经过若干扩散长度后,全部复合。
3.在反向情况下坐上题。
答:反向小注入下,P区接电源负极,N区接电源正极,势垒区电场强度增加,空间电荷增加,势垒区边界向中性区推进。
势垒区与N区交界处空穴被势垒区强电场驱向P区,漂移通过势垒区后,与P区中漂移过来的空穴复合。
中性N区平衡空穴浓度与势垒区与N区交界处空穴浓度形成浓度梯度,不断补充被抽取的空穴,对PN结反向电流有贡献。
同理,势垒区与P区交界处电子被势垒区强电场驱向N区,漂移通过势垒区后,与N区中漂移过来的电子复合。
中性P区平衡电子浓度与势垒区与P区交界处电子浓度形成浓度梯度,不断补充被抽取的电子,对PN结反向电流有贡献。
反向偏压较大时,势垒区与P区、N区交界处的少子浓度近似为零,少子浓度梯度不随外加偏压变化,反向电流饱和。
5.一硅突变pn 结的n 区ρn =5Ω⋅cm ,τp =1μs ;p 区ρp =0.1Ω⋅cm ,τn =5μs ,计算室温下空穴电流与电子电流之比、饱和电流密度,以及在正向电压0.3V 时流过p-n 结的电流密度。
解:由5n cm ρ=Ω⋅,查得143910D N cm -=⨯,3420/p cm V s μ=⋅由0.1p cm ρ=Ω⋅,查得173510A N cm -=⨯,3500/n cm V s μ=⋅∴由爱因斯坦关系可算得相应的扩散系数分别为2142010.5 cm /40p p kT Ds q μ==⨯=,2150012.5 cm /40n n kT D s q μ==⨯= 相应的扩散长度即为33.2410p L cm-===⨯37.910n L cm -===⨯对掺杂浓度较低的n 区,因为杂质在室温下已全部电离,0143910n n cm -=⨯,所以0021025314(1.510) 2.510910i n n n p cm n -⨯===⨯⨯ 对p 区,虽然N A =5⨯1017cm -3时杂质在室温下已不能全部电离,但仍近似认为p p0=N A ,0021022317(1.510) 4.510510i p p n n cm p -⨯===⨯⨯ 于是,可分别算得空穴电流和电子电流为∴0195UU 31.61010.52.510(1)(1)3.2410q q n kTkTp PPp J qD ee L --⨯⨯⨯⨯=-=-⨯ 101.3010(1)qVkTe -=⨯-019231.61012.5 4.510(1)(1)7.910qV qV p kTkTn nnn J qD ee L --⨯⨯⨯⨯=-=-⨯131.1410(1)qVkTe-=⨯-空穴电流与电子电流之比 103131.3010 1.14101.1410pn J J --⨯==⨯⨯ 饱和电流密度:0010131021.3010 1.1410 1.3010/n p S PnPnp n J qD qD A cm L L ---=+=⨯+⨯=⨯当U =0.3V 时:0.30.310100.0260.026(1) 1.3010(1) 1.3010qVkTS J J eee--=-=⨯⨯-=⨯⨯=521.2910A /cm -⨯6.条件与上题相同,计算下列电压下的势垒区宽度和单位面积上的势垒电容: ①-10V ;①0V ;①0.3V 。
解:对上题所设的p +n 结,其势垒宽度D X ===式中,1417021021910510()ln 0.026ln 0.74(1.510)n p A D D F F i k T N N V E E V q q n ⋅⨯⨯⨯=-===⨯ 外加偏压U 后,势垒高度D V 变为()D V U -,因而 ① U =-10V 时,势垒区宽度和单位面积势垒电容分别为43.9410D X cm -===⨯ 14920411.68.8510 2.610 F/cm 3.9410r T DC x εε---⨯⨯===⨯⨯ ② U =0V 时,势垒区宽度和单位面积势垒电容分别为41.0310D x cm -==⨯ 1492411.68.85109.9710 F /cm 1.0310T C ---⨯⨯==⨯⨯ ③ U =0.3V57.9710D x cm -===⨯ 正向偏压下的pn 结势垒电容不能按平行板电容器模型计算,但近似为另偏压势垒电容的4倍,即982T 4(0)49.9710410 F /cm T C C --==⨯⨯=⨯7.计算当温度从300K 增加到400K 时,硅pn 结反向电流增加的倍数。
解:根据反向饱和电流J S 对温度的依赖关系(讲义式(6-26)或参考书p.193):(3/2)(0)exp()g S E J T kTγ+∝-式中,E g (0)表示绝对零度时的禁带宽度。
由于3/2Tγ+比其后之指数因子随温度的变化缓慢得多,S J 主要是由其指数因子决定,因而1.24 1.2440012.4512001.24300(400) 2.4310(300)kS kS kJ K e e e J K e --====⨯9.已知突变结两边的杂质浓度为N A =1016cm -3,N D =1020cm -3。
①求势垒高度和势垒宽度 ②画出E (x )和V (x )图。
解:32031610,10--==cm N cm N D A平衡势垒高度为()()eV q n N N qTk q qV i D A D 94.0105.110ln 026.0ln 23620=⨯=⎪⎪⎭⎫ ⎝⎛=()43.510D X cm -=≈≈⨯11.分别计算硅n +p 结在正向电压为0.6V 、反向电压为40V 时的势垒区宽度。
已知N A =5*1017cm -3,V D =0.8V 。
解:对n+-p 结V V cm N V V V V D A R F 8.0,105,40,6.0317=⨯=-==-势垒区宽度()AD r p D qN V V x X -=≈02εε当V V cm N V V V D A F 8.0,105,6.0317=⨯===-时, ()()()cm qN V V X AF D r D 61719140103.2105106.16.08.01085.81222---⨯=⨯⨯⨯-⨯⨯⨯⨯=-=εε当V V cm N V V V D A R 8.0,105,40317=⨯=-==-时, ()()()cm qN V V X AR D r D 51719140103.3105106.1408.01085.81222---⨯=⨯⨯⨯+⨯⨯⨯⨯=+=εε12.分别计算硅p +n 结在平衡和反向电压45V 时的最大电场强度。
已知V D =0.7V ,153510D N cm -=⨯。
解:势垒宽度:D X ==⑴平衡时,即U=0V 时54.2710D X cm -==⨯ 最大场强:191554141.610510 4.2710 3.3310/8.851011.6B mm r qN X V cm εεε---⨯⨯⨯⨯⨯===⨯⨯⨯ ⑵45DV V =-时:43.4510D X cm -==⨯ 最大场强191545141.610510 3.45102.710/8.851011.6B mm r qN X V cm εεε---⨯⨯⨯⨯⨯===⨯⨯⨯13.求题5所给硅p +n 的反向击穿电压、击穿前的空间电荷区宽度及其中的平均电场强度。
解:按突变结击穿电压与低掺杂区电阻率的关系,可知其雪崩击穿电压U B = 95.1443ρ=95.14⨯751/4=318 V或按其n 区掺杂浓度9⨯1014/cm 3按下式算得U B =603164(10/)B N =60⨯ (100/9)3/4=365(V )二者之间有计算误差。
以下计算取300V 为击穿前的临界电压。
击穿前的空间电荷区宽度32.110cm D X -===⨯ 空间电荷区中的平均电场强度53300/ 1.4310 V /cm 2.110B D E U X -===⨯⨯ 注:硅的临界雪崩击穿电场强度为3⨯105 V/cm ,计算结果与之基本相符。
