MIMO信道的信道容量
MIMO信道容量极限.

MIMO 信道容量极限摘要——我们对最近的关于单用户和多用户多输入多输出(MIMO)信道的香农容量的研究结果进行了全面的概述。
尽管预测了这样的信道有着巨大的容量增益,这些预测却或多或少基于一些不切实际的前提下,比如基本的时变信道模型,信道被接收端和发送端追踪的程度如何。
更加实际一点的前提会对MIMO 技术潜在的容量增益造成很大的影响。
对于时变MIMO 信道有多种香农理论容量定义,对于每一种定义又有着不同的相关模型和要考虑的信道信息量前提条件。
我们首先对单用户MIMO 信道的遍历容量和中断容量结果进行了全面的总结。
这些结果表明多天线带来的容量增益很大程度上依赖于接收端或者发送端获得的信道信息:信道的信号噪声比,每一个天线单元的信道增益之间的相关性。
我们把注意力集中在多址接入信道(MACs)的容量区域,已知的广播信道可获得的最大速率区域,与单用户MIMO 信道相反,多用户MIMO 信道容量的获得是相当困难的。
我们总结了MIMO 广播信道和多址接入信道的结果,这些信道要么是固定的,要么发送端和接收端都能对信道的瞬时状态有着精确的了解。
MIMO 多址接入信道的容量区域和已知的广播信道可获得的最大速率区域(又叫做脏纸区域)可以通过对偶变换紧密联系起来。
这一变换方便了寻找能够达到MIMO MAC 容量区域边界上点的发送策略,也方便了寻找MIMO 广播脏纸区域的发送策略,反之亦然。
最后我们讨论了采用基站协作多小区MIMO 信道的容量结果。
基站起到了天线阵列空间分集的作用,利用这一结构的发送策略显示出巨大的容量增益。
本文对MIMO 蜂窝系统的容量问题也进行了简要讨论。
在这一领域内尚存在大量的未解决的问题,对这些未解决问题的讨论贯穿于全文。
关键字——天线相关;波束成形;广播信道(BCs);信道分布信息(CDI);信道状态信息(CSI);多小区系统;多址接入信道(MACs);多输入多输出(MIMO)信道;多用户系统;香农容量。
MIMO信道容量的隐训练序列分析法

√ s + 打S=L. c , M, ∈ , 日 . s , H s
H =厂 , , ( S )
( 2 )
式 中 , P 为训 练 阶段每 根接 收天线 的信 噪 比 ; ∈ C p 为接 收 的训 练数 据矩 阵 。 T
表示 为 s=[ 。 s ] 一 帧 ( 个 符 号 的块 ) , 5 , , 内 MI MO信号模 型可 表示 为
图 1 隐 训 练 序 列 情 况 下信 息流 的帧 结构 示 意 图
y √ s+, : H
维 加性 复数噪声 矩 阵 ; H和 的元 素为 独立 的复高 斯 随机变量 , 均值 为 0 方 差为 1 , 。
己知的统 计分 布 ( 高斯 、 瑞利 或莱 斯 ) , 这样仿 真得 到的是 该算法 的理论 性 能 。然而 , 实 际应用 中或 在
在 对某种 空时 编码 和调制算 法 的实际性 能进 行评估 时 , 须对 真实信 道 的状态 信息进 行合 理 的估 计 , 必 而
估 计 的效 果或 精度 , 将直接 影 响系统 的真实性 能 。尽管 目前 信 道估 计 可 以使 用一 些 非数 据 的辅 助 技术
失。
本 文基 于隐训 练序 列 的信 道估 计模 型 , 无需 为训 练序列 专 门分配 时 隙 , 可在 没有带 宽损失 的情 况下
有较 高的估计 精度 和低计 算 复杂度 , 有利 于实 时估计 , 实 可行 。又 利用 最 小 二乘 算 法 , 真 并 分析 信 切 仿 噪 比、 据传 输 的帧长 、 数 收发天 线 的数 目与 信道容 量下 限 的变 化关 系 。
1 系统模 型
设信 道为 平 坦 衰 落 的窄 带 信 道 , 服 从 简 并
mimo技术原理

3. MIMO的信道模型
无线通信信号特点
➢ 中尺度衰落
描述阴影衰落,变化趋向于正态(高斯)分布, 通常称为对数正态衰落。
3. MIMO的信道模型
无线通信信号特点
➢ 大尺度衰落
描述由距离引起的信号的衰减,中值信号功率与 距离长度增加的某次幂成反比变化。
3. MIMO的信道模型
无线通信信号特点
2.MIMO的空时编码
分层空时码-复用
2.MIMO的空时编码
分层空时码-复用
S/P
编 码 器 编 码 器
…… ……
调 制 器 调 制 器
空 间 交 织
交 织 器 xt1
x 交 织 器
nT t
DLST的一般结构
2.MIMO的空时编码
分层空时码-复用
2.MIMO的空时编码
分层空时码-复用
1.MIMO技术原理
空
数
射
数据 时
模
频
编
转
前
码
换
端
s
h 11 h1 2
h 1 nT
h n R nT
射
模
空
频
数
时 数据
前
转
解
端
换
码
H
r
s1(t)
s(t)=
s
2
(
t
)
s n T ( t )
h11(t,)h12(t,) H(t,)h21(t,)h22(t,)
hh21nnT T((tt,,))
陈列操纵矢量(陈列机构和去波角的函数)
a ( ,) [ 1 a 1 , a n R , ] T
第m个分量为
3. MIMO的信道模型
2、MIMO信道容量推导

二、信道容量的推导主要研究基于VBLAST 的MIMO 系统:系统:串并变换调制调制调制VBLAST 检测器y1y2ym 比特分配功率分配b1bnb2信道估计丰富的散射信道2p 1p pn 数据图2.1 采用VBLAST 结构MIMO 系统框图系统框图MIMO 信道容量的推导:信道容量的推导:(信道容量定义为MIMO 系统在单位带宽上的数据传输速率)系统在单位带宽上的数据传输速率)根据奇异值分解(SVD)理论,在k 时刻,任何一个M ×N 矩阵H 可以写成可以写成HH =UDV 式中,D 是M ×N 非负对角矩阵;U 和V 分别是M ×M 和N ×N 的酉矩阵,且有H HM =UU I 和H N =VV I ,其中M I 和N I 是M ×M 和N ×N 单位阵。
D 的对角元素是矩阵H HH 的特征值的非负平方根。
H HH 的特征值(用l 表示)定义为定义为 H l =HH y y ,0¹y式中,y 是与l 对应的M ×1维矢量,称为特征矢量。
特征值的非负平方根也称为H 的奇异值,而且U 的列矢量是H HH 的特征矢量,V 的列矢量是HH H 的特征矢量。
矩阵H HH 的非零特征值的数量等于矩阵H 的秩,用m 示,其最大值为),min(N M m =。
则可以得到接收向量。
则可以得到接收向量 H =r UDV x +n引入几个变换H r'=U r ,H x'=V x ,H'n =U n ,这样等价的信道可以描述为:'''r =Dx +n 对于M ×N 矩阵H ,秩的最大值),min(N M m =,也就是说有m 个非零奇异值。
值。
将i l 代入上式,可以得到接收信号为:代入上式,可以得到接收信号为:'''i i i i r x n l =+(m i ,,2,1 =)''i i n r =(1,2,,i m m M =++ )可以看出等效的MIMO 信道是由m 去耦平行子信道组成的。
MIMO信道容量计算公式

MIMO信道容量计算公式
MIMO(Multiple-Input Multiple-Output)是一种通过同时使用多个发射天线和接收天线来增加无线通信系统容量的技术。
MIMO技术可以利用信道的冗余和多路径效应,提高信号的传输速率和可靠性。
1.SISO信道容量计算公式:
SISO信道容量的计算公式使用香农公式,用于计算传输速率。
香农公式如下:
C = B * log2(1 + SNR)
其中,C是信道容量,B是带宽,SNR是信噪比(Signal-to-Noise Ratio)。
SISO信道容量计算公式适用于只有一个天线的系统。
2.MIMO信道容量计算公式:
C = log2(det(I + H*SNR*H^H))
其中,C是信道容量,H是MIMO信道的传输矩阵,SNR是信噪比。
除了以上基本的MIMO信道容量计算公式,还有一些进一步考虑调制方式、信道状态信息等因素的改进公式,如ZF(Zero Forcing)和MMSE (Minimum Mean Square Error)等方法,用于提高MIMO系统的容量。
这些方法考虑了天线之间的干扰和多径效应,可以优化信号的传输和接收性能。
总结起来,MIMO信道容量的计算公式可以通过SISO信道容量公式和MIMO信道容量公式来表示,具体的计算方法需要综合考虑信道状况和系
统参数,并结合数值计算方法进行分析。
通过合理设计和优化,MIMO技术可以显著提高无线通信系统的容量和性能。
同频干扰下MIMO信道容量研究

2 1 .6 1 ) 00 4 (0
1 1
同频 干 扰 下 M I MO 信 道 容量 研 究
陈 宏, 戴居 丰
C HE n , N Ho g DAIJ -e g u fn
Ap l ain 。 0 0. 6 1 : 1 1 . p i to s 2 1 4 ( 0) 1 — 3 c
Ab ta t B s d o mut u e Mut l n u Mut l O tu ( MO) sse .h i a t f a e itrees a h wi ih sr c : a e n l- sr i lpe I p t i lpe up tMI i y tms te mp c o fw nefrr e c t hg h
p we n a a g n mb r o n e e e s a h wi o p we n y t m a a i w t f e O c a n l n e e e c p we r o r a d lr e u e f it r r r e c t l w o r o s se c p ct f h y i i d C — h n e i tr r n e o r a e h x f
M O s se y t m d sg e in.
K e w o ds: c n l a a iy; o ch n l ntre e c i e e e c t no s r to; lil i pu m utpl o t t y r ha ne c p c t c — a ne i e r n e;ntr r n e o f f ie a i mu tp e n t li e upu
MIMO通信系统的信道容量分析及MATLAB仿真实现

3 MI MO 系 统 信 道 模 型
研 究 MI MO系统 必 须考虑 信 道模 型 , 设研 究 的信道 为基 于瑞 利衰 落 的随机信 道 , MI 设 MO系统 信道模 型有 J V根发 射 天线 和 M 根接 收天 线 ,信道矩 阵 H( J 表 示第 i 发射 天线 到第 7 接 收天线 的信道 衰落 系 i) , 根 根 数 ,每根 发射 天线 的功 率为 P Ⅳ,每 根接 收天 线 的噪声 功率 为 ,故 信 噪 比 S R为 : =P/ I.通过分 / N 4 】
21 0 2年 4月
Apr 201 . 2
MI MO通信系统 的信道容 量分析及 MA L B仿真实现 TA
朱琳璐
( 丽水广播 电视 大 学 ,浙 江 丽水 3 3 0 2 0 0)
摘
要 :在 多入 多 出( MO) MI 系统原 理和模 型 的基础 上 ,分析 了基 于单入 单 出(I O 、单入 多 出( I SS ) SMO) 、多
解信道特征矩阵 Q的特征值 ,由香农公式导出 MI MO信道容量 C= o:el +P( ̄) } Wl dt 【/ r 】 ,其中威沙 g { N Q
特矩 阵 Q=HH“,M <N ;Q=日“ , M ≥N ; I 是 mi( n M,N) 阶单位 矩 阵 ;W 为 每个子 信道 的带宽 ,
还是 提高 频谱 的资源 利用率 .在无线 通信 中,使 用 多输入 、多输 出( MO:Mut l Ip t lpeOup t MI lpe n u— t l— tu) i — Mu i
技术 既能增 加 系统容量 ,也 能增强 系统 性能 ,在其 他条 件相 同 的前 提下 ,可 以成倍地 提 高频谱 效率 .
‘4 1 5‘
MIMO信道容量计算公式
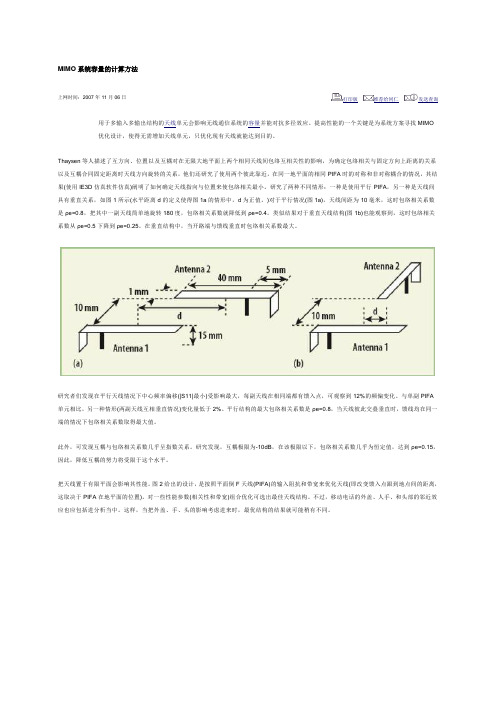
MIMO系统容量的计算方法上网时间:2007年11月06日打印版推荐给同仁发送查询用于多输入多输出结构的天线单元会影响无线通信系统的容量并能对抗多径效应。
提高性能的一个关键是为系统方案寻找MIMO优化设计,使得无需增加天线单元,只优化现有天线就能达到目的。
Thaysen等人描述了互方向、位置以及互耦对在无限大地平面上两个相同天线间包络互相关性的影响,为确定包络相关与固定方向上距离的关系以及互耦合同固定距离时天线方向旋转的关系,他们还研究了使用两个彼此靠近,在同一地平面的相同PIFA时的对称和非对称耦合的情况,其结果(使用IE3D仿真软件仿真)阐明了如何确定天线指向与位置来使包络相关最小。
研究了两种不同情形:一种是使用平行PIFA,另一种是天线间具有垂直关系,如图1所示(水平距离d的定义使得图1a的情形中,d为正值。
)对于平行情况(图1a),天线间距为10毫米,这时包络相关系数是ρe=0.8,把其中一副天线简单地旋转180度,包络相关系数就降低到ρe=0.4。
类似结果对于垂直天线结构(图1b)也能观察到,这时包络相关系数从ρe=0.5下降到ρe=0.25。
在垂直结构中,当开路端与馈线垂直时包络相关系数最大。
研究者们发现在平行天线情况下中心频率偏移(|S11|最小)受影响最大,每副天线在相同端都有馈入点,可观察到12%的频偏变化。
与单副PIFA单元相比,另一种情形(两副天线互相垂直情况)变化量低于2%。
平行结构的最大包络相关系数是ρe=0.8,当天线彼此交叠垂直时,馈线均在同一端的情况下包络相关系数取得最大值。
此外,可发现互耦与包络相关系数几乎呈指数关系。
研究发现,互耦极限为-10dB,在该极限以下,包络相关系数几乎为恒定值,达到ρe=0.15,因此,降低互耦的努力将受限于这个水平。
把天线置于有限平面会影响其性能。
图2给出的设计,是按照平面倒F天线(PIFA)的输入阻抗和带宽来优化天线(即改变馈入点跟到地点间的距离,这取决于PIFA在地平面的位置)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Pi 1/ 0 1/ i 0 P
其中 0 为某个门限值。由此得到信道容量为
i 0 i 0 (1-6)
C B log 2 (
i: i 0
i ) 0
对于有一个发送天线和多个接收天线的单入多出系统,或者有多个发送天线 一个接收天线的多入单出系统,也可以定义出收发都有理想信道信息时的容量。 这些信道可以通过多天线获得分集增益和阵列增益,但没有复用增益。当发送端 和接收端都已知信道信息时, 其容量等于信号在发送端或接收端进行最大比合并 后得到的 SISO 信道的容量为
1 引言
信道容量的计算是研究噪声信道的主要关注点之一。信道容量的定义是以任 意小的差错率传输信息的最大速率,它建立了可靠通信的基本极限。因此,信道 容量广泛应用于衡量通信系统的性能。本文的主要目标是研究与 MIMO 无线信 道有关的信道容量。 MIMO 信道的香农容量是能够以任意小的差错率传输的最大数据率。中断容 量则定义为能使中断率不超过某个数值的最大数据率。 信道容量的大小和收发两 端是否已知信道增益矩阵或其分布有关。 下文先给出不同信道信息假设下静态信 道的容量,它是其后讨论的衰落信道容量的基础。
MIMO 信道的信道容量
摘要
由于 MIMO 可以在不需要增加带宽或总发送功率耗损(transmit power expenditure)的情况下大幅地增加系统的资料吞吐量(throughput)及传送距离, 使得此技术于近几年受到许多瞩目。MIMO 的核心概念为利用多根发射天线与 多根接收天线所提供之空间自由度来有效提升无线通信系统之频谱效率, 以提升 传输速率并改善通信品质。研究 MIMO 信道的容量是对 MIMO 进行深入分析的 基础,本文分析了 MIMO 信道的容量计算方法,分别介绍了在静态信道中的注 水法、平均功率分配法信道容量,以及衰落信道中遍历容量和中断容量。 关键词:MIMO,信道容量,注水法,平均功率分配,遍历容量,中断容量
Tr ( R x )
。 于是, 我们有 H (Y ) B log2 det[eRy ]
,
I ( X ; Y ) B log 2 det[ I M r HRx H H ] (1-2)
MIMO 信道容量就是所有满足功率约束条件的输入协方差矩阵 Rx 中, 使得互 信息量最大,即
C max B log 2 det[ I M r HRx H H ] (1-3)
列数,所以 RH min( M t , M r ) 。满秩的情况称为富散射环境,此时 RH min( M t , M r ) 。 其他情况可能是低秩的, 若某个信道中的 H 的元素高度相关, 其秩可能会降为 1。 用发送与编码和接受成形对信道的输入输出 x 和 y 分别进行变换,就可以实现
后作为天线的输入, 矩阵的并行分解。 发送预编码将输入向量 x 经线性变换 x Vx
Rx ( / M t ) I M t 。在上述假设下,这样的输入协方差矩阵确实能够使信道互信息
量最大。此时互信息为
I ( x; y ) B log 2 [ I M r
可用奇异值分解将此式表示为
RH
Mt
HH H ]
I ( x; y ) B log 2 (1
i 1
i
Mt
接收成形将信道的输出 y 乘以 U H ,如图(2)
x
x Vx
x
y Hx n
y
UH y y
y
图 2 发送预编码与接收成形 发送预编码和接收成形将 MIMO 信道变换成 RH 个并行的单入单出 SISO 信道, 其
。这一点可以从奇异值分解得到: ,输出为 y 输入为 x
进行讨论。对于静态信道,如果发送端不知道信道状态或者信道的平均互信息, 那么它也无法确定该以什么样的速率发送方能保证数据的正确接收。 此时最适合 的容量定义为中断容量。 发送端以固定速率 R 来发送, 中断率表示接收端不能正 确接收的概率,也即信道 H 的互信息小于 R 的概率,其值为
out p ( H : B log 2 det[ I M
i 、输出为 y i ,噪声为 n i ,信道 了 RH 个独立的并行信道,第 i 个信道的输入为 x 增益为 i 。注意 i 之间是有关联的,他们都是 H 的函数。不过由于这些并行信 道并不相互干扰, 所以我们说这些信道总是通过发送功率联系在一起的一组独立 信道。并行分解如图(3)所示。并行信道互不干扰,使得最大似然解调的复杂 度随 RH 线性增长。此外,通过在这些信道上发送独立数据,MIMO 的数据速率 将是单天线系统的 RH 倍,即复用增益为 RH 。但需注意,每个信道的性能与 i 有 关。
2.1 MIMO 信道的并行分解
发送端和接收端都有多个天线时, 可以获得另外的一种增益, 称作复用增益。 MIMO 信道的服用增益来源于 MIMO 信道可以分解为 R 个并行的独立信道。 在这 些独立的信道上传输多路数据, 数据速率就可以比单个天线系统提高 R 倍, 这个 提高的倍数就是复用增益。 这个分解过程就用到了矩阵理论中的奇异值分解的知 识。 奇异值分解(singular value decomposition ,SVD)是线性代数中一种重要的矩
阵分解,在信号处理、统计学等领域有重要应用。奇异值分解在某些方面与对称 矩阵或 Hermite 矩阵基于特征向量的对角化类似。 然而这两种矩阵分解尽管有其 相关性,但还是有明显的不同。对称阵特征向量分解的基础是谱分析,而奇异值 分解则是谱分析理论在任意矩阵上的推广。 考虑一个 M r M t 的 MIMO 信道 ,发送端和接收端都已知信道增益矩阵 H。 令 RH 表示 H 的秩。对任意的 H,可进行奇异值分解:
Rx :Tr ( Rx )
其中 det[ A] 是矩阵 A 的行列式。很明显,最优的 Rx 取决于发送端是否知道 H 。 以下根据不同的发送端信道边信息假设来考虑这个最优问题。
1.发送端已知信道:注水法
对于给定信道矩阵为 H 的 MIMO 信道,当发送端和接收端均已知 H 时, MIMO 信道分解可以简化信道容量的分析。具体而言,信道容量等于总发送功率 在各个信道之间最优分配后, 各个独立并行信道的容量之和。最优功率分配就是 通过优化协方差矩阵使(1-3)最大化的结果。讲奇异值分解带入(1-3) ,利用 酉矩阵性质可以得到收发两端都已知信道时 MIMO 信道的容量为
C max B log 2 (1 i 2 i ) (1-4)
i:i i i 1
RH
其中 RH 是 H 的非零奇异值的个数。 由于 MIMO 信道可以分解成 RH 个并行信道, 因此称其自由度为 RH 。由于 P / 2 ,式(1-4)所示的容量也可以根据第 i 个 并行信道的功率 Pi 表示为
Ry 为
R y E[ yy H ] HRx H H I M r
可以证明,给定协方差矩阵为
Ry
(1-1)
的所有随机向量中,零均值循环对称随机向量
的熵最大。而仅当输入向量 x 是零均值循环对称复高斯随机变量时,y 才是零均 值循环对称复高斯随机变量, 所以零均值循环对称复高斯随机变量是式中 x 的最 佳分布, 功率约束条件是 从而互信息为
1 HH H I M r M t M t lim
讲此式带入式(1-7)可得,当 M t 趋于无限大时,互信息变为常数 C M r B log 2 (1 ) 。定义 M min( M t , M r ) ,则随着 M 的增大,MIMO 信道在位 置 CSTI 的情况下容量将趋于 C MB log 2 (1 ) ,随着 M 线性增长。在天线数较 少时也能观察到这种随 M 线性增长的规律。同样的,当信噪比很大时,对于任 意 M t 和 M r ,容量也随着 M min( M t , M r ) 线性增长。由于 ZMSW MIMO 信道的 秩 RH M min( M t , M r ) ,因此无 CSIT 时,高信噪比或者天线数很多时,信道容 量随信道自由度线性增长。这些结论是 MIMO 技术颇具吸引力的主要原因:只 要接收端能正确估计信道信息,即使发送端不知道信道状态,ZMSW MIMO 信道 的容量也与发送端和接收端中的最小天线数成线性增长的关系。因此 MIMO 信 道在不需要增加信号功率或带宽的情况下就可以提供很高的数据率。但需注意, 信噪比非常低时增加发送天线并无益处,容量只与接受天线数有关。这是因为信
r
Mt
HH H ] R )
(1-10)
这个概率取决于 HH H 的特征值分析,这些特征值是 H 的奇异值的平方。人们对 聚真气一直的分布问题已经进行了研究,对于 MIMO 信道中常见的情形,已经 得到了分布的结果。 当发送端和接收端的天线数目很多时, 随机矩阵理论给出了关于 H 的奇异值 分布的中心极限定理。根据这一定理,所有信道实现都有相同的互信息。作为中 心极限分布的例子,假设接收端天线数固定为 M r 那么在 ZMSW 模型下,大数定 律表明
Hale Waihona Puke 11 n1 x 2 x
1
1 y
2
2 n
2 y
3
3 n
2 x
3 y
图 1 MIMO 信道奇使用异值分解后的等效并行信道
2.2 静态信道
MIMO 信道的容量是 SISO 信道的互信息公式在矩阵信道下的扩展。 静态信道 下,接收端可以容易地对 H 做出很好的估计,因此本节假设有发送端信道边信 息(channel side information at the transmitter ,CSIT) 。在此假设下,信道容量由 信道输入向量 x 和输出向量 y 之间的互信息确定:
C max I ( X ; Y ) max[ H (Y ) H (Y | X )] (1)
p ( x) p( x)
其中 H (Y ) 是 y 的熵,H (Y | X ) 是 y|x 的熵。 由熵的定义可知,H (Y | X ) H ( n) , 其中 H ( n) 为噪声熵。噪声的熵独立于信道输入,所以最大化互信息就是最大化 y 的熵。 若给定输入向量 x 的协方差矩阵为 R x , 那么 MIMO 信道输出 y 的协方差矩阵
