《定积分及应用习题》PPT课件
合集下载
定积分及其应用ppt课件

n
xi 0, f (i )xi 0, i 1
|| T || max{x1, x2 , , xn }
n
b
lim
||T ||0
i 1
f (i )xi
f ( x)dx 0.
a
性质5的推论:(定积分不等式性质)
(1)如果在区间[a, b]上 f ( x) g( x),
则
b
a
f
(
x
)dx
b
a
g(
x)dx.
(a b)
证明 f ( x) g( x), g( x) f ( x) 0,
b
a[g( x) f ( x)]dx 0,
(a b)
即
b
g( x)dx
b
f ( x)dx 0,
a
a
于是
b
a f ( x)dx
c
b
f
(
x)dx
c
b
a f ( x)dx c f ( x)dx.
(定积分对于积分区间具有可加性)
性质4
b
b
a 1 dx a
dx b a .
性质5 如果在区间[a, b]上 f ( x) 0,
则
b
a
f
(
x
)dx
0.
(a b)
证明 f ( x) 0, f (i ) 0, (i 1,2,,n)
前
积取负号.
a
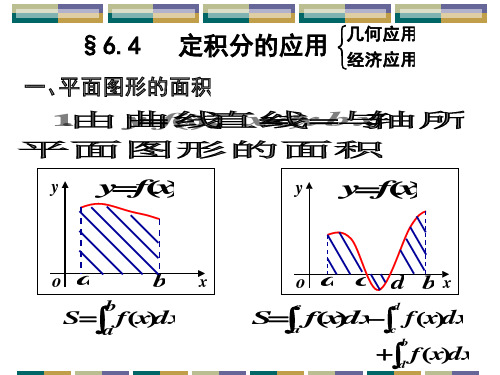
y f (x)
b
b
特别,当 f (x) 1 时,有a 1 dx (b a)1 b a .
定积分的应用96113-PPT文档资料26页
3
2x2
2
16
3
8
S右 2[
2x(x4)d ] x(22x2 3 0 1x24x)85 66
32
23
SS 1S 218
例 3 计算由曲线 y2 2x和直线 y x 4所围成
的图形的面积.
解2 选 y为积分变量 y[2,4]
(8,4)
y2 2x
4
S 2
收益 R (x )x 函 R (t)d数 t 0
作业:6.4 1(1,3)、2、5(1,3)、6、8
n
Vy(xi2xi21)| f(i)|
y
yf(x)
i1
n
i n1(xixi 1)x (ixi 1)|f(i)|o
xi1 i x i
x
(xi xi1)|f(i)|xi
y2 x y x2
(0,0)
(1,1)
(不要省略)
2.选择适当的积分变量,确定被积函数 0
选 x为积分变量 x[0,1]
x y2
y x2
x
1
被积函数x为 x2
3.代入相应的积分 算公 出式 定, 积分值
1
S (
0
xx2)dx
2 3
3
x2
1 3
x3
y4y22dy
(y2 4y y3)4 18
2
6
2
yx4
(2,2)
求平面图形面根 积据 时图 ,形 要的形状
适当的积分变计 量算 ,简 会单 使化
例4在抛物 yx线 2(0x1)上找一 P,点 使经 P 过
的水平直线与 直抛 线 x0物 ,x线 1所和 围成的
定积分的应用93820-PPT文档资料59页

y1 f1(x)
所围成,则其面积公式为:
b
A f1 ( x ) f 2 ( x ) d x .
a
o
y2 f2(x)
a
b
x
3 、若平面区域是 y—区域:
由左曲线 x1 g1( y) 、
右曲线 x2 g2( y) 、下
y
直线 y a 、上直线y b b
所围成, 则其面积公式为:
2
或
22
2
A 2 0
2x2 x2
dx
1 2
1 x2
dx
2
练习写出下列给定曲线所围成的图形面来自的定积分表达式。(7)
y2 42x
2
法一:以 y 作积分变量
1
2
A202(2y42)(1y42)dy
4
2 3
法二:以 x 作积分变量
2
y2 4x1
f(x)=x2
y
f(x)=x2
y
y f(x)=(x-1)2-1
f(x)=1
0a
①
x -1 0 2
②
x a 0 b x -1 0 2 x
③
④
解:(3)在图③中,被积f (函 x) 数1在[a,b]
上连续,f且 (x) 0,根据定积分的几何意
义,可得阴影部分积的为面A badx
y
f(x)=x2
A 0 1 [x (1 ) 2 1 ] d x 0 2 [x (1 ) 2 1 ] dx
授新课:一、直角坐标系情况
1 、 若 f ( x )在 [a , b ]上 不 都 是 非 负 的 ,
则所围成图形(如右图)
b
y
六章定积分应用ppt课件

WF(ba)
F
a
b
若F 为变力,力对
物体所作的功W=?
例1 带电量为q0与q1的正电荷分别放在空间两点, 求当q1沿a与b连线从a移到b时电场力所作的功。
解: 如图建立坐标系:在上述移动过程中,电场
对q1作用力是变化的。
(i)取r为积分变量,则 r[a,b] q0
q1
(ii)相应于[a,b]上任一小区间[r,r+dr] o a
br
的功元素
dW Fdrkq0q1dr
(iii)所求功
r2
W
b
k
a
qr0q21dr
kq0q1
(1) r
b a
kq0q1(1ab1)
例2 在底面积为S的圆柱形容器中盛有一定量的气体。在等 温条件下,由于气体膨胀,把容器中的一个活塞(面积为S) 从点a推移至b,计算在移动过程中气体压力所作的功。
解: 如图建立坐标系,活塞位置可用坐标x表示。
引力
问题的提出:从物理学知道,质量分别为m1、m2,相
距为r的两质点间的引力大小为
F Gmr1m2 2
其中G为引力系数,引力的方向沿着两质点的连线。
如何计算一根
细棒对一个质点的 引力F=?
r
o
m1
m2 x
例6 设有一长度为l、线密度为的均匀细棒,在
其中垂线上距棒a单位处有一质量为m 的质点M。
试计算该棒对质点M的引力。
x
问题的解决方法: 定积分元素法
以液面为y轴,x轴铅直向下。
设平板铅直位于液体中形状如图。
o
距离液面x、高为dx、宽为f(x) 的
矩形平板所受压力的近似值,即压力 元素为
a x x+dx
第六章定积分的几何应用0119345页PPT

b c
1
无界函数的反常积分
f(x) C (a,b], 而在点 a 的右邻域内无界,
若极限
存在 , 则称此极限为函数 f (x) 在
[a , b] 上的反常积分, 记作
无界点常称 为瑕点 类似地 , 若 f(x) C [a,b),而在 b 的左邻域内无界,
则定义
2
而在点 c 的
邻域内无界 , 则定义
d x
1
2
3
d x
( )
0 x (x 2 ) 0 1 2 3 x (x 2 )
1
( 0
2
1
3
2
3 ) 1 2 x 1 2 x 1 d x
1 2 ln x x 21 0 ln x x 21 2 ln x x 23 2 ln x x 2 3
c
b
f ( x ) d x f ( x)dx
a
c
c1
b
lim f(x)dx lim f(x)dx
10 a
20 c2
3
说明: (1) 有时通过换元 , 反常积分和常义积分可以互相转化 .
例如 ,
1
1
1 x2
0
x2
1 x2
dt
1dΒιβλιοθήκη x于 是 , 所 求 面 积 为
b
A |f(x)g (x)| dx a
17
例 1 计算由两条抛物线 y2 x和 y x2所围成的
图形的面积.
解 两曲线的交点
(0,0) (1,1) 选 x为积分变量 x[0,1]
第5章 定积分及其应用(共132页)
22
10:31:46
23
课后作业
课前预习
5.2 定积分的计算
书面作业
P128: 2;3;计算
5.2.1 变上限积分 5.2.2 牛顿-莱布尼兹公式 知识回顾与小结
10:31:46
25
5.2.1 变上限积分
设函数 f ( x ) 在闭区间
变上限积分动态演示
上述和式的极限,即得曲边梯形的面积
A lim f ( i ) x i
0
i 1 n
7
变速直线运动的路程
设某物体的运动速度 v v ( t )是时间 t 的连续函数,
T2 ]内所走过的路程 s . 求物体在时间间隔 [ T1 ,
第一步 分割
T2 ]中任意插入 n 1 个分点, 在时间间隔 [ T1 ,
微积分学基本定理
b]上连续, F ( x )是 f ( x ) 设函数 f ( x ) 在闭区间 [a , b] 上的一个原函数, 则 在 [a ,
b a
f ( x )d x F (b) F (a )
称为牛顿-莱布尼兹公式,或称为 N-L 公式.
32
N-L 公式表明:
b ]上的定积分等于它的 一个连续函数在区间 [ a ,
第三步
求和,即
求和
把 n 个子时间段内物体所走过的路程
s v ( i ) t i
i 1 n
第四步
取极限
记 max { t 1 , t2 , , t n } ,取
上述和式的极限,即得变速直线运动的路程
s lim v ( i ) t i
0
与 u x 2 复合
而成的,所以
10:31:46
23
课后作业
课前预习
5.2 定积分的计算
书面作业
P128: 2;3;计算
5.2.1 变上限积分 5.2.2 牛顿-莱布尼兹公式 知识回顾与小结
10:31:46
25
5.2.1 变上限积分
设函数 f ( x ) 在闭区间
变上限积分动态演示
上述和式的极限,即得曲边梯形的面积
A lim f ( i ) x i
0
i 1 n
7
变速直线运动的路程
设某物体的运动速度 v v ( t )是时间 t 的连续函数,
T2 ]内所走过的路程 s . 求物体在时间间隔 [ T1 ,
第一步 分割
T2 ]中任意插入 n 1 个分点, 在时间间隔 [ T1 ,
微积分学基本定理
b]上连续, F ( x )是 f ( x ) 设函数 f ( x ) 在闭区间 [a , b] 上的一个原函数, 则 在 [a ,
b a
f ( x )d x F (b) F (a )
称为牛顿-莱布尼兹公式,或称为 N-L 公式.
32
N-L 公式表明:
b ]上的定积分等于它的 一个连续函数在区间 [ a ,
第三步
求和,即
求和
把 n 个子时间段内物体所走过的路程
s v ( i ) t i
i 1 n
第四步
取极限
记 max { t 1 , t2 , , t n } ,取
上述和式的极限,即得变速直线运动的路程
s lim v ( i ) t i
0
与 u x 2 复合
而成的,所以
高等数学-定积分及其应用ppt课件.ppt
一、引例
在变速直线运动中, 已知位置函数
与速度函数
之间有关系:
物体在时间间隔
内经过的路程为
这种积分与原函数的关系在一定条件下具有普遍性 .
5.3 定积分的计算
则积分上限函数
证:
则有
定理1. 若
5.3.1 牛顿 – 莱布尼兹公式
说明:
1) 定理 1 证明了连续函数的原函数是存在的.
2) 变限积分求导:
5.6.1 广义积分
引例. 曲线
和直线
及 x 轴所围成的开口曲
边梯形的面积
可记作
其含义可理解为
1 连续函数在无限区间上的积分
定义1. 设
若
存在 ,
则称此极限为 f (x) 在区间 的广义积分,
记作
这时称广义积分
收敛 ;
如果上述极限不存在,
就称广义积分
发散 .
类似地 , 若
公式, 复化求积公式等,
并有现成的数学软件可供调用.
性质1 常数因子可提到积分号外 性质2 函数代数和的积分等于它们积分的代数和。
5.2 定积分的简单性质
性质3 若在区间 [ a , b ]上 f (x)≡K,则 性质4 定积分的区间可加性 若 c 是 [ a , b ] 内的任一点,则
的面积 .
解:
例3. 汽车以每小时 36 km 的速度行驶 ,
速停车,
解: 设开始刹车时刻为
则此时刻汽车速度
刹车后汽车减速行驶 , 其速度为
当汽车停住时,
即
得
故在这段时间内汽车所走的距离为
刹车,
问从开始刹
到某处需要减
设汽车以等加速度
车到停车走了多少距离?
在变速直线运动中, 已知位置函数
与速度函数
之间有关系:
物体在时间间隔
内经过的路程为
这种积分与原函数的关系在一定条件下具有普遍性 .
5.3 定积分的计算
则积分上限函数
证:
则有
定理1. 若
5.3.1 牛顿 – 莱布尼兹公式
说明:
1) 定理 1 证明了连续函数的原函数是存在的.
2) 变限积分求导:
5.6.1 广义积分
引例. 曲线
和直线
及 x 轴所围成的开口曲
边梯形的面积
可记作
其含义可理解为
1 连续函数在无限区间上的积分
定义1. 设
若
存在 ,
则称此极限为 f (x) 在区间 的广义积分,
记作
这时称广义积分
收敛 ;
如果上述极限不存在,
就称广义积分
发散 .
类似地 , 若
公式, 复化求积公式等,
并有现成的数学软件可供调用.
性质1 常数因子可提到积分号外 性质2 函数代数和的积分等于它们积分的代数和。
5.2 定积分的简单性质
性质3 若在区间 [ a , b ]上 f (x)≡K,则 性质4 定积分的区间可加性 若 c 是 [ a , b ] 内的任一点,则
的面积 .
解:
例3. 汽车以每小时 36 km 的速度行驶 ,
速停车,
解: 设开始刹车时刻为
则此时刻汽车速度
刹车后汽车减速行驶 , 其速度为
当汽车停住时,
即
得
故在这段时间内汽车所走的距离为
刹车,
问从开始刹
到某处需要减
设汽车以等加速度
车到停车走了多少距离?
《定积分及其应用》课件

在经济学中,供需关系决定了市场的价格。供需曲线的面积表示市场上供应和需求的关系。通过计算这个面积, 我们可以了解市场的均衡点,也就是市场上的价格。同时,通过观察供需曲线面积的变化,我们可以了解市场的 价格变动趋势。
感谢您的观看
THANKS
在曲线上的积分。
曲线的转动惯量
总结词
通过定积分计算曲线的转动惯量
详细描述
转动惯量是描述物体转动难易程度的物理量。对于一个 均匀细长的物体,其转动惯量可以通过定积分来计算。 转动惯量等于质量分布相对于某一轴的转动惯量,等于 质量密度函数在物体质量分布上的积分。
05
定积分的经济应用
收益流的现值
总结词
收益流的现值是定积分在经济中的一个重要应用,它 可以帮助我们计算未来的现金流在当前的价值。
详细描述
在金融和经济学中,我们经常需要考虑未来的收益流 ,也就是未来的现金流。由于货币的时间价值,我们 需要将未来的现金流折现到现在的价值。定积分可以 用来计算这种折现的值。
投资决策问题
总结词
投资决策问题涉及到如何分配有限的资源以获得最大 的回报。定积分可以用来解决这类问题。
定积分的几何意义
总结词
定积分的值等于函数图像与x轴所夹的面积。
详细描述
定积分的值可以通过几何意义来解释,即定积分的值等于函数图像与x轴所夹的 面积。这个面积可以是正的、负的或零,取决于函数图像在给定区间上的上下 位置。
定积分的性质
总结词
定积分具有线性性质、可加性、可减性和区间可加性等性质。
详细描述
体积的计算
总结词
定积分在计算三维空间中物体体积的问 题中起到关键作用,特别是对于旋转体 和薄片绕旋转轴旋转形成的体积。
VS
感谢您的观看
THANKS
在曲线上的积分。
曲线的转动惯量
总结词
通过定积分计算曲线的转动惯量
详细描述
转动惯量是描述物体转动难易程度的物理量。对于一个 均匀细长的物体,其转动惯量可以通过定积分来计算。 转动惯量等于质量分布相对于某一轴的转动惯量,等于 质量密度函数在物体质量分布上的积分。
05
定积分的经济应用
收益流的现值
总结词
收益流的现值是定积分在经济中的一个重要应用,它 可以帮助我们计算未来的现金流在当前的价值。
详细描述
在金融和经济学中,我们经常需要考虑未来的收益流 ,也就是未来的现金流。由于货币的时间价值,我们 需要将未来的现金流折现到现在的价值。定积分可以 用来计算这种折现的值。
投资决策问题
总结词
投资决策问题涉及到如何分配有限的资源以获得最大 的回报。定积分可以用来解决这类问题。
定积分的几何意义
总结词
定积分的值等于函数图像与x轴所夹的面积。
详细描述
定积分的值可以通过几何意义来解释,即定积分的值等于函数图像与x轴所夹的 面积。这个面积可以是正的、负的或零,取决于函数图像在给定区间上的上下 位置。
定积分的性质
总结词
定积分具有线性性质、可加性、可减性和区间可加性等性质。
详细描述
体积的计算
总结词
定积分在计算三维空间中物体体积的问 题中起到关键作用,特别是对于旋转体 和薄片绕旋转轴旋转形成的体积。
VS
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
tf3
( .x
2
)
dx1 a
6、下列积分中,值为零的是( D)
(A) 1 x 2dx; 1
(C) 1 dx; 1
(B) 2 x 3dx; 1
(D) 1 x 2 sin xdx . 1
精选课件ppt
15
7、 已知 f (0) 1 , f (2) 3 , f ' (2) 5,则 2 xf '' ( x)dx (B) 0
10
例8. 设非负函数
曲线
与直线 及坐标轴所围图形
面积为 2 , (1) 求函数
(2) a 为何值时, 所围图形绕 x 轴一周所得旋转体
体积最小 ?
解: (1)
由方程得
即
故得
精选课件ppt
11
又
(2) 旋转体体积
又 为唯一极小点, 因此
精选课件ppt
y
o
1x
时 V 取最小值 .
12
训练题
11
1. 1 x2 dx ( C )
第五章 定积分及其应用
习题课
精选课件ppt
1
一.本章提要
问题1:
曲边梯形的面积
问题2:
变速直线运动的路程
存在定理
定积分
广义积分
的定 性积 质分
牛顿-莱布尼茨公式
b
af(x)d xF (b)F (a)
定积分精选的课件应ppt用
计 算 法
定 积 分 的
2
二.本章解题类型
1.利用牛-莱直接积分 2.利用换元积分法积分.注意:换元必换限;不换元 不换限 3.比较两个定积分的大小
精选课件ppt
5
例3.比较
2
ln xdx
与
2
(1
x)dx
的大小
1
1
解一 令f(x)=1+x-lnx, 因为 f(x)11x1
∴当1<x<2时, f (x)>0.
xx
又因为f(x)在[1,2]上连续,∴f(x)在[1,2]上单增.
则, 当x>1时,f(x)>f(1)=2, 即 1+x>ln x
2
(A)12;
(B)8;
(C)7;
(D)6.
8、设
f (x)
1 1
1 ,
x 1 ex
x0 ,则定积分
,x0
2 0
f ( x 1)dx=(A)
(A)1 ln(1 1); e
(B)2 ln(1 e 2 ) ln 3;
a
a
证 令 abxt,则 xabt,dxdt
xat b, x bt a,
b
a
af(abx)d xbf(t) (d),t
b
b
a f(t)dta f(x)d,x
证毕
精选课件ppt
8
例6. 求 d ax sint2dt.
dx
解 原式= csin t2d t axsin t2dt
lnx
( A) 2
(B) 2
(C) 发散
(D) 1 2
2、 d x ln(t 2 1) dt =( A )
dx 0
(A)ln( x 2 1);
(B)ln(t 2 1);
(C)2x ln( x 2 1); (D)2t ln(t 2 1) .
精选课件ppt
13
x sin t 2dt
3、lim 0 x0
x3
=( C )
(A) 0 ;
(B)1;
(C)1 ; 3
(D) .
4.、定积分
1
e
x dx的值是( D
)
0
(A)e ;
(B)1 ; 2
1
(C)e 2;
(D)2 .
精选课件ppt
14
5 .下列式子中正确的是
(B )
5、下列积d 分中x ,使用变换正确的是 ( )
(A)
(A)dx d0
((BB))dx3
adx f
( t ) dt ,令
1 xsin 3 x
x
x 3 a1 f x(2td)xd,t 令
f (t) arctan
fx (xsi)n
t; t;
0
( (C C))ddx21
x
lbn(f1 a1
( x
tx)2d)t
2
dx,
令f
(
1x)
x
2
u;
( D(D))d 1
x2
1
xf2 d(xt,) d令t x
4.证明定积分恒等式(可作为结论掌握,如被积函 数为奇偶时的积分等.) 5.变上限积分的导数 6.求平面几何图形的面积,求旋转体的体积 7.两类广义积分求解题
精选课件ppt
3
例1.计算定积分 2 1 dx 2 x x2 1
x 22
解法一 令x=secu,则 dx=secu tanu du. u
43
的,求: (1)平面图形D的面积
(2)平面图形D绕y轴旋转一周所生成的旋转体的体积.
解 (1)平面图形D的图形如图所示
y
ye
S 01(eex)dx(exex)|10 1
y ex
(2)
Vy
e x2dy e(lny)2dy
1
1
o
x
令t lny 1 t 2etdt e2 0
e
另解(1)平面图形 A ln ydy 精选1课件ppt
ax3f(x2)dx1
a2
x(fx)d
x
0
20
证 令 x2t(x0)则 ,xt,d x1t1 2dtx 0 a
2
ax3f(x2)d
a2 3
1 1
x t2f(t) t 2d
t
t
0
0
2
0 a2
1
a2
1
tf (t)dt
a2
xf(x)dx
20
20
精选课件ppt
7
例5 证明
b
b
f(x)dx f(abx)dx
c
x
cl n xsit2 n d tx caxsit2 n d tx
ln xsit2 n dt
c
ln x
l
n xx
ax
s
c
in t2dt ax
ax
x
sin(lxn)2 1 sian 2xaxln a x
精选课件ppt
9
例7. 平面图形D是由曲线 y e x 及直线y = e 所围成
精选课件ppt
4
例2.计算定积分
2
x dx
1 1 x2
解 原式= 0
x
2
dx
x
dx
1 1 x2
0 1 x2
注:被积函数 中含绝对值 符号的定积 分方法
1d(1x2) 1d(1x2)
0
2
22
1 1x2
0 1x2
1
2
1
1
1 (1 x2)2 1 (1 x2)2
21
21
20
20
2 1 5 125 2
2
故 1 ln xdx < 1 (1 x)dx
解二 因为 1 2 lx n d x lx n |1 2 1 2 d 2 x l2 n x |1 2 2 l2 n 1
2
(1x)d
x(1x)22925
1
2 22
1
2
2
故 1 ln xdx < 1 (1 x)dx
精选课件ppt
6
例4. 证明
原式=
43sesecucustaenc2uudu1
3
du
4
u
3
4
3
4
12
解法二
原式=
令 xu 1,则 dxu 12du ,
1
2 1
2
1 u2
du
1 ( 1 )2 1
uu
1
2 1
2
du 1 u2
x 22
u
11 22
1
arccosu
2 1
2
12
解法三 令x21u ,则 x2u21(以下同学们自已完成).
