Origin分段线性拟合
Origin如何进行单段和多段的线性拟合

Origin如何进行单段和多段的线性拟合在进行数据处理时,如果需要对绘制的散点图进行线性拟合,应该怎么操作呢?针对更为复杂的情况,按照不同需要进行分段线性拟合时,怎么样才能够实现多段拟合呢?一、单段线性拟合1、首先,把数据导入origin中;2、选中需要绘制的两列数据,点击屏幕左下角,绘制散点图;3、拟合散点图:依次点击Analysis (分析)→ Fitting(拟合)→Linear Fit (线性拟合),弹出Linear Fit对话框,对话框里面不作修改,采取默认点击OK(确定)即可。
4、弹出Reminder Message(提示信息)对话框,询问是否需要转出report sheet?选中Yes,点击 OK即可。
5、现在可以看到,表格里面给出了线性拟合方程的具体信息包括斜率和截距,图中给出了线性拟合曲线。
6、如果想要更为详细的拟合数据,可以在原数据表格中点击Fit Linear1寻找。
二、多段线性拟合1、首先,把数据导入origin中,绘制散点图;可以看到的是这个散点图需要分为两段进行线性拟合,那么怎么才能实现呢?2、工具栏中选中Data(数据),点击Mask Data Points(屏蔽数据点),鼠标如图所示发生变化,拖拽鼠标选中需要屏蔽的数据点,被选中的数据点将变为红色,说明已被屏蔽;3、接下来就是对未屏蔽的散点图进行拟合,重复“单段线性拟合”中步骤3-6继续操作;得到黑色散点的线性拟合曲线,那么怎么继续对剩余部分进行线性拟合呢?4、对屏蔽点进行拟合:选中任意屏蔽点,右键弹出工作框,点击Mark,选择Swap (系统将自动交换屏蔽点和未屏蔽点,颜色发生变化);5、接下来就是剩余散点进行拟合,重复“单段线性拟合”的步骤3-6继续操作;可以看到两段拟合的曲线和相关信息都在图中展现出来。
origin拟合函数

origin拟合函数Origin是一款功能强大的数据分析软件,它提供了丰富的数据分析工具来处理实验数据,其中包括曲线拟合功能。
本文将着重介绍Origin中的曲线拟合功能,包括常见的拟合函数及其应用。
一、拟合函数在Origin中,可以通过选择不同的拟合函数来拟合所需的曲线。
常见的拟合函数有线性函数、二次函数、三次函数、指数函数、对数函数、幂函数、指数增长函数、正弦函数、余弦函数等。
下面将对这些函数进行详细介绍。
1. 线性函数一元线性函数的表达式为y=a+bx,其中a和b分别为截距和斜率,x为自变量,y为因变量。
线性函数是最简单的拟合函数之一,适用于线性关系较为明显的数据。
例如,当我们在光电效应实验中测量出光电子的动能和光子的频率时,它们之间就存在着线性关系,此时可以使用线性函数来拟合数据。
2. 二次函数三次函数的表达式为y=a+bx+cx^2+dx^3,其中a、b、c和d分别为常数,x为自变量,y为因变量。
三次函数通常用于描述抛物线,这种函数在物理和工程学中经常被应用。
例如,在材料科学中可以使用三次函数来描述一个材料的弹性行为。
4. 指数函数指数函数的表达式为y=ae^(bx),其中a和b为常数,x为自变量,y为因变量。
指数函数适用于描述随时间或位置而变化的某些现象。
例如,当我们观察放射性衰变时,衰变速率随时间的变化可以使用指数函数来拟合。
8. 正弦函数正弦函数的表达式为y=a sin(bx+c),其中a、b和c为常数,x为自变量,y为因变量。
正弦函数适用于描述像周期性的变化,例如,天文学中的多个现象,如日、月、星星的运动都是可以用正弦函数表示的。
二、常见应用在实际应用中,我们可以使用Origin中的曲线拟合功能来解决各种问题。
下面列举几种常见的应用。
1. 数据分析在实验数据分析中,使用拟合函数可以帮助我们理解和预测实验数据的变化趋势。
例如,在物理实验中,我们可以使用线性函数来分析位移和时间的关系,使用指数函数来分析辐射物质的衰变过程。
Origin 常用小技巧1 分段线性拟合
Origin 常用小技巧 1 分段线性拟合
By D. J. Liu
6 点上图中 From 和 To 后面的框中输入第二部确定的拟合范围,点击 OK,出现如下结果。
4
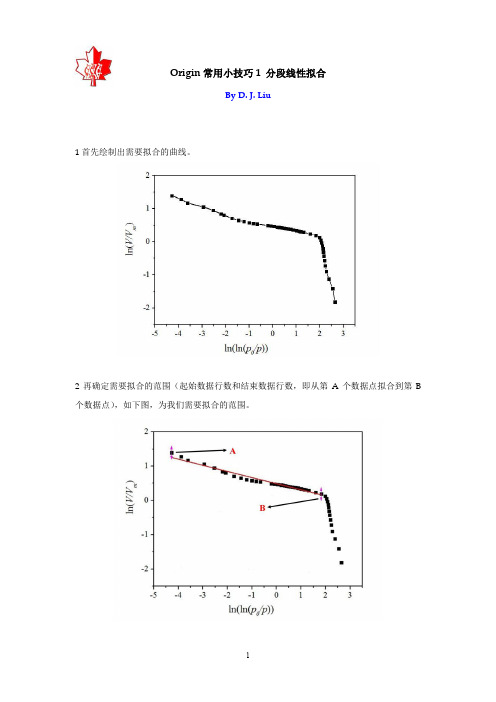
1 首先绘制出需要拟合的曲线。
2 再确定需要拟合的范围(起始数据行数和结束数据行数,即从第 A 个数据点拟合到第 B 个数据点) ,如下图,为我们需要拟合的范围。
1
3 Analysis → Fitting → Fitting Linear → Open Dialog
4 打开对话框后,如下图。
2
5 点击上图中红框的加号,展开对话框。
origin 分段函数拟合

origin 分段函数拟合
分段函数拟合是一种常用的数学方法,用于逼近复杂函数。
它将整个定义域分成多个段落,每个段落内使用简单的函数进行拟合。
这样做的目的是用一组简单的函数来近似整个函数的行为,从而简化计算和分析过程。
在分段函数拟合中,我们首先确定分段点,即将整个定义域划分为不同的段落。
然后,针对每个段落,选择一种适当的函数类型进行拟合。
常用的函数类型包括线性函数、二次函数、指数函数和对数函数等等。
在每个段落内,我们通过调整函数的参数,使得拟合函数与实际函数的取值尽可能接近。
这可以通过最小二乘法等统计方法来实现。
通过不断优化参数,我们可以得到一个在整个定义域上都较好逼近原函数的分段函数。
分段函数拟合可以应用于多个领域,如物理学、经济学和工程学等。
它可以用于描述非线性关系、曲线拟合和数据分析等问题。
通过将问题分解为多个简单的段落,分段函数拟合可以简化复杂问题的处理,并提高计算效率。
总的来说,分段函数拟合是一种有效的数学方法,可以将复杂函数近似为一组简单的函数。
通过合理选择分段点和拟合函数,我们可以得到一个在整个定义域上都较好逼近原函数的分段函数,从而简化计算和分析过程。
origin分段函数拟合

origin分段函数拟合
拟合的函数形式为:
\[ f(x) =
\begin{cases}
a_1x + b_1 & \text{if } x < x_1 \\
a_2x + b_2 & \text{if } x_1 \leq x < x_2 \\
\vdots \\
a_{n-1}x + b_{n-1} & \text{if } x_{n-2} \leq x < x_{n-1} \\ a_nx + b_n & \text{if } x \geq x_{n-1} \\
\end{cases}
\]
其中,$a_i$和$b_i$为拟合参数,$x_i$为分段点。
拟合的过程可以分为以下几步:
1. 确定分段点$x_i$的个数和位置。
可以根据数据的分布情况和特点来选择合适的分段点。
2. 对每个区间$(x_{i-1}, x_i)$内的数据进行线性拟合,得到参数$a_i$和$b_i$。
3. 将每个区间的拟合结果拼接起来,得到最终的拟合函数。
具体的拟合算法可以使用最小二乘法来求解,最小化真实数据与拟合函数之间的误差。
可以使用数值优化算法,如梯度下降法或牛顿法来求解最优的参数值。
需要注意的是,拟合的结果可能会受到分段点的选择和初始参数值的影响,因此需要进行多次尝试和调整,以找到最优的拟合结果。
origin拟合曲线选取点

在Origin中拟合曲线时,选取合适的数据点非常重要。
以下是几个建议:
1. 代表性:选择具有代表性的数据点进行拟合。
这些点应该能够反映数据整体的变化规律。
2. 分布均匀:尽量选择分布均匀的数据点,避免在某些区域选择过多的点,而其他区域选择过少的点。
3. 考虑噪声和异常值:在选择数据点时,应考虑噪声和异常值的影响。
对于噪声,可以选择滤波或平滑处理来减少其影响。
对于异常值,可以将其去除或进行特殊处理。
4. 交互式拟合:可以在Origin中采用交互式拟合方式,即手动选择需要拟合的数据点,然后进行拟合。
这样可以更灵活地选择数据点,并获得更好的拟合效果。
5. 分段拟合:对于具有不同变化趋势的数据,可以考虑采用分段拟合方法。
这样可以更好地适应数据的局部变化规律,提高拟合精度。
6. 非线性拟合:如果数据呈现出非线性变化趋势,可以选择合适的非线性拟合函数进行拟合。
在Origin中,可以通过Analysis > Fitting > Nonlinear Curve Fit菜单进行非线性拟合。
7. 拟合曲线类型:根据数据的特征和变化规律,选择合适的拟合曲线类型。
例如,线性拟合、多项式拟合、指数拟合、对数拟合等。
总之,在Origin中拟合曲线时,需要仔细考虑数据点的选择,并根
据实际情况灵活调整拟合策略,以获得最佳的拟合效果。
Origin的使用方法汇总

Polynomial Fit(多项式拟合工具)
使用【tools】菜单 【Ploynomial Fit 】命令用户可 以对多项式拟合过程中的参数进 行选择,使拟合过程按要求进行, 适合有具体要求的用户使用。
R2
n i 1 n i 1
ˆ Y Y i
i
2
Y Y
2
2
1
n i 1 n i 1
ˆ Yi Y i
i
2
Y Y
2
1
2 e i i 1
n
Y Y
i 1 i
n
2
0 R 1
一般情况下,R2的值越大,拟合得越好。
直线拟合的相关系数
平均人口数 (百万人) 48.2 48.9 49.54 50.25 51.02 51.84 52.76 56.39 54.55 55.35 56.16 56.98
若1990年该省国民收入使用额为67十亿元,平均 人口为58百万人,试估计1990年消费基金
二、非线性模型
有n组观测数据: , n 拟合 设因变量Y 和自变量X 满足: Y f X ,
在Result Log中只显示简单的拟合结果,包括截距、斜率、 标准误差、相关系数、编制偏差、拟合图形的点数和P值
在Results Log中显示所有的拟合结果,除了上面介绍的 以外,还显示t-检验值和ANOVA(方差分析)列表
选中,则进行y=Bx回归分析,不选, 则执行标准线性回归分析 选中,则按指定的斜率值进行拟合,不选, 则执行标准线性回归分析 选中,使用误差值作为权重(如果激活的是 Worksheet,必须选中一列Y误差列,如果激 活的是Graph,图中必须有误差线) 只对拟合过程中的误差参数有影响 绘制数据上、下可信范围 绘制数据上、下预期范围 执行拟合 根据拟合公式计算的X值(已知Y值) 根据拟合公式计算的Y值(已知X值)
Origin线性拟合方法

Polynomial Fit(多项式拟合工具)
使用【tools】菜单 【Ploynomial Fit 】命令用户可 以对多项式拟合过程中的参数进 行选择,使拟合过程按要求进行, 适合有具体要求的用户使用。
最后得到的拟合曲线上点的个数
表示Graph窗口中拟合直线在两端多于曲线 X值范围的百分比
可信度,设置可信范围、预期范围
n Yi Yˆi 2
n
ei2
R2
i 1 n
2
1
i 1 n
1
2
n
i 1
2
Yi Y
Yi Y
Yi Y
i 1
i 1
i 1
0 R 2 1 一般情况下,R2的值越大,拟合得越好。
直线拟合的相关系数
r R2 1 r r
r 与斜率 b1 取相同的符号
r = 1: 完全正相关 r = -1: 完全负相关 r = 0: 无线性关系
分别就k 3和k 4两种情况,
1.9
3.5
2.2
4 在Origin中对表中的数据进行拟合,
2.3
7
2.5 2.6
7.5 9.9
求出b0 ,b1,b2 , , bk。
2.9
10.9
3.1
11.9
3.4
13.5
3.8
13
4.1
11.9
4.4
9
4.7
6.5
4.8
4
4.9
1.5
5
0
5.1
-2.5
5.3
-5
Origin:线性拟合
• 1. 线性回归(basic linear regression ) • 2. 多项式回归(polynomial regression) • 3. 多重回归(multiple linear regression)
