深圳初中数学八年级下册因式分解十字相乘法课件
合集下载
十字相乘法(八年级数学精品课件)
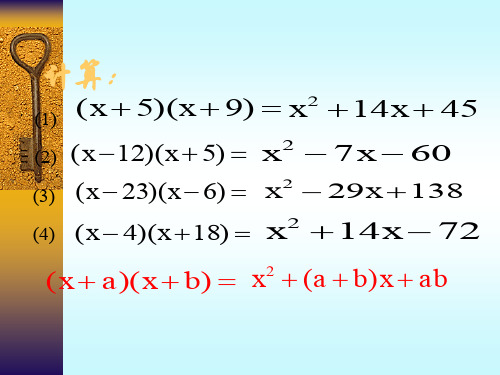
例2、把 y4-7y2-18 分 解因式
例3、把 x2-9xy+14y2 分解因式
用十字相乘法分解下列因式
1、x4-13x2+36 2、x2+3xy-4y2 3、x2y2+16xy+48 4、(2+a)2+5(2+a)-36
5、x4-2x3-48x2
例4、把 6x2-23x+10 分解因式 十字相乘法的要领是:“头尾
十字相乘法
“十字相乘法”是乘法公式: (x+a)(x+b)=x2+(a+b)x+ab的反 向运算,它适用于分解二次三 项式。
例1、把 x2+6x-7分解因式
十字相乘法(借助十字交叉线分解因式的方法)
例一:
x2 6x 7 (x 7)(x 1)
x
7
x 1
x7x 6x
因式分解:
(1) x2 14x 45= (x 5)(x 9) (2) x2 7 x 60= (x 12)(x 5)
(3) x2 29x 138= (x 23)(x 6)
(4) x2 14x 72= (x 4)(x 18) x2 (a b)x ab = (x a)(x b)
分解,交叉相乘,求和凑中,观 察试验”。
1、8x2-22x+15
2、14a2-29a-15 3、4m2+7mn-36n2
4、10(y+1)2-29(y+1)+10
例5、把(x2+5x)2-2(x2+5x)-24 分解因式
例6、把 (x2+2x+3)(x2+2x-2)-6 分解因式
十字相乘法分解因式ppt课件

(2)(x+y+12)(x+y-4)
(2).(x+y) 2+8(x+y)-48; 14
十字相乘法分解因式(2)
本节课解决两个问题: 第一:对形如ax2+bx+c (a≠0)的二次三项式 进行因式分解;
第二:对形如ax2+bxy+cy2 (a≠0)的二次三项式 进行因式分解;
15
(a1x+c1) (a2x+c2) =ax2+bx+c (a≠0)
1
一、计算:
(1) (x 5)(x 9) x2 14x 45
(2) (x 12)(x 5) x2 7x 60 (3) (x 23)(x 6) x2 29x 138
(4) (x 4)(x 18) x2 14x 72
(x a)(x b) x2 (a b)x ab
2
下列各式是因式分解吗?
x2 14x 45 (x 5)(x 9)
x2 7x 60 (x 12)(x 5)
x2 29x 138 (x 23)(x 6)
x2 14x 72 (x 4)(x 18)
3
x2 px q x2 (a b)x ab (x + a )(x + b)
1
-5
6
-5
2
-1
-1-10=-11
1
1
-5+6=1
20
练习:将下列各式分解因式
1、 7x 2-13x+6 答案(7x-6)(x-1) 2、 -y 2-4y+12 答案- (y+6)(y-2) 3、 15x2+7xy-4y 2 答案 (3x-y)(5x+4y) 4、 x 2-(a+1) x+a 答案 (x-1)(x-a)
十字相乘法因式分解课件

步骤二:寻找两个数,它们的乘积等于常数项
总结词
确定两个数的乘积与常数项相等
详细描述
在找到两个数的和与一次项的系数相等后,我们需要找到这两个数的乘积等于常数项的数。例如,在因式分解 “x^2 + 5x + 6”,我们需要找到两个数,它们的乘积为6。
步骤三:验证结果
总结词
验证分解结果的正确性
详细描述
十字相乘法因式分解
目录
CONTENTS
• 引言 • 十字相乘法的基本原理 • 十字相乘法的步骤 • 十字相乘法的应用 • 练习与挑战
01 引言
什么是十字相乘法
十字相乘法是一种数学方法,用于将 多项式因式分解为两个一次因式的乘 积。
该方法通过将多项式的常数项和一次 项系数分别分解为两个数的乘积,然 后交叉相乘得到一次项系数,从而找 到因式分解的两个一次因式。
代数式的化简
代数式化简的定义
将一个代数式通过变形、合并同 类项等方式简化。
十字相乘法的应用
在代数式化简过程中,有时需要通 过因式分解来简化代数式,而十字 相乘法是因式分解的一种常用方法 。
代数式化简的步骤
首先将代数式整理为易于因式分解 的形式,然后使用十字相乘法进行 因式分解,最后将因式分解后的代 数式进行简化。
在这个例子中,我们通过观察二次多项式的系数,找到两个数6和-1,它们的和 等于二次项的系数5,并且它们的乘积等于常数项-6,从而实现了因式分解。
03 十字相乘法的步骤
步骤一
总结词
确定两个数的和与一次项的系数相等
详细描述
在因式分解过程中,首先需要找到两个数,它们的和应等于一次项的系数。例 如,在因式分解“x^2 + 5x + 6”,我们需要找到两个数,它们的和为5。
因式分解——十字相乘法 —初中数学课件PPT

如果一个多项式适当分组,使分组 后各组之间有公因式或可应用公式,那 么这个多项式就可以用分组的方法分解 因式。
练一 练
mx+my-nx-ny ① ② ③④
①②,③④两组,得(mx+my)-(nx+ny)
解1:原式= (mx+my)-(nx+ny) =m(x+y)-n(x+y) =(x+y)(m-n)
x2+px+q= x2+(a+b)x+ab= (x+a)(x+b)
x
a
x
ax +
b
bx = (a+b)x
步骤: ①竖分二次项与常数项; ②交叉相乘,和相加; ③检验确定,横写因式.
顺口溜: 竖分常数交叉验, 横写因式不能乱.
将下列各式因式分解: 1.x2+8x+12= (x+2)(x+6) 2.x2-11x-12= (x-12)(x+1) 3.x2-7x+12= (x-3)(x-4) 4.x2-4x-12= (x-6)(x+2) 5.x2+13x+12= (x+1)(x+12) 6.x2-x-12= (x-4)(x+3)
(4)(x-1)(x+2)(x-3)(x+4)+24 解:(x-1)(x+2)(x-3)(x+4)+24
= 9a4-(4a2-4a+1)
= (x2+x-2)(x2+x-12)+24
= 9a4-(2a-1) 2 = (3a2+2a-1)(3a2-2a+1)
= (x2+x) 2-14(x2+x)+48 = (x2+x-2+px+q进行因式分解, 应重点掌握以下三个问题:
练一 练
mx+my-nx-ny ① ② ③④
①②,③④两组,得(mx+my)-(nx+ny)
解1:原式= (mx+my)-(nx+ny) =m(x+y)-n(x+y) =(x+y)(m-n)
x2+px+q= x2+(a+b)x+ab= (x+a)(x+b)
x
a
x
ax +
b
bx = (a+b)x
步骤: ①竖分二次项与常数项; ②交叉相乘,和相加; ③检验确定,横写因式.
顺口溜: 竖分常数交叉验, 横写因式不能乱.
将下列各式因式分解: 1.x2+8x+12= (x+2)(x+6) 2.x2-11x-12= (x-12)(x+1) 3.x2-7x+12= (x-3)(x-4) 4.x2-4x-12= (x-6)(x+2) 5.x2+13x+12= (x+1)(x+12) 6.x2-x-12= (x-4)(x+3)
(4)(x-1)(x+2)(x-3)(x+4)+24 解:(x-1)(x+2)(x-3)(x+4)+24
= 9a4-(4a2-4a+1)
= (x2+x-2)(x2+x-12)+24
= 9a4-(2a-1) 2 = (3a2+2a-1)(3a2-2a+1)
= (x2+x) 2-14(x2+x)+48 = (x2+x-2+px+q进行因式分解, 应重点掌握以下三个问题:
八年级数学十字相乘法因式分解(PPT)4-2

劲,茁壮生长,四季常春,不畏风雪严寒。独立的个体姿态非常优美,人们习惯把生长在岩石峭壁上的称“望人松”。适于作油松伴生树种的有元宝枫、栎
类、桦木、侧柏等。木材富含松脂,耐腐,适作建筑、家具、枕木、矿柱、电杆、人造纤维等用材。树干可割取松脂,提取松节油,树皮可提取栲胶,松节、 针叶及花粉可入药,亦可采松脂供工业用。 栽培技术编辑 、整地作床:在整地前,先施硫酸亚铁斤,然后用锨深翻厘米,再耧平作床,畦宽.米,长至米, 打埂做畦,种植厘米左右的苗按.米×.米的株行距定点挖穴,每畦一行,每亩栽株。 、挖穴栽苗:栽植油松时,每畦一行,定点在畦的中央,穴为×厘米, 下留松土4至厘米,若是草绳包装的土球,可以不解开;若是尼龙绳和塑料包装的,必须解下,免得造成栽死苗的恶果。将苗栽好后,平好畦面,就可以浇灌。 若苗叶发黄,是缺铁,需施硫酸亚铁。 [] 培育管理 、油松栽上后,在一周内施两次水,以后可松土、保墒,到五月初再浇一次,以后天气不旱不浇,到六 月可施一次肥,八月施一次硫酸亚铁。在株边挖坑点施。在松土锄草上,可天进行一次,要求认真细致,一般深达4至厘米,要求锄匀,土松无坷垃,草锄净、 拾净。 、油松整形和换头:油松在管理过程中,需注意整形和换头工作,油松在生长过程中,有的重枝,头会损坏或处于弱势,须用强健的侧技拉上、捆好,
例2 分解因式 3x2-10x+3
解:3x 2-10x+3
Hale Waihona Puke x-3=(x-3)(3x-1) 3x
-1
-9x-x=-10x
例3 分解因式 5x2-17x-12
解:5x 2-17x-12 5x
+3
=(5x+3)(x-4) x
-4
-20x+3x=-17x
点;有的油松种植人行道内侧或分车带中,于车行道边种植快长树。这样土壤避免车、人的破坏和践踏,对油松生长有利。在古典园林中作为主要景物,以 一株即成一景者极多,至于; 科学实验加盟 科学实验加盟 ;三五株组成美丽景物者更多。其他作为配景、背景、框景等用着屡见不鲜。 在园林配植中,除了适于作独植、丛植、纯林群植外,亦宜行混交种植。适于作油松伴生树枝的有元宝枫、栎类、桦木、侧柏等。 工业价值 油松树干挺拔苍
类、桦木、侧柏等。木材富含松脂,耐腐,适作建筑、家具、枕木、矿柱、电杆、人造纤维等用材。树干可割取松脂,提取松节油,树皮可提取栲胶,松节、 针叶及花粉可入药,亦可采松脂供工业用。 栽培技术编辑 、整地作床:在整地前,先施硫酸亚铁斤,然后用锨深翻厘米,再耧平作床,畦宽.米,长至米, 打埂做畦,种植厘米左右的苗按.米×.米的株行距定点挖穴,每畦一行,每亩栽株。 、挖穴栽苗:栽植油松时,每畦一行,定点在畦的中央,穴为×厘米, 下留松土4至厘米,若是草绳包装的土球,可以不解开;若是尼龙绳和塑料包装的,必须解下,免得造成栽死苗的恶果。将苗栽好后,平好畦面,就可以浇灌。 若苗叶发黄,是缺铁,需施硫酸亚铁。 [] 培育管理 、油松栽上后,在一周内施两次水,以后可松土、保墒,到五月初再浇一次,以后天气不旱不浇,到六 月可施一次肥,八月施一次硫酸亚铁。在株边挖坑点施。在松土锄草上,可天进行一次,要求认真细致,一般深达4至厘米,要求锄匀,土松无坷垃,草锄净、 拾净。 、油松整形和换头:油松在管理过程中,需注意整形和换头工作,油松在生长过程中,有的重枝,头会损坏或处于弱势,须用强健的侧技拉上、捆好,
例2 分解因式 3x2-10x+3
解:3x 2-10x+3
Hale Waihona Puke x-3=(x-3)(3x-1) 3x
-1
-9x-x=-10x
例3 分解因式 5x2-17x-12
解:5x 2-17x-12 5x
+3
=(5x+3)(x-4) x
-4
-20x+3x=-17x
点;有的油松种植人行道内侧或分车带中,于车行道边种植快长树。这样土壤避免车、人的破坏和践踏,对油松生长有利。在古典园林中作为主要景物,以 一株即成一景者极多,至于; 科学实验加盟 科学实验加盟 ;三五株组成美丽景物者更多。其他作为配景、背景、框景等用着屡见不鲜。 在园林配植中,除了适于作独植、丛植、纯林群植外,亦宜行混交种植。适于作油松伴生树枝的有元宝枫、栎类、桦木、侧柏等。 工业价值 油松树干挺拔苍
《因式分解之十字相乘法》PPT课件

因式分解之
十字相乘法
温故而知新
整式乘法中,有
(x+a)(x+b)= x2+(a+b)x+ab
口答计算结果
(1) (x+3)(x+4) (2) (x+3)(x-4) (3) (x-3)(x+4) (4) (x-3)(x-4)
两个一次二项式 整式乘法 一个二次
相乘的积
三项式
(x+a)(x+b)=x2+(a+b)x+ab
反过来 x2+(a+b)x+ab=(x+a)(x+b)
一个二次
两个一次二项式相
三项式 因式分解
乘的积
x2 px q
=
x2 (a b)x ab (x + a )(x + b)
pq
q ab, p a b
如果二次三项式
x2+px+q中的常数项系 数q能分解成两个因数a、 b的积,而且一次项系 数p又恰好是a+b,那 么x2+px+q就可以进行 如上的因式分解。
16
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
17
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
十字相乘法
温故而知新
整式乘法中,有
(x+a)(x+b)= x2+(a+b)x+ab
口答计算结果
(1) (x+3)(x+4) (2) (x+3)(x-4) (3) (x-3)(x+4) (4) (x-3)(x-4)
两个一次二项式 整式乘法 一个二次
相乘的积
三项式
(x+a)(x+b)=x2+(a+b)x+ab
反过来 x2+(a+b)x+ab=(x+a)(x+b)
一个二次
两个一次二项式相
三项式 因式分解
乘的积
x2 px q
=
x2 (a b)x ab (x + a )(x + b)
pq
q ab, p a b
如果二次三项式
x2+px+q中的常数项系 数q能分解成两个因数a、 b的积,而且一次项系 数p又恰好是a+b,那 么x2+px+q就可以进行 如上的因式分解。
16
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
17
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
因式分解(十字相乘)课件

探索因式分解在其他学科中的应用, 如物理、化学等。
感谢您的观看
THANKS
十字相乘法是一种用于因式分解的数学方法,通过将一个多项式分解为两个因式的 乘积,从而简化问题。
它基于二次多项式的根与系数之间的关系,通过构造一个交叉相乘的方程组来找到 因式。
这种方法在代数、方程求解和数学竞赛等领域有广泛应用。
十字相乘法的应用
01
02
03
04
解决一元二次方程
通过十字相乘法,可以将一元 二次方程转化为两个一次方程
通过实例分析和练习,掌握十 字相乘法的运用。
结合实际问题和数学模型,加 深对因式分解的理解和应用。
课程安排
介绍因式分解的概念和意义 。
讲解因式分解的基本方法和 步骤。
02
01
重点介绍十字相乘法的原理
和应用。
03
通过实例演示和练习,巩固 所学知识。
04
05
总结课程重点和难点,提出 学习建议。
02
因式分解的基本概念
因式分解的步骤
总结词
因式分解通常按照一定的步骤进行。
详细描述
因式分解通常按照以下步骤进行:首先观察多项式的各项,尝试将其转化为整式的积的形式;然后提取公因式; 最后利用公式法或分组法进行因式分解。在每一步中,都需要仔细分析多项式的各项,并灵活运用数学规则和技 巧。
03
十字相乘法
什么是十字相乘法
因式分解(十字相乘)ppt 课件
目录 CONTENT
• 引言 • 因式分解的基本概念 • 十字相乘法 • 因式分解的实例解析 • 练习与巩固 • 总结与回顾
01
引言
课程目标
掌握因式分解的基本 原理和方法。
因式分解(十字相乘)课件

提取公因式
将每一项的公因式提取出来, 将原多项式变成各项公因式的 乘积。
配方法
通过配方法,将不能直接提取 公因式的多项式进行因式分解。
分组分解
如果多项式中含有四个以上的 项,我们可以通过分组的方式 来进行因式分解。
常见的因式分解公式
1 平方差公式
a² - b² = (a + b)(a - b)
2 完全平方公式
因式分解(十字相乘)ppt课 件
因式分解是数学中重要的概念之一,它能够帮助我们解决各种代数问题,本 课程将详细介绍因式分解的定义、基本方法、常见公式和解题技巧。
因式分解的概念和定义
因式分解是将一个多项式拆分成多个较简单的乘积的过程,通过因式分解, 我们可以更好地理解一个多项式的结构和性质。
因式分解的基本方法和步骤
ห้องสมุดไป่ตู้
3 三项平方差公式
a² + 2ab + b² = (a + b)²
a³ - b³ = (a - b)(a² + ab + b²)
应用因式分解解决问题的例题
1
例题一
利用因式分解,求解二次方程2x² + x - 6 = 0的解。
2
例题二
利用因式分解,化简表达式(4x + 3)(2x - 5) + 7x。
总结和提醒
因式分解是解决代数问题的重要工具,通过学习和掌握因式分解的方法和技巧,我们可以更加轻松地解决各种 数学难题。
3
例题三
应用因式分解,计算多边形的面积。
因式分解的技巧和窍门
在进行因式分解时,需要灵活运用一些技巧和窍门,如提取公因式时寻找最大公约数,或使用配方法时查找合 适的形式进行配对。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例如:
3x2 2x 1
1.十字相乘法分解因式的公式:
x2+(a+b)x+ab=(x+a)(x+b)
2.能用十字相乘法来分解因式的二次三项式的系数的 特点:常数项能分解成两个数的积,且这两个数的和 恰好等于一次项的系数。
3.在用十字相乘法分解因式时,因为常数项的 分解因数有多种情况,所以通常要经过多次的 尝试才能确定采用哪组分解来进行分解因式。
x2 11x 12 (x __—__12)(x __+___1)
寻找的两数a和b的符号是如何确定的?
x2 px q (x a)(x b)
当q>0时,a、b( 同号 ),且a、b的符号和p 的符号( 相同 ).
当q<0时,a、b( 异号 ),且绝对值较大的因 数与p的符号( 相同 ).
例2、把 y4-7y2-18 分 解因式
深圳初中数学八年 级下册因式分解 ——十字相乘法
课前复习:
1.什么是因式分解?
把一个多项式分解成几个整式的积的形式,叫做把 这个多项式因式分解,也叫做把这个多项式分解因 式。
因式分解的实质是(“和差化积” )与( 整式乘法 ) 是“积化和差”的过程正好( 相反 )。
2.之前我们都学习了哪些分解因式的方法?
例3、把 x2-9xy+14y2 分解因式
把下列各式分解因式
1. x2-11x-12 2. x2+4x-12 3. x2-x-12 4. x2-5x-14 5. y2-11y+24
x2-5x+6 x2-5x-6 X2+5x-6 X2+5x+6
用十字相乘法分解下列因式
1、x4-13x2+36 2、x2+3xy-4y2 3、x2y2+16xy+48 4、(2+a)2+5(2+a)-36
思考3:
是不是所有的二次三项式都可以用十字相乘法进行因式分解呢? 如果不是,那满足什么条件的二次三项式可以用十字相乘法进行因 式分解呢?
将下列多项式因式分解
(1)x2+3x-4 (2)x2-3x-4 (3)x2+6xy-16y2 (4)x2-11xy+24y2 (5)x2y2-7xy-18
(7)(a+b)2-4(a+b)+3 (8) x4-3x3 -28x2
例6、把 (x2+2x+3)(x2+2x-2)-6 分解因式
例7、把 (x+1)(x+2)(x+3)(x+4)-3分解 因式
拓展创新
把下列各式分解因式 1、x2-4xy+4y2-6x+12y+8
2、(x2+2x)(x2+2x-11)+11 3、x n+1+3xn+2xn-1 4、(x+1)(x+3)(x+5)(x+7)+16
ab q
它们的乘积等于常数项,它们的和等于一 次项系数。
试一试:把x2+3x+2分解因式
十字相乘法(借助十字交叉线分解因式的方法)
例一:
步骤:
x2 6x 7 (x 7)(x 1) ①竖分二次项与常数项
x
7
x 1
②交叉相乘,和相加 ③检验确定,横写因式
顺口溜:
x7x 6x
竖分常数交叉验, 横写因式不能乱。
相乘法。
请大家记住公式
十字相乘法公式:
x2 (a b)x ab (x a)(x b)
定义: 利用十字交叉线来分解系数,把二次三
项式分解因式的方法叫做十字相乘法。
十字相乘法进行因式分解的关键:
(1)列出常数项分解成两个因数的积的各种可能情况;
拆分常数项
(2)尝试其中的哪两个因数的和恰好等 于一次项系数; 验证一次项
试一试:把x2+3x+2分解因式
分析∵ (+1) ×(+2)=+2
常数项
(+1)+(+2)=+3
x
1
∴x
2
一次项系数 十字交叉线
解:原式 (x 1)(x 2)
(1).因式分解竖直写; (2).交叉相乘验中项; (3).横向写出两因式;
利用十字交叉线来分解 系数,把二次三项式分 解因式的方法叫做十字
等式左边是( 二次三项式 ),二次项的系数是( 1)
等式右边是两个一次二项式(相乘 ),整个等式从 左到右将( 和差 )的形式转化成( 积 )的形式, 进行的是(因式分解 )。
x2 px q x2 (a b)x ab (x a)(x b)
那么a和b如何确定呢?满足什么条件呢?
ab p
(x 3)(x 4) x2 7x 12
(x 3)(x 4) x2 x 12 (x 3)(x 4) x2 x 12
(x 3)(x 4) x2 7x 12
(x a)(x b) x2 (a b)x ab
等式左边是两个一次二项式(相乘 ) 右边是( 二次三项式 )
5、x4-2x3-48x2
例4、把 6x2-23x+10 分解因式 十字相乘法的要领是:“头尾
分解,交叉相乘,求和凑中,观 察试验”。
1、8x2-22x+15
2、14a2-29a-15 3、4m2+7mn-36n2
4、10(y+1)2-29(y+1)+10
例5、把(x2+5x)2-2(x2+5x)-24 分解因式
课外拓展:
若 A B ,下0面两个结论对吗?
(1)A和B同时都为0,即A=0且B=0;
(2)A和B中至少有一个为0,即A=0或B=0。
请结合上面的结论,运用十字相乘法解 下列一元二次方程:
1). x2 7x 6 0 2). x2 7x 12
思考2:
我们现在所研究的都是二次项系数是1的二次三项式用十字相乘法 进行因式分解,那么当二次项的系数不是1,而是其他数字时又该 如何进行分解呢?
这个过程将( 积 )的形式,转化成( 和差 ) 的形式,进行的是(整式乘法 )运算。
(x 3)(x 4) = x2 7x 12
(x 3)(x 4) = x2 x 12 (x 3)(x 4) = x2 x 12
(x 3)(x 4) = x2 7x 12 x2 px q (x a)(x b) = x2 (a b2 7x 12
3.
2. x2 4x 12
4.
x2 8x 12
x2 11x 12
练一练:在下列各式的横线上填入“+”和“—”号。
x2 7x 12 (x __—__ 3)( x __—__ 4)
x2 8x 12 (x __+__ 2)(x __+___6)
x2 4x 12 (x __+__ 6)( x __—__ 2)
(9) 2x2-7x+3 (10) 5x2+6xy-8y2
(6)x4+13x2+36
提取公因式法
公式法
计算下列各题:
(x 3)(x 4) x2 7x 12 (x 3)(x 4) x2 x 12 (x 3)(x 4) x2 x 12 (x 3)(x 4) x2 7x 12 问:你有什么快速计算类似多项式的方法吗?
(x a)(x b) x2 (a b)x ab
3x2 2x 1
1.十字相乘法分解因式的公式:
x2+(a+b)x+ab=(x+a)(x+b)
2.能用十字相乘法来分解因式的二次三项式的系数的 特点:常数项能分解成两个数的积,且这两个数的和 恰好等于一次项的系数。
3.在用十字相乘法分解因式时,因为常数项的 分解因数有多种情况,所以通常要经过多次的 尝试才能确定采用哪组分解来进行分解因式。
x2 11x 12 (x __—__12)(x __+___1)
寻找的两数a和b的符号是如何确定的?
x2 px q (x a)(x b)
当q>0时,a、b( 同号 ),且a、b的符号和p 的符号( 相同 ).
当q<0时,a、b( 异号 ),且绝对值较大的因 数与p的符号( 相同 ).
例2、把 y4-7y2-18 分 解因式
深圳初中数学八年 级下册因式分解 ——十字相乘法
课前复习:
1.什么是因式分解?
把一个多项式分解成几个整式的积的形式,叫做把 这个多项式因式分解,也叫做把这个多项式分解因 式。
因式分解的实质是(“和差化积” )与( 整式乘法 ) 是“积化和差”的过程正好( 相反 )。
2.之前我们都学习了哪些分解因式的方法?
例3、把 x2-9xy+14y2 分解因式
把下列各式分解因式
1. x2-11x-12 2. x2+4x-12 3. x2-x-12 4. x2-5x-14 5. y2-11y+24
x2-5x+6 x2-5x-6 X2+5x-6 X2+5x+6
用十字相乘法分解下列因式
1、x4-13x2+36 2、x2+3xy-4y2 3、x2y2+16xy+48 4、(2+a)2+5(2+a)-36
思考3:
是不是所有的二次三项式都可以用十字相乘法进行因式分解呢? 如果不是,那满足什么条件的二次三项式可以用十字相乘法进行因 式分解呢?
将下列多项式因式分解
(1)x2+3x-4 (2)x2-3x-4 (3)x2+6xy-16y2 (4)x2-11xy+24y2 (5)x2y2-7xy-18
(7)(a+b)2-4(a+b)+3 (8) x4-3x3 -28x2
例6、把 (x2+2x+3)(x2+2x-2)-6 分解因式
例7、把 (x+1)(x+2)(x+3)(x+4)-3分解 因式
拓展创新
把下列各式分解因式 1、x2-4xy+4y2-6x+12y+8
2、(x2+2x)(x2+2x-11)+11 3、x n+1+3xn+2xn-1 4、(x+1)(x+3)(x+5)(x+7)+16
ab q
它们的乘积等于常数项,它们的和等于一 次项系数。
试一试:把x2+3x+2分解因式
十字相乘法(借助十字交叉线分解因式的方法)
例一:
步骤:
x2 6x 7 (x 7)(x 1) ①竖分二次项与常数项
x
7
x 1
②交叉相乘,和相加 ③检验确定,横写因式
顺口溜:
x7x 6x
竖分常数交叉验, 横写因式不能乱。
相乘法。
请大家记住公式
十字相乘法公式:
x2 (a b)x ab (x a)(x b)
定义: 利用十字交叉线来分解系数,把二次三
项式分解因式的方法叫做十字相乘法。
十字相乘法进行因式分解的关键:
(1)列出常数项分解成两个因数的积的各种可能情况;
拆分常数项
(2)尝试其中的哪两个因数的和恰好等 于一次项系数; 验证一次项
试一试:把x2+3x+2分解因式
分析∵ (+1) ×(+2)=+2
常数项
(+1)+(+2)=+3
x
1
∴x
2
一次项系数 十字交叉线
解:原式 (x 1)(x 2)
(1).因式分解竖直写; (2).交叉相乘验中项; (3).横向写出两因式;
利用十字交叉线来分解 系数,把二次三项式分 解因式的方法叫做十字
等式左边是( 二次三项式 ),二次项的系数是( 1)
等式右边是两个一次二项式(相乘 ),整个等式从 左到右将( 和差 )的形式转化成( 积 )的形式, 进行的是(因式分解 )。
x2 px q x2 (a b)x ab (x a)(x b)
那么a和b如何确定呢?满足什么条件呢?
ab p
(x 3)(x 4) x2 7x 12
(x 3)(x 4) x2 x 12 (x 3)(x 4) x2 x 12
(x 3)(x 4) x2 7x 12
(x a)(x b) x2 (a b)x ab
等式左边是两个一次二项式(相乘 ) 右边是( 二次三项式 )
5、x4-2x3-48x2
例4、把 6x2-23x+10 分解因式 十字相乘法的要领是:“头尾
分解,交叉相乘,求和凑中,观 察试验”。
1、8x2-22x+15
2、14a2-29a-15 3、4m2+7mn-36n2
4、10(y+1)2-29(y+1)+10
例5、把(x2+5x)2-2(x2+5x)-24 分解因式
课外拓展:
若 A B ,下0面两个结论对吗?
(1)A和B同时都为0,即A=0且B=0;
(2)A和B中至少有一个为0,即A=0或B=0。
请结合上面的结论,运用十字相乘法解 下列一元二次方程:
1). x2 7x 6 0 2). x2 7x 12
思考2:
我们现在所研究的都是二次项系数是1的二次三项式用十字相乘法 进行因式分解,那么当二次项的系数不是1,而是其他数字时又该 如何进行分解呢?
这个过程将( 积 )的形式,转化成( 和差 ) 的形式,进行的是(整式乘法 )运算。
(x 3)(x 4) = x2 7x 12
(x 3)(x 4) = x2 x 12 (x 3)(x 4) = x2 x 12
(x 3)(x 4) = x2 7x 12 x2 px q (x a)(x b) = x2 (a b2 7x 12
3.
2. x2 4x 12
4.
x2 8x 12
x2 11x 12
练一练:在下列各式的横线上填入“+”和“—”号。
x2 7x 12 (x __—__ 3)( x __—__ 4)
x2 8x 12 (x __+__ 2)(x __+___6)
x2 4x 12 (x __+__ 6)( x __—__ 2)
(9) 2x2-7x+3 (10) 5x2+6xy-8y2
(6)x4+13x2+36
提取公因式法
公式法
计算下列各题:
(x 3)(x 4) x2 7x 12 (x 3)(x 4) x2 x 12 (x 3)(x 4) x2 x 12 (x 3)(x 4) x2 7x 12 问:你有什么快速计算类似多项式的方法吗?
(x a)(x b) x2 (a b)x ab
