线性系统理论第一章(习题)

合集下载

线性系统分析_习题答案

专业课习题解析课程西安电子科技大学844信号与系统专业课习题解析课程第1讲第一章信号与系统（一）专业课习题解析课程第2讲第一章信号与系统（二）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为（2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)(sin )(t r t f =（7）)(2)(k t f k ε=（10）)(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。

线性系统理论复习题纲

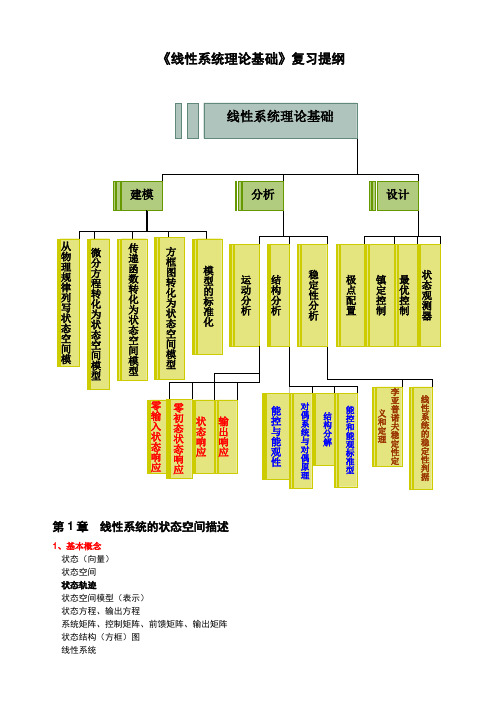
《线性系统理论基础》复习提纲第1章线性系统的状态空间描述1、基本概念状态（向量）状态空间状态轨迹状态空间模型（表示）状态方程、输出方程系统矩阵、控制矩阵、前馈矩阵、输出矩阵状态结构（方框）图线性系统时不变（定常）系统、时变系统连续时间系统、离散时间系统状态线性变换矩阵的特征值、矩阵的特征向量对角线标准型、约当标准型模态标准型正则型矩阵范德蒙矩阵传递函数矩阵2、知识要点%%知识点1：根据物理规律建立状态空间模型♦ 简单机械系统 ♦简单电气系统参考例题：例2.1.1，例2.1.2（P8）%%知识点2：微分方程模型转化为状态空间模型♦微分方程中不含输入导数项给定 ()(1)110n n n y a ya y a y bu --++++=&L ，选取状态向量12(1)n n x y x y x y -⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦&M M ，则有状态方程： 1122011010010n n n x x x x u x a a a x b -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦&&M O M M M&L输出方程： []⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n x x x y M Λ21001 例2.1.3 (注意：方框图在没有要求时可以不画出) ♦微分方程中包含输入函数导数项，且m n <给定()(1)()(1)110110n n m m n m m ya y a y a yb u b u b u b u ----++++=++++&&L L ，m n <,将其转化为()(1)110()(1)110n n n m m m m y a y a y a y u y b yb y b y b y ----⎧++++=⎪⎨=++++⎪⎩&%%%%L &%%%%L ，选取状态向量12(1)n n x yx y x y-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦%&%M M %，则有状态方程 120110100101n n x x u x a a a -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦&&M O M M &L 输出方程 12011[,,,,0,,0]m n m n x x y b b b x --⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦L L 123M例2.1.4 ♦ 微分方程中包含输入函数导数项，且n m =若()(1)()(1)110110n n n n n n n ya y a y a yb u b u b u b u ----++++=++++&&L L ，让n y y b u =-%，则转化为如下微分方程的形式()(1)(1)(1)110111100()()()n n n n n n n n n y a y a y a y b a b u b a b u b a b u -----++++=-++-+-%%%%&L L 。

线性系统理论1数学基础

a2 u a1e1 a 2 e2 a n en e1 e2 en a n
T 1 T 2 T T n
我们称 a a a 为关于基 e1 , e2 , , en 的坐标。若向量 e , e , , e 构成 R n 的另一组基，则有
1.6
广义Sylvester矩阵
AV BW VF 其中: A R W C
r n nn
(1.6.1)
nr
,BR
;V C
nn
,
; F 为n价的Jordan矩阵当取 .
定W 阵, 并令C BW , 则上式化为常规的Sylvester矩阵方程 : AV VF C (1.6.2)
矩阵的Jordan标准型与该特征值相关联的Jordan块的个数.
矩阵某特征值的代数重数:
矩阵的Jordan标准型与该特征值相关所有的Jordan块的阶数之和.
命题1.5.1 设A R 构如上述.记
n n
,其Jordan矩阵的结
i =max pi1 pi2 piq ,i=1,2, ,l
v1 v 2 v n v 1 v P 2 v n
v Rn ，有
e , e , , e n 和基 e1 , e 2 , , e n 之间的坐标我们称 P 为基 1 2
1.4有理分式矩阵及其互质分解
1.4.1 互质多项式矩阵
1.4.2 有理分式矩阵的互质分解
1.4.3 矩阵(sI A) B的右既约分解
1
W ( s ) ( sI A) B N ( s ) D ( s )的求取: 第一步:利用算法1.3.1求取幺模矩阵P ( s ) 和Q ( s )满足 : P ( s ) sI A B Q(s) 0 I 第二步 : 将幺模阵Q ( s )做如下分块 : Q11 ( s ) Q12 ( s ) Q( s) Q21 ( s ) Q22 ( s ) 其中, Q11 ( s ) R nr [ s ], Q21 ( s ) R r r [ s ]. 第三步 : 取 N ( s ) Q11 ( s ), D ( s ) Q21 ( s ) 则N ( s )与D ( s )满足右既约分解式 W ( s ) ( sI A) 1 B N ( s ) D 1 ( s )。

线性系统理论(第一章)

x1(k +1) 0.9696 0.0202 x1(k) x (k +1) = 0.0404 0.9898 x (k) , k = 0,1,2,L 2 2 7 x1(0) 10 x (0) = 7 2 9×10
016
向量方程的形式：
Y = g (x,u,t)
, t ≥ t0
008
第一章
Ø线性系统的状态空间描述为：
& = A (t ) x + B (t )u x t ≥ t0 y = C (t ) x + D (t )u
其中：
a11 (t ) L a1n (t ) A(t ) = M M an1 (t ) L ann (t )
线性系统。
017
第一章
& = A(t ) x + B (t )u x t ≥ t0 y = C (t ) x + D (t )u
D(t ) + B(t ) +
+ +
u
∫
A(t )
C (t )
y
018
第一章
若向量函数中 f 为变量
( x,u,t)
和
g ( x, u , t ) 至少包含一个元
其中： ai 和 b j 为实常数，i = 0 ,1, L , n
j = 0 ,1, L , n − 1
003
第一章
假定初始条件为零，取拉氏变换。复频率域描述，即传递函数。
bn −1 s + L + b1 s + b0 G (s) = n n −1 s + a n − 1 s + L + a1 s + a 0

线性系统理论课后答案

6 XI 给定图P2.12)和＜b)所示两个电路，试列写出其状态方S 和输出方程。

其中, 分别指定：⑹状态变组廿二叱•勺输入变M « = ef(r):输出支量尹=/(b)状态变宣组X 严气，输入变S“y(O；输出变量丿■“CP2 1解本题A 于由物理系统養立状态令问描述的基本题，意在训练正磧和熟塚运用电路定律列写岀电路的状态方程和输出方程•(1)列写P2・l(a)电路的状态方程和输山方程。

首先.考虎到电容C 和电感E 为给定电路中仅有的两个储能元件•电容端电压弋和流经电感电流了构成此电路的线性无关极人变*组，从而透取状态变*组州=%:和巧=i 符合定义要求。

基此，利用电路元件关系式和回路基尔《夫定律，定出电路方程为C 虬r dr L —+= e再由上述电路方程导出状态变量陀和i 的导》项，可得到状态变査方程规范形式，血C I •—=—(tU C d/ 1 心 1 d/L c L L表%=3山和dW/dn 并将上述方程组表为向量方程，就得到此电路的状态方程:继而.按约定输出y = A 可直接得到此电路的输出方程:(b)列写P2.i(b)电路的状态方程和«ta 方程•类似地.考虑到电容C ］和C2为给定电路中仅有的两个储能元件，电容端电压乜和七构成此电路的线性无关极大变fi 组，选取状态变量组二叱和可二叱2符合定义要求，基此，利用电路元件关系式和回路基尔霍夫定定出电路方程为dur GRpM 叱+叱之71RZ,皿6再由上述电路方程导出状态变量叱和叱的导数项，可得到状态变量方程规范形式: % 1 I 1少GR q GR 5 C,Kdr 表M 也C| /曲和 MqI方程：继而，按约定输出y =坯，可由电路导出：尸叱=%+七将其表为向*方程，就得萸i 此电路的皴出方程，八不叱~孫"6 +丽e并将上述方程组表为向量方程，就得封此电路的状态K2.6求出下列^输入输出描述的一个状态空同描述： (i) 施)二 2^2 十 18$+40u(s)『+ 6“ +11S+6 (ii) 型十妙⑴_u(j) (g + 3)2(zl)解本®属于由传递函数型输入输出描述导出狀态空间描述的基本fi 。

第一篇线性系统理论习题答案

⎡ s +1 ⎢s2 + s +1 ⎢ −1 = [1 0 1]⎢ 2 ⎢s + s +1 ⎢ 0 ⎢ ⎣
9－7 设有三维状态方程
⎡0 ⎤ ⎢1 ⎥ ⎢ ⎥ ⎢ ⎣1 ⎥ ⎦
1 s + s +1 s 2 s + s +1
2
0
⎤ 0 ⎥ ⎥ ⎡0 ⎤ s 2 + 2 s 1⎥ = 3 0 ⎥ ⎢ ⎢ s −1 ⎥ ⎥ 1 ⎥ ⎢ ⎣1⎥ ⎦ s − 1⎥ ⎦
⎡ R M ⎤ ⎡ R −1 ∵⎢ ⎥×⎢ ⎣0 T ⎦ ⎣ 0
− R −1 MT −1 ⎤ ⎡ R −1 ⎥=⎢ T− ⎦ ⎣ 0
⎡R M ⎤ ∴⎢ ⎥ ⎣0 T ⎦
9－10 解
−1
⎡ R −1 =⎢ ⎣ 0
− R −1 MT −1 ⎤ ⎥ T −1 ⎦
−1
对可控标准形 A 和 b ，计算 ( sI − A) b
+
v2
& 2 = x1 + y = x1 − C 2 x
写成矩阵形式为
1 1 x2 + U R2 R2
图 9－1 RLC 网络
⎡ R1 − & x ⎡ 1 ⎤ ⎢ L1 ⎢x ⎥=⎢ ⎣ &2 ⎦ ⎢ 0 ⎢ ⎣
⎤ ⎡ 1 ⎤ 0 ⎥ x ⎡ ⎤ ⎢ L ⎥ ⎥ ⎢ 1 ⎥ + ⎢ 1 ⎥U − 1 ⎥ ⎣ x2 ⎦ ⎢ − 1 ⎥ ⎢ R2 C 2 ⎥ ⎦ ⎣ R2 C 2 ⎥ ⎦
x1 ， x 2 有下列关系存在 x1 = x1 + x 2 x 2 = − x1 − 2 x 2
试求系统在 x 坐标中的状态方程。解 ①
&1 = x & = x2 x &2 = & & = −2 x1 − 3 x 2 + u x x

《线性系统理论》作业参考答案

x 11 e t x 21 , 21 0 , x
x11 ( t 0 ) 1 x 21 ( t 0 ) 0
，
x 12 e t x 22 , 22 0 , x
x12 ( t 0 ) 0 x 22 ( t 0 ) 1
解得
x12 e t e t 0 x11 1 ， x 21 0 x 21 1 1 (t ) x 0 e
( sI A )
1
s ( s 1) 0 2 det( sI A ) s ( s 1) 0 adj ( sI A ) 1
s 1 ( s 1) 0
2
s ( s 1) 1 s ( s 1) 1 s 1 1
2
所以 e
。
可以看出， f ( i ) 是 f ( A ) 的一个特征值。
1-3 解：(1) 特征多项式为 1 ( ) ( 1 ) .
4
验证
A 1 I 0 , ( A 1 I ) 2 0 , ( A 1 I ) 3 0 , ( A 1 I ) 4 0
At
e t 1 1 L [( sI A ) ] 0 0
e 1 1 0
t
t t 1 e te t e 1 。 t e
1-5 证明：因为 D 1 存在，所以由 D R p p
A det C B IA det D 0 BD A I D C
c
k 0
k
A
k
设 x 是属于 i 的一个非零特征向量，故
A x i x
.
2 2 因此 A x A Ax A i x i Ax i i x i x .

中国科学技术大学自动化专业《线性系统理论和设计》习题1-6章习题答案

1.7 证明：())()det(det )det(det )(det )det()det()(1111λλλλλλλA B A I T A I T T A I T AT T I B I AT T B B A ∆=-=⋅-⋅-=-=-=∆⇒=----相似，与设= 又因为特征值为特征方程()0λ∆=的根，故特征值也相同。

1.11 解：可以参照课本P18的例题1.12（1）,3,2,1)3)(2)(1()(,300020104132111===⇒---=∆⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=λλλλλλA A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==Λ∴⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⇒=--3211000105411050140010)(1113211Q A Q Q q q q q A I ，，由λ（4）,2,1,1)2)(1)(1()(4344111432124==-==⇒-+-=∆⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--λλλλλλλA ，1241243111111()0,111122,()012,12,4822 2.P I A q q q u I A q q u λλλλλξλλη⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥==--=⇒==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦==-=⎡⎤⎢⎥⎢⎥==<=⎢⎥⎢⎥⎣⎦===对于，，由对于的特征值，其代数重数由计算其对应的特征向量计算出一个特征向量，即几何重数个数小于代数重数，即标准型中存在一个对应的约当块，约当块的阶数即的指数可以利用[]4443434123414418 1.682,()001110111121,,44114412121181211212q I A q q q c q q Q q q q q Q A Q λλ-=-=⇒⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⋅-=∴==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥-⎢⎥∴Λ==⎢⎥⎢⎥⎣⎦的式计算的广义特征向量由取1.12 证明：12n 222112n n 1n-1n-112n 21n 121n 1221n n 1n-3n-3221n 21n-22n-2n-2221n n 1111(1110()()0()()(0()()λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ-⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎡⎤--⎢⎥--⎢⎥--⎢⎥==⎢⎥--⎢⎥⎢⎥--⎣⎦后一行减去前一行的倍）n-221n n 123n 2131n 1n-2n-2n-223n j i 1i j n)()111()()()()()λλλλλλλλλλλλλλλλλλ≤<≤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎡⎤⎢⎥⎢⎥=---=⎢⎥⎢⎥⎣⎦=-∏同理2.6 解：(d) 令24231211y x y x yx y x ====，，，，则状态空间方程为： u m m k m k m k mk ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--=0010020100000200112211x xx y ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=010*******y y (e) 令yx y x ==21，，则状态空间方程为： u e e t t ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=-10102x x[]x y 01= 2.7 解：(c)非线性方程： ⎩⎨⎧==21221u-x xx x[]x y 01= (d) 设⎪⎩⎪⎨⎧+=⇒=+⋅++-=⇒=+⋅+ux sx x u)(x s u x x sx x s )x (u 333221122121112，则状态空间方程可为：u ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-=310312x x[]x y 01= 另法：先求出传递函数2323s G(s)s s +=+-，按2.6（b ）方法求解。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

若 li 是 A 的特征值，试证 [1 li li 2 li n -1 ]T 是属于 li 的特征向量。 1—2 若 li 是 A 的一个特征值，试证 f (li ) 是矩阵函数 f (A) 的一个特征值。 1—3 试求下列矩阵的特征多项式和最小多项式
é l1 1 0 0 ù ê ú ê 0 l1 1 0 ú ê ú ê ú ê 0 0 l1 0 ú ê ú ê 0 0 0 l1 ú ë û é l1 1 0 0 ù ê ú ê 0 l1 0 0 ú ê ú ê ú ê 0 0 l1 0 ú ê ú ê 0 0 0 l1 ú ë û é l1 1 0 0 ù ê ú ê 0 l1 0 0 ú ê ú ê ú ê 0 0 l1 1 ú ê ú ê 0 0 0 l1 ú ë û
y =
t
ò0 g(t - t )u(t )d t
若脉冲响应 g 由图 1—12(a)给定。试问，由图 1—12(b)所示的输入而激励的输出为何？ g(t) 1 1 (a) 图 1—12 脉冲响应和输入作用 1—12 试求图 1—13 所示系统的动态方程式(略)
29
u(t) 1 2 t 1 2 (b) t
n >m
试证，给定初始状态 x(m ) = x0 下，时刻 n 的状态为 x(n )=F(n, m )x(0) 。若 A 与 n 无关，则
F(n, m ) 为何？
1—27 证明 x(n + 1) = A(n )x(n ) + B(n )u(n ) 的解为
n -1
x(n ) = F(n, m )x(m ) +
1 ù ú s+3ú 5s + 1 úú s + 2 úû
的实现，并画出其模拟图。 1—25 设{ A , B , C , D }和{ A , B , C , D }是两个线性时不变系统，其维数不一定相同。证明当且仅当
CAk B = CAk B
(k = 0,1,2 )
D=D
时，两系统零状态等价。 1—26 设 x(n+1) = A(n)x(n)定义： F(n, m ) = A(n - 1)A(n - 2) A(m ) F(m, m ) = I
= A(t )x 的状态转移矩阵，试证： 1—18 设 Φ ( t, t0 ) 为 x
t
det F ( t, t0 ) = exp ò tr[A(t )]d t
t0
= A(t )x ，方程 z = -A* (t )z 称为它的伴随方程。其中 A* (t ) 表示 A(t ) 的转置共 1—19 给定 x = A(t )x 和 z = -A* (t )z 的状态转移矩阵。试证：轭。设 F ( t, t0 ) 和 F1 ( t, t0 ) 分别是 x
且：
1 ai = - tr (Ri -1A) i i = 1,2, 3 , n
= (costsint )x 的等价时不变动态方程 1—22 试求 x
= e -At Be At x ，其中 A 、 B 为常值为方阵，求状态转移矩阵。 1—23 若 x
1—24 求真有理函数阵
é2 + s ê s +1 G(s ) = êê ê 5 êë s + 1
L =m
å F(n, l + 1)B(l )u(l )
1—28 设有 n 维、线性、时不变动态方程
= Ax + Bu x y = Cx + Du
若输入
u(t ) = u(n ) nT £ t £ (n + 1)T
n = 0,1,2
这里 T > 0 为采样周期。试证，系统在离散瞬时 0,T , 2T , 上的行为由下列离散时间方程给出：
éA Bù ú = det D ⋅ det(A - BD-1C) det êê ú êë C D úû
若 A 可逆，上式有何变化？并证明
é é a1 ù ù ê ê ú ú n ê êa ú ú 2 det êê In + êê úú [b1 b2 bn ] úú = 1 + å aibi ê ê ú ú i =1 ê êa ú ú ëê ëê n úû ûú
31
æ T At ö x(n + 1) = e At x(n ) + ç e dt ÷ Bu(n ) ÷ ç ÷ ç è ò0 ø y(n ) = Cx(n ) + Du(n )
1—29 设有理函数矩阵为
é ê ê G(s ) = ê ê ês ëê 1 2s + 1 ù ú s s(s + 1) ú ú 1 2s + 1 ú + 1 s(s + 1)2 úûú
1—16
设
é1 ê ê0 ê A=ê ê0 ê ê0 ë 1 ù ú 1 0 0 úú 0 1 -1 úú ú 0 0 1 ú û 0 1
试利用 L[e At ] = (sI - A)-1 ，求 e At 1—17 若 T-1 (t ) 存在且对所有 t 可微，试证 d -1 éd ù [T (t )] = -T-1 (t ) ê T(t ) ú T-1 (t ) dt dt ë û
其中 a 为固定常数。试问，试系统是否为线性的？是否为时不变的？是否具有因果性？ 1—9 试证：若对于任何 u1, u2 ，有 H (u1 + u2 ) = Hu1 + Hu2 则对于任意有理数 a 和任何 u ，有 H a u= a Hu。 1—10 试证，对于固定的 a ，图 1—4 所定义的移位算子 Qa 是线性时不变系统。它的脉冲响应和传递函数为何？ 1—11 考虑由下式描述的松弛系统
若输入 u 有形式 e ，其中 l1 不是 A 的特征值，试证存在初始状态，使输出 y 立即有 e l1t 的形式而不包含有任何瞬变过程。又当 l1 是传递函数的零点时，试证可选适当初始状态，使系统在输入 el1t 作用下，输出恒为零。
l1t
32
30
D(s ) = det(sI - A) = s n + a1s n -1 + a2s n -2 + + an
是 A 的特征多项式。试证
R1 = A + a1I = AR 0 + a1I R2 = A2 + a1A + a2 I = AR1 + a2 I

Rn -1 = An -1 + a1An -2 + + an -1I = ARn -2 + an -1I
1—7
线性松弛系统的脉冲响应为 g(t, t ) = e -|t -t | ( 对所有的 t, t ) 设问系统是否具有因果
性？它是时不变的吗？ 1—8 设一松弛系统，对于任何 u ，其输入和输出的关系为
ì ï u(t ) t £ a y(t ) = (Pau )(t ) = ï í ï 0 t>a ï î
1—4 给定
é1 1 0ù ê ú ê ú A = ê0 0 1ú ê ú ê0 0 1ú ë û
试求 A10 , A101, e At 。
28
1— 5 设
él 1 0 ù ê ú ê ú C = ê0 l 0ú ê ú ê0 0 lú ë û
试求能满足 e B = C 的矩阵 B 。并证明，对于任一非奇异矩阵 C ，均存在能满足 e B = C 的矩阵B 。 1—6 若 D 可逆，证明
小
结
本章首先在松弛、线性、因果性、时不变性等概念和基础上，引出了线性系统的输入输出描述和状态变量描述，并在§1—4 中对这两种描述方法进行了比较。在§1—3 中讨论了动态方程的解。解动态方程的关键所在是求出状态转移矩阵 F(t, t ) 。对于时变的情况，计算 F(t, t ) 甚为困难。对于时不变的情况，因为 F(t, t ) = e A(t -t ) ，而对矩阵指数，(1—48)式提供了一种计算途径。 §1—4 中对实现问题的讨论是初步的，实现问题的深入讨论只有在引入可控性和可观测性等概念后才有可能。定理 1—9 的充分性的证明是构造性的，它通过(1—85)式给出了构造真有理函数阵实现的一种方法。本章作为学习后续各章的准备，都是很基本的内容。许多内容可以在有关的本科教材中找到更加详细的说明。为了使读者复习必要的数学预备知识，在习题中选用一些数学练习题，见习题 1—1 至习题 1—6。
习
1—1 设有矩阵
é 0 ê ê 0 A = êê ê ê -a ëê n 1 0
题
0 1

-an -1 -a n -2
ù ú ú ú 1 úú -a1 úú û 0 0
试证， A 的特征多项式为
D(l)=det(lI - A)=ln + a1ln -1 + a2ln -2 + + an -1l1 + an
1 ù éx é 0 1 ù é x1 ù úê ú a， êê úú = êê ú êx ú 0 t x 2 êë ûú ë 2 û ëê ûú
1 ù é -1 e 2t ù é x1 ù éx úê ú b， êê úú = êê ú x x 0 1 2 úû êë 2 úû ëê ûú ëê
1—13 试求图 1—14 所示的网络动态方程描述 y 电流 + __ __ V2 +
L1 R1
C2 R2
图 1—14 线性网络 1—14 试求图 1—15 所示网络的传递函数和动态方程描述。你是否认为该传递函数是这个系统的一种好的描述？(略)
1—15 试求下列齐次方程的基本矩阵和状态转移矩阵。
计算极点多项式和零点多项式。 1—30 若λ1 不是 A 的特征值，试证下列恒等式
(sI - A)-1(s - l1 )-1 = (l1I - A)-1 (s - l1 )-1 + (sI - A)-1 (A - l1I)-1