初一数学上册第一单元有理数知识点归纳及单元测试题试卷
七年级上册数学第一章《有理数》知识点及典型例题
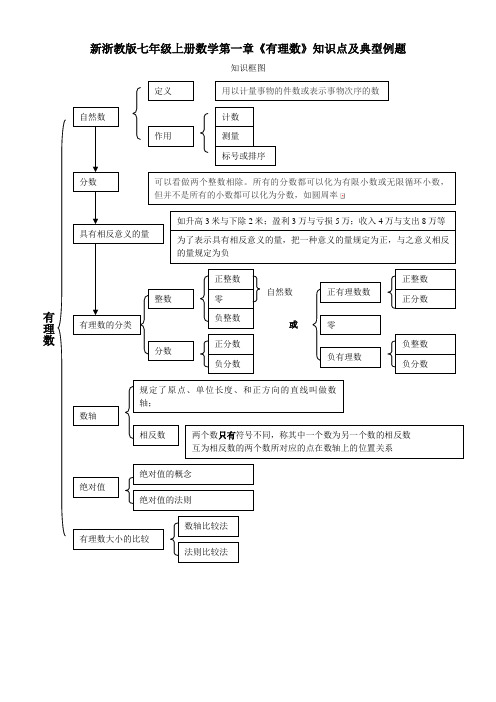
新浙教版七年级上册数学第一章《有理数》知识点及典型例题知识框图有理数自然数分数计数测量标号或排序定义作用用以计量事物的件数或表示事物次序的数可以看做两个整数相除。
所有的分数都可以化为有限小数或无限循环小数，但并不是所有的小数都可以化为分数，如圆周率有理数的分类整数分数零正整数负整数正分数负分数正有理数数负有理数零负整数负分数正整数正分数或具有相反意义的量如升高3米与下除2米；盈利3万与亏损5万；收入4万与支出8万等为了表示具有相反意义的量，把一种意义的量规定为正，与之意义相反的量规定为负数轴绝对值有理数大小的比较自然数规定了原点、单位长度、和正方向的直线叫做数轴；相反数两个数只有符号不同，称其中一个数为另一个数的相反数互为相反数的两个数所对应的点在数轴上的位置关系绝对值的概念绝对值的法则数轴比较法法则比较法将考点与相应习题联系起来考点一、关于“……说法正确的是……”的题型（只可能是选择题）1、下列语句：①带“-”号的数是负数；②如果a为正数，则-a一定是负数；③不存在既不是正数又不是负数的数；④ 00C表示没有温度，正确的有（）个A.0B.1C.2D.32、下列说法不正确的是（）A.数轴是一条直线；B.表示-1的点，离原点1个单位长度；C.数轴上表示-3的点与表示- 1的点相距2个单位长度；D.距原点3个单位长度的点表示—3或3。
3、下列说法中不正确的是（）A.－5表示的点到原点的距离是5；B. 一个有理数的绝对值一定是正数；C. 一个有理数的绝对值一定不是负数；D. 互为相反数的两个数的绝对值一定相等.4、如图：下列说法正确的是（）A.a比b大B.b比a大C.a、b一样大D.a、b的大小无法确定5、若｜a＋b|＝－（a＋b）,下列结论正确的是（）A.a＋b≤0B.a＋b<0C.a＋b=0D.a＋b>06、下列说法：①一个数的绝对值的相反数一定是负数；②只有负数的绝对值是它的相反数；③正数和零的绝对值都等于它本身；④互为相反数的两个数的绝对值相等，错误的个数是( )A.3个B.2个C.1个D.0个7、如果a表示有理数，那么下列说法中正确的是（）A.+a与-(-a)互为相反数B. +a与-a一定不相等C.-a一定是负数D. -(+a)与+(-a)一定相等8、已知字母、表示有理数，如果+=0，则下列说法正确的是（）A.、中一定有一个是负数B.、都为0C.与不可能相等D.与的绝对值相等9、下列说法正确的是（）A. -|a|一定是负数B. 只有两个数相等时，它们的绝对值才相等C. 若|a|=|b|，则a与b互为相反数D. 若一个数小于它的绝对值，则这个数为负数10、给出下面说法：①互为相反数的两个数绝对值相等；②一个数的绝对值等于它本身，这个数不是负数；③若|m|>m，则m<0；④若|a|>|b|，则a>b，其中正确的有（）A.①②③B.①②④C.①③④D.②③④考点二、具有相反意义的量、相反数、数轴、绝对值、有理数的分类等概念的直接考题1、某项科学研究，以45分钟为1个时间单位，并记每天上午10时为0，10时以前记为负，10时以后记为正，例如9：15记为-1，10：45记为1等等，以此类推，上午7：45应记为2、在时钟上，把时针从钟面数字“12”按顺时针方向拨到“6”，计做拨了“+”周，那么，把时针从“12”开始，拨了“”周后，该时针所指的钟面数字是3、若a与b互为相反数，则下列式子：①a+b=0；②a=-b；③|a|=|-b|；④a=b，其中一定成立的序号为4、数轴上到数-1所表示的点的距离为5的点所表示的数是5、绝对值最小的有理数是；绝对值最小的整数是；| 3.14 －π|= _________6、写出所有不小于-4并且小于3.2的整数：7、绝对值小于6且大于3的整数有（）A.1个B.2个C.3个D.4个8、下面关于0的说法：①是整数，也是有理数；②是正数，不是负数；③不是整数，是有理数；④是整数，也是自然数，正确的是（）A.①②B.②③C.①④D.①③9、在15，，0.15，-30，-12.8，-，-1.010010001，，-3.12112111211112……，-3.141414……中，负分数的个数是（）A.3个B.4个C.5个D.6个10、一滴墨水洒在一个数轴上，根据图中标出的数值，判断墨迹盖住的整数点的个数是（1）判断墨迹盖住的整数共有多少个？并说明理由。
人教版七年级上册数学 第一章 有理数 单元测试题 含答案 答题卡
第一章 有理数 单元测试题（一）一 选择题 （每小题3分 共30分）1.下列四个数中，在－2到 0之间的数是： （ ） A －１ Ｂ １ Ｃ －３ Ｄ ３2.下列说法正确的是： （ ） A 0表示什么也没有B 一场比赛赢4个球得＋4分， －3分表示输了３个球 Ｃ ７没有符号Ｄ 0既不是正数，也不是负数3.既是分数又是正数的是（ ）A +2B －31C 0D 2.34.下列结论正确的有（ ）个： ① 规定了原点，正方向和单位长度的直线叫数轴 ② 最小的整数是0 ③ 正数，负数和零统称有理数 ④ 数轴上的点都表示有理数A 0B 1C 2D 3 5.在数轴上，A 点和B 点所表示的数分别为－2和1，若使A 点表示的数是B 点表示的数的3倍，应把A 点 （ ） A 向左移动5个单位 B 向右移动5个单位C 向右移动4个单位D 向左移动1个单位或向右移动5个单位 6.如图，在数轴上点M 表示的数可能是( )A ．1.5B ．－1.5C ．－2.4D ．2.47.在0.75，－1，－0.75，3，0，＋5，－3这几个数中，互为相反数的有( ) A ．0对 B ．1对 C ．2对 D ．3对8.数a 在数轴上的对应点在原点左边，且|a|＝4，则a 的值为( ) A ．4或－4 B ．4 C ．－4 D ．以上都不对 9.一个数的绝对值等于它的相反数，则这个数是( ) A ．正数或0 B ．负数或0 C ．所有正数 D ．所有负数10.清晨蜗牛从树根沿着树干往上爬，树高10m ，白天爬4m ，夜间下滑3m ，它从树根爬上树顶，需（ ） A 、10天 B 、9天 C 、8天 D 、7天 二 填空题（每小题3分 共18分）1．如果向南走5米，记作+5米，那么向北走8米应记作____米． 2.已知下列各数:-4,3.5,0,-2,10,+21,其中非负数有_______ 3.在数轴上，距原点6个单位长度的点表示的数为____． 4.若a=－2020,则—a=____.5.某天早晨的气温是18℃，中午上升6℃，半夜又下降5℃，则半夜的气温是_____℃．6.如果x ＜0，y ＞0，且|x|=2，|y|=3，那么x+y=________． 三 解答题（本大题共72分） 1（30分） 计算(1)1+（－21 ）+31 +（－61） (2)(-109)+(-267)+(+109)+268(3)(－23)－(＋12)－(－56)－(－13) (4)(－813)－(＋12)－(－70)－(－813)；(5)(－3)－(－17)－(－33)－81 (6)（－12）+ 14 -（-21）+ 3 -（－2）2（8分）简答题：（1）－1和0之间还有负数吗？如有，请列举。
人教版七年级数学上册《第一章 有理数》单元复习检测试卷及参考答案
人教版七年级数学上册《第一章有理数》单元复习检测试卷一、选择题1．由四舍五入得到的近似数－8.30×104，精确到()A．百分位B．十分位C．千位D．百位2．2018年10月24日港珠澳大桥全线通车，港珠澳大桥东起香港国际机场附近的香港口岸人工岛，向西横跨伶仃洋海域后连接珠海和澳门人工岛，止于珠海洪湾，它是世界上最长的跨海大桥，被称为“新世界七大奇迹之一”，港珠澳大桥总长度55000米，则数据55000用科学记数法表示为（）A．55×105B．5.5×104C．0.55×105D．5.5×105 3．在，，0，，，这几个有理数中，负数的个数是（）A．1 B．2 C．3 D．44．，，的和比它们的绝对值的和小（）A．B．C．4 D．5．对有理数a，b，规定运算如下：a※b＝a＋ab，则－2※3的值为()A．－10 B．－8 C．－6 D．－46．下列说法：①与互为相反数；②任何有理数都可以用数轴上的点表示；③一定比a大；④近似数精确到百分位。
其中正确的个数是（）A．4个B．3个C．2个D．1个7．计算所得结果为( ) ．A．2 B．C．D．8．已知：c32=，c53=，c64=，…观察上面的计算过程，寻找规律并计算c106的值为（）A．42 B．210 C．840 D．2520二、填空题9．设有理数a，b，c满足，，则a，b，c中正数的个数为________。
10．如图，点A，B在数轴上对应的有理数分别为，a，则A，B间的距离是_____ 。
（用含a的式子表示）11．若a，b互为倒数，c，d互为相反数，则2c+2d﹣3ab的值为________。
12．若规定运算符号“★”具有性质：a★b＝a2﹣ab．例如（﹣1）★2＝（﹣1）2﹣（﹣1）×2＝3，则1★（﹣2）＝_____。
13．当n为正整数时，（﹣1）2n+1+（﹣1）2n的值是_________。
人教版七年级数学上册第一章 有理数单元测试卷(含答案)
人教版七年级数学上册第一章有理数一、选择题1．在−π3，3.1415，0，−0.333…，−227，2.010010001…中，非负数的个数（ ）A ．2个B ．3个C ．4个D ．5个2．长江干流上的葛洲坝、三峡向家坝、溪洛渡、白鹤滩、乌东德6座巨型梯级水电站，共同构成目前世界上最大的清洁能源走廊，总装机容量71695000千瓦，将71695000用科学记数法表示为（ ）A ．7.1695×107B ．716.95×105C ．7.1695×106D ．71.695×1063．生产厂家检测4个篮球的质量，结果如图所示，超过标准质量的克数记为正数，不足标准质量的克数记为负数，其中最接近标准质量的篮球是（ ）A ．B ．C ．D ．4．下列说法正确的是（ ）A ．1是最小的自然数B ．平方等于它本身的数只有1C ．任何有理数都有倒数D ．绝对值最小的数是05．计算 3−(−3) 的结果是（ ）A ．6B ．3C ．0D ．－66．下列说法：①有理数与数轴上的点一一对应；②1的平方根是它本身；③立方根是它本身的数是0，1；④对于任意一个实数a ，都可以用1a表示它的倒数．⑤任何无理数都是无限不循环小数.正确的有（ ）个.A ．0B ．1C ．2D ．37．把数轴上表示数2的点移动3个单位后，表示的数为（ ）A ．5B ．1C ．5或－1D ．5或18．如果|a|=−a ，那么a 一定是（ ）A ．正数B ．负数C ．非正数D ．非负数9．法国的“小九九”从“一 一得一”到“五五二十五”和我国的“小九九”是一样的，后面的就改用手势了.下面两个图框是用法国“小九九”计算7×8和8×9的两个示例，且左手伸出的手指数不大于右手伸出的手指数.若用法国的“小九九”计算7×9，左、右手依次伸出手指的个数是（ ）7×8=？8×9=？因为两手伸出的手指数的和为5，未伸出的手指数的积为6，所以7×8=56.7×8=10×(2+3)+3×2=56因为两手伸出的手指数的和为7，未伸出的手指数的积为2，所以8×9=72.8×9=10×(3+4)+2×1=72A ．2，4B ．1，4C ．3，4D ．3，110．如图是节选课本110页上的阅读材料，请根据材料提供的方法求和：11×2+12×3+13×4+⋅⋅⋅+12020×2021，它的值是（ ）上题是利用一系列等式相加消去项达到求和，这种方法不仅限于整数求和，如1−12=11×2①12−13=12×3②13−14=13×4③14−15=14×5④ ……继续写出上述第n 个算式，并把这些算式两边分别相加，会得到：11×2+12×3+13×4+⋅⋅⋅+1n ×(n +1)．A ．1B ．20202021C ．20192020D ．12021二、填空题11．12的相反数是 . 12．－2的绝对值是 13．定义一种新运算“⊗”，规则如下：a ⊗b =a 2−ab ，例如：3⊗1=32−3×1=6，则4⊗[2⊗(−5)]的值为 ．14．如图所示的运算程序中，若开始输入的值为−2，则输出的结果为 ．15．若a−2+|3−b |=0，则3a +2b = ．16．若a ，b ，c 都不为0，则 a |a|+b |b|+c |c|+abc|abc|的值可能是 ．三、解答题17．把下列各数在数轴上表示出来，并用“<”号把它们连接起来．−3,|−3|,32,(−2)2,−(−2)18．将有理数−2.5，0，212，2023，−35%，0.6分别填在相应的大括号里．整数：{ …}；负数：{ …}；正分数：{ …}19．小明有5张写着不同数字的卡片，完成下列各问题：（1）把卡片上的5个数在数轴上表示出来；（2）从中取出3张卡片，将这3张卡片上的数字相乘，乘积的最大值为 ；（3）从中取出2张卡片，将这2张卡片上的数字相除，商的最小值为 20．把相同的瓷碗按如图方式整齐地叠放在一起．叠放4个时，测量的高度为9.5cm；叠放6个时，测量的高度为12.5cm．（1）根据题意，可知每增加一个瓷碗，高度增加 cm；（2）求碗高；（3）若叠放10个瓷碗，高度为 cm．21．若a，b互为相反数，c，d互为倒数，m的绝对值为2．（1）直接写出a+b=______，cd=____，m=____．（2）求m−cd+3a+3bm的值．22．我们知道，|a|可以理解为|a−0|，它表示：数轴上表示数a的点到原点的距离，这是绝对值的几何意义．进一步地，数轴上的两个点A，B，分别用数a，b表示，那么A，B两点之间的距离为AB=|a−b|，反过来，式子|a−b|的几何意义是：数轴上表示数a的点和表示数b的点之间的距离，利用此结论，回答以下问题：（1）数轴上表示数8的点和表示数3的点之间的距离是_________，数轴上表示数−1的点和表示数−3的点之间的距离是_________．（2）数轴上点A用数a表示，则①若|a−3|=5，那么a的值是_________．②|a−3|+|a+6|有最小值，最小值是_________；③求|a+1|+|a+2|+|a+3|+⋯+|a+2021|+|a+2022|+|a+2023|的最小值．23．数轴上点A表示的数为10，点M，N分别以每秒a个单位长度，每秒b个单位长度的速度沿数轴运动，a，b满足|a-5|+(b-6)2=0.（1）请直接与出a= ，b= ；（2）如图1，点M从A出发沿数轴向左运动，到达原点后立即返回向右运动：同时点N从原点0出发沿数轴向左运动，运动时间为t，点P为线段ON的中点若MP=MA，求t的值：（3）如图2，若点M从原点向右运动，同时点N从原点向左运动，运动时间为t时M运动到点A的右侧，若此时以M，N，O，A为端点的所有线段的长度和为142，求此时点M对应的数.答案解析部分1．【答案】B 2．【答案】A 3．【答案】B 4．【答案】D 5．【答案】A 6．【答案】B 7．【答案】C 8．【答案】C 9．【答案】A 10．【答案】B 11．【答案】﹣ 1212．【答案】213．【答案】−4014．【答案】815．【答案】1216．【答案】0或4或﹣417．【答案】图见解答，−3<32<−(−2)<|−3|<(−2)218．【答案】解：整数：0，2023；负数：−2.5，−35%；正分数：212，0.6．19．【答案】（1）解：如图所示（2）50（3）-820．【答案】（1）1.5（2）解：设碗高为xcm ，根据题意得x+1.5×3=9.5．解方程得，x=5 ．答：碗高为5cm．（3）18.521．【答案】（1）0，1，±2；（2）1或−322．【答案】（1）5，2（2）①8或−2；②9；③1023132 23．【答案】（1）5；6（2）解：①点M未到达O时（0＜t≤2时），NP=OP=3t，AM=5t，OM=10-5t，MP=3t+10-5t即3t+10-5t=5t，解得t=10 7，②点M到达O返回，未到达A点或刚到达A点时，即当（2＜t≤4时），OM=5t-10，AM=20-5t，MP=3t+5t-10即3t+5t-10=20-5t，解得t=30 13③点M到达O返回时，在A点右侧，即t＞4时OM=5t-10，AM=5t-20，MP=3t+5t-10，即3t+5t-10=5t-20，解得t=−103（不符合题意舍去）.综上t=107或t=3013；（3）解：如下图：根据题意：NO=6t，OM=5t，所以MN=6t+5t=11t依题意：NO+OA+AM+AN+OM+MN=MN+MN+OA+MN=33t+10=142，解得t=4.此时M对应的数为20.。
七年级数学上册《第一章 有理数》单元测试题含答案(人教版)
七年级数学上册《第一章 有理数》单元测试题含答案(人教版）学校:___________班级：___________姓名：___________考号：___________一、单选题1．以下四个有理数中，绝对值最小的是（ ）A ．-2B ．2C ．0D ．12．下列选项，具有相反意义的量是（ ）A ．增加20个与减少30个B ．6个老师和7个学生C ．走了100米和跑了100米D ．向东行30米和向北行30米3．下列说法中不正确的是（ ）A ．﹣3.14既是负数，分数，也是有理数B ．0既不是正数，也不是负数，但是整数C ．﹣2000既是负数，也是整数，但不是有理数D ．0是正数和负数的分界4．我国是世界上严重缺水的国家，目前每年可利用的淡水资源总量为 27500 亿立方米，人均占有淡水量居世界第 110 位，因此我们要节约用水，其中 27500 用科学记数法表示为（ ）A ．227510⨯B ．42.7510⨯C ．52.7510⨯D ．327.510⨯5．数轴上的两点之间的距离为7，一个点表示的数是﹣3，则另一个点表示的数是（ ）A ．4B ．4或﹣10C ．﹣10D ．10或﹣46．下列各式中，积为负数的是（ ）A ．()()123-⨯-⨯B ．()()123-⨯-⨯-C ．()103-⨯⨯D ．()()()123-⨯-⨯-7．如图，在一个不完整的数轴上有A ，B ，C 三个点，若点A ，B 表示的数互为相反数，则图中点C 点表示的数是（ ）A ．2-B ．1C ．0D ．48．现定义两种运算“ ⊕ ”，“ * ”.对于任意两个整数 11a b a b a b a b ⊕=+-*=⨯-， ，则 (68)(35)⊕*⊕ 的结果是（ ）A ．69B ．90C ．100D ．112 二、填空题9．123- 的倒数是 ，-2.3的绝对值是 ． 10．5月23日，我国许多天文爱好者都拍摄了金星伴月的美丽天象，金星是距离地球最近的行星，距离大约4050万千米，用科学记数法表示这个数字为 千米．（保留两位有效数字）11．我们把向东走8步记作+8步，则向西走5步记作 步.12．大于－ 132 而小于 122的所有整数的和是 ． 13．已知|a ﹣2|+|b+1|＝0，则（a+b ）﹣（b ﹣a ）＝ .14．如图是一个简单的数值运算程序，当输入x 的值为﹣3时，则输出的数值为 ．三、计算题15．510.474( 1.53)166----16．计算：（1）()1375+-- ；（2）()()324542-÷---⨯-17．计算：（1）()15136326⎛⎫-+⨯- ⎪⎝⎭；（2）()22022351113242⎛⎫-⨯-+-÷- ⎪⎝⎭．18．如图所示，在一条不完整的数轴上从左到右有点 ,,A B C ，其中 2AB = ， 1BC = 设点 ,,A B C 所对应的数之和是 m ，点 ,,A B C 所对应的数之积是 n .（1）若以 B 为原点，写出点 ,A C 所对应的数，并计算 m 的值；若以 C 为原点， m 又是多少？（2）若原点 O 在图中数轴上点 C 的右边，且 4CO = ，求 n 的值.19．某工厂一周内计划每日生产200辆车.受各种因素影响，实际每天的产量与计划量相比的情况如下表（增加为正）（1）本周三生产了多少辆车？（2）本周的总产量与计划相比，是增加还是减少了？增加或减少的数量是多少？（3）产量最多的一天与最少的一天相比，多生产多少辆？20．早在1960年、中国登山队首次从珠穆朗玛北侧中国境内登上珠峰，近几十年，珠峰更是吸引了大批的登山爱好者，某日，登山运动员傅博准备从海拔7400米的3号营地登至海拔近7900米的4号营地，由于天气骤变，近6小时的攀爬过程中他不得不几次下撤躲避强高空风，记向上爬升的海拔高度为正数，向下撒退时下降的海拔高度为负数，傅博在这一天攀爬的海拔高度记录如下：(单位：米)+320、-55、+116、-20、+81、-43、+115.（1）傳博能按原计划在这天登至4号营地吗？（2）若在这一登山过程中，傅博所处位置的海拔高度上升或下降1米平均消耗8大卡的卡路里，则傅博这天消耗了多少卡路里？参考答案：1．C 2．A 3．C 4．B 5．B 6．D 7．B 8．B9．37-；2.310．74.110⨯11．-512．3-13．414．-115．解：原式= 510.474+1.53166-- = 510.47 1.534166+--=2-6=-4.16．（1）解：原式 1375=--65=-1=（2）解：原式 8458=-÷-+258=--+1=17．（1）解：()15136326⎛⎫-+⨯- ⎪⎝⎭()()()151363636326=⨯--⨯-+⨯-()()12906=---+-12906=-+-72=（2）解：()22022351113242⎛⎫-⨯-+-÷- ⎪⎝⎭511138162=⨯-+÷1383216=-+⨯52=-+3=-18．（1）解：以 B 为原点，点 ,A C 所对应的数分别是 2- ， 12011m =-++=-以 C 为原点 (21)(1)04m =--+-+=- ；n=---⨯--⨯-=-（2）解：(412)(41)(4)14019．（1）解：200-3=197（辆）答：本周三生产了197辆车（2）解：-8+8-3+4+14-9-25=-20 （辆）减少了20辆.答：本周与计划相比，总产量减少了，减少了20辆（3）解：产量最多的一天生产了200+14=214（辆）产量最少的一天生产了200-25=175（辆）产量最多的一天与最少的一天相比，多生产了214-175=39（辆）答：产量最多的一天与最少的一天相比，多生产39辆.20．（1）解：依题意得：-+-+-+=（米）傳博一天内的攀爬高度为：32055116208143115514-=<3号营地登至4号营地的高度为：79007400500514∴傳博能按原计划在这天登至4号营地（2）解：依题意得：傅博这天消耗了的卡路里为：()+-++-++-+⨯=⨯= 32055116208143115875086000。
初一数学七年级人教版上册第1章《有理数》单元综合测试题答案解析
初一数学七年级人教版上册第1章《有理数》单元综合测试题一．选择题1.阿里巴巴数据显示，2017年天猫商城“双11”全球狂欢交易额超957亿元，数据957亿用科学记数法表示为（）A.957×108B. 95.7×109C.9.57×1010D.0.957×1010【答案】C【解析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n是正数；当原数的绝对值＜1时，n是负数.解：将957亿用科学记数法表示约为：9.57×1010．故选：C.【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值.2.下列运算结果为正数的是（）A. ﹣32B. ﹣3÷2C. ﹣1+2D. 0×（﹣2018）【答案】C【解析】根据各个选项中的式子，可以计算出相应的结果，从而可以解答本题.解：∵-32=-9，-3÷2=-32，-1+2=1，0×（-2018）=0，∴选项C中的结果为正数，故选：C.【点评】本题考查有理数的混合运算，解答本题的关键是明确有理数混合运算的计算方法.3.在﹣2、3、﹣4、﹣5这四个数中任取两个数相乘，得到的积最大的是（）A. 20B. ﹣20C. 10D. 8【答案】A【解析】观察四个数，不难得出，选择﹣4与﹣5相乘，得到的积最大．﹣4与﹣5乘积最大，为20．故选A．【点评】本题主要掌握有理数的乘法运算法则，两数相乘，同号得正，异号得负，并把绝对值相乘．4.下列说法正确的是（）①最小的负整数是﹣1；②数轴上表示数2和﹣2的点到原点的距离相等；③当a≤0时，|a|=﹣a成立；④a+5一定比a大；⑤（﹣2）3和﹣23相等．A. 2个B. 3个C. 4个D. 5个【答案】C【解析】①最大的负整数是1，故不正确；②2和-2的绝对值相等，则数轴上表示数2和-2的点到原点的距离相等，故命题正确；③正确；④正确；⑤正确．故选C．【考点】1.有理数的乘方；2.有理数；3.数轴；4.绝对值；5.有理数大小比较．5.在﹣112，15，﹣10，0，﹣（﹣5），﹣|+3|中，负数的个数有（）A. 2个B. 3个C. 4个D. 5 个【答案】B【解析】根据正数与负数的定义求解.解：在-112，15，-10，0，-（-5），-|+3|中，负数有-112、-10、-|+3|这3个，故选：B.【点评】本题考查了正数和负数：在以前学过的0以外的数叫做正数，在正数前面加负号“-”，叫做负数，一个数前面的“+”“-”号叫做它的符号.6.如图，在数轴上点A最可能表示的数的绝对值是（）A. ﹣2.5B. 2.5C. ﹣3.5D. 3.5【答案】B【解析】根据数轴的定义即可求出答案.解：由数轴可知：点A表示的数为a，∴-3＜a＜-2,∴在数轴上点A最可能表示的数的绝对值是2.5.故选：B.【点评】本题考查数轴的性质，解题的关键是正确理解数轴的定义，本题属于基础题型.7.a，b，c三个数的位置如图所示，下列结论不正确的是（）A. a+b＜0B. b+c＜0C. b+a＞0D. a+c＞0【答案】C【解析】根据数轴上点的位置判断出a，b，c的大小，利用有理数的加法法则判断即可.解：根据数轴上点的位置得：-4＜b＜-3＜-1＜0＜1＜c，即|a|＜|c|＜|b|，∴a+b＜0，b+c＜0，b+a＜0，a+c＞0，故选：C.【点评】此题考查了有理数的加法，以及数轴，熟练掌握运算法则是解本题的关键.8.已知有理数a，b，c在数轴上对应的位置如图所示，化简|b﹣c|﹣|c﹣a|( )A. b﹣2c+aB. b﹣2c﹣aC. b+aD. b﹣a【答案】D【解析】观察数轴，可知：c＜0＜b＜a，进而可得出b﹣c＞0、c﹣a＜0，再结合绝对值的定义，即可求出|b﹣c|﹣|c﹣a|的值．观察数轴，可知：c＜0＜b＜a，∴b﹣c＞0，c﹣a＜0，∴|b﹣c|﹣|c﹣a|=b﹣c﹣（a﹣c）= b﹣c﹣a+c=b﹣a．故选D．【点评】本题考查了数轴以及绝对值，由数轴上a、b、c的位置关系结合绝对值的定义求出|b﹣c|﹣|c﹣a|的值是解题的关键．9.下列结论成立的是( )A. 若|a|＝a，则a＞0B. 若|a|＝|b|，则a＝±bC. 若|a|＞a，则a≤0D. 若|a|＞|b|，则a＞b．【答案】B【解析】若|a|=a，则a为正数或0；若|a|=|b|，则a与b互为相反数或相等；若|a|＞a，则a为正数；若|a|＞|b|，若a，b均为正数，则a＞b；若a，b均为负数，则a＜b；若a，b为一正一负或有一个为0，则a，b的大小不能确定．A．若|a|=a，则a为正数或0，故结论不成立；B．若|a|=|b|，则a与b互为相反数或相等，故结论成立；C．若|a|＞a，则a为负数，故结论不成立；D．若|a|＞|b|，若a，b均为负数，则a＜b，故结论不成立．故选B．【点评】本题考查了的知识点有：正、负数的意义、绝对值的意义，有理数的大小比较等．10.若ab≠0，则aabb+的值不可能是（）A. 0B. 1C. 2D. ﹣2 【答案】D【解析】当a、b同号时，a ba b+=±2，当a、b异号时，a ba b+=0，由此即可判断.解：当a、b同号时，a ba b+=±2，当a、b异号时，a ba b+=0，故选：D.【点评】本题考查有理数的加法法则以及乘法法则，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型.二．填空题11.计算：|-3|-1=__．【答案】2【解析】根据有理数的加减混合运算法则计算.解：|﹣3|﹣1=3-1=2.故答案为：2.【点评】考查的是有理数的加减运算、乘除运算，掌握它们的运算法则是解题的关键.12.将数轴上表示﹣1的点A向右移动5个单位长度，此时点A所对应的数为_____．【答案】4．【解析】分析：在数轴上点向右平移几个单位，则就加上几；在数轴上点向左平移几个单位，则就加上几．详解：根据题意可得：－1+5=4．【点评】本题主要考查的是数轴上点的平移法则，属于基础题型．理解平移的性质是解决这个问题的关键．13.145-的倒数是_____．【答案】521．【解析】求一个分数的倒数的方法：把这个分数的分子和分母互换位置即可，是小数的化成分数后据此求出，据此解答.解：145-=145,1 4 5的倒数是521．故答案为：5 21.【点评】本题主要考查求一个分数的倒数的方法：把这个分数的分子和分母互换位置即可.14.已知：|m﹣n|＝n﹣m，|m|＝4，|n|＝3，则m﹣n＝_______【答案】-1或-7【解析】根据绝对值的代数意义和有理数的减法法则，结合已知条件分析解答即可.∵|m-n|=n-m,|m|=4,|n|=3，∴m≤n,m=±4,n=±3，∴m=-4,n=±3，∴当m=-4,n=3时，m-n=-4-3=-7；当m=-4,n=-3时，m-n=-4-(-3)=-4+3=-1.综上所述，m-n=-1或-7.故答案为：-1或-7.【点评】熟悉“有理数的减法法则和绝对值的代数意义：正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0”是解答本题的关键.15.点A1、A2、A3、…、A n（n为正整数）都在数轴上．点A2在点A1的左边，且A1A2=1；点A3在点A2的右边，且A2A3=2；点A4在点A3的左边，且A3A4=3；…，点A2018在点A2017的左边，且A2017A2018=2017，若点A2018所表示的数为2018，则点A1所表示的数为_____．【答案】3027．【解析】根据题意得出规律：当n为奇数时，A n-A1=n-12，当n为偶数时，A n=A1-n2，把n=2018代入求出即可.解：根据题意得：当n为奇数时，A n-A1=n-12，当n为偶数时，A n-A1=-n2，2018为偶数，代入上述规律, A2018-A1=-2018/2=-1009,解得A1=3027．故答案为：3027.【点评】此题考查数字的变化规律，找出数字之间的联系，利用运算规律解决问题.16.已知a，b互为相反数，c，d互为倒数，则﹣5a+2017cd﹣5b=_____．【答案】2017【解析】根据相反数及倒数的定义得出a+b=0，cd=1，再代入所求代数式进行计算即可.解：根据题意得：a+b=0，cd=1，则原式=-5（a+b）+2017cd=-5×0+2017×1=2017．故答案为2017.【点评】本题考查的是有理数的混合运算，熟知相反数、倒数的定义是解答此题的关键.三．解答题17.计算：（1）﹣18×（125 236+-）；（2）（﹣1）3﹣（1﹣12）÷3×[2﹣（﹣3）2]．【答案】（1）-6；（2）16；【解析】分析：（1）运用乘法分配律计算可得；（2）根据有理数混合运算顺序和运算法则计算可得．详解：(1)原式＝－9－12＋15＝－6．(2)原式＝－1－12×13×(－7)＝－1＋76＝16．【点评】本题主要考查有理数的混合运算，熟练掌握有理数的混合运算的顺序和法则是解题的关键．18.已知a的相反数是2，b的绝对值是3，c的倒数是﹣1．（1）写出a，b，c的值；（2）求代数式3a（b+c）﹣b（3a﹣2b）的值．【答案】（1）a=﹣2，b=±3，c=﹣1；（2）24；【解析】（1）根据相反数、绝对值、倒数的定义解答即可；（2）把所给的整式去括号合并同类项化为最简后，再代入求值即可.（1）∵a的相反数是2，b的绝对值是3，c的倒数是﹣1，∴a=﹣2，b=±3，c=﹣1；（2）3a（b+c）﹣b（3a﹣2b）=3ab+3ac﹣3ab+2b2=3ac+2b2，∵a=﹣2，b=±3，c=﹣1，∴b2=9，∴原式=3×（﹣2）×（﹣1）+2×9=6+18=24．【点评】本题考查了代数式求值，相反数的定义，绝对值的性质，倒数的定义，是基础题，比较简单，但要注意b的两种情况．19.下表给出了七（三）班6位同学的体重情况：（单位：kg）（1）完成表中空白部分；（2）这6位同学体重的和多少千克．【答案】（1）答案见解析；（2）282千克；【解析】（1）先算出标准体重为45kg，再算出个人体重与班级平均体重的差值，填表即可；（2）将这6个人的个人体重相加即可.（1）如表：（2）﹣1+2+0﹣3+4+10+45×6=282（kg），答：这6位同学体重的和是282千克；【点评】本题考查了有理数的混合运算，以及正负数所表示的意义.20.粮库3天内进出库的粮食记录日下（单位：吨．进库的吨数记为正数，出库的吨数记为负数）：+26，﹣32，﹣25，+34，﹣38，+10．（1）经过这3天，库里的粮食是增多了还是减少了？（2）经过这3天，仓库管理员结算发现库存粮食480吨，那么3天前库存粮食是多少吨？【答案】（1）-25吨；（2）505吨；【解析】（1）理解“+”表示进库“-”表示出库，把粮库3天内发生粮食进出库的吨数相加就是库里现在的情况; （2）利用（1）中所求即可得出3天前粮库里存粮数量.（1）26+（﹣32）+（﹣25）+34+（﹣38）+10=﹣25（吨）．答：粮库里的粮食是减少了25吨；（2）480﹣（﹣25）=505（吨）．答：3天前粮库里存粮有505吨；【点评】此题主要考查了正数和负数的定义，解题关键是理解“正”和“负”的相对性，明确正数和负数的定义，并且注意0这个特殊的数字，既不是正数也不是负数.21.为了有效控制酒后驾车，交警队一辆汽车每天在一条东西方向的公路上巡视．某天早晨从A 地出发，晚上到达B 地，约定向东为正方向，当天行驶记录如下（单位：km ）：+18，﹣19，﹣13，+15，+10，﹣14，+19，﹣20．问：（1）B 地在A 地哪个方向？距A 地多少千米？（2）若该警车每千米耗油0.2L ，警车出发时，油箱中有油20L ，请问中途有没有给警车加油？若有，至少加多少升油？请说明理由．【答案】（1）在A 地的西方，距A 地4千米；（2）需加油5.6L ；【解析】（1）把这些数值相加，根据结果就可知道在那个方向，相距多少千米．（2）绝对值相加，乘以每小时耗油量即可，由此即可进行判断．解：（1）18-19-13+15+10-14+19-20=－4所以B 地在A 地的西方，相距4千米；（2）0.2×（18+19+13+15+10+14+19+20）=25.6升25.6﹣20=5.6故中途给警车加过油，至少加5.6升．【点评】本题考查有理数的加减混合运算，以及正负数的意义，从而可求出解．22.把下列各数填在相应的括号内：–19，2.3，–12，–0.92，35，0，–14，0.563，π 正数集合{ ……}；负数集合{ ……}；负分数集合{ ……}；非正整数集合{ ……}【答案】正数集合：32.30.5635，，，π⎧⎫⎨⎬⎩⎭负数集合：119120.924⎧⎫----⎨⎬⎩⎭，，，，负分数集合：10.924⎧⎫--⎨⎬⎩⎭，，非正整数集合：{}19120--，，【解析】利用正数，负数，负分数，非整数的定义进行分类即可． 正数集合：32.30.5635π⎧⎫⎨⎬⎩⎭，，， 负数集合：119120.924⎧⎫----⎨⎬⎩⎭，，，， 负分数集合：10.924⎧⎫--⎨⎬⎩⎭，， 非正整数集合：{}19120--，，23.如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动.它从A 处出发去看望B 、C 、D 处的其它甲虫，规定：向上向右走为正，向下向左走为负.如果从A 到B 记为：A→B(+1，+4)，从B 到A 记为：B→A(-1，-4)，其中第一个数表示左右方向，第二个数表示上下方向．（1）图中A→C( ， )，B→C( ， )，C→ (+1， )；（2）若这只甲虫从A 处去甲虫P 处的行走路线依次为（+2，+2），（+2，-1），（-2，+3），（-1，-2），请在图中标出P 的位置；（3）若这只甲虫的行走路线为A→B→C→D ，请计算该甲虫走过的路程；（4）若图中另有两个格点M 、N ，且M→A （3-a ，b-4），M→N （5-a ，b-2），则N →A 应记为什么？【答案】（1）3；4；2；0；D ；-2；（2）见解析；（3）10；（4）N →A 应记为(-2,-2) .【解析】（1）根据规定及实例可知A→C 记为（3，4）C→D 记为（1，-1）；A→B→C→D 记为（1，4），（2，0），（1，-1）；（2）按题目所示平移规律分别向右向上平移2个格点，再向右平移2个格点，向下平移1个格点；向左平移2个格点，向上平移3个格点；向左平移1个向下平移两个格点即可得到点P的坐标，在图中标出即可；（3）根据M→A（3-a，b-4），M→N（5-a，b-2）可知5-a-（3-a）=2，b-2-（b-4）=2，从而得到点A向右走2个格点，向上走2个格点到点N，从而得到N→A应记为什么.（1）图中A→C（+3，+4），B→C（+2，0），C→D（+1，﹣2）；故答案为：（+3，+4），（+2，0），D；（2）P点位置如图1所示；（3）如图2，根据已知条件可知：A→B表示为：（1，4），B→C；p记为（2，0）C→D记为（1，﹣2）；则该甲虫走过的路线长为：1+4+2+1+2=10；（4）由M→A（3﹣a，b﹣4），M→N（5﹣a，b﹣2），所以，5﹣a﹣（3﹣a）=2，b﹣2﹣（b﹣4）=2，所以，点A向右走2个格点，向上走2个格点到点N，所以，N→A应记为（﹣2，﹣2）．【点评】本题主要考查了利用坐标确定点的位置的方法．解题的关键是正确的理解从一个点到另一个点移动时，如何用坐标表示.。
人教版数学七年级上册单元测试卷-第一单元 有理数(含答案)
保密★启用前人教版数学七年级上册单元测试卷第一单元 有理数一、单选题1．如果规定收入为正，那么支出为负，收入2元记作2+，支出5元记作（ ）． A ．5元B ．5-元C ．3-元D ．7元2．2022的相反数是（ ） A ．12022B ．12022-C ．−2022D ．20223．下列计算结果为0的是（ ） A ．2222--B ．223(3)-+-C ．22(2)2-+D ．2333--⨯4．数轴上，把表示2的点向左平移3个单位长度得到的点所表示的数是（ ）． A ．－5B ．－1C ．1D ．55．华为最新款手机芯片“麒麟990”是一种微型处理器，每秒可进行100亿次运算，它工作2022秒可进行的运算次数用科学记数法表示为（ ） A ．140.202210⨯B ．1220.2210⨯C ．132.02210⨯D ．142.02210⨯6．下面算式与11152234-+的值相等的是（ ）A ．111324234⎛⎫⎛⎫--+- ⎪ ⎪⎝⎭⎝⎭B ．11133234⎛⎫--+ ⎪⎝⎭C ．111227234⎛⎫+-+ ⎪⎝⎭D ．11143234⎛⎫--+ ⎪⎝⎭7．观察下列三组数的运算：3(2)8-=-，328-=-；3(3)27-=-，3327-=-；3(4)64-=-，3446-=-．联系这些具体数的乘方，可以发现规律．下列用字母a 表示的式子：①当0a <时，33()a a =-；①当0a >时，33()a a -=-．其中表示的规律正确的是（ ） A ．①B ．①C ．①、①都正确D ．①、①都不正确8．数轴上，点A 对应的数是6-，点B 对应的数是2-，点O 对应的数是0.动点P 、Q 从A 、B 同时出发，分别以每秒3个单位和每秒1个单位的速度向右运动．在运动过程中，下列数量关系一定成立的是（ ）A ．2PQ OQ =B ．2OP PQ =C ．32QB PQ =D ．PB PQ =9．如图，正方形的周长为8个单位，在该正方形的4个顶点处分别标上0，2，4，6，先让正方形上表示数字6的点与数轴上表﹣3的点重合，再将数轴按顺时针方向环绕在该正方形上，则数轴上表示2017的点与正方形上的数字对应的是（ ）A ．0B ．2C ．4D ．610．如图，数轴上4个点表示的数分别为a 、b 、c 、d ．若|a ﹣d |＝10，|a ﹣b |＝6，|b ﹣d |＝2|b ﹣c |，则|c ﹣d |＝（ ）A ．1B ．1.5C ．1.5D ．2二、填空题11．用科学记数法表示的数的原数5.001×106＝___．12．已知：a 、b 互为相反数，c 、d 互为倒数，2m =，则()()220212020a b m cd ++-=______．13．东京与北京的时差为1h +，伯伯在北京乘坐早晨9:00的航班飞行约3h 到达东京，那么李伯伯到达东京的时间是____．（注：正数表示同一时刻比北京时间早的时数） 14．大家知道，550=-，它在数轴上的意义是：表示5的点与原点（即表示0的点）之间的距离．又如式子63-，它在数轴上的意义是：表示6的点与表示3的点之间的距离．类似地，式子()5a --在数轴上的意义是______． 15．有理数,,a b c 在数轴上对应点位置如图所示，用“＞”或“＜”填空：（1）｜a ｜______｜b ｜； （2）a ＋b ＋c ______0：（3）a －b ＋c ______0； （4）a ＋c ______b ； （5）c －b ______a ． 16．下列说法：①若a ，b 互为相反数，则ab＝﹣1；①如果|a +b |＝|a |+|b |，则ab ≥0；①若x 表示一个有理数，则|x +2|+|x +5|+|x ﹣2|的最小值为7； ①若abc ＜0，a +b +c ＞0，则a bc ab abc a bc ab abc+++的值为﹣2．其中一定正确的结论是____（只填序号）． 三、解答题 17．计算：(1)2(7)18(2)-⨯--÷-； (2)212316()12()234-÷--⨯-．18．画出数轴，用数轴上的点表示下列各数，并用“>”将它们连接起来： 33,2,1.5,,0,0.54---．19．比较下列各数的大小，并用“＜”号连接起来：2.5-，12，3，3--，(2)--，0．20．如图所示，在数轴上点A，B，C表示得数为﹣2，0，6，点A与点B之间的距离表示为AB，点B与点C之间的距离表示为BC，点A与点C之间的距离表示为AC．(1)求AB、AC的长；(2)点A，B，C开始在数轴上运动，若点A以每秒2个单位长度的速度向左运动，同时，点B和点C分别以每秒3个单位长度和4个单位长度的速度向右运动．请问：BC ﹣AB的值是否随着运动时间t的变化而变化？若不变，请求其值；若变化，请说明理由并判断是否有最值，若有求其最值．21．入冬以来，某品牌的羽绒服统计了在西乡市场某一周的销售情况，以每天100件为标准，超过的件数记作正数，不足的件数记作负数，记录如下：8，12，-9，6，-11，10，-2．(1)求销量最多的一天比销量最少的一天多销售______件；(2)该品牌羽绒服这一周的销售总量是多少件？若每件羽绒服的利润为130元，则这一周销售该品牌羽绒服的总利润为多少元？22．对于平面内的两点M、N，若直线MN上存在点P，使得MP=1NP成立，则称点P为点M、N的“和谐点”，但点P不是点N、M的“和谐点”.(1)如图1，点A、B在直线l上，点C、D是线段AB的三等分点，则是点A、B的“和谐点”（填“点C或“点D”）；(2)如图2，已知点E、F、G在数轴上，点E表示数－2，点F表示数1，且点F是点E、G的“和谐点”，求点G表示的数；(3)如图3，数轴上的点P表示数5，点M从原点O出发，以每秒3个单位的速度向左运动，点N从点P出发，以每秒10个单位的速度向左运动，点M、N同时出发.在M、N、P三点中，若点M是另两个点的“和谐点”，则OM= .23．计算：已知|m|＝1，|n|＝4．（1）当mn＜0时，求m+n的值；（2）求m﹣n的最大值．24．阅读下面的文字回答后面的问题：求231005555+++⋯+的值解：令231005555S=+++⋯+①将等式两边同时乘以5到：23410155555S=+++⋯+①①-①得：101455S=-①101554S-=即101231005555554-+++⋯+=问题：求231002222+++⋯+的值；参考答案：1．B【解析】【分析】结合题意，根据正负数的性质分析，即可得到答案．【详解】根据题意得：支出5元记作5-元故选：B．【点睛】本题考查了正数和负数的知识；解题的关键是熟练掌握正负数的性质，从而完成求解．2．C【解析】【分析】根据相反数的定义求解即可，只有符号不同的两个数互为相反数．【详解】解：2022的相反数是−2022．故选：C．【点睛】本题考查了相反数的定义，掌握相反数的定义是解题的关键．3．B【解析】【分析】根据有理数的乘方对各选项分别进行计算，然后利用排除法求解即可．【详解】A. 22--=−4−4=−8，故本选项错误；22B. 22-+-=−9+9=0，故本选项正确；3(3)C. 22-+=4+4=8，故本选项错误；(2)2D. 2333--⨯=−9−9=−18，故本选项错误．故选B.【点睛】此题考查有理数的乘方，解题关键在于掌握运算法则4．B【解析】【分析】根据数轴上点的坐标特点及平移的性质解答即可．【详解】解：根据题意：数轴上2所对应的点为A，将A点左移3个单位长度，得到点的坐标为2-3=-1，故选：B．【点睛】本题考查了数轴上的点与实数对应关系及图形平移的性质等有关知识．5．C【解析】【分析】科学记数法的表示形式为10na⨯的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的值与小数点移动的位数相同，题中：1亿810=．【详解】解：100亿1010=，1013102022 2.02210⨯=⨯，故选：C．【点睛】本题考查科学记数法的表示方法，关键要正确确定a的值以及n的值．6．C【解析】【分析】直接计算每个算式，对比答案即可．【详解】解：1111115 52527 23423412-+=+-++=；A 、1111111117324324324123423423412⎛⎫⎛⎫--+-=++-=+++--= ⎪ ⎪⎝⎭⎝⎭；B 、1111111111333333723423423412⎛⎫--+=++=++++= ⎪⎝⎭；C 、1111115227227723423412⎛⎫+-+=+--++= ⎪⎝⎭；D 、11111114343823423412⎛⎫--+=++++= ⎪⎝⎭，故选：C 【点睛】本题考查了有理数的加减运算，熟记有理数的加减混合运算的法则是解题的关键． 7．B 【解析】 【分析】根据三组数的运算的规律逐个判断即可得． 【详解】解：由三组数的运算得：[]333222))8((-=-==----， []3333(3)(3)27-=--=--=-，[]3334(4)(4)64-=--=--=-，归纳类推得：当0a <时，33()a a =--，式子①错误； 由三组数的运算得：3328(2)-=-=-， 33327(3)--=-=， 33464(4)--=-=，归纳类推得：当0a >时，33()a a -=-，式子①正确； 故选：B ． 【点睛】本题考查了有理数乘方的应用，正确归纳类推出一般规律是解题关键． 8．A 【解析】 【分析】设运动时间为t秒，根据题意可知AP=3t，BQ=t，AB=2，然后分类讨论:①当动点P、Q在点O左侧运动时，①当动点P、Q运动到点O右侧时，利用各线段之间的和、差关系即可解答.【详解】解:设运动时间为t秒，由题意可知: AP=3t，BQ=t，AB=|-6-(-2)|=4，BO=|-2-0|=2，①当动点P、Q在点O左侧运动时，PQ=AB-AP+BQ=4-3t+t=2(2-t)，①OQ= BO- BQ=2-t，①PQ= 2OQ ；①当动点P、Q运动到点O右侧时，PQ=AP-AB-BQ=3t-4-t=2(t-2)，①OQ=BQ- BO=t-2，①PQ= 2OQ，综上所述，在运动过程中，线段PQ的长度始终是线段OQ的长的2倍，即PQ= 2OQ一定成立.故选: A.【点睛】本题考查了数轴上的动点问题及数轴上两点间的距离，解题时注意分类讨论的运用.9．B【解析】【分析】表示2017的点在﹣1的右侧，从点﹣1到2017共2018个单位长度，根据2018÷8＝252……2，是252圈余2个单位长度，所以对应的数字就是2．【详解】解：因为正方形的周长为8个单位长度，所以正方形的边长为2个单位长度．表示2017的点与表示﹣1的点的距离等于2017﹣（﹣1）＝2018个单位长度，因为2018÷8＝252……2，所以252圈余2个单位长度，所以对应的数字是2．故选：B．【点睛】此题考查了数轴，解题的关键是找出正方形的周长与数轴上的数字的对应关系．10．D【解析】【分析】根据|a−d|＝10，|a−b|＝6得出b和d之间的距离，从而求出b和c之间的距离，然后假设a 表示的数为0，分别求出b，c，d表示的数，即可得出答案．【详解】解：①|a−d|＝10，①a和d之间的距离为10，假设a表示的数为0，则d表示的数为10，①|a−b|＝6，①a和b之间的距离为6，①b表示的数为6，①|b−d|＝4，①|b−c|＝2，①c表示的数为8，①|c−d|＝|8−10|＝2，故选：D．【点睛】本题主要考查数轴上两点间的距离、绝对值的意义，关键是要能恰当的设出a、b、c、d表示的数．11．5001000【解析】【分析】把5.001×106表示成原数的形式，就是把5.001的小数点向右移动6位即可得到．【详解】解：5.001×106＝5001000，故答案为：5001000．【点睛】本题考查了科学记数法，把科学记数法表示的数还原成原数，当n＞0时，n是几，小数点就向右移几位．12．1或-3##-3或1【解析】【分析】根据a、b互为相反数，c、d互为倒数，m的绝对值为2，可以得到a+b＝0，cd＝1，m＝±2，然后代入所求式子计算即可．【详解】解：∵a、b互为相反数，c、d互为倒数，m的绝对值为2，∴a+b＝0，cd＝1，m＝±2，当m＝2时，()()2202120112020a bm cd++-=+-=；当m＝﹣2时，()()220212013 2020a bm cd++-=-+-=-；故答案为：1或-3．【点睛】本题考查有理数的混合运算，解答本题的关键是求出a+b＝0，cd＝1，m＝±2．13．13时【解析】【分析】根据题意，9点先加上3个小时，再加上时差的1个小时，得到达到东京的时间．【详解】由题意得93113++=，∴李伯伯到达东京是下午13时．故答案是：13时．【点睛】本题考查有理数加法的实际应用，解题的关键是掌握有理数加法运算法则．14．表示a的点与表示-5的点之间的距离【解析】【分析】利用绝对值的意义即可求解．【详解】=-，它在数轴上的意义是：表示5的点与原点（即表示0的点）之间的距解：因为550-，它在数轴上的意义是：表示6的点与表示3的点之间的距离，离，式子63a--在数轴上的意义是表示a的点与表示-5的点之间的距离．所以式子()5【点睛】本题考查了绝对值，掌握绝对值的意义是解题的关键．15．<<>>>【解析】【分析】首先根据数轴可得b<a<0<c，然后再结合绝对值的性质和有理数的加减法法法则进行计算即可．【详解】解：（1）①根据数轴可得b<a<0<c，①|a|<|b|故答案为：<；（2）①a<0<c，|a|>|c|，①a+c<0，①a+b+c<0；故答案为：<；（3）①a-b>0，①a-b+c>0；故答案为：>；（4）①a >b ，①a +c >b ；故答案为：>；（5）①c >b ，①c -b >0，①c -b >a ．故答案为：>；【点睛】此题主要考查了有理数的比较大小，关键是掌握绝对值的定义和有理数的加减法法法则． 16．①①##①①【解析】【分析】根据相反数和绝对值的意义讨论即可得出答案．【详解】①若a ，b 互为相反数，则0a b +=,不能得出1a b=-，故①错误； ①当0,0a b ≥≥或0,0a b <<时，a b a b +=+成立，当0,0a b ><或0,0a b <>时，a b a b a b +=-≠+， ∴a b a b +=+成立，则0,0a b ≥≥或0,0a b <<，即0ab ≥，故①正确； ①252x x x ++++-表示x 到数2-、5-、2三个点的距离之和，所以2x =-时，252x x x ++++-取得最小值，最小值为2(5)7--=，故①正确；①当0,0,0c a b <>>且0a b c ++>时，111102abcababca bc ab abc a bc ab abc a bc ab abc--+++=+++=-+-=≠-，故①错误． 故答案为：①①．【点睛】本题考查相反数与绝对值，掌握绝对值的意义是解题的关键．17．(1)23(2)-63【解析】【分析】直接利用有理数混合运算法则计算即可．(1)解：2(7)18(2)14(9)14923-⨯--÷-=--=+=．(2) 解：21231116()12()1612()64163234412-÷--⨯-=-÷-⨯-=-+=-． 【点睛】本题考查有理数的混合运算，注意先算乘方，再算乘除，后算加减，有括号要先算括号里面的；可以结合题目特点，灵活运用结合律、分配律、交换律，从而起到简化运算的效果．18．作图见解析；33 1.500.524>>>->->-． 【解析】【分析】先在数轴上表示出各个数，再根据数轴上的点表示的数的大小规律即可得到结果．【详解】解：在数轴上表示出各个数如图所示：则可得3>1.5>0>−0.5>34->−2【点睛】本题考查了利用数轴比较有理数的大小，解题的关键是熟练掌握数轴上的点表示的数，右边的数始终大于左边的数．19．()13 2.50232-<-<<<--< 【解析】【分析】先把每个数进行化简，再根据有理数的大小排列起来即可．解：33--=-，(2)2--=， ①13 2.50232-<-<<<< ， ①13 2.50(2)32--<-<<<--<．【点睛】本题考查比较数的大小，准确的把每个数进行化简是解题的关键．20．(1)2,8AB AC ==(2)变化，当0=t 时取得最大值4【解析】【分析】（1）根据点A ，B ，C 表示的数，即可求出AB ， AC 的长；（2）根据题意分别求得点A 表示的数为-2-2t ，点B 表示的数为3t ，点C 表示的数为6+4t ，根据两点距离求得,BC AB ，进而根据整式的加减进行计算即可．(1)解：AB =0-（-2）=2， AC =()628--=．(2)当运动时间为t 秒时，点A 表示的数为-2-2t ，点B 表示的数为3t ，点C 表示的数为6+4t ， 则6436BC t t t =+-=+，()32225AB t t t =---=+ ()62544BC AB t t t ∴-=+-+=-当0=t 时，BC AB -的值最大，最大值为4．【点睛】本题考查了列代数式、数轴以及两点间的距离，解题的关键是：（1）根据三个点表示的数，求出三条线段的长度；（2）利用含t 的代数式表示出BC ，AB 的长．21．(1)23(2)该品牌羽绒服这一周的销售总量是714件，总利润为92820元【解析】（1）直接利用有理数的减法法则，用最大的数减去最小的数即可；（2）可以先求出7天的标准件数，再加上比标准多或少件数即可，利用这周销售羽绒服的总件数×130即可．(1)12(11)23--=（件）故答案为：23；(2)7×100+8+12+（-9）+6+（-11）+10+（-2）=714（件）所以该品牌羽绒服这一周的销售总量是714件．714×130=92820（元）所以这一周销售该品牌羽绒服的总利润为92820元．【点睛】本题主要考查正数和负数，正确利用有理数的运算法则是解题的关键．22．(1)点C(2)-5或7(3)45或1517或4511【解析】【分析】（1）点C、D是线段AB的三等分点，故可直接依题意判断得到答案．（2）按“和谐点”的定义列出等式，然后可求得答案．（3）设经过t秒后满足点M是点N、P的“和谐点”或点M是P、N的“和谐点”，求出t的值，进而得到答案．(1)解：①点C、D是线段AB的三等分点①12 AC BC=故点C是点A、B的“和谐点”．(2)解：点F 是点E 、G 的“和谐点”，依题意有12EF GF =， ①3EF =①6GF =①点G 为-5或7．(3)解：设时间t 秒后：①满足点M 是点N 、P 的“和谐点”，此时点M 为-3t ，点N 为5-10t ，依题意有12NM PM = ①()157532t t -=+当570t -＞时，()15757532t t t -=-=+，解得517t =①点M 为1517-，1517OM = 当570t -＜时，()()157532t t --=+，解得1511t①点M 为1511-，4511OM =①满足点M 是P 、N 的“和谐点”，此时点M 为-3t ，点N 为5-10t ，依题意有12PM NM = ①153572t t +=- ，解得15t =①45OM =综上所述，45OM =或1517或4511 【点睛】本题考查数轴上的两点距离及动点问题，熟练掌握数轴的相关知识，按定义列出等式求解是解题的关键．23．（1）±3；（2）m ﹣n 的最大值是5．【解析】【分析】由已知分别求出m =±1，n =±4；（1）由已知可得m =1，n =﹣4或m =﹣1，n =4，再求m +n 即可；（2）分四种情况分别计算即可．【详解】①|m |=1，|n |=4，①m =±1，n =±4；（1）①mn ＜0，①m =1，n =﹣4或m =﹣1，n =4，①m +n =±3；（2）分四种情况讨论：①m =1，n =4时，m ﹣n =﹣3；①m =﹣1，n =﹣4时，m ﹣n =3；①m =1，n =﹣4时，m ﹣n =5；①m =﹣1，n =4时，m ﹣n =﹣5；综上所述：m ﹣n 的最大值是5．【点睛】本题考查了有理数的运算，绝对值的运算；掌握有理数和绝对值的运算法则，能够正确分类是解题的关键．24．10122-【解析】【分析】根据题目解题过程进行求解即可；【详解】解：令231002222S =+++⋯+①将等式两边同时乘以2到：20134122222S =+++⋯+①①-①得：10122S =-①10122S =-，即23100101222222++++=⋯-．【点睛】本题主要考查有理数混合运算的应用，正确理解题意，根据题目方法步骤进行求解是解题的关键．。
人教版数学七年级上册第一章有理数《单元测试》附答案
人教版数学七年级上学期第一章有理数测试时限：100分钟满分：120分一.选择题(本大题共12个小题,每小题3分,共36分内)1.下列说法不正确的是( )A. 0是最小数B. 0的相反数是0C. 0没有倒数D. 0是绝对值最小的数2.下列各对数中,互为相反数的是( )A. +(-3)与-3B. +(+3)与-3C. -(-3)与3D. 3 与+(+3)3.若两个有理数的和是正数,那么一定有结论( )A. 两个加数都是正数B. 两个加数有一个是正数C. 一个加数正数,另一个加数为零D. 两个加数不能同为负数4.两个非零有理数的和是0,则它们的商为：( )A. 0B. -1C. +1D. 不能确定5.下列各组数中,数值相等是()A. 32和23B. ﹣23和(﹣2)3C. ﹣32和(﹣3)2D. ﹣3×22 和(﹣3×2)26.绝对值相等的两个数在数轴上对应两点的距离为10,则这两个数为( )A. 10和－10B. 0和10C. 5和－5D. 5和07.a,b,c三个数在数轴上的位置如图所示,则下列结论中错误的是( )A. b＜0B. a+c＜0C. a﹣b＞0D. b﹣c＜08.计算16×(－6)÷(-16)×6值为( )A. 1B. 36C. －1D. +69.下列交换加数的位置的变形中,正确的是A. 1-4+5-4=1-4+4-5B.13111311 34644436 -+--=+--C. 1-2+3-4=2-1+4-3D. 4.5-1.7-2.5+1.8=4.5-2.5+1.8-1.710.学校、家、书店依次坐落在一条东西走向的大街上,学校在家的东边200米,书店在家西边1000米,某同学从家里出发,向西走了500米,接着又向西走了－700米,此时该同学的位置在( )A. 在家B. 在学校C. 在书店D. 不在上述地方11.比较大小：-22,(12-)2,(13-)3,正确的是( )A. -22＞(12-)2＞(13-)3 B. (13-)3＞-22＞(12-)2C. (12-)2＞-22＞(13-)3 D. (12-)2＞(13-)3＞-2212.若(－1)2＝4,那么的值为()A. 27B. 3或－1C. 25或－1D. －1或27二、填空题(本大题共4个小题,每小题3分,共12分)13.月球距地球约为38万千米,用科学计数法表示为____________千米．14.绝对值小于6的所有数的积是_____________．15.如果数轴上的点A对应的数为-5,那么与A点相距3个单位长度的点所对应的有理数为__________．16.在﹣3,﹣2,﹣1,4,5中取出三个数,把三个数相乘,所得到的最大乘积是_．三、解答题(本大题共6个题,共72分)17.(1)将下列各数填入相应的圈内：212,5 , 0 ,1.5 ,＋2 ,－3 .(2 )说出这两个圈的重叠部分表示的是什么数的集合：．18.数轴上表示下列各数,并用“＜”号把它们连起来：1.5, 3, －2.5, 0 , －1 1 319.计算下列各题(1)15＋(-14)-15-(-025) (2)(-81)÷94×49÷(-32)(3)292324×(-12) (4)25×34-(-25)×12＋25×(-14)(5)-24-(-4)2 ×(-1)+(-3)3(6)3.25-[(-12)-(-52)+(-54)+243]20.按要求解答下列各题(1)已知a、b 互为相反数,c、d 互为倒数,x=(-2)2．试求x2 -(a + b + c×d) x +(a + b)2015 +(－c×d)2016的值．(2)已知有理数a、b、c 满足|a-1|+|b-3|+|3c-1|=0,求(a×b×c)178 ÷(a36×b7×c6)的值．21.某食品厂从生产的袋装食品中抽取20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表：(1)这批样品的质量比标准质量多还是少?多或少几克?(2)若每袋标准质量为450克,则抽样检测的总质量是多少?22.陈老师在上周五买进某公司股票1000股,每股28元,下表为本周内每日该股票的涨跌情况.(单位：元)(1)星期三收盘时,每股是多少?(2)本周内最高价是每股多少元?最低价是每股多少元?(3)已知陈老师买进股票时付了1.5%的手续费,卖出时需付成交手续费和交易税共2.5%,如果陈老师在星期五收盘时将全部股票卖出,他的收益情况如何?答案与解析一.选择题(本大题共12个小题,每小题3分,共36分内)1.下列说法不正确的是( )A. 0是最小的数B. 0的相反数是0C. 0没有倒数D. 0是绝对值最小的数【答案】A【解析】【分析】根据有理数0的意义进行分析.【详解】0不是最小的数,比0小的数是负数；0的相反数是0；0没有倒数；0是绝对值最小的数.故选A【点睛】本题考核知识点：0的意义. 解题关键点：理解有理数0的意义.2.下列各对数中,互为相反数的是( )A. +(-3)与-3B. +(+3)与-3C. -(-3)与3D. 3 与+(+3)【答案】B【解析】【分析】根据：只有符号不同的两个数互为相反数.逐个化简分析即可.【详解】A .+(-3)=-3与-3, 不是互为相反数；B.+(+3)=3与-3 , 是互为相反数；C.-(-3)=3与3, 不是互为相反数；D.3 与+(+3)=3, 不是互为相反数.故选B【点睛】本题考核知识点：相反数. 解题关键点：理解相反数的定义.3.若两个有理数的和是正数,那么一定有结论( )A. 两个加数都是正数B. 两个加数有一个是正数C. 一个加数正数,另一个加数为零D. 两个加数不能同为负数【答案】D【解析】试题分析：若两个有理数的和为正数,两个加数可能都为正数,也可能一个为正数,也可能一个加数为正数,另一个加数为0,不可能两加数为负数．故选D．考点：有理数的加法．4.两个非零有理数的和是0,则它们的商为：( )A. 0B. -1C. +1D. 不能确定【答案】B【解析】【分析】根据“互为相反数的两个数的和是0”判断出这两个数是互为相反数,互为相反数的两个数的商为-1.【详解】∵两个非零有理数的和是0∴这两个数互为相反数∴互为相反数的两个非零数的商为-1故选B【点睛】本题考查“互为相反数的两数相加得0”以及有理数除法法则,熟练掌握相关知识点是解题关键5.下列各组数中,数值相等的是()A 32和23 B. ﹣23和(﹣2)3 C. ﹣32和(﹣3)2 D. ﹣3×22 和(﹣3×2)2【答案】B【解析】【分析】原式各项利用乘方的意义计算得到结果,即可做出判断．【详解】A、32=9,23=8,数值不相等；B、﹣23=(﹣2)3=﹣8,数值相等；C、﹣32=﹣9,(﹣3)2=9,数值不相等；D、﹣3×22=﹣12,(﹣3×2)2=36,数值不相等,故选B6.绝对值相等的两个数在数轴上对应两点的距离为10,则这两个数为( )A. 10和－10B. 0和10C. 5和－5D. 5和0【答案】C【解析】【分析】绝对值相等的两个不同的数互为相反数,因为他们的距离是10,所以他们的绝对值是5.【详解】依题意可得,这两个数的绝对值是5,所以这两个数是5和－5.故选C【点睛】本题考核知识点：绝对值. 解题关键点：理解绝对值的意义.7.a,b,c三个数在数轴上的位置如图所示,则下列结论中错误的是( )A. b＜0B. a+c＜0C. a﹣b＞0D. b﹣c＜0【答案】C【解析】试题分析：根据数轴上点的特点,可知a＜b＜0＜c,且︱a︱＞︱c︱＞︱b︱,因此a+b＜0,故A正确；a+c＜0,故B正确；a-b＜0,故C错误；b-c＜0,故D正确.故选C考点：数轴8.计算16×(－6)÷(-16)×6的值为( )A. 1B. 36C. －1D. +6 【答案】B【解析】【分析】先把除法运算化为乘法运算,再根据有理数乘法法则进行计算.【详解】16×(－6)÷(-16)×6=16×(－6)×(-6)×6=36故选B【点睛】本题考核知识点：有理数乘除法. 解题关键点：把除法转化为乘法.9.下列交换加数的位置的变形中,正确的是A. 1-4+5-4=1-4+4-5B.13111311 34644436 -+--=+--C. 1-2+3-4=2-1+4-3D. 45-1.7-2.5+1.8=4.5-2.5+1.8-1.7 【答案】D【解析】【详解】A. 1−4+5−4=1−4−4+5,故错误；B.13111311=-34644436-+--+--,故错误；C. 1-2+3-4=-2+1-4+3,故错误；D. 4.5−1.7−2.5+1.8=4.5−2.5+1.8−1.7,故正确．故选D.10.学校、家、书店依次坐落在一条东西走向的大街上,学校在家的东边200米,书店在家西边1000米,某同学从家里出发,向西走了500米,接着又向西走了－700米,此时该同学的位置在( )A. 在家B. 在学校C. 在书店D. 不在上述地方【答案】B【解析】【分析】某同学从家里出发,向西走了500米,接着又向西走了－700米,相当于向东走700米,最后离家向东200米. 【详解】依题意分析可得,向西走了－700米,相当于向东走700米,所以,该同学最后离家向东200米.即在学校.故选B【点睛】本题考核知识点：负数的意义,数轴. 解题关键点：理解负数的意义.11.比较大小：-22,(12-)2,(13-)3,正确的是( )A. -22＞(12-)2＞(13-)3 B. (13-)3＞-22＞(12-)2C. (12-)2＞-22＞(13-)3 D. (12-)2＞(13-)3＞-22【答案】D 【解析】解：∵﹣22=﹣4,(﹣12)2=14,(﹣13)3=﹣127,∴(﹣12)2＞(﹣13)3＞﹣22；故选D．点睛：本题考查了有理数大小的比较,不是最简的化到最简,然后根据正数大于0,0大于负数,两个负数比较,绝对值大的反而小得出答案．12.若(－1)2＝4,那么的值为()A. 27B. 3或－1C. 25或－1D. －1或27【答案】D【解析】由题意得：－1=2解得：x=3或x=-1那么=27或-1故选D二、填空题(本大题共4个小题,每小题3分,共12分)13.月球距地球约为38万千米,用科学计数法表示为____________千米．【答案】3.8×105【解析】【分析】把一个大于10(或者小于1)的整数记为a×10n的形式(其中1 ≤| a| ＜10 )的记数法.【详解】38万=3.8×105.故答案为3.8×105【点睛】本题考核知识点：科学记数法. 解题关键点：理解科学计数法的意义.14.绝对值小于6的所有数的积是_____________．【答案】0【解析】【分析】先求出绝对值小于6的所有数,再求他们的积.要注意,其中有一个是0.【详解】绝对值小于6的所有数有无数个,但其中一个是0,所以,他们的积是0.故答案为0【点睛】本题考核知识点：有理数乘法. 解题关键点：记住0与任何数相乘等于0.15.如果数轴上的点A对应的数为-5,那么与A点相距3个单位长度的点所对应的有理数为__________．【答案】-8或-2【解析】【分析】与A点相距3个单位长度的点可能在A的左侧或在A的右侧.【详解】与A点相距3个单位长度的点可能在A的左侧或在A的右侧,所以,对应的数是：-5-3=-8,或-5+3=-2. 故答案为-8或-2【点睛】本题考核知识点：数轴上两点距离、有理数加减. 解题关键点：运用有理数加减法求两点的距离.16.在﹣3,﹣2,﹣1,4,5中取出三个数,把三个数相乘,所得到最大乘积是_．【答案】30 ；【解析】根据正数大于一切负数,同号得正,异号得负,找出乘积是正数绝对值最大的三个数相乘即可.解：最大乘积是：(-3)×(-2)×5=3×2×5=30.故答案为30.“点睛”本题考查了有理数的乘法,以及有理数的大小比较,比较简单,熟记运算法则是解题的关键.三、解答题(本大题共6个题,共72分)17.(1)将下列各数填入相应的圈内：212,5 , 0 ,1.5 ,＋2 ,－3 .(2 )说出这两个圈的重叠部分表示的是什么数的集合：．【答案】(1)见解析；(2)正整数的集合【解析】【分析】根据有理数的分类解答即可.【详解】(1)如图,(2)∵5,+2是正整数,∴两个圈的重叠部分表示的是正整数的集合.【点睛】本题考查了有理数的分类,熟练掌握有理数的两种分类方式是解答本题的关键. 有理数可分为整数和分数,整数分正整数,零和负整数；分数分正分数和负分数.有理数也可分为正有理数,零和负有理数,正有理数分为正整数和正分数,负有理数分为负整数和负分数.18.在数轴上表示下列各数,并用“＜”号把它们连起来：1.5, 3, －2.5, 0 , －1 1 3【答案】见解析【解析】【分析】先按要求画好数轴,在数轴上表示各数,根据数轴上右边的数大于左边的数进行连接. 【详解】解：如图：-2.5＜-1.3＜0＜1.5＜3.【点睛】本题考核知识点：利用数轴表示数的大小. 解题关键点：画好数轴,表示各数.19.计算下列各题(1)15＋(-14)-15-(-025) (2)(-81)÷94×49÷(-32)(3)292324×(-12) (4)25×34-(-25)×12＋25×(-14)(5)-24-(-4)2 ×(-1)+(-3)3(6)3.25-[(-12)-(-52)+(-54)+243]【答案】(1)0 (2)12(3)-35912(4) 25(5)-27 (6)-136【解析】【分析】根据有理数的运算法则,逐个计算.【详解】解：(1)15＋(-14)-15-(-0.25)=15-15- 14+0.25=0(2)(-81)÷94×49÷(-32)=81×49×49×132= 1 2(3)292324×(-12)= (30- 124) ×(-12)= 30×(-12) -1 24× (-12)=-35912(4)25×3 4-(-25)×12＋25×(-14) =25×(34+1 2-1 4) =25×1=25 (5)-24-(-4)2 ×(-1)+(-3)3 = -16+16-27= -27(6)3.25-[(-12)-(-52)+(-5 4)+243] =31 4+1 2 -5 2+5 4-243 1515234442231242423122423136=++--=--=-=- 【点睛】本题考核知识点：有理数混合运算. 解题关键点：掌握有理数运算法则.20.按要求解答下列各题(1)已知a 、b 互为相反数,c 、d 互为倒数,x=(-2)2．试求x 2 -(a + b + c×d) x +(a + b)2015 +(－c×d)2016的值． (2)已知有理数a 、b 、c 满足|a-1|+|b-3|+|3c-1|=0,求(a×b×c)178 ÷(a 36×b 7×c 6)的值．【答案】(1)13 (2)13【解析】【分析】(1)由已知可得a+b=0,cd=1,x=4,再代入原式可得；(2)由非负数性质得a-1=0,b-3=0,3c-1=0.求出a,b,c,再代入求值.【详解】解：(1)因为a 、b 互为相反数,c 、d 互为倒数,x=(-2)2所以,a+b=0,cd=1,x=4,所以,x 2 -(a + b + c×d) x +(a + b)2015 +(－c×d)2016=42-(0+1)×4+02015+(-1)2016=16-4+0+1=13.(2)因为|a-1|+|b-3|+|3c-1|=0,所以,根据非负数性质得：a-1=0,b-3=0,3c-1=0.所以,a=1,b=3,c=13, 所以,(a×b×c)178 ÷(a 36×b 7×c 6) =(1×3×13)178 ÷[136×37×(13)6] =1÷3 =13. 【点睛】本题考核知识点：非负数、倒数、相反数的应用. 解题关键点：理解非负数、倒数、相反数的性质. 21.某食品厂从生产的袋装食品中抽取20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表：(1)这批样品的质量比标准质量多还是少?多或少几克?(2)若每袋标准质量为450克,则抽样检测的总质量是多少?【答案】(1)这批样品的质量比标准质量多,多24克；(2)9024克【解析】【分析】(1)根据表格列出算式,计算得到结果,即可做出判断；(2)根据每袋标准质量为450克列出算式,计算即可得到结果．【详解】(1)根据题意得：﹣5×1﹣2×4+0×3+1×4+3×5+6×3=﹣5﹣80+4+15+18=24(克), 则这批样品的质量比标准质量多,多24克；(2)根据题意得：20×450+24=9024(克),则抽样检测的总质量是9024克．【点睛】此题考查了正数与负数,弄清题意是解本题的关键．22.陈老师在上周五买进某公司股票1000股,每股28元,下表为本周内每日该股票的涨跌情况.(单位：元)(1)星期三收盘时,每股是多少?(2)本周内最高价是每股多少元?最低价是每股多少元?(3)已知陈老师买进股票时付了1.5%的手续费,卖出时需付成交手续费和交易税共2.5%,如果陈老师在星期五收盘时将全部股票卖出,他的收益情况如何?【答案】(1)34.5元 (2)36.5元、30元(3)盈利830元．【解析】【分析】(1)根据题意得：28+4+4.5−2=34.5(元)；(2)算出每天股价,再作比较；(3)根据题意得：1000×(30−28)−1000×28×1.5%−30×1000×2.5%=830(元),可得收益.【详解】解：(1)根据题意得：28+4+4.5−2=34.5(元),则星期三收盘时,每股34.5元；(2)本周的股价分别为28+4=32(元)；32+4.5=36.5(元)；36.5−2=34.5(元)；34.5+1.5=36(元)；36−6=30(元),则本周内最高价是每股36.5元,最低价是每股30元；(3)根据题意得：1000×(30−28)−1000×28×1.5%−30×1000×2.5%=830(元),则张先生在星期五收盘时将全部股票卖出,他的收益情况为830元．【点睛】本题考核知识点：有理数运算的应用.解题关键点：理解题意,根据实际列出算式并正确运算.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初一数学上册第一单元有理数知识点归纳及测试题知识网络：一．有理数：(1)凡能写成形式的数，都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意：0即不是正数，也不是负数;-a不一定是负数，+a也不一定是正数;π不是有理数;(2)有理数的分类:①②(3)注意：有理数中，1、0、-1是三个特殊的数，它们有自己的特性;这三个数把数轴上的数分成四个区域，这四个区域的数也有自己的特性;(4)2.数轴：数轴是规定了原点、正方向、单位长度的一条直线.3.相反数：(1)只有符号不同的两个数，我们说其中一个是另一个的相反数;0的相反数还是0;(2)注意：a-b+c的相反数是-a+b-c;a-b的相反数是b-a;a+b的相反数是-a-b;(3)4.绝对值：(1)正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数;注意：绝对值的意义是数轴上表示某数的点离开原点的距离;(2)绝对值可表示为：绝对值的问题经常分类讨论;(3)(4)|a|是重要的非负数，即|a|≥0;注意：|a|·|b|=|a·b|,5.有理数比大小：(1)正数的绝对值越大，这个数越大;(2)正数永远比0大，负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小，绝对值大的反而小;(5)数轴上的两个数，右边的数总比左边的数大;(6)大数-小数>0，小数-大数<0.二．有理数法则及运算规律。
(1)同号两数相加，取相同的符号，并把绝对值相加;(2)异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值;(3)一个数与0相加，仍得这个数.2.有理数加法的运算律：(1)加法的交换律：a+b=b+a;(2)加法的结合律：(a+b)+c=a+(b+c).3.有理数减法法则：减去一个数，等于加上这个数的相反数;即a-b=a+(-b).4.有理数乘法法则：(1)两数相乘，同号为正，异号为负，并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘，有一个因式为零，积为零;各个因式都不为零，积的符号由负因式的个数决定.5.有理数乘法的运算律：(1)乘法的交换律：ab=ba;(2)乘法的结合律：(ab)c=a(bc);(3)乘法的分配律：a(b+c)=ab+ac.6.有理数除法法则：除以一个数等于乘以这个数的倒数;注意：零不能做除数，.7.有理数乘方的法则：(1)正数的任何次幂都是正数;三．乘方的定义。
(1)求相同因式积的运算，叫做乘方;(2)乘方中，相同的因式叫做底数，相同因式的个数叫做指数，乘方的结果叫做幂;(3)(4)据规律底数的小数点移动一位，平方数的小数点移动二位.2.3.近似数的精确位：一个近似数，四舍五入到那一位，就说这个近似数的精确到那一位.4.有效数字：从左边第一个不为零的数字起，到精确的位数止，所有数字，都叫这个近似数的有效数字.5.混合运算法则：先乘方，后乘除，最后加减;注意：怎样算简单，怎样算准确，是数学计算的最重要的原则.6.特殊值法：是用符合题目要求的数代入，并验证题设成立而进行猜想的一种方法,但不能用于证明.概念定义：1、大于0的数叫做正数（positive number）。
2、在正数前面加上负号“-”的数叫做负数（negative number）。
3、整数和分数统称为有理数（rational number）。
4、人们通常用一条直线上的点表示数，这条直线叫做数轴（number axis）。
数轴三要素：原点，正方向，单位长度。
难点：用点表示数5、在直线上任取一个点表示数0，这个点叫做原点（origin）。
6、一般的，数轴上表示数a的点与原点的距离叫做数a的绝对值（absolute value）。
7、由绝对值的定义可知：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0。
8、正数大于0，0大于负数，正数大于负数。
9、两个负数，绝对值大的反而小。
10、有理数加法法则（1）同号两数相加，取相同的符号，并把绝对值相加。
（2）绝对值不相等的异号两数相加，取绝对值较大的加数的负号，并用较大的绝对值减去较小的绝对值，互为相反数的两个数相加得0。
（3）一个数同0相加，仍得这个数。
11、有理数的加法中，两个数相加，交换交换加数的位置，和不变。
12、有理数的加法中，三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。
13、有理数减法法则减去一个数，等于加上这个数的相反数。
14、有理数乘法法则两数相乘，同号得正，异号得负，并把绝对值向乘。
任何数同0相乘，都得0。
15、有理数中仍然有：乘积是1的两个数互为倒数。
16、一般的，有理数乘法中，两个数相乘，交换因数的位置，积相等。
17、三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积相等。
18、一般地，一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加。
19、有理数除法法则除以一个不等于0的数，等于乘这个数的倒数。
20、两数相除，同号得正，异号得负，并把绝对值相除。
0除以任何一个不等于0的数，都得0。
21、求n个相同因数的积的运算，叫做乘方，乘方的结果叫做幂（power）。
在an 中，a叫做底数（basenumber），n叫做指数（exponeht）22、根据有理数的乘法法则可以得出负数的奇次幂是负数，负数的偶次幂是正数。
显然，正数的任何次幂都是正数，0的任何次幂都是0。
23、做有理数混合运算时，应注意以下运算顺序：（1）先乘方，再乘除，最后加减；（2）同级运算，从左到右进行；（3）如有括号，先做括号内的运算，按小括号、中括号、大括号依次进行。
24、把一个大于10数表示成a×10n 的形式（其中a是整数数位只有一位的数，n是正整数），使用的是科学计数法。
25、接近实际数字，但是与实际数字还是有差别，这个数是一个近似数（approximate number）。
26、从一个数的左边的第一个非0数字起，到末尾数字止，所有的数字都是这个数的有效数字（significant digit）知识点细解一、有理数概念1、正数与负数例1：按要求选择下列各数： 8，3，0，-1.5，14，-0.037，+0.62，-3，132，98-，+2，-7属于整数集合的有__________ 属于分数集合的有_________ _属于正数集合的有_______________ 属于负数集合的有_____________ 属于正整数集合的有____________ 属于负整数集合的有____________ 正分数集合的有_____________ 属于负分数集合的有__________ 属于非整数集合的有_________________属于非负数集合的有_________ 属于非负整数集合的有_________属于非正整数集合的有_______________例2主动学习网饮料公司生产的一种瓶装饮料外包装上印有“600±30（mL）”字样，请问“±30mL”是什么含义？质检局对该产品抽查5瓶，容量分别为603mL，611mL，589mL，573mL，627mL，问抽查产品的容量是否合格？练习：1.若密云水库的水位比标准水位高出3cm记为＋3cm，某月的水位记录中显示，1日水位为－5cm，2日水位为－1cm，3日水位为＋4cm，则（）A.1日与2日水位相差6cmB.1日与3日水位相差1cmC.2日与3日水位相差5cmD.均不正确2.篮球的质量，超过标准质量的克数记为正数，不足标准质量的克数记为负数，检查的结果如下表：篮球编号 1 2 3 4 5与标准质量的差（克）+4 +7 -3 -8 +9最接近标准质量的是_______号篮球；质量最大的篮球比质量最小的篮球重_______克.3.判断：1）最小的自然数是1；2）最小的整数是1；3）一个有理数的倒数等于它本身，则这个数是1；2.数轴例3在数轴上表示下列各数，再按大小顺序用“＜”号连接起来.-4，0，-4.5，-112，2，3.5，1，122例4如右图所示，数轴的一部分被墨水污染了，被污染的部分内含有的整数为练习：1、实数,a b在数轴上表示如图所示，则结论错误的是A.a b o+< B.0ab< C.b a-> D.0a b-<2.数轴上有一点到原点的距离是5.5，那么这个点表示的数是 _________.3.一个点从数轴的原点开始,先向右移3个单位长度,再向左移动5个单位长度,则终点表示的数是____.4.数轴上点A对应的数为-3,那么与A相距1个长度的点B所对应的数是_________.3.相反数 例5.（1）－3与 互为相反数；0的相反数是 .（2）m -的相反数是 ，1m -+的相反数是 ，1m +的相反数是 . （3）已知9,a -=那么a -的相反数是 .已知9a =-，则a 的相反数是 . 例6如果0a <，化简下列各数的符号，并说出是正数还是负数（1）()a -+； （2）()a -- （3）[]()a -+- （4）[]()a ---练习：一个数的相反数的倒数是-4,这个数是__________如果a 与-3互为相反数,那么a 等于( )4.绝对值 例7：求绝对值.：（1）0.5； （2）12-； （3）－（－3）； （4）－∣1.5∣.例8已知∣x ∣=4，∣y ∣=6，求代数式∣x+y ∣的值.练习：1、2--的倒数是 2..计算5( 4.8) 2.3⨯-+-=____________.3..绝对值不大于3的整数有4..已知3,2,0,_________.x y xy x y ==<+则的值是模拟试题1、填空： ⑴若m ，n 互为相反数，则m ＋ n ＝ . ⑵某人转动转盘，如果沿逆时针转5圈记作＋5圈，那么沿顺时针转12圈可表示成 ； ⑶某次乒乓球质量检测中，一只乒乓球超出标准0.02克记作＋0.02克，那么－0.03可表示成 ；2、如图， 两点所表示的两数的（ ）Ａ.和为正数 Ｂ.和为负数 Ｃ.积为正数Ｄ.积为负数3、.如果，那么下列关系式中正确的是（ ）.A. B. C. D. 4. 下列说法中不正确的是（ ）A.－5表示的点到原点的距离是5；B. 一个有理数的绝对值一定是正数；C. 一个有理数的绝对值一定不是负数；D. 互为相反数的两个数的绝对值一定相等. 5.一定是正数的是（ ）A.|m|＋2 B.|m| C.m －3 D.－|m|6. 如果有理数a ，b 满足a ＋b>0，ab<0，则下列式子正确的是（ ）A.当a>0，b<0时，|a|>|b|B.当a<0，b>0时，|a|>|b|C.a>0，b>0D.a<0，b<07. 某城市按以下规定收取每月煤气费，用煤气不超过60立方米，按每立方米0.8元收费；如果超过60立方米，超过部分按每立方米1.2元收费。