编译原理第4章作业答案
编译原理-第4章 语法分析--习题答案

第4章语法分析习题答案1.判断(1)由于递归下降分析法比较简单,因此它要求文法不必是LL(1)文法。
(× )LL(1)文法。
(× )(3)任何LL(1)文法都是无二义性的。
(√)(4)存在一种算法,能判定任何上下文无关文法是否是LL(1) 文法。
(√)(× )(6)每一个SLR(1)文法都是LR(1)文法。
(√)(7)任何一个LR(1)文法,反之亦然。
(× )(8)由于LALR是在LR(1)基础上的改进方法,所以LALR(× )(9)所有LR分析器的总控程序都是一样的,只是分析表各有不同。
(√)(10)算符优先分析法很难完全避免将错误的句子得到正确的归约。
(√)2.文法G[E]:E→E+T|TT→T*F|FF→(E)|i试给出句型(E+F)*i的短语、简单短语、句柄和最左素短语。
答案:画出语法树,得到:短语: (E+F)*i ,(E+F) ,E+F ,F ,i简单短语: F ,i句柄: F最左素短语: E+F3.文法G[S]:S→SdT | TT→T<G | GG→(S) | a试给出句型(SdG)<a的短语、简单短语、句柄和最左素短语。
答案:画出语法树,得到:短语:(SdG)<a 、(SdG) 、SdG 、G 、a简单(直接)短语:G 、a句柄:G最左素短语:SdG4.对文法G[S]提取公共左因子进行改写,判断改写后的文法是否为LL(1)文法。
S→if E then S else SS→if E then SS→otherE→b答案:提取公共左因子;文法改写为:S→if E then S S'|otherS'→else S|E→bLL(1)文法判定:① 文法无左递归② First(S)={if,other}, First(S')={else, }First(E)={b}Follow(S)= Follow(S')={else,#}Follow(E)={then}First(if E then S S')∩First(other)=First(else S)∩First( )=③First(S')∩Follow(S')={else}不为空集故此文法不是LL(1)文法。
编译原理第4章答案

第四章词法分析1.构造下列正规式相应的DFA:(1)1(0|1) * 101(2)1(1010* | 1(010) * 1)* 0(3)a((a|b) * |ab * a)* b(4)b((ab)* | bb) * ab解:(1)1(0|1) * 101 对应的 NFA为1101012341下表由子集法将NFA 转换为 DFA:I I0=ε-closure(MoveTo(I,0))I1=ε-closure(MoveTo(I,1))A[0]B[1]B[1]B[1]C[1,2]C[1,2]D[1,3]C[1,2]D[1,3]B[1]E[1,4]E[1,4]B[1]B[1]001101A B C D E110,1(2)1(1010 * | 1(010) * 1)* 0 对应的 NFA 为εε1101010 01234561εε101978ε下表由子集法将NFA 转换为 DFA:I I=ε-closure(MoveTo(I,0))I1= ε-closure(MoveTo(I,1))A[0]B[1,6]B[1,6]C[10]D[2,5,7]C[10]D[2,5,7]E[3,8]B[1,6]E[3,8]F[1,4,6,9] F[1,4,6,9]G[1,2,5,6,9,10]D[2,5,7]G[1,2,5,6,9,10]H[1,3,6,9,10]I[1,2,5,6,7] H[1,3,6,9,10]J[1,6,9,10]K[2,4,5,7] I[1,2,5,6,7]L[3,8,10]I[1,2,5,6,7] J[1,6,9,10]J[1,6,9,10]D[2,5,7]K[2,4,5,7]M[2,3,5,8]B[1,6]L[3,8,10]F[1,4,6,9] M[2,3,5,8]N[3]F[1,4,6,9] N[3]O[4]O[4]P[2,5]P[2,5]N[3]B[1,6]1L111111010B I KA D E F M00110 00C11G H J101NP O(3)a((a|b) * |ab * a)* b(略 )(4)b((ab) * | bb) * ab(略 )2.已知 NFA=( {x,y,z},{0,1},M,{x},{z} )其中:M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ ,M(z,1)={y},构造相应的 DFA。
编译基础学习知识原理第4章规范标准答案
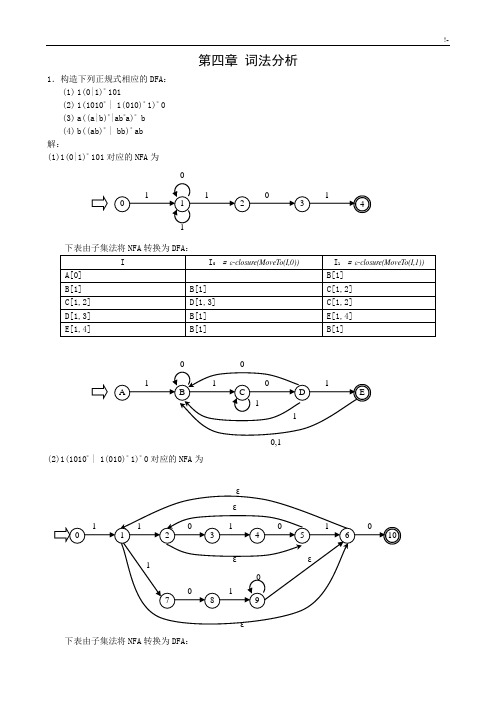
第四章 词法分析1.构造下列正规式相应的DFA :(1) 1(0|1)*101(2) 1(1010* | 1(010)* 1)*(3) a((a|b)*|ab *a)*b(4) b((ab)* | bb)*ab 解:(1)1(0|1)*101对应的NFA 为下表由子集法将NFA 转换为DFA :(2)1(1010* | 1(010)* 1)*0对应的NFA 为下表由子集法将NFA 转换为DFA :(3)a((a|b)*|ab*a)* b (略)(4)b((ab)* | bb)* ab (略)2.已知NFA=({x,y,z},{0,1},M,{x},{z})其中:M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ,M(z,1)={y},构造相应的DFA。
解:根据题意有NFA图如下0,1 下表由子集法将NFA转换为DFA:下面将该DFA最小化:(1)首先将它的状态集分成两个子集:P1={A,D,E},P2={B,C,F}(2)区分P2:由于F(F,1)=F(C,1)=E,F(F,0)=F并且F(C,0)=C,所以F,C等价。
由于F(B,0)=F(C,0)=C,F(B,1)=D,F(C,1)=E,而D,E不等价(见下步),从而B与C,F可以区分。
有P21={C,F},P22={B}。
(3)区分P1:由于A,E输入0到终态,而D输入0不到终态,所以D与A,E可以区分,有P11={A,E},P12={D}。
(4)由于F(A,0)=B,F(E,0)=F,而B,F不等价,所以A,E可以区分。
(5)综上所述,DFA可以区分为P={{A},{B},{D},{E},{C,F}}。
所以最小化的DFA如下:3.将图4.16确定化:图4.16解:下表由子集法将NFA转换为DFA:14.把图4.17的(a)和(b)分别确定化和最小化:(a) (b)解: (a):可得图(a1),由于F(A,b)=F(B,b)=C,并且F(A,a)=F(B,a)=B,所以A,B 等价,可将DFA 最小化,即:删除B ,将原来引向B 的引线引向与其等价的状态A ,有图(a2)。
编译原理第4章习题答案

S-> S’ S’->(S)SS’| First( (S)SS’) = { ( } Follow(S)=Follow(S’)= { (, ),$ }
预测分析表
非终结符 S ( S->S’ ) S->S’ $ S->S’
S’
S’->(S)SS’
S’->
S’->
S’->
冲突
仔细分析后,发现该文法 S->S(S)S| 是二义性文法。 二义性文法不可能是LL(1)文法。 例如:( ) ( )
S->aS’ S’->aS’AS’|Ɛ A->+|*
First(S) = First(aS’)={a} First(S’)= First(aS’AS’) ∪ First(Ɛ)= {a} ∪{Ɛ}= {a, Ɛ} First(A) = { +,*}
Follow(S) ={$} 因为 S->aS’,所以把Follow(S)加入到Follow(S’)中。 因为 S’->aS’AS’的第一个S’ ,所以把First(AS’)={+,*}加入到Follow(S’)中。 因为 S’->aS’AS’的第二个S’ ,所以Follow(S)加入到Follow(S’)中。 所以,Follow(S’)= {$, +,*} 对 S’->aS’AS’的A ,当A后面的S’推导出非空时,把First(S’)-{Ɛ}={a}加入到Follow(A)中。 对 S’->aS’AS’的A ,当A后面的S’推导出空时,把Follow(S’)={$,+,*}加入到Follow(A)中。 所以,Follow(A)= {a, +,*,$} 对于S’->aS’AS’|Ɛ,因为First(aS’AS’) ∩Follow(S’)={a} ∩{$,+,*}=空集,所以没有冲突。 对于A->+|*,因为First(+) ∩First(*)={+} ∩{*}=空集,所以没有冲突。 所以该文法是LL(1)文法。
编译原理第四章参考答案

编译原理第四章参考答案1.1考虑下⾯⽂法G1S->a|^|(T)T->T,S|S消去G1的左递归。
然后对每个⾮终结符,写出不带回溯的递归⼦程序。
答::(1)消除左递归:S->a|^|(T)T-> ST’T’->,S T’|ε(2)first(S)={ a , ^ , ( } first(T)= { a , ^ , ( } first(T’)={ , ε}First(a)={a},First(^)={^},First( (T) )={ ( }S的所有候选的⾸符集不相交First(,ST’)={,} ,First(ε)={ε},T’的所有候选的⾸符集不相交Follow(T’)=Follow(T)={ )}first(T’)∩Follow(T’)={}所以改造后的⽂法为LL(1)⽂法。
不带回溯的递归⼦程序如下:S( ){if (lookahead=’a’) advance;Else if(lookahead=’^’) advance;Else if(lookahead=’(’){advance;T();if(lookahead=’)’) advance;else error();}Else error();}T( ){S( );T’( ):}T’->,S T’|εT’( ){if (lookahead=’,’){advance;T’();}Else if(lookahead=Follow(T’)) advance;Else error;}有⽂法G(S):S→S+aF|aF|+aFF→*aF|*a(1)改写⽂法为等价⽂法G[S’],消除⽂法的左递归和回溯(2)构造G[S’]相应的FIRST和FOLLOW集合;(3)构造G[S’]的预测分析表,以此说明它是否为LL(1)⽂法。
(4)如果是LL(1)⽂法,请给出句⼦a*a+a*a*a的预测分析过程该⽂法为LL(1)⽂法,因为它的预测分析表中⽆冲突项。
编译原理龙书第四章答案

编译原理龙书第四章答案编译原理是计算机科学中的一门基础课程,是用于教授计算机程序的设计、构建和优化的学科,常常被用于编写编译器和解释器。
在编译原理课程中,龙书(Compilers: Principles, Techniques, and Tools)是一本经典的教材,其中第四章主要讲述了词法分析器的设计和实现。
以下是第四章的答案,按照列表划分:1. 什么是词法分析器?词法分析器(Lexical Analyzer)是编译器的组成部分之一,它用于将程序中的字符序列转换为一系列单词或词法单元(Lexeme),以便后续的语法分析和语义分析使用。
2. 词法分析器的工作流程是什么?词法分析器的工作流程如下:(1)读入字符序列。
(2)将字符序列划分为一个个词法单元,或者检查字符序列是否合法。
(3)生成一个词法单元序列,并将其传递给语法分析器。
3. 词法单元的定义是什么?词法单元是编程语言中的一个基本单元,它是对代码中的一个单一概念进行编码的基本方式。
例如,在C语言中,词法单元包括关键字(如int,if,while等)、标识符(Identifier,即自定义变量名)、运算符和特殊符号等。
4. 有哪些方法可以实现词法分析器?可以使用正则表达式、自动机等方法实现词法分析器。
其中,正则表达式可以表示字符串的集合,因此可以将其用于识别单词类别;自动机是根据输入字符序列转换状态的一种计算模型,因此可以用于实现有限自动机(Deterministic Finite Automaton)和非确定有限自动机(Nondeterministic Finite Automaton)等。
5. DFA和NFA分别是什么?DFA和NFA都是有限自动机的一种,但在转换动作上有所不同。
DFA 是确定的有限自动机,即在状态转换时只有唯一的一个选择;而NFA 是非确定的有限自动机,即在状态转换时可以有多个选择。
6. DFA和NFA之间有什么关系?DFA和NFA虽然在转换动作上不同,但它们可以互相转化。
编译原理第4章答案

第四章 词法分析1.构造下列正规式相应的DFA :(1) 1(0|1)*101(2) 1(1010*| 1(010)*1)*0 (3) a((a|b)*|ab *a)*b (4) b((ab)*| bb)*ab 解:(1)1(0|1)*101对应的NFA 为下表由子集法将NFA 转换为DFA :(2)1(1010*| 1(010)*1)*0对应的NFA 为 10,1下表由子集法将NFA转换为DFA:(3)a((a|b)*|ab *a)*b (略) (4)b((ab)*| bb)*ab (略)2.已知NFA=({x,y,z},{0,1},M,{x},{z})其中:M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ,M(z,1)={y},构造相应的DFA 。
解:根据题意有NFA 图如下下表由子集法将NFA 转换为DFA :0,1下面将该DFA最小化:(1)首先将它的状态集分成两个子集:P1={A,D,E},P2={B,C,F}(2)区分P2:由于F(F,1)=F(C,1)=E,F(F,0)=F并且F(C,0)=C,所以F,C等价。
由于F(B,0)=F(C,0)=C,F(B,1)=D,F(C,1)=E,而D,E不等价(见下步),从而B与C,F可以区分。
有P21={C,F},P22={B}。
(3)区分P1:由于A,E输入0到终态,而D输入0不到终态,所以D与A,E可以区分,有P11={A,E},P12={D}。
(4)由于F(A,0)=B,F(E,0)=F,而B,F不等价,所以A,E可以区分。
(5)综上所述,DFA可以区分为P={{A},{B},{D},{E},{C,F}}。
所以最小化的DFA如下:3.将图确定化:1101111解:下表由子集法将NFA 转换为DFA :4.把图的(a)和(b)分别确定化和最小化:(a) (b)解: (a):下表由子集法将NFA 转换为DFA :0,1a可得图(a1),由于F(A,b)=F(B,b)=C,并且F(A,a)=F(B,a)=B,所以A,B 等价,可将DFA 最小化,即:删除B ,将原来引向B 的引线引向与其等价的状态A ,有图(a2)。
编译原理第四章作业答案

非终结符
FIRSTVT
LASTVT
E
+ * ↑( i
+ * ↑) i
T
* ↑( i
* ↑) i
F
↑( i
↑)i
P
(i
)i
2).关系 1.由#E#,知 # = # ;由(E)知 ( = ) 2.求 < 关系 考察对象:文法中终结符号在前,非终结符号在后的相邻符号对 由#E # < FIRSTVT(E) 由+T + < FIRSTVT(T) 由*F * < FIRSTVT(F) 由↑F ↑< FIRSTVT(F) 由(E ( < FIRSTVT(E)
T→F
F→-P
F→P
P→(E)
P→i
(1) 构造 G 的算符优先矩阵;
(2) 指出 G 不是算符优先文法,即指出具有多重定义的优先矩阵元素;
(3)将 G 改写为算符优先文法。
解:
(1)求每个非终结符号的 FIRSTVT 集和 LASTVT 集
S→E
E→E-T|T
T→T*F|F
F→-P|P
P→(E)|i
Z 11 Z 12 Z 13
(S
A
B ) = (φ (S ) + () [S ] + [])Z 21
Z 22
Z
23
Z 31 Z 32 Z 33
Z 11 Z 12 Z 13 ε φ φ A B φ Z 11 Z 12 Z 13
Z 21
Z 22
Z
23
=
φ
ε
φ
+
ε
φ
φ
Z
21
Z 22
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章
习题:考虑上下文无关文法: S->S S +|S S *|a 以及串aa + a*
(1)给出这个串的一个最左推导
S -> S S *
-> S S + S *
-> a S + S *
-> a a + S *
-> aa + a*
(3)给出这个串的一棵语法分析树
习题:下面是一个只包含符号a和b的正则表达式的文法。
它使用+替代表示并运算的符号|,以避免和文法中作为元符号使用的竖线相混淆:
rexpr rexpr + rterm | rterm
rterm rterm rfactor | rfactor
rfactor rfactor * | rprimary
rprimary a | b
1)对这个文法提取公因子
2)提取公因子的变换使这个文法适用于自顶向下的语法分析技术吗?
3)提取公因子之后,原文法中消除左递归
4)得到的文法适用于自顶向下的语法分析吗?
解
1)提取左公因子之后的文法变为
rexpr rexpr + rterm | rterm
rterm rterm rfactor | rfactor
rfactor rfactor * | rprimary
rprimary a | b
2)不可以,文法中存在左递归,而自顶向下技术不适合左递归文法
3)消除左递归后的文法
rexpr -> rterm rexpr’
rexpr’-> + rterm rexpr’|ε
rterm-> rfactor rterm’
rterm’-> rfactor rterm’|ε
rfactor-> rprimay rfactor’
rfactor’-> *rfactor’|ε
rprimary-> a | b
4)该文法无左递归,适合于自顶向下的语法分析
习题:为下面的每一个文法设计一个预测分析器,并给出预测分析表。
可能要先对文法进行提取左公因子或消除左递归
(3)S->S(S)S|ε
(5)S->(L)|a L->L,S|S
解
(3)
①消除该文法的左递归后得到文法
S->S’
S’->(S)SS’|ε
②计算FIRST和FOLLOW集合
FIRST(S)={(,ε} FOLLOW(S)={),$}
FIRST(S’)={(,ε} FOLLOW(S’)={),$}
③
(5)
①消除该文法的左递归得到文法
S->(L)|a
L->SL’
L’->,SL’|ε
用类Pascal语言的一个预测分析器:
PROCEDURE S
BEGIN
if (lookahead==’(')
THEN BEGIN
match ('(');
L;
match (')');
END;
ELSE IF (lookahead=='a')
THEN match('a')
ELSE error
END;
PROCEDURE L;
BEGIN
S;
WHILE (lookahead ==',');
BEGIN
match (',');
S;
END;
END;
②计算FIRST与FOLLOW集合
FIRST(S)={(,a} FOLLOW(S)={ ),, ,$}
FIRST(L)={(,a} FOLLOW(L)={ ) }
FIRST(L’)={,,ε} FOLLOW(L’)={ ) }
③构建预测分析表
非终结符号输入符号
(),a$ S S->(L)S->a
L L->SL’L->SL’
L’L’->εL’->,SL’
习题计算练习的文法的FIRST和FOLLOW集合
3)S S(S)S|ε
5)S(L)|a,L L,S|S
解:
3)FIRST(S)={ ε,( } FOLLOW(S)={ (,),$ }
5)FIRST(S)={ (,a } FOLLOW(S)={ ),,,$ }
FIRST(L)={ (,a } FOLLOW(L)={ ),, }
习题 为练习中的增广文法构造SLR 项集,计算这些项集的GOTO 函数,给出这个文法的语法分析表。
这个文法是SLR 文法吗? S SS+|SS*|a 解:
①构造该文法的增广文法如下
S ’->S S->SS+ S->SS* S->a
②构造该文法的LR(0)项集如下
③GOTO 函数如下
GOTO(I0,S)=I1 GOTO(I0,a)=I2
GOTO(I1,S)=I3 GOTO(I1,a)=I2 GOTO(I1,$)=acc
GOTO(I3,S)=I3 GOTO(I3,+)=I4 GOTO(I3,*)=I5 GOTO(I3,a)=I2 ④构造该文法的语法分析表
状态
ACTION
GOTO +
* a $ S 0 S2 1 1 S2 acc 3 2 R3 R3 R3 R3 3 S4 S5 S2 3 4 R1 R1 R1 R1 5
R2
R2
R2
R2
注:FOLLOW(S ’)=FOLLOW(S)={+,*,a,$}
这个文法是SLR 文法,因为语法分析表中没有重复的条目
习题说明下面文法 S SA|A A a
是SLR(1)的,而不是LL(1)的。
证明:
1) 可以求得FIRST(SA)=FIRST(A)={a},故该文法不是LL(1)文法 2) 构造该文法的增广文法的语法分析表如下
I0 S ’->.S S->.SS+ S->.SS* S->.a I1 S ’->S. S->+ S->* S->.SS+ S->.SS* S->.a I2 S->a. I3 S->SS.+ S->SS.* S->+ S->* S->.SS+
S->.SS*
S->.a
I4 S->SS+. I5 S->SS*.
①构造增广文法
S’->S
S->SA
S->A
A->a
②构造LR(0)项集族
③GOTO函数如下
GOTO(I0,S)=I1 GOTO(I0,A)=I2 GOTO(I0,a)=I3
GOTO(I1,A)=I4 GOTO(I1,a)=I3 GOTO(I1,$)=acc
④构建语法分析表如下(FOLLOW(A)=FOLLOW(S)={a,$})
可以看到该语法分析表中没有重复的条目故该文法是SLR(1)文法
习题说明下面的文法
S->Aa|bAc|dc|bda
A->d
是LALR(1)的,但不是SLR(1)的
证明:
1、构造该文法的SLR(1)语法分析表
①构造增广文法
S’->S
S->Aa
S->bAc
S->dc
S->bda
A->d
②构造LR(0)项集族
③GOTO函数
GOTO(I0,S)=I1 GOTO(I0,A)=I2 GOTO(I0,b)=I3 GOTO(I0,d)=I4 GOTO(I1,$)=acc GOTO(I2,a)=I5 GOTO(I3,A)=I6 GOTO(I3,d)=I7 GOTO(I4,c)=I8 GOTO(I6,c)=I9 GOTO(I7,a)=I10
④构建SLR语法分析表如下(FOLLOW(A)={a,c})
可以看到在图中存在二义性的条目,故该文法不是SLR(1)文法
2、构造该文法的LALR(1)语法分析表
①构造该增广文法的LR(1)项集族如下
③GOTO函数
GOTO(I0,S)=I1 GOTO(I0,A)=I2 GOTO(I0,b)=I3 GOTO(I0,d)=I4 GOTO(I1,$)=acc GOTO(I2,a)=I5 GOTO(I3,A)=I6 GOTO(I3,d)=I7
GOTO(I4,c)=I8 GOTO(I6,c)=I9 GOTO(I7,a)=I10
可见该分析表中不存在二义性的条目,故该文法是LALR(1)文法
习题说明下面的文法
S->Aa|bAc|Bc|bBa
A->d
B->d
是LR(1)的,但不是LALR(1)的
证明:
1、构造该文法的LR(1)语法分析表
①构造该文法的增广文法
S’->S
S->Aa
S->bAc
S->Bc
S->bBa
A->d
B->d
②构造该增广文法的LR(1)项集族如下
②项集合并:没有可以合并的项集
③GOTO 函数
GOTO(I0,S)=I1 GOTO(I0,A)=I2 GOTO(I0,b)=I3 GOTO(I0,B)=I4 GOTO(I0,d)=I5 GOTO(I1,$)=acc GOTO(I2,a)=I6 GOTO(I3,A)=I7 GOTO(I3,B)=I8 GOTO(I3,d)=I9 GOTO(I4,c)=I10 GOTO(I7,c)=I11 GOTO(I8,a)=I12
2、 构造该文法的LALR(1)语法分析表 ①合并LR(1)项集族 I5和I9可以合并为I59。
