【初中数学】浙江省温州市实验中学2015年初中毕业生学业考试数学一模试卷 浙教版
浙江省温州市初中数学毕业生学业考试第一次模拟考试试卷
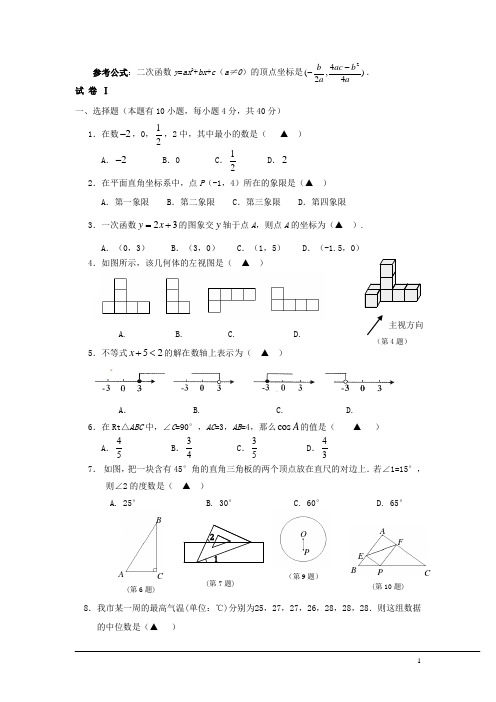
参考公式:二次函数y =ax 2+bx +c (a ≠0)的顶点坐标是)44,2(2ab ac a b --.试 卷 Ⅰ一、选择题(本题有10小题,每小题4分,共40分) 1.在数2-,0,12,2中,其中最小的数是( ▲ ) A .2-B .0C .12D .22.在平面直角坐标系中,点P (-1,4)所在的象限是(▲ ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 3.一次函数23y x =+的图象交y 轴于点A ,则点A 的坐标为(▲ ). A .(0,3) B .(3,0) C .(1,5) D .(-1.5,0) 4.如图所示,该几何体的左视图是( ▲ )A. B. C. D. 5.不等式52x +<的解在数轴上表示为( ▲ )A . B. C. D.6.在Rt △ABC 中,∠C =90°,AC =3,AB =4,那么cos A 的值是( ▲ ) A .54 B .43 C .53 D .34 7. 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.若∠1=15°,则∠2的度数是( ▲ )A. 25°B. 30°C. 60°D. 65°8.我市某一周的最高气温(单位:℃)分别为25,27,27,26,28,28,28.则这组数据的中位数是(▲ )(第4题)主视方向21(第7题)O P(第9题)(第6题)ABC (第10题)E PABCFA .28B .27C .26D .259.如图,⊙O 的半径为5,若OP =3,,则经过点P 的弦长可能是 ( ▲ )A .3B .6C .9D .12 10.如图,在△ABC 中,AB =3,AC =4,BC =5,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC于F ,则EF 的最小值为( ▲ )A . 2B .2.2C .2.4D .2.5卷Ⅱ二、填空题(本题有6小题,每小题5分,共30分)11.计算:23()a = ▲ .12.如图,AB ∥CD ,∠A =∠B =90°,AB =3,BC =2,则AB 与CD 之间的距离为 ▲ . 13.如图,在正方形ABCD 的外侧,作等边△ADE ,则∠AEB= ▲ . 14.在“感恩一日捐”捐赠活动中,某班40位同学捐款金额统计如下,则在这次活动中,该班同学捐款金额的平均数是 ▲ 元.金额(元)2030 36 50 100 学生数(人) 375151015.某商品按标价八折出售仍能盈利b 元,若此商品的进价为a 元,则该商品的标价为▲ 元.(用含,a b 的代数式表示) 16.如图,5AB =,线段AB 的两端点在函数10(0)y x x=>的图象上,AC ⊥轴于点C ,BD ⊥y 轴于点D ,线段AC ,BD 相交于点E .当DO =2CO 时,图中阴影部分的面积等于 ▲ .三、解答题(本题有8小题,共80分)17.(本题10分)(1)计算:2(5)(2)418-+-⨯- (2)解方程组: 21,3211x y x y +=⎧⎨-=⋅⎩.18.(本题8分)如图,已知E ,F 是四边形ABCD 对角线AC 上的两点,AE =CF ,BE =FD ,BE ∥FD .求证:四边形ABCD 是平行四边形.DCAB(第12题)(第16题)yxAD CBOEEADBAE(第13题)19.(本题8分)不透明的布袋里装有红、蓝、黄三种颜色小球共40个,它们除颜色外其余都相同,其中红色球20个,蓝色球比黄色球多8个. (1)求袋中蓝色球的个数.(2)求摸出1个球是黄色球的概率.(3)现再将2个黄色球放入布袋,搅匀后,求摸出1个球是黄色球的概率. 20.(本题8分)如图,某河堤的横断面是梯形ABCD ,BC ∥AD ,BE ⊥AD 于点E ,AB =50米,BC =30米,∠A =60°,∠D =30°.求AD 的长度.21.(本题10分)如图,AB 是⊙O 的直径,BC 是⊙O 的切线, D 是⊙O 上一点,且AD ∥OC . (1)求证:△ADB ∽△OBC .(2)若AB =6,BC =4.求AD 的长度 .(结果保留根号)22.(本题10分)如图,正比例函数(0)y kx k =≠经过点A (2,4), AB ⊥x 轴于点B . (1)求该正比例函数的解析式.(2)将△ABO 绕点A 逆时针旋转90︒得到△ADC ,写出点C 的坐标,试判断点C 是否在直线113y x =+的图象上,并说明理由.23.(本小题12分)今年小芳家添置了新电器.已知今年5月份的用电量是240千瓦时. (1)若今年6月份用电量增长率是7月份用电量增长率的1.5倍,设今年7月份用电量增长率为x ,(第20题)D OBACyx(第22题)(第21题)补全下列表格内容(用含x 代数式表示) 月份6月份7月份月增长率x用电量(单位:千瓦时)(2)在(1)的条件下,预计今年7月份的用电量将达到480千瓦时,求今年7月份用电量增长率x 的值.(精确到1%)(3)若今年6月份用电量增长率是7月份用电量增长率的n 倍,6月份用电量为360千瓦时,预计今年7月份的用电量将不低于500千瓦时.则n 的最大值为 .(直接写出答案)24.(本题14分) 如图,经过原点的抛物线22y x mx =-与x 轴的另一个交点为A .过点1(1,)2P m +作直线PH y ⊥轴于点H ,直线AP 交y 轴于点C .(点C 不与点H 重合)(1)当2m =时,求点A 的坐标及CO 的长.(2)当1m >时,问m 为何值时32CO =?(3)是否存在m ,使 2.5CO HC =?若存在,求出所有满足要求的m 的值,并定出相对应的点C 坐标;若不存在,请说明理由.数学答卷纸一、选择题(本题有10小题,每小题4分,共40分)HOPACxy(第24题)二、填空题(本题有6小题,每小题5分,共30分)三、解答题(本题有8小题,共80分)18.(本题8分)证明:19. (本题8分) (1)EFABCD(第18题)20.(本题8分)(第20题)21. (本题10分)(1)(2)(第21题)22.(本题10分)(1)y24.(本题14分) (1)23.(本题12分) (1) 月份6月份7月份增长率x用电量 (单位:千瓦时)(2)(3)n 的最大值为 .(直接写出答案) (2)PCy(2)(3)参考答案及评分标准一、选择题(本题共10小题,每小题4分,共40分) 1.A 2.B3.A4.B5.D6.B 7.C 8.B 9.C 10.C二、填空题(本题有6小题,每小题5分,共30分) 11.6a 12.2 13.15° 14.55 15.54+ab ()16.174三、解答题(本题有8小题,共80分) 17.(本题10分)(1)原式=258--(3分) 21(1)(2)3211(2)x y x y +=⎧⎨-=⎩=17-(2分) 解:(1)+(2)得412,3x x =∴= (2分) 把3x =代如(1)得321,1y y +=∴=-(2分)3,1x y =⎧∴⎨=-⋅⎩ (1分) 18.(本题8分)证明:∵BE ∥FD∴∠BEF =∠DFE∴∠BEA =∠DFC (2分) ∵AE =CF ,BE =FD∴△ABE ≌△CDF (SAS) (2分) ∴∠BAE =∠DCF , AB =CD (2分) ∴AB ∥CD∴四边形ABCD 是平行四边形. (2分)19.(本题8分)(1)14 (3分)(2)320(3分) EFABCD(第18题)(3)421(2分)20.(本题8分)解:画CF ⊥AD 于点F . ∵BE ⊥AD∴3sin 502532BE AB A ==⨯= (2分) ∴222250(253)25AE AB BE =-=-=∵BC ∥AD ,CF ⊥AD∴CF=BE 253=, (2分)25375tan 33CF FD D ===, EF =BC=30 (2分)∴253075130AD AE EF FD =++=++=米 (2分) 21.(本题10分)证明:(1)∵AB 是⊙O 的直径,BC 是⊙O 的切线, ∴∠D =∠OBC =90° (2分) ∵AD ∥OC∴∠A =∠COB (2分) ∴△ADB ∽△OBC (1分) (2)∵AB =6, ∴OB =3, ∵BC =4,2222345OC OB BC ∴=+=+= (2分)∵△ADB ∽△OBC∴6,,35AD AB AD OB OC =∴= (2分) 185AD ∴= (1分)22.(本题10分)解:(1)∵正比例函数(0)y kx k =≠经过点A (2,4)∴42k = (2分)2k ∴=(第21题)(第20题)FD OBACyx(第22题)2y x ∴= (2分)(2) ∵A (2,4),AB ⊥x 轴于点B∴2,4OB AB ==∵△ABO 绕点A 逆时针旋转90︒得到△ADC∴2,4DC OB AD AB ==== (2分) ∴C (6,2) (2分)∵当6x =时,161323y =⨯+=≠ ∴点C 不在直线113y x =+的图象上 (2分)23.(本题12分)(1) (每空格2分)月份6月份7月份增长率 1.5x用电量(单位:千瓦时) 240(1 1.5)x +240(1)(1 1.5)x x ++(2)480240(1)(1 1.5)x x =++, (2分) 解得13x =或2x =-(不合题意舍去), 133%3x ∴=≈ (2分) (3)9724.(本题14分)解:(1)当2m =时,24y x x =-,令0y =,解得120,4,(4,0)x x A ==∴ (2分)∵HP ∥OA ,∴△CHP ∽△COA ,∴HP CHOA CO =∵113,4,2HP m OA OH =+===⋅ ∴340.5CHCH =+∴ 1.5,2HC CO HC HO =∴=+= (2分)(2),HP CH OA CO =31,2,,12HP m OA m CO CH =+===⋅HOPACxy(图1)11,32 1.5m m m +∴=∴= (3分) (3)①当1m >时(如图1), ,HP CH OA CO =1,2,HP m OA m =+= 2.5CO HC =11,2 2.5m m +∴= 5m ∴=-(舍去) (2分) ②当01m <<时(如图2),∵,CO HC <,又∵ 2.5CO HC =,∴0,CH <∵0,CH >∴不存在m 的值使 2.5CO HC =. (1分) ③当10m -<<时(如图3), ,HP CHOA CO=1,2,HP m OA m =+=- 2.5CO HC = 115,2 2.59m m m +∴=∴=--1152.5,,,2714CO HC CO HC HC CO =+=∴== 5(0,)14C ∴ (2分) ④当1m <-时(如图4), ,HP CHOA CO =1,2,HP m OA m =--=- 2.5CO HC = 11,52 2.5m m m --∴=∴=-- 1152.5,,,236CO HC CO HC HC CO =-=∴== 5(0,)6C ∴ (2分)综上所述当59m =-时,点5(0,)14C ;当5m =-时,点5(0,)6C ∴.PACHOPA Cxy(图3)HOP ACxy(图4)。
浙江省温州市2015中考数学试题(WORD版,附答案)

浙江省2015年初中毕业升学考试(温州卷)数 学 试 题 卷一、选择题(本题有10小题,每小题4分,共40分)1. 给出四个数0,3,21,-1,其中最小的是 A. 0 B. 3 C. 21 D. -1 2. 将一个长方体内部挖去一个圆柱(如图所示),它的主视图是3. 某校学生参加体育兴趣小组情况的统计图如图所示。
若参加人数最少的小组有25人,则参加人数最多的小组有A. 25人B. 35人C. 40人D. 100人4. 下列选项中的图形,不属于...中心对称图形的是 A. 等边三角形 B. 正方形 C. 正六边形 D. 圆5. 如图,在△ABC 中,∠C=90°,AB=5,BC=3,则cosA 的值是A. 43B. 34C. 53D. 54 6. 若关于x 的一元二次方程0442=+-c x x 有两个相等实数根,则c 的值是A. -1B. 1C. -4D. 47. 不等式组⎩⎨⎧≤->+2121x x 的解是 A. 1<x B. x ≥3 C. 1≤x <3 D. 1<x ≤38. 如图,点A 的坐标是(2,0),△ABO 是等边三角形,点B 在第一象限。
若反比例函数xk y =的图象经过点B ,则k 的值是 A. 1 B. 2C.3 D. 329. 如图,在Rt ∠AOB 的平分线ON 上依次取点C ,F ,M ,过点C作DE ⊥OC ,分别交OA ,OB 于点D ,E ,以FM 为对角线作菱形FGMH ,已知∠DFE=∠GFH=120°,FG=FE 。
设OC=x ,图中阴影部分面积为y ,则y 与x 之间的函数关系式是A. 223x y = B. 23x y = C. 232x y = D. 233x y =10. 如图,C 是以AB 为直径的半圆O 上一点,连结AC ,BC ,分别以AC ,BC 为边向外作正方形ACDE ,BCFG ,DE ,FG ,,的中点分别是M ,N ,P ,Q 。
2015年浙江省温州市中考数学试卷-答案

8.【答案】C
【解析】如答图,过点B作 于点D,
∵点A的坐标是(2,0),△ABO是等边三角形,
∴ .∴由勾股定理得,
∵点B在第一象限,∴点B的坐标是 .
∵反比例函数 的图象经过点B,∴ ,故选C.
【考点】反比例函数综合题,曲线上点的坐标与方程的关系,等边三角形的性质,勾股定理
9.【答案】B
【解析】∵ON是 的平分线, ,∴△ODE是等腰直角三角形.
∵ ,∴ .
∵ ,∵ .
∴ ,∴
又∵菱形FGMH中, ,∴ ∴ ,故选B.
【考点】由实际问题列函数关系式,角平分线的性质,等腰直角三角形的判定和性质,含30度角直角三角形的性质,菱的性质
10.【答案】C
【解析】如答图,连接OP、OQ,
浙江省温州市2015年初中毕业升学考试
数学答案解析
第Ⅰ卷
一、选择题
1.【答案】D
【解析】根据实数的大小比较法则,正数大于0,0大于负数,两个负数相比,绝对值大的反而小,因此, ,故选D.
【考点】实数的大小比较
2.【答案】A
【解析】根据从正面看得到的图形是主视图,可得,主视图是长方形的中间有个看不到小长方形,故选A.
19.【答案】(1)∵ .
∴ .
∴从高到低确定三名应聘者的排名顺序为甲、丙、乙.
(2)由题意可知,甲的面试考核低于80分,不符合公司规定;
;
∴根据规定,乙将被录用.
【解析】(1)根据算术平均数的公式计算即可.
(2)根据规定先剔除笔试、面试、体能分分别低于80分、80分、70分的人,再根据加权平均数的计算结果确定录用者.
【考点】中心对称图形
5.【答案】D
2015年浙江省温州实验中学中考一模数学试卷和答案PDF

2. (4 分)如图,桌面上有一个一次性纸杯,它的主视图应是(
A.
B.
C. 3. (4 分)要使分式 A足( B.x≠1 C.x=﹣2 ) D.x=1 ) D. (0,4)
4. (4 分)一次函数 y=2x+4 的图象与 x 轴的交点坐标是( A. (﹣2,0) B. (0,﹣2) C. (4,0)
22. (10 分)如图,在⊙O 中,∠AOB=150°,∠ABC=45°,延长 OB 到 D, 使 BD=OB,连接 CD. (1)求证:CD 与⊙O 相切; (2)若 CD=6,求弓形 BC(劣弧所对)的面积. (结果保留 π 和根号)
23. (12 分)今年 3 月 12 日植树节前夕,我校购进 A,B 两个品种的树苗,已知 A 种比 B 种树苗多 20 元,买一株 A 种树苗和 2 株 B 种树苗共需 110 元. (1)问 A,B 两种树苗每株分别是多少元? (2)4 月,为美化校园,学校花费 4000 元再次购入 A,B 两种树苗,已知 A 种
A.
B.
+1
C.
D.2
二、填空题(本题有 6 小题,每小题 5 分,共 30 分)
第 2 页(共 23 页)
11. (5 分)分解因式:a2﹣3a= 12. (5 分)方程 x2﹣4=0 的解是
. . .
13. (5 分) 如图, 已知 AB∥CD∥EF, 若 AC: CE=2: 3, BD=6, 那么 BF=
19. (8 分)如图,已知 A(﹣2,﹣2) 、B(n,4)是一次函数 y=kx+b 的图象 和反比例函数 y= 的图象的两个交点. (1)求反比例函数和一次函数的解析式; (2)求△AOB 的面积.
20. (10 分)如图,在正方形 ABCD 中,点 G 是 CD 上任意一点,连接 BG,作 AE⊥BG 于点 E,CF⊥BG 于点 F. (1)求证:BE=CF; (2)若 BC=2,CF= ,求 EF 的长.
2015年浙江省温州高级中等学校招生考试数学试卷

2015年浙江省初中毕业生学业考试(温州市卷)数学试题(含答案全解全析)第Ⅰ卷(选择题,共40分)一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)1.给出四个数0,,,-1,其中最小的是()A.0B.C.D.-12.将一个长方体内部挖去一个圆柱(如图所示),它的主视图是()3.某校学生参加体育兴趣小组情况的统计图如图所示.若参加人数最少的小组有25人,则参加人数最多的小组有()A.25人B.35人C.40人D.100人4.下列选项中的图形,不属于...中心对称图形的是()A.等边三角形B.正方形C.正六边形D.圆5.如图,在△ABC中,∠C=90°,AB=5,BC=3,则cos A的值是()A. B. C. D.6.若关于x的一元二次方程4x2-4x+c=0有两个相等实数根,则c的值是()A.-1B.1C.-4D.4的解是()7.不等式组-A.x<1B.x≥3C.1≤x<3D.1<x≤38.如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限.若反比例函数y=的图象经过点B,则k的值是()A.1B.2C.D.29.如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE.设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是()A.y=x2B.y=x2C.y=2x2D.y=3x210.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG.DE,FG,,的中点分别是M,N,P,Q.若MP+NQ=14,AC+BC=18,则AB的长为()A.9B.C.13D.16第Ⅱ卷(非选择题,共110分)二、填空题(本题有6小题,每小题5分,共30分)11.分解因式:a2-2a+1=.12.一个不透明的袋中只装有1个红球和2个蓝球,它们除颜色外其余均相同.现随机从袋中摸出两个球,颜色是一红一蓝的概率是.13.已知扇形的圆心角为120°,弧长为2π,则它的半径为.14.方程=的根是.15.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室总占地面积最大为m2.16.图甲是小明设计的带菱形图案的花边作品.该作品由形如图乙的矩形图案拼接而成(不重叠、无缝隙).图乙中,=,EF=4cm,上下两个阴影三角形的面积之和为54cm2,其内部菱形由两组距离相等的平行线交叉得到,则该菱形的周长为cm.三、解答题(本题有8小题,共80分.解答需写出必要的文字说明、演算步骤或证明过程)17.(本题10分)(1)计算:20150++2×-;(2)化简:(2a+1)(2a-1)-4a(a-1).18.(本题8分)如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.(1)求证:AB=CD;(2)若AB=CF,∠B=30°,求∠D的度数.19.(本题8分)某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序;(2)该公司规定:笔试、面试、体能得分分别不得低于80分、80分、70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用.20.(本题8分)各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何计算它的面积?奥地利数学家皮克(G.Pick,1859~1942年)证明了格点多边形的面积公式:S=a+b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图1,a=4,b=6,S=4+×6-1=6.(1)请在图2中画一个格点正方形,使它的内部只含有4个格点,并写出它的面积;(2)请在图3中画一个格点三角形,使它的面积为,且每条边上除顶点外无其他格点......图1图2图321.(本题10分)如图,AB是半圆O的直径,CD⊥AB于点C,交半圆于点E,DF切半圆于点F.已知∠AEF=135°.(1)求证:DF∥AB;(2)若OC=CE,BF=2,求DE的长.22.(本题10分)某农业观光园计划将一块面积为900m2的园圃分成A,B,C三个区域,分别种植甲、乙、丙三种花卉,且每平方米栽种甲3株或乙6株或丙12株.已知B区域面积是A的2倍,设A区域面积为x(m2).(1)求该园圃栽种的花卉总株数y关于x的函数表达式;(2)若三种花卉共栽种6600株,则A,B,C三个区域的面积分别是多少?(3)已知三种花卉的单价(都是整数)之和为45元,且差价均不超过10元.在(2)的前提下,全部栽种共需84000元.请写出甲、乙、丙三种花卉中,种植面积最大的花卉总价.23.(本题12分)如图,抛物线y=-x2+6x交x轴正半轴于点A,顶点为M,对称轴MB交x轴于点B,过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.(1)求点A,M的坐标;(2)当BD为何值时,点F恰好落在该抛物线上?(3)当BD=1时,①求直线MF的解析式,并判断点A是否落在该直线上;②延长OE交FM于点G,取CF中点P,连结PG,△FPG,四边形DEGP,四边形OCDE的面积分别记为S1,S2,S3,则S1∶S2∶S3=.24.(本题14分)如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ∶AB=3∶4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C 作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.(1)用关于x的代数式表示BQ,DF;(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长;(3)在点P的整个运动过程中,①当AP为何值时,矩形DEGF是正方形?②作直线BG交☉O于另一点N,若BN的弦心距为1,求AP的长(直接写出答案).答案全解全析:一、选择题1.D根据正数大于0,0大于负数,知-1<0<<.故选D.2.A根据从主视方向看得到的图形是主视图,可得主视图是长方形,且该长方形中有两条虚线.故选A.3.C由题意知参加人数最少的小组有25人,占25%,∴参加体育兴趣小组的总人数为25÷25%=100(人).∴参加人数最多的小组有100×(1-25%-35%)=100×40%=40(人).故选C.4.A根据中心对称图形的概念进行判断.5.D在△ABC中,∠C=90°,AB=5,BC=3,根据勾股定理,得AC=4.∴cos A==.故选D.6.B∵关于x的一元二次方程4x2-4x+c=0有两个相等实数根,∴Δ=(-4)2-4·4·c=0⇒c=1.故选B.⇒⇒1<x≤3.故选D.7.D由-8.C如图,过点B作BD⊥x轴于点D.∵点A的坐标是(2,0),△ABO是等边三角形,∴OB=OA=2,OD=1.由勾股定理得BD=.∵点B在第一象限,∴点B的坐标是(1,).∵反比例函数y=的图象经过点B,∴=⇒k=.故选C.9.B∵ON是Rt∠AOB的平分线,DE⊥OC,∴△ODE是等腰直角三角形.∵OC=x,∴DE=2x.∵∠DFE=120°,∴∠EDF=30°.∴CF=x.∴S△DEF=·2x·x=x2.在菱形FGMH中,∠GFH=120°,又FG=FE,∴S菱形FGMH=2S△DEF.∴y=3S△DEF=x2.故选B.10.C如图,连结OP、OQ,∵DE,FG,,的中点分别是M,N,P,Q,∴O,P,M三点共线,O,Q,N三点共线.∵四边形ACDE,四边形BCFG是正方形,∴AE=CD=AC,BG=CF=BC.设AB=2r,则OM=MP+r,ON=NQ+r.∵点O,M分别是AB,ED的中点,∴OM是梯形ABDE的中位线.∴OM=(AE+BD)=(AE+CD+BC)=(2AC+BC),即MP+r=(2AC+BC).同理,得NQ+r=(2BC+AC).两式相加,得MP+NQ+2r=(AC+BC).∵MP+NQ=14,AC+BC=18,∴14+2r=×18⇒2r=13,即AB=13.故选C.二、填空题11.答案(a-1)2解析a2-2a+1=a2-2·a·1+12=(a-1)2.12.答案解析共有3种等可能的结果:(红球,蓝球1),(红球,蓝球2),(蓝球1,蓝球2),颜色是一红一蓝的情况有两种:(红球,蓝球1),(红球,蓝球2),∴随机从袋中摸出两个球,颜色是一红一蓝的概率是.13.答案3解析由弧长公式得=2π,解得r=3.14.答案x=2解析=⇒3x=2x+2⇒x=2.经检验,x=2是原方程的根.∴方程=的根是x=2.15.答案75解析设垂直于现有墙的一面墙长为x m,建成的饲养室总占地面积为y m2,则利用现有墙的长为(27+3-3x)m,∴y=x(30-3x)=-3x2+30x=-3(x-5)2+75.∵-3<0,∴当x=5时,y max=75,即能建成的饲养室总占地面积最大为75m2.16.答案解析如图,连结MN、PQ,设MN=2x cm,PQ=2y cm,∵=,∴可设AB=6k cm(k>0),则BC=7k cm.∵上下两个阴影三角形的面积之和为54cm2,∴2··3k+54=6k·7k,即(2x+7k)·3k+54=42k2.①易知四边形DENM、四边形AFMN是平行四边形,∴DE=AF=MN=2x cm.∵EF=4cm,∴4x+4=7k,即2x=-.②将②代入①得,-·3k+54=42k2,化简得7k2+4k-36=0.解得k1=2,k2=-(舍去).∴AB=12cm,BC=14cm,MN=5cm,∴x=.易证△MCD∽△MPQ,∴=-,解得y=.∴PM===(cm).∴菱形MPNQ的周长为4×=(cm).评析本题主要考查平行四边形,菱形的性质以及相似三角形的性质.三、解答题17.解析(1)原式=1+2-1=2.(2)原式=4a2-1-4a2+4a=4a-1.18.解析(1)证明:∵AB∥CD,∴∠B=∠C.∵AE=DF,∠A=∠D,∴△ABE≌△DCF,∴AB=CD.(2)∵AB=CF,AB=CD,∴CD=CF,∴∠D=∠CFD.∵∠B=∠C=30°,∴∠D=75°.19.解析(1)甲==84,乙==80,丙==81,∴甲>丙>乙,∴排名顺序为甲、丙、乙.(2)由题意可知,只有甲不符合规定.∵乙'=85×60%+80×30%+75×10%=82.5,丙'=80×60%+90×30%+73×10%=82.3,∴录用乙.20.解析(1)画法不唯一,如图①或图②.(2)画法不唯一,如图③,图④等.21.解析(1)证明:连结OF,∵DF切半圆O于点F,∴DF⊥OF.∵∠AEF=135°,四边形ABFE为圆内接四边形,∴∠B=45°.∴∠FOA=90°,∴AB⊥OF,∴DF∥AB.(2)连结OE,∵BF=2,∠FOB=90°,∴OB=OF=2.∵OC=CE,CE⊥AB,OE=OF=2,∴CE=.∵DC∥OF,DF∥AB,∴四边形OCDF是平行四边形,∴DC=OF=2.∴DE=DC-CE=2-.22.解析(1)y=3x+6·2x+12(900-3x),即y=-21x+10800.(2)当y=6600时,-21x+10800=6600,解得x=200.∴2x=400,900-3x=300.答:A的面积是200m2,B的面积是400m2,C的面积是300m2.(3)种植面积最大的花卉总价为36000元.23.解析(1)令y=0,则-x2+6x=0,解得x1=0,x2=6,∴A(6,0),∴对称轴是直线x=3,∴M(3,9).(2)∵OE∥CF,OC∥EF,C(2,0),∴EF=OC=2,∴BC=1.∴点F的横坐标为5.∵点F落在抛物线y=-x2+6x上,∴F(5,5),BE=5.∵==,∴DE=2BD,∴BE=3BD,∴BD=.(3)①当BD=1时,BE=3,∴F(5,3).设MF的解析式为y=kx+b,-将M(3,9),F(5,3)代入,得解得∴y=-3x+18.∵当x=6时,y=-3×6+18=0,∴点A落在直线MF上.②3∶4∶8.评析本题主要考查二次函数与几何问题的综合,主要涉及二次函数图象与坐标轴的交点坐标,点是否在抛物线上,函数与方程综合等知识点.24.解析(1)在Rt△ABQ中,∵AQ∶AB=3∶4,AQ=3x,∴AB=4x,∴BQ=5x.又∵OD⊥m,l⊥m,∴OD∥l.∵OB=OQ,∴AH=BH=AB=2x,∴CD=2x,∴FD=CD=3x.(2)∵AP=AQ=3x,PC=4,∴CQ=6x+4.作OM⊥AQ于点M(如图①),∴OM∥AB.图①∵☉O是△ABQ的外接圆,∠BAQ=90°,∴点O是BQ中点,∴QM=AM=x,∴OD=MC=x+4.∴OE=BQ=x,∴ED=2x+4,∴S矩形DEGF=DF·DE=3x(2x+4)=90,∴x1=-5(舍去),x2=3,∴AP=3x=9.(3)①若矩形DEGF是正方形,则ED=FD.Ⅰ.点P在点A的右侧时(如图①),∴2x+4=3x,解得x=4,∴AP=3x=12.Ⅱ.点P在点A的左侧时,i.当点C在点Q右侧,(i)0<x<时(如图②),图②∵ED=4-7x,FD=3x,∴4-7x=3x,解得x=,∴AP=.(ii)≤x<时(如图③),图③∵ED=7x-4,DF=3x,∴7x-4=3x,解得x=1(舍去).ii.当点C在点Q左侧或重合时,即x≥(如图④),图④DE=7x-4,DF=3x,∴7x-4=3x,解得x=1,∴AP=3.综上所述,当AP为12或或3时,矩形DEGF是正方形.②AP的长为6或.略解:连结NQ,由点O到BN的弦心距为1,得NQ=2.当点N在AB的左侧时(如图⑤),图⑤过点B作BK⊥EG于点K,∵GK=x,BK=x,∴∠GBK=45°.易知BK∥AQ,∴AI=AB=4x,∴IQ=x,∴NQ==2,∴x=2,∴AP=6.当点N在AB的右侧时(如图⑥),图⑥过点B作BJ⊥GE于点J,∵GJ=x,BJ=4x,∴tan∠GBJ=,∴AI=16x,∴QI=19x,∴NQ==2,∴x=,∴AP=.评析本题考查动点问题,主要涉及动点与图形运动.分类讨论是解决动点问题的必经过程,也是中考必考内容.难度比较大.。
浙江省2015年温州学业水平模拟数学试卷带答案

2015年浙江省温州学业水平模拟数学试卷第I 卷(选择题)1, =⋂P M ( )A .[)+∞,1B .[)+∞,0C .()+∞,0D .()+∞,12 )A 3.过点P ),2(m -和Q )4,(m 的直线斜率为1,那么m 的值为( ) A.1 B.4 C.1或3 D.1或44.直线0x y +=与圆22(2)4x y -+=相交所得线段的长度为 ( )A .2 D5.已知角θ的终边上有一点 P ( ( )A 6.已知函数||5)(x x f =,)()(2R a x ax x g ∈-=,若1)]1([=g f ,则=a ( ) A.1 B. 2 C. 3 D. -17( )A 8.在等差数列{a n }中,a 1+a 9=10,则a 5的值为( ). A .5B .6C .8D .109.函数y =cos 2x 在下列哪个区间上是减函数( )10.下列函数中,既是偶函数又在区间()0,+∞上存在零点的是( ) B.x y e -= C. D.21y x =--11.已知n m ,是两条不同直线, γβα,,是三个不同平面,则下列正确的是( ) A .若αn αm //,//,则n m // B .若γβγα⊥⊥,,则βα//C .若βm αm //,//,则βα//D .若αn αm ⊥⊥,,则n m //12.已知a 、b 为单位向量,其夹角为60︒,则(2a -b )·b =( )A. -1B. 0C. 1D.2 13.设R b a ∈,,则“4>+b a ”是“2,2>>b a 且”的( ) (A )充分条件 (B )必要条件(C )充分必要条件 (D )既非充分又非必要条件14.已知角α为第二象限角,,53sin =α则=α2sin ( ) A.2512- B.2512 C.24- D.2415.为了得到sin 2y x =的图象,只需将 ( )ABCD16.[2013·宁波质检]如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA 1⊥平面A 1B 1C 1,正视图是正方形,俯视图是正三角形,该三棱柱的侧视图面积为( )17.若变量x 、y 满足约束条件⎪⎩⎪⎨⎧≥≥≤-≤+0,024y x y x y x ,则y x +2的最大值是( )A.2B.4C.7D.8 18.已知x>0,y>0,x +2y +2xy =8,则x +2y 的最小值是( )A .3B .19. )A .x y ±=B .x y 4±= D .x y 2±= 20.2log 510+log 50.25=( )A .0B .1C .2D .421.设等比数列{}n a 的前n 项和为n S ,且510S =,1030S =,则15S =( ) A .60 B .70 C .90 D .4022.如图所示,四棱锥S -ABCD 的底面为正方形,SD ⊥底面ABCD ,则下列结论中不正确的是 ( ).A .AC ⊥SBB .AB ∥平面SCDC .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D .AB 与SC 所成的角等于DC 与SA 所成的角23.如图,半径为2的⊙O 中,∠AOB =90°,D 为OB 的中点,AD 的延长线交⊙O 于点E ,则线段DE 的长为( )A 24.若双曲线C :222(0)x y m m -=>与抛物线x y 162=的准线交于,AB 两点,且,则m 的值是( )A.116B. 80.C. 52D.2025.已知ABC ∆的面积为,则ABC ∆的周长等于 ( )____________. 27.已知42a =,lg x a =,则x =________.28.设{}n a 是公差不为零的等差数列,12a =且136,,a a a 成等比数列,则2014a = .29.在▱ABCD 中,=a,=b,=3,M 为BC 的中点,则=______(用a,b 表示).30.已知二面角α―ΑΒ―β为600,在平面β内有一点P ,它到棱AB 的距离为2,则点P 到平面α的距离为三、解答题(题型注释)31.已知数列{}n a 是等差数列,且12a =,12312a a a ++=. ⑴ 求数列{}n a 的通项公式;⑵ 令nn n b a =⋅3*(N )n ∈,求数列{}n b 的前n 项和.32.如图,在△ABC 中,已知45B ∠=,D 是BC 边上一点,AD=10,AC=14,DC=6,求AB 的长.33.如图,在五面体ABCDEF 中,已知DE ⊥平面ABCD ,//AD BC ,o 60BAD ∠=,2AB =,1DE EF ==.(1)求证://BC EF ;(2)求三棱锥B DEF -的体积.34.已知曲线E 上任意一点P 到两个定点4.(1)求曲线E 的方程;(2)设过(0,-2)的直线l 与曲线E 交于,C D 两点,且0OC OD ⋅=(O 为原点),求直线l 的方程.参考答案1.A 2.D3.A 4.D 5.B 6.A 7.B 8.A 9.C 10.C 11.D 12.B 13.B 14.C 15.B 16.A 17.C 18.B 19.D 20.C 21.B 22.D 23.C 24.D 25.C26.{}|16x x -≤≤272829.-a+b 3031.(1)2n (232.33.(1)BC 平行于平面ADEF ,(234.(1)(2)直线l 的方程是22y x =-或22y x =--。
2015学年浙江省温州中考数学年试题答案
山东省临沂市2015年初中学生学业考试数学答案解析第Ⅰ卷【解析】如图:35=,故a a为:故选B。
故选D。
【考点】反比例函数与一次函数的交点问题第Ⅱ卷AB A⨯sin=4-AB BDAD BD=3721.【答案】(1)条形统计图如图:∵O切BC【考点】切线的性质,扇形面积的计算24.【答案】(1)303760(18)503600(923)x x y x x +⎧=⎨+⎩≤≤≤≤ (2)010560a 当<<时,方案二合算,当10560a >时,方案一合算 【解析】(1)当18x ≤≤时,每平方米的售价应为:4000(8)30303760y x x =--⨯=+(元/平方米)当923x ≤≤时,每平方米的售价应为:4000(8)50503600y x x =+-⨯=+(元/平方米)。
∴303760(18)503600(923)x x y x x +⎧=⎨+⎩≤≤≤≤。
(2)第十六层楼房的每平方米的价格为:501636004400⨯+=(元/平方米), 按照方案一所交房款为:14400120(18%)485760W a a =⨯⨯--=-(元), 按照方案二所交房款为:24400120(110%)475200W =⨯⨯-=(元),当12W W >时,即485760475200a ->,解得:010560a <<, 当12W W <时,即485760475200a -<,解得:10560a >, ∴010560a 当<<时,方案二合算;当10560a >时,方案一合算。
【考点】利用一次函数解决问题25.【答案】(1)AF 与BE 的数量关系是:AF BE =,位置关系是:AF BE ⊥。
答案是:相等,互相垂直; (2)结论仍然成立。
理由是:∵正方形ABCD 中,AB AD CD ==,∴在ADE △和DCF △中,AE DF AD CD DE CF =⎧⎪=⎨⎪=⎩,∴ADE DCF △≌△, ∴DAE CDF ∠=∠,又∵正方形ABCD 中,90BAD ADC ∠=∠=︒, ∴BAE ADF ∠=∠,∴在ABE △和ADF △中,AB DA BAE ADF AE DF =⎧⎪∠=∠⎨⎪=⎩,∴ABE ADF △≌△ ,∴BE AF =,ABM DAF ∠=∠, 又∵90DAF BAM ∠+∠=︒, ∴90ABM BAM ∠+∠=︒,∴在ABM △中,180()90AMB ABM BAM ∠=︒-∠+∠=︒, ∴BE AF ⊥;(3)第(1)问中的结论都能成立.理由是:∵正方形ABCD 中,AB AD CD ==,∴在ADE △和DCF △中,AE DF AD CD DE CF =⎧⎪=⎨⎪=⎩,∴ADE DCF △≌△, ∴DAE CDF ∠=∠,又∵正方形ABCD 中,90BAD ADC ∠=∠=︒, ∴BAE ADF ∠=∠,∴在ABE △和ADF △中,AB DA BAE ADF AE DF =⎧⎪∠=∠⎨⎪=⎩,∴ABE ADF △≌△,∴BE AF =,ABM DAF ∠=∠, 又∵90DAF BAM ∠+∠=︒ ,90ABM BAM ∴∠+∠=︒,⊥。
2015年浙江省温州市中考数学试卷-答案
∴点 O、P、M 三点共线,点 O、Q、N 三点共线. ∵ACDE,BCFG 是正方形, ∴ AE CD AC,BG CF BC .
∵ OC x ,∴ DE 2x .
∵ DFE 120 ,∵ EDF 30 .
∴ CF
x 3
3 3
x
,∴SDEF源自1 2 2x 3x 3
3 x2 3
又∵菱形 FGMH 中, GFH 120,FG FE ,∴ S菱形FGMH 2 SDEF ∴ y 3 SDEF 3x2 ,故选 B.
∵点 B 在第一象限,∴点 B 的坐标是 (1, 3) .
∵反比例函数 y k 的图象经过点 B,∴ 3 k k 3 ,故选 C.
x
1
【考点】反比例函数综合题,曲线上点的坐标与方程的关系,等边三角形的性质,勾股定理
9.【答案】B
【解析】∵ON 是 RtAOB 的平分线, DE OC ,∴△ODE 是等腰直角三角形.
2 / 12
设 AB 2r ,则 OM MP r, ON NQ r .
∵点 O、M 分别是 AB、ED 的中点,
∴OM 是梯形 ABDE 的中位线.
∴ OM 1 AE BD 1 AE CD BC 1 2AC BC ,即 MP r 1 2AC BC .
整式方程求解,然后解一元一次方程,最后检验即可求解:
3 / 12
2 3 3x 2x 2 x 2 , x x 1 经检验, x 2 是原方程的根 ∴方程 2 3 的根是 x 2 .
2015年浙江省温州市初中毕业生学业考试第一次模拟考试数学试卷【附答案】
AC2015年初中毕业生学业考试第一次模拟考试数学试卷2015.03一、选择题(本题有10小题,每小题4分共40分) 1.计算:2+(-1)的结果是( )A .-1B . -3C .1D .3 2.下列运算结果正确的是( )A .236a a a ⋅= B .235()a a = C .235a a a += D .32a a a -= 3.函数2y x=的图象所在的象限是( ) A .第一、二象限 B . 第一、三象限 C .第二、三象限 D .第二、四象限4.如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )...D .5.二次函数22y =+(x-1)的图象上最低点的坐标是( )A .(1,2)B .(1,2)-C .(1,2)-D .(1,2)--6.如图,点A 、B 、C 在⊙O 上,∠A=50°,则∠BOC 的度数为( )A .130°B .50°C .65°D .100°7.如图,已知Rt △ABC 中,∠C =90°,AC =4,tanA =,则BC 的长是( ) A .2 B .8 C .2D .48.已知五箱梨的质量(单位:kg )分别为:18,20,21,18,19,则这五箱梨质量的中位数和众数分别为( ) A .AC ⊥BD B .∠A+∠B=180° C .AB=AD D .∠A ≠∠C10.如图,点C 是以AB 为直径的半圆上的一动点,分别以AC 、BC 为直径作半圆,它们交出两弯新月(图中阴影部分),当点C 从点A 沿弧线向终点B 运动过程中, 两弯新月面积的和(图中阴影部分) 变化情况是( )(9题图)(7题图) (6题图)A .逐渐变小B .逐渐变大C . 先变小后变大D .先变大后变小二、填空题(本题有6小题,每小题5分共30分) 11.分解因式:ax ﹣a = ___________ .12.已知扇形的圆心角为120°,半径为3cm ,则扇形的面积为___________ cm 2. 13.如图,直线a,b 被直线c 所截.若a ∥b,∠1=40°,∠2=70°,则∠3= ________度.14.写出一个过点(0,3),且函数值y 随自变量x 的增大而减少的一次函数关系式:_________. 15.某种商品,在甲商场10元可买x 件,在乙商场10元可买(x+1)件,则每件该商品乙商场比甲商场便宜________________元(用含x 的代数式表示).16.如图,在平面直角坐标系中,点A 、C 的坐标分别为(5,0)、(0,3),直线kx y =与矩形ABCO 的边CB ,BA 交于点P ,以OP 为直径的圆与矩形ABCO 的边最多有_______个交点,此时k 的取值范围是___________.三、解答题(本大题共有8小题,共80分) 17.(本题10分)(1)计算:1)13(80-+--(2)先化简,再求值:4)4()2(2--++m m m ,其中2=m .18.(本题8分)如图,将矩形ABCD 沿BD 对折,点A 落在E 处,BE 与CD 相交于F ,若AD =3,BD =6.(1)求证:△EDF ≌△CBF ; (2)求∠EB C .19.(本题8分)如图1、如图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形边长均为1.点A 和点B 在小正方形的顶点上.请在两张方格纸中各画一个Rt △ABC ,b(16题图)(10题图)使得点C 在小正方形的顶点上,且所画的两个三角形不全等.20.(本题8分)在一个不透明的箱子里,装有红、白、黑各一个球,它们除了颜色之外没有其他区别.(1)随机地从箱子里取出1个球,则取出红球的概率是多少?(2)随机地从箱子里取出1个球,放回搅匀再取第二个球,请你用画树状图或列表的方法求两次取出相同颜色球的概率.21.(本题10分) 如图,已知二次函数y =a (x ﹣h )2+的图象经过原点O (0,0),A (2,0).(1)写出该函数图象的对称轴;(2)若将线段OA 绕点O 逆时针旋转60°到OA ′,试判断点A ′是否为该函数图象的顶点?22. (本题10分)如图,AB 是⊙O 的直径,点C 在BA 的延长线上,直线CD 与⊙O 相切于点D ,弦DF ⊥AB 于点E ,线段CD=10,连结BD 。
【初中数学】浙江省温州市2015年毕业生升学考试数学模拟试卷 浙教版
2015年温州市毕业生升学考试数学模拟试卷姓名一、选择题(本题有10小题,每题4分,共40分) 1.下列各数中,倒数是3-的数是( ) A .3 B .3- C .31 D . 13- 2.桌面上放着1个长方体和1个圆柱体,按下图所示的方式摆放在一起,其左视图是( )3某行政区划调整为5镇10街道,市区总人口687498人,将这个总人口数保留两个有效数字并用科学记数法表示,则为( ) A .6.8×105B .6.9×105C .68×104D .69×1044.下列运算正确的是( )A .22a a a ∙= B .()22ab ab =C .()325aa = D .624a a a ÷=5.如图,Rt △ABC 中,∠C=90°,若AB=5,sinA=53,则AC 的长是( ) A. 3 B.4 C.5 D. 6(第5题图) (第6题图) (第7题图)6.如图,△ABC 内接于⊙O ,AD 是⊙O 的直径,∠ABC =35°,则∠CAD 的度数是( )A .35°B .45°C .55°D .65°7.周老师对九(1)班全班同学“每分钟跳绳次数”进行了测试,把所得数据绘制成如图所示的频数分布直方图.若将不低于160个/分的成绩(成绩为整数)评为优秀,则该班此次 成绩优秀的同学人数占全班人数的百分比是( )A .56%B .46%C .44%D .28% 8.抛物线22y x x =-与坐标轴的交点个数为( )A .0个B .1个C .2个D .3个9.在平面直角坐标系XOY 中,以原点O 为圆心的圆过点A (13,0),直线34y kx k =-+与圆O 交于B 、C 两点,则弦BC 的长的最小值为( )A .24 B. 25 C. 26 D 28(第9题图) (第10题图) (第13题图)10.如图所示,点C 是以AB 为直径的半圆上的一动点,分别以AC ,BC 为直径作半圆,它们交出两弯新月(图中阴影部分),则当点C 从点A 沿弧线向终点B 运动过程中,两弯新月面积的和(图中阴影部分)变化情况是( ) A .不变 B .逐渐变大C .先变小后变大D .先变大后变小二、填空题(本题有6个小题,每小题5分,共30分) 11.因式分解:216a b b - = ___ ______ .12.点(3-,2)在一个反比例函数的图象上,则这个反比例函数的解析式是 ______ . 13.一个材质均匀的正方体的每个面上标有数字1,2,3中的其中一个,其展开图如图所示,随机抛掷此正方体一次,则朝上与朝下的两面上数字不相同的概率是 _________ . 14.如图所示,半径为1的圆心角为60°的扇形纸片OAB 在直线L 上向右做无滑动的滚动.且滚动至扇形O ′A ′B ′处,则顶点O 所经过的路线总长是 _________ .(第14题图) (第15题图) (第16题图)15.如图,在四边形ABCD 中,∠ABC=∠ADC=90°,对角线AC 、BD 交于点P ,且AB=BD ,AP= 4PC= 4,则cos ∠ACB 的值是 _________ .16.如图,Rt △ABC 的斜边AB 在x 轴上,OA =OB =6,点C 在第一象限,∠A =30°, P (m ,n )是线段BC 上的动点,过点P 作BC 的垂线a ,以直线a 为对称轴,将线段OB 轴对称变换后得线段O ′B ′,(1) 当点B ′ 与点C 重合时,m 的值为 ;(2)当线段O ′B ′与线段AC 没有公共点时,m 的取值范围是 .2015年温州市毕业生升学考试数学模拟卷姓名一、选择题1、 2、 3、 4、 5、 6、 7、 8、 9、 10、 二、填空题11、 12、 13、 14、 15、 16、 、 三、解答题(本大题有8小题,共80分)17.(本题8分) (1)计算:|2|)31()31(1-+++-;(2)解方程:0222=--x x .18、(本题8分)如图,点P 是菱形ABCD 的对角线BD 上一点,连接CP 并延长,交AD 于E ,交BA 的延长线点F .问:(1)图中△APD 与哪个三角形全等?并说明理由; (2)求证:△APE ∽△FPA ;(3)猜想:线段PC ,PE ,PF 之间存在什么关系?并说明理由.19.(本题8分)如图所示,在8×8的网格中,我们把△ABC 在图1中作轴对称变换,在图2中作旋转变换,已知网格中的线段ED 、线段MN 分别是边AB 经两种不同变换后所得的像,请在两图中分别画出△ABC 经各自变换后的像,并标出对称轴和旋转中心(要求:不写作法,作图工具不限,但要保留作图痕迹). 20.(本题8分)七(1) 班进行“品学兼优生”的推选工作,经过自荐和第一轮筛选后,甲、乙两名同学进入终选.下表为甲、乙两位同学的得分情况.其中人气分的计算办法是:根据班级同学和主科老师的投票结果,同学1票记3分,老师1票记10分,两个分数相加即为人气分.(1)求甲的人气分m 的值. (2)经全班同学讨论决定, 候选人的最终得分将根据如图 所示的百分比折算后记入总分, 求乙的最终得分. 21.(本题10分) 如图,已知AB 是半圆O 的直径,过点O 作弦AD 的垂线交半圆O 于点E ,交AC 于点C ,使BED C ∠=∠.(1)判断直线AC 与圆O 的位置关系,并证明你的结论;(2)若8AC =,4cos 5BED ∠=,求AD 的长.C OBE D22.(本题12分)如图1所示,已知温沪动车铁路上有A、B、C三站,B、C两地相距280千米,甲、乙两列动车分别从B、C两地同时沿铁路匀速相向出发向终点C、B站而行,甲、乙两动车离A地的距离y(千米)与行驶时间表x(时)的关系如图2所示,根据图象,解答以下问题:(1)填空:路程a=_________,路程b=_________.点M的坐标为______.与行驶时间x之间的函数关系式.(2)求动车甲离A地的距离y甲(3)补全动车乙的大致的函数图象.(直接画出图象)23.(本题12分)宏远商贸公司有A、B两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:(1)已知一批商品有A、B两种型号,m,质量一共是10.5吨,体积一共是203求A、B两种型号商品各有几件?m,其收费方式有以下两(2)物流公司现有可供使用的货车每辆额定载重3.5吨,容积为6 3种:①按车收费:每辆车运输货物到目的地收费600元;②按吨收费:每吨货物运输到目的地收费200元.要将(1)中的商品一次或分批运输到目的地,宏远商贸公司应如何选择运送、付费方式运费最少?并求出该方式下的运费是多少元?24.(本题14分)如图,在平面直角坐标系中,经过点A (1,3)的直线交y 轴正半轴于P ()0,m ,交x 轴于点B ,过P 作PQ ⊥AP ,交x 轴于点Q ,AC ⊥y 轴,垂足为C ,其中3m ≠. (1)当03m <<时,求证:△ACP ∽△POQ ; (2)求OQ 的长; (3)求m 为何值时,△APQ 与△POQ 相似.2015年温州市毕业生升学考试数学模拟参考答案一、选择题(每小题4分,共40分) DBBDB CACAA 提示:15、二、填空题(每小题5分,共30分) 11.()()44b a a +- ; 12.x y 6-= 13.23;14.43π ; 15 .9159,36242m m ≤<<≤或 14、15、16、三、解答题(共80分)17(本题8分)x=±(1)6 (2)118、(本小题8分)如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD 于E,交BA的延长线点F.问:(1)图中△APD与哪个三角形全等?并说明理由;(2)求证:△APE∽△FPA;(3)猜想:线段PC,PE,PF之间存在什么关系?并说明理由.解:(1)△APD≌△CPD.理由:∵四边形ABCD是菱形,∴AD=CD,∠ADP=∠CDP.又∵PD=PD,∴△APD≌△CPD.(+3分)证明:(2)∵△APD≌△CPD,∴∠DAP=∠DCP,∠FPA=∠FPA,∴△AP E∽△FPA.(+5分)猜想:(3)PC2=PE•PF.理由:∵△APE∽△FPA,∴.∴PA2=PE•PF.∵△APD≌△CPD,∴PA=PC.∴PC2=PE•PF.(+8分)19:解答:解:所画图形如下所示:各得4分20:m=95,93,9.21、解:(1)AC 与O 的相切.证明如下:OC AD ⊥∵290AOC ∴∠+∠=°.又2C BED ∠=∠=∠ , 90AOC C ∠+∠=∴°.AB AC ⊥∴ -----------------------(-+4分) 即AC 与O 的相切. -----------------------(-+5分)(2)解:连接BD .AB ∵是O 直径,90ADB ∴∠=︒在Rt AOC ∆中,90CAO ∠=︒,8AC = ,90ADB ∠= °.4cos cos 5C BED ∠=∠=.6AO ∴=,12AB ∴=在Rt ABD ∆中,4cos 2cos 5BED ∠=∠=,4cos 2125AD AB ∴=⋅∠=⨯=485.----------------------(+10分)22、解:(1)根据图象可知:a=100km ,b=180km , (+1分) V 甲==280×=160km/h , (+2分)=小时, ∴点M 的坐标为:(,0); (+3分) (2)当0≤x ≤时,设y 甲=k 1x+b 1,把(,0)与(0,100)代入,,解得:,∴y 甲=﹣160x+100; (+5分) 当<x ≤1时,y 甲=k 2x+b 2, 把(,0)与(1,180)代入,CA OBE D1 2,解得:,∴y甲=160x﹣100;(+7分)(3)QV乙==200,∴动车乙从A站B站的时间为:100÷200=0.5(小时),(+8分)∴动车乙从A站到B站的函数图象经过(1.4,100),函数图象如图所示.(+10分)23、(本题12分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
温州市实验中学2015年初中毕业生学业考试数学一模试卷参考公式:二次函数y=ax 2+bx+c 的顶点坐标是)4ab 4ac ,2a b (2--.试题卷Ⅰ一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)1.下列四个数2-,0,0.5...的是( ▲ ) A .2-B .0C .0.5 D2.如图,桌面上有一个一次性纸杯,它的主视图应是( ▲ )A .B .C .D .3.要使分式21x x +-有意义,则x 的取值应满足( ▲ ) A .2x ≠- B .1x ≠ C .2x =- D .1x =4.一次函数24y x =+的图象与x 轴的交点坐标是( ▲ )A .(-2,0)B .(0,-2)C .(4,0)D .(0,4) 5.一名射击爱好者7次射击的中靶环数如下(单位:环):7,10,9,8,7,9,9,这7个数据的中位数 是( ▲ )A .7环B .8环C .9环D .10环6.如图,AC 是旗杆AB 的一根拉线,测得BC =6米,ACB ∠=50°,则拉线AC 的长为( ▲ )A .6sin 50︒B .6cos50︒C .6sin 50︒ D .6cos50︒l 1(第6题图) (第7题图)7.如图,直线1l ∥2l ,1∠=35°,2∠=75°,则3∠等于( ▲ )A .55°B .60°C .65°D .70° 8.小明为研究反比例函数2y x=的图象,在-2、-1、1中任意取一个数为横坐标,在-1、2中(第2题图) 主视方向任意取一个数为纵坐标组成点P 的坐标,点P 在反比例函数2y x=的图象上的概率是( ▲ )A .16B .13C .12D .239.如图,Rt ABC ∆中,90ACB ∠=︒,30B ∠=︒,2AC =,将ABC ∆绕点C 逆时针旋转至A B C ''∆,使得点A '恰好落在AB 上,A B ''与BC 交于点D ,则AB . C(第9题图) (第10题图)10.如图,矩形OABC 的顶点A 在y 轴上,C 在x 轴上,双曲线ky x=与AB 交于点D ,与BC 交于点E ,DF x ⊥轴于点F ,EG y ⊥轴于点G ,交DF 于点H ,若矩形OGHF 和矩形HDBE 的面积分别是1和2,则k 的值为( ▲ ) A .125 B 1 C .52D . 试题卷Ⅱ二、填空题(本题有6小题,每小题5分,共30分) 11.分解因式:23a a -= ▲ . 12.方程240x -=的解是 ▲ .13.如图,已知AB ∥CD ∥EF ,若:AC CE =2:3,BD =6,那么BF = ▲ . 14.如图,AB 是O 的直径,点C ,D 在O 上,且在AB 的同侧,若40AOD ∠=︒,则C ∠的度数为 ▲ .A(第14题图) (第15题图) (第16B'D A'CA B题图)15.如图,将长方形ABCD 分割成1个灰色长方形与148个面积相等的小正方形.若灰色长方形的长与宽之比为5:3,则:AD AB = ▲ .16.如图,在四边形ABCD 中,AD ∥BC ,B Rt ∠=∠,60C ∠=︒,AD =4,CD =8,点E 在BC 上,点F 在CD 上,现将四边形ABCD 沿EF 折叠,若点C 洽与点A 重合,EF 为折痕,则CE = ▲ , sin AFE ∠= ▲ . 三、解答题(本题有8小题,共80分)17.(本题10分)(10(3)tan 45π+--︒; (2)化简:2(2)(3)x x x +--.18.(本题6分)如图,在直角坐标系中有一个格点三角形ABC (顶点都在格点上的三角形),已知A (- 2,1),B (- 3,4),C (- 4,1),直线MN 过点M (2,5),N (5,2). (1)请在图中作出格点三角形ABC 关于x 轴对称的格点三角形'''A B C (A ,B ,C 的对应点依次为'A ,'B ,'C );(2)连结AM,AN ,则tan MAN ∠= .19.(本题8分)如图,已知A (-2,-2)、B (n ,4)是一次函数y kx b =+的图象和反比例函数my x=的图象的两个交点. (1)求反比例函数和一次函数的解析式; (2)求AOB ∆的面积.20.(本题10分)如图,在正方形ABCD 中,点G 是CD 上任意一点,连接BG ,作AE BG ⊥于点E ,CF BG ⊥于点F . (1)求证:BE CF =; (2)若BC =2,65CF =,求EF 的长. 21.(本题10分)某校举办初中生演讲比赛,每班派一名学生参赛,现某班有A 、B 、C 三G FEDC BA(第20题图)(第19题图)BAO xy(第18题图)名学生竞选,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表和图①:(1)请将表和图1中的空缺部分补充完整;(2)竞选的最后一个程序是由本校的300名学生代表进行投票,每票计1分,三名候选人的得票情况如图2(没有弃权票,每名学生只能推荐一人).①若将笔试、口试、得票三项测试得分按4:3:3的比例确定最后成绩,请计算学生A 的最后成绩;②若规定得票测试分占20%,要使学生B 最后得分不低于91分,则笔试成绩在总分中所占比例的取值范围应是 ▲ .22.(本题10分)如图,在O 中,AOB ∠=150°,ABC ∠=45°.延长OB 到D ,使BD OB =,连结CD . (1)求证:CD 与O 相切;(2)若CD =6,求弓形BC (劣弧所对)的面积. (结果保留π和根号)23.(本题12分)今年3月12日植树节前夕,我校购进A 、B 两个品种的树苗,已知A 种比B 种每株多20元,买1株A 种树苗和2株B 种树苗共需110元.(1)问A 、B 两种树苗每株分别是多少元?(2)4月,为美化校园,学校花费4000元再次购入A 、B 两种树苗,已知A 种树苗数量不少于B 种数量的一半,则此次至多购买B 种树苗多少株?C 25%B 40%A 35%笔试口试CB A竞选人分数/分757080859095100(第22题图)DBOAC图1图224.(本题14分)如图,抛物线2(0)y ax bx c a =++≠的图象经过点A ,B ,C ,已知点A的坐标为(-3,0),点B 坐标为(1,0),点C 在y 轴的正半轴,且CAB ∠=30°. (1)求抛物线的函数解析式;(2)若直线l :yx +m 从点C 开始沿y 轴向下平移,分别交x 轴、y 轴于点D 、E .①当m >0时,在线段AC 上否存在点P ,使得点P ,D ,E 构成等腰直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.②以动直线l 为对称轴,线段AC 关于直线l 的对称线段A C '' 与二次函数图象有交点,请直接写出m 的取值范围.参考答案一、选择题(本题有10小题,每小题4分,共40分.) lD AC OBExylD AC OBExy (第24题图)备用图二、填空题(本题有6小题,每小题5分,共30分)三、解答题(本题有8小题,共80分)17.(本题10分)(10(3)tan 45π+--︒;411=+- ......(3分)4= ......(2分)(2)化简:2(2)(3)x x x +--解:原式= 22443++-+x x x x ......(3分) = 74+x ......(2分) 18. (本题6分)(1) 作出△'''A B C ...... (3分) (2) 3tan 4∠=MAN ...... (3分)19.(本题8分)⎩⎩∴22=+y x ......(2分)(2)将一次函数22=+y x 与y 轴的交点记为C (0,2)......(1分) ∴112221322∆∆∆=+=⨯⨯+⨯⨯=AOB AOC BOC S S S ......(3分)20.(本题10分)证明:(1)∵AE ⊥BG , CF ⊥BG ,∴∠AEB=∠BFC=90°......(1分)又∵∠ABE+∠FBC=90°, ∠ABE+∠BAE=90°∴∠FBC =∠BAE......(2分) ∵AB=BC∴△ABE ≌△BCF......(1分) ∴BE=CF ......(1分) (2)∵CF ⊥BG, BC=2, CF=65∴BF 2285=-==BC CF ......(3分)又∵BE=CF=85......(1分) ∴EF=BF-BE=862555=-=......(1分)21.(本题10分)(1)90......(1分),C 口试补充如下......(1分)G FE DCBA(第20题图)(2)①A 得票情况:30035%105? ...... (1分)A 的最后成绩:8549031053433???++ ...... (3分)92.5= ...... (1分)答:A 的最后成绩为92.5分.②取值范围:0.2x 0.8# ...... (3分)22.(本题10分) 解:(1)连结OC ,∵OA=OB,∠AOB=150°∴∠OAB=∠OBA=15°......(1分) 又∵∠ABC=45°∴∠OBC=60° ......(1分)∵OC=OB ,BD=OB∴∠OCB=60°,∠BCD=∠D=30°......(2分) ∴∠OCD=90°∴半径OC ⊥CD......(1分) ∴CD 与⊙O 相切 (2)作OH ⊥BC ,∵∠COB=60°,OB=OC∴∠COH=30°,∴OH =......(1分) 在Rt △OCD 中,∠D=30°,CD=6∴OC = ......(1分 ∴OH=3......(1分)∴S 弓形AB =S 扇形OBC -S △OBC = (2601323602ππ⨯-⨯=- ....(2分)23.(本题12分)解:(1)设A 种树苗每株x 元,B 种树苗每株y 元, 可得方程202110x y x y -=⎧⎨+=⎩......(4分)解得5030x y =⎧⎨=⎩∴A 种树苗每株50元,B 种树苗每株30元 ......(2分) (2)设购买A 种树苗a 株,B 种树苗b 株。
由题意可得50304000a b +=,则3805a b =- ..........(2分)由题意可得318052b b -≥,解得 80011b ≤ .....(2分) ∵b 为正整数,且被5整除,所以b 最大值为70 ∴至多购买B 树苗70棵. ......(2分)24.(本题14分)解:(1)在Rt △AOC 中,∠CBA =30°∵A(-3,0) ,即OA=3∴即C(0(1分)设抛物线解析式为2=+y ax bx 将A (-3,0),B (1,0)代入得930⎧+=⎪⎨-+=⎪⎩a b a b .解得⎧=⎪⎪⎨⎪=⎪⎩a b ......(2分)∴2=-+y x ......(1分) (2)由题意可知,OE=m ,,∠(i )如图,当PD ⊥DE ,DP=DE ,作PQ ⊥x 轴 ∴∠PQD=∠EOD=90°,∠PDQ+∠EDO=90°,∠EDO+∠DEO=90°, ∴∠DEO=∠PDQ=30° ∴△DPQ ≌△EDO (AAS )∴DQ=OE=m,∵∠PAQ=∠PDQ=30°∴PA=PD∴AQ=DQ=m∴m=3,∴m==......(2分)(ii)如图,当PE⊥DE,DP=DE,作PQ⊥y轴同理可得,∴∴6m==-......(2分)(iii)如图,当DP⊥DE,DP=PE,作DM⊥AC,EN⊥AC同理可得∴=, ∴9m==-......(2分)(3)m≤≤......(4分)。
