ilovenili_ABAQUS有限元网格划分基础
有限元网格划分和收敛性
一、基本有限元网格概念1.单元概述几何体划分网格之前需要确定单元类型。
单元类型的选择应该根据分析类型、形状特征、计算数据特点、精度要求和计算的硬件条件等因素综合考虑。
为适应特殊的分析对象和边界条件,一些问题需要采用多种单元进行组合建模。
2.单元分类选择单元首先需要明确单元的类型,在结构有限元分析中主要有以下一些单元类型:平面应力单元、平面应变单元、轴对称实体单元、空间实体单元、板单元、壳单元、轴对称壳单元、杆单元、梁单元、弹簧单元、间隙单元、质量单元、摩擦单元、刚体单元和约束单元等。
根据不同的分类方法,上述单元可以分成以下不同的形式。
3.按照维度进行单元分类根据单元的维数特征,单元可以分为一维单元、二维单元和三维单元。
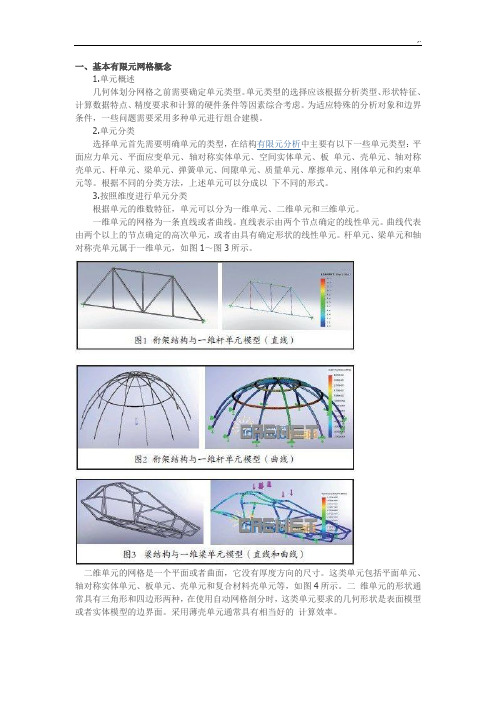
一维单元的网格为一条直线或者曲线。
直线表示由两个节点确定的线性单元。
曲线代表由两个以上的节点确定的高次单元,或者由具有确定形状的线性单元。
杆单元、梁单元和轴对称壳单元属于一维单元,如图1~图3所示。
二维单元的网格是一个平面或者曲面,它没有厚度方向的尺寸。
这类单元包括平面单元、轴对称实体单元、板单元、壳单元和复合材料壳单元等,如图4所示。
二维单元的形状通常具有三角形和四边形两种,在使用自动网格剖分时,这类单元要求的几何形状是表面模型或者实体模型的边界面。
采用薄壳单元通常具有相当好的计算效率。
三维单元的网格具有空间三个方向的尺寸,其形状具有四面体、五面体和六面体,这类单元包括空间实体单元和厚壳单元,如图5所示。
在自动网格划分时,它要求的是几何模型是实体模型(厚壳单元是曲面也可以)。
4.按照插值函数进行单元分类根据单元插值函数多项式的最高阶数多少,单元可以分为线性单元、二次单元、三次单元和更高次的单元。
线性单元具有线性形式的插值函数,其网格通常只具有角节点而无边节点,网格边界为直线或者平面。
这类单元的优点是节点数量少,在精度要求不高或者结果数据梯度不太大的情况下,采用线性单元可以得到较小的模型规模。
有限元网格划分(讲稿) 27页PPT文档
Surface 采 用quad
Face 采用 quad
通过 sweep quad 创建Hex
Associated points 用于网格生成 Points 可 associated 于 curve 、 surface 硬点布置受global model tolerance 限制 被关联几何网格生成亦受限制 仅应用于 Paver 关联点亦可给被关联去除
在线curve或边edge上设置mesh seed 用以控制欲建模型的元素数目 与大小。
mesh seed 也用于调整网格密度 MSC.Patran 提供多种方法产生 seed
Uniform seed bias (等间隔) Non-uniform seed bias (不等间隔) Curve based seeding (依曲线参数而定) Tabular (列表输入) PCL function (PCL函数)
性,可进行parasolid 装配
有限元网格划分基础
ISOMESH 与 TETMESH的区别
由原丝体创建简单体 用Isomesh 划网格 附加工作多,但可使用hex
元素
Parasolid 体(复杂体)
简单体分割
对 parasolid 体直接划mesh
有限元网格划分基础
左图是一个硬点的
例子。说明了硬点 与网格之间的关系
硬线用于面网格生成 硬线布置受global model tolerance 限制 被关联几何网格生成亦受限制 硬线本身可加mesh seeded 仅应用于 Paver 关联线亦可给被关联去除
有限元网格划分基础
IsoMesher 可用于参数体
有限元网格划分基础
Mirror Plane
通过Create/Element/Edit菜单可以手动创建单元 需要注意的是:
ABAQUS有限元软件基本操作说明

Abaqus仿真分析操作说明1.单位一致性(未列出参照国际单位)长度:米(m)力:牛(N)质量:千克(kg)时间:秒(s)强度(压力):帕(Pa)能量:焦耳(J)密度:千克/立方米(kg/m3)加速度:米/平方秒(m/s2)2.模型(part)的建立首先用三维绘图软件(CAD、PROE、SOLIDEDGE、SOLIDWORKS等)将模型画好。
3.模型(part)导入ABAQUS软件①将模型另存为sat或stp(step),示意图如下;文件名最好存为英文字母。
②模型另存为sat或stp(step)格式后,到“选项”进行设置,设置完成后将模型另存好(存放位置自设,能找到就好),示意图如下;③打开已经安装好的ABAQUS软件,选中左上角“文件→导入→部件”,示意图如下;导出模型单位由mm改为m。
选中后隐藏的部件不能导入ABAQUS软件。
版本设为ABAQUS软件版本。
双击所有参数均为默认,确定就好。
4.模型(part)的参数设置和定义到上面这一步骤,模型导入已经完成,接下来就是一些参数的设置和分析对象的定义。
具体的分析步骤按照下图所示一步一步完成即可。
(1)(2)(3)(4)(6)(5)(7)(1)“属性”步完成材料的定义。
具体参数设置见下图:1.双击“创建材料”2.自定义名称3.自定义材料描述4.在“通用”下双击“密度”进行参数设置5.输入材料密度,单位kg/m3。
6.在“力学”下双击“弹性”进行参数设置。
7.输入材料杨氏模量(Pa)和泊松比(无单位),单击“确定”完成参数设置。
8.双击“创建截面”,“类别”和“类型”默认。
9.单击“继续”。
10.参数默认,单击“确定”。
11.双击“指定截面”。
12.单击模型指定截面。
13.单击“完成”,完成截面指定。
14.模型变绿,指定截面成功;同时“属性”步参数定义结束。
(2)“装配”步完成分析对象的选定。
具体操作见下图:1.切换到下一步(装配)。
3.选中要分析的部件,单击“确定”,完成“装配”步。
Abaqus实例教程——网格划分

Abaqus实例教程——⽹格划分Workshop 9⾃動型與掃掠型網格建構技術: 幫浦模型w9-meshing.avi Introduction(介紹)在本練習中你將會使⽤ABAQUS/CAE 中的Mesh 模組來為整個幫浦組裝模型建構有限元素網格. 需要做的⼯作包括將網格屬性指定給每⼀個組件, 指定網格的種⼦點, 以及建⽴網格. Modifying the pump housing element type(修改幫浦外殼元素類型)1.從../IntroClass/workshops/ pump⽬錄啟動 ABAQUS/CAE 並且開啟模型的資料檔Pump.cae.2.在模型樹中, 將零件PUMP-1展開並在其中的Mesh上快點兩下將⼯作環境切換到 Mesh 模組然後在PUMP-1上開始⼯作.3.按照以下的步驟來製做⼀個組別(set)在其中將包含組成幫浦外殼的全部元素:a.在模型樹中, 將零件PUMP-1展開並在其中的Sets 上快點兩下.b.在Create Set對話框中, 選取Element作為組別類型. 將此組別取名為pump-mesh然後按下Continue按鈕.c.使⽤拉⽅框的⽅式將幫浦外殼的全部元素都選起來. 如果有必要的話可以使⽤選取過濾器. 選好之後按下Done按鈕.4.使⽤Query指令來確認⽬前你所指定到網格中的元素類型:a.從上⽅的下拉式功能表中, 選取Tools→Query功能選項.會彈出Query對話框.b.從其中所列出來的General Queries中, 選取Element然後按下Apply按鈕. 在任⼀元素上點⼀下並注意在訊息區中所列出來的元素編號, 類型, 以及節點連接順序, 如圖 W9–1 中所⽰. 重複這個程序檢查此網格中的其它元素.Figure W9–1 Selected element attributes.c.按下在Query對話框中的Cancel按鈕結束此查詢指令.5.幫浦外殼的元素類型是線性四⾯體元素(C3D4), 他並不適合⽤在有接觸狀況的分析. 所以, 要將幫浦外殼的元素類型改成⼆階四⾯體元素(C3D10M):a.從上⽅的下拉式功能表中, 選取Mesh→Element Type功能選項.b.當提⽰你所要選取的區域的類型時, 按下在提⽰區右側的Sets按鈕.c.在彈出來的Region Selection對話框中, 選取pump-mesh這⼀組然後按下Continue.d.在Element Type對話框中, 檢閱⽬前的設定. 將Geometric Order之下的Quadratic選項打開. 注意元素類型此時改成 C3D10M 了. 按下OK按鈕.e.在Region Selection對話框中, 按下Cancel.6.使⽤Query指令來檢查這些網格中的元素類型, 已經被變更了.Generating the bolt mesh(建螺絲的網格)1.從上⽅的⽬前⼯作環境提⽰列中的Object欄位處, 選取bolt將之設成圖形區的⽬前⼯作物件.這個螺絲會以⿈⾊顯⽰出來, 表⽰他此時只能以掃掠型網格建構技巧來將之建構成六⾯體元素的網格. 我們將使⽤⼀階⾮協調模式的六⾯體元素 (C3D8I) 在這個螺絲上的邊緣以局部種⼦點為 8 來建構網格.2.從上⽅的下拉式功能表中, 選取Seed→Edge by Number功能選項.3.在畫⾯上拉⼀個⽅框來將螺絲上的全部邊緣都選取起來.4.當提⽰區詢問你沿著邊緣的元素數⽬時, 輸⼊8.5.從上⽅的下拉式功能表中, 選取Mesh→Element Type功能選項來更改此螺絲上的元素類型.6.使⽤在畫⾯上拉⼀個⽅框的⽅式來將整個螺絲選取起來.7.在Element Type的對話框中, 將在Element Controls⾴之下的Incompatiblemodes(⾮協調模式)打開. 然後按下OK按鈕.8.從上⽅的下拉式功能表中, 選取Mesh→Part功能選項來將此螺絲網格建⽴起來.在提⽰區中, 按下Yes就可以建⽴此網格了.9.完成此動作後檢閱⼀下整個網格. 整個螺絲的網格如圖 W9–2 中所⽰.Generating the cover mesh(建底蓋的網格)1.從上⽅的⽬前⼯作環境提⽰列中的Object欄位處, 選取cover將之設成圖形區的⽬前⼯作物件.這個底蓋會以橘⾊顯⽰出來, 表⽰他如果沒有先加以分割的話是沒有辦法將之建構成六⾯體元素的網格的. 為了這個練習的緣故, 我們將使⽤四⾯體的⾃動網格建⽴技巧來建⽴此底蓋的網格. 使⽤整體性的元素⼤⼩ 0.35 以及元素類型為 C3D10M.2.從上⽅的下拉式功能表中, 選取Mesh→Controls功能選項. 在Mesh Controls對話框中, 選取Tet作為元素的形狀然後按下OK按鈕.這個零件現在會變成粉紅⾊, 表⽰他可以使⽤⾃動型網格建構技巧來建構其網格.3.指定整個網格的元素⼤⼩ (Seed→Part) 為0.35還有將螺絲孔的邊緣設定其局部的邊緣網格數量 (Seed→Edge By Number) 為8.4.將此底蓋上的元素類型 (Mesh→Element type) 更改成⼆階四⾯體元素(C3D10M).5.⽣成底蓋上的元素. 在此底蓋板上的網格如圖 W9–2 中所⽰.Generating the gasket mesh(建襯墊的網格)1.從上⽅的⽬前⼯作環境提⽰列中的Object欄位處, 選取gasket將之設成圖形區的⽬前⼯作物件.這個襯墊會以⿈⾊顯⽰出來, 表⽰他此時只能以掃掠型網格建構技巧來將之建構成六⾯體元素的網格.2.指定整個網格的元素⼤⼩(Seed→Part) 為0.25.3.將線性六⾯體襯墊元素 (GK3D8) 指定給這個襯墊使⽤ (Mesh→Element type並選⽤其中Gasket元素家族).4.⽣成襯墊上的元素. 在此襯墊上的網格如圖W9–3中所⽰.Figure W9–2 Bolt and cover meshes.Figure W9–3 Gasket mesh.5.查看⼀下整個組裝的網格, 在上⽅的⽬前⼯作環境提⽰列中的Object欄位處切換成Assembly選項. 整個建好網格的組裝如圖 W9–4 所⽰.Figure W9–4 Meshed assembly.6.將整個模型資料存檔Pump.cae, 並結束 ABAQUS/CAE 程式.。
有限元的网格划分技术

有限元的网格划分技术对于有限元分析来说,网格划分是其中最关键的一个步骤,网格划分的好坏直接影响到解算的精度和速度。
网格化有三个步骤:定义单元属性(包括实常数)、在几何模型上定义网格属性、划分网格。
定义网格的属性主要是定义单元的外形、大小。
单元大小基本上在线段上定义,可以用线段数目或长度大小来划分,可以在线段建立后立即声明,或整个实体模型完成后逐一声明。
采纳BottOm-UP方式建立模型时,采纳线段建立后立即声明比较便利且不易出错。
例如声明线段数目和大小后,叁制对象时其属性将会一•起夏制,完成上述操作后便可进行网格化命令。
网格化过程也可以逐步进行,即实体模型对象完成到某个阶段就进行网格话,如所得结果满足,则连续建立其他对象并网格化。
网格的划分可以分为自由网格(free meshing)、映射网格(mapped meshing)和扫略网格(SWeeP meshing)等。
一、自由网格划分自由网格划分是自动化程度最高的网格划分技术之一,它在面上可以自动生成三角形或四边形网格,在体上自动生成四周体网格。
通常状况下,可采用ANSYS的智能尺寸掌握技术(SMARTSIZE命令)来自动掌握网格的大小和疏密分布,也可进行人工设置网格的大小(AESIZE、LESIZE、KESIZE、ESIZE等系列命令)并掌握疏密分布以及选择分网算法等( MOPT 命令)。
对于简单几何模型而言,这种分网方法省时省力,但缺点是单元数量通常会很大,计算效率降低。
同时,由于这种方法对于三维简单模型只能生成四周体单元,为了获得较好的计算精度,建议采纳二次四周体单元(92号单元)。
假如选用的是六面体单元,则此方法自动将六面体单元退化为阶次全都的四周体单元,因此,最好不要选用线性(•阶次)的六面体单元(没有中间节点,比如45号单元),由于该单元退化后为线性的四周体单元,具有过大的刚度,计算精度较差;假如选用二次的六面体单元(比如95 号单元),由于其是退化形式,节点数与其六面体原型单元全都,只是有多个节点在同一位置而己,因此,可以采用TCHG命令将模型中的退化形式的四周体单元变化为非退化的四周体单元(如92号单元),削减每个单元的节点数量,提高求解效率。
ilovenili_ABAQUS有限元网格划分基础

ABAQUS有限元网格划分基础Simwe会员ilovenili摘要:ABAQUS中的MESH步可以产生一个集合的网格划分,根据分析的需要,你可以对网格划分的方式进行控制,系统会自动产生不同的网格划分。
当你修改PART步和ASSEMBLY步中的参数时,系统在此步会自动生成适合于这个模型的网格划分。
当然,由于ABAQUS在网格划分方面的功能还不够强大,不能够完全按照作者的意图随心所欲的进行划分,因此,可以用Patran或Hypermesh等软件生成网格,然后导入至CAE中。
下面我们讲述一下ABAQUS对二维的结构化网格划分。
关键词:网格,逻辑,二维,三结点单元,四结点单元1二维结构化网格划分:具有以下特征的二维区域才可以进行结构化网格划分:1.1区域内没有孔洞,孤立的边,或者是孤立的点。
1.2模型区域有三到五条逻辑边(我们可以把近乎直线的两条边看作是一条逻辑边,如下图所示)组成,每条边之间相互连接。
(如红线所示的两条边均可以看作是一条逻辑边)一般来讲,在三种划分方法中,结构化划分方法能够最好的对CAE所产生的网格进行控制。
如果你想用完全四边形元素对一个四条边区域进行网格划分,那么网格单元的边在边界上必须分布均匀。
对于三边形或五边形区域,限制条件将会更加复杂。
当使用结构化划分时,系统会考虑种子分布(所谓的种子分布是指种子的空间排布,与种子的数量无关。
比如说,种子分布关心的是种子到底是沿着一条边均匀的排列还是在这条边的末端更加集中一些).不过,在两个区域过渡的地方网格必须协调,比如说,两个相邻的区域分别用的是结构化和自由网格划分,那么系统就可能调节网格区域的结点以使得过渡区域的网格划分协调,正因为如此,可能使得实际的元素结点不相互匹配。
当你用结构化主导四边形元素划分一个四边形区域时,系统会插入一个单独的三角形,由此产生的网格很好的与种子相匹配,如下图所示:然而,当你用结构化主导四边形元素划分三边或五边形区域时,系统将不会插入任何三角形,由此产生的网格使用的是完全四边形元素;而且网格也可能与种子不匹配。
在ABAQUS中进行的微观组织结构的有限元网格划分

在ABAQUS中进行的微观组织结构的有限元网格划分摘要:详细地介绍了使用开发的软件TransMesh和商业化有限元软件ABAQUS,对二维异质体材料微观组织结构进行面向对象的有限元网格划分技术。
这一技术运用C语言和Python脚本语言,在有限元软件ABAQUS中成功的再现了二维异质体材料微观组织结构的体积代表单元(RVE),并通过软件TransMesh 实现了参数化有限元网格划分。
通过将ABAQUS和自主开发的TransMesh软件相结合,在国内率先系统地掌握了二维异质体材料微观组织结构的有限元网格划分技术,为微观组织结构的有限元模拟的顺利进行奠定了基础。
关键词:异质体微观组织结构软件TransMesh 有限元网格划分异质体材料的微观组织结构对于材料的宏观物理和力学性能有着直接的影响。
随着有限元方法和计算技术的发展,人们可以利用有限元的方法来模拟微观组织结构,以达到材料微观组织结构的‘性能导向型’设计与预测的目的。
在用有限元进行微观组织结构模拟的过程中,网格划分是至关重要的。
在国外,进行微观组织结构的有限元网格划分选用的是专门的有限元网格划分软件,而国内没有类似的软件。
另外,在对各种不同的异质体材料微观组织结构进行有限元网格划分方面,没有发现专门的文献,更谈不上网格划分技术的系统化。
有鉴于此,在微观组织结构可视化的基础上,选择大型通用有限元软件ABAQUS和自己开发的软件TransMesh系统的进行了异质体材料微观组织结构的有限元网格划分,为今后的异质体材料微观组织结构的有限元模拟与分析提供了有效的手段。
1. 问题的提出任何一个问题的有限元分析,通常由三个步骤组成:前处理,模拟计算和后处理[1]。
与众多的有限元分析软件相比,ABAQUS具有超强的模拟计算和通用的分析能力,同时在前处理功能上也暴露出了明显的不足。
这种不足在对复杂微观组织结构建模的过程中表现地尤为突出。
对于大多数宏观物体而言,无论直接通过ABAQUS/CAE所提供的绘图功能,或者是通过ABAQUS本身与绘图功能强大的CAD软件的接口,都可以用手工作图的方式建立相应的模型。
有限元网格划分原则

有限元网格划分原则划分网格是建立有限元模型的一个重要环节,它要求考虑的问题较多,需要的工作量较大,所划分的网格形式对计算精度和计算规模将产生直接影响。
为建立正确、合理的有限元模型,这里介绍划分网格时应考虑的一些基本原则。
1 网格数量网格数量的多少将影响计算结果的精度和计算规模的大小。
一般来讲,网格数量增加,计算精度会有所提高,但同时计算规模也会增加,所以在确定网格数量时应权衡两个因素综合考虑。
在决定网格数量时应考虑分析数据的类型。
在静力分析时,如果仅仅是计算结构的变形,网格数量可以少一些。
如果需要计算应力,则在精度要求相同的情况下应取相对较多的网格。
同样在响应计算中,计算应力响应所取的网格数应比计算位移响应多。
在计算结构固有动力特性时,若仅仅是计算少数低阶模态,可以选择较少的网格,如果计算的模态阶次较高,则应选择较多的网格。
在热分析中,结构内部的温度梯度不大,不需要大量的内部单元,时可划分较少的网格。
2. 网格疏密网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分布特点。
在计算数据变化梯度较大的部位(如应力集中处),为了较好地反映数据变化规律,需要采用比较密集的网格。
而在计算数据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。
这样,整个结构便表现出疏密不同的网格划分形式。
划分疏密不同的网格主要用于应力分析(包括静应力和动应力),而计算固有特性时则趋于采用较均匀的网格形式。
这是因为固有频率和振型主要取决于结构质量分布和刚度分布,不存在类似应力集中的现象,采用均匀网格可使结构刚度矩阵和质量矩阵的元素不致相差太大,可减小数值计算误差。
同样,在结构温度场计算中也趋于采用均匀网格。
3. 单元阶次许多单元都具有线性、二次和三次等形式,其中二次和三次形式的单元称为高阶单元。
选用高阶单元可提高计算精度,因为高阶单元的曲线或曲面边界能够更好地逼近结构的曲线和曲面边界,且高次插值函数可更高精度地逼近复杂场函数,所以当结构形状不规则、应力分布或变形很复杂时可以选用高阶单元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ABAQUS有限元网格划分基础
Simwe会员ilovenili
摘要:ABAQUS中的MESH步可以产生一个集合的网格划分,根据分析的需要,你可以对网格划分的方式进行控制,系统会自动产生不同的网格划分。
当你修改PART步和ASSEMBLY步中的参数时,系统在此步会自动生成适合于这个模型的网格划分。
当然,由于ABAQUS在网格划分方面的功能还不够强大,不能够完全按照作者的意图随心所欲的进行划分,因此,可以用Patran或Hypermesh等软件生成网格,然后导入至CAE中。
下面我们讲述一下ABAQUS对二维的结构化网格划分。
关键词:网格,逻辑,二维,三结点单元,四结点单元
1二维结构化网格划分:
具有以下特征的二维区域才可以进行结构化网格划分:
1.1区域内没有孔洞,孤立的边,或者是孤立的点。
1.2模型区域有三到五条逻辑边(我们可以把近乎直线的两条边看作是一条逻辑边,如下图所示)组成,每条边之间相互连接。
(如红线所示的两条边均可以看作是一条逻辑边)
一般来讲,在三种划分方法中,结构化划分方法能够最好的对CAE所产生的网格进行控制。
如果你想用完全四边形元素对一个四条边区域进行网格划分,那么网格单元的边在边界上必须分布均匀。
对于三边形或五边形区域,限制条件将会更加复杂。
当使用结构化划分时,系统会考虑种子分布(所谓的种子分布是指种子的空间排布,与种子的数量无关。
比如说,种子分布关心的是种子到底是沿着一条边均匀的排列还是在这条边的末端更加集中一些).不过,在两个区域过渡的地方网格必须协调,比如说,两个相邻的区域分别用的是结构化和自由网格划分,那么系统就可能调节网格区域的结点以使得过渡区域的网格划分协调,正因为如此,可能使得实际的元素结点不相互匹配。
当你用结构化主导四边形元素划分一个四边形区域时,系统会插入一个单独的三角形,由此产生的网格很好的与种子相匹配,如下图所示:
然而,当你用结构化主导四边形元素划分三边或五边形区域时,系统将不会插入任何三角形,由此产生的网格使用的是完全四边形元素;而且网格也可能与种子不匹配。
如果两条边所成的角度很小的话,系统会自动将这两条边看作成一条逻辑边.因此,对于一个五边形区域而言,将会应用一个四边形的网格划分模式。
如下所示:
如果你想用结构化四边形元素对一个区域进行网格划分,那么这个区域必须要有比较规则的形状,否则系统将会生成一个无效的网格。
下图即为所展示的无效的网格。
如果发生上图这种网格中包含无效的元素,我们可以用三种方法去纠正①调整网格种子的位置②利用Redefine the region corners命令③将区域分割为更小且形状更规则的区域。
运用这三种方法所得的结果如下图所示:
2下面我们将要介绍的是用于元素控制的四种基本类型。
2.1Full integration:完全积分:所谓完全积分是指当单元具有规则形状时,所用的高斯积分点可以对单元刚度矩阵中的多项式进行精确的积分。
线性单元如果要完全积分,则在每个方向需要两个积分点。
而二次单元如果要完全积分则在每一方向需要三个积分点。
如下所示:
注意,只有当能确切的认为在你的模型中载荷将产生小位移时,才可采用完全积分线性单元。
而如果你怀疑载荷产生的位移类型,则应采用不同的单元类型。
在复杂的应力状态下,完全积分二次单元也可能发生琐死。
因此,如果在模型中有此单元,则应仔细的检查计算的结果。
但是,对于模拟局部应力集中区域,完全积分线性单元将是非常有用的。
2.2Reduced integration:减缩积分:只有四边形和六面体单元才能采用减缩积分;而所有的锲形、四面体和三角形实体单元采用完全积分,尽管它们可以与减缩积分的六面体或四边形单元在相同的网格中。
减缩积分单元比完全积分单元在每个方向上少用一个积分点。
减缩积分线性单元只在单元中心有一个积分点。
对于减缩积分四边形单元,其积分点的位置如下所示:
注意:线性减缩积分单元由于存在着所谓沙漏(hourglassing)数值问题而过于柔软。
在ABAQUS中,对减缩积分单元引入少量的人工“沙漏刚度”(hourglass stiffness)以限制沙漏模式的扩展。
当模型中应用更多的单元时,这种刚度在限制沙漏模式是更有效的,这意味着只要采用合理的细网格线性减缩积分单元就会给出可接受的结果。
线性减缩积分单元对变形的要求不严格;因此可在变形较大的任何模拟中采用划分较细的此类单元。
二次减缩单元也有沙漏模式。
但是在正常的网格中这种模式几乎不可能扩展,并且在网格足够细时很少成为问题。
C3D20R的1×6网格确实表现出一些沙漏性,但更精确的网格则没有这种现象。
即使受复杂应力状态,二次减缩积分单元也不易受影响而导致锁死。
因此,一般来说,除了包含较大应变的大位移模拟和一些接触分析外,这些单元对最通用的应力/位移模拟是最好的选择。
2.3Incompatible modes:非协调单元:非协调单元可以用来克服完全积分一阶单元的剪力自锁问题。
剪力自锁是由于单元的位移场不能模拟与弯曲相联系的运动学现象而引起的,那么可把能够增强单元位移梯度的附加自由度引入到一阶单元。
在弯曲问题中,用非协调单元可得到与二次单元相当的结果,且计算费用明显降
低。
非协调单元之所以有用,是因为它们如果应用得当,则在很低花费时仍可以得到较高的精度。
但必须注意保证单元扭曲是非常小的,然而当网格较复杂时这一点是很难保证的;因此,对于具有这种几何形状的模型,你应再一次考虑应用减缩积分二次单元,因为它们对网格扭曲不太敏感。
2.4Hybrid formulation:杂交单元:对于ABAQUS的每一个实体单元,如所有减缩积分单元和非协调单元,都可得到一个杂交单元形式。
当材料是不可压缩的(泊松比=0.5)或非常接近于不可压缩(泊松比﹥0.495)时采用杂交单元。
橡胶是一种具有不可压缩性质的材料。
不能用规则单元来模拟不可压缩材料的反应(除了平面应力情况),这是因为在单元中的压应力是不确定的。
建议:如何使用实体单元?
在模拟计算中,如果要想以合理的费用达到精确的结果,则正确的选择单元是非常关键的。
当使用ABAQUS经验更多时,你无疑会针对各种应用的特殊要求,自己建立选择单元的规则。
但是当你开始使用ABAQUS时应参考下面的建议:
2.4.1如果不需要模拟非常大的应变或进行一个复杂的,改变接触条件的问题,则应采用二次减缩积分单元(CAX8R,CRE8R,CPS8R.C3D20R等)。
2.4.2如果存在应力集中,则应在局部采用二次完全积分单元(CAX8,CPE8,CPS8,C3D20等)。
它们可在较低费用下对应力梯度提供最好的解决。
2.4.3对含有非常大的网格扭曲模拟(大应变分析),采用细网格划分的线性减缩积分单元(CAX4R,CPE4R.CPS4R,C3D8R等)。
2.4.4对接触问题采用线性减缩积分单元或非协调单元(CAX4I,CPE4I,CPS4II,C3D8I 等)的细网格划分。
2.4.5如果在模型中采用非协调单元应使网格扭曲减至最小。
2.4.6三维情况应尽可能采用块状单元(六面体)。
它们在最小费用下给出了最好的结果。
当几何形状复杂时,完全采用块状单元构造网格会很困难;因此可能有必要采用楔形和四面体单元。
这些单元的线性形式,如C3D6和C3D4,众所周知是较差的单元(若需要时,划分较细的网格以使结果达到合理的精度);因此,只有在完成网格万不得已的情况下才会应用这些单元,即使那时,这些单元也应远离需要精确求解的区域。
2.4.7一些前处理程序包括网格划分方法,它们可用四面体单元构造任意形状的网格。
只要采用二次四面体单元(C3D10),其结果对小位移问题应该是合理的。
但运行将比采用相应的块体单元网格花费更多的时间。
你不应采用只包含线性四面体单元(C3D4)的网格,因为如果不用大量的单元其结果将是不准确的。
参考文献:
[1] ABAQUS/Standard User’s Manual
[2] ABAQUS/CAE User’s Manual
[3] ABAQUS/Standard 有限元软件入门指南 庄茁等 译。
