第二讲 面板数据回归模型
第二讲面板数据线性回归模型
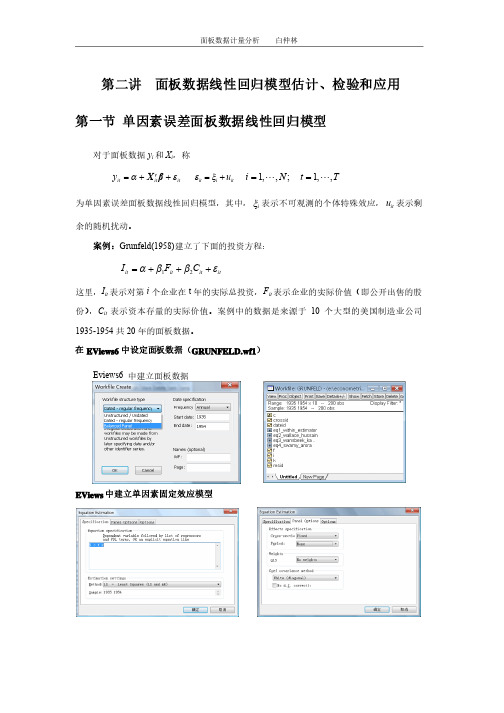
Eviews6 中建立面板数据中建立面板数据 EViews中建立单因素固定效应模型1.1 混合回归模型1 面板数据混合回归模型假设1 ε ~ N (0, σ2I NT ) 对于面板数据y i 和X i ,无约束的线性回归模型是y i = Z i δi + εi i =1, 2, … , N(4.1) 其中'i y = ( y y i 1, … , y iT ),Z i = [ ιT , X i ]并且X i 是T×K 的,'i δ是1×(K +1)的,εi 是T×1的。
的。
注意:各个体的回归系数δi 是不同的。
是不同的。
如果面板数据可混合,则得到有约束模型如果面板数据可混合,则得到有约束模型y = Zδ + ε (4.2)其中Z ′ = ('1Z ,'2Z , … ,'N Z ),u ′ = ('1ε,'2ε, … ,'N ε)。
2 混合回归模型的估计当满足可混合回归假设时,当满足可混合回归假设时,()1''ˆZ Z Z Y −=δ在假设1下,对于Grunfeld 数据,基于EViews6建立的混合回归模型建立的混合回归模型3 面板数据的可混合性检验假设检验原理:基于OLS/ML 估计,对约束条件的检验。
估计,对约束条件的检验。
(1) 面板数据可混合的检验 推断面板数据可混合的零假设是:推断面板数据可混合的零假设是:10H :对于所有的i 都有δi = δ. 检验约束条件的统计量是Chow 检验的F 统计量统计量()()1res ures 'uresSSE SSE (N )K'SSEN T K−−−()(y X x u u =−+−βy x −效应检验检验面板数据固定效应模型设定的零假设是:检验面板数据固定效应模型设定的零假设是:()()()1resuresures SSE SSE N SSE NT N K −−−−ξi 是独立于it u ,对于所有的(y x u αβξ=+++和随机效应的Hausman检验不能拒绝零假设。
面板数据回归分析

引言概述:正文内容:一、理论基础1.面板数据的概念和特点2.面板数据模型的基本假设3.面板数据回归分析的理论基础和背景4.面板数据回归模型的常见形式5.面板数据回归模型的参数估计方法二、面板数据的处理与描述统计1.面板数据的基本处理方法2.面板数据的描述统计分析3.面板数据的基本图表分析4.面板数据的异方差和自相关检验5.面板数据的稳健标准误估计与统计推断三、面板数据的固定效应模型1.固定效应模型的基本原理2.固定效应模型的参数估计方法3.固定效应模型的推断性分析4.固定效应模型的诊断检验5.固定效应模型的应用与解释四、面板数据的随机效应模型1.随机效应模型的基本原理2.随机效应模型的参数估计方法3.随机效应模型和固定效应模型的比较4.随机效应模型的推断性分析5.随机效应模型的应用和实证研究五、面板数据的时间序列模型1.面板数据时间序列模型的基本原理2.面板数据时间序列模型的参数估计方法3.面板数据时间序列模型的推断性分析4.面板数据时间序列模型的预测和预测精度评估5.面板数据时间序列模型的应用案例分析总结:本文探讨了面板数据回归分析的相关理论和方法,并提供了详细的应用案例和实证分析。
面板数据回归分析是一种重要的数据分析工具,可以有效应用于经济学领域的研究和实践中。
掌握面板数据回归分析的理论模型和技术方法,对于深入研究经济问题,解决实际经济问题具有重要意义。
在未来的研究和实践中,面板数据回归分析将继续发挥重要作用,为我们提供更多洞察经济现象的途径。
引言概述:面板数据回归分析是经济学领域常用的一种统计分析方法,它用于研究多个个体(如国家、公司、家庭等)在不同时间点上的变化情况,使得我们能够更全面地理解经济现象。
本文将详细介绍面板数据回归分析的基本概念、模型设定、估计方法以及结果解释等,旨在帮助读者更好地理解和应用面板数据回归分析。
正文内容:一、面板数据回归分析的基本概念1.1面板数据的定义与分类1.2面板数据的特点与优势二、面板数据回归模型的设定2.1固定效应模型2.1.1模型假设2.1.2模型设定及估计方法2.2随机效应模型2.2.1模型假设2.2.2模型设定及估计方法2.3混合效应模型2.3.1模型假设2.3.2模型设定及估计方法三、面板数据回归模型的估计方法3.1最小二乘法估计(OLS)3.2差分法估计(FD)3.3广义矩估计(GMM)3.4最大似然估计(MLE)四、面板数据回归模型结果的解释与分析4.1固定效应模型结果的解释与分析4.2随机效应模型结果的解释与分析4.3混合效应模型结果的解释与分析五、面板数据回归分析的拓展应用5.1异方差面板数据回归分析5.2面板数据回归模型中的内生性问题5.3面板数据回归模型的非线性扩展总结:面板数据回归分析作为一种重要的经济学研究方法,在许多领域中都有广泛的应用。
面板数据模型 (2)

面板数据模型1. 引言面板数据模型(Panel Data Model)是一种针对面板数据分析的统计模型。
面板数据也称为纵向数据或者长期追踪数据,在经济学和社会科学领域广泛应用。
面板数据由包含多个个体和多个时间点的观测数据组成,可以提供比截面数据(cross-sectional data)更多的信息。
本文将介绍面板数据模型的基本概念、应用领域、建模方法和相关统计分析技术。
2. 面板数据模型的基本概念2.1 面板数据的构成面板数据由个体维度和时间维度两个维度构成。
个体维度指的是一组被观察的个体,可以是人、公司、地区等;时间维度指的是一段时间内的观测点,可以是年、月、季度等。
面板数据是在个体和时间维度上的交叉观测数据。
2.2 面板数据的类型面板数据分为平衡面板数据和非平衡面板数据。
平衡面板数据指的是所有个体在每个时间点上都有观测值;非平衡面板数据指的是个体在某些时间点上缺少观测值。
2.3 面板数据模型的优势相比于截面数据和时间序列数据,面板数据有以下几个优势:•能够控制个体固定效应:面板数据模型可以减少个体固定效应的干扰,提高模型的解释能力;•能够捕捉个体间的异质性:面板数据模型可以捕捉个体之间的差异和变动,提供更全面的分析结果;•提供更多的信息和数据点:面板数据相对于时间序列数据,提供了更多的观测点,可以提高统计分析的准确性。
3. 面板数据模型的应用领域面板数据模型在经济学、金融学、社会学等领域广泛应用,具体领域包括但不限于:•劳动经济学:分析个体的劳动供给行为和工资决定因素;•金融学:评估公司和证券的风险和收益;•医学研究:研究药物治疗的效果和副作用;•教育经济学:评估教育政策的效果和影响;•发展经济学:分析发展中国家的经济增长和贫困问题。
4. 面板数据模型的建模方法面板数据模型的建模方法主要包括固定效应模型(Fixed Effects Model)和随机效应模型(Random Effects Model)。
面板数据模型 (2)

面板数据模型面板数据模型是一种用于可视化面板的数据结构。
面板是一种数据可视化工具,它可以将数据以图表、表格、图像等形式展示出来,帮助用户更直观地理解数据。
1. 什么是面板数据模型?面板数据模型是一种用于表示面板数据的数据结构。
它由以下几个要素组成:•数据源(Data Source):数据源是面板中使用的数据的来源。
数据源可以是各种类型的数据,包括数据库、文件、API接口等。
面板可以从一个或多个数据源中获取数据。
•指标(Metric):指标是面板中展示的数据的具体指标。
指标可以是一些统计数据,如平均值、总和、最大值等。
面板可以同时展示多个指标。
•维度(Dimension):维度是用于分类和分组数据的属性。
维度可以是日期、地理位置、产品类型等。
面板可以通过维度对数据进行分组,从而提供更多的数据分析维度。
•图表类型(Chart Type):面板可以根据数据的特点选择合适的图表类型进行展示。
常见的图表类型有折线图、柱状图、散点图等。
2. 面板数据模型的关键元素面板数据模型由以下几个关键元素组成:•表格(Table):表格是面板中最基本的展示方式,它将数据以表格的形式展示出来。
表格由多行和多列组成,每行表示一个数据项,每列表示一个指标或维度。
表格可以方便地查看每个数据项的具体数值。
•图表(Chart):图表是面板中常用的展示方式,它以图形的形式展示数据。
图表可以根据数据的特点选择不同的类型,如折线图可以展示数据的趋势变化,柱状图可以展示数据的比较关系。
•过滤器(Filter):过滤器可以用于筛选展示的数据。
通过设置过滤器,用户可以根据需要过滤掉一些数据,只展示感兴趣的数据。
过滤器可以设置在维度上,也可以设置在指标上。
•时间轴(Time Range):时间轴是面板中用于选择数据展示时间范围的工具。
用户可以通过时间轴选择展示的时间跨度,如按小时、按天、按周等。
3. 应用举例以下是一个简单的面板数据模型的应用举例:---title: 面板数据模型示例---# 面板数据模型示例## 数据源本面板使用的数据源为数据库中的销售数据。
面板数据回归分析

Y i i 0 1 X 1 i 2 X 2 i 3 X 3 i u i , i 1 , 2 , ,N
Y i tY i1 (X 1 i t X 1 i)2 (X 2 it X 2 i)3 (X 3 it X 3 i) u it u i,
7.1 面板数据模型
7.1.2 面板数据模型 Y iti01X 1 it2X 2it3X 3itu i,t
i1 ,2 , ,N ;t1 ,2 , ,T
➢ 假设 2: Var(uit) u2,
Cov(uit,uis) E(uituis) 0, t s, Cov(uit,ujt) E(uitujt) 0, i j, Cov(uit,ujs) E(uitujs) 0, (i,t) ( j, s), i 1,2,, N;t 1,2,,T
7.3 随机效应模型估计
7.3.2 用EViews7.2估计随机效应模型
数据导入、数据结构转换以及模型设定 与固定效应模型估计一样,不同的是在 panel option的cross section中选Random,2 还有 u2 和 的估计方法
7.3 随机效应模型估计
7.3.2 用EViews7.2估计随机效应模型
7.2 固定效应模型估计
7.2.2 用EViews7.2估计固定效应模型
例子7.2 教育的回报
EViews操作:
7.3 随机效应模型估计
7.3.1 随机效应模型估计 7.3.2 用EViews7.2估计随机效应模型
7.3 随机效应模型估计
7.3.1 随机效应模型估计
Y it01X 1it2X2it3X3itvi,t vitiui,t i1,2, ,N ;t1,2, ,T
面板数据回归(Panel Data)

随机效应面板模型 Random-Effect Panel Model
id year y
x1 x2 x3 x4
1001 1 2000 25 400 2400 7.78
0 1000 6.91
1003 3
0
20 30 30 3.43
• 如果总体很大,抽取的样本单位具有较大 的随机性,那么与个体有关的效应将被视 为具有随机分布的性质
基本假设
yit ci xit uit
• 假设RE.1
• (a) 严格外生性
E(uit|xi,ci)=0,
t=1,2,⋯,T
xi=xi1,xi2,⋯,xiT
• 如果Ti对于每个单位都相同,叫平衡面板 (Balanced Panel)
• 如果Ti对于每个单位不都相同,叫不平衡面 板(Unbalanced Panel)
– 对于非平衡面板数据,我们关心非平衡是否是内 生的
• 比如,yit是收入,随着时间流逝富人更容易退出样本,因 为他们的时间成本比较高,此时数据的非平衡就是内生引起 的 • 此时,即使最初的模型是线性模型,yit的条件期望是xit 的 线性函数,我们需要非线性的样本选择方法
– 所谓的POLS方法,是指对所有跨i和t的观测值 进行OLS回归,对模型进行POLS回归
– 但是个体异质性往往和解释变量相关,此时用 POLS估计得到的估计量是有偏且不一致的, 此偏差称为异质性偏差(heterogeneity bias), 这是遗漏(不随时间变化的)变量引起的偏差
严格外生性假设
• 检验假设:H0: σ2c = 0,即vit不存在序列相关
第16章:面板数据回归模型
提供更多个体动态行为的信息 例如,对于失业问题,截面数据能告诉 我们在某个时点上哪些人失业,而时间序列 数据能告诉我们某个人就业与失业的历史, 但这两种数据均无法告诉我们是否失业的总 是同一批人(意味着低流转率,low turnover rate),还是失业的人群总在变动 (意味着高流转率,high turnover rate) 面板数据可能解决此类问题
477.6000 488.1951 512.0038 529.4399 595.4147 627.1859 720.5337 754.6824 756.4338 738.1251
412.4400 445.6976 450.5022 474.4142 510.8094 571.2644 639.0028 666.0424 707.5816 650.5806
陈文静
22
为什么使用面板数据?
(7)解决遗漏变量问题 在计量经济建模过程中,遗漏变量偏差是 一个普遍存在的问题,遗漏变量常常是不可 观测的个体差异或“异质性”造成的,如果 这种个体差异“不随时间而改变”,则面板 数据提供了解决遗漏变量的方法。
暨南大学经济学院统计系
陈文静
23
为什么使用面板数据?
352.8409
356.1099 376.3157 389.0615 417.7114 459.3653 519.7328 550.2303 574.9075
300.5505
311.4781 316.4172 324.9145 347.8568 381.5282 424.2052 425.7236 422.8841
暨南大学经济学院统计系 陈文静 14
表
中国城乡居民消费——收入统计数据
第二讲 面板数据回归模型
第二讲 面板数据回归模型2.1面板数据回归模型的一般形式 面板数据模型的一般形式如下:it Kk kit ki it u x y +=∑=1β (2.1)其中,N ,,,,i "321=,表示N 个个体;T ,,,,t "321=,表示已知的T 个时点。
it y 是被解释变量对个体i 在t 时的观测值;kit x 是第k 个非随机解释变量对于个体i 在t 时的观测值;ki β是待估计的参数;it u 是随机误差项。
用矩阵表示为i i i i =+Y X βU (N ,,,,i "321=) (2.1’)其中,121i i i iT T y y y ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#Y ,112111222212i i Ki i i Ki i iTiTKiT T K x x x x x x x x x ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦""##"#"X , 121×⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=K Ki i i i βββ#β,121i i iiT T u u u ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#U .2.2 面板数据回归模型的分类通常,对模型(2.1)将做许多限制性假设,使其成为不同类型的面板数据回归模型。
一般来说,常用的面板数据回归模型有如下九种模型,下面分别介绍它们。
1混合回归模型从时间上看,不同个体之间不存在显著性差异;从截面上看,不同截面之间也不存在显著性差异,那么就可以直接把面板数据混合在一起,用普通最小二乘法(OLS )估计参数。
即估计模型12Kit k kit it k y x u ββ==++∑ (2.2)=+Y X U β (2.2’)其中,121N NT ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#Y Y Y Y ,12N NT K×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#X X X X ,121×⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=K K βββ#β,121N NT ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#U U U U .实际上,混合回归模型(Pooled Regression Models )假设了解释变量对被解释变量的影响与个体无关。
面板数据回归分析报告
v 2V(avit)r 2u 2 ;
Co (vit,v vis) 2,ts
2021/4/26
29
7.3 随机效应模型估计
7.3.1 随机效应模型估计 Y it01X 1 it2X 2it3X 3itvit, vitiuit,i1 ,2, ,N ;t1 ,2, ,T
• 上述模型不存在内生性,OLS估计有一致性,但是 v it 不满足不相关假设,OLS估计不是最优估计,要获得 最优估计,需要作变换
•
14、抱最大的希望,作最大的努力。2 022年5 月4日 星期三2 022/5/ 42022/ 5/42022 /5/4
•
15、一个人炫耀什么,说明他内心缺 少什么 。。202 2年5月 2022/5 /42022 /5/4202 2/5/45 /4/2022
•
16、业余生活要有意义,不要越轨。2 022/5/ 42022/ 5/4May 4, 2022
第7章
面板数据回归分析
2021/4/26
精品
1
面板数据回归分析
7.1 面板数据模型
7.1.1 面板数据 7.1.2 面板数据模型
7.2 固定效应模型估计
7.2.1 固定效应模型估计 7.2.2 用EViews7.2估计固定效应模型
2021/4/26
2
面板数据回归分析
7.3 随机效应模型估计
7.3.1 随机效应模型估计 7.3.2 用EViews7.2估计随机效应模型
7.3.1 随机效应模型估计
Y it01X 1it2X2it3X3itvit, vitiuit,i1,2, ,N ;t1,2, ,T
• 随机效应假设了 i 与模型自变量不相关, 因此关心的问题不再是内生性,而是如何 提高估计的有效性,即探索复合误差项 vit i uit 的方差结构。
如何使用Stata进行面板数据回归分析
如何使用Stata进行面板数据回归分析Stata是一种流行的统计软件,广泛用于经济学、社会学、医学和其他社会科学领域的数据分析和建模。
面板数据回归分析是一种常用的统计方法,用于研究在时间和横截面上变化的数据。
本文将介绍如何使用Stata进行面板数据回归分析。
一、数据准备在进行面板数据回归分析之前,首先需要准备好面板数据集。
面板数据集包括多个个体在不同时间点上的观测值。
通常,面板数据可分为两种类型:平衡面板数据和非平衡面板数据。
平衡面板数据指的是每个个体在每个时间点上都有观测值,而非平衡面板数据则允许个别个体在某些时间点上缺失观测值。
准备好数据后,可以使用Stata导入数据集。
可以使用命令“use 文件路径/文件名”来加载数据集。
确保数据集的格式正确,并且数据已按照面板数据的要求进行排序。
二、面板数据回归模型面板数据回归模型是通过建立个体和时间的固定效应模型来进行的。
常见的面板数据回归模型包括固定效应模型(Fixed Effects Model)和随机效应模型(Random Effects Model)。
1. 固定效应模型固定效应模型是一种控制个体固定特征的面板数据回归模型。
固定效应模型通过添加个体固定效应来控制个体固有特征,假设个体固定效应与解释变量无关。
可以使用命令“xtreg 因变量自变量1 自变量2, fe”来估计固定效应模型。
2. 随机效应模型随机效应模型是一种包含个体和时间随机效应的面板数据回归模型。
随机效应模型允许个体和时间效应与解释变量相关,并且具有更强的灵活性。
可以使用命令“xtreg 因变量自变量1 自变量2, re”来估计随机效应模型。
三、结果解释和分析在进行面板数据回归分析后,可以对结果进行解释和分析。
常见的结果输出包括回归系数、标准误、t值和p值等。
1. 回归系数回归系数表示自变量对因变量的影响程度。
回归系数的符号表示影响方向,正系数表示正向影响,负系数表示负向影响。
回归系数的绝对值大小表示影响程度的强弱。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二讲 面板数据回归模型2.1面板数据回归模型的一般形式 面板数据模型的一般形式如下:it Kk kit ki it u x y +=∑=1β (2.1)其中,N ,,,,i "321=,表示N 个个体;T ,,,,t "321=,表示已知的T 个时点。
it y 是被解释变量对个体i 在t 时的观测值;kit x 是第k 个非随机解释变量对于个体i 在t 时的观测值;ki β是待估计的参数;it u 是随机误差项。
用矩阵表示为i i i i =+Y X βU (N ,,,,i "321=) (2.1’)其中,121i i i iT T y y y ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#Y ,112111222212i i Ki i i Ki i iTiTKiT T K x x x x x x x x x ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦""##"#"X , 121×⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=K Ki i i i βββ#β,121i i iiT T u u u ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#U .2.2 面板数据回归模型的分类通常,对模型(2.1)将做许多限制性假设,使其成为不同类型的面板数据回归模型。
一般来说,常用的面板数据回归模型有如下九种模型,下面分别介绍它们。
1混合回归模型从时间上看,不同个体之间不存在显著性差异;从截面上看,不同截面之间也不存在显著性差异,那么就可以直接把面板数据混合在一起,用普通最小二乘法(OLS )估计参数。
即估计模型12Kit k kit it k y x u ββ==++∑ (2.2)=+Y X U β (2.2’)其中,121N NT ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#Y Y Y Y ,12N NT K×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#X X X X ,121×⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=K K βββ#β,121N NT ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#U U U U .实际上,混合回归模型(Pooled Regression Models )假设了解释变量对被解释变量的影响与个体无关。
关于参数的这种假设被广泛应用,但是,在许多问题的研究中,混合回归模型并不适用(Mairesse & Griliches ,1990)。
2 固定效应模型在面板数据线性回归模型中,如果对于不同的截面或不同的时间序列,只是模型的截距项是不同的,而模型的斜率系数是相同的,则称此种模型为固定效应模型(fixed effects regression model )。
固定效应模型分为3种类型,即个体固定效应模型(entity fixed effects regression model )、时点固定效应模型(time fixed effects regression model )和时点个体固定效应模型(time and entity fixed effects regression model )。
(1)个体固定效应模型个体固定效应模型是对于不同的纵剖面时间序列(个体)只有截距项不同的模型2Kit i k kit it k y x u λβ==++∑ (2.3)或者表示为矩阵形式()N T =⊗++Y I X U ιλβ (2.3’)其中,N T ⊗I ι是N 阶单位矩阵N I 和T 阶列向量()11'T ,,="ι的克罗内克积,121N N λλλ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#λ,()2131122322231i i Ki i i Ki i iT iT KiT T K x x x x x x x x x ×−⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦""##"#"X ,()121N NT K ×−⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#X X X X ,()2311K K βββ−×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#β. (2)时点固定效应模型时点固定效应模型就是对于不同的截面(时点)有不同截距的模型。
如果确知对于不同的截面,模型的截距显著不同,但是对于不同的时间序列(个体)截距是相同的,那么应该建立时间固定效应模型it Kk kit k t it u x y ++=∑=2βγ (2.4)其矩阵表示为()N T =⊗++Y I X U ιγβ (2.5)其中,T N I ⊗ι是N 阶列向量()'N ,,11"=ι和T 阶单位矩阵T I 的克罗内克积,121T T γγγ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#γ,()2131122322231i i Ki i i Ki i iT iT KiT T K x x x x x x x x x ×−⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦""##"#"X ,()121N NT K ×−⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#X X X X ,()2311K K βββ−×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#β. (3)时点个体固定效应模型时点个体固定效应模型就是对于不同的截面(时点)、不同的时间序列(个体)都有不同截距的模型。
如果确知对于不同的截面、不同的时间序列(个体)模型的截距都显著地不相同,那么应该建立时点个体固定效应模型,表示如下,2Kit i t k kit it k y x u λγβ==+++∑ (2.6)其矩阵表示为()()N T N T =⊗+⊗++Y I I X U ιλιγβ(2.7) 其中,N ,,,,i "321=,表示N 个个体;T ,,,,t "321=,表示已知的T 个时点。
实际上,如果模型(2.1)中存在缺失了随时点或个体变化的不可观测的重要确定性解释变量,则在模型中应该引入虚拟变量,设定模型为固定效应模型。
对于固定效应模型可以采用在模型中加虚拟变量的方法估计回归参数,并称这种回归为最小二乘虚拟变量(The Least Square Dummy Variable )回归,简记为LSDV 回归。
也可以采用广义最小二乘法的协方差分析(Analysis of Covariance )法估计固定效应模型参数,简记为ANCOVA 回归。
3 随机效应模型 如果模型it Kk kit k it u x y ++=∑=21ββ (2.8)中缺失了分别随个体和时间变化的不可观测随机性因素时,可以通过对误差项的分解来描述这种信息的缺失,即,将模型误差项分解为3个分量it i t it u u v w =++ (2.9)其中,u i ,v t 和w it 分别表示个体随机误差分量、时间随机误差分量和混合随机误差分量。
同时,还假定u i ,v t ,w it 之间互不相关,各自分别不存在截面自相关、时间自相关和混合自相关。
这时,模型(2.1)被称为随机效应模型或误差分解模型。
对于误差分解模型可以采用广义最小二乘法(GLS )估计模型参数。
4 确定系数面板数据模型在面板数据模型(2.1)中,如果解释变量对被解释变量的影响随着个体的变化是不同的确定性参数时,称模型(2.1)为确定系数面板数据模型。
确定系数面板数据模型的矩阵形式为Zellner (1962)的似不相关回归模型(Seemingly Unrelated Regressions )=+Y X U β (2.10)其中,12000000N NT NK×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦""##%#X X X X ,121i i i ki K βββ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#β,121N KN ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#ββββ 5 随机系数面板数据模型面板数据模型(2.1)揭示了不同个体的相同经济现象,于是,如果N 个个体是从某个总体随机抽取的一个样本时,面板数据模型(2.1)的参数列向量i β就是随机向量。
另外,如果个体间是空间相关时,面板数据模型(2.1)的N 个参数列向量的集合{}12i |i ,,,N ="β可以被看成是同一个总体的N 个样本。
这时,称面板数据回归模型(2.1)为随机系数回归模型(Random Coefficient Regression Model ),即,i i =+ββv (12i ,,,N =")其中,β是固定向量,i v 是零均值的随机向量。
从而,面板数据模型(2.1)可以表示为()i i i i =++Y X v U βi i i =+Y X W β (2.11)其中,i i i i =+W X v U 。
这样,利用广义最小二乘法估计模型(2.11)得到的估计量()()111ˆ=''−−−βΩΩX X X Y 比混合回归模型(2.2)的估计量更有效,其中,Ω是⎛⎞⎜⎟⎜⎟=⎜⎟⎜⎟⎝⎠#1N W W W W 的方差协方差矩阵。
有关面板数据静态回归模型的分类和模型设定可用图2.1概括。
图 2.1 线性面板数据模型概述6 平均个体回归模型首先,对每个个体在时点上建立模型,并估计参数。
然后,计算各个体的参数估计值的平均值,将此值作为面板模型的参数估计。
对于给定的个体i ,估计多元回归模型it Kk kit ki it u x y +=∑=1β (T ,,,,t "321=)的参数ki β的估计量kiˆβ;然后,以N 个个体参数估计量的均值 11Nkkii ˆˆNββ==∑ (K ,,,,k "321=) (2.12)作为模型参数ki β的估计量。
一般来说,当面板数据的个体较少、时间序列较长,且个体差异不显著时,才会用平均个体回归方法估计模型参数。
这种面板数据通常是宏观经济的面板数据。
7 平均时间回归模型先对各变量的数据在时间上计算平均值,然后对按时间平均的截面数据回归。
即估计截面数据的多元回归模型i Kk .ki k .i u x y +=∑=1β (N ,,,,i "321=) (2.13)其中,.i y 和.ki x 分别是被解释变量和解释变量在时间上的平均值。
当面板数据的个体较多、时间序列较短,且时间差异不显著时,可用平均时间回归方法估计模型参数,且Pesaran (1995)指出,即使对于动态面板数据模型,该估计也是无偏的和一致的。
