大学物理-静电场练习题及答案
大连理工大学大学物理作业2(静电场二)及答案详解
1．如图所示，把点电荷q +从高斯面外P 移到R 处()OP OR =，O 为S 上一点，则[ ].A 穿过S 的电通量e φ发生改变，O 处E变.B e φ不变，E 变。
.C e φ变，E 不变。
.D e φ不变，E不变。
答案：【B 】[解]闭合面外的电荷对穿过闭合面的电通量无贡献，或者说，闭合面外的电荷产生的电场，穿过闭合面的电通量的代数和为零；移动点电荷，会使电荷重新分布，或者说改变电荷的分布，因此改变了O 点的场强。
2．半径为R 的均匀带电球面上，电荷面密度为σ，在球面上取小面元S ∆，则S ∆上的电荷受到的电场力为[ ]。
.A 0 .B 22Sσε∆ .C2S σε∆ .D2204SRσπε∆答案：【B 】解：应用高斯定理和叠加原理求解。
如图所示。
面元S ∆上的电荷受到的库仑力是其他电荷在面元S ∆处产生的总电场强度1E与面元S ∆上的电荷量S Q ∆=∆σ的乘积：111E S E Q F∆=∆=σ。
面元S ∆处电场强度E是面元S ∆电荷在此产生的电场强度2E 与其他电荷在面元S∆处产生的总电场强度1E 的矢量和，21E E E+=。
首先，由高斯定理求得全部球面分布电荷在面元S ∆处产生的总电场强度 R E ˆ0εσ=其次，面元S ∆上的电荷量S Q ∆=∆σ对于面元S ∆来说，相当于无限大带电平面，因此，面元S ∆上的电荷量S Q ∆=∆σ在面元S ∆处产生的电场强度为R E ˆ202εσ=由叠加原理，其他电荷在面元S ∆处产生的总电场强度为 R E E E ˆ2021εσ=-=面元S ∆上的电荷量S Q ∆=∆σ受到的库仑力为RS R S E S E Q F ˆ2ˆ2020111εσεσσσ∆=∆=∆=∆= 注：本题可以用叠加原理直接进行计算，太麻烦。
3．如图所示，一个带电量为q 的点电荷位于立方体的A 角上，则通过侧面abcd 的电场强度通量等于[ ]。
.A06q ε .B 012q ε .C24qε .D48q ε答案：【C 】[解] ：如果以A 为中心，再补充上7个相同大小的立方体，则组成一个边长为小立方体边长2倍大立方体，点电荷q 位于大立方体的中心。
大学物理静电场练习题带标准答案
大学物理静电场练习题带答案————————————————————————————————作者：————————————————————————————————日期：大物练习题（一）1、如图，在电荷体密度为ρ的均匀带电球体中，存在一个球形空腔，若将带电体球心O 指向球形空腔球心O '的矢量用a 表示。
试证明球形空腔中任一点电场强度为 . A 、03ρεa B 、0ρεa C 、02ρεa D 、3ρεa2、如图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R ．试求环中心O 点处的场强A 、02πR λε-B 、0πRλε- C 、00ln 22π4λλεε+ D 、00ln 2π2λλεε+3、 如图所示，一导体球半径为1R ,外罩一半径为2R 的同心薄导体球壳, 外球壳所带总电荷为Q ,而内球的电势为0V ，求导体球和球壳之间的电势差 （填写A 、B 、C 或D ，从下面的选项中选取）。
A 、1020214R Q V R R πε⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ B 、102024R Q V R R πε⎛⎫- ⎪⎝⎭C 、0024Q V R πε- D 、1020214R Q V R R πε⎛⎫⎛⎫+-⎪ ⎪⎝⎭⎝⎭4.如图所示，电荷面密度为1σ的带电无限大板A 旁边有一带电导体B ，今测得导体表面靠近P 点处的电荷面密度为2σ。
求：（1）P 点处的场强 ；（2）导体表面靠近P 点处的电荷元S ∆2σ所受的电场力 。
A 、20σεB 、202σεC 、2202S σε∆D 、220S σε∆5．如图，在一带电量为Q 的导体球外，同心地包有一各向同性均匀电介质球壳，其相对电容率为r ε，壳外是真空，则在壳外P 点处(OP r =)的场强和电位移的大小分别为［ ］Q Opr)（A ）2200,44r Q QE D rr εεε==ππ； （B ）22,44r Q QE D r r ε==ππ； （C ）220,44Q QE D r r ε==ππ； （D ）2200,44Q QE D r r εε==ππ。
大学物理静电场练习题带答案
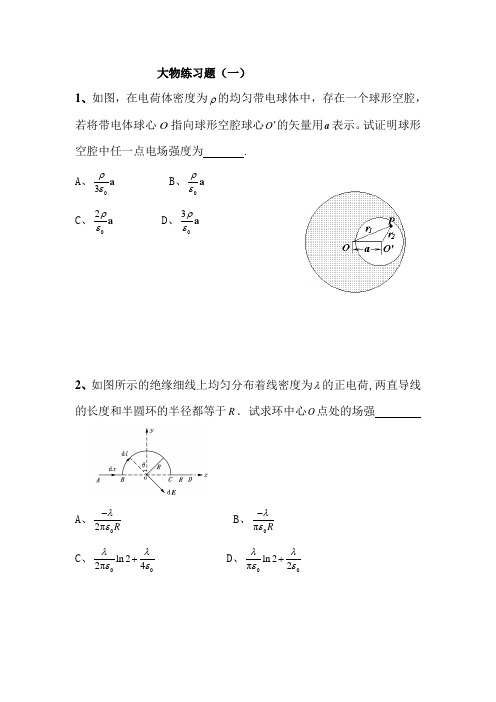
大物练习题（一）1、如图，在电荷体密度为ρ的均匀带电球体中，存在一个球形空腔，若将带电体球心O指向球形空腔球心O'的矢量用a表示。
试证明球形空腔中任一点电场强度为 .A、3ρεa B、ρεaC、2ρεa D、3ρεa2、如图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R．试求环中心O点处的场强A、2πRλε- B、πRλε-C、00ln22π4λλεε+ D、00ln2π2λλεε+3、 如图所示，一导体球半径为1R ,外罩一半径为2R 的同心薄导体球壳, 外球壳所带总电荷为Q ,而内球的电势为0V ，求导体球和球壳之间的电势差 （填写A 、B 、C 或D ，从下面的选项中选取）。
A 、1020214R Q V R R πε⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ B 、102024R Q V R R πε⎛⎫- ⎪⎝⎭C 、0024Q V R πε- D 、1020214R Q V R R πε⎛⎫⎛⎫+-⎪ ⎪⎝⎭⎝⎭4.如图所示，电荷面密度为1σ的带电无限大板A 旁边有一带电导体B ，今测得导体表面靠近P 点处的电荷面密度为2σ。
求：（1）P 点处的场强 ；（2）导体表面靠近P 点处的电荷元S ∆2σ所受的电场力 。
A 、20σεB 、202σεC 、2202S σε∆D 、220S σε∆5．如图，在一带电量为Q 的导体球外，同心地包有一各向同性均匀电介质球壳，其相对电容率为r ε，壳外是真空，则在壳外P 点处(OP r =)的场强和电位移的大小分别为［ ］Q Opr（A ）2200,44r Q QE D rr εεε==ππ； （B ）22,44r Q QE D r r ε==ππ； （C ）220,44Q QE D r r ε==ππ； （D ）2200,44Q QE D r r εε==ππ。
6、在一点电荷产生的静电场中，一块电介质如图放置，以点电荷所在处为球心作一球形闭合面，则对此球形闭合面： （A ）高斯定理成立，且可用它求出闭合面上各点的场强；（B ）高斯定理成立，但不能用它求出闭合面上各点的场强； （C ）由于电介质不对称分布，高斯定理不成立； （D ）即使电介质对称分布，高斯定理也不成立。
大学物理C-练习三静电场答案
练 习 三 静电场一、填空题1.点电荷q 1、q 2、q 3 和q 4 在真空中的分布如图所示．图中S 为闭合曲面，则通过该闭合曲面的电场强度通量sE dS ⎰r r g Ñ=____120()q q ε+________，式中的E r是点电荷___q 1、q 2、 q 3、q 4____在闭合曲面上任一点产生的场强的矢量和．2.在边长为a 的正方体中心处放置一电荷为Q 的点电荷，则正方体顶角处的电场强度的大小为_______203Q a πε______3.一半径为R 的均匀带电圆环，电荷线密度为λ． 设无穷远处为电势零点，则圆环中心O 点的电势U ＝_______2λε________． 4.一半径为R 的均匀带电导体球壳，带电荷为Q ．球壳内、外均为真空．设无限远处为电势零点，则壳内各点电势U =_______04Q Rπε_______．5.在点电荷q 的电场中，把一个－×10-9 C 的电荷，从无限远处(设无限远处电势为零)移到离该点电荷距离 0.1 m 处，克服电场力作功×10-5 J ，则该点电荷q ＝_____ -2×10-7C___________．(真空介电常量0＝×10-12 C2·N -1·m -2 )6.一电荷为Q 的点电荷固定在空间某点上，将另一电荷为q 的点电荷放在与Q 相距r 处．若设两点电荷相距无限远时电势能为零，则此时的电势能We ＝_____04Qq rπε____________．7. 图示BCD 是以O 点为圆心，以R 为半径的半圆弧，在A 点有一电荷为+q 的点电荷，O 点有一电荷为－q的点电荷．线段BA = R ．现将一单位正电荷从B 点沿半圆弧轨道BCD 移到D 点，3q •SA q • 1q •2q •1q • 1q •则电场力所作的_______06q Rπε______________。
2024年大学物理静电学题库及答案
一、选择题:（每题3分） 1、 在坐标原点放一正电荷Ｑ，它在P 点(x =+1,ｙ=0)产生的电场强度为.目前,另外有一个负电荷-2Q ，试问E应将它放在什么位置才能使P 点的电场强度等于零？ （A) x 轴上x >1． (Ｂ） x 轴上0<x <1． (C) x 轴上x ＜0. (D) y 轴上y >0. (E) y 轴上y ＜0. [ ]2、一均匀带电球面，电荷面密度为σ，球面内电场强度到处为零，球面上面元ｄ S 带有σ d S 的电荷,该电荷在球面内各点产生的电场强度(A) 到处为零. (B ） 不一定都为零． （C) 到处不为零． （D ） 无法判定 ． ［ ］３、在边长为a 的正方体中心处放置一电荷为Q 的点电荷,则正方体顶角处的电场强度的大小为： (A) ． (B) .2012a Q επ206a Qεπ (C)． (D ）． 203a Q επ20a Qεπ［ ]４、电荷面密度分别为＋σ和-σ的两块“无限大”均匀带电的平行平板,如图放置，则其周围空间各点电场强度 随位置坐标ｘ变化的关系曲线为：（设场强方向向右为正、向左为负) [ Ａ ]σ(D)5、设有一“无限大”均匀带正电荷的平面.取x 轴垂直带电平面，坐标原点在带电平面上,则其周围空间各点的电场强度随距离平面的位置E坐标x 变化的关系曲线为（要求场强方向沿x 轴正向为正、反之为负)： ［ C] ６、设有一“无限大”均匀带负电荷的平面．取ｘ轴垂直带电平面，坐标原点位于带电平面上，则其周围空间各点的电场强度E 随距离平面的位置坐标ｘ变化的关系曲线为(要求场强方向沿x 轴正向为正、反之为负): [ B ](B)x7、有关电场强度定义式,下列说法中哪个是正确的？ 0/q F E= (A) 场强的大小与试探电荷ｑ0的大小成反比． E(B) 对场中某点，试探电荷受力与ｑ0的比值不因ｑ0而变.F (C ） 试探电荷受力的方向就是场强的方向.F E（D) 若场中某点不放试探电荷q 0,则＝0,从而=0． [ B ]F E 8、将一个试验电荷q 0 (正电荷)放在带有负电荷的大导体附近Ｐ点处（如图），测得它所受的力为F ．若考虑到电荷q ０不是足够小,则 （A) F / q 0比P 点处原先的场强数值大． (Ｂ） F / q 0比P 点处原先的场强数值小. (C) F / ｑ0等于Ｐ点处原先场强的数值． (D ） F / q 0与Ｐ点处原先场强的数值哪个大无法确定. ［ A ]9、下面列出的真空中静电场的场强公式，其中哪个是正确的？ (A) 点电荷ｑ的电场：.(r 为点电荷到场点的距离) 204rq E επ=（B) “无限长”均匀带电直线(电荷线密度λ)的电场：r rE302ελπ=(为带电直线到场点的垂直于直线的矢量) r（Ｃ） “无限大”均匀带电平面(电荷面密度σ)的电场：02εσ=E P 0(D) 半径为R 的均匀带电球面(电荷面密度σ)外的电场：r rR E302εσ= (为球心到场点的矢量） r10、下列几个说法中哪一个是正确的?(A)电场中某点场强的方向，就是将点电荷放在该点所受电场力的方向．(B)在以点电荷为中心的球面上， 由该点电荷所产生的场强到处相同．D ＩRECTION （C ） 场强可由定出,其中q 为试验电荷，ｑ可正、可负,为q F E / =F试验电荷所受的电场力． （Ｄ) 以上说法都不正确． [ ］ 11、一电场强度为的均匀电场,的方向与沿ｘ轴正向，E E如图所示．则通过图中二分之一径为Ｒ的半球面的电场强度通量为 （A) πR 2E ． (Ｂ） πR 2E / ２．(C) 2πR 2E ． （Ｄ) 0． 高斯面内无电荷 [ ]12、已知一高斯面所包围的体积内电荷代数和∑q ＝0，则可肯定： （Ａ） 高斯面上各点场强均为零． （B ） 穿过高斯面上每一面元的电场强度通量均为零. (Ｃ) 穿过整个高斯面的电场强度通量为零． （D) 以上说法都不对． ［ ］1３、一点电荷，放在球形高斯面的中心处．下列哪一个情况,通过高斯面的电场强度通量发生变化: (Ａ) 将另一点电荷放在高斯面外. （B ） 将另一点电荷放进高斯面内． (Ｃ) 将球心处的点电荷移开,但仍在高斯面内. （Ｄ） 将高斯面半径缩小. [］ 14、点电荷Ｑ被曲面Ｓ所包围 ， 从无穷远处引入另一点电荷q 至曲面外一点，如图所示,则引入前后： （A) 曲面Ｓ的电场强度通量不变，曲面上各点场强不变. (B) 曲面S 的电场强度通量变化,曲面上各点场强不变. (C) 曲面Ｓ的电场强度通量变化,曲面上各点场强变化. （D ） 曲面Ｓ的电场强度通量不变，曲面上各点场强变化． [ ]１5、半径为R 的均匀带电球面的静电场中各点的电场强度的大小E 与距球心的距离r 之间的关系曲线为:［ B ］E Or(D)E ∝1/r 216、半径为R 的均匀带电球体的静电场中各点的电场强度的大小E 与距球心的距离r 的关系曲线为:［ Ｂ ］17、半径为R 的“无限长”均匀带电圆柱体的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为： [ B ]18、半径为R 的均匀带电球面，若其电荷面密度为σ，则在距离球面Ｒ处的电场强度大小为: (A) . （Ｂ)． εσ2εσ (Ｃ) ． ﻩ (D)． [04εσ8εσC ］(C)(B)(C)(B)19、高斯定理 ⎰⎰⋅=VSV S E 0/d d ερ (A) 适合用于任何静电场． (Ｂ) 只适合用于真空中的静电场． （C ） 只适合用于具备球对称性、轴对称性和平面对称性的静电场. (Ｄ) 只适合用于虽然不具备（C)中所述的对称性、但能够找到适宜的高斯面的静电场． ［ A]20、依照高斯定理的数学体现式可知下述各种说法中，正确的是: ⎰∑⋅=Sq S E 0/d ε (A) 闭合面内的电荷代数和为零时，闭合面上各点场强一定为零. (B ） 闭合面内的电荷代数和不为零时,闭合面上各点场强一定到处不为零． (C) 闭合面内的电荷代数和为零时,闭合面上各点场强不一定到处为零． （D) 闭合面上各点场强均为零时,闭合面内一定到处无电荷． [ ］21、有关高斯定理的了解有下面几个说法，其中正确的是: (A ） 假如高斯面上到处为零,则该面内必无电荷.E (B) 假如高斯面内无电荷，则高斯面上到处为零. E (C ） 假如高斯面上到处不为零，则高斯面内必有电荷. E (D) 假如高斯面内有净电荷，则通过高斯面的电场强度通量必不为零. [ ] 22、如图所示,两个同心均匀带电球面,内球面半径为R 1、带有电荷Q 1,外球面半径为R 2、带有电荷Q 2，则在外球面外面、距离球心为ｒ处的P 点的场强大小Ｅ为：(A ）. 20214rQ Q επ+（B)． ()()2202210144R r Q R r Q -π+-πεε（Ｃ) .()2120214R R Q Q -π+ε(D). [ ］2024r Q επ ２3、 如图所示，两个“无限长”的、半径分别为R 1和R ２的共轴圆柱面，均匀带电,沿轴线方向单位长度上的所带电荷分别为λ1和λ2,则在外圆柱面外面、距离轴线为ｒ处的P 点的电场强度大小E 为： (A) .r0212ελλπ+(B). ()()20210122R r R r -π+-πελελ (C) ． ()20212R r -π+ελλ (Ｄ)． [ ]20210122R R ελελπ+π 24、A 和Ｂ为两个均匀带电球体，A 带电荷＋q ,B 带电荷-ｑ,作一与Ａ同心的球面Ｓ为高斯面，如图所示.则 (A) 通过S 面的电场强度通量为零，S 面上各点的场强为零.(B ） 通过Ｓ面的电场强度通量为q / ε０，S 面上场强的大小为． 20π4rq E ε=（C) 通过S 面的电场强度通量为(－ ｑ) / ε0,S 面上场强的大小为．20π4rq E ε= (D ） 通过Ｓ面的电场强度通量为q ／ ε0,但Ｓ面上各点的场强不能直接由高斯定理求出. [ D ］２5、在空间有一非均匀电场，其电场线分布如图所示.在电场中作二分之一径为R 的闭合球面Ｓ，已知通过球面上某一面元∆S 的电场强度通量为∆Φｅ，则通过该球面其他部分的电场强度通量为(A ） - ∆Φe ． (B). e SR Φ∆∆π24(Ｃ) . (D) ０.[ A ]e SSR Φ∆∆∆-π2426、半径为Ｒ的“无限长”均匀带电圆柱面的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为： [ Ｂ ](B)(C)E O r(A)E ∝1/r２7、静电场中某点电势的数值等于 (A)试验电荷ｑ0置于该点时具备的电势能． (B)单位试验电荷置于该点时具备的电势能. （C)单位正电荷置于该点时具备的电势能． （D ）把单位正电荷从该点移到电势零点外力所作的功. [ ］ 2８、如图所示,边长为ｌ的正方形,在其四个顶点上各放有等量的点电荷．若正方形中心Ｏ处的场强值和电势值都等于零,则：（Ａ） 顶点a 、b 、c 、d 处都是正电荷.(B) 顶点ａ、b 处是正电荷,c 、d 处是负电荷. （C) 顶点a 、c 处是正电荷,b 、d 处是负电荷. (Ｄ) 顶点a 、b 、c 、ｄ处都是负电荷．［ ］29、如图所示,边长为 ０.３ m 的正三角形a ｂｃ,在顶点ａ处有一电荷为10-8 C 的正点电荷，顶点b 处有一电荷为-10－8 C 的负点电荷,则顶点ｃ处的电场强度的大小E 和电势U 为： (=9×10-9 041επＮ m /Ｃ2)(Ａ） E ＝0,U ＝０． (Ｂ） E ＝1００0 V/m,U ＝0. (Ｃ） Ｅ=10０0 Ｖ／m,U =60０ Ｖ. (D ） Ｅ= V/m ，U =60０ V. ［ ］ba 30、如图所示,半径为R 的均匀带电球面，总电荷为Ｑ，设无穷远处的电势为零，则球内距离球心为ｒ的P 点处的电场强度的大小和电势为： (A) E ＝0,． rQU 04επ= (Ｂ） E =0，. RQU 04επ=（C) , ．204r QE επ=rQ U 04επ=(D) ,． ［ ］204r Q E επ=RQU 04επ=３1、有关静电场中某点电势值的正负，下列说法中正确的是： （A ） 电势值的正负取决于置于该点的试验电荷的正负． (B) 电势值的正负取决于电场力对试验电荷作功的正负. (C) 电势值的正负取决于电势零点的选用． （D) 电势值的正负取决于产生电场的电荷的正负. [ C ] 32、在边长为a 的正方体中心处放置一点电荷Q ,设无穷远处为电势零点，则在正方体顶角处的电势为: （A) . (B) ． aQ 034επa Q032επ (C) ． （D)． [ ］aQ06επaQ012επ ３３、 图中所示为一球对称性静电场的电势分布曲线,r 表示离对称中心的距离．请指出该电场是由下列哪一个带电体产生的． (Ａ) 半径为Ｒ的均匀带正电球面. (B) 半径为R 的均匀带正电球体． (C) 正点电荷. (D) 负点电荷. [ ］ ３4、 图中所示为一球对称性静电场的电势分布曲线，r 表示离对称中心的距离．请指出该电场是由下列哪一个带电体产生的． (A) 半径为R 的均匀带负电球面． (Ｂ) 半径为R 的均匀带负电球体. (C) 正点电荷． （D ） 负点电荷. [ ］35、二分之一径为R 的均匀带电球面,带有电荷Q ．若要求该球面上的电势值为零,则无限远处的电势将等于(A) . (Ｂ) ０． RQ 0π4ε (C) ． （D ） ∞． RQ0π4ε-[ ］3６、 真空中有一点电荷Q ，在与它相距为ｒ的a点处有一试验电荷q .现使试验电荷q 从a 点沿半圆弧轨道运动到b 点,如图所示．则电场力对q 作功为 (A). (Ｂ） ． 24220r r Qq π⋅πεr r Qq 2420επ (C) ． (Ｄ) ０． r r Qqππ204ε[ ]3７、点电荷-q 位于圆心O 处,Ａ、B 、Ｃ、D 为同一圆周上的四点,如图所示．现将一试验电荷从A 点分别移动到Ｂ、C 、D 各点，则 (Ａ) 从A 到Ｂ，电场力作功最大．（B) 从Ａ到C ，电场力作功最大． (Ｃ) 从A 到Ｄ，电场力作功最大． (D ） 从Ａ到各点，电场力作功相等． ［ ]38、如图所示，边长为a 的等边三角形的三个顶点上,分别放置着三个正的点电荷q 、２q 、３q .若将另一正点电荷Q 从无穷远处移到三角形的中心O 处，外力所作的功为： (A) . （Ｂ）. aqQ023επaqQ03επ (Ｃ) ． (D) ． ［ ］aqQ0233επaqQ032επ39、在已知静电场分布的条件下,任意两点P 1和P 2之间的电势差决定于 （Ａ) P １和P ２两点的位置.A3q2 (B) P 1和P 2两点处的电场强度的大小和方向． (C) 试验电荷所带电荷的正负. （D) 试验电荷的电荷大小. [ ］ ４0、如图所示，直线MN 长为２l ，弧ＯＣD 是以Ｎ点为中心，l 为半径的半圆弧，N 点有正电荷+q ,M 点有负电荷-q ．今将一试验电荷+q 0从O 点出发沿途径OCDP 移到无穷远处，设无穷远处电势为零，则电场力作功 (A) A <0 , 且为有限常量． (B ） A >0 ,且为有限常量. (Ｃ) A =∞. (D) A ＝0． ［ ] 4１、已知某电场的电场线分布情况如图所示．现观测到一负电荷从M 点移到Ｎ点．有人依照这个图作出下列几点结论,其中哪点是正确的? (Ａ) 电场强度ＥM <ＥN . (B ） 电势U M ＜U Ｎ． (C) 电势能ＷM <W Ｎ． (D) 电场力的功A >0．［ ] 42、已知某电场的电场线分布情况如图所示．现观测到一负电荷从M 点移到N 点．有人依照这个图作出下列几点结论,其中哪点是正确的? (A) 电场强度E M ＞E N ． (B) 电势ＵM >U N . (C) 电势能W M ＜W N ． (D ） 电场力的功A >0.- [ ］ 4３、在电荷为-Ｑ的点电荷A 的静电场中，将另一电荷为q 的点电荷B 从a 点移到b 点.ａ、b 两点距离点电荷A 的距离分别为r １和r 2，如图所示．则移动过程中电场力做的功为 (Ａ)． (B ） . ⎪⎪⎭⎫ ⎝⎛-π-21114r r Q ε⎪⎪⎭⎫ ⎝⎛-π210114r r qQ ε (C). (Ｄ) ［ ]⎪⎪⎭⎫ ⎝⎛-π-210114r r qQ ε()1204r r qQ -π-ε 44、带有电荷-ｑ的一个质点垂直射入开有小孔的两带电平行板之间，如图所示．两平行板之间的电势差为U ,距离为d ，则此带电质点通过电场后它的动能增量等于 (Ａ) ． (B) ＋ｑＵ． dqU- (C) －qU ． （D). ［ ］qU 214５、在匀强电场中,将一负电荷从Ａ移到B ,如图所示．则：(A)电场力作正功，负电荷的电势能减少. (B)电场力作正功,负电荷的电势能增加． (C)电场力作负功，负电荷的电势能减少. (D)电场力作负功,负电荷的电势能增加. [ ] 46、 图中实线为某电场中的电场线，虚线表示等势(位）面，-q dO U-E由图可看出： (Ａ) E A >ＥB ＞E C ，U A ＞U B ＞U Ｃ. （B) ＥA <E B ＜ＥC ，U A <U B ＜U C ． (Ｃ) E A >ＥB >E Ｃ，U A <U B <U C ． (Ｄ) ＥA <E B <ＥC ,U A ＞U B ＞U Ｃ. ［ ］４7、电子的质量为m e ，电荷为-e ,绕静止的氢原子核(即质子)作半径为r 的匀速率圆周运动，则电子的速率为 （A) ． (B) ． k r m ee rm ke e (Ｃ） ． (D) . rm kee 2rm kee 2(式中ｋ=１ / （4πε０) )［]４8、质量均为m ，相距为r 1的两个电子，由静止开始在电力作用下(忽视重力作用)运动至相距为r 2，此时每一个电子的速率为 (A ）． (B ） ． ⎪⎪⎭⎫⎝⎛-21112r r m ke ⎪⎪⎭⎫⎝⎛-21112r r m ke （Ｃ) . (D) 电场力做的功是两个电子动能和 ⎪⎪⎭⎫ ⎝⎛-21112r r m k e⎪⎪⎭⎫⎝⎛-2111r r m k e (式中k =１ / (4πε0） ) [ ]49、相距为r 1的两个电子,在重力可忽视的情况下由静止开始运动到相距为ｒ2,从相距r 1到相距ｒ2期间,两电子系统的下列哪一个量是不变的? （Ａ) 动能总和； (B) 电势能总和； (Ｃ） 动量总和； (D) 电相互作用力. ［ ]5０、一电偶极子放在均匀电场中,当电偶极矩的方向与场强方向不一致时,其所受的合力和F合力矩为:M (Ａ） ＝0，= 0. (B) = 0，0. F MF M≠ (C) 0，=０．（D) 0，0. ［ ]F ≠MF ≠M≠ 51、真空中有两个点电荷M 、Ｎ，相互间作用力为，当另一点电荷Ｑ移近这两个点电荷F时，Ｍ、Ｎ两点电荷之间的作用力 (A) 大小不变,方向变化. ﻩ(Ｂ) 大小变化，方向不变. (C) 大小和方向都不变． ﻩ(D) 大小和方向都改. [ ]５2、设有一带电油滴，处在带电的水平放置的大平行金属板之间保持稳定,如图所示.若油滴取得了附加的负电荷，为了继续使油滴保持稳定,应采取下面哪个措施？ (Ａ） 使两金属板相互接近些. (B) 变化两极板上电荷的正负极性． (C ） 使油滴离正极板远某些. （D) 减小两板间的电势差． ［］-+５3、正方形的两对角上,各置电荷Q ，在其他两对角上各置电荷q ，若Q 所受合力为零，则Q 与q 的大小关系为 (Ａ) Q ＝－2q . （B) Q =-q .22 （C ） Q ＝-４q ． (Ｄ) Ｑ=－2q ． ［ ］54、电荷之比为1∶3∶5的三个带同号电荷的小球Ａ、B 、C ，保持在一条直线上，相互间距离比小球直径大得多．若固定A 、Ｃ不动,变化Ｂ的位置使B 所受电场力为零时，与AB BC 的比值为 (A) 5. （Ｂ） １／５． (C). (D ） 1/. [ ]555５、面积为S 的空气平行板电容器,极板上分别带电量±q ,若不考虑边缘效应，则两极板间的相互作用力为 (A)． (B ） ．S q 02εSq 022ε (C ） . （D) ． 2022S q ε202Sq ε［ ］5６、充了电的平行板电容器两极板(看作很大的平板)间的静电作用力F 与两极板间的电压U 的关系是： (Ａ) F ∝U ． (B) F ∝１／U ． (C ） F ∝1/U 2． （Ｄ) F ∝Ｕ ２． ［ ]57、 有一带正电荷的大导体,欲测其附近P 点处的场强,将一电荷量为q 0 (q 0 >０ )的点电荷放在P 点,如图所示，测得它所受的电场力为F .若电荷量q 0不是足够小,则 （A) F / q 0比Ｐ点处场强的数值大. (B) F / q 0比P 点处场强的数值小． (C) F / q 0与P 点处场强的数值相等． (D) Ｆ/ q 0与P 点处场强的数值哪个大无法确定． [ ］58、有关高斯定理,下列说法中哪一个是正确的? (A) 高斯面内不包围自由电荷,则面上各点电位移矢量为零． D (B) 高斯面上到处为零，则面内必不存在自由电荷. D （C) 高斯面的通量仅与面内自由电荷有关. D（D) 以上说法都不正确. [］5９、有关静电场中的电位移线，下列说法中,哪一个是正确的? (A) 起自正电荷,止于负电荷,不形成闭合线，不中断. （B ） 任何两条电位移线相互平行． (Ｃ) 起自正自由电荷，止于负自由电荷,任何两条电位移线在无自由电荷的空间不相交． （Ｄ） 电位移线只出目前有电介质的空间． ［ ]q P60、两个半径相同的金属球，一为空心,一为实心,把二者各自孤立时的电容值加以比较，则 (A) 空心球电容值大. （B) 实心球电容值大. (C) 两球电容值相等．(D ） 大小关系无法确定. [ ]二、填空题（每题４分）6１、静电场中某点的电场强度,其大小和方向与＿_＿____＿_____＿_____＿____＿＿ _______＿___＿＿_____＿__＿＿____＿___＿＿_＿___＿_相同.62、电荷为-5×1０-9 C 的试验电荷放在电场中某点时,受到 ２0×1０-9 Ｎ的向下的力，则该点的电场强度大小为__＿＿_______＿__＿__＿___，方向__＿____＿＿＿__.６3、静电场场强的叠加原理的内容是:___＿________＿＿_＿___＿_＿______＿_________＿___＿____＿＿_________＿＿___＿__＿_______________＿____＿__＿___＿_____＿___＿____＿＿___＿_＿_＿＿__＿＿_＿__＿________＿_______＿______＿＿_＿_＿＿__．６4、在静电场中,任意作一闭合曲面，通过该闭合曲面的电场强度通量的⎰∙S Ed 值仅取决于 ,而与 无关.65、半径为R 的半球面置于场强为的均匀电场中，其对E 称轴与场强方向一致,如图所示．则通过该半球面的电场强度通量为＿＿＿＿_＿＿_＿__＿＿＿＿___. 6６、电荷分别为q 1和q ２的两个点电荷单独在空间各点产生的静电场强分别为和1E ,空间各点总场强为＝＋.目前作一封闭曲面Ｓ，2E E 1E 2E 如图所示,则如下两式分别给出通过Ｓ的电场强度通量＝________＿_＿_＿_＿＿＿＿________＿___, ⎰⋅S E d 1＝____＿_______＿＿____＿＿__＿_＿__＿____.⎰⋅S E d 67、一面积为Ｓ的平面,放在场强为的均匀电场中，已知 与平面间的夹角为E E θ(<π／2),则通过该平面的电场强度通量的数值Φｅ＝_______＿__＿____＿_＿____．６8、如图，点电荷q 和－ｑ被包围在高斯面Ｓ内,则通过该高斯面的电场强度通量=___________＿＿,式中为⎰⋅S S E d E __＿_＿＿_＿_____＿___处的场强．69、二分之一径为R 的均匀带电球面，其电荷面密度为σ.该球面内、外的场强分布为(表示r从球心引出的矢径): ＝____________＿_＿＿______（r ＜Ｒ ）, ()r E ＝_＿＿_＿＿_＿＿__＿______＿___(r ＞R )． ()r E70、二分之一径为R 的“无限长”均匀带电圆柱面，其电荷面密度为σ.该圆柱面内、外场强分布为(表示在垂直于圆柱面的平面上,从轴线处引出的矢径）: r ＝____＿＿____＿_＿＿________(ｒ<R ), ()r E =＿__＿＿_＿___＿___＿＿_＿__＿_(r ＞R ).()r E 71、在点电荷+q 和-q 的静电场中,作出如图所示的三个闭合面S 1、Ｓ2、S 3,则通过这些闭合面的电场强度通量分别是:Φ１＝_＿____＿＿，Φ2＝___＿＿___＿＿_,Φ3＝_________＿72、在静电场中,任意作一闭合曲面，通过该闭合曲面的电场强度通量的⎰∙S E d 值仅取决于 ,而与 无关．73、一闭合面包围着一个电偶极子，则通过此闭合面的电场强度通量Φｅ＝__＿_____＿＿＿＿___＿_．７４、图中曲线表示一个球对称性静电场的电势分布，r 123表示离对称中心的距离.这是___＿______＿_______＿＿_＿__＿＿__________________的电场．75、二分之一径为R 的均匀带电球面,其电荷面密度为σ．若要求无穷远处为电势零点,则该球面上的电势U ＝___＿_＿____＿__＿＿_＿__＿． 7６、电荷分别为ｑ１，q 2,q 3的三个点电荷分别位于同一圆周的三个点上，如图所示．设无穷远处为电势零点，圆半径为Ｒ,则ｂ点处的电势Ｕ＝_____＿__＿__ .77、描述静电场性质的两个基本物理量是＿＿_＿____＿___＿＿;它们的定义式是＿________＿_＿____和_＿__＿____________＿__＿____＿＿__＿_＿__＿_＿_＿_＿_.７8、静电场中某点的电势,其数值等于___＿＿___＿_＿___＿＿＿__________＿__ 或 ____＿____＿_＿＿__＿__＿______＿＿___＿_＿＿＿＿___.79、一点电荷q ＝10－９ C,Ａ、Ｂ、C 三点分别距离该点电荷1０ ｃm 、20 cm 、3０ cm.若选B 点的电势为零,则Ａ点的电势为_＿＿______＿_＿__,C 点的电势为_______＿_＿_＿_＿__．(真空介电常量ε0＝8.８５×10-12 Ｃ2·N -1·m －2)q 13q８0、电荷为－Q 的点电荷，置于圆心O 处，b 、c 、d为同一圆周上的不一样点,如图所示.现将试验电荷+q 0从图中a 点分别沿ａb 、ac 、ａd 途径移到对应的ｂ、c 、d 各点,设移动过程中电场力所作的功分别用A 1、Ａ2、A 3表示，则三者的大小的关系是__＿＿_____＿______＿___＿_．(填＞，＜，＝)81、如图所示,在一个点电荷的电场中分别作三个电势不一样的等势面A ,B ,Ｃ.已知U Ａ>U Ｂ>U C ,且U Ａ－ＵB =U B －U C ,则相邻两等势面之间的距离的关系是：R B -ＲＡ＿_____ R C －R B . (填＜，=，＞）82、一电荷为Q 的点电荷固定在空间某点上,将另一电荷为q 的点电荷放在与Q 相距r 处．若设两点电荷相距无限远时电势能为零,则此时的电势能W e ＝___＿＿____＿__＿_＿__＿____＿_．83、如图所示，在电荷为ｑ的点电荷的静电场中,将一电荷为q 0的试验电荷从a 点经任意途径移动到ｂ点，外力所作的功A ＝_＿____＿__＿____.84、真空中电荷分别为q １和ｑ2的两个点电荷，当它们相距为r 时,该电荷系统b的相互作用电势能Ｗ＝＿___＿__＿＿_＿__＿__．(设当两个点电荷相距无穷远时电势能为零) 85、在静电场中，一质子（带电荷ｅ=1.６×10-１9 C)沿四分之一的圆弧轨道从A 点移到Ｂ点(如图),电场力作功8．0×10－15 Ｊ．则当质子沿四分之三的圆弧轨道从B 点回到Ａ点时,电场力作功A ＝＿__＿_____＿＿______＿__．设A 点电势为零,则B 点电势U =___＿__________＿_____.８6、静电力作功的特点是_______＿_＿＿___＿______＿_＿____＿_＿__＿_____＿_＿__＿＿ ____＿＿_＿__＿＿_＿______＿______＿＿_____,因而静电力属于_＿_＿____＿＿_______力．87、静电场的环路定理的数学表示式为:_________＿________＿＿＿＿．该式的物理意义是:___＿_____＿____＿___＿____＿___＿_________＿＿＿_＿_____＿_＿_____＿＿____＿_＿_＿__＿＿＿＿__＿＿＿__＿_______＿__＿_＿_______＿___＿＿．该定理表白,静电场是_＿_＿＿_ ＿__＿__________＿＿＿__＿_＿________场.A８８、一电荷为Q 的点电荷固定在空间某点上，将另一电荷为ｑ的点电荷放在与Q 相距r 处.若设两点电荷相距无限远时电势能为零，则此时的电势能W ｅ=__＿__＿＿___＿_____＿_______.8９、 图示为某静电场的等势面图,在图中画出该电场的电场线. ９０、图中所示以O 为心的各圆弧为静电场的等势（位)线图，已知U 1<U ２＜U 3,在图上画出a 、b 两点的电场强度的方向，并比较它们的大小.E a __＿＿_＿＿＿ E ｂ(填<、＝、＞).91、一质量为m ,电荷为q 的粒子，从电势为U Ａ的Ａ点,在电场力作用下运动到电势为ＵB 的B 点．若粒子抵达B 点时的速率为v B ,则它在A 点时的速率v Ａ=__＿_＿__＿__＿__＿___＿＿＿_＿_____.92、一质量为m 、电荷为q 的小球,在电场力作用下，从电势为U 的a 点,移动到电势为零的b 点．若已知小球在b 点的速率为ｖb ，则小球在a 点的速率ｖaO U U= ___＿＿＿______＿___＿__＿__．９3、一质子和一α粒子进入到同一电场中，二者的加速度之比,a p ∶a α＝＿___＿_＿____＿＿___. 94、带有N 个电子的一个油滴，其质量为m ,电子的电荷大小为ｅ.在重力场中由静止开始下落(重力加速度为g ),下落中穿越一均匀电场区域，欲使油滴在该区域中匀速下落，则电场的方向为____＿__＿__________，大小为___＿＿_＿__＿___．95、在静电场中有一立方形均匀导体,边长为a ．已知立方导体中心O 处的电势为Ｕ0,则立方体顶点A 的电势为＿＿____＿_____. ９６、一孤立带电导体球，其表面处场强的方向__＿___＿____＿表面;当把另一带电体放在这个导体球附近时,该导体球表面处场强的方向＿_＿_____＿_____＿＿＿表面．97、如图所示,将一负电荷从无穷远处移到一个不带电的导体附近，则导体内的电场强度__＿＿＿_＿____＿_＿，导体的电势____＿_____＿＿＿_．（填增大、不变、减小） 9８、一空气平行板电容器,两极板间距为ｄ,充电后板间电压为U .然后将电源断开,在两板间平行地插入一厚度为d /3的金属板,则板间电压变成U ' ＝_＿＿______＿＿_____ ．99、一孤立带电导体球，其表面处场强的方向_____＿＿_____表面;当把另一带电体放在这个导体球附近时,该导体球表面处场强的方向_＿＿＿___________＿_表面．10０、A 、B 两个导体球，相距甚远，因此均可当作是孤立的．其中A 球本来带电,B 球不带电,现用一根细长导线将两球连接，则球上分派的电荷与球半径成__＿＿__比.101、如图所示，两同心导体球壳,内球壳带电荷+ｑ，外球壳带电荷-2q ．静电平衡时，外球壳的电荷分布为: 内表面_______＿___ ; 外表面＿_＿_＿__＿___ ．1０2、如图所示，将一负电荷从无穷远处移到一个不带电的导体附近，则导体内的电场强度_＿_____＿__＿___，导体的电势___＿_________＿．(填增大、不变、减小） 103、一金属球壳的内、外半径分别为R 1和R ２,带电荷为Ｑ.在球心处有一电荷为q 的点电荷,则球壳内表面上的电荷面密度 =＿______＿_＿_＿_＿．104、二分之一径为Ｒ的均匀带电导体球壳，带电荷为Q ．球壳内、外均为真空．设无限远处为电势零点，则壳内各点电势Ｕ =________＿_____. 105、一平行板电容器，上极板带正电，下极板带负电，其间布满相对介电常量为εr ＝ 2的各向同性均匀电介质,如图所示．在图上大体画出电介质内任一点P 处自由电荷产生的场强 , 束缚电荷产生的场强和总场强．0E E ' E1０6、两个点电荷在真空中相距d 1 = 7 cm 时的相互作用力与在煤油中相距ｄ2 ＝ 5c ｍ时的相互作用力相等，则煤油的相对介电常量εr =___＿____＿_＿＿_＿__＿＿_.107、如图所示,平行板电容器中充有各向同性均匀电介质.图中画出两组带有箭头的线分别表示电场线、电位移线．则其中（1)为＿＿_________＿＿_____线，(2）为＿＿＿＿__＿___________线.108、一个半径为R 的薄金属球壳,带有电荷q ,壳内布满相对介电常量为εｒ的各向同性均匀电介质．设无穷远处为电势零点，则球壳的电势U = __＿_____＿＿____＿__＿_____＿_＿______．(1)(2)109、一平行板电容器,两板间布满各向同性均匀电介质，已知相对介电常量为εr .若极板上的自由电荷面密度为σ ,则介质中电位移的大小Ｄ＝___________＿,电场强度的大小E =__＿＿______＿_____＿___. １10、一个半径为Ｒ的薄金属球壳,带有电荷q,壳内真空,壳外是无限大的相对介电常量为εr的各向同性均匀电介质.设无穷远处为电势零点,则球壳的电势Ｕ =＿__＿__＿______＿__＿_＿＿________.111、一平行板电容器,充电后切断电源，然后使两极板间布满相对介电常量为εr 的各向同性均匀电介质.此时两极板间的电场强度是本来的______＿____＿倍；电场能量是本来的____＿＿__＿＿＿倍. 1１２、一平行板电容器,充电后与电源保持联接，然后使两极板间布满相对介电常量为εｒ的各向同性均匀电介质,这时两极板上的电荷是本来的__＿___倍;电场强度是本来的_________倍；电场能量是本来的__＿______倍.11３、在相对介电常量为εr的各向同性的电介质中,电位移矢量与场强之间的关系是___＿_＿________＿＿＿＿_ .114、分子的正负电荷中心重叠的电介质叫做______＿__＿_＿___ 电介质 .在外电场作用下，分子的正负电荷中心发生相对位移，形成＿______＿_______＿＿＿____＿_.1１5、一平行板电容器，两板间布满各向同性均匀电介质，已知相对介电常量为εr ．若极板上的自由电荷面密度为σ，则介质中电位移的大小Ｄ＝_＿__________，电场强度的大小E =___＿_____＿___＿__＿___.１16、一平行板电容器充电后切断电源，若使二极板间距离增加,则二极板间场强＿__________＿＿＿___，电容__＿____＿_＿_____＿____． (填增大或减小或不变) 117、一个孤立导体，当它带有电荷q而电势为Ｕ时，则定义该导体的电容为C＝___＿___＿_＿_＿__,它是表征导体的__＿_＿＿__＿_______的物理量．1１８、一个孤立导体,当它带有电荷q而电势为U时,则定义该导体的电容为C =___＿＿_＿__＿____，它是表征导体的＿______＿______＿_的物理量.1１9、两个空气电容器1和2，并联后接在电压恒定的直流电源上，如图所示．今有一块各向同性均匀电介质板迟缓地插入电容器1中，则电容器组的总电荷将＿＿____＿___，电容器组储存的电能将_＿________．(填增大,减小或不变）12０、真空中均匀带电的球面和球体，假如二者的半径和总电荷都相等,则带电球面的电场能量W 1与带电球体的电场能量W ２相比,Ｗ1________ Ｗ2 (填＜、＝、>)．三、计算题：(每题10分)121、如图所示,真空中一长为Ｌ的均匀带电细直杆，总电荷为ｑ，试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度.1２2、用绝缘细线弯成的半圆环,半径为R ，其上均匀地带有正电荷Q ,试求圆心Ｏ点的电场强度.１23、如图所示，一长为10 c ｍ的均匀带正电细杆，其电荷为１.５×１0-8 C,试求在杆的延长线上距杆的端点5 c ｍ处的P 点的电场强度．（=9×109 N ·ｍ2/C ２ ) 041επ 124、真空中一立方体形的高斯面,边长a ＝０.1 m,位于图中所示位置.已知空间的场强分布为： Ｅx =b ｘ , Ｅy =0 ， E z ＝0.常量b ＝100０ N/(C ·m)．试求通过该高斯面的电通量Lq。
大学物理-静电场(一)(带答案)
一、库仑定律和电场力1.关于摩擦一物体后，物体呈现正电性的一种解释是：在摩擦过程中，[ ]A.物体获得了中子。
B.物体获得了质子。
C.物体失去了电子。
D.物体失去了中子。
【答案】：C2.两条平行的无限长直均匀带电线，相距为d，线电荷密度分别为±λ，若已知一无限长均匀带电直线的场强分布为λ2πε0r方向垂直于带电直线，则其中一带电直线上的单位长度电荷受到另一带电直线的静电作用力大小为[ ]A.λ24πε0d2B.λ24πε0dC.λ22πε0d2D.λ22πε0d【答案】：D3.关于电荷与电场，有下列几种说法，其中正确的是［］A.点电荷的附近空间一定存在电场；B.电荷间的相互作用与电场无关；C.若电荷在电场中某点受到的电场力很大，则表明该点的电场强度一定很大；D.在某一点电荷附近的任一点，若没放试验电荷，则该点的电场强度为零。
【答案】：A4. 两个静止不动的点电荷的带电总量为2q，为使它们间的排斥力最大，各自所带的电荷量分别为［］A.q2,3q 2B.q3,5q 3C.q,qD.−q2,5q 2【答案】：C5.关于电场力和电场强度，有下列几种说法，其中正确的是［］A.静电场的库仑力的叠加原理和电场强度的叠加原理彼此独立、没有联系；B.两静止点电荷之间的相互作用力遵守牛顿第三定律；C.在以点电荷为中心的球面上，由该点电荷所产生的电场强度处处相同；D.以上说法都不正确。
【答案】：B6.—点电荷对放在相距d处的另一个点电荷的作用力为F，若两点电荷之间的距离减小一半，此时它们之间的静电力为[ ]A.4FB.2FC.0.5FD.0.25F【答案】：A7.如图所示为一竖直放置的无穷大平板，其上均匀分布着面电荷密度为σ的正电荷，周围激发的电场强度大小为σ2ε0，方向沿水平方向向外且垂直于平板。
在其附近有一水平放置的、长度为l的均匀带电直线，直线与平板垂直，其线电荷密度为λ，则该带电直线所受到的电场力大小为[ ]A.σλ2πε0ln lB.σλ2ε0ln lC.σλl2πε0D.σλl2ε0【答案】：D8.质量为m、电荷为-e的电子以圆轨道绕静止的氢原子核旋转，其轨道半径为r，旋转频率为γ，动能为E，则下列几种关系中正确的是［］A.E=e8πε0rB.γ2=32ε02E3me4C.E=e 24πε0rD.γ2=32ε0E3me2【答案】：B9.电偶极子在非均匀电场中的运动状态[ ]A.只可能有转动运动；B.不可能有转动运动；C.只可能有平动运动；D.既可能有转动运动，也可能有平动运动。
大学静电场试题及答案
大学静电场试题及答案一、选择题1. 静电场中的电场线是从正电荷出发，终止于负电荷。
A. 正确B. 错误答案：A2. 电场强度的方向是正电荷所受电场力的方向。
A. 正确B. 错误答案：A3. 电场中某点的电势与该点的电场强度大小无关。
A. 正确B. 错误答案：A4. 电容器的电容与两极板间的距离成反比。
A. 正确B. 错误答案：B5. 电场中某点的电势与该点的电场强度方向无关。
A. 正确B. 错误答案：A二、填空题1. 电场强度的定义式为_______，其中E表示电场强度，F表示电场力，q表示试探电荷。
答案：E = F/q2. 电势差的定义式为_______，其中U表示电势差，W表示电场力做的功，q表示试探电荷。
答案：U = W/q3. 电容器的电容公式为_______，其中C表示电容，Q表示电荷量，V表示电势差。
答案：C = Q/V4. 电场力做功的公式为_______，其中W表示功，q表示电荷量，U表示电势差。
答案：W = qU5. 电场中某点的电势与该点的电场强度大小_______关系。
答案：无关三、简答题1. 简述电场强度和电势的概念及其物理意义。
答案：电场强度是描述电场强弱和方向的物理量，其大小等于单位正电荷在该点所受的电场力，方向与正电荷所受电场力的方向相同。
电势是描述电场能的性质的物理量，它表示单位正电荷在电场中从某点移到参考点（通常取无穷远处）所做的功。
2. 电容器的电容与哪些因素有关？请简述其关系。
答案：电容器的电容与电容器的几何尺寸、两极板间的距离以及介质的介电常数有关。
电容与两极板的面积成正比，与两极板间的距离成反比，与介质的介电常数成正比。
四、计算题1. 一个平行板电容器，其极板面积为0.05平方米，两极板间的距离为0.01米，介质为空气（介电常数ε₀=8.85×10^-12 F/m）。
求该电容器的电容。
答案：C = ε₀ * A / d = 8.85×10^-12 * 0.05 / 0.01 =4.425×10^-11 F2. 已知电场中某点的电势为100V，试探电荷为-2C，求该点的电场强度。
大学物理静电场作业题参考答案
解得 q 2l sin 4 0mg tan 7.3.4 长 l =15.0cm的直导线AB上均匀地分布着线密度 =5.0x10-9C·m-1的正电荷．试
求：(1)在导线的延长线上与导线B端相距 a1 =5.0cm处 P 点的场强；(2)在导线的垂直 平分线上与导线中点相距 d2 =5.0cm 处 Q 点的场强．
S
(D) 曲 面 S 的 电 场 强 度 通 量 不 变 ， 曲 面 上 各 点 场 强 变
化．
题 7.1（2）图
[答案 D ]
（3）在电场中的导体内部的 [ ] （A）电场和电势均为零； （B）电场不为零，电势均为零； （C）电势和表面电势相等； （D）电势低于表面电势。 [答案：C]
（4）两个同心均匀带电球面，半径分别为 Ra 和 Rb (Ra＜Rb), 所带电荷分别为 Qa 和
Uo
4U1
4
8.99
109
1.25 5
108 102
8.99 103V
(2)根据电势差的定义，有UO q0 (U UO )
选取无穷远处为电势零点WO q0 (U UO ) 8.99 106 J
电场力做负功，说明实际需要外力克服电场力做功。
题 7.3.11 图 7.3.11 如题7.3.11图所示，在 A ，B 两点处放有电量分别为+ q ,- q 的点电荷，AB
解：如题 7.3.4 图所示
(1) 在带电直线上取线元 dx ，其上电量 dq 在 P 点产生场强为 dEP
1 4π 0
dx (a x)2
EP
dE P
4π 0
l 2 l 2
dx (a x)2
4π 0
[ a
1
l
1 a
大学物理C-练习三静电场答案
练 习 三 静电场一、填空题1.点电荷q 1、q 2、q 3 和q 4 在真空中的分布如图所示．图中S为闭合曲面，则通过该闭合曲面的电场强度通量sE dS ⎰r r g Ñ=____120()q q ε+________，式中的E r 是点电荷___q 1、q 2、 q 3、q 4____在闭合曲面上任一点产生的场强的矢量和．2.在边长为a 的正方体中心处放置一电荷为Q 的点电荷，则正方体顶角处的电场强度的大小为_______203Q aπε______3.一半径为R 的均匀带电圆环，电荷线密度为λ． 设无穷远处为电势零点，则圆环中心O 点的电势U ＝_______2λε________． 4.一半径为R 的均匀带电导体球壳，带电荷为Q ．球壳内、外均为真空．设无限远处为电势零点，则壳内各点电势U =_______04Q Rπε_______．5.在点电荷q 的电场中，把一个－1.0×10-9 C 的电荷，从无限远处(设无限远处电势为零)移到离该点电荷距离 0.1 m 处，克服电场力作功1.8×10-5 J ，则该点电荷q ＝_____ -2×10-7 C___________．(真空介电常量0＝8.85×10-12 C2·N -1·m -2 )6.一电荷为Q 的点电荷固定在空间某点上，将另一电荷为q 的点电荷放在与Q 相距r 处．若设两点电荷相距无限远时电势能为零，则此时的电势能We ＝_____04Qq rπε____________．7. 图示BCD 是以O 点为圆心，以R 为半径的半圆弧，在A 点有一电荷为+q 的点电荷，O 点有一电荷为－q 的点电荷．线段BA = R ．现将一单位正电荷从B 点沿半圆弧轨道BCD 移到D 点，则电场力所作的_______6q Rπε______________。
二、选择题1. 如图所示，任一闭合曲面S 内有一点电荷q ，O 为S 面上任一点，若将q 由闭合曲面内的P 点移到T 点，且OP =OT ，那么 （ D ） (A) 穿过S 面的电通量改变，O 点的场强大小不变；(B) 穿过S 面的电通量改变，O 点的场强大小改变； (C) 穿过S 面的电通量不变，O 点的场强大小改变； q O STP 3q •SA q • 1q •2q •1q • 1q •(D) 穿过S 面的电通量不变，O 点的场强大小不变。
《大学物理》静电场练习题及答案
《大学物理》静电场练习题及答案一、简答题1、为什么在无电荷的空间里电场线不能相交?答案：由实验和理论知道，静电场中任一给定点上，场强是唯一确定的，即其大小和方向都是确定的．用电场线形象描述静电场的空间分布时，电场线上任一点的切线方向表示该点的场强方向．如果在无电荷的空间里某一点上有几条电场线相交的话，则过此交点对应于每一条电场线都可作出一条切线，这意味着交点处的场强有好几个方向，这与静电场中任一给定点场强具有唯一确定方向相矛盾，故无电荷的空间里电场线不能相交．2、简述静电场中高斯定理的文字内容和数学表达式。
答案：在真空中的静电场内，通过任意封闭曲面的电通量等于该封闭曲面所包围的所有电荷电量的代数和的01ε倍。
0ε∑⎰=⋅内S SqS d E3、写出静电场的环路定理，并分别说明其物理意义。
答案：静电场中，电场强度的环流总是等于零(或0l=⋅⎰l d E)，静电场是保守场。
4、感生电场与静电场有哪些区别和联系?5、在电场中某一点的电场强度定义为0q F E=.若该点没有试验电荷，那么该点的电场强度又如何? 为什么?答案： 电场中某一点的电场强度是由该电场自身性质所决定，与这一点有无试验电荷没有任何关系。
6、在点电荷的电场强度公式中，如果0→r ，则电场强度E 将趋于无限大。
对此，你有什么看法? 答案： 这表明，点电荷只是我们抽象出来的一个物理模型，当带电体较小而作用距离较大时使用点电荷模型较为方便、精确。
但当作用距离r 很小时，点电荷模型的误差会变大，这时我们不能再用点电荷的电场强度公式而要采用更精确的模型。
二、选择题1、如图所示，两个同心均匀带电球面，内球面半径为1R 、带有电荷1Q ，外球面半径为2R 、带有电荷2Q ，则在外球面外面、距离球心为r 处的P 点的场强大小E 为 ( A ) A 、20214r Q Q επ+B 、()()2202210144R r Q R r Q -π+-πεε C 、()2120214R R Q Q -+επ D 、2024r Q επ2、A 和B 为两个均匀带电球体，A 带电荷q +，B 带电荷q -，作一与A 同心的球面S 为高斯面，如图所示。
大连理工大学大学物理作业及答案详解1-22
大连理工大学大学物理作业及答案详解作业1 （静电场一）1．关于电场强度定义式，下列说法中哪个是正确的？[ ] A ．场强E 的大小与试探电荷0q 的大小成反比。
B ．对场中某点，试探电荷受力F 与0q 的比值不因0q 而变。
C ．试探电荷受力F 的方向就是场强E 的方向。
D ．若场中某点不放试探电荷0q ，则0F =，从而0E =。
答案： 【B 】[解]定义。
场强的大小只与产生电场的电荷以及场点有关，与试验电荷无关，A 错；如果试验电荷是负电荷，则试验电荷受的库仑力的方向与电场强度方向相反，C 错；电荷产生的电场强度是一种客观存在的物质，不因试验电荷的有无而改变，D 错；试验电荷所受的库仑力与试验电荷的比值就是电场强度，与试验电荷无关，B 正确。
2．一个质子，在电场力作用下从A 点经C 点运动到B 点，其运动轨迹如图所示，已知质点运动的速率是递增的，下面关于C 点场强方向的四个图示哪个正确？[ ]答案： 【D 】[解]a m E q=，质子带正电且沿曲线作加速运动，有向心加速度和切线加速度。
存在向心加速度，即有向心力，指向运动曲线弯屈的方向，因此质子受到的库仑力有指向曲线弯屈方向的分量，而库仑力与电场强度方向平行（相同或相反），因此A 和B 错；质子沿曲线ACB 运动，而且是加速运动，所以质子受到的库仑力还有一个沿ACB 方向的分量（在C 点是沿右上方），而质子带正电荷，库仑力与电场强度方向相同，所以，C 错，D 正确。
3．带电量均为q +的两个点电荷分别位于X 轴上的a +和a -位置，如图所示，则Y 轴上各点电场强度的表示式为E = ，场强最大值的位置在y = 。
答案：y a qy23220)(2+=πε，2/a y ±= [解]21E E += )(422021y a qE E +==πε关于y 轴对称：θcos 2,01E E E y x ==j y a qyj E E y 23220)(2+==∴πε沿y 轴正向的场强最大处0=dydEy y a y y a dy dE 2)(23)(25222322⨯+-+∝-- 2/a y = 2/a y ±=处电场最强。
大学物理第05章 静电场习题解答
第5章 静电场习题解答5.1一带电体可作为点电荷处理的条件是（ C ） （A ）电荷必须呈球形分布。
（B ）带电体的线度很小。
（C ）带电体的线度与其它有关长度相比可忽略不计。
（D ）电量很小。
5.2图中所示为一沿 x 轴放置的“无限长”分段均匀带电直线，电荷线密度分别为+λ（x >0）和 -λ（x < 0），则 oxy 坐标平面上点（0，a ）处的场强 E 为：（ B ） ( A ) 0 ( B )02aλπεi ( C )04a λπεi ( D ) ()02aλπε+i j 5.3 两个均匀带电的同心球面，半径分别为R 1、R 2(R 1<R 2)，小球带电Q ，大球带电-Q ，下列各图中哪一个正确表示了电场的分布 （ d ）(C) (D)5.4 如图所示，任一闭合曲面S 内有一点电荷q ，O 为S 面上任一点，若将q 由闭合曲面内的P 点移到T 点，且OP =OT ，那么 （ d ）(A) 穿过S 面的电通量改变，O 点的场强大小不变； (B) 穿过S 面的电通量改变，O 点的场强大小改变； (C) 穿过S 面的电通量不变，O 点的场强大小改变；(D) 穿过S 面的电通量不变，O 点的场强大小不变。
5.5如图所示，a 、b 、c 是电场中某条电场线上的三个点，由此可知 （ c ） (A) E a >E b >E c ； (B) E a <E b <E c ； (C) U a >U b >U c ； (D) U a <U b <U c 。
5.6关于高斯定理的理解有下面几种说法，其中正确的是 （ c ）(A) 如果高斯面内无电荷，则高斯面上E处处为零；(B) 如果高斯面上E处处不为零，则该面内必无电荷； (C) 如果高斯面内有净电荷，则通过该面的电通量必不为零；(D) 如果高斯面上E处处为零，则该面内必无电荷。
5.7 下面说法正确的是 [ D ](A)等势面上各点场强的大小一定相等； (B)在电势高处，电势能也一定高； (C)场强大处，电势一定高；(D)场强的方向总是从电势高处指向低处.5.8 已知一高斯面所包围的体积内电量代数和0i q =∑ ，则可肯定：[ C ] （A ）高斯面上各点场强均为零。
(完整版)大学物理静电场练习题及答案
练习题7-1 两个点电荷所带电荷之和为 Q，它们各带电荷为多少时，互相间的作用力最大 ?解 : 这是一个条件极值问题。
设此中一个点电荷带电 q，则另一个点电荷带电Q q ，两点电荷之间的库仑力为1Q q qFr 24 0由极值条件 dF dq0 ，得q 1 Q 2又因为d2 F1dq2 2 0 r 2<0这表示两电荷均分电荷Q 时，它们之间的互相作用力最大。
7-2 两个相同的小球，质量都是 m，带等值同号的电荷 q，各用长为 l 的细线挂在同一点，如图7-43 所示。
设均衡时两线间夹角 2很小。
（ 1）试证均衡时有以下的近似等式成立：123q lx0 mg2式中 x 为两球均衡时的距离。
(2)假如 l= 1.20 m， m=10 g，x=5.0 cm，则每个小球上的电荷量 q 是多少 ?(3)假如每个球以10 9 C s-1的变化率失掉电图 7-43 练习题 7-2 图荷，求两球相互趋近的刹时相对速率dx/dt 是多少 ?解：(1)带电小球受力解析如图解所示。
小球平衡时，有FTsinTcos mg由此二式可得tanFmg因为 很小，可有 tanx 2l ，再考虑到Fq20 x 24可解得21xq l 32 0mg（2）由上式解出3120 mgx22.38 108 Cql（3） 因为1 1dx l3 2 dq 2x dq3dt2 0 mgqdt3q dt3带入数据解得1.4010 3 m s-1合力的大小为F F x 2F 1cos212e 2x224d0 x2x 2d22132e 2 x44 x2d 2 3 2令 dF dx0 ，即有8e 2138x 24x2d23 22 4x 2d25 2由此解得 粒子受力最大的地点为xd2 2第七章静电场7-4 由相距较近的等量异号电荷构成的系统称电偶极子，生物细胞膜及土壤颗粒表面的双电层可视为好多电偶极子的会集。
所以，电偶极子是一个十分重要的物理模型。
《大学物理》练习题及详细解答-—真空中的静电场
、 两点间的电势差为
17．细长圆柱形电容器由同轴的内、外圆柱面构成，其半径分别为 和 ，两圆柱面间为真空。电容器充电后内、外两圆柱面之间的电势差为 。求：
（1）内圆柱面上单位长度所带的电量 ；
（2）在离轴线距离 处的电场强度大小。
解：（1）电场分布具有轴对称性，取同轴闭合圆柱面为高斯面，圆柱面高为 ，底面圆半径为 ，应用高斯定理求解。
解：（1）均匀带电的细圆环在 点处产生的场强大小为（参见教材中均匀带电圆环轴线上的场强公式）
，方向沿 向右
粒子所受的电场力的大小
，方向沿 向右
（2）在细圆环上取 ， 在 点产生的电势为
点的电势为
由动能定理得，
（2）电荷在顶点时，将立方体延伸为边长 的立方体，使 处于边长 的立方体中心，则通过边长 的正方形各面的电通量
对于边长 的正方形，如果它不包含 所在的顶点，则 ，如果它包含 所在顶点，则 。
9. 两个无限大的平行平面都均匀带电，电荷的面密度分别为 和 ，试求空间各处场强。
解：如图所示，电荷面密度为 的平面产生的场强大小为
，方向沿 轴负方向
利用几何关系， ， 统一积分变量，得
因为所有的细圆环在在 点产生的场强方向均沿为 轴负方向，所以球心处电场强度的大小为
方向沿 轴负方向。
7.一“无限大”平面，中部有一半径为 的圆孔，设平面上均匀带电，电荷面密度为 ，如图所示。试求通过小孔中心 并与平面垂直的直线上各点的场强。
解：应用补偿法和场强叠加原理求解。
当 时， ， ，所以
（2）当 时， ，所以
当 时， ，所以
负号表示场强方向沿径向指向球心。
12. 一厚度为 的无限大的带电平板，平板内均匀带电，其体电荷密度为 ，求板内外的场强。
大学物理题库-第5章 静电场习题(含答案解析)
真空中的静电场一 选择题1．两个等量的正电荷相距为2a ，P 点在它们的中垂线上，r 为P 到垂足的距离。
当P 点电场强度大小具有最大值时，r 的大小是：[ ]（A ）42a r =（B ）32a r = （C ）22ar = （D ）a r 2= 2．如图5-1所示，两个点电荷的电量都是q +，相距为a 2，以左边点电荷所在处为球心，以a 为半径作一球形高斯面，在球面上取两块相等的小面积1S 和2S ，设通过1S 和2S 的电通量分别为1Φ和2Φ，通过整个球面的电通量为Φ，则[ ]（A ）021εq=ΦΦ>Φ,（B ）0212,εq=ΦΦ<Φ（C ）021εq=ΦΦ=Φ,（D ）021εq=ΦΦ<Φ,3．在静电场中，高斯定理告诉我们 [ ]（A ）高斯面内不包围电荷，则高斯面上各点E的量值处处相等；（B ）高斯面上各点E只与面内电荷有关，与面外电荷无关；（C ）穿过高斯面的E（D ）穿过高斯面的E 通量为零，则高斯面上各点的E必为零； 4．如图5-2所示，两个“无限长”的同轴圆柱面，半径分别为1R 和2R ，其上均匀带电，沿轴线方向单位长度上的带电量分别为1λ和2λ，则在两圆柱面之间、距轴线为r 的P 点处的场强大小为：[ ]（A ）r 012πελ （B ）r 0212πελλ+ （C ）()r R -2022πελ （D ）()1012R r -πελ5．电荷面密度为+σ和-σ的两块“无限大”均匀带电平行平板，放在与平面垂直的x2-5 图1 - 5 图轴上a +和a -位置，如图5-3所示。
设坐标圆点o 处电势为零，则在a x a +<<-区域的电势分布曲线为： （ ）6．真空中两个平行带电平板A 、B ，面积均为S ，相距为)(S d d <<2，分别带电量q +和q -，则两板间相互作用力的大小为：[ ]（A ）204d q πε （B ）Sq 0ε （C ）Sq 022ε （D ）不能确定7．静电场中，下列说法哪一个是正确的？[ ]（A ）正电荷的电势一定是正值； （B ）等势面上各点的场强一定相等；（C ）场强为零处，电势也一定为零； （D ）场强相等处，电势梯度矢量一定相等。
大学物理静电场习题答案
［ B ］
a
b
4.（1076） 点电荷-q位于圆心O处，A、B、C、D为同一圆周上的四点，如图所示．现将一 试验电荷从A点分别移动到B、C、D各点，则 (A) 从A到B，电场力作功最大． (B) 从A到C，电场力作功最大． (C) 从A到D，电场力作功最大． -q (D) 从A到各点，电场力作功相等． ［D ］ A B O
R dEx
dq
d
x
dE
O dEy
dEx dE cos, dEy dE sin
对各分量分别求和
0 Ex sin cos d 0 4 0 R
0 0 2 Ey sin d 0 4 0 R 8 0 R
所以
0 E Ex i E y j j 8 0 R
O
a aBiblioteka xa 4.(1025) 电荷面密度分别为+δ和－δ的两块“无限大”均匀带电平行平面，分别与x x 轴垂直相交于x1＝a，x2＝－a 两点．设坐标原点O处电势为零，试求空间 - 的电势分布表示式并画出其曲线．
z
a
+
解：由高斯定理可得场强分布为： E =-δ/ ε0 (－a＜x＜a) E=0 (－∞＜x＜－a ，a＜x＜＋∞) 由此可求电势分布：在－∞＜x≤－a区间
Rb Rc Ra A BC
E1=λ1 / 2πε0r，方向由B指向A
B、C间场强分布为 B、A 间电势差
E2=λ2 / 2πε0r，方向由B指向C
1 U BA E1 d r Rb 2 0
Ra
Rb dr 1 Rb r 2 0 ln Ra
Ra
C
B A
E2 E1
《大学物理》真空中的静电场练习题及答案解析
《大学物理》真空中的静电场练习题及答案解析一 选择题1. 下列几个说法中哪一个是正确的 （B ）（A ）电场中某点场强的方向，就是将点电荷放在该点所受电场力的方向（B ）电场中某点的场强大小与试验电荷无关。
（C ）场强大小由 E =F /q 可知，某点的场强大小与试验电荷受力成正比，与电量成反比。
（D ）在以点电荷为中心的球面上，由该点电荷所产生的场强处处相同2. 如图所示为一沿 x 轴放置的“无限长”分段均匀带电直线，电荷线密度分别为+λ、-λ，则 oxy坐标平面上点（0，a ）处的场强E 的方向为（ A ）( A )x 正方向 （B ） x 负方向 （C ）y 正方向（D ）y 负方向3.如图所示，一个带电量为q 的点电荷位于正立方体的中心上，则通过其中一侧面的电场强度通量等于：（ B ）（A）04εq (B)06εq (C) 024εq (D) 027εq第2题图 第3题图 4．关于高斯定理0ε∑⎰⎰=⋅=Φi s e q s d E ，下列说法中正确的是（ C ）（A ）如果高斯面无电荷，则高斯面上的电场强度处处为零（B ）如果高斯面上的电场强度处处为零，则高斯面内无电荷（C ）如果高斯面上的电场强度处处为零，则通过高斯面的电通量为零（D ）若通过高斯面的电通量为零，则高斯面上的电场强度处处为零5.如图所示，闭合曲面S 内有一点电荷q ，P 为S 面上一点，在S 面外A 点有一点电荷,q ，将其移到B 点，则（ B ）（A ）通过S 面的电通量不变，P 点的电场强度不变。
（B ）通过S 面的电通量不变，P 点的电场强度变化。
（C ）通过S 面的电通量改变，P 点的电场强度不变。
（D ）通过S 面的电通量改变，P 点的电场强度变化。
6．下列说法中正确的是（ D ）（A ）场强为0的点电势也为0 （B ）场强不为0的点电势也不为0（C ）电势为0的点，则电场强度也一定为0（D ）电势在某一区域为常数，则电场强度在该区域必定为01.B2.A3.B4.C5.D 、6D二 填空题1、在点电荷的q +，q -电场中，作如图所示的三个高斯面，求通过321S S 、、S ，球面的电通量分别为________________、_______________、______________。
大连理工大学大学物理作业4(静电场四)及答案详解
作业4 静电场四导线穿过外球壳上的绝缘小孔与地连接，外球壳上带有正电荷，则内球壳上[ ]。
.A 不带电荷.B 带正电 .C 带负电荷.D 外表面带负电荷，内表面带等量正电荷答案：【C 】解：如图，由高斯定理可知，内球壳内表面不带电。
否则内球壳内的静电场不为零。
如果内球壳外表面不带电（已经知道内球壳内表面不带电），则两壳之间没有电场，外球壳内表面也不带电；由于外球壳带正电，外球壳外表面带正电；外球壳外存在静电场。
电场强度由内球壳向外的线积分到无限远，不会为零。
即内球壳电势不为零。
这与内球壳接地（电势为零）矛盾。
因此，内球壳外表面一定带电。
设内球壳外表面带电量为q （这也就是内球壳带电量），外球壳带电为Q ，则由高斯定理可知，外球壳内表面带电为q -，外球壳外表面带电为Q q +。
这样，空间电场强度分布r r qr E ˆ4)(201πε=，（两球壳之间：32R r R <<）r r Qq r E ˆ4)(202πε+= ，（外球壳外：r R <4）其他区域（20R r <<，43R r R <<），电场强度为零。
内球壳电势为041)11(4ˆ4ˆ4)()(403202020214324322=++-=⋅++⋅=⋅+⋅=⋅=⎰⎰⎰⎰⎰∞∞∞R Q q R R q r d r rQq r d r r q r d r E r d r E l d E U R R R R R R R πεπεπεπε则04432=++-R QR q R q R q ，4324111R R R R Q q +--=由于432R R R <<，0>Q ，所以0<q即内球壳外表面带负电，因此内球壳负电。
2．真空中有一组带电导体，其中某一导体表面某处电荷面密度为σ，该处表面附近的场强大小为E ，则0E σ=。
那么，E 是[ ]。
.A 该处无穷小面元上电荷产生的场 .B 导体上全部电荷在该处产生的场 .C 所有的导体表面的电荷在该处产生的场 .D 以上说法都不对答案：【C 】解：处于静电平衡的导体，导体表面附近的电场强度为0E σ=，指的是：空间全部电荷分布，在该处产生的电场，而且垂直于该处导体表面。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
练习题7-1 两个点电荷所带电荷之和为Q ，它们各带电荷为多少时，相互间的作用力最大?解: 这是一个条件极值问题。
设其中一个点电荷带电q ，则另一个点电荷带电q Q -， 两点电荷之间的库仑力为()241r qq Q F -=πε由极值条件0d d =q F，得Q q 21= 又因为202221d d r q F πε-=<0这表明两电荷平分电荷Q 时，它们之间的相互作用力最大。
7-2 两个相同的小球，质量都是m ，带等值同号的电荷q ，各用长为l 的细线挂在同一点，如图7-43所示。
设平衡时两线间夹角2θ很小。
（1）试证平衡时有下列的近似等式成立：31022⎪⎪⎭⎫⎝⎛=mg l q x πε式中x 为两球平衡时的距离。
(2)如果l = 1.20 m ，m =10 g ，x =5.0 cm ，则每个小球上的电荷量q 是多少?(3)如果每个球以-19s C 1001⋅⨯-.的变化率失去电 图7-43 练习题7-2图 荷，求两球彼此趋近的瞬时相对速率d x /d t 是多少? 解：(1)带电小球受力分析如图解所示。
小球平衡时，有FT =θsinmg T =θcos由此二式可得mgF =θtan因为θ很小，可有()l x 2tan ≈θ，再考虑到2024x q F πε=可解得31022⎪⎪⎭⎫ ⎝⎛=mg l q x πε（2）由上式解出C 10382282130-⨯±=⎪⎪⎭⎫⎝⎛±=.l mgx q πε （3） 由于tq q x t q q mg l t x d d 32d d 322d d 31310=⎪⎪⎭⎫ ⎝⎛==-πευ 带入数据解得-13s m 10401⋅⨯=-.υ合力的大小为2222201222412cos 2⎪⎭⎫ ⎝⎛+⋅⎪⎭⎫ ⎝⎛+⋅⋅===d x x d x e F F F x πεθ()23222043241dx xe +=πε令0d d =x F ，即有()()0482341825222232202=⎥⎥⎦⎤⎢⎢⎣⎡+⋅-+d x x d x e πε 由此解得α粒子受力最大的位置为22d x ±=7-4 由相距较近的等量异号电荷组成的体系称电偶极子，生物细胞膜及土壤颗粒表面的双电层可视为许多电偶极子的集合。
因此，电偶极子是一个十分重要的物理模型。
图7-45所示的电荷体系称电四极子，它由两个电偶极子组合而成，其中的q 和l 均为已知，对图7-44中的P 点(OP 平行于正方形的一边)，证明当x » l 时4043x plE p πε≈其中，p=ql 称电偶极矩。
解：电四极子可看成两个电偶极子的组合。
设左边和右边两个电偶极子在P 点产生的场强分别为E 左和E 右，由教材例题7-3可知()()302 4l p E x πε=+左方向向下 ()()3024l p E x πε=-右方向向上其中，p =ql 。
P 点处的合场强为()()()()3223332200022232444ll l l x l p p p E E E x x x πεπεπε+=-=-=-+⎡⎤-⎣⎦左右由于x » l上式可简化为()403 4plE xπε=方向向上 证毕。
7-5 如图7-46所示，长为l 的细直线OA 带电线密度为λ，求下面两种情况下在线的延长线上距线的端点O 点为b 的P 点的电场强度： (1)λ为常量，且λ>0；(2) λ=kx ，k 为大于零的常量，(0≤x ≤1)。
解：(1)将带电直线分割成无数个长度元d x ，d x 的坐标是x 。
它所带的电荷元d q =λd x ，d q 在P 点产生的电场强度的大小为()2d 41d b x xE +⋅=λπε因为所有电荷元产生的场强方向都相同，所以场强的矢量叠加可用代数方法 相加。
于是带电直线在P 点产生的电场强度为 ()⎰+⋅=lb x xE 02d 41λπε ⎪⎭⎫ ⎝⎛+-=l b b 1140πελ()l b b l+=04πελ 方向沿x 轴的负方向。
(2) 同样取电荷微元d q =λd x =kx d x ()2d 41d b x xkx E +⋅=πε同理()⎰+⋅=lb x xkx E 02d 41πε⎪⎭⎫⎝⎛+-+=b l l b l b k ln 40πε 方向沿x 轴的负方向。
7-6 一个半径为R 的半圆细环上均匀地分布电荷Q ，求环心处的电场强度。
解：分析在求环心处的电场强度时，不能将带电半圆环视作点电荷。
现将其抽象为带电半圆弧线．在弧线上取线元d l ，其电荷l RQ q d d π=，此电荷元可视为点电荷，它在O点的电场强度为020d 41d r E Rq ⋅=πε 因圆环上电荷对y 轴呈对称性分布，电场分布也是轴对称的，则有0d ==⎰Lx x E E点O 的合电场强度为 习题7-6用图θπεθsin d 41sin d -d -20RqE E E E LLLy y ⋅-====⎰⎰⎰其中，负号表示场强方向与y 方向相反。
将l RQq d d π=，θd d R l =，带入上式，积分得 2022022sin 4RQ RQ E επθεππ－=-=⎰负号表示场强方向与y 方向相反7-7 一个半径为R的带电圆盘，电荷面密度为σ，求：（1）圆盘轴线上距盘心为x处的任一点P的电场强度；（2）当R→∞时，P点的电场强度为多少?（3）当x »R时，P点的电场强度又为多少?练习题7-7用图解：（1）在半径为R的带电圆盘上取半径为r、外半径为r+d r的细圆环，如图所示。
利用教材中例题7-5的结果可知，该细圆环上的电荷在P点产生的场强为()()3232222200d 2dd44x S x r rEx r x rσσππεπε==++于是，整个圆盘上的电荷在P点产生的场强为()()⎥⎥⎦⎤⎢⎢⎣⎡+-=+=⎰21222322122RxxrxrdrxE Rεσεσ（1）当R→∞时，R »x。
此时，上式可化为2Eσε=即此时可将带电圆盘看作无限大带电平面。
（3）当x »R时，可将带电圆盘看作点电荷，此时P点电场强度为22200444R qEx xσππεπε==7-8 图7-47为两个分别带有电荷的同心球壳系统。
设半径为1R 和2R 的球壳上分别带有电荷1Q 和2Q ，求：（1）I 、II 、III 三个区域中的场强； （2）若1Q =－2Q ，各区域的电场强度又为多少？画出此时的电场强度分布曲线 (即E －r 关系曲线)。
解：（1）在区域I ，做半径为r ﹤R 1的球形高斯面。
因为高斯面无电荷，根据高斯定理 S d S⋅⎰⎰ E =∑ii q内1ε即 0421=r E π可得区域I 中的电场强度为E 1= 0在区域II ，以12R r R <<为半径做球形高斯面。
因为此高斯面的电荷为Q 1，由高斯定理得S d S⋅⎰⎰ E =∑ii q1ε1224επQ r E =由此可解得区域II 的电场强度为12204Q E r πε=在区域III ，做半径r ﹥R 2的球形高斯面。
由于该高斯面的电荷为Q 1+Q 2，由高斯定理可得S d S⋅⎰⎰3 E =∑ii q1ε21234επQ Q r E +=E 3 =1224Q Q r πε+图7-47 练习题7-8用图（2）当1Q =－2Q 时，根据以上结果易知区域I 的场强为E 1= 0区域II 的场强为12204Q E rπε=区域III 的场强为E 3= 0根据上述结果可画出如图所示E r -关系曲线。
7-12 水分子的电偶极矩为-306.1310C m ⨯⋅，如果这个电偶极矩是由一对点电荷±e 引起的(e 为电子电量)，那么，它们的距离是多少?如果电偶极矩的取向与强度为6-110N C ⋅的电场方向一致，要使这个电偶极矩倒转成与电场相反的方向需要多少能量(用eV 表示)? 解：（1）由电偶极矩的定义e p ql =得3011196.1310 3.8310(m)1.610e p l q ---⨯===⨯⨯ （2）若使电偶极矩倒转需要能量为A ，则1961119522 1.61010 3.83101.6107.6610(eV)A q q eEl+-----=⋅+⋅=⨯⨯⨯⨯⨯=⨯=⨯E l E l7-13 计算练习题7-8中Ⅰ、Ⅱ、Ⅲ区域中的电势。
解：（1）根据题7-8所得Ⅰ、Ⅱ、Ⅲ区域中的电场分布，01=E ;12204Q E r πε=;2210341r Q Q E +=πε 可得区域I 的电势为1212212 1 123 11222 00 d d d d d d 44E rrR R rR R R R R U E r E r E rQ Q Q r r r rπεπε∞∞∞=⋅=+++=+⎰⎰⎰⎰⎰⎰由此解得12101214Q Q U R R πε⎛⎫=+ ⎪⎝⎭区域Ⅱ的电势分布为2212223 021 d d d 4E r R rrR Q Q U E r E r r R πε∞∞•⎛⎫==+=+ ⎪⎝⎭⎰⎰⎰ 区域Ⅲ的电势分布为1233 0 d d 4E r rrQ Q U E r rπε∞∞•+===⎰⎰（2）若12Q Q =-，则区域Ⅰ的电势为1212211 123 1201012 d d d d d 4114E rrR R rR R R R U E r E r E rQ rrQ R R πεπε∞∞=⋅=++=⎛⎫=- ⎪⎝⎭⎰⎰⎰⎰⎰区域Ⅱ的电势为2122 0211 d d 4E r R rrQ U E r r R πε∞•⎛⎫===- ⎪⎝⎭⎰⎰区域Ⅲ的电势为 33 d d 0E r rrU E r ∞∞•===⎰⎰7-14 “无限长”均匀带电圆柱面，半径为R ，单位长度上带电量为+λ。
试求其电势分布。
(提示：选取距带电圆柱面轴线为R 的0P 点为电势零点)解：由于电荷分布具有轴对称性，所以应用高斯定理很容易求出电场强度分布为0 (r ＜ R )E=rE 02πελ=（r ＞ R ） 电场强度方向垂直于带电圆柱面沿径向。
选某一距带电直线为R 的0P 点为电势零点， 如本题解图所示。
当r ＜ R 时 0d d 0⎰⎰=⋅=⋅=Rrp PU r E r E这个结果可以一般地表示为当r ＞ R 时r rr E U P P RrRrd 2d d 00⎰⎰⎰'==⋅=πελr E R r ln 2ln 200πελπελ+-=rRln 20πελ=. ..页脚7-16 同轴电缆是由两个很长且彼此绝缘的同轴金属圆柱体构成，如图7－49所示。
设圆柱体的电势为1U ，半径为1R ；外圆柱体的电势为2U ，外圆柱体的半径为2R ，两圆柱体之间为空气。