中考数学第二轮复习:图表信息问题
中考数学第二轮专题复习图表信息型问题和阅读理解型问题 新人教版

中考数学冲刺第二轮专题复习——图表信息型问题和阅读理解型问题一、图表信息型问题1、图表信息型问题的特点:由图象(表)来获取信息.从而达到解题目的的题型。
2、图表信息型问题的主要类型:(1)图像信息型,即教材介绍的基本函数图象(如直线、双曲线、抛物线);(2)图形信息型,主要是几何问题;(3)统计图表型,即结合实际情境描绘的不规则图象(如折线型、统计图表等).这种题型一般是由图象给出的数据信息,探求两个变量之间的关系,进行数、形之间的互换.题型可涉及填空、选择和解答。
3、图表信息型考我们什么?(1)注重考查数形之间的转化能力,(2)考察发现问题、解决问题的能力4、解答图表信息型问题的步骤:(1)观察图像,获取有效信息;(2)对获取的信息进行整理,理清各量之间的关系;(3)通过建模解决问题。
第一种类型:图像信息型,即教材介绍的基本函数图象(如直线、双曲线、抛物线)【例1】(2012 绍兴)小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则表示父亲、母亲离家距离与时间之间的关系是(只需填序号).第二种类型:图形信息型,主要是几何问题【例2】(2011 绍兴)取一张矩形纸片按照图1、图2中的方法对折,并沿图3中过矩形顶点的斜线(虚线)剪开,把剪下的①这部分展开,平铺在桌面上.若平铺的这个图形是正六边形,则这张矩形纸片的宽和长之比为.【例3】(2010 绍兴)如图为某机械装置的截面图,相切的两圆⊙O1,⊙O2均与⊙O的弧AB 相切,且O1O2∥l1(l1为水平线),⊙O1,⊙O2的半径均为30mm,弧AB的最低点到l1的距离为30mm,公切线l2与l1间的距离为100mm.则⊙O的半径为()A.70mm B.80mm C.85mm D.100mm【例4】(2011 贵阳)用长度一定的不锈钢材料设计成外观为矩形的框架(如图①②③中的一种)设竖档AB=x米,请根据以上图案回答下列问题:(题中的不锈钢材料总长度均指各图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行)(1)在图①中,如果不锈钢材料总长度为12米,当x为多少时,矩形框架ABCD的面积为3平方米?(2)在图②中,如果不诱钢材料总长度为12米,当x为多少时,矩形架ABCD的面积S最大?最大面积是多少?(3)在图③中,如果不锈钢材料总长度为a米,共有n条竖档,那么当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?第三种类型:统计图表型,即结合实际情境描绘的不规则图象(如折线型、统计图表等)【例5】(2011 衢州)下列材料来自2006年5月衢州有关媒体的真实报道:有关部门进行民众安全感满意度调查,方法是:在全市内采用等距抽样,抽取32个小区,共960户,每户抽一名年满16周岁并能清楚表达意见的人,同时,对比前一年的调查结果,得到统计图如下:写出2005年民众安全感满意度的众数选项是;该统计图存在一个明显的错误是.【例6】(2011 湖州)班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生发言次数进行了统计,并绘制成如下频数分布折线图(图1).(1)请根据图1,回答下列问题:①这个班共有名学生,发言次数是5次的男生有人、女生有人;②男、女生发言次数的中位数分别是次和次;(2)通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数的扇形统计图如图2所示,求第二天发言次数增加3次的学生人数和全班增加的发言总次数.二、阅读理解型问题1、阅读理解型的主要题型:(1)阅读特殊范例,推出一般结论;(2)阅读解题过程,总结解题思路和方法;(3)阅读新知识,研究新问题等。
中考数学复习常考图表信息类题型解析(题目类型解析+真题反馈)(共19张PPT)

2019/3/9
请根据图中提供的信息,解答下列问题: (1) 在这次抽样调查中,共调查了___________名学生; (2) 补全条形统计图,并在扇形统计图中计算C类所对应扇形的圆心角的 度数; (3) 根据抽样调查结果,估计该校2000名学生中“家长和学生都未参与” 的人数。
2019/3/9
各类情况条形统计图 人数 240 200 160 120 80 40 240
2019/3/9
a元,蓝色地砖每块b元, 解: (1)设红色地砖每块 4000a 6000b 0.9 86000,
答:红色地砖每块8元,蓝色地砖每块10元. (2)设购置蓝色地砖x块,则购置红色地砖(12000-x)块,所需的总费用为 y元. 由题意知x≥(12000-x),得x≥4000,又x≤6000, ∴ 4000≤x≤6000. 当4000≤x<5000时,y=10x+8×0.8(12000-x),即y=76800+3.6x, ∴ x=4000时,y有最小值91200; 当5000≤x≤6000时,y=0.9×10x+8×0.8(12000-x)=2.6x+76800. ∴ x=5000时,y有最小值89800. ∵89800<91200,∴购买蓝色地砖5000块,红色地砖7000块,费用最少,
2019/3/9
典例选讲
例1 实数a,b,c在数轴上的对应点的位置如图所示,则正确 的结论是 (B )
A. a>4
B.c-b>0
C.ac>0
D.a+c>0
2019/3/9
典例选讲
例2 利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系 统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表 示0.将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生 所在班级序号,其序号为a×23+b×22+c×21+d×20.如图2第一行数字从 左到右依次为0,1,0,1,序号为0×23+1×22+0×21+1×20=5,表示 该生为5班学生.表示6班学生的识别图案是 ( B )
2019年安徽数学中考二轮复习专题三:图表信息问题课件(39张PPT)

解、处理数据的能力.
【例 2】
(2018·温州 )温州某企业安排 65名工人生产甲、乙两种产
品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需
求和生产经验,乙产品每天产量不少于 5件,当每天生产5件时,每件可 获利120元,每增加1件,当天平均每件获利减少 2元.设每天安排x人生 产乙产品. (1)根据信息填表. 产品种类 每天工人数/人 每天产量/件 x 每件产品可获利润/元
【解析】
(1) 方法一 : 设 AE = a , 分别用含 a 的代数式表示 BE ,
AB,根据题意建立y关于x的函数表达式;方法二:先分别用含x,y的代
数式表示CF和DF,再根据2BC+2CF+3DF=80,确定y与x之间的函数 表达式,并写出自变量的取值范围;(2)用配方法把二次函数配成顶点形 式,结合抛物线的开口方向和自变量取值范围确定二次函数的最值 .
【点拨】 此类问题容易出错的地方是:(1)由于不能用含x,y代数 式表示线段长 , 导致无法求解 ; (2)在配方时 ,对于二次项系数不是 1的
容易与解一元二次方程相混淆 ,导致错误;(3)求二次函数的最值时,由
于没有考虑自变量取值范围导致错误.
●类型二
表格类信息型
用表格呈现数据信息,比较直观、简洁,在日常生活中使用极为普 遍,工厂的产值、股市的行情、话费的计算等,表格信息型问题近年来 成为了中考数学试题的一道亮丽风景.解答这类问题关键是分析表格数 据,抽取有效信息,找出内在规律,需要同学们具备一定的分析、理
2x(元 ); (2) 每天生产甲产品可获得的利润比生产乙产品可获得的利润多 550 元 , 所以 15×2(65 - x) = x(130 - 2x) + 550 , 得一元二次方程 x2 - 80x + 700=0,解得x1=10,x2=70(不合题意,舍去),所以130-2x=110,每
中考第二轮专题复习—第三讲 图表信息型问题

☆◇☆中考数学中的图表信息型问题☆◇☆所谓图表信息问题,就是根据实际问题中所呈现出来的图像、图表信息,要求考生依据这些给出的信息通过整理、分析、加工等手段解决的一类问题,主要考查同学们识图看表的能力以及处理信息的能力.解答这类试题的关键是对图表信息认真分析、合理利用,按照题意要求,准确地输出信息.信息时代的到来,呼唤信息型的中考试题.由于此类问题命题背景广泛、蕴含知识丰富,突出对考生获取、整理与加工信息能力的考查,因而倍受命题者青睐,近年来在各地的中考试题中出现的频率越来越高.图象信息题是指由图象(表)来获取信息.从而达到解题目的的题型,这类问题来源广泛,形式灵活,突出对考生收集、整理和加工信息能力的考查.是近几年中考的热点.解图象信息题的关键是“识图”和“用图”.解这类题的一般步骤是:(1)观察图象,获取有效信息;(2)对已获信息进行加工、整理,理清各变量之间的关系;(3)选择适当的数学工具,通过建模解决问题.题型1此类题目一般以表格的形式出现,通过表格对数据进行收集、整理,得出与解题相关的信息,从而解决实际应用问题.题型2此类题目以图形、图象的形式出现,在图形的形式出现时,题型新颖,给出的形式有形象的人物及各自的语言表述,在活泼的氛围里,给出题目具体内容,在考查学生的建模能力,有时候用不等式,有时候用方程;在图象的形式出现时,有时用函数图象的形式出现,有时以统计图的形式出现,它要把所给的图象或图形的信息进行分类、提取加工,再合成。
例1、某次时装表演会预算中,票价定为每张100元,容纳观众人数不超过2000人,毛利润y(百元)关于观众人数x(百人)之间的函数图象如图2-1-3所示,当观众人数超过1000人时,表演会组织者需向保险公司缴纳定额平安保险费5000元(不列人成本费用人请解答下列问题:(1)求当观众人数不超过1000人时,毛利润y关于观众人数的函数解析式和成本费用S(百元)关于观众人数x的函数解析式;(2)若要使这次表演会获得36000.元的毛利润,那么需售出多少张门票?需支付成本费用多少元?注:当观众人数不超过1000人时,表演会的毛利润一门票收人一成本费用;当观众人数超过1000人时,表演会的毛利润=门票收入-成本费用-平安保险费.解:(1)由图2-1-3知,当 0≤x ≤10与10<x ≤20时,y 都是x 的一次函数.当0≤x ≤10时,设y 关于x 的函数解析式为y =kx +b ,把点(0,-100),(10,400)代入函数解析式,得10050 10400100b k k b b =-=⎧⎧⎨⎨+==-⎩⎩,解得:所以y =50x -100(0≤x ≤10),S =100x -(50x -100)=50x +100(0≤x ≤10)(2)当10<x ≤20时,由题意,知 50x -100=360.所以x =9.2,S =50x +100 =50×9.2+100=560.当10<x ≤2 0时,设y =mx +n .把点(10,350)(20,850)代入函数解析式,得1035050 20850150m n m m n n +==⎧⎧⎨⎨+==-⎩⎩,解得:所以y =50x -150(10<x ≤20),S =100x -(50x -150)-50=50x +100(10<x ≤20)当y =360时,50x -150=360,解得x =10.2.所以S =50×10.2+100=610.答:需售门票 920张或 1020张,相应地需支付成本费用分别为56000元或 61000元. 点拨:正确理解题意,注意单位的统一.例2、(07无锡)某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙地时正好用了2小时,已知摩托车行驶的路程(S 千米)与行驶的时间t (小时)之间的函数关系由如图6—1的图象ABCD 给出,若这辆摩托车平均每行驶100千米的耗油量为2升,根据图中给出的信息,从甲地到乙地,这辆摩托车共耗油升.分析:由题意知,摩托车的耗油量与从甲地到乙地所用时间无关,而只与所行驶的路程有关;而由图像可以得到信息,从甲地到乙地的路程为45千米.故耗油量应为45100×2=0.9(升).解:0.9升.说明:本题中摩托车的耗油量与所用时间无关,故从甲地到乙地的行驶时间2小时则属于过剩信息,在解题中要学会合理地排除.时)例3、某村实行合作医疗制度,村委会规定:(一)每位村民年初缴纳合作医疗基金a 元;设一位村民当年治病花费的医疗费为x 元,他个人实际承担的医疗费用(包括医疗费中个人承担的部分和缴纳的合作医疗基金)为y 元.(1)当0≤x≤b 时,y =a ;当b <x≤5000时,y=(用含有a 、b 、c 、x 的式子表示).(2)下表是该村4位村民2001年治疗花费的医疗费和个人实际承担的费用,根据表(3)村民个人一年最多承担医疗费用多少元? (2002年威海市中考试题) 分析:解决本题的关键是要能看懂表格,从第一个表格中我们不难得到如下信息:村民个人实际承担的费用是由两部分组成的,其一是合作医疗基金a ;其二是超过b 元不超过5000元部分的c%.由此,很容易写出用a 、b 、c 、x 表示y 的关系式.从第二个表格中可以看出,村民甲、乙两人的治疗花费的医疗费不同,但个人承担的费用却相同,这说明他们实际上承担的是合作医疗基金,由此可以得出a=30.进而将丙、丁两人的x 、y 具体值代入所列出的关系式中,构成方程组,从而可求出a 、b 、c 的值.而第3小问其实就是求所得到的函数式的最大值,由一次函数的性质可知,当x=5000时取最大值.解:(1)y =(x -b )c%+a ;(2)甲、乙两人花费的医疗费不同,但实际承担的费用相同(都是30元),说明他们两人花费的医疗费都不超过b 元,因此,他们实际承担的费用就是缴纳的合作医疗基金,即a =30.丙、丁两人实际承担的医疗费用超过了30元,说明他们一年得医疗费超过了b 元,但不足5000元,所以⎩⎨⎧=+-=+-830%)150(,5030%)90(c b c b 解得 ⎩⎨⎧==.50,50c b ∴ 当b <x ≤5000时,y =(x -50)50%+30, 即 152y x =+. (3)将x =5000代入,得 y =5000×0.5+5=2505,∴ 村民个人一年最多承担医疗费2505元.说明:本题就其实质来说是一个应用分段函数解决的实际问题,关键是要能根据表格中提供的信息,搞清个人实际所承担的医疗费用,同时要对第二个表格中所反映出的信息进行分析,搞清四位村民所花费的医疗费x 所在的范围,从而确定是否代入所列出的关系式去求解,而不能盲目行事。
中考数学第二轮复习:图表信息问题

1
专 题 解 读
2
考情透析 图表信息题是中考常考的一种新题型,它是通过图象、 图形及表格等形式给出信息,通过认真阅读、观察、 分析、加工、处理等手段解决的一类实际问题.主要 考查同学们的读图、识图、用图能力,以及分析问题、 解决问题的能力.图表信息问题往往和“方程(组)、不 等式(组)、函数、统计与概率”等知识结合考查.
11
二、表格信息题
以表格的形式给出数据信息是这类信息题的特征,分析表中的数据,能从表
格中发现两个量之间存在规律,归纳出相应的关系式是解决此类问题的关键.
12
【例题2】 (2012· 浙江台州)某汽车在刹车后行驶的距离s(单
位:米)与时间t(单位:秒)之间的关系的部分数据如下表:
时间t(秒) 行驶距离s(米)
4
专 题 突 破
5
一、图象信息题
此类题目主要是运用函数图象(一次函数、二次函数、反比例函数的 图象等)表示物体的变化规律(体现在两个变量之间的数量关系),考查
数形结合的思想和函数建模能力.解答时往往根据图象的形状、位置、 变化趋势等信息来判断、分析、解决问题.
6
【例题1】 (2012· 浙江义乌)周末,小明骑自行车从家里出
10
(3)设从家到乙地的路程为m km,
则点 E(x1,m),点 C(x2,m),分别代 入 y=60x-80,y=20x-10, m+80 m+10 得:x1= , x2 = . 60 20 10 1 ∵x2-x1= = , 60 6 m+10 m+80 1 ∴ - = , 20 60 6 解得:m=30. ∴从家到乙地的路程为 30 km.
14
分析 (1)描点作图即可. (2)首先判断函数为二次函数.用待定系数法,由 所给的任意三点即可求出函数解析式. (3)①将函数解析式表示成顶点式(或用公式求), 即可求得答案.
备考2023年中考数学二轮复习-统计与概率_数据收集与处理_频数(率)分布表-综合题专训及答案
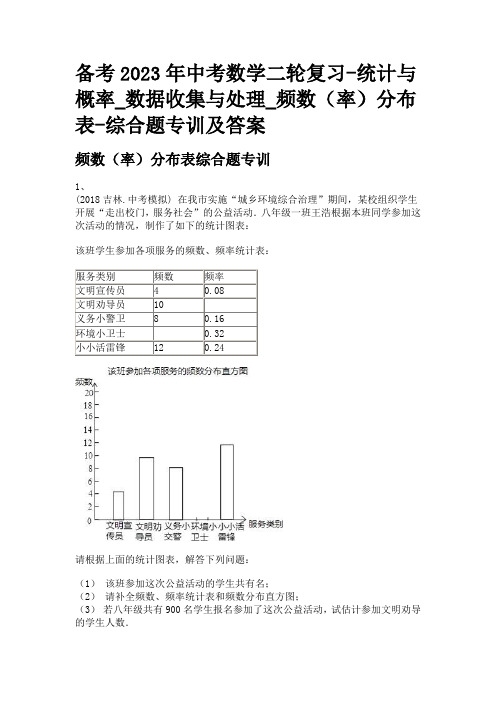
备考2023年中考数学二轮复习-统计与概率_数据收集与处理_频数(率)分布表-综合题专训及答案频数(率)分布表综合题专训1、(2018吉林.中考模拟) 在我市实施“城乡环境综合治理”期间,某校组织学生开展“走出校门,服务社会”的公益活动.八年级一班王浩根据本班同学参加这次活动的情况,制作了如下的统计图表:该班学生参加各项服务的频数、频率统计表:服务类别频数频率文明宣传员 4 0.08文明劝导员10义务小警卫8 0.16环境小卫士0.32小小活雷锋12 0.24请根据上面的统计图表,解答下列问题:(1)该班参加这次公益活动的学生共有名;(2)请补全频数、频率统计表和频数分布直方图;(3)若八年级共有900名学生报名参加了这次公益活动,试估计参加文明劝导的学生人数.2、(2018玄武.中考模拟) 某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:请根据所给信息,解答下列问题:(1) a=,b=;(2)请补全频数分布直方图;(3)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?3、(2017昆山.中考模拟) 国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:获奖等次频数频率一等奖10 0.05二等奖20 0.10三等奖30 b优胜奖 a 0.30鼓励奖80 0.40请根据所给信息,解答下列问题:(1) a=,b=,(2)补全频数分布直方图;(3)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?(4)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.4、(2019南浔.中考模拟) 为了庆祝中国人民海军成立70周年,某市举行了“海军知识”竞赛,为了了解竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示。
备考2024年中考数学二轮复习-利用统计图表分析实际问题-单选题专训及答案

备考2024年中考数学二轮复习-利用统计图表分析实际问题-单选题专训及答案利用统计图表分析实际问题单选题专训1、(2018房山.中考模拟) 某班体育委员对本班所有学生一周锻炼时间(单位:小时)进行了统计,绘制了统计图,如图所示,根据统计图提供的信息,下列推断正确的是()A . 该班学生一周锻炼时间的中位数是11B . 该班学生共有44人C . 该班学生一周锻炼时间的众数是10D . 该班学生一周锻炼12小时的有9人2、(2020西宁.中考模拟) 为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是()体温(℃)36.136.236.336.436.536.6人数(人)48810x2A . 这些体温的众数是8B . 这些体温的中位数是36.35C . 这个班有40名学生D . x=83、(2018黄浦.中考模拟) 一个民营企业10名员工的月平均工资如下表,则能较好反映这些员工月平均工资水平的是()人次1112113工资3032 1.5 1.220.8(工资单位:万元)A . 平均数;B . 中位数;C . 众数;D . 标准差.4、(2019温州.中考模拟) 某班预开展社团活动,对全班42名学生开展“你最喜欢的社团”问卷调查(每人只选一项),并将结果制成如下统计表,则学生最喜欢的项目是()社团名称篮球足球唱歌器乐人数(人)11x98A . 篮球B . 足球C . 唱歌D . 器乐5、(2019秀洲.中考模拟) 某电动车厂2018年第三、四季度各月产量情况如图所示。
某电动车厂2018年第三、四季则下列说法错误的是( )A . 7月份产量为300辆B . 从10月到11月的月产量增长最快C . 从11月到12月的月产量减少了20%D . 第四季度比第三季度的产量增加了70%6、(2019绍兴.中考模拟) 以下是某手机店1~4月份的两个统计图,分析统计图,对3、4月份三星手机的销售情况四个同学得出的以下四个结论,其中正确的为()A . 4月份三星手机销售额为65万元B . 4月份三星手机销售额比3月份有所上升C . 4月份三星手机销售额比3月份有所下降D . 3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额7、(2019温州.中考模拟) 小红同学5月份各项消费情况的扇形统计图如图所示,其中小红在学习用品上共支出100元,则她在午餐上共支出()A . 50元B . 100元C . 150元D . 200元8、(2018西湖.中考模拟) 右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是()A . 13,13B . 14,14C . 13,14D . 14,139、(2018福清.中考模拟) 下图是某学校全体教职工年龄的频数分布直方图(统计中采用“上限不在内”的原则,如年龄为36岁统计在36≤x<38小组,而不在34≤x<36小组),根据图形提供的信息,下列说法中错误的是()A . 该学校教职工总人数是50人B . 年龄在40≤x<42小组的教职工人数占该学校总人数的20%C . 教职工年龄的中位数一定落在40≤x<42这一组D . 教职工年龄的众数一定在38≤x<40这一组10、(2018龙湾.中考模拟) 如图是某手机店去年8﹣12月份某品牌手机销售额统计图,根据图中信息,可以判断相邻两个月该品牌手机销售额变化量最大的是()A . 8月至9月B . 9月至10月C . 10月至11月D . 11月至12月11、(2018龙湾.中考模拟) 下面的统计图反映了我市2011﹣2016年气温变化情况,下列说法不合理的是()A . 2011﹣2014年最高温度呈上升趋势B . 2014年出现了这6年的最高温度C . 2011﹣2015年的温差成下降趋势D . 2016年的温差最大12、(2019嘉兴.中考真卷) 年月日第届中国国际大数据产业博览会召开.某市在五届数博会上的产业签约金额的折线统计图如图.下列说法正确的是()A . 签约金额逐年增加B . 与上年相比,2019年的签约金额的增长量最多C . 签约金额的年增长速度最快的是2016年D . 2018年的签约金额比2017年降低了22.98%13、(2018合肥.中考模拟) 为了解初三学生的体育锻炼时间,小华调查了某班45名同学一周参加体育锻炼的情况,并把它绘制成折线统计图.由图可知,一周参加体育锻炼时间等于9小时的人数是()A . 5B . 18C . 10D . 414、(2019威海.中考真卷) 甲、乙施工队分别从两端修一段长度为380米的公路.在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.施工时间/天123456789累计完成施工量/3570105140160215270325380米下列说法错误的是( )A . 甲队每天修路20米B . 乙队第一天修路15米C . 乙队技术改进后每天修路35米D . 前七天甲,乙两队修路长度相等15、(2019五华.中考模拟) (2019·五华模拟) 如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是()A . 平均数是6B . 中位数是6.5C . 众数是7D . 平均每周锻炼超过6小时的人数占该班人数的一半16、(2018河池.中考模拟) 数学小组的同学为了解“阅读经典”活动的开展情况,随机调查了50名同学,对他们一周的阅读时间进行了统计,并绘制成下图.这组数据的中位数和众数分别是()A . 中位数和众数都是8小时B . 中位数是25人,众数是20人C . 中位数是13人,众数是20人,D . 中位数是6小时,众数是8小时17、(2019巴中.中考真卷) 如图所示,是巴中某校对学生到校方式的情况统计图.若该校骑自行车到校的学生有200人,则步行到校的学生有()A . 120人B . 160人C . 125人D . 180人18、(2018泸州.中考真卷) 某校对部分参加夏令营的中学生的年龄(单位:岁)进行统计,结果如下表:年龄1314151617人数12231则这些学生年龄的众数和中位数分别是()A . 16,15B . 16,14C . 15,15D . 14,1519、(2019醴陵.中考模拟) 若干名工人某天生产同一种玩具,生产的玩具数整理成条形图(如图所示).则他们生产的玩具数的平均数、中位数、众数分别为()A . 5,5,4B . 5,5,5C . 5,4,5D . 5,4,420、(2019盘龙.中考模拟) 如图分别是某班全体学生上学时乘车、步行、骑车人数分布的条形统计图和扇形统计图(两图都不完整),下列结论错误的是( )A . 该班总人数为50人B . 骑车人数占20%C . 乘车人数是骑车人数的2.5倍D . 步行人数为30人21、(2020嘉兴.中考模拟) 乐乐把报纸上看到甲、乙两公司2013年年的销售收入情况如图所示:关于两家公司年的销售收入的增长速度,下列说法正确的是()A . 甲快B . 乙快C . 一样快D . 无法比较22、(2020呼和浩特.中考模拟) 小明家1至6月份的用水量统计如图所示,则5月份的用水量比4月份增加的百分率为( )A . 25%B . 20%C . 50%D . 33%23、(2020广元.中考真卷) 下列各图是截止2020年6月18日的新冠肺疫情统计数据,则以下结论错误的是()A . 图1显示印度新增确诊人数大约是伊朗的两倍.每百万人口的确诊人数大约是伊朗的B . 图1显示俄罗斯当前的治愈率高于四班牙C . 图2显示海外新增确诊人数随时间的推移总体呈增长趋势D . 图3显示在2-3月之间,我国现有确诊人数达到最多24、(2021福建.中考模拟) 随着智能手机的普及,“支付宝支付”和“微信支付”等手机支付方式倍受广大消费者的青睐,某商场对2019年7−12月中使用这两种手机支付方式的情况进行统计,得到如图所示的折线图,根据统计图中的信息,得出以下四个推断,其中不合理的是()A . 6个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多;B . 6个月中使用“微信支付”的消费总额比使用“支付宝支付”的消费总额大;C . 6个月中11月份使用手机支付的总次数最多;D . 9月份平均每天使用手机支付的次数比12月份平均每天使用手机支付的次数多;25、(2021辉.中考模拟) 为了解高校学生对5G移动通信网络的消费意愿,从在校大学生中随机抽取了1000人进行调查,下面是大学生用户分类情况统计表和大学生愿意为5G套餐多支付的费用情况统计图(例如,早期体验用户中愿意为5G套餐多支付10元的人数占所有早期体验用户的50%).用户分类人数A:早期体验用户(目前已升级为5G用户)260人B:中期跟随用户(一年内将升级为5G用户)540人C:后期用户(一年后才升级为5G用户)200人下列推断中,不合理的是()A . 早期体验用户中,愿意为5G套餐多支付10元,20元,30元的人数依次递减B . 后期用户中,愿意为5G套餐多支付20元的人数最多C . 愿意为5G套餐多支付10元的用户中,中期跟随用户人数最多D . 愿意为5G套餐多支付20元的用户中,后期用户人数最多26、(2020东城.中考模拟) 党的十八大以来,全国各地认真贯彻精准扶贫方略,扶贫工作力度、深度和精准度都达到了新的水平,为2020年全面建成小康社会的战略目标打下了坚实基础.以下是根据近几年中国农村贫困人口数量(单位:万人)及分布情况绘制的统计图表的一部分.年份人数地区201720182019东部30014747中部1112181西部1634916323(以上数据来源于国家统计局)根据统计图表提供的信息,下面推断错误的是()A . 2018年中部地区农村贫困人口为597万人B . 2017﹣2019年,农村贫困人口数量都是东部最少C . 2016﹣2019年,农村贫困人口减少数量逐年增多D . 2017﹣2019年,虽然西部农村贫困人口减少数量最多,但是相对于东、中部地区,它的降低率最低27、(2020朝阳.中考模拟) 生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的天数据,整理后绘制成统计表进行分析.日均可回收物回收量(千吨)合计频数123频率0.050.100.151表中组的频率满足.下面有四个推断:①表中的值为20;②表中的值可以为7;③这天的日均可回收物回收量的中位数在组;④这天的日均可回收物回收量的平均数不低于3.所有合理推断的序号是()A . ①②B . ①③C . ②③④D . ①③④28、(2021潍坊.中考真卷) 如图为2021年第一季度中国工程机械出口额TOP10国家的相关数据(同比增速是指相对于2020年第一季度出口额的增长率),下列说法正确的是()A . 对10个国家出口额的中位数是26201万美元B . 对印度尼西亚的出口额比去年同期减少C . 去年同期对日本的出口额小于对俄罗斯联邦的出口额D . 出口额同比增速中,对美国的增速最快29、(2021赤峰.中考真卷) 五一期间,某地相关部门对观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整),下列结论错误的是()A . 本次抽样调查的样本容量是5000B . 扇形统计图中的m为10%C . 若五一期间观光的游客有50万人,则选择自驾方式出行的大约有20万人D . 样本中选择公共交通出行的有2400人30、为了减轻学生课外作业负担,数学老师准备按照学生每天课外作业完成量(完成题目个数)实行分档布置作业.作业量分档递增,计划使第一档、第二档和第三档的作业量覆盖全校学生的70%,20%和10%,为合理确定各档之间的界限,随机抽查了该校500名学生过去一个阶段完成作业量的平均数(单位:个);绘制了统计图.如图所示,下面四个推断合理的是( )A . 每天课外作业完成量不超过15个题的该校学生按第二档布置作业B . 每天课外作业完成量超过21个的该校学生按第三档布置作业C . 该校学生每天课外作业完成量的平均数不超过18D . 该校学生每天课外作业完成量的中位数在15﹣18之间利用统计图表分析实际问题单选题答案1.答案:A2.答案:A3.答案:B4.答案:B5.答案:C6.答案:B7.答案:D8.答案:D9.答案:D10.答案:C11.答案:C12.答案:C13.答案:B14.答案:D15.答案:A16.答案:A17.答案:B18.答案:A19.答案:B20.答案:D21.答案:A22.答案:B23.答案:24.答案:25.答案:26.答案:27.答案:28.答案:29.答案:30.答案:。
数学中考复习《图表信息题》课件(14张ppt)

练习3 某气象研究中心观测一场沙尘暴从发生到结
束的全过程,开始时风速平均每小时增加2 千米/时,4小时后,沙尘暴经过开阔荒漠地,风速变为平 均每小时增加4千米/时,一段时间,风速保持不变,当沙 尘暴遇到绿色植被区时 ,其风速平均每小时减少1千米/时, 最终停止,结合风速y与时间x的图象如图,回答下列问题:
运输公司的甲、乙两种货车,已知过去两次租用这 种货车情况如下表(两种货车均为满载)
甲种货车辆数(辆) 乙种货车辆数(辆) 累计运输吨数(吨)
第一次 第二次
2
5
3
6
15.5 35
现租用该公司甲种货车5辆及乙种货车一辆刚好 运完这批货物,如果按每吨运费30元计算,货主应 付运费多少元?
解:设甲乙两种货车满载时的载重量分别
y(千米/时)
(32)
(1)在y轴( ) 内填入相应的数值;
(8)
O 4 10
25
x(小时)
(2)沙尘暴从发生到结束,共经过了多少小时?
(2)沙尘暴从发生到结束,共经过了多少小时?
(3)求出当x≥25时,风速y(千米/时)与时间
x(小时)之间的函数关系式。
解3:2÷(12=)32由(题小意时得)(:32)y(千米B/时) C(25,32)
1 2
x+2
(2)观察图象,当x>-4 时,y> 0;
当x =-4 时,y=0;当x <-4 时,y<0;
(3)观察图象,当x=2时,y= 3 , y
当y=1时x= -2 ; 3
(4)不解方程,求
2 1
1 2
x+2=0的解;x=-4
1
-4 -3 -2 -1-1 o 1 2 3 x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解
度:
(1)由图象,得:小明骑车速
10÷0.5=20(km/ h). 在甲地游玩的时间是 1-0.5=0.5(h).
(2)妈妈驾车速度:20×3=60(km/h)
如图,设直线BC解析式为y=20x+ b1,
9
把点 B(1,10)代入得 b1=-10. ∴直线 BC 解析式为 y=20x-10 ①. 设直线 DE 解析式为 y=60x+b2, 4 把点 D3,0代入得 b2=-80. ∴直线 DE 解析式为 y=60x-80 ②. 联立①②,得 x=1.75,y=25. ∴交点 F(1.75,25). ∴小明出发 1.75 小时(105 分钟)被妈妈追上, 此时离家 25 km.
分析 (1)用路程除以时间即可得到速度;在甲地 游玩的时间是1-0.5=0.5小时. (2)求得线段BC所在直线的解析式和DE所在直线 的解析式后,求得交点坐标即可求得被妈妈追上 的时间.
8
(3)设从家到乙地的路程为m km,则点E(x1,m),点C(x2,m)分别 代入两直线方程,依妈妈比小明早10分钟到达乙地列式求解.
此类题是通过常见的统计图表(频数分布表、频率分布直方图、 条形统计图、折线统计图、扇形统计图等)给出数据信息和变 化规律的常考题型.考查读图、识图能力和分析数据、处理数 据的能力,同时考查学生“用数据说话”的应用意识.
20
【例题3】 (2012· 浙江衢州)据衢州市2011年国民经济和社会发 展统计公报显示,2011年衢州市新开工的住房有商品房、廉 租房、经济适用房和公共租赁房四种类型.老王对这四种 新开工的住房套数和比例进行了统计,并将统计结果绘制 成下面两幅统计图,请你结合图中所给信息解答下列问题:
18
2 s2 -5t2+15t2 = =-5t2+15,∵t1<t2 t2 t2 s1 s2 ∴ - =-5t1+15-(-5t2+15)=5(t2-t1)>0 t1 t2 s1 s2 ∴ > . t1 t2 其实际意义是刹车后到t2时间内的平均速度小于到t1时
间内的刹车后平均速度.
19
三、统计图表信息题
14
分析 (1)描点作图即可. (2)首先判断函数为二次函数.用待定系数法,由 所给的任意三点即可求出函数解析式. (3)①将函数解析式表示成顶点式(或用公式求), 即可求得答案.
s1 s2 ②求出 与 ,用差值法比较大小. t1 t2
15
解 (1)描点如图所示:
16
(2)由散点图可知该函数为二次函数. 设二次函数的解析式为:s=at2+bt+c,
0 0
0.2 2.8
0.4 5.2
0.6 7.2
0.8 8.8
1.0 10
1.2 10.8
„ „
(1)根据这些数据在给出的坐标系中画出相应的点;
(2)选择适当的函数表示s与t之间的关系,求出相应
的函数解析式;
13
(3)①刹车后汽车行驶了多长距离才停止?
②当t分别为t1,t2(t1<t2)时,对应s的值分别为s1,s2, 请比较与的大小,并解释比较结果的实际意义.
∵抛物线经过点(0,0),∴c=0.
又由点(0.2,2.8),(1,10)可得:
0.04a+0.2b=2.8, a=-5, 解得: a+b=10, b=15.
经检验,其余各点均在s=-5t2+15t上. ∴二次函数的解析式为:s=-5t2+15t.
17
(3)①汽车刹车后到停止时的距离即汽车滑行的最大 距离. 32 45 2 ∵s=-5t +15t=-5t-2 + , 4 3 45 ∴当 t= 时,滑行距离最大,为 . 2 4 45 因此,刹车后汽车行驶了 米才停止. 4 ②∵s=-5t2+15t, ∴s1=-5t2+15t1,s2=-5t2+15t2 1 2 -5t2+15t1 s1 1 ∴ = =-5t1+15 t1 t1
发到野外郊游.从家出发0.5小时后到达甲地,游玩一 段时间后按原速前往乙地.小明离家1小时20分钟后, 妈妈驾车沿相同路线前往乙地,如图是他们离家的路程 y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的 速度是小明骑车速度的3倍.
7
(1)求小明骑车的速度和在甲地游玩的时间; (2)小明从家出发多少小时后被妈妈追上?此时离家多 远? (3)若妈妈比小明早10分钟到达乙地,求从家到乙地的 路程.
3
思路分析 解决这类题的基本思路是“细读图表→分析→理清 关系→解决问题”,具体做法: 1.细读图表:(1)通过整体阅读,搜索有价值的信 息;(2)重视数据变化;(3)注意图表细节.这些 细节往往起提示作用. 2.理清关系:对已获取的信息加工、整合,理清 各变量之间的关系. 3.选择适当的数学工具,通过建立数学模型,解 决问题.
4
专 题 突 破
5
一、图象信息题
此类题目主要是运用函数图象(一次函数、二次函数、反比例函数的 图象等)表示物体的变化规律(体现在两个变量之间的数量关系),考查
数形结合的思想和函数建模能力.解答时往往根据图象的形状、位置、 变化趋势等信息来判断、分析、解决问题.
6
【例题1】 (2012· 浙江义乌)周末,小明骑自行车从家里出
专题二 图表信息问题
1
专 题 解 读
2
考情透析 图表信息题是中考常考的一种新题型,它是通过图象、 图形及表格等形式给出信息,通过认真阅读、观察、 分析、加工、处理等手段解决的一类实际问题.主要 考查同学们的读图、识图、用图能力,以及分析问题、 解决问题的能力.图表信息问题往往和“方程(组)、不 等式(组)、函数、统计与概率”等知识结合考查.
10
(3)设从家到乙地的路程为m km,
则点 E(x1,m),点 C(x2,m),分别代 入 y=60x-80,y=20x-10, m+80 m+10 得:x1= ,x2= . 60 20 10 1 ∵x2-x1= = , 60 6 m+10 m+80 1 ∴ - = , 20 60 6 解得:m=30. ∴从家到乙地的路程为 30 km.
11
二、表格信息题
以表格的形式给出数据信息是这类信息题的特征,分析表中的数据,能从表
格中发现两个量之间存在规律,归纳出相应的关系式是解决此类问题的关键.
12
【例题2】 (2012· 浙江台州)某汽车在刹车后行驶的距离s(单
位:米)与时间t(单位:秒)之间的关系的部分数据如下表:
时间t(秒) 行驶距离s(米)
