材料力学柴国鈡第10章答案
材料力学第2版 课后习题答案 第10章 强度理论

解: t ≥
pD =
2[σ ]
3×106 ×1 2 × 300×106
= 0.01m = 1.0cm
2
9-8 铸铁圆柱形容器外直径D = 20 cm,壁厚t=2cm,受内压强p=4MPa,并在容器两端
受轴向压力P=200 kN作用,设 µ = 0.25 ,
许用拉应力[σ +]=25 MPa,(1)用第二强
论作强度校核。 解:
σ
4 xd
=
σ 2 + 3τ 2
σ
= 1202 + 3× 402 = 138MPa < [σ ]
τ
σ τ
题 9-3 图
所以安全。
9-4 某梁在平面弯曲下,已知危险截面上作用有弯矩M=50.9 kN ⋅ m ,剪力FS=134.6 kN,截面为No. 22b工字钢,[σ ]=160 MPa,试根据第三强度理对梁作主应力校核。
σ
m xd
=
σ
1
−
σ σ
+ b − b
σ3
= 1.027 −
256 × (−101.027)
625
=
42.4MPa
9-12 内径为d,壁厚为t的圆筒容器,内部盛有比重为γ ,高度为H的液体,竖直吊装如
图示。试按第三强度理论沿容器器壁的母线绘制圆筒的相当应力σ
3 xd
图(不计端部影响)。
解:
σ
y
=
πd2 4
应力校核。
70
(+)
(−) 30
( Q −图)
(−) 20
(−) 30
24.44 (+)
(M −图)
(−) 20
Wz
范钦珊版材料力学习题全解 第10章 压杆的稳定问题

= π3 Ed 4 32l 2
4、第四种方式
屈曲形式如解图 d 所示,两杆作为整体绕 z 轴屈曲
µ=2
结构的临界载荷
x FP
x FP
y
O
y
O
习题 10—9 解图 d
7
5、第五种方式
FPcr
= π2 EI z ( µl ) 2
= π2 E ⋅ 2 ⋅ (πd 4
4l 2
64
+ πd 2 4
⋅ ( a )2 2
10-5 正三角形截面压杆,其两端为球铰链约束,加载方 向通过压杆轴线。当载荷超过临界值,压杆发生屈曲时,横截 面将绕哪一根轴转动?现有四种答案,请判断哪一种是正确 的。
(A) 绕 y 轴; (B) 绕通过形心 C 的任意轴; (C) 绕 z 轴; (D) 绕 y 轴或 z 轴。 解:因为过正多边形截面形心的任意轴均为形心主轴,且 惯性矩相等。所以,正确答案是 B。
FAB
cosθ
=
3 cotθ 2
⋅ FP
,
FQ = FP
σ max
=
MB W
+
FNx A
≤ [σ ] ,
0.3FP 185 ×10−8
+
3 2
cot θ
⋅
FP
30.6 ×10−4
≤ 160 ×106 ,
FP ≤ 73.5kN<FPcr = 118kN
所以,托架所能承受的最大载荷为 73.5kN。
10-11 长 l=50 mm,直径 d=
习题 10-2 图
解:各杆内力如解图所示,由各受杆内力情况可知,正确答案是 A。
10-3 图中四杆均为圆截面直杆,杆长相同,且均为轴向加载,关于四者临界载荷的大 小,有四种解答,试判断哪一种是正确的(其中弹簧的刚度较大)。
材料力学答案第十章
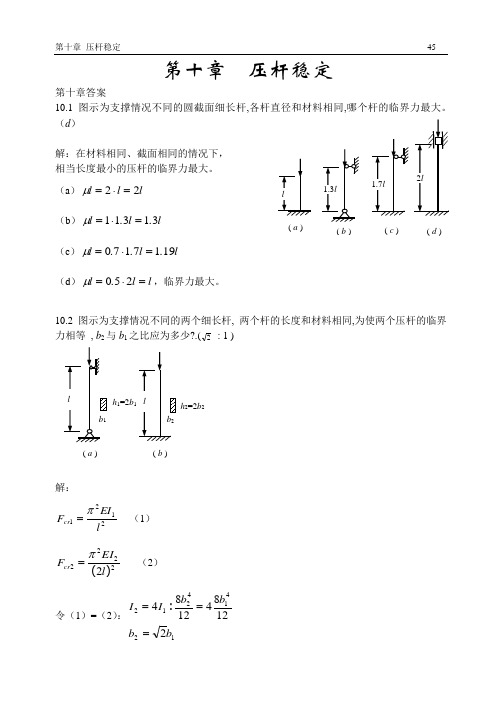
第十章 压杆稳定第十章答案10.1图示为支撑情况不同的圆截面细长杆,各杆直径和材料相同,哪个杆的临界力最大。
(d )解:在材料相同、截面相同的情况下, 相当长度最小的压杆的临界力最大。
(a )l l l 22=⋅=μ (b )l .l .l 31311=⋅=μ (c )l .l ..l 1917170=⋅=μ(d )l l .l =⋅=250μ,临界力最大。
10.2图示为支撑情况不同的两个细长杆, 两个杆的长度和材料相同,为使两个压杆的临界力相等 , b 2与b 1之比应为多少?.(2 : 1 )解:2121l EI F cr π=(1)22222)(l EI F cr π=(2)令(1)=(2):12414212212841284b b b b I I ===:( a)( b) ( c) ( d )( a ) ( b ) h 1=2b h 2=2b 210.3 铰接结构ABC 由截面和材料相同的细长杆组成,若由于杆件在ABC 平面内失稳而引起破坏,试确定荷载F 为最大时(两个杆同时失稳时)的θ (0<θ<π/2)角。
(θ=arctan (1/3)=18.44°) 解:θπcos F l EIF cr ==21212)( (1)θπsin F l EIF cr ==22222)( (2)(1/3))(:(2)(1)arctan cos l sin l l l tan ====θθ3130302222110.4图示压杆,型号为20a 工字钢,在xoz 平面内为两端固定,在xoy 平面内为一端固定,一端自由,材料的弹性模量E = 200GPa ,比例极限σp = 200MPa ,试求此压杆的临界力。
(F c r = 402.2kN )解:(1)柔度计算 查表知:6010012158122=-=========bE a ,E.AI i .A I i s p y y zz σλλσπλs 0p 23558mm A mm,mm,(2)xoz 平面内失稳:7894121200050..i l .y ===y λ 为中柔度杆,kN MPa,7048197===-=A F .b a cr cr y cr σλσ (2) (2)xoy 平面内失稳:169858180002..i l Z ===Z λ 为中柔度杆,kN MPa,6901194===-=A F .b a cr cr z cr σλσx10.5 结构如图,二杆的直径均为d =20mm ,材料相同,材料的弹性模量E = 210GPa , 比例极限σP = 200MPa ,屈服极限 σs = 240MPa ,强度安全系数n =2 ,规定的稳定安全系数n st =2.5 ,试校核结构是否安全。
材料力学 第五版 第10章 高等教育出版社
横截面上的正应力为 FNd ρω 2 D 2 σd = = A 4
12
材 料 力 学 Ⅱ 电 子 教 案
例 10-4 直径d =100 mm的圆轴,右端有重量 P =0.6 kN,直径 - D=400 mm的飞轮,以均匀转速n =1 000 r/min旋转(图a)。在 轴的左端施加制动力偶Md(图b),使其在t=0.01s内停车。不 计轴的质量。求轴内的最大切应力τdmax。
B
z
A C
1.5m 1.5m
B
z
(a)
(b)
22
材 料 力 学 Ⅱ 电 子 教 案
动荷载·交变应力 第十章 动荷载 交变应力
P h
解:
1. 图a
由型钢查得20b号工字钢的 A Wz和Iz分别为
1.5m 1.5m
B
z
Wz=250×103 mm3,Iz=2 500×104 mm4 梁的最大静应力为
σ st ,max
6
(1) (2) (3)
FN d = K d P
材 料 力 学 Ⅱ 电 子 教 案
钢索横截面上的动应力为
FN d P σd = = K d = K dσ st A A
(4)
式中,σ st =
P 为静应力。 A
由(3),(4)式可见,动荷载等于动荷载因数与静荷载 的乘积;动应力等于动荷载因数与静应力的乘积。即用动荷因 数反映动荷载的效应。
动荷因数为
2h 2 × 20 = 1+ 1+ = 14.7 ∆st 0.214 3 梁的最大动应力为 Kd = 1 + 1 +
σ d = K dσ st ,max = 14.7 × 6 = 88.2 MPa
材料力学习题册答案-第10章动载荷

第十章 动载荷、选择题1在用能量法计算冲击应力问题时,以下假设中(D )是不必要的。
A 冲击物的变形很小,可将其视为刚体;B 被冲击物的质量可以忽略,变形是线弹性的;C 冲击过程中只有应变能、势能和动能的变化,无其它能量损失;D 被冲击物只能是杆件。
2•在冲击应力和变形实用计算的能量法中,因不计被冲击物的质量,所以计算结果与实际 情况相比(D )。
A 冲击应力偏大,冲击变形偏小;B 冲击应力偏小,冲击变形偏大;C 冲击应力和冲击变形均偏大;D 冲击应力和冲击变形均偏小。
3.四种圆柱及其冲击载荷情况如图所示,柱C 上端有一橡胶垫。
其中柱( 大动应力最大。
IW、计算题1重量为P 的重物从高度H 处自由下落到钢质曲拐上, 试按第三强度准则写出危险点的相 当应力。
D )内的最解:在C 点作用静载荷P 时,BC 段产生弯曲变形, AB 段产生弯扭组合变形, C 点的静位 移:Pa 3Pl 3 Palstf C f B AB aa 3EI BC 3EI AB GI PAB ’ L 2HK d 1 JV sth 3d 4 d 4式中, I BC, I AB I PAB 12b 64 32危险点在A 截面的上下端,静应力为:.M 2 T 2 P a 2 l 2r3 W Z W Z弹簧支座,重量为 P 250 N 的重物从高度H 50 mm 自由下落到梁的中点C 处。
若铝 合金的弹性模量 E 70 GPa ,试求冲击时梁内的最大正应力。
解:在C 点作用静载荷P 时,AB 梁为静不定问题,变形协调条件为梁中点变形等于弹簧变 形,故有:式中,W Zd 3 32则动应力为:d K d r3 K d P . a 2I 2W Z2、图示横截面为b h 75mm 25mm 的铝合金简支梁,在跨中增加一刚度 K 18 kN/m 的代入数值可计算出:由结构对称,可知R A R B 50 N(资料素材和资料部分来自网络,供参考。
材料力学习题解hfut

6
w2 = A2 sinkx2 + B2 coskx 2 +
Fc x2 2F
当 x1 = 0,w1 = 0 → B1 = 0 当 x 2 = 0,w2 = 0 → B2 = 0 当 x1 = x2 = 或写成
l F ′ = − w2 ′ ,w1 = w2 = c ,w1 2 c
kl Fc l Fc A1sin 2 + 4 F = c kl Fc l Fc = A2 sin + c 2 4F kl Fc kl Fc A1 kcos 2 + 2 F = − A2 kcos 2 − 2 F
Fc F x1 − Fw1,M ( x 2 ) = c x 2 − Fw2 2 2
′′ + k 2 w1 = w1
式中,
Fc 2 F ′′ + k 2 w2 = c k 2 x2 k x1,w2 2F 2F k2 = F EI
Fc x1 2F
通解为
w1 = A1sinkx1 + B1coskx1 +
式中,
k12 =
以上二微分方程的通解为
F F 2 ,k 2 = EI 1 EI 2
w1 = A1sink1 x1 + B1cosk1 x1 + δ w2 = A2 sink 2 x 2 + B2 cosk 2 x 2 + δ
定未知常数的条件为
′=0 x1 = 0,w1 = 0,w1 x1 = l ′ = w2 ′ ,w1 = w2,w1 x2 = 0 x2 = l,w2 = δ
或简化成
sin
4k 2 EI kl kl kl kl [sin − (1 − )cos ] = 0 2 2 2 2 cl
第10章课后习题答案

第10章课后习题答案10-1证明当升角与当量摩擦角符合时,螺纹副具有自锁性。
当时,螺纹副的效率所以具有自锁性的螺纹副用于螺旋传动时,其效率必小于50%。
10-2解由教材表10-1、表10-2查得,粗牙,螺距,中径螺纹升角,细牙,螺距,中径螺纹升角对于相同公称直径的粗牙螺纹和细牙螺纹中,细牙螺纹的升角较小,更易实现自锁。
10-3解查教材表10-1得粗牙螺距中径小径螺纹升角普通螺纹的牙侧角,螺纹间的摩擦系数当量摩擦角拧紧力矩由公式可得预紧力拉应力查教材表9-1得35钢的屈服极限拧紧所产生的拉应力已远远超过了材料的屈服极限,螺栓将损坏。
10-4解(1)升角当量摩擦角工作台稳定上升时的效率:(2)稳定上升时加于螺杆上的力矩(3)螺杆的转速螺杆的功率(4)因,该梯形螺旋副不具有自锁性,欲使工作台在载荷作用下等速下降,需制动装置。
其制动力矩为10-5解查教材表9-1得Q235的屈服极限,查教材表10-6得,当控制预紧力时,取安全系数由许用应力查教材表10-1得的小径由公式得预紧力由题图可知,螺钉个数,取可靠性系数牵曳力10-6解此联接是利用旋转中间零件使两端螺杆受到拉伸,故螺杆受到拉扭组合变形。
查教材表9-1得,拉杆材料Q275的屈服极限,取安全系数,拉杆材料的许用应力所需拉杆最小直径查教材表10-1,选用螺纹()。
10-7解查教材表9-1得,螺栓35钢的屈服极限,查教材表10-6、10-7得螺栓的许用应力查教材表10-1得,的小径螺栓所能承受的最大预紧力所需的螺栓预紧拉力则施加于杠杆端部作用力的最大值10-8解在横向工作载荷作用下,螺栓杆与孔壁之间无间隙,螺栓杆和被联接件接触表面受到挤压;在联接接合面处螺栓杆则受剪切。
假设螺栓杆与孔壁表面上的压力分布是均匀的,且这种联接的预紧力很小,可不考虑预紧力和螺纹摩擦力矩的影响。
挤压强度验算公式为:其中;为螺栓杆直径。
螺栓杆的剪切强度验算公式其中表示接合面数,本图中接合面数。
材料力学_xt10

计算题10-1、图示矩形截面杆h=200mm ,b=100mm ,P=20KN ,试计算最大正应力。
(cl-xtzj11) 10-2 人字架及承受的载荷如图所示。
试求截面I I -上的最大正应力和a 点的正应力。
10-3 悬臂吊如图所示,起重量(包括电葫芦)G =30kN ,横梁BC 为工字钢,许用应力[σ]=140MPa ,试选择工字钢的型号(可近似按G 行至梁中点位置计算)。
10-4 图示悬臂梁自由端受一与z 轴成ϕ角的横向力P 作用,该力可分解为垂直分力ϕcos P P z =和水平分力ϕsin P P y =。
试据叠加法写出任一截面上任一点K 的正应力计算式,并确定该梁危险点的位置及其应力的计算式。
10-5 斜杆AB 的横截面为100×100mm 2的正方形,若P =3kN ,试求其最大拉应力和最大压应力。
10-6 砖砌烟囱高H =30m ,底截面I I -的外径d 1=3m ,内径d 2=2m ,自重G 1=2000kN ,受q =1kN/m 的风力作用。
试求:(a )烟囱底截面上的最大压应力。
(b )若烟囱的基础埋深h =4m ,基础及填土自重按G 2=1000kN 计算,土壤的许用压应力MPa 3.0][=σ,圆形基础的直径D 应为多大?注:计算风力时,可省去烟囱直径的变化,把它看作是等截面的。
10-7 图示一矩形截面杆,用应变片测得杆件上、下表面的轴向应变分别为a ε=1×10-3,b ε=0.4×10-3,材料的弹性模量E =210GPa 。
试绘制横截面的正应力分布图;并求拉力P 及其偏心距e 的数值。
10-8 一矩形截面短柱,受图示偏心压力P 作用,已知许用拉应力[t σ]=30MPa ,许用压应力[c σ]=90MPa ,求许可压力[P ]。
10-9 材料为灰铸铁HT15-33的压力机框架如图所示。
许用拉应力为[]30=t σMPa ,许用压应力为[]80=c σMPa 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10.1 一端固定一端铰支的工字形截面细长压杆,已知弹性模量GPa 208=E ,截面尺寸200mm×100mm ×7mm ,杆长m l 10=,试确定压杆的临界压力。
解:4337.16796532121869312200100mm I x =⨯-⨯=4332.11719831271861210072mm I y =⨯+⨯=因为x y I I <,故y I I =()()kN N l EI F cr 1.49101.49100007.02.117198310208323222=⨯=⨯⨯⨯⨯==πμπ10.2 两端固定的圆截面钢质压杆,直径为50mm ,受轴向压力F 作用。
已知GPa 210=E 和MPa 200=p σ,试确定能够使用欧拉公式的最短压杆长度l 。
解:8.10120010210505.044322=⨯⨯==≥⨯⨯===πσπλμμλp p E l d l i l可得:mm l 2545≥10.3 截面为矩形h b ⨯的压杆,两端用柱销联接(在y x -平面内弯曲时,可视为两端铰支;在zx -平面内弯曲时,可视为两端固定)。
已知GPa 200=E ,MPa 200=p σ,试求:(1)当mm 30=b ,mm50=h 时,压杆的临界压力;(2)若使压杆在两个平面(y x -和z x -面)内失稳的可能性相同时,求b 和h 的比值。
解:43331250012503012mm bh I z =⨯==,1=z μ,故()()kNN l EI F z z cr 1171011723001312500102003232221=⨯=⨯⨯⨯⨯==πμπ43311250012305012mm hb I y =⨯==,5.0=y μ,故()()kN N l EI F y y cr 1681016823005.0112500102003232222=⨯=⨯⨯⨯⨯==πμπ故kN F cr 117=。
若使压杆在两个平面(y x -和z x -面)内失稳的可能性相同,则要求()()21124124332222=⇒=⇒=⇒=h b hb bh I I l EI l EI yz y y z z μπμπ10.4 两端铰支的细长压杆,圆形横截面的直径为d 。
假设压杆只发生弹性变形,材料的热膨胀系数为α。
若温度升高T ∆,求临界压力与T ∆的关系。
解:T E Tl EAl F N ∆=⇒∆=ασαcr T E σασ≤∆=42d TE F cr πα∆≥10.5 图示圆截面压杆mm 40=d ,材料M P a 235=s σ。
试求可用经验公式λσ12.1304-=cr 计算临界应力时的最小杆长。
解:s cr σλσ≤-=12.13042.9412.123530412.1304=-=-≥s σλ mm l l i l 7.13452.94107.0≥⇒≥⨯==μλ10.6 图示结构,圆杆BD 的直径mm 50=d ,材料GPa 200=E ,100=p λ,试求结构的临界压力cr F 。
解:F F NB 5.2=p i l λμλ≥=⨯⨯==16050420001,故适用欧拉公式 NA E A F cr NBcr 32232221015145016010200⨯=⨯⨯⨯===ππλπσ kN F F NBcr cr 6.605.2==10.7 由三根细长压杆构成的支架,A 、B 、C 位于同一水平面,三杆截面均为圆形,直径为d ,材料的弹性模量为E ,90=p λ。
A 、B 、C 、D 均为铰链节点。
竖直力F 的作用线恰好通过等边三角形ABC 的形心G 。
已知h AB DG ==,d h 20=。
试确定最大允许的力F。
解:由于对称性,三杆轴力相同,不妨假设为N F 。
三杆的杆长均为h h h l 3323322=+⎪⎪⎭⎫ ⎝⎛= 由竖直方向的平衡方程,有()N N NN F Fl h F GDB F F 2332333cos 3===∠= 4.923316033834321===⨯⨯⨯==d h d h i lμλ因为p λλ>,适用于欧拉公式,故223224λπλπσEd A E A F cr Ncr === 即,223833233λπEd F F Ncr cr ==10.8 图中AB 为刚杆,圆截面细长杆1、2为两端铰支约束,材料、长度、直径均相同,求临界压力cr F 。
解:只有当1、2杆均失稳,整个结构才失稳。
()243222164l Ed l EI F F cr cr πμπ=== 由平衡方程,有2432121643223l Ed F F F a F a F a F cr cr cr cr cr cr π=+=⇒⋅+⋅=⋅10.9 如图所示的杆系ABC ,由两根细长压杆通过铰支相连,压杆的横截面尺寸和材料相同。
试求使得临界压力F 值最大时的角度β( 90<β)。
解:设AB 距离为l ,则AC 长度为l 23,BC 长度为2l 。
由AC 杆,有22,34l EIF AC cr π=,则有βπβsin 34sin 22,1l EI F F AC cr cr == 由BC 杆,有22,4l EIF BC cr π=,则有βπβcos 4cos 222l EI F F BC cr == 综合考虑,只有当21cr cr F F =,临界压力F 值最大,故有31tan =β, 4.18=β10.10 图示蒸汽机的活塞杆AB ,所受压力KN F 120=,m l 8.1=,截面为圆形,直径mm 75=d ,材料为钢,GPa 210=E ,MPa 240=p σ。
规定的稳定安全因数8=st n ,试校核活塞杆的稳定性。
解:964/7518001=⨯==ilμλ 9.9224010210322=⨯⨯==πσπλp p E因为p λλ>,适用于欧拉公式,故()()()kNN l Ed l dEl EI F cr 99410994180064751021064643243324324222=⨯=⨯⨯⨯⨯====πμπμππμπ828.8120994>===F F n cr st 故,活塞杆满足稳定性要求。
10.11 发动机连杆由Q235钢制成,如图所示。
若m l 21=,m l 7.12=,mm b 30=,mm h 60=,材料的弹性模量GPa E 210=。
规定的稳定安全因数0.3=st n ,试确定最大工作压力F 。
解:查表得,Q235钢:100=p λ,临界应力的欧拉公式为:λσ12.1304-=cr x -z 平面:mm b i y 66.8123012===14.9866.817005.02=⨯==y y y i l μλx -y 平面:mm h i z 3.17126012===,5.1153.17200011=⨯==z z z i l μλ故5.115=λ,发动机连杆失稳发生x -y 平面。
因为p λλ>,适用于欧拉公式,故MPa E cr 1555.1151021023222=⨯⨯==πλπσkN N A F cr cr 2801028030601553=⨯=⨯⨯==σ最大工作压力为kN n F F st cr 2.933280===。
10.12 悬臂梁AB 用一根外径mm 40=D 和内径mm 30=d 的钢管BC 支撑,梁和钢管的材料均为pA235Q 。
当一个重N 250的块体Q 从mm 8=h 的高度落到B 点,试校核压杆BC 的稳定性。
已知m 3=a ,m 2=b ,梁AB 的惯性矩4cm 2450=I ,材料的弹性模量GPa 200=E ,规定的稳定安全因数8.2=st n 。
(提示:本题待学习动载荷一章后,再行求解) 解:mm d D i 5.124304042222=+=+=,1605.1220001=⨯==i b μλ因为100=>p λλ,故适用于欧拉公式,则()()()kNN b d D E l EI F cr 4.42104.4220006430401020064324433244322=⨯=⨯-⨯⨯⨯=-==ππμπ 如图结构承受静载荷Q 作用,则变形协调条件BC B l w ∆=,有()()()N Aa bI A Qa R EA Rb EI a R Q 55.247300043040245000002000343040300025033322223333=⎪⎪⎭⎫ ⎝⎛⨯-⨯+⨯⨯-⨯⨯⨯=+=⇒=-ππ故()mm EIa R Q w B33105.43-⨯=-=,故动荷因素为6.60105.416112113=⨯++=++=-Bd w h k故,kN N R k F d BC d 67.35.367355.2476.60,==⨯== 因为,st BC d cr n F F n >===5.1167.34.42, 故压杆BC 满足稳定性要求。
10.13 图示构架,AB 为刚性杆,AC 、BD 、BE 均为细长杆,且它们的材料、横截面均相同,横截面面积为A ,惯性矩为I ,力F 作用于AB 杆的中点。
设材料的弹性模量为E ,稳定安全系数3=st n ,求许可载荷[]F 。
解:由平衡方程,可得2FF NA =,22F F F NBE NBD == AC 杆:2122,cr NA cr F a EI F ==π 2212a EIF cr π=BD 或BE 杆:()222222,cr NBD cr F aEIF ==π 2222a EIF cr π=故,222a EIF cr π=,[]2232a EIn FF stcr π==。
10.14 钢杆的尺寸、受力和支座情况如图所示。
已知材料的比例极限M Pa 200=p σ,屈服极限M Pa 240=s σ,弹性模量GPa 200=E ,直线公式的系数MPa 304=a ,MPa 12.1=b 。
试求其工作安全系数。
解:3.9920010200322=⨯⨯==πσπλp p E1.5712.1240304=-=-=b a s s σλ 左边杆:754/249005.0=⨯==i l μλ因为s p λλλ>>,适用于直线公式,故MPa b a cr 2207512.1304=⨯-=-=λσkN N A F cr cr 5.99105.9942422032=⨯=⨯⨯==πσ右边杆:804/288007.0=⨯==i l μλ因为s p λλλ>>,适用于直线公式,故MPa b a cr 2148012.1304=⨯-=-=λσkN N A F cr cr 97100.9742821432=⨯=⨯⨯==πσ综合,可得整个结构的临界压力为kN F cr 97=,故其工作安全系数为23.33097===F F n cr10.15 图示结构ABC 为矩形截面杆,mm 60=b 、mm 100=h 、m 4=l ,BD 为圆截面杆,mm 60=d ,两杆材料均为235Q 钢,GPa 200=E ,MPa 200=p σ,均布载荷m /kN 1=q ,稳定安全系数3=st n 。
