三重积分练习题

合集下载

7三重积分练习共51页文档

2a
yy2 f(x,y)d.x
2a
例3. 求
1
d
y1sinxd
x.
0 yx
解：由于
1 sinx dx
是“积不出”的，怎么办？
yx
要改换积分次序. 先画积分区域D的图形.
由积分表达式知，D： y x 1, 0 y 1
画曲线 x=y 和 x=1，直线y=0, y=1. 如图：
故
原式 =
D
a 0
1 2b2(a 224aa42)8 1a2b2
ax
y 5x
例4 计算二重积分 (x6,y其)d中xdy
D
D是由三条线 y x ,y 所5 x 围,x 成 1 的区域.
yx
x 1
解易知积分区域可表为
D :0 x 1 ,x y 5 x
于是
1 5x
(x6y)dxdy dx (x6y)dy
sinx x
dxdy
y
1
d
xsinx xd
y
1s inx xdx
0 0x
0x
y= x
1
s
inxdxcox1 s1co1s
0
0
0
D
x
例. 设D：a x b, c y d. f(x, y)=f1(x)·f2(y)可积，
则
b
d
f(x ,y )daf1 (x )dx cf2 (y )d.y
3d
D
6
24ssiinnr2rdr15(2
3)
机动目录上页下页返回结束
解：积分区域如图
记 f (x, y) = | y – x | y–x, 当y x时,
= x–y, 当y < x时,

三重积分题

三重积分题一、计算三重积分∫∫∫_V (x2 + y2 + z2) dV，其中V是由x2 + y2 ≤ 1, 0 ≤ z ≤ 1定义的圆柱体。

A. π/2B. πC. 3π/2D. 2π（答案：D）二、三重积分∫∫∫_V xyz dV，在区域V: 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1内的值为？A. 0B. 1/2C. 1D. 3/2（答案：A）三、计算三重积分∫∫∫_V (x + y + z) dV，其中V是由0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1定义的立方体。

A. 0B. 1C. 3/2D. 2（答案：C）四、三重积分∫∫∫_V (sin(x)cos(y)z) dV，在区域V: 0 ≤ x ≤π, 0 ≤ y ≤π, 0 ≤ z ≤ 1内的值为？A. 0B. 1C. -1D. 2（答案：A）五、计算三重积分∫∫∫_V e(x+y+z) dV，其中V是由0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤z ≤ 1定义的立方体，并假设e的近似值为2.718。

A. e - 1B. e2 - 1C. e3 - 1D. e4 - 1（答案：C）注：此题需要用到e的幂次性质进行积分。

六、三重积分∫∫∫_V (x2y2z2) dV，在区域V: -1 ≤ x ≤ 1, -1 ≤ y ≤ 1, -1 ≤ z ≤ 1内的值为？A. 0B. 1/8C. 1/4D. 1（答案：A）七、计算三重积分∫∫∫_V (1/(1+x2+y2+z2)) dV，其中V是由x2 + y2 + z2 ≤ 1定义的球体。

A. π2/2B. π2C. 2π2D. 4π2（答案：A）注：此题需要用到球坐标变换进行积分。

八、三重积分∫∫∫_V (cos(x2+y2+z2)) dV，在区域V: 0 ≤ x ≤√π, 0 ≤ y ≤√π, 0 ≤ z ≤√π，且假设cos的近似值在积分中可直接使用，其值为？A. 0B. (π(3/2))/2 * (sin(π) - sin(0))C. π(3/2) * (cos(π) - cos(0))D. -π(3/2) * (sin(π) - sin(0))（答案：B）注：此题需要注意到cos函数的周期性，并正确计算积分上下限。

数学分析21.5三重积分(含习题及参考答案)

第二十一章重积分5三重积分一、三重积分的概念引例：设一空间立体V 的密度函数为f(x,y,z)，为求V 的质量M ，将V 分割成n 个小块V 1,V 2,…,V n . 每个小块V i 上任取一点(ξi ,ηi ,ζi ), 则 M=i ni i i i T V f ∆∑=→10),,(lim ζηξ, 其中△V i 是小块V i 的体积, T =}{max 1的直径i ni V ≤≤.概念：设f(x,y,z)是定义在三维空间可求体积有界区域V 上的有界函数. 用若干光滑曲面所组成的曲面网T 来分割V ，把V 分成n 个小区域 V 1,V 2,…,V n .记V i 的体积为△V i (i=1,2,…,n)，T =}{max 1的直径i ni V ≤≤.在每个V i 中任取一点(ξi ,ηi ,ζi ), 作积分和i ni i i i V f ∆∑=1),,(ζηξ.定义1：设f(x,y,z)为定义在三维空间可求体积的有界闭区域V 上的函数，J 是一个确定的数. 若对任给的正数ε，总存在某一正数δ，使得对于V 的任何分割T ，只要T <δ，属于分割T 的所有积分和都有J V f i ni iii-∆∑=1),,(ζηξ<ε，则称f(x,y,z)在V 上可积，数J 称为函数f(x,y,z)在V 上的三重积分，记作J=⎰⎰⎰VdV z y x f ),,(或J=⎰⎰⎰Vdxdydz z y x f ),,(，其中f(x,y,z)称为被积函数，x, y, z 称为积分变量，V 称为积分区域.注：当f(x,y,z)=1时，⎰⎰⎰VdV 在几何上表示V 的体积.三积重分的条件与性质：1、有界闭域V 上的连续函数必可积；2、如界有界闭区域V 上的有界函数f(x,y,z)的间断点集中在有限多个零体积的曲面上，则f(x,y,z)在V 上必可积.二、化三重积分为累次积分定理21.15：若函数f(x,y,z)在长方体V=[a,b]×[c,d]×[e,h]上的三重积分存在，且对任意(x,y)∈D=[a,b]×[c,d], g(x,y)=⎰he dz z y xf ),,(存在，则积分⎰⎰Ddxdy y x g ),(也存在，且⎰⎰⎰Vdxdydz z y x f ),,(=⎰⎰⎰Dhedz z y x f dxdy ),,(.证：用平行于坐标轴的直线作分割T ，把V 分成有限多个小长方体 V ijk =[x i-1,x i ]×[y j-1,y j ]×[z k-1,z k ].设M ijk , m ijk 分别是f(x,y,z)在V ijk 上的上确界和下确界，对任意(ξi ,ηj )∈[x i-1,x i ]×[y j-1,y j ], 有m ijk △z k ≤⎰-kk z z j i dz z f 1),,(ηξ≤M ijk △z k .现按下标k 相加，有∑⎰-kz z j i kk dz z f 1),,(ηξ=⎰he j i dz zf ),,(ηξ=g(ξi ,ηj )，以及∑∆∆∆kj i k j i ijkz y x m,,≤j i ji j i y x g ∆∆∑,),(ηξ≤∑∆∆∆kj i k j i ijk z y x M ,,.两边是分割T 的下和与上和. 由f(x,y,z)在V 上可积，当T →0时，下和与上和具有相同的极限，∴g(x,y)在D 上可积，且⎰⎰⎰Dhedz z y x f dxdy ),,(=⎰⎰⎰Vdxdydz z y x f ),,(.推论：若V={(x,y,z)|(x,y)∈D, z 1(x,y)≤z ≤z 2(x,y)} ⊂[a,b]×[c,d]×[e,h]时，其中D 为V 在Oxy 平面上的投影，z 1(x,y), z 2(x,y)是D 上的连续函数，函数f(x,y,z)在V 上的三重积分存在，且对任意(x,y)∈D, G(x,y)=⎰),(),(21),,(y x z y x z dz z y x f 亦存在，则积分⎰⎰Ddxdy y x G ),(存在，且⎰⎰⎰Vdxdydz z y x f ),,(=⎰⎰D dxdy y x G ),(=⎰⎰⎰Dy x z y x z dz z y x f dxdy ),(),(21),,(.证：记F(x,y,z)=⎩⎨⎧∈∈V V z y x ，Vz y x ，z y x f \),,(0),,(),,(0 , 其中V 0=[a,b]×[c,d]×[e,h].对F(x,y,z)应用定理21.15，(如图)则有⎰⎰⎰Vdxdydz z y x f ),,(=⎰⎰⎰0),,(V dxdydzz y x F=⎰⎰⎰⨯d][c,b][a,),,(hedz z y x F dxdy =⎰⎰⎰Dy x z y x z dz z y x f dxdy ),(),(21),,(.例1：计算⎰⎰⎰+Vy x dxdydz22，其中V 为由平面x=1, x=2, z=0, y=x 与z=y 所围区域(如图).解：设V 在xy 平面上投影为D ，则 V={(x,y,z)|z 1(x,y)≤z ≤z 2(x,y),(x,y)∈D},其中D={(x,y)|0≤y ≤x,1≤x ≤2}, z 1(x,y)=0, z 2(x,y)=y, 于是⎰⎰⎰+V y x dxdydz 22=⎰⎰⎰+D y y x dz dxdy 022=⎰⎰+D dxdy y x y 22=⎰⎰+21022x dy y x y dx=⎰212ln 21dx =2ln 21.例2：计算⎰⎰⎰++Vdxdydz z y x )(22，其中V 是由⎩⎨⎧==0x y z 绕z 轴旋转一周而成的曲面与z=1所围的区域.解：V={(x,y,z)|22y x +≤z ≤1,(x,y)∈D}, 其中D={(x,y)|x 2+y 2≤1},⎰⎰⎰++Vdxdydz z y x )(22=⎰⎰⎰+++Dyx dz z y x dxdy 12222)(=⎰⎰⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛+-+Ddxdy y x y x 2121)(2222=⎰⎰⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-πθ201022121rdrr r d=⎰πθ20407d =207π.定理21.16：若函数f(x,y,z)在长方体V=[a,b]×[c,d]×[e,h]上的三重积分存在，且对任意x ∈[a,b], 二重积分I(x)=⎰⎰Ddydz z y x f ),,(存在，则积分⎰⎰⎰baDdydz z y x f dx ),,(也存在，且⎰⎰⎰Vdxdydz z y x f ),,(=⎰⎰⎰baDdydz z y x f dx ),,(.证：用平行于坐标轴的直线作分割T ，把V 分成有限多个小长方体 V ijk =[x i-1,x i ]×[y j-1,y j ]×[z k-1,z k ], 记D jk =[y j-1,y j ]×[z k-1,z k ], 设M ijk , m ijk 分别是f(x,y,z)在V ijk 上的上确界和下确界，对任意ξi ∈[x i-1,x i ], 有m ijk △D jk ≤⎰⎰jkD i dydz z y f ),,(ξ≤M ijk △D jk .现按下标j,k 相加，有∑⎰⎰k j D i jkdydz z y f ,),,(ξ=⎰⎰Di dydz z y f ),,(ξ=I(ξi )，以及∑∆∆∆kj i k j i ijkz y x m,,≤i ii x I ∆∑)(ξ≤∑∆∆∆kj i k j i ijk z y x M ,,.两边是分割T 的下和与上和. 由f(x,y,z)在V 上可积，当T →0时，下和与上和具有相同的极限，∴I(x)在D 上可积，且⎰⎰⎰baDdydz z y x f dx ),,(=⎰⎰⎰Vdxdydz z y x f ),,(.推论：(如图)若V ⊂[a,b]×[c,d]×[e,h], 函数f(x,y,z)在V 上的三重积分存在，且对任意固定的z ∈[e,h], 积分φ(z)=⎰⎰zD dxdy z y x f ),,(存在，其中D z是截面{(x,y)|(x,y,z)∈V}, 则⎰he dz z )(ϕ存在，且⎰⎰⎰Vdxdydz z y x f ),,(=⎰h edz z )(ϕ=⎰⎰⎰heD zdxdy z y x f dz ),,(.证：证法与定理21.16证明过程同理.例3：计算I=⎰⎰⎰⎪⎪⎭⎫ ⎝⎛++V dxdydz c z b y a x 222222, 其中V 是椭球体222222c z b y a x ++≤1.解：I=⎰⎰⎰⎪⎪⎭⎫ ⎝⎛++V dxdydz c z b y a x 222222=⎰⎰⎰V dxdydz a x 22+⎰⎰⎰V dxdydz b y 22+⎰⎰⎰Vdxdydz c z 22.其中⎰⎰⎰V dxdydz a x 22=⎰⎰⎰-a a V xdydz dx a x 22,V x 表示椭圆面2222c z b y +≤1-22ax 或⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-2222222211a x c z a xb y ≤1. 它的面积为π⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-222211a x c a x b =πbc ⎪⎪⎭⎫⎝⎛-221a x. ∴⎰⎰⎰V dxdydz a x 22=⎰-⎪⎪⎭⎫ ⎝⎛-a a dx a x a bcx 22221π=154πabc. 同理可得：⎰⎰⎰V dxdydz b y 22=⎰⎰⎰V dxdydz cz 22=154πabc.∴I=3(154πabc)=54πabc.三、三重积分换元法规则：设变换T ：x=x(u,v,w), y=y(u,v,w), z=z(u,v,w)，把uvw 空间中的区域V ’一对一地映成xyz 空间中的区域V ，并设函数x=x(u,v,w), y=y(u,v,w), z=z(u,v,w)及它们的一阶偏导数在V ’内连续且函数行列式J(u,v,w)=wz v z uz w yv y u yw x v x u x ∂∂∂∂∂∂∂∂∂≠0, (u,v,w)∈V ’. 则当f(x,y,z)在V 上可积时，有 ⎰⎰⎰Vdxdydz z y x f ),,(=⎰⎰⎰'V dudvdw w v u J w v u z w v u y w v u x f |),,(|)),,(),,,(),,,((.常用变换公式： 1、柱面坐标变换：T ：⎪⎩⎪⎨⎧+∞<<∞-=≤≤=+∞<≤=z z ，z ，r y r ，r x πθθθ20sin 0cos , J(r,θ,z)=100cos sin 0sin cos θθθθr r -=r, 即有 ⎰⎰⎰Vdxdydz z y x f ),,(=⎰⎰⎰'V dz rdrd z r r f θθθ),sin , cos (.V ’为V 在柱面坐标变换下的原象.注：(1)虽然柱面坐标变换并非是一对一的，且当r=0时，J(r,θ,z)=0，但结论仍成立.(2)柱面坐标系中r=常数, θ=常数, z=常数的平面分割V ’变换到xyz 直角坐标系中，r=常数是以z 轴为中心轴的圆柱面，θ=常数是过z 轴的半平面，z 的常数是垂直于z 轴的平面(如图).例4：计算⎰⎰⎰+Vdxdydz y x )(22, 其中V 是曲面2(x 2+y 2)=z 与z=4为界面的区域.解法一：V={(x,y,z)|2(x 2+y 2)≤z ≤4, (x,y)∈D}, D={(x,y)|x 2+y 2≤2}.⎰⎰⎰+Vdxdydz y x )(22=⎰⎰⎰++4)(22222)(y x Ddzy x dxdy=⎰⎰+-+Ddxdy y x y x )](24)[(2222=⎰⎰-202220)24(rdrr r d πθ=⎰-2053)2(4dr r r π=⎰-2053)2(4dr r r π=38π.解法二：V 在xy 平面上的投影区域D=x 2+y 2≤2. 按柱坐标变换得 V ’={(r,θ,z)|2r 2≤z ≤4, 0≤r ≤2, 0≤θ≤2π}.∴⎰⎰⎰+V dxdydz y x )(22=⎰⎰⎰'V dz drd r θ2=⎰⎰⎰42320202r dz r dr d πθ=38π.2、球坐标变换：T ：⎪⎩⎪⎨⎧≤≤=≤≤=+∞<≤=πθϕπϕθϕθϕ20cos 0sin sin 0cos sin ，r z ，r y r ，r x ,J(r,φ,θ)=0sin cos sin sin cos sin sin sin sin cos cos cos sin ϕϕθϕθϕθϕθϕθϕθϕr co r r r r --=r 2sin φ≥0, 即有⎰⎰⎰Vdxdydz z y x f ),,(=⎰⎰⎰'V d drd rr r r f θϕϕϕθϕθϕsin )cos ,sin sin , cos sin (2,V ’为V 在球坐标变换T 下的原象.注：(1)球坐标变换并不是一对一的，并且当r=0或φ=0或π时，J=0. 但结论仍成立.(2)球坐标系中r=常数, φ=常数, θ=常数的平面分割V ’变换到xyz 直角坐标系中，r=常数是以原点为中心的球面， φ=常数是以原点为顶点, z 轴为中心轴的圆锥面，θ=常数是过z 轴的半平面(如图).例5：求由圆锥体z ≥22y x +cot β和球体x 2+y 2+(z-a)2≤a 2所确定的立体体积，其中β∈⎪⎭⎫⎝⎛2,0π和a(>0)为常数.解：球面方程x 2+y 2+(z-a)2=a 2可表示为r=2acos φ, 锥面方程z=22y x +cot β可表示为φ=β. ∴V ’={(r,φ,θ)|0≤r ≤2acos φ, 0≤φ≤β, 0≤θ≤2π}. ∴⎰⎰⎰VdV =⎰⎰⎰ϕβπϕϕθcos 202020sin a dr r d d =⎰βϕϕϕπ033sin cos 316d a =343a π(1-cos 4β).例6：求I=⎰⎰⎰Vzdxdydz , 其中V 为由222222c z b y a x ++≤1与z ≥0所围区域.解：作广义球坐标变换：T ：⎪⎩⎪⎨⎧===ϕθϕθϕcos sin sin cos sin cr z br y ar x , 则J=abcr 2sin φ. V 的原象为V ’={(r,φ,θ)|0≤r ≤1, 0≤φ≤2π, 0≤θ≤2π} ∴⎰⎰⎰Vzdxdydz =⎰⎰⎰⋅1022020sin cos dr abcr cr d d ϕϕϕθππ=⎰2022sin 4πϕϕπd abc =42abc π.习题1、计算下列积分：(1)⎰⎰⎰+Vdxdydz z xy )(2, 其中V=[-2,5]×[-3,3]×[0,1]；(2)⎰⎰⎰Vzdxdydz y x cos cos , 其中V=[0,1]×[0,2π]×[0,2π]；(3)⎰⎰⎰+++Vz y x dxdydz3)1(, 其中V 是由x+y+z=1与三个坐标面所围成的区域； (4)⎰⎰⎰+Vdxdydz z x y )cos(, 其中V 由y=x , y=0, z=0及x+z=2π所围成.解：(1)⎰⎰⎰+VdV z xy )(2=⎰⎰⎰+--1023352)(dz z xy dy dx =⎰⎰--⎪⎭⎫⎝⎛+335231dy xy dx =⎰-522dx =14.(2)⎰⎰⎰VzdV y x cos cos =⎰⎰⎰202010cos cos ππzdz ydy xdx =21.(3)⎰⎰⎰+++Vz y x dxdydz 3)1(=⎰⎰⎰---+++y x x z y x dz dy dx 1031010)1(=⎰⎰-⎥⎦⎤⎢⎣⎡-++x dy y x dx 1021041)1(121=⎰⎪⎭⎫ ⎝⎛-+-+1041211121dx x x =1652ln 21-. (4)⎰⎰⎰+VdV z x y )cos(=⎰⎰⎰-+xxdz z x y dy dx 20020)cos(ππ=⎰⎰-xydydx x 020)sin 1(π=⎰-20)sin 1(21πdx x x =21162-π.2、试改变下列累次积分的顺序： (1)⎰⎰⎰+-yx xdz z y x f dy dx 01010),,(；(2)⎰⎰⎰+220110),,(y x dz z y x f dy dx .解：(1)积分区域V={(x,y,z)|0≤z ≤x+y, 0≤y ≤1-x, 0≤x ≤1}； ∵V 在xy 平面上的投影区域D xy ={(x,y)|0≤y ≤1-x, 0≤x ≤1} ∴I=⎰⎰⎰+-yx xdz z y x f dy dx 01010),,(=⎰⎰⎰+-yx ydz z y x f dx dy 01010),,(.∵V 在yz 平面上的投影区域D yz ={(y,z)|0≤y ≤1, 0≤z ≤1} ∴I=⎰⎰⎰-yydx z y x f dz dy 10010),,(+⎰⎰⎰--yy z y dx z y x f dz dy 1110),,(=⎰⎰⎰--yy z zdx z y x f dy dz 1010),,(+⎰⎰⎰-yz dx z y x f dy dz 10110),,(.∵V 在xz 平面上的投影区域D yz ={(x,z)|0≤x ≤1, 0≤z ≤1} ∴I=⎰⎰⎰-xxdy z y x f dz dx 10010),,(+⎰⎰⎰--xx z x dy z y x f dz dx 1110),,(=⎰⎰⎰--xx z zdy z y x f dx dz 1010),,(+⎰⎰⎰-xz dy z y x f dx dz 10110),,(.(2)积分区域V={(x,y,z)|0≤z ≤x 2+y 2, 0≤y ≤1, 0≤x ≤1}；∵V 在xy 平面上的投影区域D xy ={(x,y)|0≤y ≤1, 0≤x ≤1}；在yz 平面上的投影区域D yz ={(x,y)|0≤y ≤1, 0≤z ≤1+y 2}；在xz 平面上的投影区域D yz ={(x,y)|0≤x ≤1, 0≤z ≤1+x 2}； ∴I=⎰⎰⎰+2201010),,(y x dz z y x f dy dx =⎰⎰⎰+220110),,(y x dz z y x f dx dy=⎰⎰⎰10010),,(2dx z y x f dz dy y +⎰⎰⎰-+1110222),,(y z y ydxz y x f dz dy=⎰⎰⎰10110),,(dx z y x f dy dz z +⎰⎰⎰--111212),,(yz z dx z y x f dy dz .=⎰⎰⎰10010),,(2dy z y x f dz dx x +⎰⎰⎰-+1110222),,(x z x x dyz y x f dz dx=⎰⎰⎰10110),,(dy z y x f dx dz z +⎰⎰⎰--111212),,(x z z dy z y x f dx dz .3、计算下列三重积分与累次积分：(1)⎰⎰⎰Vdxdydz z 2, 其中V 由x 2+y 2+z 2≤r 2和x 2+y 2+z 2≤2rz 所确定；(2)⎰⎰⎰--+-22222221010y x yx x dz z dy dx .解：(1) 由x 2+y 2+z 2≤2rz, 得S: x 2+y 2≤2rz-z 2, 0≤z ≤2r , 又由x 2+y 2+z 2≤r 2, 得Q: x 2+y 2≤r 2-z 2,2r≤z ≤r ∴⎰⎰⎰Vdxdydz z 2=⎰⎰⎰Sr dxdy z dz 220+⎰⎰⎰Qrr dxdyz dz 22=⎰-2022)2(r dz z rz z π+⎰-rr dz z r z 2222)(π=480595r π. (2)应用柱坐标变换：V ’={(r,θ,z)|r ≤z ≤22r -, 0≤r ≤1, 0≤θ≤2π}, ∴⎰⎰⎰--+-22222221010y x yx x dz z dy dx =⎰⎰⎰-2221020r rdz z rdr d πθ=⎰---1322]2)2[(6dr r r r r π.=⎰---10322]2)2[(6dr r r r r π=)122(15-π.4、利用适当的坐标变换，计算下列各曲面所围成的体积. (1)z=x 2+y 2, z=2(x 2+y 2), y=x, y=x 2；(2)2⎪⎭⎫ ⎝⎛+b y a x +2⎪⎭⎫ ⎝⎛c z =1 (x ≥0, y ≥0, z ≥0, a>0, b>0, c>0). 解：(1)V={(x,y,z)|x 2+y 2≤z ≤2(x 2+y 2), (x,y)∈D}, 其中D={(x,y)|0≤x ≤1, x 2≤y ≤x }. ∴⎰⎰⎰V dxdydz =⎰⎰+Ddxdy y x )(22=⎰⎰+xx dyy x dx 2)(2210=⎰⎥⎦⎤⎢⎣⎡-+-1063223)()(dx x x x x x =353. (2)令x=arsin 2φcos θ, y=brcos 2φcos θ, z=crsin θ, 则J=0cos sin cos cos sin 2sin cos cos cos cos cos sin 2sin sin cos sin 2222θθθϕϕθϕθϕθϕϕθϕθϕcr c br br b ar ar a ---=2abcr 2cos φsin φcos θ,又V ’={(r,φ,θ)|0≤r ≤1, 0≤φ≤2π, 0≤θ≤2π}. ∴⎰⎰⎰Vdxdydz =⎰⎰⎰1022020sin cos cos 2dr r d d abc ππϕϕϕθθ=3abc.5、设球体x 2+y 2+z 2≤2x 上各点的密度等于该点到坐标原点的距离，求这球体的质量.解：依题意，球体的质量M=⎰⎰⎰≤++++xz y x dV z y x 2222222,应用球面变换得V ’={(r,θ,φ)|-2π≤θ≤2π, 0≤φ≤π, 0≤r ≤2sin φcos θ}. ∴M=⎰⎰⎰-θϕπππϕϕθcos sin 203022sin dr r d d =⎰⎰-πππϕϕθθ05224sin cos 4d d =58π.6、证明定理21.16及其推论. 证：证明过程见定理21.16及其推论.7、设V=⎭⎬⎫⎩⎨⎧≤++1),,(222222c z b y a x z y x , 计算下列积分：(1)⎰⎰⎰---Vdxdydz c z b y a x 2222221；(2)⎰⎰⎰++Vc z by ax dxdydz e 222222.解：应用球面变换得V ’={(r,θ,φ)| 0≤θ≤2π, 0≤φ≤π, 0≤r ≤1}. (1)⎰⎰⎰---VdV cz b y a x 2222221=⎰⎰⎰-10220201sin dr r abcr d d ϕϕθππ =42πabc . (2)⎰⎰⎰++Vc z b y ax dV e222222=⎰⎰⎰12020sin dr e abcr d d r ϕϕθππ=)2(4-e abc π.。

考研数学三重积分练习

习题9 三重积分一、填空题1、若{}22(,,)|1,01x y z x y z Ω=+≤≤≤，则d z v Ω⎰⎰⎰= 。

2、d z v Ω⎰⎰⎰＝，其中222{(,,)|1,0}x y z x y z z Ω=++≤≥3、曲面z =被1z =截下部分的面积为。

4、曲面22z x y =+被1z =截下部分的体积为。

5、锥面z =被柱面22z x =所割下部分的面积为。

二、解答题1、I=d x v Ω⎰⎰⎰，其中Ω是由1x y z ++=与三个坐标平面所围的闭区域。

2、()x y z dxdydz Ω++⎰⎰⎰ 其中Ω：由平面1x y z ++=及三坐标面所围成的区域。

3、I=22()d x y v Ω+⎰⎰⎰，其中Ω是由2222x y z z ++= 所围成的闭区域。

4、I＝⎰⎰⎰Ω+•dvyxz)(22，其中Ω是由球面222yxz--=与圆锥面22yxz+=所围成的闭区域。

5、⎰⎰⎰Ω++dvzyx)(222，Ω＝｛2224,0x y z z++≤≥｝。

6、⎰⎰⎰Ω+•dvyxz)(22，Ω是由球面222yxz--=与圆锥面22yxz+=所围成的闭区域。

7、⎰⎰⎰Ω++dvzyx222，Ω是由球面zzyx2222=++所围成的闭区域。

8、求函数22y x z +=在区域D ：x 4y x x 222≤+≤上与z=0所围成的体积。

9、求由平面1,0,0,0=++===z y x z y x 所围成的几何体的体积。

10、在由椭圆1422≤+y x 绕其长轴旋转一周而成的椭球体上，沿长轴方向打一穿过中心的圆孔，并使剩下部分的体积恰好等于椭球体体积的一半，求该圆孔的直径。

练习题6三重积分练习题

第九章练习题6：三重积分王克金三重积分的性质 1.(),,f x y z dv Ω⎰⎰⎰存在的充分条件是（）A（A ）(),,f x y z 在有界闭区域Ω上连续（B ）(),,f x y z 在有界闭区域Ω上有界（C ）(),,f x y z 在区域Ω上连续（D ）(),,f x y z 在区域Ω上有界答案：（A ）解 B 、D 有界不一定可积，C 区域无界，连续不一定可积，故只有A2. 有界闭区域Ω由平面10,20x y z x y z +++=+++=及三个坐标面围成，设[]()3212ln(3),I x y z dxdydz I x y z dxdydz ΩΩ=+++=++⎰⎰⎰⎰⎰⎰，则利用三重积分性质知12,I I 的关系为（）A（A ）12I I ≤ （B ）12,I I 的大小不具体计算无法比较（C ）12I I ≥ （D ）12,I I 的值计算不出来，故无法比较它们的大小答案：（A ）解被积函数均可视为x y z ++的函数，在积分区域内，21x y z -≤++≤-，[]32ln(3)ln 21()x y z x y z +++≤<≤++，故A 成立3.有界闭区域Ω由平面10,2x y z x y z +++=+++=及三个坐标面围成，设[]()3212ln(3),I x y z dxdydz I x y z dxdydz ΩΩ=+++=++⎰⎰⎰⎰⎰⎰，则利用三重积分性质知12,I I 的关系为__________答案：12I I ≤解在Ω内，[]330ln(3)(ln2)1x y z ≤+++≤≤，()214x y z ≤++≤，故12I I ≤三重积分的奇偶性1.设Ω为3R 中关于xy 面的对称区域，(,,)f x y z 为Ω上的连续函数，1Ω为Ω在xy 面上方部分，则当(,,)f x y z 为关于_____的奇函数时，(,,)0;f x y z dv Ω=⎰⎰⎰则当(,,)f x y z 为关于_____的偶函数时，1(,,)___(,,)f x y z dv f x y z dv ΩΩ=⎰⎰⎰⎰⎰⎰。

三重积分习题

931 化三重积分⎰⎰⎰Ω=dxdydz z y x f I ),,(为三次积分其中积分区域分别是(1)由双曲抛物面xy z 及平面x y 10 z 0所围成的闭区域解积分区域可表示为 {(x y z )| 0z xy 0y 1x 0x 1} 于是 ⎰⎰⎰-=xyx dzz y x f dy dx I 01010),,((2)由曲面z x 2y 2及平面z 1所围成的闭区域解积分区域可表示为}11 ,11 ,1|),,{(2222≤≤--≤≤--≤≤+=Ωx x y x z y x z y x于是 ⎰⎰⎰+----=111112222),,(y x x xdz z y x f dy dx I(3)由曲面z x 22y 2及z 2x 2所围成的闭区域解曲积分区域可表示为}11 ,11 ,22|),,{(22222≤≤--≤≤---≤≤+=Ωx x y x x z y x z y x于是 ⎰⎰⎰-+----=22222221111),,(x y x x x dz z y x f dy dx I提示曲面z x 22y 2与z 2x 2的交线在xOy 面上的投影曲线为x 2+y 2=1(4)由曲面cz xy (c 0) 12222=+by a x z 0所围成的在第一卦限内的闭区域解曲积分区域可表示为}0 ,0 ,0|),,{(22a x x a ab yc xyz z y x ≤≤-≤≤≤≤=Ω于是 ⎰⎰⎰-=c xy x a a b adz z y x f dy dx I 000),,(22提示区域的上边界曲面为曲面c z xy 下边界曲面为平面z 02 设有一物体占有空间闭区域{(x y z )|0x 1 0y 1 0z 1} 在点(x y z )处的密度为(x y z )x y z 计算该物体的质量解 ⎰⎰⎰⎰⎰⎰++==Ω101010)(dz z y x dy dx dxdydz M ρ⎰⎰++=1010)21(dy y x dx⎰⎰+=++=1010102)1(]2121[dx x dx y y xy 23)1(21102=+=x3如果三重积分⎰⎰⎰Ωdxdydz z y x f ),,(的被积函数f (xy z )是三个函数f 1(x )、f 2(y )、f 3(z )的乘积即f (x y z ) f 1(x )f 2(y )f 3(z ) 积分区域{(x y z )|a x b c y d l z m } 证明这个三重积分等于三个单积分的乘积即⎰⎰⎰⎰⎰⎰=Ωmldcbadzz f dy y f dx x f dxdydz z f y f x f )()()()()()(321321证明 ⎰⎰⎰Ωdxdydz z f y f x f )()()(321dx dy dz z f y f x f ba dcml]))()()(([321⎰⎰⎰=dx dy dz z f y f x f b a d c m l]))()()(([321⎰⎰⎰=⎰⎰⎰=m ldcb adx dy y f dz z f x f )])()()()([(231dx x f dy y f dz z f bam ld c)]())()()([(123⎰⎰⎰=⎰⎰⎰=d cbam ldx x f dy y f dz z f )())()()((123⎰⎰⎰=d cmlb adzz f dy y f dx x f )()()(3214计算⎰⎰⎰Ωdxdydzz xy 32 其中是由曲面z xy 与平面y x x 1和z 0所围成的闭区域解积分区域可表示为 {(x y z )| 0z xy 0y x 0x 1}于是 ⎰⎰⎰Ωdxdydz z xy 32⎰⎰⎰=xyxdz z dy y xdx 030210⎰⎰=xxy dy z y xdx 004210]4[⎰⎰=x dy y dx x 051054136412811012==⎰dx x5 计算⎰⎰⎰Ω+++3)1(z y x dxdydz 其中为平面x 0 y 0 z 0x y z 1所围成的四面体解积分区域可表示为 {(x y z )| 0z 1x y 0y 1x 0x 1}于是 ⎰⎰⎰Ω+++3)1(z y x dxdydz ⎰⎰⎰---+++=y x x dz z y x dy dx 1031010)1(1 ⎰⎰--++=xdy y x dx 1021]81)1(21[dx x x ⎰+-+=10]8183)1(21[ )852(ln 21-=提示⎰⎰⎰Ω+++3)1(z y x dxdydz ⎰⎰⎰---+++=y x x dz z y x dy dx 1031010)1(1 ⎰⎰---+++-=xyx dy z y x dx 101021])1(21[⎰⎰--++=x dy y x dx 10210]81)1(21[ dx y y x x-⎰-++-=101]81)1(21[dx x x ⎰+-+=10]8183)1(21[ 102]16183)1ln(21[x x x +-+= )852(ln 21-=6计算⎰⎰⎰Ωxyzdxdydz其中为球面x 2y 2z 21及三个坐标面所围成的在第一卦限内的闭区域解积分区域可表示为}10 ,10 ,10|),,{(222≤≤-≤≤--≤≤=Ωx x y y x z z y x 于是 ⎰⎰⎰Ωxyzdxdydz ⎰⎰⎰---=222101010x y x xyzdz dy dx⎰⎰---=2102210)1(21x dy y x xy dx ⎰-=1022)1(81dx x x 481=7计算⎰⎰⎰Ωxzdxdydz其中是由平面z 0 z y y 1以及抛物柱面y x 2所围成的闭区域解积分区域可表示为 {(x y z )| 0z y x 2y 1 1x 1}于是 ⎰⎰⎰Ωxzdxdydz ⎰⎰⎰-=yx zdz dy xdx 01112⎰⎰-=1211221x dy y xdx)1(61116=-=⎰-dx x x8计算⎰⎰⎰Ωzdxdydz其中是由锥面22y x Rh z +=与平面zh (R 0h 0)所围成的闭区域解当0z h 时过(0 0 z )作平行于xOy 面的平面截得立体的截面为圆D z 222)(z h R y x =+ 故D z 的半径为z h R 面积为222z h R π 于是⎰⎰⎰Ωzdxdydz⎰⎰⎰zD hdxdy zdz 0⎰==h h R dz z hR 0223224ππ9 利用柱面坐标计算下列三重积分(1)⎰⎰⎰Ωzdv其中是由曲面222y x z --=及z x 2y 2所围成的闭区域解在柱面坐标下积分区域可表示为 021222ρρ-≤≤z于是 ⎰⎰⎰Ωzdv ⎰⎰⎰-=1022022ρρπρρθzdz d d ⎰--=1042)2(212ρρρρπdπρρρρπ127)2(1053=--=⎰d(2)⎰⎰⎰Ω+dvy x )(22 其中是由曲面x 2y 22z 及平面z 2所围成的闭区域解在柱面坐标下积分区域可表示为02 02222≤≤z ρ于是 dv y x )(22+Ω⎰⎰⎰dz d d θρρρ⋅=Ω⎰⎰⎰2⎰⎰⎰=22123202ρπρρθdz d d⎰⎰-=205320)212(ρρρθπd d ⎰==ππθ2031638d10 利用球面坐标计算下列三重积分(1)⎰⎰⎰Ω++dvz y x )(222 其中是由球面x 2y 2z 21所围成的闭区域解在球面坐标下积分区域可表示为 02 00r 1于是 ⎰⎰⎰Ω++dv z y x )(222⎰⎰⎰Ω⋅=θϕϕd drd r sin 4⎰⎰⎰=104020sin dr r d d ππϕϕθπ54=(2)⎰⎰⎰Ωzdv其中闭区域由不等式x 2y 2(z a )2a 2 x 2y 2z 2 所确定解在球面坐标下积分区域可表示为ϕπϕπθcos 20 ,40 ,20a r ≤≤≤≤≤≤于是⎰⎰⎰⎰⎰⎰ΩΩ⋅=θϕϕϕd drd r r zdv sin cos 2⎰⋅=404)cos 2(41cos sin 2πϕϕϕϕπd a4405467cos sin 8a d a πϕϕϕππ==⎰11 选用适当的坐标计算下列三重积分(1)⎰⎰⎰Ωxydv其中为柱面x 2y 21及平面z 1 z 0 x 0 y 0所围成的在第一卦限内的闭区域解在柱面坐标下积分区域可表示为10 ,10 ,20≤≤≤≤≤≤z ρπθ于是 ⎰⎰⎰Ωxydv ⎰⎰⎰Ω⋅⋅=dz d d θρρθρθρsin cos⎰⎰⎰==101032081cos sin dz d d ρρθθθπ别解用直角坐标计算⎰⎰⎰Ωxydv ⎰⎰⎰-=1010102dz ydy xdx x ⎰⎰-=21010x ydy xdx ⎰-=103)22(dx x x 81]84[1042=-=x x (2)⎰⎰⎰Ω++dvz y x 222 其中是由球面x 2y 2z 2z 所围成的闭区域解在球面坐标下积分区域可表示为ϕπϕπθcos 0 ,20 ,20≤≤≤≤≤≤r于是 ⎰⎰⎰Ω++dv z y x 222⎰⎰⎰⋅=ϕππϕϕθcos 022020sin dr r r d d10cos 41sin 2204πϕϕϕππ=⋅=⎰d(3)⎰⎰⎰Ω+dvy x )(22 其中是由曲面4z 225(x 2y 2)及平面z 5所围成的闭区域解在柱面坐标下积分区域可表示为 525 ,20 ,20≤≤≤≤≤≤z ρρπθ于是 ⎰⎰⎰Ω+dv y x )(22⎰⎰⎰=52520320ρπρρθdz d dπρρρπ8)255(2203=-=⎰d(4)⎰⎰⎰Ω+dvy x )(22 其中闭区域由不等式Az y x a ≤++≤<2220 z所确定解在球面坐标下积分区域可表示为Ar a ≤≤≤≤≤≤ ,20 ,20πϕπθ于是 ⎰⎰⎰Ω+dv y x )(22θϕϕθϕϕϕd drd r r r sin )sin sin cos sin (2222222⎰⎰⎰Ω+=)(154sin 55420320a A dr r d d Aa -==⎰⎰⎰πϕϕθππ12 利用三重积分计算下列由曲面所围成的立体的体积(1)z 6x 2y 2及22y x z +=解在柱面坐标下积分区域可表示为0 2 02 z 62于是 ⎰⎰⎰⎰⎰⎰ΩΩ==dz d d dv V θρρ⎰⎰⎰-=262020ρρπρρθdz d d⎰=--=2032332)6(2πρρρρπd(2)x 2y 2z 22az (a 0)及x 2y 2z 2(含有z 轴的部分)解在球面坐标下积分区域可表示为ϕπϕπθcos 20 ,40 ,20a r ≤≤≤≤≤≤于是 ⎰⎰⎰⎰⎰⎰ΩΩ==θϕϕd drd r dv V sin 2⎰⎰⎰=ϕππϕϕθcos 2024020sin a dr r d d34033sin cos 382a d a πϕϕϕππ==⎰(3)22y x z +=及zx 2y 2解在柱面坐标下积分区域可表示为 02 01 2z于是 6)(2103210202πρρρπρρθρρπ=-===⎰⎰⎰⎰⎰⎰⎰Ωd dz d d dv V(4)225y x z --=及x 2y 24z解在柱面坐标下积分区域可表示为 22541 ,20 ,20ρρρπθ-≤≤≤≤≤≤z于是 ⎰⎰⎰-=22541220ρρπρρθdz d d V)455(32)45(22022-=--=⎰πρρρρπd13 球心在原点、半径为R 的球体在其上任意一点的密度的大小与这点到球心的距离成正比求这球体的质量解密度函数为222),,(z y x k z y x ++=ρ 在球面坐标下积分区域可表示为02r R于是 ⎰⎰⎰Ω++=dv z y x k M 2224220sin R k dr r kr d d R πϕϕθππ=⋅=⎰⎰⎰。

练习105(三重积分的计算(投影法))- 答案

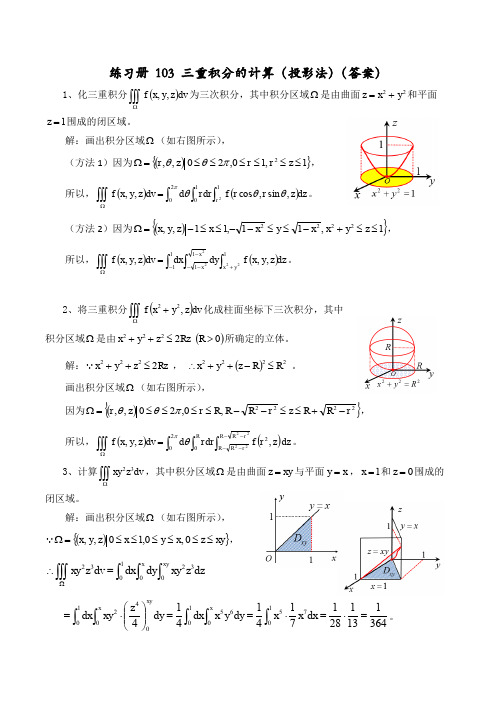
练习册 103 三重积分的计算（投影法）（答案）1、化三重积分()⎰⎰⎰Ωdv z y x f ,,为三次积分，其中积分区域Ω是由曲面22y x z +=和平面1=z 围成的闭区域。

解：画出积分区域Ω（如右图所示），（方法1）因为(){}1 ,10,20 ,,2≤≤≤≤≤≤=Ωz r r z r πθθ，所以，()()dz z r r f rdr d dv z y x f r ⎰⎰⎰⎰⎰⎰=Ω110202,sin ,cos ,,θθθπ。

（方法2）因为(){}1 ,11,11 ,,2222≤≤+-≤≤--≤≤-=Ωz y x x y x x z y x ，所以，()()dz z y x f dy dx dv z y x f y x x x ⎰⎰⎰⎰⎰⎰+----Ω=111112222,,,,。

2、将三重积分()⎰⎰⎰Ω+dv z y x f ,22化成柱面坐标下三次积分，其中积分区域Ω是由()0 2222>≤++R Rz z y x 所确定的立体。

解： 2222Rz z y x ≤++ ， () 2222R R z y x ≤-++∴。

画出积分区域Ω（如右图所示），因为(){}2222 ,0,20 ,,r R R z r R R R r z r -+≤≤--≤≤≤≤=Ωπθθ，所以，()()dz z r f rdr d dv z y x f r R R r R R R ⎰⎰⎰⎰⎰⎰----Ω=2222 ,,,2020πθ。

3、计算⎰⎰⎰Ωdv z xy 32，其中积分区域Ω是由曲面xy z =与平面x y =，1=x 和0=z 围成的闭区域。

解：画出积分区域Ω（如右图所示），(){}xy z x y x z y x ≤≤≤≤≤≤=Ω0 ,0,10 ,, ，dz z xy dy dx dv z xy xyx ⎰⎰⎰⎰⎰⎰=∴Ω0320103236411312817141414107506510004210=⋅=⋅==⎪⎪⎭⎫ ⎝⎛⋅=⎰⎰⎰⎰⎰dx x x dy y x dx dy z xy dx x x xy。

高等数学三重积分例题

高等数学三重积分例题一、计算三重积分∭_varOmega z dV，其中varOmega是由锥面z = √(x^2)+y^{2}与平面z = 1所围成的闭区域。

1. 利用柱坐标计算在柱坐标下x = rcosθ，y = rsinθ，z = z，dV = rdzdrdθ。

锥面z=√(x^2)+y^{2}在柱坐标下就是z = r。

由锥面z = r与平面z = 1所围成的闭区域varOmega，其在柱坐标下的范围为：0≤slantθ≤slant2π，0≤slant r≤slant1，r≤slant z≤slant1。

2. 计算积分则∭_varOmegaz dV=∫_0^2πdθ∫_0^1rdr∫_r^1zdz。

先计算关于z的积分：∫_r^1zdz=(1)/(2)(1 r^2)。

再计算关于r的积分：∫_0^1r×(1)/(2)(1 r^2)dr=(1)/(2)∫_0^1(rr^3)dr=(1)/(2)((1)/(2)-(1)/(4))=(1)/(8)。

最后计算关于θ的积分：∫_0^2πdθ = 2π。

所以∭_varOmegaz dV=(1)/(8)×2π=(π)/(4)。

二、计算三重积分∭_varOmega(x + y+z)dV，其中varOmega是由平面x = 0，y = 0，z = 0及x + y+z = 1所围成的四面体。

1. 利用直角坐标计算对于由平面x = 0，y = 0，z = 0及x + y + z=1所围成的四面体varOmega，其范围为0≤slant x≤slant1，0≤slant y≤slant1 x，0≤slant z≤slant1 x y。

则∭_varOmega(x + y + z)dV=∫_0^1dx∫_0^1 xdy∫_0^1 x y(x + y + z)dz。

2. 计算积分先计算关于z的积分：∫_0^1 x y(x + y+z)dz=(x + y)z+(1)/(2)z^2big|_0^1 x y=(x + y)(1 x y)+(1)/(2)(1 x y)^2展开得x + y-(x^2+2xy + y^2)+(1)/(2)(1 2x 2y+x^2+2xy + y^2)进一步化简为x + y x^2-2xy y^2+(1)/(2)-x y+(1)/(2)x^2+xy+(1)/(2)y^2即(1)/(2)-x^2-xy (1)/(2)y^2。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

三重积分练习题
1．计算cos()I y x z dxdydz Ω
=
+⎰⎰⎰，Ω由抛物柱面y =平面0,0,2
y z x z π
==+=
所围区域。

（
28
16
π-）
2．计算I z dxdydz Ω
=⎰⎰⎰
，Ω由z =与223x y z +=围成。

（134
π
）
3．计算I Ω
=⎰⎰⎰
，Ω为由2221x y z ++≤和z ≥所围区域。

（
20
π
）
4．已知()f x 连续，222
()[()]F t z f x y dxdydz Ω
=++⎰⎰⎰，222:0,z h x y t Ω≤≤+≤，求：
()F t '和2
0()
lim t F t t
+
→。

5．设Ω为平面1(0,0,0)x y z
a b c a b c
++=>>>与三个坐标平面围成的四面体区域，求
(,,)I a b c z dxdydz Ω
=⎰⎰⎰；
若又设a b c h ++=为定值，问,,a b c 怎样取值时，(,,)I a b c 最大，并求此最大值。

（24
,241536
a b c h ） 6．将22()I f x y dxdydz Ω
=
+⎰⎰⎰
化为球坐标下的三次积分，其中222:1,x y z Ω++≤
0,0x y ≥≥。

7．设()f u 具有连续导数，求2222
4
01lim
t x y z t f dxdydz t π→++≤⎰⎰⎰。

（(0)f '，若(0)0f =；∞，若(0)0f ≠）
8．计算22
()I x y dxdydz Ω
=+⎰⎰⎰，其中Ω为平面曲线
{
2
20
y z x ==绕z 轴旋转一周形成的曲面与平面8z =所围成的区域。

（10243
π
）
9．计算I Ω
=
⎰⎰⎰，其中Ω为22,1,1y x z y =+==之间。

10．设2
2
2
{(,,)|1,0}x y z x y z x y z Ω=++≤++≥，计算三重积分：
（1）22233323x y z I dxdydz x y z Ω+-=++⎰⎰⎰；（2）333
333
6233x y z I dxdydz x y z Ω
+++=+++⎰⎰⎰ 11．求2
22(),,0I x y z dv x
y z z h Ω
=
++Ω+≤≤≤⎰⎰⎰由所围立体。

12．计算下列三重积分
（1）222222
ln(1)1z x y z I dxdydz x y z Ω
+++=+++⎰⎰⎰，其中222
1x y z Ω++≤为。

（2）2
22()
222(),4,0,0,0x
y z I x z e dv x y z x y z -++Ω
=+Ω≤++≤≥≥≥⎰⎰⎰由1所围
（3）222
,:1x
I e dv x y z Ω
=Ω++≤⎰⎰⎰。

10．解：分析本题中被积函数比较复杂，而积分区域具有关于,,x y z 轮换不变性，所以可以利用积分值与积分变量名称无关这一特点进行计算。

（1）因为222
333333333
x y z dV dV dV x y z x y z x y z ΩΩΩ
==++++++⎰⎰⎰⎰⎰⎰⎰⎰⎰ 所以
原式=222
333333333
230x y z dV dV dV x y z x y z x y z ΩΩΩ
+-=++++++⎰⎰⎰⎰⎰⎰⎰⎰⎰ （2）因为333
333333333
111333x y z dV dV dV x y z x y z x y z
ΩΩΩ+++==+++++++++⎰⎰⎰⎰⎰⎰⎰⎰⎰ 所以
原式=333
333333333
11123333x y z dV dV dV x y z x y z x y z
ΩΩΩ++++++++++++++⎰⎰⎰⎰⎰⎰⎰⎰⎰ =333333333333
1112[]333x y z dV dV dV x y z x y z x y z ΩΩΩ++++++++++++++⎰⎰⎰⎰⎰⎰⎰⎰⎰ =333333
(1)(1)(1)42233x y z dV V x y z πΩ
+++++==+++⎰⎰⎰ 12．解：
（1）22
2
cos ln (1)sin 1r r I r drd d r
ϕϕθϕΩ
+=
+⎰⎰⎰
=
32212
ln (1)
sin cos 0(sin cos 0)1r r d d dr d r
πππϕϕϕθϕϕϕ+==+⎰
⎰⎰
⎰
（2）
2
2
2222
2333
1
(sin cos cos )sin (sin cos sin cos )(25)
4r r I r e r drd d d d e r dr e e
ππ
ϕθϕϕϕθ
π
ϕθϕθϕϕ-Ω
-=+⋅=+⋅=
-⎰⎰⎰⎰⎰⎰
（3）由对称性，知 2
22221
cos 20
1(0)
2
2sin 2z
r x y z z I e dv d d e r dr π
πϕϕθϕπ++≤≥===-⎰⎰⎰⎰⎰
⎰。