立体几何理-高考理科数学试题专题分类汇编
高考数学(理)(全国通用)复习高考试题分类汇编 : 立体几何 (含解析)

第八章 立体几何第一节 空间几何体及其表面积和体积题型85 空间几何体的表面积与体积1.(2017江苏6)如图所示,在圆柱12O O 内有一个球O ,该球与圆柱的上、下面及母线均相切.记圆柱12O O 的体积为1V ,球O 的体积为2V ,则12V V 的值是 .1.解析 设球O 的半径为r ,由题意212V r r =π⋅,3243V r =π,所以1232V V =.故填32.2.(2017天津理10)已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为 .2.解析 设正方体的边长为a ,则226183a a =⇒=.外接球直径为正方体的体对角线,所以23==R ,344279πππ3382==⨯=V R . 3.(2107全国1卷理科16)如图所示,圆形纸片的圆心为O ,半径为5 cm ,该纸片上的等边三角形ABC 的中心为O .D ,E ,F 为圆O 上的点,DBC △,ECA △,FAB △分别是以BC ,CA ,AB 为底边的等腰三角形.沿虚线剪开后,分别以BC ,CA ,AB 为折痕折起DBC △,ECA △,FAB △,使得D ,E ,F 重合,得到三棱锥.当ABC △的边长变化时,所得三棱锥体积(单位:3cm )的最大值为_______.3.解析 由题意,联结OD ,交BC 于点G ,如图所示,则OD BC ⊥,OG =,即OG 的长度与BC 的长度成正比.设OG x =,则BC =,5DG x =-,三棱锥的高h =,2132ABC S x =⋅⋅=△,则13ABC V S h =⋅△令()452510f x x x =-,50,2x ⎛⎫∈ ⎪⎝⎭,()3410050f x x x '=-,令()0f x '>,即4320x x -<,2x <,当()0f x '<,得522x <<,所以()f x 在()0,2上单调递增,在52,2⎛⎫ ⎪⎝⎭上单调递减.故()()280f x f =≤,则V ,所以体积的最大值为3.题型86 旋转体的表面积、体积及球面距离4.(2107全国3卷理科8)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( ). A .πB .3π4C .π2D .π44.解析 如图所示,由题可知球心在圆柱体的中心处,圆柱体上、下底面圆的半径r =23ππ4V r h ==.故选B.题型87 几何体的外接球与内切球第二节 空间几何体的直观图与三视图题型88 斜二测画法与直观图——暂无 题型89 空间几何体的三视图5.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是( ). A.π12+ B. π32+ C. 3π12+ D. 3π32+5.解析 由三视图可知,直观图是由半个圆锥与一个三棱锥构成,半圆锥体积为()2111=13232S π⨯π⨯⨯=,三棱锥体积为211=213=132S ⎛⎫⨯⨯⨯ ⎪⎝⎭,所以几何体体积1212S S S π=+=+.故选A .6.(2017全国1卷理科7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( ).A.10B.12C.14D.166. 解析 由三视图可画出立体图,如图所示,该多面体只有两个相同的梯形的面, ()24226S =+⨯÷=梯,6212S =⨯=全梯.故选B.7.(2107全国2卷理科4)如图所示,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( ). A .90π B .63π C .42π D .36π7.解析 该几何体可视为一个完整的圆柱减去一个高为6的圆柱的一半,如图所示. 2211π310π3663π22=-=⋅⋅-⋅⋅⋅=V V V 总上.故选B.8.(2017北京理7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( ).A.B.C. D.28. 解析 几何体四棱锥如图所示,最长棱为正方体的体对角线,即l =故选B.9.(2017山东理13)由一个长方体和两个14圆柱体构成的几何体的三视图如图所示,则该几何体的体积为 .9. 解析 该几何体的体积为21112211242V π=π⨯⨯⨯+⨯⨯=+.第三节 空间点、直线、平面之间的位置关系题型90 证明“点共面”“线共面”“点共线”或“线共点” ——暂无 题型91 截面问题——暂无10.(2017江苏18)如图所示,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm ,容器Ⅰ的底面对角线AC 的长为cm ,容器Ⅱ的两底面对角线EG ,11E G 的长分别为14cm 和62cm . 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm . 现有一根玻璃棒l ,其长度为40cm (容器厚度、玻璃棒粗细均忽略不计).(1)将l 放在容器Ⅰ中,l 的一端置于点A 处,另一端置于侧棱1CC 上,求l 没入水中部分 的长度;(2)将l 放在容器Ⅱ中,l 的一端置于点E 处,另一端置于侧棱1GG 上,求l 没入水中部分的长度.AC A 11容器ⅠE G 1H 1容器Ⅱ10.解析 (1)由正棱柱的定义,1CC ⊥平面ABCD ,所以平面11A ACC ⊥平面ABCD ,1CC AC ⊥.记玻璃棒的另一端落在1CC 上点M 处,如图所示为截面11A ACC的平面图形.因为AC =40AM =,所以30MC ==,从而3sin 4MAC ∠=.记AM 与水面的交点为1P , 过点1P 作11PQ AC ⊥,1Q 为垂足,则11PQ ⊥平面ABCD ,故1112PQ =,从而11116sin PQ AP MAC==∠.答:玻璃棒l 没入水中部分的长度为16cm .问(1)AC 1A 1CMP 1Q 1(2)如图所示为截面11E EGG 的平面图形,O ,1O 是正棱台两底面的中心.由正棱台的定义,1OO ⊥平面EFGH , 所以平面11E EGG ⊥平面EFGH ,1O O EG ⊥. 同理,平面11E EGG ⊥平面1111E F G H ,111O O E G ⊥. 记玻璃棒的另一端落在1GG 上点N 处.过G 作11GK E G ⊥,K 为垂足,则132GK OO ==. 因为 14EG =,1162E G =,所以16214242KG -==,从而1GG =40==.设1EGG α∠=,ENG β∠=,则114sin sin cos 25KGG KGG απ⎛⎫=+==⎪⎝⎭∠∠.因为2απ<<π,所以3cos 5α=-. 在ENG △中,由正弦定理可得4014sin sin αβ=,解得7sin 25β=. 因为02βπ<<,所以24cos 25β=, 于是()()sin sin sin =NEG αβαβ=π--=+∠sin cos cos sin αβαβ+4243735255255⎛⎫=⨯+-⨯= ⎪⎝⎭. 记EN 与水面的交点为2P ,过2P 作22P Q EG ⊥,2Q 为垂足,则22P Q ⊥平面EFGH ,故2212P Q =,从而22220sin PQ EP NEG==∠.答:玻璃棒l 没入水中部分的长度为20cm .问(2)G O E Q 2P 2NG 1KE 1O 1评注 此题本质上考查解三角形的知识,但在这样的大背景下构造的应用题让学生有畏惧之感,且该应用题的实际应用性也不强.也有学生第(1)问采用相似法解决,解法如下:AC =40AM =,所以30CM ==,1112PQ =,所以由11AP A Q CM △△∽,111PQ AP CM AM =,即1123040AP =,解得116AP =. 答:玻璃棒l 没入水中部分的长度为16cm .题型92 异面直线的判定——暂无第四节 直线、平面平行的判定与性质题型93 证明空间中直线、平面的平行关系11.(2107浙江19(1))如图所示,已知四棱锥P ABCD -,PAD △是以AD 为斜边的等腰直角三角形,//BC AD ,CD AD ⊥,22PC AD DC CB ===,E 为PD 的中点. (1)证明://CE 平面PAB .11.解析 (1)如图所示,设PA DE 的中点为F ,联结EF ,FB .A BDPE因为E ,F 分别为PD ,PA 的中点,所以//EF AD ,且1=2EF AD . 又因为//BC AD ,12BC AD =,所以//EF BC ,且=EF BC ,所以四边形BCEF 为平行四边形,所以//CE BF ,又BF ⊂平面PAB ,所以//CE 平面PAB .H QPN MF DBCEA12.(2017江苏15)如图所示,在三棱锥A BCD -中,AB AD ⊥,BC BD ⊥, 平面ABD ⊥平面BCD , 点,E F (E 与,A D 不重合)分别在棱,AD BD 上,且EF AD ⊥. 求证:(1)EF ∥平面ABC ; (2)AD AC ⊥.ABDCEF12.解析 (1)在平面ABD 内,因为AB AD ⊥,EF AD ⊥,且点E 与点A 不重合,所以//EF AB .又因为EF ⊄平面ABC ,AB ⊂平面ABC ,所以//EF 平面ABC . (2)因为平面ABD ⊥平面BCD ,平面ABD平面BCD BD =,BC ⊂平面BCD ,BC BD ⊥,所以BC ⊥平面ABD .因为AD ⊂平面ABD ,所以BC AD ⊥. 又AB AD ⊥,BCAB B =,AB ⊂平面ABC ,BC ⊂平面ABC ,所以AD ⊥平面ABC .又因为AC ⊂平面ABC ,所以AD AC ⊥.13.(2017全国2卷理科19)如图所示,在四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底面ABCD ,12AB BC AD ==,o 90BAD ABC ∠=∠=, E 是PD 的中点. (1)求证:直线//CE 平面PAB ;EM DCBAP13.解析 (1)令PA 的中点为F ,联结EF ,BF ,如图所示.因为点E ,F 为PD ,PA 的中点,所以EF 为PAD △的中位线,所以=1//2EF AD .又因为90BAD ABC ∠=∠=︒,所以BC AD ∥.又因为12AB BC AD ==,所以=1//2BC AD ,于是=//EF BC .从而四边形BCEF 为平行四边形,所以CE BF ∥.又因为BF PAB ⊂面,所以CE ∥平面PAB.题型94 与平行有关的开放性、探究性问题第五节 直线、平面垂直的判定与性质题型95 证明空间中直线、平面的垂直关系14.(2017江苏15)如图所示,在三棱锥A BCD -中,AB AD ⊥,BC BD ⊥, 平面ABD ⊥平面BCD , 点,E F (E 与,A D 不重合)分别在棱,AD BD 上,且EF AD ⊥. 求证:(1)EF ∥平面ABC ; (2)AD AC ⊥.ABDCEF14.解析 (1)在平面ABD 内,因为AB AD ⊥,EF AD ⊥,且点E 与点A 不重合,所以//EF AB .又因为EF ⊄平面ABC ,AB ⊂平面ABC ,所以//EF 平面ABC . (2)因为平面ABD ⊥平面BCD ,平面ABD平面BCD BD =,BC ⊂平面BCD ,BC BD ⊥,所以BC ⊥平面ABD .因为AD ⊂平面ABD ,所以BC AD ⊥. 又AB AD ⊥,BCAB B =,AB ⊂平面ABC ,BC ⊂平面ABC ,所以AD ⊥平面ABC .又因为AC ⊂平面ABC ,所以AD AC ⊥.15.(2017全国1卷理科18(1))如图所示,在四棱锥P ABCD -中,//AB CD ,且90BAP CDP ∠=∠=.(1)求证:平面PAB ⊥平面PAD ;DCBAP15. 解析 (1)证明:因为90BAP CDP ∠=∠=,所以PA AB ⊥,PD CD ⊥.又因为AB CD ∥,所以PD AB ⊥.又因为PD PA P =,PD ,PA ⊂平面PAD ,所以AB ⊥平面PAD .又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD .16.(2017全国3卷理科19(1))如图所示,四面体ABCD 中,ABC △是正三角形,ACD △是直角三角形,ABD CBD ∠=∠,AB BD =.(1)求证:平面ACD ⊥平面ABC ;16.解析 ⑴如图所示,取AC 的中点为O ,联结BO ,DO . 因为ABC △为等边三角形,所以BO AC ⊥,AB BC =.由AB BC BD BD ABD DBC =⎧⎪=⎨⎪∠=∠⎩,得ABD CBD ≅△△,所以AD CD =,即ACD △为等腰直角三角形, 从而ADC ∠为直角.又O 为底边AC 中点,所以DO AC ⊥. 令AB a =,则AB AC BC BD a ====,易得2a OD =,OB = 所以222OD OB BD +=,从而由勾股定理的逆定理可得2DOB π∠=,即OD OB ⊥. 由OD AC OD OB AC OB O AC ABC OB ABC⊥⎧⎪⊥⎪⎪=⎨⎪⊂⎪⊂⎪⎩平面平面,所以OD ⊥平面ABC . 又因为OD ⊂平面ADC ,由面面垂直的判定定理可得平面ADC ⊥平面ABC .BEC DAO题型96 与垂直有关的开放性、探索性问题——暂无第六节 空间向量与立体几何题型97 空间向量及其运算 题型98 空间角的计算17.(2017全国2卷理科10)已知直三棱柱111ABC A B C -中,120ABC ∠=,2AB =,11BC CC ==,则异面直线1AB 与1BC 所成角的余弦值为( ).ABCD17.解析 设M ,N ,P 分别为AB ,1BB ,11B C 的中点,则1AB 和1BC 的夹角为MN 和NP 夹角或其补角(异面线所成角为π02⎛⎤ ⎥⎝⎦,).可知112MN AB ==,112NP BC ==,取BC 的中点Q ,联结,,PQ MQ PM ,则可知PQM △为直角三角形.1=PQ ,12MQ AC =.在ABC △中,2222c o s A C A B B C A B B C AB C =+-⋅⋅∠14122172⎛⎫=+-⨯⨯⋅-= ⎪⎝⎭,即AC,则MQ =,则在MQP △中,MP =. 在PMN △中,222cos 2MN NP PM PNM MN NP +-∠=⋅⋅222+-==. 又异面直线所成角为π02⎛⎤ ⎥⎝⎦,.故选C.18.(2107山东理17)如图所示,几何体是圆柱的一部分,它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120得到的,G 是DF 的中点. (1)设P 是CE 上的一点,且AP BE ⊥,求CBP ∠的大小; (2)当3AB =,2AD =,求二面角E AG C --的大小.18.解析 (1)因为AP BE ⊥,AB BE ⊥,AB ,AP ⊂平面ABP ,ABAP A =,所以BE ⊥平面ABP .又BP ⊂平面ABP ,所以BE BP ⊥.又120EBC ∠=︒,所以30CBP ∠=︒.(2)以B 为坐标原点,分别以BE ,BP ,BA 所在的直线为x ,y ,z 轴,建立如图所示的空间直角坐标系.由题意得(0,0,3)A ,(2,0,0)E,G,(C -,则(2,0,3)AE =-,AG =,(2,0,3)CG =.设111(,,)x y z =m 是平面AEG 的一个法向量,由00AE AG ⎧⋅=⎪⎨⋅=⎪⎩m m,可得11112300x z x -=⎧⎪⎨=⎪⎩,取12z =,可得平面AEG的一个法向量(3,2)m =. 设222(,,)x y z =n 是平面ACG 的一个法向量,由00AG CG ⎧⋅=⎪⎨⋅=⎪⎩n n,可得22220230x x z ⎧=⎪⎨+=⎪⎩,取22z =-,可得平面ACG的一个法向量(3,2)=-n . 从而1cos ,2⋅==⋅m n m n m n ,易知二面角E AG C --为锐角.因此所求的角为60︒.19.(2017江苏22)如图所示,在平行六面体1111ABCD A B C D -中,1AA ⊥平面ABCD ,且2AB AD ==,1AA =120BAD ∠=︒. (1)求异面直线1A B 与1AC 所成角的余弦值; (2)求二面角1B A D A --的正弦值.A 1B 1C 1D 1ABCD19.解析 在平面ABCD 内,过点A 作AE AD ⊥,交BC 于点E . 因为1AA ⊥平面ABCD ,所以1AA AE ⊥,1AA AD ⊥.如图所示,以{}1,,AE AD AA 为正交基底,建立空间直角坐标系A xyz -.BB y因为2AB AD ==,1AA =120BAD ∠=︒. 则()0,0,0A,)1,0B -,()0,2,0D,)E,(1A,1C .(1)(13,1,A B =-,(13,1,AC =,则111111cos ,A BAC A B AC A B AC ⋅=1,177-⋅==-.因此异面直线1A B 与1AC 所成角的余弦值为17. (2)平面1A DA 的一个法向量为()3,0,0AE =.设(),,x y z =m 为平面1BA D 的一个法向量,又(13,1,A B =-,()BD =,则100A B BD ⎧⋅=⎪⎨⋅=⎪⎩m m,即030y y --=+=⎪⎩. 不妨取3x =,则y =,2z =,所以()=m 为平面1BA D 的一个法向量. 从而cos ,AE AE AE ⋅=m mm34⋅==,设二面角1B A D A --的大小为θ,则3cos 4θ=. 因为[]0,θ∈π,所以sin θ==.因此二面角1B A D A --的正弦值为4. 20.(2017全国1卷理科18)如图所示,在四棱锥P ABCD -中,//AB CD ,且90BAP CDP ∠=∠=.(1)求证:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=,求二面角A PB C --的余弦值.DCBAP20. 解析 (1)证明:因为90BAP CDP ∠=∠=,所以PA AB ⊥,PD CD ⊥.又因为AB CD ∥,所以PD AB ⊥.又因为PD PA P =,PD ,PA ⊂平面PAD ,所以AB ⊥ 平面PAD .又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD .(2)取AD 的中点O ,BC 的中点E ,联结PO ,OE ,因为AB CD ∥,所以四边形ABCD 为平行四边形,所以OE AB ∥.由(1)知,AB ⊥平面PAD ,所以OE ⊥平面PAD .又PO ,AD ⊂平面PAD ,所以OE PO ⊥,OE AD ⊥.又因为PA PD =,所以PO AD ⊥,从而PO ,OE ,AD 两两垂直.以O为坐标原点,建立如图所示的空间直角坐标系O xyz -, 设2PA =,所以()00D ,,)20B ,,(00P ,()20C ,,所以(0PD =,,(22PB =,,()00BC =-,.设()x y z =n ,,为平面PBC 的一个法向量,由00PB BC ⎧⋅=⎪⎨⋅=⎪⎩n n,得200y +=-=⎪⎩.令1y =,则z ,0x =,可得平面PBC 的一个法向量(01=n ,. 因为90APD ∠=︒,所以PD PA ⊥,又知AB ⊥平面PAD ,PD ⊂平面PAD , 所以PD AB ⊥,又PA AB A =,所以PD ⊥平面PAB . 即PD 是平面PAB的一个法向量,(0PD =,,,从而cos PD PD PD ⋅===⋅n n n,由图知二面角A PB C--为钝角,所以它的余弦值为21.(2017全国2卷理科19)如图所示,在四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底面ABCD ,12AB BC AD ==,o 90BAD ABC ∠=∠=, E 是PD 的中点. (1)求证:直线//CE 平面PAB ;(2)点M 在棱PC 上,且直线BM 与底面ABCD 所成的锐角为45,求二面角M AB D --的余弦值.EM DCBAP21.解析 (1)令PA 的中点为F ,联结EF ,BF ,如图所示.因为点E ,F 为PD ,PA的中点,所以EF 为PAD △的中位线,所以=1//2EF AD .又因为90BAD ABC ∠=∠=︒,所以BC AD ∥.又因为12AB BC AD ==,所以=1//2BC AD ,于是=//EF BC .从而四边形BCEF 为平行四边形,所以CE BF ∥.又因为BF PAB ⊂面,所以CE ∥平面PAB .(2)以AD 的中点O 为坐标原点,建立如图所示的空间直角坐标系.设1AB BC ==,则()000O ,,,()010A -,,,()110B -,,,()100C ,,,()010D ,,,(00P .点M 在底面ABCD 上的投影为M ',所以MM BM ''⊥,联结BM '.因为45MBM '∠=,所以MBM '△为等腰直角三角形.因为POC △为直角三角形,OC =,所以60PCO ∠=. 设MM a '=,CM '=,1OM '=.所以100M ⎛⎫' ⎪ ⎪⎝⎭,,.BM a a '===⇒=112OM '==-.所以100M ⎛⎫'- ⎪ ⎪⎝⎭,,102M ⎛- ⎝⎭,112AM ⎛=- ⎝⎭,(100)AB =,,. 设平面ABM 的法向量11(0)y z =,,m ,则110AM y ⋅=+=m,所以(02)=,m ,易知平面ABD 的一个法向量为(001)=,,n,从而cos ,⋅==⋅m n m n m n .故二面角M AB D --.22.(2017全国3卷理科19)如图所示,四面体ABCD 中,ABC △是正三角形,ACD △是直角三角形,ABD CBD ∠=∠,AB BD =.(1)求证:平面ACD ⊥平面ABC ;(2)过AC 的平面交BD 于点E ,若平面AEC 把四面体ABCD 分成体积相等的两部分,求二面角––D AE C 的余弦值.22.解析 ⑴如图所示,取AC 的中点为O ,联结BO ,DO . 因为ABC △为等边三角形,所以BO AC ⊥,AB BC =.由AB BC BD BD ABD DBC =⎧⎪=⎨⎪∠=∠⎩,得ABD CBD ≅△△,所以AD CD =,即ACD △为等腰直角三角形, 从而ADC ∠为直角.又O 为底边AC 中点,所以DO AC ⊥. 令AB a =,则AB AC BC BD a ====,易得2a OD =,OB = 所以222OD OB BD +=,从而由勾股定理的逆定理可得2DOB π∠=,即OD OB ⊥. 由OD AC OD OB AC OB O AC ABC OB ABC⊥⎧⎪⊥⎪⎪=⎨⎪⊂⎪⊂⎪⎩平面平面,所以OD ⊥平面ABC . 又因为OD ⊂平面ADC ,由面面垂直的判定定理可得平面ADC ⊥平面ABC .BEC DAO⑵由题意可知V V D ACE B ACE --=,即B ,D 到平面ACE 的距离相等,即点E 为BD 的中点. 以O 为坐标原点,OA 为x 轴正方向,OB 为y 轴正方向,OD 为z 轴正方向,设AC a =,建立空间直角坐标系,则()0,0,0O ,,0,02a A ⎛⎫ ⎪⎝⎭,0,0,2a D ⎛⎫ ⎪⎝⎭,B ⎛⎫ ⎪ ⎪⎝⎭,,4a E ⎛⎫ ⎪ ⎪⎝⎭,易得24a a AE ⎛⎫=- ⎪ ⎪⎝⎭,,0,22a a AD ⎛⎫=- ⎪⎝⎭,,0,02a OA ⎛⎫= ⎪⎝⎭. 设平面AED 的法向量为()1111=,,x y z n ,平面AEC 的法向量为()2222=,,x y z n ,则1100AE AD ⎧⋅=⎪⎨⋅=⎪⎩n n,取1=n ;220AE OA ⎧⋅=⎪⎨⋅=⎪⎩n n,取(20,1,=n .设二面角D AE C --为θ,易知θ为锐角,则1212cos θ⋅==⋅n n n n.23.(2017北京理16)如图所示,在四棱锥P ABCD -中,底面ABCD 为正方形,平面PAD ⊥平面ABCD ,点M 在线段PB 上,//PD 平面MAC,PA PD ==4AB =.(1)求证:M 为PB 的中点; (2)求二面角B PD A --的大小;(3)求直线MC 与平面BDP 所成角的正弦值.23.解析 (1)设,AC BD 的交点为E ,联结ME . 因为PD ∥平面MAC ,平面MAC平面PBD ME =,所以PD ME ∥.因为ABCD 是正方形,所以E 为BD 的中点,所以M 为PB 的中点.MP EDCBA(2)取AD 的中点O ,联结OP ,OE . 因为PA PD =,所以OP AD ⊥.又因为平面PAD ⊥平面ABCD ,且OP ⊂平面PAD ,所以OP ⊥平面ABCD . 因为OE ⊂平面ABCD ,所以OP OE ⊥.因为ABCD 是正方形,所以OE AD ⊥.如图所示,建立空间直角坐标系O xyz -,则P ,(2,0,0)D ,(2,4,0)B -,(4,4,0)BD =-,(2,0,PD =.设平面BDP 的法向量为(,,)x y z =n ,则00BD PD ⎧⋅=⎪⎨⋅=⎪⎩n n,即44020x y x -=⎧⎪⎨=⎪⎩. 令1x =,则1y =,z ==n .平面PAD 的法向量为(0,1,0)=p ,所以1cos ,||||2⋅==<>n p n p n p .由题知二面角B PD A --为锐角,所以它的大小为3π.(3)由(1)知1,M ⎛- ⎝⎭,(2,4,0)C ,(3,2,)2MC =-. 设直线MC 与平面BDP 所成角为α,则2sin cos ,9MC MC MCα⋅===<>n n n . 所以直线MC 与平面BDP . 24.(2017天津理17)如图所示,在三棱锥P ABC -中,PA ⊥底面ABC ,90BAC ∠=.点D E N ,,分别为棱PA ,PC ,BC 的中点,M 是线段AD 的中点,4PA AC ==,2AB =.(1)求证://MN 平面BDE ; (2)求二面角C EM N --的正弦值;(3)已知点H 在棱PA 上,且直线NH 与直线BE 所成角的余弦值为21,求线段AH 的长.NM ED CBAP24.解析 如图所示,以A 为坐标原点,{},,AB AC AP 为基底,建立如图所示的空间直角坐标系,依题意可得(000)A ,,,(200)B ,,,(040)C ,,,(004)P ,,,(002)D ,,,(022)E ,,,(001)M ,,,(120)N ,,.(1)证明:()0,2,0DE =,()2,0,2DB =-.设(,,)x y z =n 为平面BDE 的一个法向量, 则0DE DB ⎧⋅=⎪⎨⋅=⎪⎩n n ,即20220y x z =⎧⎨-=⎩,不妨设1z =,可得(1,0,1)=n .又()1,2,1MN =-,可得0MN ⋅=n ,因为MN ⊄平面BDE ,所以//MN 平面BDE . (2)易知1(1,0,0)=n 为平面CEM 的一个法向量.设2(,,)x y z =n 为平面EMN 的一个法向量,则220EM MN ⎧⋅=⎪⎨⋅=⎪⎩n n ,因为(0,2,1)EM =--,(1,2,1)MN =-,所以2020y z x y z --=⎧⎨+-=⎩. 不妨设1y =,可得2(4,1,2)=--n .因此有121212cos ,|||⋅==n n n n |n n,于是12sin ,=n n . 所以二面角C EM N --.(3)依题意,设()04AH h h =剟,则H (0,0,h ),进而可得(1,2,)NH h =--,(2,2,2)BE =-.由已知得||cos ,||||NH BE NH BE NH BE h ⋅===2102180h h -+=, 解得85h =或12h =.所以线段AH 的长为85或12. 25.(2107浙江19)如图所示,已知四棱锥P ABCD -,PAD △是以AD 为斜边的等腰直角三角形,//BC AD ,CD AD ⊥,22PC AD DC CB ===,E 为PD 的中点. (1)证明://CE 平面PAB ;(2)求直线CE 与平面PBC 所成角的正弦值.25.解析 (1)如图所示,设PA DE 的中点为F ,联结EF ,FB . 因为E ,F 分别为PD ,PA 的中点,所以//EF AD ,且1=2EF AD . 又因为//BC AD ,12BC AD =,所以//EF BC ,且=EF BC ,所以四边形BCEF 为平行四边形,所以//CE BF ,又BF ⊂平面PAB ,所以//CE 平面PAB .H QPN MF DBCEA(2)分别取BC ,AD 的中点为M ,N .联结PN 交EF 于点Q ,联结MQ .因为E ,F ,N 分别是PD ,PA ,AD 的中点,所以Q 为EF 的中点,在平行四边形BCEF 中,//MQ CE .由PAD △为等腰直角三角形,得PN AD ⊥.A DPE由DC AD ⊥,N 是AD 的中点,所以12ND AD BC ==,且BC DN ∥,所以四边形BCDN 是平行四边形,所以CD BN ∥,所以BN AD ⊥.又BNPN N =,所以AD ⊥平面PBN ,由//BC AD ,得BC ⊥平面PBN ,又BC ⊂平面PBC ,所以平面PBC ⊥平面PBN . 过点Q 作PB 的垂线,垂足为H ,联结MH .MH 是MQ 在平面PBC 上的射影,所以QMH ∠是直线CE 与平面PBC 所成的角.设1CD =.在PCD △中,由2PC =,1CD =,PD =CE =,又BC ⊥平面PBN ,PB ⊂平面PBN ,所以BC PB ⊥.在PBN △中,由1PN BN ==,PB ==QH PB ⊥,Q 为PN 的中点,得14QH =.在Rt MQH △中,14QH =,MQ =sin QMH ∠=所以直线CE 与平面PBC 所成角的正弦值是8. 26.(2107浙江9)如图所示,已知正四面体–D ABC (所有棱长均相等的三棱锥),P ,Q ,R 分别为AB ,BC ,CA 上的点,AP PB =,2BQ CRQC RA==,分别记二面角––D PR Q ,––D PQ R ,––D QR P 的平面角为α,β,γ,则( ).A .γαβ<<B .αγβ<<C .αβγ<<D .βγα<<26.解析 如图所示,设点D 在底面ABC 内的射影为O ,判断O 到PR ,PQ ,QR 的距离,O 到哪条线段的距离越小,对应的二面角就越大.显然有,αβ,γ均为锐角.1P 为三等分点,O 到1PQR △三边的距离相等.动态研究问题:1P P ®,所以O 到QR 的距离不变,O 到PQ 的距离减少,O 到PR 的距离变大.所以αγβ<<.1题型99 空间距离的计算——暂无题型100 与空间角、空间距离有关的开放性、探索性问题——暂无27.(2017全国3卷理科16)a ,b 为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在的直线与a ,b 都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论:①当直线AB 与a 成60角时,AB 与b 成30角; ②当直线AB 与a 成60角时,AB 与b 成60角; ③直线AB 与a 所成角的最小值为45; ④直线AB 与a 所成角的最小值为60;其中正确的是________.(填写所有正确结论的编号).27.解析 由题意知,a ,b ,AC 三条直线两两相互垂直,作出图像如图所示.不妨设图中 所示的正方体的边长为1,故1AC =,AB =AB 以直线AC 为旋转轴旋转,则点A 保持不变,点B 的运动轨迹是以C 为圆心,1为半径的圆.以C 为坐标原点,以CD 为x 轴 正方向,CB 为y 轴正方向,CA 为z 轴正方向,建立空间直角坐标系.则(1,0,0)D ,(0,0,1)A ,直线a 的方向单位向量(0,1,0)=a ,1=a .B 点起始坐标为(0,1,0) ,直线b 的方向单位向量(1,0,0)=b ,1=b .设B 点在运动过程中的坐标()cos ,sin ,0B θθ', 其中θ为B C '与CD 的夹角,[0,2π)θ∈.那么'AB 在运动过程中的向量(cos ,sin ,1)AB θθ'=-,2AB '= 设AB '与直线a 所成夹角为π0,2α⎡⎤∈⎢⎥⎣⎦,则(cos ,sin ,1)(0,1,0)cos 2AB θθαθ⎡-⋅==∈⎢'⎣⎦a , 所以ππ,42α⎡⎤∈⎢⎥⎣⎦,故③正确,④错误.设AB '与直线b 所成夹角为π[0,]2β∈,(cos ,sin ,1)(1,0,0)cos AB AB AB θθβθ'⋅-⋅==''b b b. 当AB '与直线a 夹角为60︒时,即π3α=, sin3πθα=. 因为22cos sin 1θθ+=,所以cos θ=.从而1cos 2βθ=. 因为π0,2β⎡⎤∈⎢⎥⎣⎦,所以π=3β,此时AB '与b 的夹角为60︒.所以②正确,①错误.故填② ③.28.(2017天津理17)如图所示,在三棱锥P ABC -中,PA ⊥底面ABC ,90BAC ∠=.点D E N ,,分别为棱PA ,PC ,BC 的中点,M 是线段AD 的中点,4PA AC ==,2AB =.(1)求证://MN 平面BDE ; (2)求二面角C EM N --的正弦值;(3)已知点H 在棱PA 上,且直线NH 与直线BE ,求线段AH 的长.NM ED BAP28.解析 如图所示,以A 为坐标原点,{},,AB AC AP 为基底,建立如图所示的空间直角坐标系,依题意可得(000)A ,,,(200)B ,,,(040)C ,,,(004)P ,,,(002)D ,,,(022)E ,,,(001)M ,,,(120)N ,,.(1)证明:()0,2,0DE =,()2,0,2DB =-.设(,,)x y z =n 为平面BDE 的一个法向量, 则0DE DB ⎧⋅=⎪⎨⋅=⎪⎩n n ,即20220y x z =⎧⎨-=⎩,不妨设1z =,可得(1,0,1)=n .又()1,2,1MN =-,可得0MN ⋅=n ,因为MN ⊄平面BDE ,所以//MN 平面BDE . (2)易知1(1,0,0)=n 为平面CEM 的一个法向量.设2(,,)x y z =n 为平面EMN 的一个法向量,则220EM MN ⎧⋅=⎪⎨⋅=⎪⎩n n ,因为(0,2,1)EM =--,(1,2,1)MN =-,所以2020y z x y z --=⎧⎨+-=⎩. 不妨设1y =,可得2(4,1,2)=--n .因此有121212cos ,|||⋅==n n n n |n n,于是12sin ,=n n . 所以二面角C EM N --. (3)依题意,设()04AH h h =剟,则H (0,0,h ),进而可得(1,2,)NH h =--,(2,2,2)BE =-.由已知得||cos ,||||NH BE NH BE NH BE h ⋅===2102180h h -+=, 解得85h =或12h =.所以线段AH 的长为85或12.题型101 立体几何中的最值问题探究与扩展——暂无。
全国高考数学试题分类汇编 理科逐题详解 立体几何
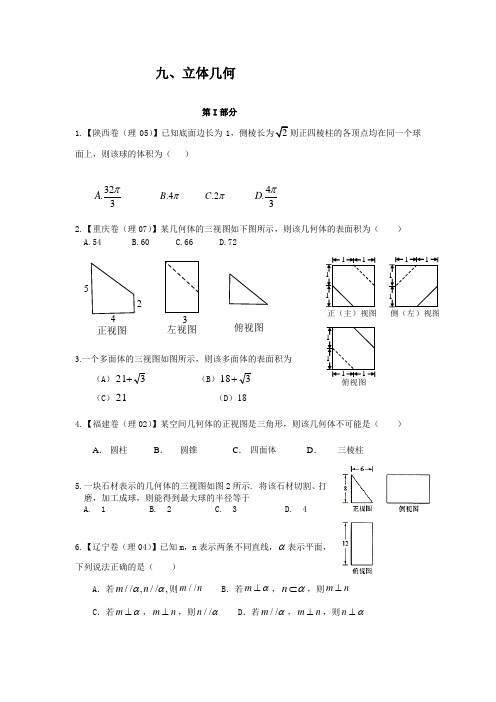
九、立体几何第I 部分1.【陕西卷(理05)】已知底面边长为1,侧棱长为2则正四棱柱的各顶点均在同一个球面上,则该球的体积为( )32.3A π .4B π .2C π 4.3D π2.【重庆卷(理07)】某几何体的三视图如下图所示,则该几何体的表面积为( ) A.54 B.60 C.66 D.723.一个多面体的三视图如图所示,则该多面体的表面积为(A )321+ (B )318+(C )21(D )184.【福建卷(理02)】某空间几何体的正视图是三角形,则该几何体不可能是( ) A . 圆柱 B . 圆锥 C . 四面体 D . 三棱柱5.一块石材表示的几何体的三视图如图2所示. 将该石材切割、打磨,加工成球,则能得到最大球的半径等于A. 1B. 2C. 3D. 46.【辽宁卷(理04)】已知m ,n 表示两条不同直线,α表示平面,下列说法正确的是( )A .若//,//,m n αα则//m nB .若m α⊥,n α⊂,则m n ⊥C .若m α⊥,m n ⊥,则//n αD .若//m α,m n ⊥,则n α⊥俯视图左视图正视图3245正(主)视图侧(左)视图俯视图1111111111117.【全国大纲卷(08)】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( ) A .814πB .16πC .9πD .274π8.【四川卷(理08)】如图,在正方体1111ABCD A B C D -中,点O 为线段BD 的中点。
设点P 在线段1CC 上,直线OP 与平面1A BD 所成的角为α,则sin α的取值范围是A .3[,1]3B .6[,1]3C .622[,]33D .22[,1]39.【辽宁卷(理07)】某几何体三视图如图所示,则该几何体的体积为( )A .82π-B .8π-C .82π-D .84π-10.【全国大纲卷(11)】已知二面角l αβ--为060,AB α⊂,AB l ⊥,A 为垂足,CD β⊂,C l ∈,0135ACD ∠=,则异面直线AB 与CD 所成角的余弦值为( )A .14 B .24 C .34 D .1211.【全国新课标Ⅰ(理12)】如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为A .62B .42C .6D .412.【全国新课标Ⅱ(理06)】如图,网格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( ) A. 1727 B. 59 C. 1027 D. 1313.【全国新课标Ⅱ(理11)】直三棱柱ABC-A 1B 1C 1中,∠BCA=90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC=CA=CC 1,则BM 与AN 所成的角的余弦值为( )A. 110B. 25C. 3010D.2214.【北京卷(理07)】在空间直角坐标系Oxyz 中,已知()2,0,0A ,()2,2,0B ,()0,2,0C ,()1,1,2D ,若 1S ,2S ,3S 分别表示三棱锥D ABC -在xOy ,yOz ,zOx 坐标平面上的正投影图形的面积,则( )(A )123S S S == (B )12S S =且 31S S ≠ (C )13S S =且 32S S ≠ (D )23S S =且 13S S ≠15.【广东卷(理07)】若空间中四条两两不同的直线1234,,,l l l l ,满足122334,,l l l l l l ⊥⊥⊥,则下列结论一定正确的是A.14l l ⊥B.14//l lC.14,l l 既不垂直也不平行D.14,l l 的位置关系不确定 16.【湖北卷(理05)】在如图所示的空间直角坐标系xyz O -中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为A.①和②B.③和①C. ④和③D.④和②17.【湖北卷(理08)】.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,另相乘也。
高考数学近三年真题立体几何(理科专用)

三年专题 立体几何(选择题、填空题)(理科专用)1.【2022年新高考1卷】南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5m 时,相应水面的面积为140.0km 2;水位为海拔157.5m 时,相应水面的面积为180.0km 2,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5m 上升到157.5m 时,增加的水量约为(√7≈2.65)( ) A .1.0×109m 3B .1.2×109m 3C .1.4×109m 3D .1.6×109m 32.【2022年新高考1卷】已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且3≤l ≤3√3,则该正四棱锥体积的取值范围是( ) A .[18,814]B .[274,814]C .[274,643]D .[18,27]3.【2022年新高考2卷】已知正三棱台的高为1,上、下底面边长分别为3√3和4√3,其顶点都在同一球面上,则该球的表面积为( ) A .100πB .128πC .144πD .192π4.【2021年甲卷理科】2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86(单位:m ),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A ,B ,C 三点,且A ,B ,C 在同一水平面上的投影,,A B C '''满足45A C B ∠'''=︒,60A B C ''∠'=︒.由C 点测得B 点的仰角为15︒,B B '与C C '的差为100;由B 点测得A 点的仰角为45︒,则A ,C 两点到水平面A B C '''的高度差A A C C ''- 1.732≈)( )A .346B .373C .446D .4735.【2021年甲卷理科】已如A ,B ,C 是半径为1的球O 的球面上的三个点,且,1A CBC A C B C ⊥==,则三棱锥O A B C-的体积为( )A 12B 12C 4D 46.【2021年新高考1的母线长为( )A .2B .C .4D .7.【2021年新高考2卷】正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )A .201+B .2C .563D 38.【2020年新课标1卷理科】埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A 4B 2C 4D 29.【2020年新课标1卷理科】已知,,A B C 为球O 的球面上的三个点,⊙1O 为A B C的外接圆,若⊙1O 的面积为4π,1A BB C A C O O ===,则球O 的表面积为( )A .64πB .48πC .36πD .32π10.【2020年新课标2卷理科】如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M ,在俯视图中对应的点为N ,则该端点在侧视图中对应的点为( )A .EB .FC .GD .H11.【2020年新课标2卷理科】已知△ABC 4的等边三角形,且其顶点都在球O的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( )AB .32C .1D 212.【2020年新课标3卷理科】下图为某几何体的三视图,则该几何体的表面积是( )A.B .C .D .13.【2020年新高考1卷(山东卷)】日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O ),地球上一点A 的纬度是指OA 与地球赤道所在平面所成角,点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷,若晷面与赤道所在平面平行,点A 处的纬度为北纬40°,则晷针与点A 处的水平面所成角为( )A .20°B .40°C .50°D .90°14.【2022年新高考1卷】已知正方体ABCD −A 1B 1C 1D 1,则( ) A .直线BC 1与DA 1所成的角为90° B .直线BC 1与CA 1所成的角为90° C .直线BC 1与平面BB 1D 1D 所成的角为45°D .直线BC 1与平面ABCD 所成的角为45°15.【2022年新高考2卷】如图,四边形ABCD 为正方形,ED ⊥平面ABCD ,FB ∥ED,AB =ED =2FB ,记三棱锥E −ACD ,F −ABC ,F −ACE 的体积分别为V 1,V 2,V 3,则( )A .V 3=2V 2B .V 3=V 1C .V 3=V 1+V 2D .2V 3=3V 116.【2021年新高考1卷】在正三棱柱111A B CA B C -中,11A BA A ==,点P 满足1B P BC B B λμ=+,其中[]0,1λ∈,[]0,1μ∈,则( )A .当1λ=时,1A B P△的周长为定值B .当1μ=时,三棱锥1P A B C-的体积为定值C .当12λ=时,有且仅有一个点P ,使得1AP B P⊥D .当12μ=时,有且仅有一个点P ,使得1AB ⊥平面1A BP17.【2021年新高考2卷】如图,在正方体中,O 为底面的中心,P 为所在棱的中点,M ,N 为正方体的顶点.则满足M NO P⊥的是( )A .B .C .D .18.【2020年新课标3卷理科】已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.19.【2020年新高考1卷(山东卷)】已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2,∠BAD=60°.以1D BCC 1B 1的交线长为________.20.【2020年新高考2卷(海南卷)】已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为BB1、AB的中点,则三棱锥A-NMD1的体积为____________三年专题立体几何(解答题)(理科专用)1.【2022年全国甲卷】在四棱锥P−ABCD中,PD⊥底面ABCD,CD∥AB,AD=DC=CB=1 ,AB=2,DP=√3.(1)证明:BD⊥PA;(2)求PD与平面PAB所成的角的正弦值.2.【2022年全国乙卷】如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC 的中点.(1)证明:平面BED⊥平面ACD;(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.3.【2022年新高考1卷】如图,直三棱柱ABC−A1B1C1的体积为4,△A1BC的面积为2√2.(1)求A 到平面A 1BC 的距离;(2)设D 为A 1C 的中点,AA 1=AB ,平面A 1BC ⊥平面ABB 1A 1,求二面角A −BD −C 的正弦值.4.【2022年新高考2卷】如图,PO 是三棱锥P −ABC 的高,PA =PB ,AB ⊥AC ,E 是PB 的中点.(1)证明:OE//平面PAC ;(2)若∠ABO =∠CBO =30°,PO =3,PA =5,求二面角C −AE −B 的正弦值. 5.【2021年甲卷理科】已知直三棱柱111A B C A B C -中,侧面11A AB B为正方形,2A BB C ==,E ,F 分别为A C 和1C C 的中点,D 为棱11AB 上的点.11B FA B ⊥(1)证明:B F D E⊥;(2)当1BD为何值时,面11B BC C与面D F E 所成的二面角的正弦值最小?6.【2021年乙卷理科】如图,四棱锥P A B C D==,P D D C-的底面是矩形,P D⊥底面A B C D,1M为B C的中点,且P B A M⊥.(1)求B C;(2)求二面角A P M B--的正弦值.7.【2021年新高考1卷】如图,在三棱锥A B C D-中,平面A B D⊥平面B C D,A B A D=,O为B D的中点.(1)证明:O A C D⊥;(2)若OCD是边长为1的等边三角形,点E在棱A D上,2--=,且二面角E B C DD E E A的大小为45︒,求三棱锥A B C D-的体积.8.【2021年新高考2卷】在四棱锥Q A B C D-中,底面A B C D是正方形,若====.A D Q D Q A Q C2,3(1)证明:平面Q A D ⊥平面A B C D ; (2)求二面角BQ D A--的平面角的余弦值.9.【2020年新课标1卷理科】如图,D 为圆锥的顶点,O 是圆锥底面的圆心,A E 为底面直径,A EA D=.A B C是底面的内接正三角形,P 为D O 上一点,6P OO=.(1)证明:P A ⊥平面P B C ;(2)求二面角BP C E--的余弦值.10.【2020年新课标2卷理科】如图,已知三棱柱ABC -A 1B 1C 1的底面是正三角形,侧面BB1C 1C是矩形,M ,N 分别为BC ,B 1C 1的中点,P 为AM 上一点,过B 1C 1和P 的平面交AB于E ,交AC 于F .(1)证明:AA 1∥MN ,且平面A 1AMN ⊥EB 1C 1F ;(2)设O 为△A 1B 1C 1的中心,若AO ∥平面EB 1C 1F ,且AO =AB ,求直线B 1E 与平面A 1AM N 所成角的正弦值.11.【2020年新课标3卷理科】如图,在长方体1111A B C D A B C D -中,点,E F 分别在棱11,D DB B 上,且12D EE D =,12B FF B =.(1)证明:点1C 在平面A E F 内;(2)若2A B=,1A D=,13A A=,求二面角1AE F A --的正弦值.12.【2020年新高考1卷(山东卷)】如图,四棱锥P -ABCD 的底面为正方形,PD ⊥底面A BCD .设平面P AD 与平面PBC 的交线为l .(1)证明:l ⊥平面PDC ;(2)已知PD =AD =1,Q 为l 上的点,求PB 与平面QCD 所成角的正弦值的最大值. 13.【2020年新高考2卷(海南卷)】如图,四棱锥P -ABCD 的底面为正方形,PD ⊥底面A BCD .设平面P AD 与平面PBC 的交线为l .(1)证明:l⊥平面PDC ;(2)已知PD =AD =1,Q 为l 上的点,QB ,求PB 与平面QCD 所成角的正弦值.。
高考数学立体几何分类汇编(理)

2011-2018新课标(理科)立体几何分类汇编一、选填题【2012新课标】(11)已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =;则此棱锥的体积为( )()A 26 ()B 36 ()C 23 ()D 22【2013新课标1】6、如图,有一个水平放置的透明无盖的正方体容器,容器高8cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚度,则球的体积为 ( )A 、500π3cm 3B 、866π3cm 312C 、1372π3cm 3D 、2048π3cm 3【2014新课标2】11. 直三棱柱ABC A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为( )A.110 B.25 C.3010 D.22 【2015新课标2】(9)已知A,B 是球O 的球面上两点,∠AOB=90,C 为该球面上的动点,若三棱锥O-ABC 体积的最大值为36,则球O 的表面积为( )A .36π B.64π C.144π D.256π【2016新课标1】(11)平面a 过正方体ABCD -A 1B 1C 1D 1的顶点A ,a //平面CB 1D 1,a ⋂平面ABCD =m ,a ⋂平面ABA 1B 1=n ,则m 、n 所成角的正弦值为( )(A)32 (B)22 (C)33 (D)13【2016新课标3】10. 在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球,若AB ⊥BC ,AB =6,BC =8,AA 13,则V 的最大值是( )(A )4π (B )9π2 (C )6π (D )32π3 【2017新课标1】16.如图,圆形纸片的圆心为O ,半径为5 cm ,该纸片上的等边三角形ABC 的中心为O 。
高考数学 立体几何试题分类汇编 理 试题
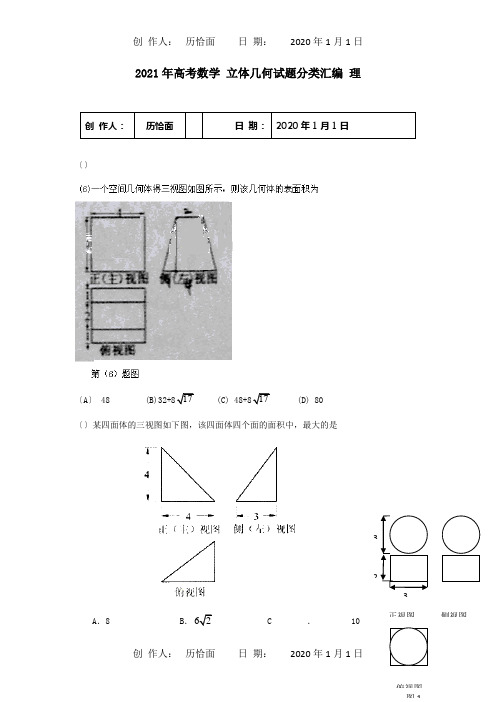
2021年高考数学立体几何试题分类汇编理创作人:历恰面日期:2020年1月1日〔〕〔A〕 48 (B)32+817 (C) 48+817 (D) 80〔〕某四面体的三视图如下图,该四面体四个面的面积中,最大的是A.8 B.62C.10 3正视图侧视图D .82〔〕设图一是某几何体的三视图,那么该几何体的体积为〔 〕 A .9122π+ B .9182π+ C .942π+ D .3618π+ 答案:B解析:有三视图可知该几何体是一个长方体和球构成的组合体,其体积3439+332=18322V ππ=⨯⨯+()。
〔〕如图l —3.某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,那么该几何体的体积为A.63B.93C.123D.183〔〕321,,ααα是三个互相平行的平面,平面21,αα之间的间隔 为1d ,平面32,αα之间的间隔 为2d .直线l 与321,,ααα分别交于321,,P P P .那么”“3221P P P P =是”“21d d =的 ( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 答案:C解析:平面321,,ααα平行,由图可以得知:假如平面间隔 相等,根据两个三角形全等可知3221P P P P =假如3221P P P P =,同样是根据两个三角形全等可知21d d =〔〕如图,四棱锥S —ABCD 的底面为正方形,SD ⊥底面ABCD ,那么以下结论中不正确的选.....项是.. A .AC ⊥SBB .AB ∥平面SCDC .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D .AB 与SC 所成的角等于DC 与SA 所成的角〔〕球的直径SC =4,A ,B 是该球球面上的两点,AB =3, 30=∠=∠BSC ASC ,那么棱锥S —ABC 的体积为A .33B .32C .3D .1〔全国2〕直二面角l αβ--,点,A AC l α∈⊥,C 为垂足,,,B BD l D β∈⊥为垂足.假设AB=2,AC=BD=1,那么D 到平面ABC 的间隔 等于(A)23 (B)33 (C)63(D) 1 【思路点拨】此题关键是找出或者做出点D 到平面ABC 的间隔 DE ,根据面面垂直的性质不难证明AC ⊥平面β,进而β⊥平面平面ABC,所以过D 作DE BC ⊥于E ,那么DE 就是要求的间隔 。
高考数学立体几何分类汇编(理)

新课标(理科)立体几何分类汇编一、选填题【2012新课标】(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( B ) ()A 6 ()B 9 ()C 12 ()D 18 【解析】选B 。
该几何体是三棱锥,底面是俯视图,高为3,此几何体的体积为11633932V =⨯⨯⨯⨯=【2012新课标】(11)已知三棱锥S ABC -的所有顶点都在球O的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =;则此棱锥的体积为( A )()A 26 ()B 36 ()C 23 ()D 22【解析】ABC ∆的外接圆的半径33r =,点O 到面ABC 的距离2263d R r =-=,SC 为球O 的直径⇒点S 到面ABC 的距离为2623d =此棱锥的体积为113262233436ABC V S d ∆=⨯=⨯⨯=另:13236ABC V S R ∆<⨯=排除,,B C D【2013新课标1】6、如图,有一个水平放置的透明无盖的正方体容器,容器高8cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚度,则球的体积为 ( A )A 、500π3cm 3B 、866π3cm 312C 、1372π3cm 3D 、2048π3cm 3【解析】设球的半径为R ,则由题知球被正方体上面截得圆的半径为4,球心到截面圆的距离为R-2,则222(2)4R R =-+,解得R=5,∴球的体积为3453π⨯=500π33cm ,故选A.【2013新课标1】8、某几何函数的三视图如图所示,则该几何的体积为( A )A 、16+8πB 、8+8πC 、16+16πD 、8+16π 【解析】由三视图知,该几何体为放到的半个圆柱底面半径为2 高为4,上边放一个长为4宽为2高为2长方体,故其体积为21244222π⨯⨯+⨯⨯ =168π+,故选A .【2013新课标2】4. 已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足l ⊥m ,l ⊥n ,l α,lβ,则( D ).A .α∥β且l ∥αB .α⊥β且l ⊥βC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l 【解析】因为m ⊥α,l ⊥m ,lα,所以l ∥α.同理可得l ∥β。
高考数学(理)真题专题汇编:空间立体几何

高考数学(理)真题专题汇编:空间立体几何一、选择题(本题共9道小题,每小题0分,共0分)1.【来源】2019年高考真题——数学(浙江卷)设三棱锥V -ABC 的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点),记直线PB 与直线AC 所成角为α,直线PB 与平面ABC 所成角为β,二面角P -AC -B 的平面角为γ,则( )A. ,βγαγ<<B. ,βαβγ<<C. ,βαγα<<D. ,αβγβ<<2.【来源】2019年高考真题——数学(浙江卷)祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V Sh =柱体,其中S 是柱体的底面积,h 是柱体的高,若某柱体的三视图如图所示,则该柱体的体积(cm 3)是( )A. 158B. 162C. 182D. 3243.【来源】2019年高考真题——理科数学(全国卷Ⅱ) 设α,β为两个平面,则α∥β的充要条件是 A .α内有无数条直线与β平行 B .α内有两条相交直线与β平行 C .α,β平行于同一条直线D .α,β垂直于同一平面4.【来源】2019年高考真题——理科数学(全国卷Ⅲ)如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED的中点,则A.BM=EN,且直线BM、EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM、EN是异面直线D.BM≠EN,且直线BM,EN是异面直线5.【来源】0(08年全国卷2)已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于()A.1 B. C. D.26.【来源】0(08年四川卷文)若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为的菱形,则该棱柱的体积等于( )(A)(B)(C)(D)7.【来源】0(08年北京卷)如图,动点在正方体的对角线上.过点作垂直于平面的直线,与正方体表面相交于.设,,则函数的图象大致是()8.【来源】2011年高考数学理(安徽)一个空间几何体得三视图如图所示,则该几何体的表面积为(A)48+(B)32817+(C)48817(D)509.【来源】2011年高考数学理(全国新课标)在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为二、填空题10.【来源】2019年高考真题——理科数学(北京卷)已知l,m是平面α外的两条不同直线.给出下列三个论断:①l⊥m;②m∥α;③l⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:__________.某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.12.【来源】2019年高考真题——理科数学(天津卷)已知四棱锥的底面是边长为2的正方形,侧棱长均为5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为 .13.【来源】2019年高考真题——理科数学(全国卷Ⅱ)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.(本题第一空2分,第二空3分.)学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体ABCD -A 1B 1C 1D 1挖去四棱锥O -EFGH 后所得几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,16cm 4cm AB =BC =, AA =,3D 打印所用原料密度为0.9 g/cm 3,不考虑打印损耗,制作该模型所需原料的质量为___________.15.【来源】(07年浙江卷文)已知点O 在二面角α-AB -β的棱上,点P 在α内,且∠POB =45°.若对于β内异于O 的任意一点Q ,都有∠POQ ≥45°,则二面角α-AB -β的取值范围是_________.16.【来源】2011年高考数学理(全国新课标)已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且6,23AB BC ==,则棱锥O ABCD -的体积为 。
高考数学试题分类汇编立体几何理

立体几何一、选择题1、(2016年北京高考)某三棱锥的三视图如图所示,则该三棱锥的体积为( )A.16 B.13 C.12D.1 【答案】A2、(2016年山东高考)有一个半球和四棱锥组成的几何体,其三 视图如右图所示,则该几何体的体积为(A )π32+31 (B )π32+31 (C )π62+31 (D )π62+1【答案】C3、(2016年全国I 高考)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是(A )17π (B )18π (C )20π (D )28π【答案】A4、(2016年全国I 高考)平面α过正方体ABCD -A 1B 1C 1D 1的顶点A ,α//平面CB 1D 1,αI 平面ABCD =m ,αI 平面ABB 1 A 1=n ,则m ,n 所成角的正弦值为(A (B )2 (C (D )13【答案】A5、(2016年全国II 高考)右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A )20π (B )24π (C )28π (D )32π 【答案】C6、(2016年全国III 高考)如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为(A )18+(B )54+(C )90 (D )81 【答案】B7、(2016年全国III 高考)在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,13AA =,则V 的最大值是(A )4π (B )92π(C )6π (D )323π【答案】B二、填空题1、(2016年上海高考)如图,在正四棱柱1111D C B A ABCD -中,底面ABCD 的边长为3,1BD 与底面所成角的大小为32arctan,则该正四棱柱的高等于____________【答案】2、(2016年四川高考)已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是__________.3、(2016年天津高考)已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位:m ),则该四棱锥的体积为_______m 3.【答案】24、(2016年全国II 高考) ,αβ是两个平面,,m n 是两条直线,有下列四个命题: (1)如果,,//m n m n αβ⊥⊥,那么αβ⊥.[ (2)如果,//m n αα⊥,那么m n ⊥. (3)如果//,m αβα⊂,那么//m β.(4)如果//,//m n αβ,那么m 与α所成的角和n 与β所成的角相等. 其中正确的命题有 ..(填写所有正确命题的编号) 【答案】②③④5、(2016年浙江高考)某几何体的三视图如图所示(单位:cm ),则该几何体的表面积是 cm 2,体积是 cm 3.【答案】72 32 6、(2016年浙江高考)如图,在△ABC 中,AB =BC =2,∠ABC =120°.若平面ABC 外的点P 和线段AC 上的点D ,满足PD =DA ,PB =BA ,则四面体PBCD 的体积的最大值是 .【答案】12三、解答题1、(2016年北京高考) 如图,在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,AB AD ⊥,1AB =,2AD =,AC CD =(1)求证:PD ⊥平面PAB ;(2)求直线PB 与平面PCD 所成角的正弦值;(3)在棱PA 上是否存在点M ,使得//BM 平面PCD ?若存在,求AMAP的值;若不存在,说明理由.【解】⑴∵面PAD 面ABCD AD =面PAD ⊥面ABCD∵AB ⊥AD ,AB ⊂面ABCD ∴AB ⊥面PAD ∵PD ⊂面PAD ∴AB ⊥PD 又PD ⊥PA ∴PD ⊥面PAB⑵取AD 中点为O ,连结CO ,PO∵CD AC ==∴CO ⊥AD ∵PA PD = ∴PO ⊥AD以O 为原点,如图建系易知(001)P ,,,(110)B ,,,(010)D -,,,(200)C ,,,则(111)PB =-,,,(011)PD =--,,,(201)PC =-,,,(210)CD =--,, 设n 为面PDC 的法向量,令00(,1)n x y =,011,120n PD n n PC ⎧⋅=⎪⎛⎫⇒=-⎨⎪⎝⎭⋅=⎪⎩,,则PB 与面PCD 夹角θ有sin cos ,1n PB n PB n PBθ⋅=<>==⑶假设存在M 点使得BM ∥面PCD设AM APλ=,()0,','M y z由(2)知()0,1,0A ,()0,0,1P ,()0,1,1AP =-,()1,1,0B ,()0,'1,'AM y z =-有()0,1,AM AP M λλλ=⇒- ∴()1,,BM λλ=--∵BM ∥面PCD ,n 为PCD 的法向量 ∴0BM n ⋅=即102λλ-++=∴1=4λ∴综上,存在M 点,即当14AM AP =时,M 点即为所求.2、(2016年山东高考)在如图所示的圆台中,AC 是下底面圆O 的直径,EF 是上底面圆O '的Ox yz PABC D直径,FB 是圆台的一条母线.(I )已知G ,H 分别为EC ,FB 的中点,求证:GH ∥平面ABC ; (II )已知EF =FB =12AC=,AB =BC .求二面角F BC A --的余弦值.【解】(Ⅰ)连结FC ,取FC 的中点M ,连结HM GM,, 因为GM//EF ,EF 在上底面内,GM 不在上底面内, 所以GM//上底面,所以GM//平面ABC ; 又因为MH//BC ,⊂BC 平面ABC ,⊄MH 平面ABC ,所以MH//平面ABC ; 所以平面GHM//平面ABC ,由⊂GH 平面GHM ,所以GH//平面ABC . (Ⅱ) 连结OB ,BC AB = OB A ⊥∴O以为O 原点,分别以O O OB,OA,'为z y,x,轴, 建立空间直角坐标系.BC AB ,32AC 21FB EF ==== ,3)(22=--='FO BO BF O O ,于是有)0,0,3A(2,)0,0,3C(-2,)0,3B(0,2,)3,3F(0,, 可得平面FBC 中的向量)3,(30,-BF =,)0,,(3232CB =, 于是得平面FBC 的一个法向量为)1,3,3(1-=n , 又平面ABC 的一个法向量为)1,0,0(2=n , 设二面角A -BC -F 为θ,B则7771cos ===θ. 二面角A -BC -F 的余弦值为77.3、(2016年上海高考)将边长为1的正方形11AAOO (及其内部)绕的1OO 旋转一周形成圆柱,如图,AC 长为2π,11A B 长为3π,其中1B 与C 在平面11AAOO 的同侧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何
1.【2018年浙江卷】已知四棱锥S-ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S-AB-C的平面角为θ3,则
A. θ1≤θ2≤θ3
B. θ3≤θ2≤θ1
C. θ1≤θ3≤θ2
D. θ2≤θ3≤θ1
【答案】 D
从而因为,所以即,选 D.
点睛:线线角找平行,线面角找垂直,面面角找垂面.
2.【2018年浙江卷】某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是
A. 2
B. 4
C. 6
D. 8
【答案】 C
【解析】分析:先还原几何体为一直四棱柱,再根据柱体体积公式求结果.
详解:根据三视图可得几何体为一个直四棱柱,高为2,底面为直角梯形,上下底分别为1,2,梯形的高
为2,因此几何体的体积为选C.
点睛:先由几何体的三视图还原几何体的形状,再在具体几何体中求体积或表面积等.
3.【2018年理新课标I卷】已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为
A. B. C. D.
【答案】 A
详解:根据相互平行的直线与平面所成的角是相等的,所以在正方体中,平面与线所成的角是相等的,所以平面与正方体的每条棱所在的直线所成角都是相等的,同理平面也满足与正方体的每条棱所在的直线所成角都是相等,要求截面面积最大,则截面的位置为夹在两
个面与中间的,且过棱的中点的正六边形,且边长为,所以其面积为,故选 A.
点睛:该题考查的是有关平面被正方体所截得的截面多边形的面积问题,首要任务是需要先确定截面的位
置,之后需要从题的条件中找寻相关的字眼,从而得到其为过六条棱的中点的正六边形,利用六边形的面
积的求法,应用相关的公式求得结果.+
4.【2018年理新课标I卷】某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点在正视图上的对应点为,圆柱表面上的点在左视图上的对应点为,则在此圆柱侧面上,从到的路径中,最
短路径的长度为
A. B.
C. D. 2
【答案】 B
【解析】分析:首先根据题中所给的三视图,得到点M和点N在圆柱上所处的位置,点M在上底面上,点N 在下底面上,并且将圆柱的侧面展开图平铺,点M、N在其四分之一的矩形的对角线的端点处,根据平面上
两点间直线段最短,利用勾股定理,求得结果.
详解:根据圆柱的三视图以及其本身的特征,可以确定点M和点N分别在以圆柱的高为长方形的宽,圆柱
底面圆周长的四分之一为长的长方形的对角线的端点处,所以所求的最短路径的长度为,故
选B.
点睛:该题考查的是有关几何体的表面上两点之间的最短距离的求解问题,在解题的过程中,需要明确两
个点在几何体上所处的位置,再利用平面上两点间直线段最短,所以处理方法就是将面切开平铺,利用平
面图形的相关特征求得结果.
5.【2018年全国卷Ⅲ理】设是同一个半径为4的球的球面上四点,为等边三角形且其
面积为,则三棱锥体积的最大值为
A. B. C. D.
【答案】 B
详解:如图所示,点M为三角形ABC的重心,E为AC中点,当平面时,三棱锥体积最大,此时,,,,点M为三角形ABC的重心,,中,有,,
,故选 B.
点睛:本题主要考查三棱锥的外接球,考查了勾股定理,三角形的面积公式和三棱锥的体积公式,判断出
当平面时,三棱锥体积最大很关键,由M为三角形ABC的重心,计算得到,再由勾股定理得到OM,进而得到结果,属于较难题型。
6.【2018年理数全国卷II】在长方体中,,,则异面直线与所成角的余弦值为
A. B. C. D.
【答案】 C。
