北师大版数学八年级下册第三次月考试题
初二数学下册第三次月考试卷(带答案)

初二数学下册第三次月考试卷(带答案)学校:___________班级:___________姓名:___________考号:___________【不等关系、不等式的基本性质与不等式的解集(100分)】1.(5分)用不等号填空:(1)-π__________-3;(2)x2__________0;(3)|x|+|y|__________|x+y|;(4)(-5)÷(-1)__________(-6)÷(-7);(5)当a__________0时,|a|=-a.2.(3分)若a>b,则下列不等式变形正确..的是()A.ac2>bc2B.ab>1 C.-ca>-cb D.3a-c>3b-c3.(3分)下列不等式变形中,一定正确....的是()A.若ac>bc,则a>bB.若a>b,则am2>bm2C.若ac2>bc2,则a>bD.若m>n,则-m2>-n24.(3分)若关于x的不等式mx+1>0的解集为x<15,则关于x的不等式(m-1)x>-1-m的解集为_______________.5.(8分)若|x-4|+(5x-y-m)2=0,求当y≥0时,m的取值范围.6.(6分)已知x=3是不等式mx+2<1-4m的一个解,如果m是整数,求m的最大值.7.(7分)若不等式2x<4的解都能使不等式x-a<5成立,求a的取值范围.8.(3分)实数a,b,c满足a<b<0<c,则下列式子中正确..的是()A.ac>bcB.|a-b|=a-bC.-a<-b<cD.-a-c>-b-c9.(3分)在△ABC中,若AB=8,BC=6,则第三边AC的长度m的取值范围是__________;若m的值为偶数,则m=______________________________. 10.(3分)若实数a是不等式2x-1>5的解,但实数b不是不等式2x-1>5的解,则下列选项中,正确..的是()A.a<bB.a>bC.a≤bD.a≥b11.(6分)若不等式a(x-1)>x+1-2a的解集为x<-1,求a的取值范围.12.(7分)已知不等式3x-a≤0的正整数解有3个:1,2,3,求a的取值范围.13.(7分)题目:2x+13-x+52≥______已知这道题的正确答案是x≥7,且“______”是一个常数项,请求出“______”中的数.14.(4分)若关于x的不等式|x-2|+|x+3|≥a对于x取任何值都成立,请直接写出a的取值范围.15.(7分)(1)比较a2+b2与2ab的大小关系:①当a=3,b=5时,a2+b2__________2ab;②当a=-3,b=5时,a2+b2__________2ab;③当a=b=1时,a2+b2__________2ab.(2)根据上述结果请你猜想a2+b2与2ab的大小关系:__________ 并进行验证.16.(7分)已知关于x的不等式ax+2x<2a+4.(1)当a=1时,求该不等式的解集;(2)a取何值时,该不等式有解?并求出解集.17.(每题3分,共18分)解下列不等式:(1)2(x-3)<3(x-1);(2)2y3-1<y4+4;(3)5(x-2)+8<6(x-1)+7;(4)2x-13-3x-12<1;(5)x-x-12≤2-x+23;(6)x-3(x-3)<3[x-2(x-2)].【一元一次方程、不等式的应用(20分)】18.[一元一次不等式](8分)矿山爆破时,为了确保安全,点燃引火线后,人要在爆破前转移到300m以外的安全地区.引火线燃烧的速度是0.8cm/s,人离开的速度是5m/s,问:引火线的长度至少应为多少cm?19.[一元一次方程](8分)上海浦东机场(PVG)到新加坡樟宜机场(SIN)的直线距离约为5000km,一架波音式飞机的速度约为800km/h;一架普通飞机的速度约为500km/h.两架飞机都从上海飞往新加坡.普通飞机航班先出发,3h后,波音式飞机航班出发,问:波音式飞机什么时候追上普通飞机,这时离新加坡樟宜机场还有多远?20.(4分)现有若干本连环画册分给小朋友,如果每人分8本,那么不够分,现在如果每人分7本,还多10本,则小朋友人数最少有()A.7人B.8人C.10人D.11人参考答案阅卷提示:提供的答案除选择题和填空题外,不一定都是唯一正确的,对于那些与此答案不同的答案正确的同样给分.评分标准只是根据一种思路与方法给出的,在阅卷时会出现各种不同情况,可根据本评分标准的精神制定出具体的方案,但不要与评分标准有太大的偏离.【不等关系、不等式的基本性质与不等式的解集(100分)】1.(1)<;(2)≥;(3)≥;(4)>;(5)≤.(每空1分,共5分)2.D(3分)3.C(3分).(3分)4.x<-235.m≤20.(8分)6.-1.(6分)7.a≥-3.(7分)8.D(3分)9.2<m<14;(2分) 4或6或8或10或12. (1分)10.B(3分)11.a<1.(6分)12.9≤a<12.(7分)13.“______”中的数为-1.(7分)14.a≤5.(4分)15.(1)①>;②>;③=.(每空1分,共3分)(2)a2+b2≥2ab,(1分)证明过程略.(3分)16.(1)x<2;(2分)(2)当x≠-2时有解;(1分)解集:x<2或x>2(每个解集2分,共4分)17.(1)x>3;(2)y≤12;(3)x>3;(4)x>-1;(5)x≤1;(6)x<3. (每题3分,共18分)【一元一次方程、不等式的应用(20分)】18.48cm.(8分)19.5h后追上(5分),距新加坡还有1000km.(3分)20.D(4分)。
2021年(北师大版)八年级下学期第三次月考数学试题卷及答案
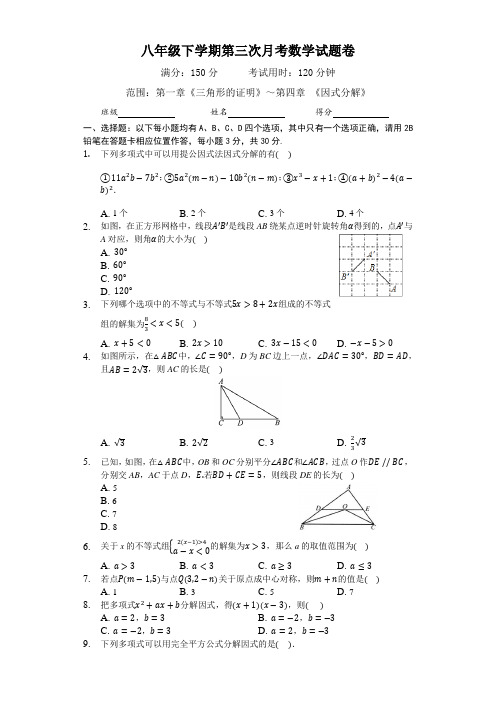
八年级下学期第三次月考数学试题卷满分:150分考试用时:120分钟范围:第一章《三角形的证明》~第四章《因式分解》班级姓名得分一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B 铅笔在答题卡相应位置作答,每小题3分,共30分.1.下列多项式中可以用提公因式法因式分解的有()①11a2b−7b2;②5a2(m−n)−10b2(n−m);③x3−x+1;④(a+b)2−4(a−b)2.A. 1个B. 2个C. 3个D. 4个2.如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为()A. 30°B. 60°C. 90°D. 120°3.下列哪个选项中的不等式与不等式5x>8+2x组成的不等式<x<5()组的解集为83A. x+5<0B. 2x>10C. 3x−15<0D. −x−5>04.如图所示,在△ABC中,∠C=90°,D为BC边上一点,∠DAC=30°,BD=AD,且AB=2√3,则AC的长是()A. √3B. 2√2C. 3D. 2√335.已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过点O作DE//BC,分别交AB,AC于点D,E.若BD+CE=5,则线段DE的长为()A. 5B. 6C. 7D. 82(x−1)>4的解集为x>3,那么a的取值范围为()6.关于x的不等式组{a−x<0A. a>3B. a<3C. a≥3D. a≤37.若点P(m−1,5)与点Q(3,2−n)关于原点成中心对称,则m+n的值是()A. 1B. 3C. 5D. 78.把多项式x2+ax+b分解因式,得(x+1)(x−3),则()A. a=2,b=3B. a=−2,b=−3C. a=−2,b=3D. a=2,b=−39.下列多项式可以用完全平方公式分解因式的是().A. 9p2−4q2B. a2+2ab−b2C. 9m2−24m+16D. −x2−4xy+4y210.如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连结HN.则在点M运动过程中,线段HN长度的最小值是()A. 6B. 3C. 2D. 1.5二、填空题(本大题共5小题,共20.0分)11.如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动.如果点P,Q同时出发,用t(s)表示移动的时间,当t=时,△POQ是等腰三角形.12.不等式组{x+1>0a−13x<0的解集是x>−1,则a的取值范围是______.13.已知点A(1,−2),B(−1,2),E(2,a),F(b,3),若将线段AB平移至EF,点A,E为对应点,则a+b的值为________.14.边长为a,b的长方形的周长为12,面积为10,则a2b+ab2的值为.15.为迎接建国70周年,某商店购进A,B,C三种纪念品共若干件,且A,B,C三种纪念品的数量之比为8:7:9.一段时间后,根据销售情况,补充三种纪念品后,库存总数量比第一次多200件,且A,B,C三种纪念品的比例为9:10:10.又一段时间后,根据销售情况,再次补充三种纪念品,库存总数量比第二次多170件,且A,B,C三种纪念品的比例为7:6:6.已知第一次三种纪念品总数量不超过1000件,则第一次购进A种纪念品______件.三、解答题(本大题共10小题,共100.0分)16.(8分)解不等式:x6−1>x−23,并把它的解集在数轴上表示出来.17.(10分)如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且∠ABD=∠ACD,∠EAD=∠BAC(1)求证:AE=AD;(2)若∠ACB=65°,求∠BDC的度数.18.(10分)在ABC中,CA=CB,∠ACB=90°.点P是平面内不与点A、C重合的任意一点,连接AP,将线段AP绕点P逆时针旋转90°得到线段DP,连接AD,BD,CP.(1)如图1,求BDCP的值及直线BD与直线CP相交所成的较小角的度数;(2)如图2,若点E、F分别是CA、CB的中点,点P在直线EF上,当点C,P,D在同一直线上时,求ADCP的值.19.(10分)(1)解不等式组:{x−3(x−1)>5x−35−1≤x+12(2)因式分解3x3−12x2y+12xy220.(8分)如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“和谐数”.如4=22−02,12=42−22,20=62−42,因此,4,12,20都是“和谐数”.36和2020这两个数是“和谐数”吗?为什么?21.(10分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和格点O.(1)平移△ABC,使得点A与点O重合,画出平移后的△A′B′C′;(2)画出△ABC关于点O成中心对称的△DEF;(3)判断△A′B′C′与△DEF是否成中心对称.22.(10分)我国沪深股市交易中,如果买、卖一次股票均需付交易金额的0.5%作费用.张先生以每股5元的价格买入“西昌电力”股票1000股,若他期望获利不低于1000元,问他至少要等到该股票涨到每股多少元时才能卖出?(精确到0.01元)23.(10分)如图,已知在等腰三角形ABC中,AB=AC,∠BAC=80°,AD⊥BC,AD=AB,连接BD并延长,交AC的延长线于点E,求∠E的度数.24.(12分)阅读理解应用待定系数法:设某一多项式的全部或部分系数为未知数、利用当两个多项式为恒等式时,同类项系数相等的原理确定这些系数,从而得到待求的值.待定系数法可以应用到因式分解中,例如问题:因式分解:x3−1.因为x3−1为三次多项式,若能因式分解,则可以分解成一个一次多项式和一个二次多项式的乘积.所以我们可以猜想x3−1可以分解成(x−1)(x2+ax+b),展开等式右边得:x3+ (a−1)x2+(b−a)x−b,根据待定系数法原理,等式两边多项式的同类项的对应系数相等:a−1=0,b−a=0,−b=−1,从而可以求出a=1,b=1.所以x3−1=(x−1)(x2+x+1).(1)若x取任意值,等式x2+5x+3=x2+(2−a)x+3恒成立,则a=____;(2)已知多项式x3+2x+12有因式x+2,请用待定系数法求出该多项式的另一因式;(3)请判断多项式x4+x2+1是否能分解成两个整系数二次多项式的乘积,如果能分解,请求出分解结果;如果不能分解,请说明理由.25.(12分)如图,在四边形ABCD中,AD//BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.已知AD=2cm,BC=5cm.(1)求证:FC=AD;(2)求AB的长.答案1.B2.C3.C4.A5.A6.D7.C8.B9.C10.B11.103或1012.a≤−1313.−114.6015.32016.解:x<−2.解集在数轴上表示略.17.证明:(1)∵∠BAC=∠EAD∴∠BAC−∠EAC=∠EAD−∠EAC即:∠BAE=∠CAD在△ABE和△ACD中{∠ABE=∠ACD AB=AC∠BAE=∠CAD,∴△ABE≌△ACD(ASA),∴AE=AD;(2)解:∵∠ACB=65°,AB=AC,∴∠ABC=∠ACB=65°,∴∠BAC=180°−∠ABC−∠ACB=180°−65°−65°=50°,∵∠ABD=∠ACD,∠AOB=∠COD,∴∠BDC=∠BAC=50°.18.解:(1)如图1中,设BD交AC于点O,BD交PC于点E.∵∠PAD=∠CAB=45°,∴∠PAC=∠DAB,∵ABAC =ADAP=√2,∴△DAB∽△PAC,∴∠PCA=∠DBA,BDPC =ABAC=√2,∵∠EOC=∠AOB,∴∠CEO=∠OAB=45°,∴直线BD与直线CP相交所成的较小角的度数为45°.(2)如图2中,当点D在线段PC上时,延长AD交BC的延长线于H.∵CE=EA,CF=FB,∴EF//AB,∴∠EFC=∠ABC=45°,∵∠PAO=45°,∴∠PAO=∠OFH,∵∠POA=∠FOH,∴∠H=∠APO,∵∠APC=90°,EA=EC,∴PE=EA=EC,∴∠EPA=∠EAP=∠BAH,∴∠H=∠BAH,∴BH=BA,∵∠ADP=∠BDC=45°,∴∠ADB=90°,∴BD⊥AH,∴∠DBA=∠DBC=22.5°,∵∠ADB=∠ACB=90°,∴A,D,C,B四点共圆,∠DAC=∠DBC=22.5°,∠DCA=∠ABD=22.5°,∴∠DAC=∠DCA=22.5°,∴DA=DC,设AD=a,则DC=AD=a,PD=√22a,∴ADCP =aa+√22a=2−√2.如图3中,当点P在线段CD上时,同法可证:DA=DC,设AD=a,则CD=AD=a,PD=√22a,∴PC=a−√22a,∴ADPC =a−√22a=2+√2.19.解:(1)解:{x−3(x−1)>5①x−35−1≤x+12②解①得x<−1,解②得x≥−7,则该不等式组的解集为:−7≤x<1.(2)3x3−12x2y+12xy2=3x(x2−4xy+4y2)=3x(x−2y)220.解:36和2020都是和谐数.理由如下:设a=(n+2)2−n2=(n+2−n)(n+2+n)=2(2n+2)=4(n+1),令36=4(n+1),解得n=8.∴36=102−82.同理:令2020=4(n+1),解得n=504.∴2020=5062−5042.21.解:(1)如图,△A′B′C′即为所求作.(2)如图,△DEF即为所求作.(3)△A′B′C′与△DEF成中心对称,对称中心是线段A′D与线段FC′的交点.22.解:设涨到每股x元时卖出,根据题意得1000x−(5000+1000x)×0.5%≥5000+1000,解这个不等式得x≥1205,199即x≥6.06.答:至少涨到每股6.06元时才能卖出.23.解:∠E=30°.24.解:(1)−3;(2)设另一个因式为(x2+ax+b),(x+2)(x2+ax+b)=x3+(a+2)x2+(2a+b)x+2b=x3+2x+12∴a+2=0,2b=12,∴a=−2,b=6,∴多项式的另一因式为x2−2x+6;(3)多项式x4+x2+1能分解成两个整系数二次多项式的乘积.设多项式x4+x2+1能分解成①(x2+1)(x2+ax+b)或②(x2+x+1)(x2+ax+1),①(x2+1)(x2+ax+b)=x4+ax3+bx2+x2+ax+b=x4+ax3+(b+1)x2+ax+b∴a=0,b+1=1由b+1=1得b=0≠1∴舍去②(x2+x+1)(x2+ax+1)=x4+(a+1)x3+(a+2)x2+(a+1)x+1∴a+1=0,a+2=1,解得a=−1.即x4+x2+1=(x2+x+1)(x2−x+1);∴x4+x2+1能分解成两个整系数二次三项式的乘积.25.证明:(1)∵AD//BC(已知),∴∠ADC=∠ECF(两直线平行,内错角相等),∵E是CD的中点(已知),∴DE=EC(中点的定义).∵在△ADE与△FCE中,{∠ADC=∠ECFDE=EC∠AED=∠CEF,∴△ADE≌△FCE(ASA),∴FC=AD;(2)∵△ADE≌△FCE,∴AE=EF,AD=CF,∴BE是线段AF的垂直平分线,∴AB=BF=BC+CF,∵AD=CF,AD=2cm,BC=5cm.∴AB=BC+AD=2+5=7(cm).。
20xx-20xx学年北师大八年级下月考数学试卷(3月)含答案解析.doc

2015-2016 学年北师大八年级下月考数学试卷(3 月) 含答案解析2015-2016 学年四川省成都七中育才学校八年级(下)月考数学试卷(3 月份)一、选择题:1.下列标志既是轴对称图形又是中心对称图形的是()A.B.C.D.2.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是()A.,,B.1,,C.6, 7,8 D.2, 3,43.如图,△ ABC 与△ A′ B′关C于′ O 成中心对称,下列结论中不成立的是()A . OC=OC′B .OA=OA′C. BC=B′ C′D .∠ ABC= ∠ A′ C′ B′4.无论 x 取何值,下列不等式总是成立的是()A . x+5> 0B .x+5 < 0 C.﹣( x+5)2< 0D.( x+5)2≥05.如图,△ ABC 中 BD 、 CD 平分∠ ABC 、∠ ACB 过 D 作直线平行于BC,交 AB 、 AC 于E、 F,当∠ A 的位置及大小变化时,线段EF 和 BE+CF 的大小关系是()A . EF=BE+CF B. EF> BE+CF C. EF< BE+CF D.不能确定6.关于 x 的不等式组的解集为x>1,则 a 的取值范围是()A . a> 1B . a< 1 C. a≥1D. a≤17.给出四个命题:①若 a> b,c=d,则 ac>bd;②若 ac> bc,则 a> b;2 2③若 a> b,则 ac > bc ;正确的有()A.1个 B.2个 C.3个 D.4个8.某商品原价 5 元,如果跌价x% 后,仍不低于 4 元,那么()A . x≤ 20B. x< 20C. x≥ 20D .x> 209.如图,△ABC 中, AB=AC .∠ A=36°, AB 的中垂线 DE 交 AC 于 D ,交 AB 于 E,下述结论:( 1) BD 平分∠ABC ;( 2) AD=BD=BC ;( 3)△ BDC 的周长等于 AB+BC ;( 4)D 是 AC 中点.其中正确的是()A .①② B.①②③C.②③④D.①②③④10.如图,已知 ? ABCD 中,AE ⊥BC 于点 E,以点 B 为中心,取旋转角等于∠ABC ,把△ BAE 顺时针旋转,得到△BA′E′,连接 DA′.若∠ADC=60°,∠ ADA′=50°,则∠ DA′E′的大小为()A . 130 °B. 150 °C. 160 °D. 170 °二、填空题:11.不等式( a﹣b) x> a﹣b 的解集是x< 1,则 a 与 b 的大小关系是.12.将一箱苹果分给若干位小朋友,若每位小朋友分 5 个苹果,则还剩12 个苹果,若每位小朋友分8 个苹果,则有一位小朋友分到了苹果但不足8 个,则有小朋友个,苹果个.13.一次函数的图象如图所示,当﹣3<y<3时,x的取值范围是.14.如图,把正△ ABC 沿 AB 边平移到△A′ B′的C位′置,它们的重叠部分(即图中阴影部分)的面积是△ABC 的面积的一半,若AB=,则此三角形移动的距离 A A′是.15.如图,在Rt △ ABC 中,∠ C=90°,AC=1 , BC=,点O为Rt△ABC内一点,连接A0 、BO、CO,且∠ AOC= ∠ COB=BOA=120°,按下列要求画图(保留画图痕迹):以点 B 为旋转中心,将△ AOB绕点B顺时针方向旋转60°,得到△ A′O′B(得到 A 、O 的对应点分别为点 A′、O′),则∠A′BC=,OA+OB+OC=.三、计算题:16.( 1)解不等式(2)解不等式组,并写出该不等式组的整数解.17.已知二元一次方程组的解x、y均是正数,(1)求 a 的取值范围.(2)化简 |4a+5|﹣ |a﹣ 4|.18.如图 1,等边△ABC 中, D 是 AB 上一点,以CD 为边向上作等边△ CDE,连结AE.(1)求证: AE ∥ BC ;(2)如图 2,若点 D 在 AB 的延长线上,其余条件均不变,(1)中结论是否成立?请说明理由.19.某工厂用如图所示的长方形和正方形纸板做横式、竖式两种长方体形状的无盖包装纸盒.若有长方形纸板 171 张,正方形纸板 82 张,要做横式、竖式纸盒共 50 个(1)若按纸盒的生产个数来分,有哪些生产方案?(2)已知横式纸盒的利润为每个 8 元,竖式纸盒的利润为每个 10 元,若仅从销售的利润考虑,以上哪种方案的利润最大?最大利润是多少元?20.正方形 ABCD 中,点 E、 F 分别是边 AD 、 AB 的中点,连接 EF.(1)如图1,若点 G 是边 BC 的中点,连接FG,则 EF 与 FG 关系为:;(2)如图2,若点 P 为 BC 延长线上一动点,连接FP,将线段 FP 以点 F 为旋转中心,逆时针旋转 90°,得到线段 FQ,连接 EQ,请猜想 BF 、EQ、BP 三者之间的数量关系,并证明你的结论.(3)若点 P 为 CB 延长线上一动点,按照(2)中的作法,在图 3 中补全图形,并直接写出BF 、EQ、BP 三者之间的数量关系:.2015-2016 学年四川省成都七中育才学校八年级(下)月考数学试卷( 3 月份)参考答案与试题解析一、选择题:1.下列标志既是轴对称图形又是中心对称图形的是( )A .B .C .D .【考点】 中心对称图形;轴对称图形.【分析】 根据中心对称图形与轴对称图形的概念判断即可.【解答】 解: A 、是轴对称图形,是中心对称图形.故正确;B 、是轴对称图形,不是中心对称图形.故错误;C 、不是轴对称图形,是中心对称图形.故错误;D 、是轴对称图形,不是中心对称图形.故错误. 故选: A .2.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )A . ,,B .1,,C .6, 7,8D .2, 3,4【考点】 勾股定理的逆定理.【分析】 知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.【解答】 解: A 、( ) 2+( ) 2≠( ) 2,不能构成直角三角形,故错误;B 、 12+( ) 2=( )2,能构成直角三角形,故正确;22 2 ,不能构成直角三角形,故错误;C 、6 +7 ≠82 22,不能构成直角三角形,故错误.D 、2 +3≠4故选: B .3.如图, △ ABC 与△ A ′ B ′关C 于′ O 成中心对称,下列结论中不成立的是( )A . OC=OC ′B .OA=OA ′C . BC=B ′ C ′D .∠ ABC= ∠ A ′ C ′ B ′ 【考点】 中心对称.【分析】 根据中心对称的性质即可判断. 【解答】 解:对应点的连线被对称中心平分, A , B 正确;成中心对称图形的两个图形是全等形,那么对应线段相等, C 正确.故选 D .4.无论 x 取何值,下列不等式总是成立的是()A . x+5> 0B .x+5 < 0 C.﹣( x+5)2< 0 D.( x+5)2≥0【考点】不等式的性质.【分析】根据不等式的基本性质对各选项进行逐一分析即可.【解答】解: A 、∵ x+5 >0,∴ x>﹣ 5,故本选项错误;B、∵ x+5< 0,∴x<﹣ 5,故本选项错误;C、∵ ﹣( x+5)2<0,∴ x≠﹣ 5,故本选项错误;2D、∵( x+5)≥0,∴ x 为任意实数,故本选项正确.5.如图,△ ABC 中 BD 、 CD 平分∠ ABC 、∠ ACB 过 D 作直线平行于BC,交 AB 、 AC 于E、 F,当∠ A 的位置及大小变化时,线段EF 和 BE+CF 的大小关系是()A . EF=BE+CF B. EF> BE+CF C. EF< BE+CF D.不能确定【考点】等腰三角形的判定与性质;平行线的性质.【分析】由平行的性质和角平分线的定义可得ED=BE ,DF=CF ,可得到EF=BE+CF .【解答】解:∵ EF∥ BC,∴∠ EDB= ∠DBC ,∵BD 平分∠ABC ,∴∠ EBD= ∠DBC ,∴∠ EBD= ∠EDB ,∴ED=BE ,同理可得FD=CF ,∴EF=ED+DF=BE+CF ,故选 A.6.关于 x 的不等式组的解集为x>1,则 a 的取值范围是()A . a> 1B . a< 1 C. a≥1D. a≤1【考点】不等式的解集.【分析】解两个不等式后,根据其解集得出关于 a 的不等式,解答即可.【解答】解:因为不等式组的解集为x> 1,所以可得a≤1,故选 D7.给出四个命题:①若 a> b,c=d,则 ac>bd;②若 ac > bc ,则 a > b ;22③若 a > b ,则 ac > bc ;正确的有( )A .1 个B .2 个C .3 个D .4 个 【考点】 不等式的性质.【分析】 根据不等式的基本性质对各选项依次进行判断,找出正确的即可解答.特别注意的特殊性.【解答】 解:① 若 a >b , c=d ,则 ac > bd ,当 c=d ≤0时不成立,故错误; ②若 ac > bc ,则 a > b ,当 c < 0 时错误;③若 a > b ,则 ac 2> bc 2,当 c=0 时不成立,错误;④若 ac 2> bc 2,则 a > b ,正确. 正确的有 ④1 个, 故选 A .8.某商品原价 5 元,如果跌价 x% 后,仍不低于 4 元,那么()A . x ≤ 20B . x < 20C . x ≥ 20D .x > 20【考点】 一元一次不等式的应用.【分析】 根据商品原价 5 元,跌价 x%后,仍不低于 4 元,进而得出不等式进而求出即可.【解答】 解:由题意可得出: 5( 1﹣ x%) ≥4,解得: x ≤20. 故选: A .9.如图, △ABC 中, AB=AC .∠ A=36°, AB 的中垂线 DE 交 AC 于 D ,交 AB 于 E ,下述结论:( 1) BD 平分 ∠ABC ;( 2) AD=BD=BC ;( 3) △ BDC 的周长等于 AB+BC ;( 4) D 是 AC 中点.其中正确的是()A . ①②B . ①②③C .②③④D . ①②③④【考点】 等腰三角形的性质.【分析】 首先,由图中的已知条件, 找出所需要的各个角的角度. 注意此题中的三角形比较特殊,顶角 A 为 36°,两个底角是 72°;可利用这些特殊条件进行求解. 【解答】 解: ∵∠ A=36°, AB=AC , ∴∠ ABC= ∠ C=72°; ∵DE 是 AB 的垂直平分线, ∴AD=BD , ∠A= ∠ABD=36° ,∴∠ ABD= ∠ DBC=36° ,即 BD 是∠ ABC 的角平分线; 因此( 1)正确.在△ BDC 中, ∵∠ DBC=36° , ∠ C=72°;∴∠ BDC= ∠ C=72°;∴BD=BC=AD ;因此( 2)正确.∵AD=BD=BC ,∴BD+BC+CD=AD+CD+BC=AC+BC=AB+BC;因此( 3)正确.故选 B.10.如图,已知 ? ABCD 中,AE ⊥BC 于点 E,以点 B 为中心,取旋转角等于∠ABC ,把△ BAE 顺时针旋转,得到△BA′E′,连接 DA′.若∠ADC=60°,∠ ADA′=50°,则∠ DA′E′的大小为()A . 130 °B. 150 °C. 160 °D. 170 °【考点】旋转的性质;平行四边形的性质.【分析】根据平行四边形对角相等、邻角互补,得∠ ABC=60° ,∠ DCB=120° ,再由∠A′DC=10°,可运用三角形外角求出∠ DA′B=130°,再根据旋转的性质得到∠BA′E′=∠BAE=30°,从而得到答案.【解答】解:∵四边形 ABCD 是平行四边形,∠ ADC=60° ,∴∠ ABC=60°,∠ DCB=120°,∵∠ ADA′=50°,∴∠ A′DC=10°,∴∠ DA′B=130°,∵AE ⊥ BC 于点 E,∴∠ BAE=30°,∵△ BAE 顺时针旋转,得到△BA′E′,∴∠ BA′E′=∠ BAE=30°,∴∠ DA′E′=∠ DA′B+∠BA′E′=160.°故选: C.二、填空题:11.不等式( a﹣b) x> a﹣b 的解集是x< 1,则 a 与 b 的大小关系是a< b.【考点】不等式的解集.【分析】本题需先根据不等式(a﹣ b) x> a﹣ b 的解集是x< 1,得出 a﹣ b 的关系,即可求出答案.【解答】解:∵不等式( a﹣ b)x> a﹣ b 的解集是x< 1,∴a﹣ b< 1,∴a< b,则 a 与 b 的大小关系是 a<b.故答案为: a< b.12.将一箱苹果分给若干位小朋友,若每位小朋友分 5 个苹果,则还剩12 个苹果,若每位小朋友分8 个苹果,则有一位小朋友分到了苹果但不足8 个,则有小朋友 5 或 6个,苹果37或42个.【考点】一元一次不等式组的应用.【分析】设小朋友为 x 人,根据每位小朋友分 5 个苹果,则还剩 12 个苹果,表示出苹果的个数,再由每位小朋友分 8 个苹果,根据人数为 x 人,表示出需要苹果的个数,减去苹果的总数,即为最后一名小朋友分到的苹果数,再利用最后一位小朋友分到了苹果,但不足8 个列出关于x 的不等式,求出不等式的解集,在解集中找出正整数解得到x 的值,即为小朋友的人数,即可得到一箱苹果的个数.【解答】解:设有x 位小朋友,则苹果为(5x+12 )个,依题意得: 0< 8x﹣( 5x+12 )< 8,可化为:,解得: 4< x<,∵x是正整数,∴x 取 5 或 6,当 x=5 时, 5x+12=37 ;当 x=6 时, 5x+12=42 ,∴有两种情况满足题意:① 这一箱苹果有37 个,小朋友有 5 位;②这一箱苹果有42 个,小朋友有 6 位,故答案为: 5 或 6; 37 或 42.13.一次函数的图象如图所示,当﹣3<y< 3 时, x 的取值范围是0< x< 4.【考点】一次函数的图象.【分析】根据图象找到y=3 和 y= ﹣ 3 所对应的x 的值,然后填空.【解答】解:根据图象知,当y=3 时, x=0 ;当 y= ﹣ 3 时, x=4 ;∴当﹣ 3< y< 3 时, x 的取值范围是0< x< 4.故答案是: 0< x< 4.14.如图,把正△ ABC 沿 AB 边平移到△A′ B′的C位′置,它们的重叠部分(即图中阴影部分)的面积是△ABC 的面积的一半,若AB=,则此三角形移动的距离 A A′是﹣1.【考点】平移的性质.【分析】根据题意可知△ ABC 与阴影部分为相似三角形,且面积比为2:1,所以 AB :A′B= :1,推出 A′ B=1,从而得到 AA′的长.【解答】解:∵△ ABC 沿 AB 边平移到△ A′B′的C′位置,∴AC ∥ A′C,′∴△ ABC ∽△ A′BD,∴=(2,) =∴AB : A′B= : 1,∵AB= ,∴A′B=1,∴AA′=﹣ 1.故答案为﹣ 1.15.如图,在Rt △ ABC 中,∠ C=90°,AC=1 , BC=,点O为Rt△ABC内一点,连接A0 、BO、CO,且∠ AOC= ∠ COB=BOA=120°,按下列要求画图(保留画图痕迹):以点 B为旋转中心,将△ AOB绕点B顺时针方向旋转60°,得到△ A′O′B(得到 A 、O 的对应点分别为点 A′、O′),则∠A′BC= 90°,OA+OB+OC=2.【考点】作图 -旋转变换.【分析】(1)先根据三角函数的定义求出∠ ABC 的度数,再根据旋转的性质得 OA=O′A′,BO=BO′,BA′ =BA=4,∠ OBO′=∠ ABA′ =60 °,∠BO′ A′=∠ BOA=120°,则∠CBA′=∠ CBA+ ∠ ABA′=90°;(2)先判断△ BOO′为等边三角形,所以OO′=BO,∠BOO′=∠ BO′O=60°,再证明点C、O、O′、 A′共线,从而得到A′ C=OC+OB+OA,然后利用勾股定理计算A′C即可.∴tan∠ABC= == , AB= =4 ,∴∠ ABC=30°,∵将△ AOB 绕点 B 顺时针方向旋转60°,得到△ A′O′B(得到 A 、 O 的对应点分别为点A′、O′),∴OA=O′A′, BO=BO′, BA′=BA=4,∠ OBO′=∠ ABA′=60°,∠ BO′A′=∠ BOA=120°,∴∠ A′BC=∠ CBA+ ∠ ABA′=30°+60°=90;°(2)∵ BO=BO′,∠OBO′=∠ ABA′=60°∴△ BOO′为等边三角形,∴OO′=BO,∠ BOO′=∠BO′O=60°,而∠ BOC=120°,∴∠ COO′=∠BOC+ ∠BOO′=60°+120°=180,°∴点 O′在直线 CO 上,同理可得点O、O′、 A′共线,∴A′C=OC+OO′+O′A′=OC+OB+OA,∵∠ CBA′=∠ CBA+ ∠ ABA′=30°+60°=90,°∴A′C= = =2 ,即 OA+OB+OC=2 .故答案为90°, 2 .三、计算题:16.( 1)解不等式(2)解不等式组,并写出该不等式组的整数解.【考点】解一元一次不等式组;一元一次不等式组的整数解.【分析】(1)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集;(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,然后求得不等式组的整数解即可.【解答】解:( 1)根据题意得,解①得 x≤2,解② 得 x>﹣ 4.则不等式组的解集是:﹣4<x≤2;(2),解① 得 x≤1,解②得 x>﹣ 2.则不等式组的解集是:﹣2<x≤1.17.已知二元一次方程组的解x、y均是正数,(1)求 a 的取值范围.(2)化简 |4a+5|﹣ |a﹣ 4|.【考点】二元一次方程组的解;解一元一次不等式组.【分析】( 1)先解方程组,再根据 x> 0, y>0,解关于 a 的不等式组,即可得出 a 的取值范围;(2)根据 a 的取值范围,化简即可.【解答】解:解二元一次方程组得,∵x> 0, y> 0,∴x> 0, y> 0,∴,解得﹣< a< 4;(2)∵ ﹣<a<4,∴|4a+5|﹣ |a﹣ 4|=4a+5+a﹣ 4=5a+1 .18.如图 1,等边△ABC 中, D 是 AB 上一点,以 CD 为边向上作等边△ CDE,连结 AE .(1)求证: AE ∥ BC ;(2)如图 2,若点 D 在 AB 的延长线上,其余条件均不变,( 1)中结论是否成立?请说明理由.【考点】全等三角形的判定与性质;等边三角形的性质.【分析】(1)根据已知条件先证出∠BCD= ∠ ACE ,再根据 SAS 证出△ DBC ≌△ ACE ,得出∠ B=∠ CAE= ∠BAC=60°,从而得出∠B+ ∠BAE=180 ,再根据平行线的判定即可证出AE ∥BC;(2)根据( 1)证出的△ DBC ≌△ ACE ,得出∠ BDC= ∠ AEC ,在△DMC 和△ AME 中,根据 AA 证出△ DMC ∽△ AME ,得出∠ EAM= ∠DCM=60°,再根据∠DCA+ ∠ CAE= ∠DCE+ ∠ECA+CEA=180°+∠ ECA ,即可得出AE ∥ BC.【解答】证明:( 1)∵∠ BCA= ∠ DCE=60°,∴∠ BCA ﹣∠ACD= ∠DCE﹣∠ACD ,即∠ BCD= ∠ ACE ,∵△ ABC 和△ DCE 是等边三角形,∴BC=AC , DC=EC ,在△ BDC 与△ ACE 中,,∴△ DBC ≌△ ACE ( SAS),∴∠ B=∠ CAE ,∴∠ B=∠ CAE= ∠BAC=60°,∴∠ CAE+ ∠BAC= ∠BAE=120°,∴∠ B+∠ BAE=180 ,∴AE ∥BC;(2)不成立,证明如下:∵△ DBC ≌△ ACE ,∴∠ BDC= ∠ AEC ,在△ DMC 和△AME 中,∵∠ BDC= ∠ AEC (已证),∴∠ DMC= ∠ EMA ,∴△ DMC ∽△ EMA ,∴∠ EAM= ∠ DCM=60°,∴∠ EAC=120°,又∵∠ DCA+ ∠ CAE= ∠ DCE+ ∠ ECA+CEA=180°+∠ ECA ,∴AE ∥BC.19.某工厂用如图所示的长方形和正方形纸板做横式、竖式两种长方体形状的无盖包装纸盒.若有长方形纸板 171 张,正方形纸板 82 张,要做横式、竖式纸盒共 50 个(1)若按纸盒的生产个数来分,有哪些生产方案?(2)已知横式纸盒的利润为每个8 元,竖式纸盒的利润为每个10 元,若仅从销售的利润考虑,以上哪种方案的利润最大?最大利润是多少元?【考点】一元一次不等式组的应用;一次函数的应用.【分析】(1)设生产横式的无盖长方体包装盒x 个,则生产竖式的无盖长方体包装盒(50 ﹣x)个,根据题意可得两个关系式为: A 种纸盒使用长方形纸板的个数+B 种纸盒使用长方形纸板的个数≤长方形纸板的张数, A 种纸盒使用正方形纸板的个数+B 种纸盒使用正方形纸板的个数≤正方形纸板的张数,把相关数值代入求正整数解即可;(2)设销售利润为W 元,生产横式纸盒x 个,根据题意可得:总利润=横式纸盒的利润×横式纸盒的个数+竖式纸盒的利润×竖式纸盒的个数,再根据函数关系式确定x 的值,即可得到答案.【解答】解:( 1)设生产横式的无盖长方体包装盒x 个,则生产竖式的无盖长方体包装盒(50﹣ x)个.由题意得,解得, 29≤x≤32.∵x 是整数,∴x1=29 , x2=30 , x3=31, x4=32 .答:有 4 种生产方案,分别是:生产横式包装盒29 个,竖式包装盒21 个;生产横式包装盒30 个,竖式包装盒20 个;生产横式包装盒31 个,竖式包装盒19 个;生产横式包装盒 32 个,竖式包装盒 18 个.(2)设销售利润为 W 元,生产横式纸盒 x 个,则w=8x+10 ( 50﹣ x) =﹣ 2x+500第 14 页(共 17 页)∴当 x=29 时, W 最大,最大值为442 元;答:生产横式纸盒 29 个,竖式纸盒21 个,最大利润为442 元.20.正方形ABCD 中,点 E、 F 分别是边AD 、 AB 的中点,连接EF.(1)如图 1,若点 G 是边 BC 的中点,连接 FG,则 EF 与 FG 关系为:EF⊥ FG ,EF=FG;(2)如图 2,若点 P 为 BC 延长线上一动点,连接FP,将线段FP 以点 F 为旋转中心,逆时针旋转90°,得到线段 FQ,连接 EQ,请猜想 BF 、EQ、BP 三者之间的数量关系,并证明你的结论.(3)若点 P 为 CB 延长线上一动点,按照(2)中的作法,在图 3 中补全图形,并直接写出BF 、EQ、BP 三者之间的数量关系:BF+BP=EQ.【考点】全等三角形的判定与性质;正方形的性质.【分析】( 1)根据线段中点的定义求出AE=AF=BF=BG ,然后利用“边角边”证明△AEF 和△BFG 全等,根据全等三角形对应边相等可得EF=FG,全等三角形对应角相等可得∠AFE= ∠ BFG=45°,再求出∠ EFG=90°,然后根据垂直的定义证明即可;(2)取 BC 的中点 G,连接 FG,根据同角的余角相等求出∠1=∠ 3,然后利用“边角边”证明△ FQE 和△FPG 全等,根据全等三角形对应边相等可得QE=FG , BF=BG ,再根据BG+GP=BP 等量代换即可得证;(3)根据题意作出图形,然后同(2)的思路求解即可.【解答】解:( 1)∵点 E、 F 分别是边AD 、AB 的中点, G 是 BC 的中点,∴A E=AF=BF=BG ,在△ AEF 和△BFG 中,,∴△ AEF ≌△ BFG ( SAS ),∴E F=FG ,∠AFE= ∠ BFG=45°,∴E F ⊥ FG, EF=FG ;(2) BF+EQ=BP .理由:如图2,取 BC 的中点 G,连接 FG,则 EF⊥ FG,EF=FG ,∴∠ 1+∠ 2=90°,又∵∠ 2+∠3=90°,∴∠ 1=∠ 3,在△ FQE 和△FPG 中,,∴△ FQE≌△ FPG( SAS),∴QE=PG 且 BF=BG ,∵BG+GP=BP ,∴B F+EQ=BP ;(3)如图 3 所示, BF+BP=EQ .2016年5月21日。
最新北师大版八年级数学下册第三次月考试卷

北师大版八年级数学下册第三次月考试题一、选择题(每小题3分,共30分)1.下下列图案中,不是中心对称图形的是( )A .B .C .D .2.不等式2x +1>﹣3的解集在数轴上表示正确的是( )A .B .C .D .3.若m n >,下列不等式一定成立的是( ) A .22m n ->+B .22m n >C .22m n -> D .22m n >4.如果一个n 边形每个外角都是30°,那么n 是( ) A .十一B .十二C .十三D .十四5.下面式子从左边到右边的变形是因式分解的是( ) A .x 2﹣x ﹣2=x (x ﹣1)﹣2 B .x 2﹣4x +4=(x ﹣2)2 C .(x +1)(x ﹣1)=x 2﹣1D .x ﹣1=x (1﹣)6.下列命题中,逆命题是真命题的是( ) A .矩形的两条对角线相等 B .正多边形每个内角都相等 C .对顶角相等D .对角线互相垂直的四边形是菱形7.如图,若平行四边形ABCD 的周长为40cm ,BC =AB ,则BC =( )A .16cmB .14cmC .12cmD .8cm8.若关于x 的方程=有增根,则m 的值为( )A .1B .2C .3D .49.小如图,在Rt ABC ∆中,90B ∠=︒,30A ∠=︒,DE 垂直平分斜边AC ,交AB 于D ,E 是垂足,连接CD ,若2BD =,则AB 的长是( )A .23B .4C .43D .610.某市在建地铁的一段工程要限期完成,甲工程队单独做可如期完成,乙工程队单独做要误期6天,现由两工程队合做4天后,余下的由乙工程队独做,正好如期完成,求该工程规定的工期是多少天?设规定的工期为x 天,根据题意,下列方程错误的是( ) A .4()+=1B .C .D .二、填空题(每小题3分,共12分) 11.若分式的值为零,则x 的值等于 .12.如图,有一块长32米,宽24米的草坪,其中有两条宽2米的直道把草坪分为四块,则草坪的面积是平方米.13.若代数式的值大于﹣1且小于等于2,则x的取值范围是.14.已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=2,则AC 的长等于.三、解答题(78分)15.(6分)把下列各式因式分解:(1)a3﹣4a2+4a (2)a2(x﹣y)+b 2(y﹣x)16.(6分)解不等式组:,并把解集在数轴上表示出来.17.(6分)先化简再求值:(﹣)÷,其中x=11﹣18.(6分)作图题:在△ABC中,点D是AB边的中点,请你过点D作△ABC的中位线DE 交AC于点E.(不写作法,保留作图痕迹)19.(8分)如图,平行四边形ABCD中,点E是AD的中点,连结CE并延长,与BA的延长线交于点F,证明:EF=EC.20.(8分)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,﹣1)、B(1,﹣2)、C(3,﹣3).(1)将△ABC向上平移4个单位长度得到△A1B1C1,请画出△A1B1C1;(2)请画出与△ABC关于原点的中心对称的△A2B2C2;(3)请写出A1、A2的坐标.21.(8分)(阅读理解题)在解分式方程时,小明的解法如下:解:方程两边都乘以x﹣3,得2﹣x=﹣1﹣2①.移项得﹣x=﹣1﹣2﹣2②.解得x③.(1)你认为小明在哪一步出现了错误?(只写序号),错误的原因是.(2)小明的解题步骤完善吗?如果不完善,说明他还缺少哪一步?答:.(3)请你解这个方程.22.(9分)如图,等边ABC∆的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使12CF BC=,连接CD和EF.(1)求证:DE CF=;(2)求EF的长;(3)求四边形DEFC的面积.23.(9分)某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.(1)求甲、乙两种商品每件的价格各是多少元?(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么,最多可购买多少件甲种商品?24.(12分)如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.(1)求证:四边形DEFG是平行四边形;(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.北师大版八年级数学下册期中试题一、选择题(每小题3分,共30分)1.下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.2.已知等腰三角形的一边长为2,周长为8,那么它的腰长为()A.2 B.3 C.2或3 D.不能确定3.如果a>b,下列各式中不正确的是()A.a﹣3>b﹣3 B.>C.﹣2a<﹣2b D.﹣2a>﹣2b4.如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在边AC上点E处,若∠A=25°,则∠ADE的大小为()A.40°B.50°C.65°D.75°5.已知不等式组有解,则a的取值范围为()A.a>﹣2 B.a≥﹣2 C.a<2 D.a≥26.如果关于x的不等式3x﹣a≤﹣1的解集如图所示,则a的值是()A.a≤﹣1 B.a≤﹣2 C.a=﹣1 D.a=﹣27.用反证法证明:“一个三角形中,至少有一个内角大于或等于60°”.应假设()A.一个三角形中没有一个角大于或等于60°B.一个三角形中至少有一个角小于60°C.一个三角形中三个角都大于等于60°D.一个三角形中有一个角大于等于60°8.如图,一次函数y=kx+b(k、b为常数,且k≠0)与正比例函数y=ax(a为常数,且a ≠0)相交于点P,则不等式kx+b<ax的解集是()A.x>1 B.x<1 C.x>2 D.x<2二、填空题(每小题3分,共24分)9.三角形的两边长分别是3和7,则其第三边x的范围为.10.写出“全等三角形的面积相等”的逆命题.11.不等式x+3>2的负整数解为.12.已知xy=,x+y=5,则2x3y+4x2y2+2xy3=.13.等腰三角形腰上的高与腰的夹角为47°,则这个三角形的顶角为度.14.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为.15.如图,在△ABC中,∠B=30°,ED垂直平分BC,ED=3.则CE长为.16.如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为.三、解答题(72分)17.(6分)分解因式:(a2+1)2﹣4a2.18.(8分)解不等式组,并把解集在数轴上表示出来:19.(8分)如图,已知点A(﹣2,﹣1)、B(﹣5,﹣5)、C(﹣2,﹣3),点P(﹣6,0).(1)将△ABC绕点P逆时针旋转90°得△A1B1C1,画出△A1B1C1,并写出点C的对应点C1的坐标为;(2)画出△ABC关于原点成中心对称的图形△A2B2C2,并写出点A的对应点A2的坐标为.20.(8分)小丽准备用35元买牛奶和面包,已知一盒牛奶3.5元,一个面包5元,她买了4盒牛奶,她最多还能买多少个面包?21.(8分)在保护地球爱护家园活动中,校团委把一批树苗分给初三(1)班同学去栽种.如果每人分2棵,还剩42棵;如果前面每人分3棵,那么最后一人得到的树苗少于5棵(但至少分得一棵).那么初三(1)班至少有多少名同学?最多有多少名同学?22.(10分)如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O (1)求证:OB=OC;(2)若∠ABC=50°,求∠BOC的度数.23.(12分)为了更好治理洋澜湖水质,保护环境,市治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.A型B型价格(万元/台)a b处理污水量(吨/月)240 180(1)求a,b的值;(2)经预算:市治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;(3)在(2)问的条件下,若每月要求处理洋澜湖的污水量不低于1860吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.24.(12分)【问题】如图①,点D是∠ABC的角平分线BP上一点,连接AD,CD,若∠A与∠C互补,则线段AD与CD有什么数量关系?【探究】探究一:如图②,若∠A=90°,则∠C=180°﹣∠A=90°,即AD⊥AB,CD⊥BC,又因为BD平分∠ABC,所以AD=CD,理由是:.探究二:若∠A≠90°,请借助图①,探究AD与CD的数量关系并说明理由.【理论】点D是∠ABC的角平分线BP上一点,连接AD,CD,若∠A与∠C互补,则线段AD 与CD的数量关系是.【拓展】已知:如图③,在△ABC中,AB=AC,∠A=100°,BD平分∠ABC.求证:BC=AD+BD。
北师大版2022-2023学年八年级数学第三次月考测试题(附答案)

2022-2023学年八年级数学第三次月考测试题(附答案)一、单项选择题(共18分)1.(﹣2)0的值为()A.﹣2B.0C.1D.22.下面四幅作品分别代表二十四节气中的“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是()A.B.C.D.3.下列计算结果正确的是()A.a12÷a3=a4B.(﹣a3)2=a6C.a2•a5=a10D.(﹣3a)2=6a2 4.现需要在某条街道l上修建一个核酸检测点P,向居住在A,B小区的居民提供核酸检测服务,要使P到A,B的距离之和最短,则核酸检测点P符合题意的是()A.B.C.D.5.下列对△ABC的判断,错误的是()A.若AB=AC,∠B=60°,则△ABC是等边三角形B.若∠A:∠B:∠C=3:4:7,则△ABC是直角三角形C.若∠A=20°,∠B=80°,则△ABC是等腰三角形D.若AB=BC,∠C=40°,则∠B=40°6.如图,将图1中的一个小长方形变换位置得到如图2所示的图形,根据两个图形中阴影部分的面积关系得到的等式是()A.(a+b)2=a2+2ab+b2B.(a﹣b)2=a2﹣2ab+b2C.a2﹣b2=(a+b)(a﹣b)D.(a+2b)(a﹣b)=a2+ab﹣2b2二、填空题。
(共18分)7.分解因式:x2﹣25=.8.若点A位于第三象限,则点A关于y轴的对称点落在第象限.9.已知4m=5,4n=9,则4m+n的值为.10.如图,在△ABC中,AB=AC,AB的垂直平分线交边AB于点D,交边AC于点E,若△ABC与△EBC的周长分别是15,9,则BC=.11.如图,某山的山顶E处有一个观光塔EF,已知该山的山坡面与水平面的夹角∠EAB为30°,山高EB为120米,点C距山脚A处180米,CD∥AB,交EB于点D,在点C处测得观光塔顶端F的仰角∠FCD为60°,则观光塔EF的高度是米.12.有一三角形纸片ABC,∠A=70°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两个纸片均为等腰三角形,则∠C的度数可以是.三、解答题(共30分)13.计算:(1)﹣a2•3a+(2a)3.(2)(a+b)(a﹣b)﹣b(2a﹣b).14.如图,在△ABC中,点E,F在边AC上,∠DAF=∠BCA,BE∥DF,AD=BC.(1)求证:△BCE≌△DAF.(2)当AE=EB,∠CFD=130°,∠C=35°时,求∠ABC的度数.15.先化简,再求值:(x2+xy+y2)(x﹣y),其中x=1,y=﹣2.16.在棋盘中建立如图所示的平面直角坐标系,其中A(﹣1,1),B(4,3),C(4,﹣1)处各有一颗棋子.(1)如图1,依次连接A,B,C,A,得到一个等腰三角形(BC为底边),请在图中画出该图形的对称轴.(2)如图2,现x轴上有两颗棋子P,Q,且PQ=1(P在Q的左边),依次连接A,P,Q,B,使得AP+PQ+QB的长度最短,请在图2中标出棋子P,Q的位置,并写出P,Q 的坐标.17.为了推进节能减排,助力实现碳达峰、碳中和,某市新换了一批新能源公交车(如图1).图2、图3分别是该公交车双开门关闭、打开中某一时刻的俯视(从上面往下看)示意图.ME,EF,FN是门轴的滑动轨道,∠E=∠F=90°,两门AB,CD的门轴A,B,C,D都在滑动轨道上,两门关闭时(如图2),点A,D分别在点E,F处,门缝忽略不计(B,C重合),两门同时开启时,点A,D分别沿E→M,F→N的方向同时以相同的速度滑动,如图3,当点B到达点E处时,点C恰好到达点F处,此时两门完全开启,若EF=1米,AB=CD,在两门开启的过程中,当∠ABE=60°时,求BC的长度.四、解答题(共24分)18.课本再现:(1)如图1,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.求证:△ADE是等边三角形.课本中给出一种证明方法如下:证明:∵△ABC是等边三角形,∴∠A=∠B=∠C.∵DE∥BC,∴∠ADE=∠B,∠AED=∠C,∴∠A=∠ADE=∠AED,∴△ADE是等边三角形.“想一想,本题还有其他证法吗?”给出的另外一种证明方法,请补全:证明:∵△ABC是等边三角形,∴∠B=∠C,∠A=60°.∵DE∥BC,∴∠B=∠ADE,∠C=①,∴②=③,∴AD=AE.(④)∴△ADE是等腰三角形.又∵∠A=60°,∴△ADE是等边三角形.(2)如图2,等边三角形ABC的两条角平分线相交于点D,延长BD至点E,使得AE =AD,求证:△ADE是等边三角形.19.下列方框中的内容是小宇分解因式的解题步骤.分解因式:(x2+4x+3)(x2+4x+5)+1.解:设y=x2+4x.原式=(y+3)(y+5)+1(第一步)=y2+8y+16(第二步)=(y+4)2(第三步)=(x2+4x+4)2.(第四步)请回答下列问题:(1)小宇分解因式中第二步到第三步运用了.A.提公因式法B.平方差公式法C.两数和的完全平方公式法D.两数差的完全平方公式法(2)小宇得到的结果能否继续因式分解?若能,直接写出分解因式的结果;若不能,请说明理由.(3)请对多项式(x2+2x+6)(x2+2x﹣4)+25进行因式分解.20.如图,在△ABC中,∠B=∠C,D,E分别是线段BC、AC上的一点,且AD=AE.(1)如图1,若∠BAC=90°,D为BC中点,则∠2的度数为;(2)如图2,用等式表示∠1与∠2之间的数量关系,并给予证明.五、解答题(共18分)21.如图,在Rt△ABC中,ACB=90°,∠A=30°,BC=2.三角尺中30°角的顶点D 在边AB上,两边分别与△ABC的边AC,BC相交于点E,F,且DE始终与AB垂直.(1)△BDF是三角形.(填特殊三角形的名称)(2)在平移三角尺的过程中,AD﹣CF的值是否变化?如果不变,求出AD﹣CF的值;如果变化,请说明理由.(3)当平移三角尺使EF∥AB时,求AD的长.22.综合与探究.【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如,由图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题.【直接应用】(1)若x+y=3,x2+y2=5,求xy的值.【类比应用】(2)若x(3﹣x)=2,则x2+(3﹣x)2=.【知识迁移】(3)将两块全等的特制直角三角板(∠AOB=∠COD=90°)按如图2所示的方式放置,其中点A,O,D在同一直线上,点B,O,C也在同一直线上,连接AC,BD.若AD=14,S△AOC+S△BOD=50,求一块直角三角板的面积.六、解答题(本大题共12分)23.综合与实践.课间,小鑫在草稿纸上画了一个直角三角形.如图1,在Rt△ABC中,∠ACB=90°,他想到了作AC的垂直平分线ED,交AC于点E,交AB于点D.他和同桌开始探讨线段AD与BD的大小关系.(1)尝试探究:当∠A=30°时,直接写出线段AD与BD的大小关系:AD BD.(填“>”、“<”或“=”)(2)得出结论:若∠A为任意锐角,则线段AD与BD的大小关系是AD BD,请说明理由.(填“>”、“<”或“=”)(3)应用结论:利用上面的结论继续研究,如图2,P是△FHG的边HG上的一个动点,PM⊥FH于点M,PN⊥FG于点N,FP与MN交于点K.当点P运动到某处时,MN与FP正好互相垂直,此时FP平分∠HFG吗?请说明理由.参考答案一、单项选择题(共18分)1.解:(﹣2)0=1.故选:C.2.解:A、不是轴对称图形,本选项错误;B、不是轴对称图形,本选项错误;C、不是轴对称图形,本选项错误;D、是轴对称图形,本选项正确.故选:D.3.解:A.a12÷a3=a9,选项A不符合题意;B.(﹣a3)2=a6,选项B符合题意;C.a2•a5=a7,选项C不符合题意;D.(﹣3a)2=9a2,选项D不符合题意;故选:B.4.解:作A点关于直线l的对称点,连接对称点和点B交l于点P,P即为所求.故选:A.5.解:A.若AB=AC,∠B=60°,则∠A=60°,∠C=60°,所以△ABC是等边三角形,故此选项判断正确,不符合题意;B.若∠A:∠B:∠C=3:4:7,则∠C=90°,所以△ABC是直角三角形,故此选项判断正确,不符合题意;C.若∠A=20°,∠B=80°,则∠C=80°,所以△ABC是等腰三角形,故此选项判断正确,不符合题意;D.若AB=BC,∠C=40°,则∠B=100°,故此选项判断错误,符合题意.故选:D.6.解:图①中阴影部分的面积可以看作两个正方形的面积差,即a2﹣b2,图②是长为a+b,宽为a﹣b的长方形,因此面积为(a+b)(a﹣b),由于图①、图②阴影部分的面积相等可得,a2﹣b2=(a+b)(a﹣b),故选:C.二、填空题。
北师大版八年级下第三次月考数学试题

北师大版八年下册第三次月考考试试题 数学注意事项:1:全卷分A 卷和B 卷,A 卷满分100分,B 卷满分50分;考试时间120分钟。
2:答题应答在答题卡内;在草稿纸,试卷上答题无效。
A 卷(共100分) 第Ⅰ卷(选择题,共30分)一、选择题:(每小题3分,共30分)每小题均有四个选项,其中只有一项符合题目要求。
1. 下列不等式一定成立的是A.a a 34>B.b b 2->-C.x x -<-43D.c c 23>2. 下列由左到右变形,属于因式分解的是A.94)32)(32(2-=-+x x xB.1)2(411842-+=-+x x x xC. )3)(3(9)(2--+-=--b a b a b aD. 22244)2(y xy x y x +-=- 3. 下列四个分式的运算中,其中运算结果正确的有①b a b a +=+211; ②()3232a a a =;③b a b a b a +=++22;④31932-=--a a a ; A.0个 B. 1个 C. 2个 D. 3个 4.化简:329122++-m m 的结果是 A.962-+m m B.32-m C.32+m D.9922-+m m5.如图,点C 是线段AB 的黄金分割点)(BC AC >,下列结论错误的是A.ACBCAB AC =B.BC AB BC ⋅=2C.215-=ABAC D.618.0≈ACBC6.已知230.5x y z==,则322x y z x y +--+的值是A .17 B.7 C.1 D.137.已知1,2,3xy yz zx x y y z z x===+++,则x 的值是 A .1 B.125 C.512D.-1 8. 在△ABC 中,AB=12,AC=10,BC=9,AD 是BC 边上的高.将△ABC 按如图所示的方式折叠,使点A 与点D 重合,折痕为EF ,则△DEF 的周长为 A.9.5 B.10.5 C.11 D.15.59. 在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下 A.小明的影子比小强的影子长 B.小明的影子比小强的影子短 C.小明的影子和小强的影子一样长 D.无法判断谁的影子长 10. 如图所示,给出下列条件: ①B ACD ∠=∠;②ADC ACB ∠=∠;③AC ABCD BC=;④2AC AD AB =. 其中单独能够判定ABC ACD △∽△的个数为ABCD E A.1 B.2 C.3 D.4第Ⅱ卷(共70分)二、填空题:(每小题4分,共l6分) 11.若2y -7x =0,则x ∶y 等于12. 分解因式:.221x x ++=________________。
八年级数学下学期第三次月考试题试题2

第HY 学2021-2021学年八年级下学期第三次月考数学试题〔无答案〕北师大版一、选择题〔一共10小题,每一小题3分,一共30分〕 1-x x 在实数范围内有意义,那么x 的取值范围为 〔 〕 ≥0 C.x ≠≥0且x ≠1x x x --=+-34231的解是...〔. 〕. A ...0. B ...2. C ...3. D ..无解...3.一组数据为1,5,3,4,5,6,这组数据的极差、众数、中位数分别为 〔 〕A.4,4,5B.5,5,C.5,5,4D.5,3,24.如图,在平行四边形ABCD 中,∠B =80°,AE 平分∠BAD 交BC 于点E ,CF ∥AE 交AE 于点F ,那么∠1= 〔 〕A .40°B .50°C .60°D .80°5.如图,正方形ABCD 的边长为 ,那么图中阴影局部的面积为 cm 2. ( )A. 8B. 6 C6.以下命题中,真命题是 〔 〕A 、有两边相等的平行四边形是菱形B 、有一个角是直角的四边形是矩形C 、四个角相等的菱形是正方形D 、两条对角线互相垂直且相等的四边形是正方形7. 如图,: ABC 为直角三角形,∠B =90︒,AB 垂 cm24直x 轴,M 为AC 中点。
假设A 点坐标为(3,4),M 点坐标为(-1,1),那么B 点坐标为 〔 〕A .(3,-4)B .(3,-3)C . (3,-2)D .(3,-1)8.在反比例函数x k y =的图象上有四点A(x 1,y 1)、B(x 2,y 2)、C(x 3,y 3),D(2,0.5)且x 1<x 2<0<x 3,那么以下各式中,正确的选项是( )A .123y y y <<B .321y y y <<C .213y y y <<D .312y y y <<9.|x -3|+〔y -5〕2+z 2-8z +16=0,那么以x ,y ,z 为边的三角形面积为 ( )A .4B .6C .12D .不能确定 10.如图,在等腰梯形ABCD 中,AB∥CD,AD=BC=5,DC=7,AB=13,点P 从点A 出发,以3个单位/秒的速度沿AD →DC 向终点C运动,同时点Q 从点B 出发,以1个单位/秒的速度沿BA 向终点A 运动,在运动期间,当四边形PQBC 为平行四边形时,运动时间是为( )A .3SB .4SC .5SD .6S二. 填空题(本大题一一共10小题, 每一小题3分, 一共30分)11. 42)13(3102+----⎪⎭⎫ ⎝⎛--= 。
新北师大版八年级下册第三次月考

博恒实验学校2018—2019学年度第二学期二次月考模拟考试卷八年级数学一、选择题(本题共12小题,每小题3分,共36分,答案写在答题卡上)1.下列四种汽车标志,其中既是中心对称图形,又是轴对称图形的是()A.B.C.D.2.下面四个多项式中,能进行因式分解的是()A.x 2+y 2B.x 2﹣y C.x 2﹣1D.x 2+x+13.不等式组的解集在数轴上表示正确的是()4.已知等腰△ABC 的两边长分别为2和3,则等腰△ABC 的周长为()A.7B.8C.6或8D.7或85.如果分式有意义,那么x 的取值范围是()A.x≠0B.x≤﹣3C.x≥﹣3D.x≠﹣36.将下列多项式分解因式,结果中不含因式x﹣1的是()A.x 2﹣1B.x(x﹣2)+(2﹣x)C.x 2﹣2x+1D.x 2+2x+17.若x>y,则下列式子中错误的是()A.x﹣3>y﹣3B.>C.x+3>y+3D.﹣3x>﹣3y8.如图在直角△ABC 中,∠BAC=90°,AB=8,AC=6,DE 是AB 边的垂直平分线,垂足为D,交边BC 于点E,连接AE,则△ACE 的周长为()A.16B.15C.14D.139、某农场开挖一条480米的渠道,开工后每天比原计划多挖20米,结果提前4天完成任务,若设原计划每天挖x 米,那么求x 时所列方程正确的是()A、B、C、D、10.如图,将一个含30°角的直角三角板ABC 绕点A 顺时针旋转得到''C AB △,点B、A、'C 在同一条直线上,则旋转角'∠BAB的度数是A.60°B.90°C.120°D.150°11、正方形ACD 在坐标系中的位置如图所示,将正方形ABCD 绕D 点顺时针方向旋转90°后,点B 的坐标为()A.(2,2)B.(4,1)C.(3,1)D.(4,0)(11题)(12题)12.直线l 1:y=k 1x+b 与直线l 2:y=k 2x 在同一平面直角坐标系中的图象如图所示,则关于x 的不等式k 1x+b>k 2x 的解为()A.x>﹣1B.x<﹣1C.x<﹣2D.无法确定二、填空题(本题共4小题,毎小题3分,共12分)13.分解因式:=-222x14.若关于x 的分式方程=1的解为正数,那么字母a15.点P(﹣4,5)关于x 轴对称的点16.在△ABC 中,∠C=90°,AB=10,AD 是△ABC 的一条角平分线.若CD=3,则△ABD班级:姓名:学号:………………………………………………………………密…………………………….封………………………….线…………………………………………………………………………三、解答题(共18分)17.(本题5分)分解因式:1.122--xxx x18.(本题5分)解不等式组:,并将解集在数轴上表示出来.19.(本题5分)先化简,再求值:(﹣x﹣1)÷,其中x=,y=.20.(本题6分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC 的顶点均在格点上,请按要求完成下列步骤:(1)画出将△ABC 向上平移3个单位后得到的△A 1B 1C 1;(2)画出将△A 1B 1C 1绕点C 1按顺时针方向旋转90°后所得到的△A 2B 2C 1.21.(本题8分)某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵5元,用360元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.(1)求甲、乙两种商品每件的价格各是多少元?(2)若商店计划购买这两种商品共40件,且投入的经费不超过1150元,那么,最多可购买多少件甲种商品?22.(本题8分)如图,M 是△ABC 的边BC 的中点,AN 平分∠BAC,BN⊥AN 于点N,延长BN 交AC 于点D,已知AB=10,BC=15,MN=3(1)求证:BN=DN;(2)求△ABC 的周长.23.(本题9分)阅读下列解题过程:已知a,b,c 为△ABC 的三边长,且满足a 2c 2﹣b 2c 2=a 4﹣b 4,试判断△ABC 的形状.解:∵a 2c 2﹣b 2c 2=a 4﹣b 4,①∴c 2(a 2﹣b 2)=(a 2+b 2)(a 2﹣b 2),②∴c 2=a 2+b 2,③∴△ABC 为直角三角形.④回答下列问题:(1)在上述解题过程中,从哪一步开始出现错误?该步的序号为:;(2)错误的原因为:;(3)请你将正确的解答过程写下来.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北师大版2012——2013学第三次月考考试试题 数学
注意事项:
1:全卷分A 卷和B 卷,A 卷满分100分,B 卷满分50分;考试时间120分钟。
2:答题应答在答题卡内;在草稿纸,试卷上答题无效。
A 卷(共100分) 第Ⅰ卷(选择题,共30分)
一、选择题:(每小题3分,共30分)每小题均有四个选项,其中只有一项符合题目要求。
1. 下列不等式一定成立的是
A.a a 34>
B.b b 2->-
C.x x -<-43
D.c c 2
3>
2. 下列由左到右变形,属于因式分解的是
A.94)32)(32(2-=-+x x x
B.1)2(411842
-+=-+x x x x C. )3)(3(9)(2--+-=--b a b a b a D. 22244)2(y xy x y x +-=- 3. 下列四个分式的运算中,其中运算结果正确的有
①b a b a +=+211; ②()3
23
2a a
a =;③
b a b a b a +=++22;④31932
-=--a a a ; A.0个 B. 1个 C. 2个 D. 3个 4.化简:32
9
122
++-m m 的结果是 A.9
62
-+m m B.32-m C.32
+m D.9922-+m m
5.如图,点C 是线段AB 的黄金分割点)(BC AC >,下列结论错误的是
A.
AC
BC
AB AC = B.BC AB BC ⋅=2 C.2
1
5-=
AB AC D.618.0≈AC BC
6. 在△ABC 中,AB=12,AC=10,BC=9,AD 是BC 边上的高.将△ABC 按如图所示的方式折叠,使点A 与点D 重合,折痕为EF ,则△DEF 的周长为 A.9.5 B.10.5 C.11 D.15.5
7. 在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下 A.小明的影子比小强的影子长 B.小明的影子比小强的影子短 C.小明的影子和小强的影子一样长 D.无法判断谁的影子长 8. 如图所示,给出下列条件: ①B ACD ∠=∠;②ADC ACB ∠=∠; ③
AC AB
CD BC
=;④2AC AD AB =g . 其中单独能够判定ABC ACD △∽△的个数为
A.1
B.2
C.3
D.4
9.已知
1,2,3xy yz zx
x y y z z x
===+++,则x 的值是 A .1 B.
125 C.5
12
D.-1 10.已知230.5x y z
==
,则322x y z x y +--+的值是
B
A .17 B.7 C.1 D.13
第Ⅱ卷(共70分)
二、填空题:(每小题4分,共l6分)
11.若2y -7x =0,则x ∶y 等于
12. 分解因式:.221x x ++=________________。
13.如图,在△ABC 中,D,E 分别是边AC 、BC 的中点,若DE=4, 则AB=________________。
14.如图,在△ABC 中,点D 是射线BC 上任意一点,DH 交AB 于点H ,交AC 于点E ,则∠HEC 与∠AHE 的大小关系是
H
E
D
C
B
A
13题图 14题图
三、解答题:(本大题共6个小题,共54分) 1 5. (本小题满分12分,每题6分) (1)分解因式:22(1)24x xy y ++-
(2)解不等式组:2031212
3x x x +≥⎧⎪
-+⎨<⎪⎩,并写出该不等式组的最小整数解。
16.先将231
()11x x x x x x
---+g
化简,然后不等式组. 的自然数解中,自选一个你喜欢的x 的值代入化简后的式子求值(6分)
17. 若方程组⎩⎨⎧+=++=+3654,
2m y x m y x 的解x ,y 均为正数,求m 的取值范围。
(6分)
18.花石镇组织10辆汽车装运完A 、B 、C 三种不同品质的湘莲共100吨到外地销售,按计划10辆汽车都要装满,且每辆汽车只能装同一种湘莲,根据下表提供的信息,
解答以下问题:(10分)
(1)设装运A 种湘莲的车辆数为x ,装运B 种湘莲的车辆数为y ,求y 与x 之间的
函数关系式;
(2)如果装运每种湘莲的车辆数都不少于2辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
19.如图,已知:DE∥BC,DF∥AC,AD=6,BD=4,DE=7(10)
(1)试说明:△ADE∽△DBF;
(2)求线段BF的长。
20.如图所示,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B(10分)
(1)求证:△ADF~ △DEC
(2)若AB=4,AD=33,AE=3,求AF的长
A D
FFFFFFFFFFFFFF
B E C
B卷(共50分)
一、填空题:(每小题4分,共20分)
21.若关于x的不等式2x<3(x-3)+1和(3x+2)×
4
1
>x+a的解相同,且有四个整数解,a的取值范围________________.
22..巳知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8.点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,矩形DECF,且DE:CE=2:3,矩形的面积是________________。
23.如图,△ABC中,∠ABC+∠CBA=∠ACB,CD是斜边AB上的高,AD=9,BD=4,那么CD=________________,AC=________________.
C
A
D B
24.雨后初晴,一学生在运动场上玩耍,从他前面2米远一小积水处,他看到了旗杆顶端的倒影。
如果旗杆低端到积水的距离为40m,该生的眼部高度是1.5m,那么旗杆的高度是_______________m。
F E
D
C B
A
25.矩形ABCD中,由8个面积均为1的小正方形组成的L型模版如图12所示放置,则矩形ABCD的周长_______________。
A D
F
B
E C
二、解答题:(本大题3个小题,共30分)
26.如图,在△ABC中,∠A与∠B互余,CD⊥AB,垂足为点D,DE∥BC,交AC与点E,求证:AD:AC=CE:BD(10)
C
E
A
D B
27.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交于点D,过点C作CE⊥AD于E,CE的延长线交AB于点F,过点E作EG∥BC交AB于G,AE·AD=16,AB=4 5 .(1)求证:CE=EF;(2)求EG的长. 28..已知:在菱形ABCD中,O是对角线BD上的一动点.(12分)
(1)如图甲,P为线段BC上一点,连接PO并延长交AD于点Q,当O是BD的点时,求证:OP OQ
=;
(2)如图乙,连结AO并延长,与DC交于点R,与BC的延长线交于点S.若460,10
AD DCB BS
===
,∠,求AS和OR的长.
A
B E
D
F G
C。
